实验7-测量螺线管的磁场 (2)
用霍尔元件测螺线管磁场实验报告 PDF

用霍尔元件测螺线管磁场实验报告 PDF本次实验的主要目的是利用霍尔元件测量螺线管所产生的磁场,研究其特性并探索影响磁场强度的因素。
实验装置:1. 螺线管:一种通电后可以产生磁场的装置,包括线圈和磁芯。
2. 霍尔元件:一种基于霍尔效应原理的元件,通过测量磁场的垂直分量而得到磁场强度。
3. 直流电源:提供螺线管所需要的电流。
4. 多用表:测量霍尔元件输出的电压。
5. 电位器:用于调整霍尔元件的工作点。
实验步骤:1. 将螺线管连接至电源,设定电流大小,使其产生磁场。
2. 按照实验装置连接图将霍尔元件连接至多用表。
4. 移动霍尔元件位置,测量不同位置下的磁场强度并记录数据。
5. 改变螺线管的电流大小,重复步骤4,记录不同电流下的磁场强度数据。
实验结果及讨论:在实验过程中,我们通过测量霍尔元件在不同位置下的电压输出,得到了螺线管产生的磁场强度数据,如表1所示。
|位置 x(cm)|电流 I(A)|霍尔元件输出电压 V(mV)|磁场强度 B(T)||:- - - - :-|:- - - - :-|:- - - - :-|:- - - - :-||1 |0.5 |25.8 |0.64 ||2 |0.5 |19.2 |0.48 ||3 |0.5 |12.6 |0.315 ||4 |0.5 |6.0 |0.15 ||5 |0.5 |0.6 |0.015 ||1 |1 |51.6 |1.28 ||2 |1 |38.4 |0.96 ||3 |1 |25.2 |0.63 ||4 |1 |12.0 |0.3 ||5 |1 |1.2 |0.03 ||1 |1.5 |77.4 |1.92 ||2 |1.5 |57.6 |1.44 ||3 |1.5 |37.8 |0.945 ||4 |1.5 |18.0 |0.45 ||5 |1.5 |1.8 |0.045 |表1:不同位置、不同电流下的磁场强度及霍尔元件输出电压数据由表1可知,在同一电流下,随着霍尔元件离螺线管距离的增加,磁场强度不断降低。
螺线管磁场测定实验

磁力线是平行于轴线的直线系,渐近两端口时,这些直线变为从两端口离散的曲线,说明其 内部的磁场在很大一个范围内是近似均匀的, 仅在靠近两端口处磁感应强度才显著下降, 呈 现明显的不均匀性。 根据上面理论计算, 长直螺线管一端的磁感应强度为内腔中部磁感应强 度的 1/2。 四三、实验内容 1.霍尔元件输出特性测量 A. 仔细阅读本实验仪使用说明书后, 按图 5-4 连接 THQDX-1 电磁学实验装置上 10mA 恒流源、直流毫伏表、1A 恒流源和实验仪之间相对应的 Is、VH 和 IM 各组连线,Is 及 IM 换 向开关投向上方, 表明 Is 及 IM 均为正值 (即 Is 沿 X 方向, B 沿 Z 方向) , 反之为负值。 VH、 Vσ切换开关投向上方测 VH,投向下方测 Vσ。经教师检查后方可开启测试仪的电源。 注意: 图 5-3 中虚线所示的部分线路即样品各电极及线包引线与对应的双刀开关之间连线已 由制造厂家连接好。 必须强调指出:决不允许将 THQDX-1 电磁学实验装置上的“1A 恒流源”误接到实验仪的 “Is 输入”或“VH 输出” 处,否则一旦通电,霍尔元件即遭损坏!
( 1 2 1 L ) ( D )2 2 2
式中 D 为长直螺线管直径,L 为螺线管长度。 磁感应强度为最大,且等于
1
BO = μ0NI 2 M(
1 L 2 1 1+ ( L )2 ( D )2 2 2
1 1) ( L )2 ( D )2 2 2
1 L 2
=μ0NIM
(11) L D2 由于本实验仪所用的长直螺线管满足 L>>D,则近似认为 BO =μ0 NIM
实验四
螺线管磁场测定实验
霍尔效应法测定螺线管轴向磁感应强度分布 置于磁场中的载流体, 如果电流方向与磁场垂直, 则在垂直于电流和磁场的方向会产生一附 加的横向电场, 这个现象是霍普斯金大学研究生霍尔于 1879 年发现的, 后被称为霍尔效应。 随着半导体物理学的迅速发展, 霍尔系数和电导率的测量已成为研究半导体材料的主要方法 之一。 通过实验测量半导体材料的霍尔系数和电导率可以判断材料的导电类型、 载流子浓度、 载流子迁移率等主要参数。 若能测量霍尔系数和电导率随温度变化的关系, 还可以求出半导 体材料的杂质电离能和材料的禁带宽度。 如今, 霍尔效应不但是测定半导体材料电学参数的 主要手段,而且随着电子技术的发展,利用该效应制成的霍尔器件,由于结构简单、频率响 应宽(高达 10GHz) 、寿命长、可靠性高等优点,已广泛用于非电量测量、自动控制和信息 处理等方面。在工业生产要求自动检测和控制的今天,作为敏感元件之一的霍尔器件,将有 更广阔的应用前景。了解这一富有实用性的实验,对日后的工作将有益处。 一、实验目的 1.掌握测试霍尔元件的工作特性。 2.学习用霍尔效应法测量磁场的原理和方法。 3.学习用霍尔元件测绘长直螺线管的轴向磁场分布。 二、实验设备 1.QX-2 螺线管磁场实验仪 2.THQDX-1 电磁学实验装置上的 1A 恒流源、10mA 恒流源、直流毫伏表 三、实验原理 1.霍尔效应法测量磁场原理 霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。 当带电粒子 (电子或空穴) 被约束在固体材料中, 这种偏转就导致在垂直电流和磁场的方向上产生正负 电荷的聚积,从而形成附加的横向电场,即霍尔电场。对于图 5-1(a)所示的 N 型半导体 试样,若在 X 方向的电极 D、E 上通以电流 Is,在 Z 方向加磁场 B,试样中载流子(电子) 将受洛仑兹力
大学物理实验报告 螺线管磁场的测量

实验报告螺线管磁场的测量霍尔效应是导电材料中的电流与磁场相互作用而产生电动势的效应。
1879年美国霍普金斯大学研究生霍尔在研究金属导电机理时发现了这种电磁现象,故称霍尔效应。
后来曾有人利用霍尔效应制成测量磁场的磁传感器,但因金属的霍尔效应太弱而未能得到实际应用。
随着半导体材料和制造工艺的发展,人们又利用半导体材料制成霍尔元件,由于它的霍尔效应显著而得到实用和发展,现在广泛用于非电量的测量、电动控制、电磁测量和计算装置方面。
在电流体中的霍尔效应也是目前在研究中的“磁流体发电”的理论基础。
近年来,霍尔效应实验不断有新发现。
1980年原西德物理学家冯·克利青研究二维电子气系统的输运特性,在低温和强磁场下发现了量子霍尔效应,这是凝聚态物理领域最重要的发现之一。
目前对量子霍尔效应正在进行深入研究,并取得了重要应用,例如用于确定电阻的自然基准,可以极为精确地测量光谱精细结构常数等。
在磁场、磁路等磁现象的研究和应用中,霍尔效应及其元件是不可缺少的,利用它观测磁场直观、干扰小、灵敏度高、效果明显。
本实验采取电放大法,应用霍尔效应对螺线管磁场进行测量。
关键词:霍尔效应;霍尔元件;电磁场;磁场一、实验目的1.了解螺线管磁场产生原理。
2.学习霍尔元件用于测量磁场的基本知识。
3.学习用“对称测量法”消除副效应的影响,测量霍尔片的UH -IS(霍尔电压与工作电流关系)曲线和UH -IM,B-IM(螺线管磁场分布)曲线。
二、实验原理霍尔效应从本质上讲,是运动的带电粒子在磁场中受洛伦兹力的作用而引起的偏转。
当带电粒子(电子或空穴)被约束在固体材料中,这种偏转就导致在垂直电流和磁场的方向上产生正负电荷在不同侧的聚积,从而形成附加的横向电场。
如图所示,磁场B位于Z 轴的正向,与之垂直的半导体薄片上沿X轴正向通以电流IS(称为工作电流),假设载流子为电子(N型半导体材料),它沿着与电流IS相反的X轴负向运动。
由于洛伦兹力fL作用,电子即向图中虚线箭头所指的位于Y轴负方向的B侧偏转,并使B侧形成电子积累,而相对的A侧形成正电荷积累。
螺线管磁场测定

螺线管磁场测定本实验仪用集成霍耳传感器测量通电螺线管内直流电流与霍耳传感器输出电压之间关系,证明霍耳电势差与螺线管内磁感应强度成正比,了解和熟悉霍耳效应的重要物理规律;用通电长直螺线管中心点磁感应强度理论计算值作为标准值来校准集成霍耳传感器的灵敏度;熟悉集成霍耳传感器的特性和应用;用该集成霍耳传感器测量通电螺线管内的磁感应强度与位置刻度之间的关系,作磁感应强度与位置的关系图。
从而学会用集成霍耳元件测量磁感应强度的方法。
一、实验目的1.了解和掌握集成线性霍耳元件测量磁场的原理和方法;2.学会测量霍耳元件灵敏度的方法。
3.精确测量通电螺线管磁场分布,二、实验原理霍耳元件的作用(如右图2所Array示):若电流I流过厚度为d的半导体薄片,且磁场B垂直于该半导体,是电子流方向由洛伦茨力作用而发生改变,在薄片两个横向面a、b之间应产生电势差,图2 霍耳元件这种现象称为霍耳效应。
在与电流I、磁场B垂直方向上产生的电势差称为霍耳电势差,通常用U H 表示。
霍耳效应的数学表达式为:IB K IB dR U H HH ==)((1) 其中R H 是由半导体本身电子迁移率决定的物理常数,称为霍耳系数。
B 为磁感应强度,I 为流过霍耳元件的电流强度,K H 称为霍耳元件灵敏度。
虽然从理论上讲霍耳元件在无磁场作用(即B=0)时,U H =0,但是实际情况用数字电压表测时并不为零,这是由于半导体材料结晶不均匀及各电极不对称等引起附加电势差,该电势差U 0称为剩余电压。
随着科技的发展,新的集成化(IC)元件不断被研制成功。
本实验采用SS95A 型集成霍耳传感器(结构示意图如图3所示)是一种高灵敏度集成霍耳传感器,它由霍耳元件、放大器和薄膜电阻剩余电压补偿组成。
测量时输出信号大,并且剩余电压的影响已被消除。
对SS95A 型集成霍耳传感器,它由三根引线,分别是:“V +”、“V -”、“V out ”。
其中“V +”和“V -”构成“电流输入端”,“V out ”和“V -”构成“电压输出端”。
螺线管内磁场的测量实验报告

螺线管内磁场的测量实验报告引言螺线管是一种常见的电磁设备,广泛应用于电磁学、物理学和工程学等多个领域。
测量螺线管内部磁场的分布和特性对于优化螺线管设计和应用具有重要意义。
本实验旨在通过测量螺线管内部磁场分布的实验,探究螺线管的特性和应用。
实验目的1.测量螺线管内磁场的分布,探究螺线管的磁场特性。
2.了解螺线管内磁场与电流和线圈结构的关系。
3.探索螺线管的应用前景和优化设计方向。
实验步骤实验器材准备1.螺线管实验装置2.磁场测量仪器(例如磁力计)3.直流电源实验操作1.搭建螺线管实验装置,确保装置稳固可靠。
2.连接磁场测量仪器到螺线管上,调节仪器到合适的量程。
3.设置直流电源的电流大小,并接入螺线管。
4.在不同电流下,测量螺线管内磁场的分布情况,记录数据。
实验结果与分析螺线管内部磁场的分布情况通过实验测量,得到了螺线管在不同电流下的内部磁场分布情况。
以下是一组典型的实验结果数据:•电流1A时,螺线管内部磁场分布如下:1.距离螺线管中心10cm处的磁场强度为0.5T;2.距离螺线管中心20cm处的磁场强度为0.3T;3.距离螺线管中心30cm处的磁场强度为0.2T。
•电流2A时,螺线管内部磁场分布如下:1.距离螺线管中心10cm处的磁场强度为1.0T;2.距离螺线管中心20cm处的磁场强度为0.6T;3.距离螺线管中心30cm处的磁场强度为0.4T。
螺线管内部磁场与电流的关系从实验结果可以看出,随着电流的增加,螺线管内部磁场的强度也随之增加。
这是因为电流通过螺线管产生了磁场,而磁场的强度与电流成正比。
螺线管内部磁场与线圈结构的关系通过多次实验可以观察到,螺线管的线圈结构对内部磁场分布有着重要影响。
线圈的半径、匝数以及线圈间距等参数会直接影响螺线管内部磁场的分布情况。
进一步的实验可以探究各个参数对磁场分布的具体影响。
螺线管的应用前景和优化设计方向螺线管由于其产生强磁场的特性,在许多领域具有广泛的应用前景。
新型螺线管磁场测定实验报告
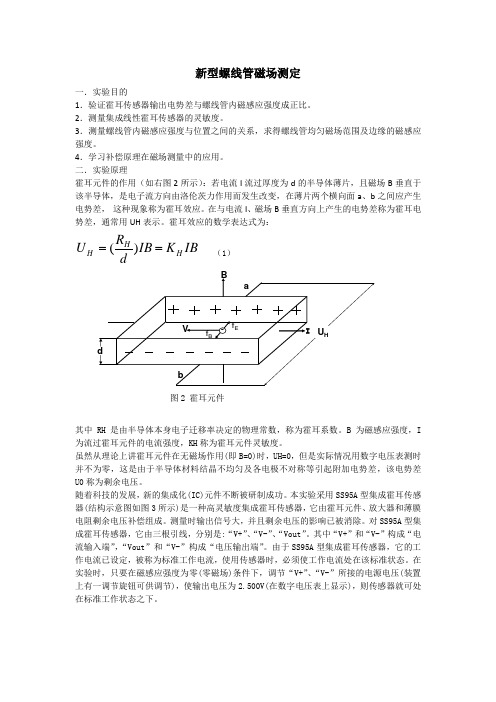
新型螺线管磁场测定一.实验目的1.验证霍耳传感器输出电势差与螺线管内磁感应强度成正比。
2.测量集成线性霍耳传感器的灵敏度。
3.测量螺线管内磁感应强度与位置之间的关系,求得螺线管均匀磁场范围及边缘的磁感应强度。
4.学习补偿原理在磁场测量中的应用。
二.实验原理霍耳元件的作用(如右图2所示):若电流I 流过厚度为d 的半导体薄片,且磁场B 垂直于该半导体,是电子流方向由洛伦茨力作用而发生改变,在薄片两个横向面a 、b 之间应产生电势差, 这种现象称为霍耳效应。
在与电流I 、磁场B 垂直方向上产生的电势差称为霍耳电势差,通常用UH 表示。
霍耳效应的数学表达式为:IB K IB dR U H H H==)( (1)其中RH 是由半导体本身电子迁移率决定的物理常数,称为霍耳系数。
B 为磁感应强度,I 为流过霍耳元件的电流强度,KH 称为霍耳元件灵敏度。
虽然从理论上讲霍耳元件在无磁场作用(即B=0)时,UH=0,但是实际情况用数字电压表测时并不为零,这是由于半导体材料结晶不均匀及各电极不对称等引起附加电势差,该电势差U0称为剩余电压。
随着科技的发展,新的集成化(IC)元件不断被研制成功。
本实验采用SS95A 型集成霍耳传感器(结构示意图如图3所示)是一种高灵敏度集成霍耳传感器,它由霍耳元件、放大器和薄膜电阻剩余电压补偿组成。
测量时输出信号大,并且剩余电压的影响已被消除。
对SS95A 型集成霍耳传感器,它由三根引线,分别是:“V+”、“V-”、“Vout ”。
其中“V+”和“V-”构成“电流输入端”,“Vout ”和“V-”构成“电压输出端”。
由于SS95A 型集成霍耳传感器,它的工作电流已设定,被称为标准工作电流,使用传感器时,必须使工作电流处在该标准状态。
在实验时,只要在磁感应强度为零(零磁场)条件下,调节“V+”、“V-”所接的电源电压(装置上有一调节旋钮可供调节),使输出电压为2.500V(在数字电压表上显示),则传感器就可处在标准工作状态之下。
螺线管内的磁场的测量-实验报告
University of Science and Technology of China96 Jinzhai Road, Hefei Anhui 230026,The People ’s Republic of China螺线管内的磁场的测量实验报告李方勇 PB05210284 05010 第29组2号(周五下午)2006.10.26实验题目 螺线管内的磁场的测量实验实验目的1、测量通电螺线管线圈内的磁感应强度,讨论通电螺线管线圈内部I 、L 、x 和B 之间关系;2、计算出真空中的磁导率。
实验仪器① 螺线管线圈;②大电流电源;③磁场强度计;④探针(霍耳元件);⑤导线和有机玻璃支架等。
实验原理按照Biot-Savart 定律可以推出在螺线管内任意一点P 的磁感应强度B 为:⎰--=-+=2/2/2102/32220)cos (cos 2])([2L L nI l x R IndlR B ββμμ 式中 221)2/(2/cos L x R L x +++=β 222)2/(2/cos L x R L x -+-=β螺线管的长为L ,x 为螺线管中点到P 点的距离。
I 为通过螺线管的电流。
n 为螺线管单位长度的匝数。
图3-1通电螺线管磁场分布实验内容1、 按下图装好仪器设备,将螺线管接到电流源上,将霍耳元件(探针)接到磁强计上,并将探针头放在螺线管的中央 a 点处。
选择磁强计的测量范围为20mT ,利用磁强计的”Compensation”钮调零。
图3-2. 实验设备接线图2、 实验测量:(螺线管总圈数N=30 )(1)测量螺线管内电流I 变化时a 点的磁感应强度B 。
将螺线管的b 点放在16cm 处,c 点放在24cm 处,此时线圈长L 为8cm 。
调节电流源从0开始每次增加2A ,记录B ,但要注意每次测量时都要将电流源打到0点,将磁强计重新调零。
(2)以a 点为中点,改变b 、c 点的距离,使线圈长L 分别为8、10、15、20、25、30、35、40cm ,分别纪录B ,注意每次测量时都要将电流源打到0点,将磁强计重新调零。
霍尔效应法测量螺线管磁场
霍尔效应法测量螺线管磁场实验报告【实验目的】1.了解霍尔器件的工作特性。
2.掌握霍尔器件测量磁场的工作原理。
3.用霍尔器件测量长直螺线管的磁场分布。
4.考查一对共轴线圈的磁耦合度。
【实验仪器】长直螺线管、亥姆霍兹线圈、霍尔效应测磁仪、霍尔传感器等。
【实验原理】1.霍尔器件测量磁场的原理图1 霍尔效应原理如图1所示,有-N 型半导体材料制成的霍尔传感器,长为L ,宽为b ,厚为d ,其四个侧面各焊有一个电极1、2、3、4。
将其放在如图所示的垂直磁场中,沿3、4两个侧面通以电流I ,则电子将沿负I 方向以速度运动,此电子将受到垂直方向磁场B 的洛仑兹力m e F ev B =⨯u u r u r u r作用,造成电子在半导体薄片的1测积累过量的负电荷,2侧积累过量的正电荷。
因此在薄片中产生了由2侧指向1侧的电场H E u u u r,该电场对电子的作用力H H F eE =u u r u u u r ,与m e F ev B =⨯u u r u r u r反向,当两种力相平衡时,便出现稳定状态,1、2两侧面将建立起稳定的电压H U ,此种效应为霍尔效应,由此而产生的电压叫霍尔电压H U ,1、2端输出的霍尔电压可由数显电压表测量并显示出来。
如果半导体中电流I 是稳定而均匀的,可以推导出H U 满足:IH H H IBU R K IB d=⋅=⋅, 式中,H R 为霍耳系数,通常定义/H H K R d =,H K 称为灵敏度。
由H R 和H K 的定义可知,对于一给定的霍耳传感器,H R 和H K 有唯一确定的值,在电流I 不变的情况下,与B 有一一对应关系。
2.误差分析及改进措施由于系统误差中影响最大的是不等势电势差,下面介绍一种方法可直接消除不等势电势差的影响,不用多次改变B 、I 方向。
如图2所示,将图2中电极2引线处焊上两个电极引线5、6,并在5、6间连接一可变电阻,其滑动端作为另一引出线2,将线路完全接通后,可以调节滑动触头2,使数字电压表所测电压为零,这样就消除了1、2两引线间的不等势电势差,而且还可以测出不等势电势差的大小。
螺线管轴向磁场的测定.
螺线管轴向磁场的测定【实验目的】1.学习用霍尔效应测量磁场的原理和方法。
2. 学习用霍尔元件测绘长直螺线管的轴向磁场分布。
【实验原理】 1.霍尔效应霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。
当带电粒子(电子或空穴)被约束在固体材料中,这种偏转就导致在垂直电流和磁场方向上产生正负电荷的聚积,从而形成附加的横向电场,即霍尔电场H E 。
如图1所示的半导体试样,若在X 方向通以电流S I ,在Z 方向加磁场B ,则在Y 方向即试样 A-A /电极两侧就开始聚集异号电荷而产生相应的附加电场。
电场的指向取决于试样的导电类型。
对图1(a)所示的N 型试样,霍尔电场逆Y 方向,(b)的P 型试样则沿Y 方向。
即有)(P 0)()(N 0)(型型⇒>⇒<Y E Y E H H显然,霍尔电场H E 是阻止载流子继续向侧面偏移,当载流子所受的横向电场力H eE 与洛仑兹力B v e 相等,样品两侧电荷的积累就达到动态平衡,故有v e eE H = (1)其中H E 为霍尔电场,v 是载流子在电流方向上的平均漂移速度。
设试样的宽为b,厚度为d,载流子浓度为n ,则bd v ne I S = (2)由(1)、(2)两式可得:dB I R d BI ne b E V S H S H H ===1 (3)即霍尔电压H V (A 、A /电极之间的电压)与B I S 乘积成正比与试样厚度d 成反比。
比例系数neR H 1=称为霍尔系数,它是反映材料霍尔效应强弱的重要参数。
只要测出H V(伏)以及知道S I (安)、B (高斯)和d (厘米)可按下式计算H R (厘米3/库仑):XYZR H =810×BI dV S H (4) 上式中的108是由于磁感应强度B 用电磁单位(高斯)而其它各量均采用CGS 实用单位而引入。
2.霍尔系数H R 与其它参数间的关系 根据H R 可进一步确定以下参数:(1)由H R 的符号(或霍尔电压的正负)判断样品的导电类型。
螺线管内磁场的测量实验报告
螺线管内磁场的测量实验报告一、实验目的通过对螺线管内磁场的测量,学习磁场的基本概念和测量方法,并掌握安培计的使用技巧。
二、实验原理1. 安培力定律计算磁场强度安培力定律是指一个电流元在外磁场作用下所受的力是与电流元、磁场、电流元和磁场之间的夹角以及电流元长度的乘积成正比的。
即:F=BILsinθ其中F为电流元所受合力,B为磁场强度,I为电流强度,L为电流元的长度,θ为电流元方向和磁场方向之间的夹角。
2. 安培计测量磁场强度安培计是一种用于测量电流的仪器,可以通过测量电流元所受的磁场力来计算磁场的强度。
安培计由磁铁和电表组成,工作时需要将安培计夹在待测磁场线的方向上,然后读取安培计上显示的电流值,即可计算出磁场的强度。
三、实验内容和步骤1. 实验器材:螺线管、安培计、导线等。
2. 实验步骤:(1)将螺线管与电源相连接,设定电流值为I=1A。
(2)将安培计放置于螺线管内,与待测磁场方向垂直,并记录安培计上显示的电流值。
(3)将螺线管和安培计的位置互换,放置电流元所在位置,记录安培计上显示的电流值。
(4)重复上述步骤,分别在不同位置测量磁场的强度,并记录数据。
四、实验结果和分析1. 实验数据记录:位置 1 2 3 4电流值(A) 1 1 1 1测量值1(mA) 17 14 12 11测量值2(mA) 16 13 11 10平均值(mA) 16.5 13.5 11.5 10.52. 计算分析:安培计上显示的电流值与磁场强度成正比。
通过实验数据可知,电流值为1A时,测量值在不同位置上的平均值分别为16.5mA、13.5mA、11.5mA和10.5mA。
根据安培力定律,可以计算出螺线管内磁场的强度:B=F/IL其中F为安培计测量的磁场力,I为电流强度,L为电流元的长度。
假设电流元长度为10cm,可得到如下计算结果:位置 F(N) B(T)1 0.033 0.332 0.027 0.273 0.023 0.234 0.021 0.21通过计算可知,在螺线管内部不同位置测得的磁场强度大约为0.21T到0.33T之间,其中距离电源较近的位置磁场强度相对较大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、观察互感现象
取x=5cm,f=1000Hz,I=45.0mA U=0.ห้องสมุดไป่ตู้86V,反接后 U=0.586V。
两次测量的V值相同。这是因为互感现象中,由电磁感应定律,根据电压比等于匝数比,电流比等于匝数反比,从而两次电压相等。
2、
x/cm
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
U/V
1.000
1.000
1.000
1.000
1.000
1.000
0.998
0.996
0.990
0.989
x/cm
10.0
11.0
12.0
12.5
13.0
13.5
14.0
14.5
15.0
15.5
U/V
0.976
0.962
0.934
本实验采用探测线圈法测量直螺线管中产生的交变磁场。图6.3.2-2是实验装置的示意图。当螺线管A中通过一个低频的交流电流 时,在螺线管内产生一个与电流成正比的交变磁场
(2)
其中CP是比例常数。把探测圈A1放在螺线管线圈内部或附近,在A1中将产生感生电动势。探测线圈的尺寸比1较小,匝数比较少。若其截面积为S,匝数为N1,线圈平面的发线与磁场方向的夹角为θ,则穿过线圈的磁通链数为
频率f=375Hz I=50.0mA U=0.108V
分析:得出的电压值几乎相等,感应电动势大小与频率电流的乘积呈正比。
C、 (1)
(7)
(1)x=0,f=750Hz,I=25.0mA对应U=0.228V:
用公式(1)计算得B=0.000396T,用公式(7)计算得B=0.000417T(2)x=l,f=750Hz,I=25.0mA对应U=0.110V:
实验报告
25系05级鄂雁祺2006年5月10日PB05025003
实验题目:测量螺线管的磁场
实验目的:学习测量交变磁场的一种方法,加深理解磁场的一些特性及电磁感应定律。
实验原理:
1、有限长载流直螺线管的磁场
长为2l,匝数为N的单层密绕的直螺线管产生的磁场。当导线中流过电流I时,由毕奥-萨伐尔定律可以计算出在轴线上某一点P的磁感应强度为
0.392
0.440
0.490
U/V(375Hz)
0.070
0.092
0.118
0.142
0.168
0.185
0.206
0.230
x=l
频率f=1500Hz I=12.5mA U=0.114V
频率f=750Hz I=25.0mA U=0.110V
频率f=375Hz I=50.0mA U=0.108V
用公式(1)计算得B=0.000199T,用公式(7)计算得B=0.000202T
(3)结果分析:
串入磁场参加感应的线圈x=0时是x=15时的两倍,产生的感应磁场强度也有对应得倍数关系,且两个公式在这里是等效的。
2、测量直螺线管轴线上的磁场分布
(1)V(x)-x曲线
(2)得到的图像可以看作B(x)-x图像,因为在公式(7) 中,B和V有正比的关系,中间(x=0-10cm左右)的磁场大小是几乎恒定的,即螺线管内部的磁场几乎是匀强的,在此x>12cm之后,磁场开始锐减。
2、研究螺线管中磁感应强度B与电流I和感生电动势V之间的关系,测量螺线管中的磁感应强度。
A、不同频率的V-I曲线:
分析:U-I斜率之比与频率呈正比,即频率越高,电压随电流增加的速度越快。
B、频率f=1500Hz I=12.5mA U=0.114V
频率f=750Hz I=25.0mA U=0.110V
(3)
根据法拉第定律,线圈中的感生电动势为
(4)
通常测量的是电压的有效值。设E(t)有效值为V,B(t)有效值为B,则有
(5)
由此得出磁感应强度
(6)
其中r1是探测线圈的半径,f是交变电源的频率。在测量过程中如始终保持A和A1在同一轴线上,此时 ,则螺线管中的磁感应强度为
(7)
在实验装置中,在待测螺线管回路中串接毫安计用于测量螺线管导线中交变电流的有效值。在探测线圈A1两端连接数字毫安计用于测量A1种感生电动势的有效值。
0.910
0.878
0.814
0.742
0.610
0.460
0.308
x/cm
16.0
16.5
17.0
17.5
18.0
U/V
0.202
0.138
0.096
0.074
0.056
3、取x=5cm,f=1000Hz,I=45.0mA U=0.586V
反接后 U=0.586V
数据处理:
1、改装后的电路图(加入单刀双掷开关)
数据记录:
1、螺线管A: , ,
探测线圈A1: ,
x=0
I/mA
15.0
20.0
25.0
30.0
35.0
40.0
45.0
50.0
U/V(1500Hz)
0.308
0.410
0.508
0.606
0.706
0.810
0.910
1.002
U/V(750Hz)
0.150
0.196
0.228
0.294
0.344
(1)
式中 为单位长度上的线圈匝数,R为螺线管半径,x为P点到螺线管中心处的距离。由曲线显示,在螺线管内部磁场近于均匀,只在端点附近磁感应强度才显著下降。当l>>R时, 与场点的坐标x无关,而在螺线管两端 为内部B值的一半。无限长密绕直螺线管是实验室中经常使用到的产生均匀磁场的理想装置。
2、测线圈法测量磁场
思考题:
用探测线圈法测量磁场时,为何产生磁场的导体中必须通过低频交流电而不能通过高频交流电?
答:螺线管可以看成是一个电感线圈,如果用高频的交流电,对信号源阻碍作用很大,即感抗很大,影响测量。
