动力计算 结构力学共179页
合集下载
结构力学 结构的动力计算

输出 (动力反应)
第二类问题:参数(或系统)的识别 结构 (系统)
输入 (动荷载)
输出 (动力反应)
第三类问题:荷载识别 输入 (动荷载) 结构 (系统)
输出 (动力反应)
第四类问题:控制问题
输入 (动荷载)
结构 (系统)
控制系统 (装置、能量)
输出 (动力反应)
2.结构动力计算的目的 研究结构在动荷载作用下的反应规 律,找出动荷载作用下结构的最大动内 力和最大动位移,为结构的动力可靠性 设计提供依据。
第13章
结构的动力计算
§13-1 动力计算的特点和动力自由度
一.动荷载及其分类
动荷载是指其大小、方向和作用位置随 时间变化的荷载.由于荷载随时间变化较快 ,所产生的惯性力不容忽视。因此,考虑惯 性力的影响是结构动力学的最主要特征。 静荷载只与作用位置有关,而动荷载 是坐标和时间的函数。
动荷载按其随时间的变化规律进行分类:
质量 m 在 t 时刻的位移y(t)是由此时作 用在质量上的惯性力产生的,位移方程为:
y(t ) [m(t )] y
整理,
m(t ) y 1
y (t ) 0
(a) (b)
单自由度体系: k
1
式(13-1)或(a)称为单自由度体系 自由振动运动方程(微分方程)
二.自由振动运动方程的解
由式(13-4)
y (t ) A sin(t ) A sin(t 2 ) A sin[ (t 2 ) ] y (t 2 )
y(t)是周期函数
T 2
-自振周期(固有周期) -自振频率(固有频率)
2 T
1. 结构自振周期 T 和自振频率 的各种等 价计算公式
结构力学动力计算

沿质点的可位移方向虚设单位荷载,作 图
M1
m
EI EI
L
图乘法得 柔度系数
自振频率
M1M1 2l3
EI 3EI
1
2m
3EI 4ml 3
L
L
L
自振周期
T 2 2 4m l3
3EI
M1图
m
EI
L
1
结构力学(2)
浙大宁波理工学院土建学院
算例.求图示体系的自振频率和周期,C端最大位移
A
∞
B
C
k
10个自由度 9个自由度
结构力学(2)
浙大宁波理工学院土建学院
10.2 单自由度体系的自由振动
1.自由振动运动微分方程
• 自由振动-由初位移或初速度引起的,在运动中无动荷载作 用的振动。
• 分析自由振动的目的 确定结构的动力特性,自振频率,自振周期。
结构力学(2)
浙大宁波理工学院土建学院m
静平衡方程
代入初始条件得
y(t 0) y0 Asin y(t 0) v0 Acos
解得
振幅: A
y02
v02
2
初始相位角:
tan1 y0
v0
结构力学(2)
浙大宁波理工学院土建学院
算例 求图示体系的自振频率和自振周期。(P359)
自振频率和自振周期是体系固有的, 只与内在因素有关,与外在因素无关。 算法:柔度法
动荷载: F(t) 刚度系数: k
柔度系数: =1/k
位移:y(t)
质量: m
时间:t
速度: y(t) dy
加速度:
dt y(t)
d
2y
dt 2
结构力学(2)
M1
m
EI EI
L
图乘法得 柔度系数
自振频率
M1M1 2l3
EI 3EI
1
2m
3EI 4ml 3
L
L
L
自振周期
T 2 2 4m l3
3EI
M1图
m
EI
L
1
结构力学(2)
浙大宁波理工学院土建学院
算例.求图示体系的自振频率和周期,C端最大位移
A
∞
B
C
k
10个自由度 9个自由度
结构力学(2)
浙大宁波理工学院土建学院
10.2 单自由度体系的自由振动
1.自由振动运动微分方程
• 自由振动-由初位移或初速度引起的,在运动中无动荷载作 用的振动。
• 分析自由振动的目的 确定结构的动力特性,自振频率,自振周期。
结构力学(2)
浙大宁波理工学院土建学院m
静平衡方程
代入初始条件得
y(t 0) y0 Asin y(t 0) v0 Acos
解得
振幅: A
y02
v02
2
初始相位角:
tan1 y0
v0
结构力学(2)
浙大宁波理工学院土建学院
算例 求图示体系的自振频率和自振周期。(P359)
自振频率和自振周期是体系固有的, 只与内在因素有关,与外在因素无关。 算法:柔度法
动荷载: F(t) 刚度系数: k
柔度系数: =1/k
位移:y(t)
质量: m
时间:t
速度: y(t) dy
加速度:
dt y(t)
d
2y
dt 2
结构力学(2)
结构力学教程——第15章 结构的动力计算

k m
24EI mh3
T 2 mh3
24EI
3. 结构的自振周期与频率
例5 计算结构水平振动和竖直振动时的自振频率,忽略自重。
m
1l
EI 常数
l
22
l
l
水平振动 柔度法 δ
M
4 EI
1 l 2
l 2
l 2
2 3
l3 3EI
1
m
3EI ml 3
3. 结构的自振周期与频率
刚度法 k
C1 和 C2 可由初始条件确定,设初始位移和初始速度分别为
y(0) y0 y(0) v0
C1 y0
C2
v0
y(t)
y0
cos t
v0
sin t
2. 自由振动微分方程的解
yy
T
y(t)
y0
cos t
v0
sin t
0
t y cos t
-y
y
T
v
0
v
y T
A
t
v sin t
A sin
t
3. 结构的自振周期与频率
拓展——定性分析 例:图示三根单跨梁,EI为常数,在梁中点有集中质量m,
不考虑梁的质量,试比较三者的自振频率。
m
m
m
l/2
l/2
l/2
l/2
l/2
l/2
1
l3 48EI
2
7l 3 768EI
3
l3 192EI
1
1
m1
48EI ml 3
2
1
m 2
768EI 7ml 3
1
1
结构力学 结构动力计算

Y st yt mg yt
⑶质点沿水平方向振动时,水平总线位移 Y yt
§10—2
运动方程为:
单自由度体系的自由振1 动
k
m
mY kY W 0
st
y(t)
Y(t)
因为 Y (t) st y(t) Y (t) y(t) -kY -mY
所以 my k[ y(t) st ] W
⑵阻尼力与质点速度平方成正比,固体在流体中运动受到的阻力。
⑶阻尼力与质点的速度无关,摩擦力属于此类。
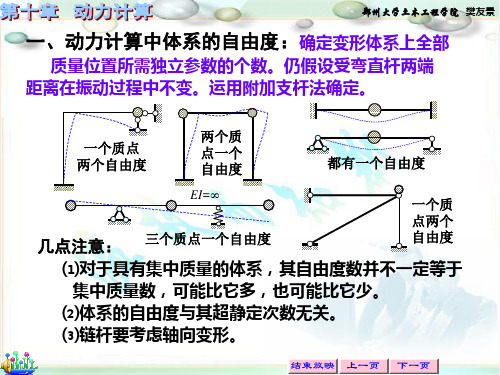
§10—1 动力计算的特点和动力体系自由度
关于阻尼力的理论很多,为计算方便我们选用粘滞阻尼理论。
理论假定:阻尼力的大小与质点的运动速度成正比,方向与质 点的 运动速度方向相反。即:
R
cv
c
dy dt
w
又 k st kW W
my ky(t) W W
my ky(t) 0
§10—2 单自由度体系的自由振动
可见,重力对动位移y (t ) 的运动方程无影响。 质量围绕静力平衡位置进行振动。
aa
a a
W mymax
l m
ymax st a (W mymax)
st
a
ymax
Mmax (W mymax)l
§10—2 单自由度体系的自由振动
单自由度体系的动力分析虽简单但很重要体现在两个方面:
⑴很多实际动力学问题,可按单自由度体系进行分析和计算,而所 得结果基本上能反映其实际的动力特点。
⑵单自由度体系的动力分析是多自由度体系动力分析的基础。
一、振动模型的建立
对于各种单自由度体系的振动,都可以用一个弹簧质块模型的振动来描述, 因为它们有相同的运动规律和运动微分方程。
⑶质点沿水平方向振动时,水平总线位移 Y yt
§10—2
运动方程为:
单自由度体系的自由振1 动
k
m
mY kY W 0
st
y(t)
Y(t)
因为 Y (t) st y(t) Y (t) y(t) -kY -mY
所以 my k[ y(t) st ] W
⑵阻尼力与质点速度平方成正比,固体在流体中运动受到的阻力。
⑶阻尼力与质点的速度无关,摩擦力属于此类。
§10—1 动力计算的特点和动力体系自由度
关于阻尼力的理论很多,为计算方便我们选用粘滞阻尼理论。
理论假定:阻尼力的大小与质点的运动速度成正比,方向与质 点的 运动速度方向相反。即:
R
cv
c
dy dt
w
又 k st kW W
my ky(t) W W
my ky(t) 0
§10—2 单自由度体系的自由振动
可见,重力对动位移y (t ) 的运动方程无影响。 质量围绕静力平衡位置进行振动。
aa
a a
W mymax
l m
ymax st a (W mymax)
st
a
ymax
Mmax (W mymax)l
§10—2 单自由度体系的自由振动
单自由度体系的动力分析虽简单但很重要体现在两个方面:
⑴很多实际动力学问题,可按单自由度体系进行分析和计算,而所 得结果基本上能反映其实际的动力特点。
⑵单自由度体系的动力分析是多自由度体系动力分析的基础。
一、振动模型的建立
对于各种单自由度体系的振动,都可以用一个弹簧质块模型的振动来描述, 因为它们有相同的运动规律和运动微分方程。
结构力学课件 动力计算
M AC 3i A 3i 3i(1 A ) M AB i i i 3 A 3 3 ( A 1) 2 2 2
l
l
M 1 2
M AB 6i M AB , FQBA 1 2 2l 12i k k11 r11l m 1 2
弹簧反力 FRC 5m 2a,
2k FRC 5m 2 a 2 , 弹簧变形 2a 5m k k
结束放映 上一页 下一页
郑州大学土木工程学院 樊友景
例3:求图示体系的 自振频率。 ⑶间接应用公式
A
l/2
B m B θ
EI=∞ l/2
C k C
l/2
D m D
A
设梁绕A点转角为θ, 2 2 2 l 3l 5ml •则梁绕A点转动的惯性 JA m m 2 2 2 为其对A点的转动惯量. A k B C D 11 •与其相应的刚度为梁 l θ=1 绕A点转动刚度k11 。 kl k11 kl 2 •用转动刚度k11代替刚 度系数k,转动惯量JA k11 k kl 2 2k 2 代替质量m代入公式 m J 5ml / 2 5m
1 192 EI m 5ml 3 192 90 105 1 134.16 s 5 300 43
结束放映
EI
F sin t
m
1
l/2
l/2
k
δ
k 1/2
上一页
下一页
郑州大学土木工程学院 樊友景
例5:已知图示梁中质量 m=300kg,EI=90×105N· m2, l=4m,k=48EI/l3,F=20kN,θ=80s-1。
结束放映
上一页
下一页
l
l
l
M 1 2
M AB 6i M AB , FQBA 1 2 2l 12i k k11 r11l m 1 2
弹簧反力 FRC 5m 2a,
2k FRC 5m 2 a 2 , 弹簧变形 2a 5m k k
结束放映 上一页 下一页
郑州大学土木工程学院 樊友景
例3:求图示体系的 自振频率。 ⑶间接应用公式
A
l/2
B m B θ
EI=∞ l/2
C k C
l/2
D m D
A
设梁绕A点转角为θ, 2 2 2 l 3l 5ml •则梁绕A点转动的惯性 JA m m 2 2 2 为其对A点的转动惯量. A k B C D 11 •与其相应的刚度为梁 l θ=1 绕A点转动刚度k11 。 kl k11 kl 2 •用转动刚度k11代替刚 度系数k,转动惯量JA k11 k kl 2 2k 2 代替质量m代入公式 m J 5ml / 2 5m
1 192 EI m 5ml 3 192 90 105 1 134.16 s 5 300 43
结束放映
EI
F sin t
m
1
l/2
l/2
k
δ
k 1/2
上一页
下一页
郑州大学土木工程学院 樊友景
例5:已知图示梁中质量 m=300kg,EI=90×105N· m2, l=4m,k=48EI/l3,F=20kN,θ=80s-1。
结束放映
上一页
下一页
l
建筑力学结构的动力计算

结构力学
由式可知,位移是由初位移y引起的余弦运动和由初速度v引起的正弦
运动的合成,为了便于研究合成运动, 令
y A sin ,...
(e)式改写成
v A cos 来自y (t ) y cos t
y(t ) Asin( t )......... .......... f ) ...(
结构力学
三、结构的自振周期和频率
由式
y(t ) Asin( t )
y T A
及图可见位移方程是一个周期函数。
0
t
-A
周期-T
2
,
工程频率- f
1 ( Hz ), T 2
圆频率- 2f
2 T
计算频率和周期的几种形式
k 1 g g m m W st
m
W
.y
d
+
I(t)
弹性力 S (t ) ky(t ) k ( y j yd )
恒与位移反向
与加速度反向
y y y 惯性力 I (t ) m(t ) m( j d )
淮海工学院土木工程学院
第十三章 结 构 的 动 力 计 算
结构力学
y y y 惯性力 I (t ) m(t ) m( j d )
2
单自由度体系强迫 振动的微分方程
ky m P(t )
y
m y
淮海工学院土木工程学院
第十三章 结 构 的 动 力 计 算
结构力学
一、动荷载为简谐荷载
y 2 y
2
P(t ) F sin t
A F m( 2 2 )
F sin t m
《结构力学》第15章 结构的动力计算
my t EA
(2 2 2)l
y(t) 1 2 22
2 2 FP (t)
13-3 单自由度体系的强迫振动
my my
m
m
l/2
F 2my t FP (t)
M图
2 EI
1 2
l 2
l
2 3
l 2
1 l 22
考虑稳态振动
y t Asin t m
F
2 2
sin t
F
m2 (1
2 2
)
sin t
F k
1
1
2 2
sin t
yst sin t
13-1 动力计算的特点和动力自由度
2 动荷载的分类 ◆第一类——周期荷载:荷载随时间作周期性的变化。
非简谐性的周期荷载 t
FP (t) FP
典型的周期荷载是 简谐荷载。机器转
t 动部分引起的荷载 属于2简00谐4年荷8载月
简谐荷载:可用正弦或余弦函数表示
13-1 动力计算的特点和动力自由度
◆第二类——冲击荷载:荷载在很短的时间内急剧增大或减小。
1 m g W g st
T 2 m T 2 W g T 2 st g
13-2 单自由度体系的自由振动
自振周期的特性 (1)自振周期只与体系的质量和刚度有关,与外界因素无关。 (2)自振周期与质量的平方根成正比,与刚度的平方根成反比。 (3)自振周期相近的体系,动力性能基本一致。
m
齐次通解
y t C1 sin t C2 cost
非齐次特解
