结构动力计算习题
结构力学(2)习题库
15 结构的动力计算判断题体系的振动自由度等于集中质量数。
（）图示体系具有1个振动自由度。
（）图示体系具有2个振动自由度。
（）图示体系具有3个振动自由度。
（）图示体系具有2个振动自由度。
（）图示体系具有2个振动自由度。
（）结构的自振频率除与体系的质量分布状况、杆件刚度有关外，还与干扰力有关。
（）自由振动是指不受外界干扰力作用的振动。
（）自由振动是由初位移和初速度引起的，缺一不可。
（）有阻尼单自由度体系的阻尼比越大，自振频率越小。
（）临界阻尼现象是指起振后振动次数很少且振幅很快衰减为零的振动。
（）惯性力并不是实际加在运动质量上的力。
（）计算一个结构的自振周期时，考虑阻尼比不考虑所得的结果要大。
（）临界阻尼振动时质点缓慢地回到平衡位置且不过平衡点。
（）阻尼力总是与质点加速的方向相反。
（）在某些情形下建立振动微分方程式时，不考虑重力的影响是因为重力为恒力。
（）图示结构的自振频率为w，在干扰力P(t)=P sin qt作用下，不管频率q怎样改变，动位移y(t)的方向总是和P(t)的方向相同。
（）计算图示振动体系的最大动内力和动位移时可以采用同一个动力系数。
（）不论干扰力是否直接作用在单自由度体系的质量m上，都可用同一个动力系数计算任一点的最大动位移。
（）单自由度体系受迫振动的最大动位移的计算公式y max=my j中，y j是质量m的重量所引起的静位移。
（）多自由度体系作自由振动，一般包括所有的振型，不可能出现仅含某一主振型的振动。
（）解得图(a)所示两个自由度体系的两个主振型为图(b)和图(c)，此解答是正确的。
（）图(a)与图(b)所示梁的自由振动频率w A、w B相比，w A>w B。
（）填空题动力荷载是指＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿荷载。
振动自由度的定义是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。
若要改变一个结构的自振周期，可以从两个方面着手：1、＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿；2、＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。
结构动力学课后习题答案
结构动力学课后习题答案结构动力学是研究结构在动态载荷作用下的响应和行为的学科。
它涉及到结构的振动、冲击响应、疲劳分析等方面。
课后习题是帮助学生巩固课堂知识、深化理解的重要手段。
以下内容是结构动力学课后习题的一些可能答案，供参考：习题1：单自由度系统自由振动分析解答：对于一个单自由度系统，其自由振动的频率可以通过以下公式计算：\[ f = \frac{1}{2\pi}\sqrt{\frac{k}{m}} \]其中，\( k \) 是系统的刚度，\( m \) 是系统的总质量。
系统自由振动的振幅随着时间的衰减可以通过阻尼比 \( \zeta \) 来描述，其衰减系数 \( \delta \) 可以通过以下公式计算：\[ \delta = \sqrt{1-\zeta^2} \]习题2：单自由度系统受迫振动分析解答：当单自由度系统受到周期性外力作用时，其受迫振动的振幅可以通过以下公式计算：\[ A = \frac{F_0}{\sqrt{(k-m\omega^2)^2+(m\zeta\omega)^2}} \] 其中，\( F_0 \) 是外力的幅值，\( \omega \) 是外力的角频率。
习题3：多自由度系统模态分析解答：对于多自由度系统，可以通过求解特征值问题来得到系统的模态。
特征值问题通常表示为：\[ [K]{\phi} = \lambda[M]{\phi} \]其中，\( [K] \) 是系统的刚度矩阵，\( [M] \) 是系统的质量矩阵，\( \lambda \) 是特征值，\( {\phi} \) 是对应的特征向量，即模态形状。
习题4：结构的冲击响应分析解答：对于结构的冲击响应分析，通常需要考虑冲击载荷的持续时间和冲击能量。
结构的冲击响应可以通过冲击响应谱（IRF）来分析，它描述了结构在不同频率下的响应。
冲击响应分析的结果可以用来评估结构的耐冲击性能。
习题5：疲劳分析解答：结构的疲劳分析需要考虑结构在重复载荷作用下的寿命。
结构动力学_克拉夫(第二版)课后习题
例题E2-1 如图E2-1所示，一个单层建筑理想化为刚性大梁支承在无重的柱子上。
为了计算此结构的动力特性，对这个体系进行了自由振动试验。
试验中用液压千斤顶在体系的顶部（也即刚性大梁处）使其产生侧向位移，然后突然释放使结构产生振动。
在千斤顶工作时观察到，为了使大梁产生0.20in[0.508cm]位移需要施加20 kips[9 072 kgf]。
在产生初位移后突然释放，第一个往复摆动的最大位移仅为0.16 in[0. 406 cm]，而位移循环的周期为1.4 s。
从这些数据可以确定以下一些动力特性：（1）大梁的有效重量；（2）无阻尼振动频率；（3）阻尼特性；（4）六周后的振幅。
2- 1图E2-1所示建筑物的重量W为200 kips，从位移为1.2 in（t=0时）处突然释放，使其产生自由振动。
如果t=0. 64 s时往复摆动的最大位移为0.86 in，试求(a)侧移刚度k；(b)阻尼比ξ；(c)阻尼系数c。
2-2 假设图2- la 所示结构的质量和刚度为：m= kips ·s 2/in ，k=40 kips/in 。
如果体系在初始条件in 7.0)0(=υ、in/s 6.5)0(=υ&时产生自由振动，试求t=1.0s 时的位移及速度。
假设：(a) c=0（无阻尼体系）； (b) c=2.8 kips ·s/in 。
2-3 假设图2- 1a 所示结构的质量和刚度为：m=5 kips ·s 2/in ，k= 20 kips/in ，且不考虑阻尼。
如果初始条件in 8.1)0(=υ，而t=1.2 s 时的位移仍然为1.8 in ，试求：(a) t=2.4 s 时的位移； (b)自由振动的振幅ρ。
例题E3-1 一种便携式谐振荷载激振器，为在现场测量结构的动力特性提供了一种有效的手段。
用此激振器对结构施以两种不同频率的荷载，并分别测出每种情况下结构反应的幅值与相位。
由此可以确定单自由度体系的质量、刚度和阻尼比。
10结构的动力计算习题解答,重庆大学,文国治版教材课后答案
第10章 结构的动力计算习题解答习题10.1 是非判断题(1) 引起单自由度体系自由振动的初速度值越大，则体系的自振频率越大。
（ ） (2) 如果单自由度体系的阻尼增大，将会使体系的自振周期变短。
（ ） (3) 在土木工程结构中，阻尼对自振周期的影响很小。
（ ）(4) 由于各个质点之间存在几何约束，质点体系的动力自由度数总是小于其质点个数。
（ ）(5) 多自由度的自振频率与引起自由振动的初始条件无关。
（ ） (6) n 个自由度体系有n 个自振周期，其中第一周期是最长的。
（ ）(7) 如果考虑阻尼，多自由度体系在简谐荷载作用下的质点振幅就不能用列幅值方程的方法求解。
（ ）【解】(1) 错误。
体系的自振频率与初速度无关，由结构本身的特性所决定。
(2) 错误。
由阻尼结构的自振频率2r 1ωωξ=-可知，阻尼增大使自振频率减小，自振周期变长。
(3) 正确。
(4) 错误。
由动力自由度的概念知，动力自由度数与计算假定有关，而与集中质量数目和超静定次数无关。
(5) 正确。
(6) 正确。
(7) 正确。
习题10.2 填空题(1) 单自由度体系运动方程为2P 2()/y y y F t m ξωω++=，其中未考虑重力，这是因为__________。
(2) 单自由度体系自由振动的振幅取决于__________。
(3) 若要改变单自由度体系的自振周期， 应从改变体系的__________或__________着手。
(4) 若由式()211βθω=-求得的动力系数为负值，则表示__________。
(5) 习题10.2(5)图所示体系发生共振时，干扰力与__________平衡。
c k WF sin θ tP 12-2(5)习题 图习题10.2(5)图(6) 求习题10.2(6)图所示质点系的自振频率时(EI ＝常数)，其质量矩阵[M ]=__________。
mm2m12-2(6)习题 图mF sin θ tP 12-2(7)习题 图习题10.2(6)图 习题10.2(7)图(7) 习题10.2(7)图所示体系不考虑阻尼，EI ＝常数。
[美]R.克里夫《结构动力学》补充详解及习题解
![[美]R.克里夫《结构动力学》补充详解及习题解](https://img.taocdn.com/s3/m/198055225627a5e9856a561252d380eb629423b8.png)
前言结构动力学是比较难学的一门课程，但是你一旦学会并且融会贯通，你就会为成为结构院士、大师和总工垫定坚实的基础。
结构动力学学习的难点主要有以下两个方面。
1 概念难理解，主要表现在两个方面，一是表达清楚难，如果你对概念理解的很透彻，那么你写的书对概念的表述也会言简意赅，切中要害（克里夫的书就是这个特点），有的书会对一个概念用了很多文字进行解释，但是还是没有说清楚，也有的书受水平限制，本身表述就不清楚。
二是理解难，有点只可意会不可言传的味道，老师讲的头头是道，自己听得云山雾绕。
2 公式推导过程难，一是力学知识点密集，推导过程需要力学概念清析，并且需要每一步的力学公式熟悉；二是需要一定的数学基础，而且有的是在本科阶段并没有学习的数学知识。
克里夫《结构动力学》被称为经典的结构动力学教材，但是也很难看懂。
之所以被称为经典，主要就是对力学的概念表达的语言准确，概念清楚。
为什么难懂呢？是因为公式的推导过程比较简单，省略过多。
本来公式的推导过程既需要力学概念清楚也需要数学公式熟悉，但是一般人不是力学概念不清楚，就是数学公式不熟悉，更有两者都不熟悉者。
所以在学习过程中感觉很难，本学习详解是在该书概念清楚的基础上，对力学公式推导过程进行详细推导，并且有的加以解释，帮助你在学习过程中加深理解和记忆。
达到融会贯通，为你成为结构院士、大师和总工垫定坚实的基础。
以下黑体字是注释，其它为原书文字。
[美] R∙克里夫《结构动力学》辅导学习详解第1章结构动力学概述… …第Ⅰ篇单自由度体系第2章基本动力体系的组成… …§2-5 无阻尼自由振动分析如上一节所述，有阻尼的弹簧-质量体系的运动方程可表示为mv̈(t)+cv̇(t)+kν(t)=p(t)（2-19）其中ν(t)是相对于静力平衡位置的动力反应；p(t)是作用于体系的等效荷载，它可以是直接作用的或是支撑运动的结构。
为了获得方程（2-19）的解，首先考虑方程右边等于零的齐次方程，即mv̈(t)+cv̇(t)+kν(t)=0（2-20）mv(t)+kν(t)=0（2-20a）此处公式应该为mv(t)+kν(t)=0，因为该节是无阻尼自由振，而且（2-20）的解，式（2-21）也是公式mv(t)+kν(t)=0的解在作用力等于零时产生的运动称为自由振动，现在要研究的即为体系的自由振动反应。
结构动力学习题
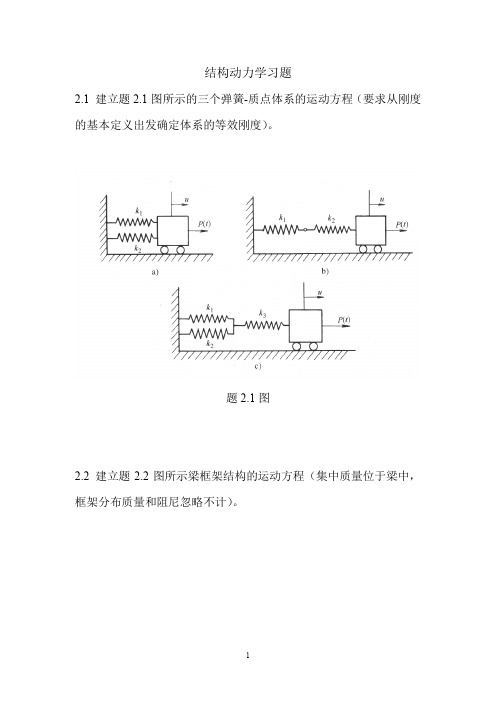
结构动力学习题2.1 建立题2.1图所示的三个弹簧-质点体系的运动方程（要求从刚度的基本定义出发确定体系的等效刚度）。
题2.1图2.2 建立题2.2图所示梁框架结构的运动方程（集中质量位于梁中，框架分布质量和阻尼忽略不计）。
题2.2图2.3 试建立题2.3图所示体系的运动方程，给出体系的广义质量M、广义刚度K、广义阻尼C和广义荷载P(t)，其中位移坐标u(t)定义为无重刚杆左端点的竖向位移。
题2.3图2.4 一总质量为m1、长为L的均匀刚性直杆在重力作用下摆动。
一集中质量m2沿杆轴滑动并由一刚度为K2的无质量弹簧与摆轴相连，见题 2.4图。
设体系无摩擦，并考虑大摆角，用图中的广义坐标q1和q2建立体系的运动方程。
弹簧k2的自由长度为b。
题2.4图2.5 如题2.5图所示一质量为m1的质量块可水平运动，其右端与刚度为k的弹簧相连，左端与阻尼系数为c的阻尼器相连。
摆锤m2以长为L的无重刚杆与滑块以铰相连，摆锤只能在图示铅垂面内摆动。
建立以广义坐标u和θ表示的体系运动方程（坐标原点取静平衡位置）。
题2.5图2.6如题2.6图所示一质量为m1的质量块可水平运动，其上部与一无重刚杆相连，无重刚杆与刚度为k2的弹簧及阻尼系数为c2的阻尼器相连，m1右端与刚度为k1的弹簧相连，左端与阻尼系数为c1的阻尼器相连。
摆锤m2以长为L的无重刚杆与滑块以铰相连，摆锤只能在图示铅垂面内摆动。
建立以广义坐标u和θ表示的体系运动方程（坐标原点取静平衡位置，假定系统作微幅振动，sinθ=tanθ=θ）。
计算结果要求以刚度矩阵，质量矩阵，阻尼矩阵的形式给出。
3.1单自由度建筑物的重量为900kN，在位移为3.1cm时（t＝0）突然释放，使建筑产生自由振动。
如果往复振动的最大位移为2.2cm（t ＝0.64s），试求：（1）建筑物的刚度k；（2）阻尼比ξ；（3）阻尼系数c。
3.2 单自由度体系的质量、刚度为m＝875t，k＝3500kN/m，且不考虑阻尼。
结构动力学例题复习题含答案-2021年推荐必备
结构动力学例题复习题第十六章结构动力学【例 16- 1 】不计杆件分布质量和轴向变形，确定图 16-6 所示刚架的动力自由度。
图 16-6【解】各刚架的自由度确定如图中所示。
这里要注意以下两点：1．在确定刚架的自由度时，引用受弯直杆上任意两点之间的距离保持不变的假定。
根据这个假定并加入最少数量的链杆以限制刚架上所有质量的位置，则刚架的自由度数目即等于所加链杆数目。
2．集中质量的质点数并不一定等于体系的自由度数，而根据自由度的定义及问题的具体情形确定。
【例 16- 2 】试用柔度法建立图 16-7a 所示单自由度体系，受均布动荷载作用的运动方程。
【解】本题特点是，动荷载不是作用在质量上的集中荷载。
对于非质量处的集中动荷载的情况，在建立运动方程时，一般采用柔度法较为方便。
设图 a 质量任一时刻沿自由度方向的位移为 y （向下为正）。
把惯性力、阻尼力及动荷载，均看作是一个静荷载，则在其作用下体系在质量处的位移y ，由叠加原理（见图 b 、 c 、 d 及 e ），则式中，，。
将它们代入上式，并注意到，，得图 16-7经整理后可得式中，，称为等效动荷载或等效干扰力。
其含义为：直接作用于质量上所产生的位移和实际动荷载引起的位移相等。
图 a 的相当体系如图 f 所示。
【例 16- 3 】图 16-8 a 为刚性外伸梁， C 处为弹性支座 , 其刚度系数为，梁端点 A 、 D 处分别有和质量，端点 D 处装有阻尼器 c ，同时梁 BD 段受有均布动荷载作用，试建立刚性梁的运动方程。
【解】因为梁是刚性的，这个体系仅有一个自由度，故它的动力响应可由一个运动方程来表达，方程可以用直接平衡法来建立。
这个单自由度体系可能产生的位移形式如图 b 所示，可以用铰 B 的运动作为基本量，而其它一切位移均可利用它来表示。
图 16-8以顺时针向为正。
则 A 点有位移和加速度； D 点有位移和加速度及速度； C 点约束反力为。
由，有将惯性力、阻尼力及约束反力代入上式，得经整理，运动方程为小结：例 16- 2 及例 16- 3 讨论的是单自由度的一般情况下的运动方程的建立。
结构力学练习题及答案
结构力学练习题及答案(总42页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一． 是非题（将判断结果填入括弧：以O 表示正确，X 表示错误）（本大题分4小题，共11分） 1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。
（ ）.2 . (本小题 4分)用力法解超静定结构时，只能采用多余约束力作为基本未知量。
（ ）3 . (本小题 2分)力矩分配中的传递系数等于传递弯矩与分配弯矩之比，它与外因无关。
（ ）4 . (本小题 2分)用位移法解超静定结构时，基本结构超静定次数一定比原结构高。
（ ）二． 选择题（将选中答案的字母填入括弧内）（本大题分5小题，共21分） 1 （本小题6分）图示结构EI=常数，截面A 右侧的弯矩为：（ ）A ．2/M ；B ．M ；C ．0； D. )2/(EI M 。
2. （本小题4分）图示桁架下弦承载，下面画出的杆件内力影响线，此杆件是：（ ） Ａ.ch; ; ; .23. (本小题 4分)图a 结构的最后弯矩图为：A. 图b;B. 图c;C. 图d;D.都不对。
（ ）( a) (b) (c) (d)4. (本小题 4分)用图乘法求位移的必要条件之一是： A.单位荷载下的弯矩图为一直线； B.结构可分为等截面直杆段； C.所有杆件EI 为常数且相同； D.结构必须是静定的。
( ) 5. （本小题3分）图示梁A 点的竖向位移为（向下为正）：( )Ａ．F P l 3/(24EI); B. F P l 3/(!6EI); C. 5F P l 3/(96EI); D. 5F P l 3/(48EI).三（本大题 5分）对图示体系进行几何组成分析。
=1F P482四（本大题 9分）图示结构B 支座下沉4 mm ，各杆EI=×105 kN·m 2，用力法计算并作M 图。
五（本大题 11分） 用力矩分配法计算图示结构，并作M 图。
结构动力计算课后习题答案
结构动力计算课后习题答案结构动力计算课后习题答案在学习结构动力学这门课程时，我们经常会遇到各种各样的习题。
这些习题旨在帮助我们巩固所学的知识，并提供实践的机会。
在这篇文章中，我将为大家提供一些结构动力计算课后习题的答案，希望能对大家的学习有所帮助。
1. 计算一个简支梁的固有频率。
答案：简支梁的固有频率可以通过以下公式计算：f = (1/2π) * √(k/m)其中，f为固有频率，k为刚度，m为质量。
在简支梁的情况下，刚度k等于弹性模量E乘以截面面积A除以长度L。
质量m等于密度ρ乘以截面面积A除以长度L。
2. 计算一个悬臂梁的固有频率。
答案：悬臂梁的固有频率可以通过以下公式计算：f = (1/2π) * √(3k/m)在悬臂梁的情况下，刚度k等于弹性模量E乘以截面面积A的三次方除以长度L的四次方。
质量m等于密度ρ乘以截面面积A除以长度L。
3. 计算一个简支梁的振动模态。
答案：简支梁的振动模态可以通过以下公式计算：f_n = (n^2 * v) / (2L)其中，f_n为第n个振动模态的频率，v为波速，L为长度。
n为振动模态的序号，从1开始。
4. 计算一个悬臂梁的振动模态。
答案：悬臂梁的振动模态可以通过以下公式计算：f_n = (2n-1) * (v/4L)其中，f_n为第n个振动模态的频率，v为波速，L为长度。
n为振动模态的序号，从1开始。
5. 计算一个简支梁的最大挠度。
答案：简支梁的最大挠度可以通过以下公式计算：δ_max = (5qL^4) / (384EI)其中，δ_max为最大挠度，q为均布载荷，L为长度，E为弹性模量，I为截面惯性矩。
6. 计算一个悬臂梁的最大挠度。
答案：悬臂梁的最大挠度可以通过以下公式计算：δ_max = (qL^4) / (8EI)其中，δ_max为最大挠度，q为均布载荷，L为长度，E为弹性模量，I为截面惯性矩。
以上是一些常见的结构动力计算课后习题的答案。
通过解答这些习题，我们可以更好地理解结构动力学的概念和原理，提高我们的计算能力和问题解决能力。
结构动力计算课后习题答案
结构动力计算课后习题答案结构动力计算是土木工程和机械工程领域中的一个重要分支，它涉及到结构在动力作用下的响应分析。
这门课程的课后习题通常要求学生运用所学的理论，解决实际工程问题。
以下是一些可能的习题答案示例，请注意，这些答案是基于假设的习题内容，实际的习题答案应根据具体的题目来确定。
习题1：单自由度系统的动力响应假设有一个单自由度系统，其质量为m，阻尼系数为c，刚度系数为k。
系统受到一个简谐激励F(t) = F0 * sin(ωt)，其中F0是激励力的幅值，ω是激励频率。
求系统的稳态响应。
答案：对于单自由度系统，其运动方程可以表示为：\[ m\ddot{x}(t) + c\dot{x}(t) + kx(t) = F_0 \sin(\omega t) \]稳态响应可以通过求解上述方程的特解来获得。
特解的形式为：\[ x(t) = X \sin(\omega t + \phi) \]其中，振幅X和相位角φ可以通过以下公式计算：\[ X = \frac{F_0}{\sqrt{(\omega^2 m - \omega^2)^2 +(c\omega)^2}} \]\[ \phi = \arctan\left(\frac{c\omega}{\omega^2 m -\omega^2}\right) \]习题2：多自由度系统的模态分析考虑一个两自由度系统，其质量矩阵、刚度矩阵和阻尼矩阵分别为：\[ M = \begin{bmatrix} m_1 & 0 \\ 0 & m_2 \end{bmatrix},\quad K = \begin{bmatrix} k_1 & k_c \\ k_c & k_2\end{bmatrix}, \quad C = \begin{bmatrix} c_1 & 0 \\ 0 & c_2\end{bmatrix} \]求系统的自然频率和模态形状。
克拉夫《结构动力学》习题答案汇总
第二章 自由振动分析2-1（a ） 由例22T π=22()W K T gπ= 因此 max ()()D t kT νν= 其中 k=0、1、2……T D =0.64sec 如果ξ 很小，T D =T∴ 222200()49.9/0.64sec 386/sec kipsk kips in in π==⇒ 50/k kips in = （b ）211lnln n n v v v v δ+≡=δξ=→=1.2ln 0.3330.86δ==0.0529ξ==0.33320.05302δπξξπ=→==⇒ 5.3%ξ= (a ’)D ω=2T πω=T T =249.950/1k kips in ξ==- (c)2c m ξω=W m g=2T πω=4c T gπωξ=T T =241W c Tg πξξ=- 2240.05292000.64sec386/sec 10.0529kipsc in π=-0.539sec/c kips in =⋅ T=T D0.538sec/c kips in =⋅ ⇒0.54sec/c kips in =⋅2-22k mω=→4.47ω== (1/sec ) (0)(0)()sin (0)cos tD D Dv v t et v t ξωξωνωωω-⎡⎤⎛⎫+⎢⎥ ⎪=+⎢⎥ ⎪⎝⎭⎣⎦∴ (0)(0)()sin (0)(0)(0))cos t D D D v v t e t v v v t ξωξωνξωωξωξωωω-⎛⎫⎡⎤+⎧⎫⎡⎤ ⎪⎢⎥=-++-⎨⎬⎢⎥ ⎪⎢⎥⎣⎦⎩⎭⎣⎦⎝⎭()22(0)(0)()(0)cos sin D t D D Dv v t e v t t ξωξωξωωνωωω-⎛⎫⎡⎤++ ⎪⎣⎦=- ⎪ ⎪⎝⎭D ω=→()(0)cos (0)(0)sin t D D D t e v t v v t ξωωνωξωωω-⎛⎫⎡⎤=-+ ⎪⎢⎥⎣⎦⎝⎭()(0)cos tD D t ev t t ξωνωω-⎛⎫⎪= ⎪⎝⎭0.055922(2)(4.47)c cc m ξω=== (a) c=0→0ξ=→D ωω=∴ 5.6(1)sin 4.470.7cos 4.47 1.384.47v t in ==+=- (1) 5.6cos 4.47 4.47(0.7)sin 4.47 1.69/sec v t in ==-=⇒(1) 1.4v in =-,(1) 1.7/sec v in = (b)c=2.8→0.0559(2.8)0.157ξ==4.41D ω== (1/sec ) (0.157)(4.41)5.60.7(0.157)(4.47)(1)sin 4.410.7cos 4.414.41t e ν-⎡+⎤⎛⎫==+⎪⎢⎥⎝⎭⎣⎦(1)0.764t in ν==-(0.157)(4.41)(1) 5.6cos 4.41 4.41t e ν-⎛⎫== ⎪⎝⎭(1) 1.10/sec t in ν==⇒(1)0.76v in =-,(1) 1.1/sec v in =第三章 谐振荷载反应3-1根据公式有 ()()21sin sin 1R t w t wt ββ⎡⎤=-⎢⎥-⎣⎦0.8wwβ== ()()2.778sin 0.8sin1.25R t wt wt=-将t ω以80°为增量计算)(t R 并绘制曲线如下：80° 160° 240° 320° 400° 480° 560° 640° 720° 800° 00.547 1.71 -0.481 -3.214 0.357 4.33 -0.19 -4.9244.9241.25w w =tω)(t R3-2解：由题意得：22m kips s in =⋅ ， 20k kips in = ， (0)(0)0v v == ，w w =3.162w rad ===8wt π=（a ）0c =()()1sin cos 2R t wt wt wt =-将8wt π=代入上式得：()412.566R t π=-=- （b ）0.5c k s =⋅0.50.0395222 3.162c c c c mw ξ====⨯⨯()()(){}1exp 1cos exp sin 2R t wt wt wt wt ξξξξ=--+-⎡⎤⎡⎤⎣⎦⎣⎦将8wt π=代入上式得：()7.967R t =- （c ） 2.0c k s =⋅2.00.1582223.162c c c c mw ξ====⨯⨯()()(){}1exp 1cos exp sin 2R t wt wt wt wt ξξξξ=--+-⎡⎤⎡⎤⎣⎦⎣⎦将8wt π=代入上式得：() 3.105R t =-3-3解：（a ）：依据共振条件可知：10.983sec w w rad =====由2L T V w π==得：10.9833662.96022wL V ft s ππ⨯===（b ）：()()()122max2221212tgo v v ξββξβ⎡⎤+⎢⎥=⎢⎥-+⎣⎦1w w β==0.4ξ= 1.2go v in =代入公式可得：max 1.921tv in =（c ）：2L T V w π=='45min 66V h ft s ==226611.51336V w rad s ec L ππ⨯'===11.5131.04810.983w w β'===0.4ξ=代入数据得 ：()()()122max22212=1.85512tgov v in ξββξβ⎡⎤+⎢⎥=⎢⎥-+⎣⎦3-4解：按照实际情况，当设计一个隔振系统时，将使其在高于临界频率比β=在这种情况下，隔振体系可能有小的阻尼。
结构力学动力计算习题
m
m l l l
练习题 .按先处理法求图示连续梁的刚度方程 8 .按先处理法求图示连续梁的刚度方程 (不
考虑梁的轴向变形）。 考虑梁的轴向变形）。
2kN 5 k N .m
1 2EI 2 EI
4kN 1 2 k N /m
3 EI 4
4m
4m
4m
练习题
9. 求图示结构各元的杆端力，并画出内力图。 求图示结构各元的杆端力，并画出内力图。
E = 10 kN m , θ = 20s , 5 3 k = 3 × 10 N/m, P = 5 × 10 N, W = 9.8kN
5 2 -1
Psinθ t
W 2m 2m
k
练习题 图示刚架杆自重不计，各杆EI=常数。 EI=常数 7. 图示刚架杆自重不计，各杆EI=常数。求自 振频率及振型，并画出振型图。 振频率及振型，并画出振型图。
练习题 10. 按后处理法求图示结构的结点荷载列阵 。 按后处理法求图示结构的结点荷载列阵{P}。 各杆EI=常数。 常数。 各杆 常数
4 kN 5 kN 2 6 kN /m 1
2 0 kN. m 3
4 3 kN
6
5
4m
4m
4m
m1
EI
l
m2
2EI 2EI l
练习题
5. 图示三铰刚架各杆 图示三铰刚架各杆EI=常数，杆自重不计。 常数， 常数 杆自重不计。
求自振频率与主振型。 求自振频率法。 用柔度法。
练习题
3
f11 = 1 × ( 1 × l × l × 2 × l ) × 4 = l EI 2 2 3 2 3EI l3 f 22 = f11 = f12 = f 21 = 0 3EI
结构动力学【习题课】(单自由度体系1)
EI l
m
4.图 所示结构周期为T 则图b 4.图a所示结构周期为Ti,则图b所示体系的周期为
T =
T1 + T + T
2 2 2
2 3
ki m
k1 k2 k3 m
(a) 5.图示体系的自振频率为 5.图示体系的自振频率为 .
(b)
EI = ∞ k
l l
m
6.图示体系的动力自由度为5. 6.图示体系的动力自由度为5. 图示体系的动力自由度为 EI=常数
第1 、2 章
小结 动力特性计算 公式法 能量守恒 幅值方程 动力反应计算 简谐荷载 周期荷载 阶跃荷载 冲击荷载 一般荷载
动荷载及其分类 自由度及其确定 运动方程的建立 惯性力法 虚功法 运动方程的求解方法 经典解法 频域解法 时域解法 数值解法 确定动力特性的试验方法 阻尼力假定及阻尼的影响
1.若使单自由度体系的阻尼增大,其结果是周期变短. 1.若使单自由度体系的阻尼增大,其结果是周期变短. 若使单自由度体系的阻尼增大 错
EA = ∞
7.体系的振幅和自振频率与初始条件有关. 7.体系的振幅和自振频率与初始条件有关. 体系的振幅和自振频率与初始条件有关
8.在图示体系中,若要使其自振频率增大,可以 8.在图示体系中,若要使其自振频率增大, 在图示体系中 A.增大 ; A.增大P; 增大 C.增大 ; C.增大m; 增大 B.增大EI; B.增大EI; 增大 D.增大 l . D.增大
ωD = ω 1−ξ 2
&& + 2ξω y + ω 2 y = P ( t ) / m & y
)
2.单自度体系运动方程为 2.单自度体系运动方程为 其中未考虑质体重力,这是因为( 其中未考虑质体重力,这是因为(
中国大学MOOC结构动力学习题含答案-精品
中国大学MOOC结构动力学习题（含答案）1、忽略杆件的轴向变形和分布质量，图示结构动力自由度的个数（）oA、1B、2C、3D、4答案：22、忽略杆件的轴向变形和分布质量，图示结构动力自由度的个数（）oA、1B、2C、3D、4答案：23、忽略杆件的轴向变形和分布质量，图示结构动力自由度的个数（）oA、0B、1C、2D、3答案：24、在很短时间内，荷载值急剧增大或急剧减小的荷载是（）oA、可变荷载B、偶然荷载C、冲击荷载D、爆炸答案：冲击荷载5、动力自由度的个数（）集中质量的个数。
图所示刚架结构，不计分布质量，动力自由度个数为（）o 此题为多项选择题。
请帮忙给出正确答案和分析，谢谢! •日目•2EI:一.c（A）2个（B）3个（C）4个（D）5个答案：B自由度个数有3个，因此正确答案为（B）。
1、一、单项选择题（每题2分，共6分）答案：ABDAC二.实验探究题（共20分）2、二、填空题（每题2分，共4分）1.相比静力计算，动力计算列平衡方程时，在所考虑的力系中要包括。
2. 爆炸荷载属于。
答案：1、从力系平衡角度建立自由振动微分方程的方法是（）oA、刚度法B、柔度法C、静力法D、动力法答案：刚度法2、忽略杆件的轴向变形和均布质量，各图质点的质量、杆长、质点位置相同，杆件EI相同且为常数。
结构自振频率最大的是（）oA、coaB、3bC、3cD、3d答案：3a3、与单自由度体系自由振动的频率有关的量是（）oA、初速度vOB、初位移yOC、相位角aD、质量m答案：阻尼越大，振幅越大4、按照GB50009-2012《建筑结构荷载规范》，高度为2001Tl的高耸钢筋混凝土结构的基本周期一般为（）0A、0.14sB、1.4sC、14sD、140s答案：1.4s5、yst是指（）oA.自然伽码与电阻率B.方位与井斜C.工具与井斜D.工具面与方位答案：A1、一、填空题（每题5分，共20分）答案：【计分规贝"：Am=K/c2.72X10-268.41X10- 4437.82X10-4；145.94X10-42、二、计算题（每题20分，共80分）答案：【计分规则】：一、回答问题（每题2分、共10分）二、分析（每题10分、共30分）三、计算题（第1题40分, 第2题20分、共60分）1、当。
结构动力学习题
第九章 结构动力计算一、是非题1、结构计算中，大小、方向随时间变化的荷载必须按动荷载考虑。
2、忽略直杆的轴向变形，图示结构的动力自由度为4个。
3、仅在恢复力作用下的振动称为自由振动。
4、单自由度体系其它参数不变，只有刚度EI 增大到原来的2倍，则周期比原来的周期减小1/2。
5、图 a 体 系 的 自 振 频 率 比 图 b 的 小 。
l /2l /2l /2l /2(a)(b)6、单 自 由 度 体 系 如 图 ，W =98.kN ，欲 使 顶 端 产 生 水平 位 移 ∆=001.m ，需 加 水 平 力 P =16kN ，则 体 系 的 自振 频 率 ω=-40s 1。
∆7、结构在动力荷载作用下，其动内力与动位移仅与动力荷载的变化规律有关。
8、由于阻尼的存在，任何振动都不会长期继续下去。
9、桁 架 ABC 在 C 结 点 处 有 重 物 W ，杆 重 不 计 ，EA 为 常 数 ，在 C 点 的 竖 向 初 位 移 干 扰 下 ，W 将 作 竖 向 自 由 振 动 。
AC10、不 计 阻 尼 时 ，图 示 体 系 的 运 动 方 程 为 ：m m X X h EI EI EI EI X X P t 00148242424012312⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭+--⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭=⎧⎨⎩⎫⎬⎭()二、选择题1、图 示 体 系 ，质 点 的 运 动 方 程为 ：A ．()()()y l P s in m y EI =-77683θ t /；B ．()()m y EI y lP s in /+=19273θ t ；C ．()()m y EI y l P s in /+=38473θ t ；D ．()()()y l P s in m y EI =-7963θ t / 。
ll0.50.52、在 图 示 结 构 中 ，若 要 使 其 自 振 频 率 ω增 大 ，可 以A ．增 大 P ；B ．增 大 m ；C ．增 大 E I ； D ．增 大 l 。
结构动力学习题答案
结构动力学习题答案结构动力学学习题答案结构动力学是一门研究结构在外部力作用下的运动和响应的学科。
在学习结构动力学时，学生通常会遇到各种各样的学习题，这些学习题既考验了学生对知识的掌握程度，又帮助他们加深对结构动力学理论的理解。
下面我们就来看一些结构动力学学习题的答案。
1. 什么是结构动力学？结构动力学是研究结构在外部力作用下的振动特性和响应的学科。
它主要研究结构在地震、风载等外部力作用下的动力响应，以及结构的振动特性和控制。
2. 结构的自由振动频率如何计算？结构的自由振动频率可以通过结构的刚度矩阵和质量矩阵来计算。
首先需要求解结构的特征值和特征向量，然后根据特征值来计算结构的自由振动频率。
3. 结构的阻尼比对结构动力学有什么影响？阻尼比是衡量结构在振动过程中能量损失的比例。
阻尼比越大，结构的振动响应越快速衰减；阻尼比越小，结构的振动响应越慢。
因此，阻尼比对结构的振动特性和稳定性有着重要的影响。
4. 结构的地震响应如何进行分析？结构的地震响应可以通过有限元分析、时程分析和频率响应分析等方法进行。
这些方法可以帮助工程师评估结构在地震作用下的受力情况，从而指导结构的设计和加固。
5. 结构的振动控制方法有哪些？结构的振动控制方法包括主动控制、被动控制和半主动控制等。
主动控制是通过外部激励来控制结构的振动；被动控制是通过阻尼器、减震器等被动装置来控制结构的振动；半主动控制则是结合了主动和被动控制的特点，通过智能控制系统来控制结构的振动。
通过以上学习题的答案，我们可以看到结构动力学是一个复杂而又有趣的学科，它涉及到结构的振动特性、动力响应和振动控制等多个方面。
通过对这些学习题的学习和理解，我们可以更好地掌握结构动力学的理论知识，为今后的工程实践打下坚实的基础。
龙驭球《结构力学Ⅱ》配套题库-课后习题(结构动力计算续论)【圣才出品】
第15章结构动力计算续论15-1 试求图示体系的第一频率和第一主振型。
各杆EI相同。
图15-1解：第一频率和第一主振型，发生在反对称荷载情况下。
所以取半边结构，如图（a）所示，横梁上的质量为，下求柔度系数。
图15-2对应质量集中点，施加单位力，作出图，用图乘法求出相应的柔度系数，第一频率为，振型为15-2 试求图示三层刚架的自振频率和主振型，设楼面质量分别为m1=270 t，m2=270 t，m3=180 t；各层的侧移刚度分别为k1=245 MN／m，k2=196 MN／m，k3=98 MN／m；横梁刚度为无限大。
图15-3解：采用刚度法求解由振动控制方程，由可得，，，三层刚架的自振频率为即三层刚架的主振型为(2)(0.667,0.667,1.000)TY=--15-3 设在题15-2的三层刚架的第二层作用一水平干扰力F P(t)：20 kN．sinθr,每分钟振动200次。
试求图示各楼层的振幅值。
图15-4 解：由题意可知，计算，荷载幅值向量为所以解方程，得到振幅向量为：15-4 试用振型叠加法重做题l0-23。
解：（1）由题10-23得到：，，设频率方程为解得，。
从而（2）求主振型由上述的计算结果，（3）建立广义坐标体系（4）计算广义质量和广义荷载（5）求正则坐标（6）求楼层振幅15-5 设在题10—22的两层刚架二层楼面处沿水平方向作用一突加荷载F P，试用振型叠加法求第一、二层楼面处的振幅值和柱端弯矩的幅值。
解：由题10-22可知，且在突加荷载作用下的广义荷载为求正则坐标求质点位移。
结构动力学练习题
结构动力学练习题作业一图示L 型刚架，其单长质量m ，BA ，BC 两杆EI = ∞，刚架所受荷载及约束见题图,试求广义单自由度系统的*m ，*k ， *c ，)(*t F ，写出其运动方程。
解：取BA 的节点A 的转角Y 为基本未知量，则其他各力处相应的位移均可用Y 表示，各个力亦可用Y 及其导数表示。
（题目中力和位移均为广义力和广义位移），各力的表达式：*22d F c l Y = *2s F kl Y =*222240(())lIdr F JY m d m r r d Y d πρρθθ==++⎰⎰33331(2)347()34ml ml ml Y ml Y ππ=+-=-其中θcos lr =。
*201()()()()6lx F t pf t l x dx pl f t l =-=⎰ 由直接平衡法得钢架的运动方程为：322231()2()746ml Y cl Y kl Y pl f t π-++= 简化为：****()m Y c Y k Y F t ++=其中：3*)473(l m m π-=*2*22c cl k kl ==)(61)(2*t f pl t F =作业二试确定图示体系的广义物理特性***,,k c m 和广义荷载)(*t P ，这些特性都根据位移坐标)(t z 定义，计算结果用所给物理特性及尺寸表达。
解：以)(t z 为基本变量，其他各力处相应的位移均可用)(t z 表示，各力亦可用)(t z 及其导数表示。
2211()228o l J m ml ==2()/o z t l α=11()()()2o o F kz t J kz t mz t α=+=+'111()()2F F kz t mz t ==+221(3)33A J m l ml ==()3A z t lα=()I F A A M J mlz t α==()33()d M cz t l lcz t =⨯='133()()2F M lkz t mlcz t =+ 22()0()2()lP t M P t xdx P t l ==⎰由直接平衡法可得：'1()FI d P t F M M M M +=+223()3()3()()2()21()3()3()2()2mlz t lcz t lkz t mlz t P t l mlz t lcz t lkz t P t l +=++-+-=简化为：****()()()()m z tc z t k z t P t ++=其中：****21323()2()m mlc lc k lkP t P t l =-==-=作业三试计算图示结构集中质体处作无阻尼受迫振动的振幅值。
《结构动力学》-第0章-习题课
《例》一质量为M、半径为r的均质实心圆柱体在质 量为m的车子上无滑动地滚动。车辆用弹簧常数为 k1、k 2的弹簧连接，并在水平表面自由滑动。用拉 格朗日方程求系统的运动微分方程。
解：系统的动能为
1 2 1 1 2 1 Mx2 J OO 2 T mx 2 2 2
1 J O Mr 2 2 x2 x1 O r
利用频率方程 k 2 m 0 ，令行列式
50 20 0.10 2 0 2020 00.1
图 二自由度结构
2 展开行列式，解 4 700 2 6000 0 ；得 12 100,2 600 ；
2 mg k
重力作用下质量m的静位移是
L3 1 1 2 mg ( ) 3EI k
或者悬臂梁与弹簧是 串联系统
系统的固有频率为
2 n
g 3kEI m(k L3 3EI )
《例》 如图所示系统，绳索一端接一质量 m，另一端绕过一转动惯量为J的滑轮与弹 簧相接，弹簧的另一端固定。设绳索无伸 长，绳索与滑轮之间无滑动。求该系统的 固有频率。 解：系统的势能为 系统的动能为
m c( x y) k ( x y) x
或用相对位移z描述的运动微分方程：
m c z k z m z y
令 y Ae i t 代入得
c z k z m A 2 e i t mz
方程的解为：
z Ze
i ( t )
《例》 如图所示，一弹簧质量系统从一倾斜角为30º的光滑 斜面下滑。求弹簧与墙壁开始接触到脱离接触的时间。
《例》列出图示系统运动微分方程。
《例》重量G=35kN的发电机置于简支梁的中点上（如图 1），已知梁的惯性矩I=0.000088m4，E=210GPa，发电机 转动时其离心力的垂直分量为Fsinωt，且F=10kN。若不 考虑阻尼，试求当发电机每分钟的转数为n=500r/min时， 梁的最大弯矩和挠度（梁的自重可略去不计）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
160结构动力计算习题一．选择题8-1 体系的动力自由度是指（ ）。
A ．体系中独立的质点位移个数B ．体系中结点的个数C ．体系中质点的个数D ．体系中独立的结点位移的个数 8-2 下列说法中错误的是（ ）。
A ．质点是一个具有质量的几何点；B ．大小、方向作用点随时间变化的荷载均为动荷载；C ．阻尼是耗散能量的作用；D ．加在质点上的惯性力，对质点来说并不存在 8-3 图示体系EI =常数，不计杆件分布质量，动力自由度相同的为（ ）。
题8-3图A ．（a ）、（b ）、（c ）B ．（a ）、（b ）C ．（b ）、（c ）D ．（a ）、（c ） 8-4图示体系不计杆件分布质量，动力自由度相同的为（ ）。
(b )(c )题8-4图A ．（a ）、（b ）、（c ）B ．（a ）、（b ）C ．（b ）、（c ）D ．（a ）、（c ）8-5 若要提高单自由度体系的自振频率，需要（ ）。
A ．增大体系的刚度B ．增大体系的质量C ．增大体系的初速度D ．增大体系的初位移 8-6不计阻尼影响时，下面说法中错误的是（ ）。
A ．自振周期与初位移、初速度无关；B ．自由振动中，当质点位移最大时，质点速度为零；C ．自由振动中，质点位移与惯性力同时达到最大值；D ．自由振动的振幅与质量、刚度无关 8-7 若结构的自振周期为T ，当受动荷载)(P t F =t F θsin 0作用时，其自振周期T （ ）。
A ．将延长B ．将缩短C ．不变D ．与荷载频率θ的大小有关8-8 若图（a ）、（b ）和（c ）所示体系的自振周期分别为a T 、b T 和c T ，则它们的关系为（ ）。
(a)(b)(c)题8-8图A ．a T >b T >c TB ．a T >c T >b TC ．a T <c T <b TD ．a T =c T <b T 8-9 振幅计算公式βst y A =中的st y 为（ ）。
A ．结构上的静荷载引起的位移；B ．动荷载幅值作为静荷载引起的位移；C ．惯性力幅值引起的位移；D ．结构上的动荷载引起的位移 8-10 对于简谐荷载作用情况，下面说法正确的是（ ）。
161A ．动力系数一定大于1；B ．计阻尼时的动力系数比不计阻尼的大；C ．动力系数等于振幅除以荷载幅值作为静荷载引起的静位移；D ．增大频比会使动力系数减小8-11 多自由度体系的自振频率和振型取决于（ ）。
A ．体系的初位移B ．体系的初速度C ．体系的初位移和初速度D ．体系的质量和刚度 8-12 下面说法中，正确的一项是（ ）。
A ．与单自由度体系一样，多自由度体系中也有这样的关系11111/δk =B ．对称体系的振型均为对称振型C ．按振型作自由振动时，各质点速度的比值与各质点位移的比值相同D ．多自由度体系作自由振动时，各质点的位移比值不随时间变化 8-13 图示对称体系有（ ）题8-13图A ．一个对称振型和一个反对称振型；B ．一个对称振型和两个反对称振型；C ．两个对称振型和一个反对称振型；D ．两个对称振型和两个反对称振型 8-14 下面说法中，错误的一项是（ ）。
A ．两个自由度体系有两个发生共振的可能状态；B ．受同频同相位的简谐荷载作用的多自由度体系（不计阻尼），在平稳阶段动荷载与位移同时达到幅值；C ．分析多自由度体系在简谐荷载作用下的动力反应时可不计阻尼影响；D ．简谐荷载作用下，多自由度体系上各点的位移动力系数不同 8-15 下面说法中，错误的一项是（ ）。
A ．能量法得到的基本频率一定大于或等于基本频率的精确值；B ．用满足位移边界条件的位移函数代入能量法求基频的公式中一定会得到基频的近似值；C ．能量法是基于能量守恒原理得到的；D ．若已知体系的振型，由能量法公式可求自振频率的精确解。
8-16 图示简支梁，质量分布集度为m ，抗弯刚度为EI ，跨度为l 。
基本振型为（ ）。
A ．图（a ）；B ．图（b ）；C ．图（c ）；D ．图（d ）。
(a)(b)(c)(d)题8-16图8-17 若求题8-16中简支梁的基本频率，应选用的位移函数为（ ）。
A ．x l π2cos1-；B ．x l πcos ；C ．x l π2sin ；D ．x lπsin 。
二．填充题8-18 在动荷载作用下， 力不容忽视，内力和位移是 的函数。
8-19 一台转速为300转/分的机器，开动时对结构的作用相当于一个简谐荷载)(P t F =t F θsin 0，荷载频率为 。
8-20 图示体系的刚度系数为 。
162题8-20图8-21 质量为m ，刚度系数为k 的单自由度体系，初位移0y 引起的自由振动（不计阻尼）的振幅为 。
8-22 图示体系竖向振动的自振频率为 。
题8-22图题8-23图8-23 图示体系的自振频率为 。
8-24 已知图示体系中的弹簧刚度系数3/3l EI k=，体系的自振周期为 。
题8-24图题8-25图8-25已知图示体系中的弹簧刚度系数3/3l EI k =，体系竖向振动的自振周期为 。
8-26 阻尼对单自由度体系自由振动的 影响小，可以不计阻尼；对 影响较大。
8-27 图示体系受静力荷载P F 作用。
当荷载被突然撤去，结构开始振动。
若不计阻尼，质点的振幅为 。
m题8-27图8-28 某单自由度体系受简谐荷载作用，已知荷载频率为结构自振频率的0.5倍，不计阻尼时的动力系数为 。
8-29 简谐荷载作用时，阻尼在 情况下对动力系数的影响不容忽视。
8-30 体系按振型作自由振动时，各质点的振动频率 ，各质点振幅 。
8-31 振型对质量正交的表达式为 ；对刚度正交的表达式为 。
8-32 刚度矩阵与柔度矩阵的关系为 。
8-33 体系按某一振型作自由振动时，各质点位移的大小、方向均随 变化，但它们的不变。
8-34 图示体系的质量矩阵为 。
题8-34图8-35 简谐荷载作用下，体系的平稳振动阶段是指 。
三．计算题8-36 试求图示体系的自振频率和自振周期。
163（a（b）c（d题8-36图8-37 图示简支梁上装有一台重量为35kN 的电机，电机开动时产生的离心力在竖向的分力为)(P t F =t F θsin 0。
已知：0F =10kN ，电机转速为500r/min ；梁的惯性矩48800cm =I ，弹性模量21GPa =E 。
不计梁重，不计阻尼，试求梁的振幅和最大动弯矩。
题8-37图8-38 在图示结构的梁上装有电机，试求电机开动时柱端最大水平位移和最大柱端弯矩。
已知：集中于梁上的结构重量（包括梁、电机以及柱的一部分）为W =20kN ，0F =250N ，电机转速n =550转/分，柱子的线刚度cm N 1088.58⋅⨯=i 。
不计阻尼。
F 8-38图F 8-39图8-39 图示结构受简谐荷载)(P t F =0F sin θt 作用。
已知：m =300kg ，EI 23m kN 100.9⋅⨯=，0F =20kN ，θ=80-1s 。
试求（1）ξ=0，（2）ξ=0.05时平稳阶段质点的最大位移及最大动弯矩图。
8-40 试用柔度法计算图示体系的振型和自振频率。
已知：l =1m ，m m m ==21，mg =1kN ，482cm .68=I ，MPa 1025⨯=E 。
题8-40图题8-41图8-41试用柔度法计算图示体系的振型和自振频率。
已知：m m =1，m m 22=。
8-42 试用柔度法计算图示体系的振型和自振频率。
1648-42图8-43图8-43 试用刚度法计算图示体系的振型和自振频率。
8-44 试求图示体系的振型和自振频率。
已知体系的柔度矩阵为EI l 31/96005/84⎥⎦⎤⎢⎣⎡。
8-44图题8-45图8.45 图示悬臂梁的长度为3m ，惯性矩44cm 104.2⨯=I ，弹性模量24kN/cm 102.1⨯=E 。
梁上装有两台电机，重量均为30kN ，转速为300转/分，产生的离心力为5kN 0=F 。
试求当只有电机2运转时的稳态振幅。
不计梁重，不计阻尼。
8-46图示两层框架结构，已知：100t 1=m ，120t 2=m ，柱的线刚度m 14MN 1⋅=i ，m 20MN 2⋅=i 。
荷载幅值5kN 0=F ，机器转速为150转/分。
试求楼层最大位移。
0F 8-46图8-47 试用能量法计算例题8-8中结构的基本频率。
8-48 另选位移函数重作例题8-15。
参考答案8-1 A ； 8-2 B ；8-3 C ；（a ）3；（b ）2；（c ）2 8-4 C ；（a ）2；（b ）2；（c ）3 8-5 A ； 8-6 D ； 8-7 C ； 8-8 D ； 8-9 B ； 8-10 C ； 8-11 D ； 8-12 C ； 8-13 B ； 8-14 C ； 8-15 B ； 8-16 A ； 8-17 D ； 8-18 惯性，时间 8-19 31.4 rad/s 8-20 3/6l EI 8-210y8-22 )(2121k k m k k +1658-23m k /28-24EIml 623π8-25EIml 3223π8-26 自振周期、频率，振幅8-27EIl F 323P8-28 4/38-29 共振或频比接近1 8-30 相同，比值不变 8-31 0T =j i MY Y )(j i ≠，0T =j i KY Y )(j i ≠8-32I k δ=8-33 时间，比值 8-34⎥⎦⎤⎢⎣⎡m m 200 8-35 按荷载频率振动的阶段8-36 （a ）38ml EI=ω，EI ml T 823π=（b ）324mh EI=ω，EImh T2423π=（c ）343ml EI =ω，EIml T 3423π=（d ）33ml EI =ω，EIml T 323π=8-37m/N 10215.77-⨯=δ，22s /388=ω，22s /78.2738=θ，m 1019.13-⨯=A ，m 65kN .1⋅=M （注意：质量m =W /g ）8-38N/m 1092.36⨯=k ，232s /1092.1⨯=ω，22s /3314=θ，m1082.876-⨯=A ，m N 4.516⋅=M8-39 （1）m 1082.23-⨯=A动玩具图（2）m 1078.23-⨯=A动玩具图8-40 设两个质点的位移向下为正。
rad/s 5.351=ω，rad/s 7.1172=ω ⎭⎬⎫⎩⎨⎧-=16.31Y ，⎭⎬⎫⎩⎨⎧=128.02Y 8-41设两个质点的位移向右为正。
31843.0ml EI =ω，3230.1ml EI =ω⎭⎬⎫⎩⎨⎧-=145.01Y ，⎭⎬⎫⎩⎨⎧=145.42Y 8-423122.1ml EI=ω，3221.8ml EI =ω⎭⎬⎫⎩⎨⎧=1096.01Y ，⎭⎬⎫⎩⎨⎧-=143.102Y 8-43设两个质量的位移向右为正。