等腰三角形、等边三角形的判定(唐基海)
等腰三角形和等边三角形的性质

等腰三角形和等边三角形的性质等腰三角形和等边三角形是基础的几何形状,它们有着特殊的性质和特点。
在本文中,我们将一起探讨等腰三角形和等边三角形的性质,并分析它们在几何学中的重要性。
一、等腰三角形的性质等腰三角形是指具有两条边相等的三角形。
以下是等腰三角形的主要性质:1. 两底角相等:等腰三角形的底边是两边相等的边,因此,其对应的底角相等。
即∠A = ∠C,其中A、C为等腰三角形的两个底角。
2. 顶角平分底角:等腰三角形的顶角恰好平分了底角。
也就是说,等腰三角形的顶角∠B恰好等于底角∠A和∠C的一半。
3. 等腰三角形的高线:等腰三角形的高线是连接顶点与底边垂直的线段。
在等腰三角形ABC中,高线BD垂直于底边AC,并且BD是AC的中线(即BD=DC)。
4. 等腰三角形的中线:等腰三角形中线是分别连接底边中点与顶点的线段。
在等腰三角形ABC中,中线BE与底边AC相等(即BE=EC)。
二、等边三角形的性质等边三角形是指三条边相等的三角形。
以下是等边三角形的主要性质:1. 三个内角相等:等边三角形的三个内角都相等,即∠A = ∠B =∠C = 60°。
2. 三条高线重合:等边三角形的三条高线分别由顶点向底边上的三个顶点所引。
这三条高线相交于同一个点,也就是等边三角形的垂心。
3. 等边三角形的中线:等边三角形的中线是分别连接底边中点与顶点的线段,也就是等边三角形的高线。
由于等边三角形的三边相等,中线也为等边三角形三边的中线。
三、等腰三角形和等边三角形的重要性等腰三角形和等边三角形在几何学中具有重要的应用和特点。
以下是它们的一些重要性:1. 判定等腰三角形:利用等腰三角形的性质,我们可以通过两条边的长度相等来判定一个三角形是否为等腰三角形。
2. 判定等边三角形:等边三角形的三条边相等,因此,我们可以通过三条边的长度相等来判定一个三角形是否为等边三角形。
3. 等腰三角形的应用:等腰三角形的性质常常应用在各类数学问题中,如三角函数、三角恒等式、三角面积等计算中。
等腰三角形与等边三角形

等腰三角形与等边三角形三角形是几何学中最基本的图形之一,具有许多有趣的性质和特征。
其中,等腰三角形和等边三角形是两种特殊的三角形,它们各自具有独特的性质和特点。
在本文中,我们将探讨等腰三角形和等边三角形的定义、性质以及它们与普通三角形之间的关系。
一、等腰三角形等腰三角形是指具有两条边相等的三角形。
换句话说,等腰三角形的两个底角相等。
例如,在一个三角形ABC中,如果边AB和边AC相等,那么这个三角形就是一个等腰三角形。
等腰三角形通常可以通过画一条中线或高的方式进行辅助辨识,因为中线和高可以将等腰三角形分成两个等腰三角形或两个全等的直角三角形。
等腰三角形具有一些独特的性质。
首先,等腰三角形的顶角(即顶点对应的角)等于两个底角之和,也就是说,如果∠A=∠B,那么∠C=2∠A。
其次,等腰三角形的两个底角相等,如果∠B=∠C,那么边AB=边AC。
二、等边三角形等边三角形是指三条边相等的三角形。
在一个等边三角形ABC中,边AB、边BC和边AC都相等。
等边三角形同时也是等腰三角形,因为它的两个底角相等。
等边三角形具有一些独特的性质。
首先,等边三角形的三个内角都是60度。
其次,等边三角形是对称的,可以通过任意一个高或任意一条中线进行折叠,将三角形的三个顶点都叠在一起。
三、等腰三角形与等边三角形的关系等腰三角形与等边三角形之间存在一种特殊的关系。
事实上,等边三角形是一种特殊的等腰三角形,它的两个底角都是60度,等于等边三角形的顶角。
在几何图形中,我们可以通过构造等边三角形来证明一些等腰三角形的性质。
例如,如果我们知道一个等腰三角形的两个底角相等,我们可以通过构造一个等边三角形,从而得出这个等腰三角形的两个底角都等于60度。
此外,等腰三角形也可以通过构造来证明等边三角形。
如果我们知道一个等腰三角形的两个底角都等于60度,我们可以通过构造一条辅助线来将等腰三角形分成两个等边三角形,从而得出这个等腰三角形的三条边都相等。
等腰三角形与等边三角形的性质

等边三角形1.等边三角形的性质:三边相等;三角都是60°;三边上的中线、高、角平分线相等2.等边三角形的判定:三个角都相等的三角形是等边三角形;有一个角是60°的等腰三角形是等边三角形;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半注意:推论1是判定一个三角形为等边三角形的一个重要方法.推论2说明在等腰三角形中,只要有一个角是600,不论这个角是顶角还是底角,就可以判定这个三角形是等边三角形。
推论3反映的是直角三角形中边与角之间的关系.3.由学生解答课本148页的例子;4.补充:已知如图所示, 在△ABC 中, BD 是AC 边上的中线, DB ⊥BC 于B, ∠ABC=120o , 求证: AB=2BC分析 由已知条件可得∠ABD=30o , 如能构造有一个锐角是30o 的直角三角形, 斜边是AB,30o 角所对的边是与BC 相等的线段,问题就得到解决了.证明: 过A 作AE ∥BC 交BD 的延长线于E∵DB ⊥BC(已知)∴∠AED=90o (两直线平行内错角相等)在△ADE 和△CDB 中⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(已知对顶角相等已证CD AD BDC ADE CBD E∴△ADE ≌△CDB(AAS)∴AE=CB(全等三角形的对应边相等)∵∠ABC=120o ,DB ⊥BC(已知)∴∠ABD=30o在Rt △ABE 中,∠ABD=30o∴AE=21AB(在直角三角形中,如果一个锐角等于30o , 那么它所对的直角边等于斜边的一半) B∴BC=21AB 即AB=2BC 点评 本题还可过C 作CE ∥AB5、训练:如图所示,在等边△ABC 的边的延长线上取一点E,以CE 为边作等边△CDE,使它与△ABC 位于直线AE 的同一侧,点M 为线段AD 的中点,点N 为线段BE 的中点,求证:△CNM 是等边三角形.分析 由已知易证明△ADC ≌△BEC,得BE=AD,∠EBC=∠DAE,而M 、N 分别为BE 、AD 的中点,于是有BN=AM ,要证明△CNM 是等边三角形,只须证MC=CN ,∠MCN=60o ,所以要证△NBC ≌△MAC ,由上述已推出的结论,根据边角边公里,可证得△NBC ≌△MAC证明:∵等边△ABC 和等边△DCE ,∴BC=AC ,CD=CE ,(等边三角形的边相等)∠BCA=∠DCE=60o (等边三角形的每个角都是60)∴∠BCE=∠DCA∴△BCE ≌△ACD (SAS )∴∠EBC=∠DAC (全等三角形的对应角相等)BE=AD (全等三角形的对应边相等)又∵BN=21BE ,AM=21AD (中点定义) ∴BN=AM∴△NBC ≌△MAC (SAS )∴CM=CN (全等三角形的对应边相等)∠ACM=∠BCN (全等三角形的对应角相等)∴∠MCN=∠ACB=60o∴△MCN 为等边三角形(有一个角等于60o 的等腰三角形是等边三角形)。
等边三角形的判定

A
∴ AB=AC,(等角对等边).
∴AB=BC=AC(等式性质). ∴ △ABC是等边三角形(等边三角形意义)
归纳:
定理:三个角都相等的三角形是等边三角形 A
在△ABC中, ′
∵∠A=∠B=∠C(已知), ∴△ABC是等边三角形 B C
(三个角都相等的三角形是等边三角形).
练一练:
已知:如图,△ABC是等边三角 形,DE∥BC,分别交AB,AC于点D,E. 求证: △ADE是等边三角形. 证明:∵△ABC等边三角形(已知), ∴ ∠A=∠B=∠A=600(已知), 又∵ DE∥BC(已知), B D 1
练一练:
1。房梁的一部分如图所示,其中 BC⊥AC,∠A=300,AB=7.4m,点D是AB的中点,DE⊥AC,垂 D 足为E.
B
求:BC,DE的长.
解:∵BC⊥AC,∠A=300,AB=7.4m(已知),
A
300
E
C
∴ BC=AB/2=7.4÷2=3.7(在直角三角形中, 如果有一个锐角等 于300,那么它所对的直角边等于斜边的一半), 又∵ AD=AB/2=7.4÷2=3.7(中点意义), ∴ DE=AD/2=3.7÷2=1.85(在直角三角形中, 如果有一个锐 角等于300,那么它所对的直角边等于斜边的一半). 答:BC=3.7m,DE=1.85m. 老师提示:对于含300角的直角三角形边之间,角之间的关系要作为常 识去认可.
第4课时
等边三角形
温故知新:
等腰三角形:
性质定理:
等腰三角形的两个底角相等,简称:等边对等角
推论1: 等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合(三线合一)
推论2: 等腰三角形两底角的平分线、两腰的高线、中线分别相等.
等腰三角形和等边三角形课件

02
等腰三角形的顶角记作$angle
A$,底角记作$angle
B$和
$angle C$。
性质
等腰三角形是轴对称 图形,有一条对称轴 ,即高线所在的直线 。
等腰三角形的三线合 一,即中线、垂线和 角平分线三线重合。
等腰三角形的两底角 相等,记作$angle B = angle C$。
等腰三角形的判定
巧。
中学数学竞赛
在中学数学竞赛中,等腰三角形和 等边三角形也是常见的考察内容, 旨在提高学生的数学素养和思维能 力。
大学生数学竞赛
在大学生数学竞赛中,等腰三角形 和等边三角形也经常出现,涉及的 知识点包括几何学、三角学和解析 几何等。
05
练习题与答案解析
基础练习题
题目1
一个等腰三角形的顶角是 70度,求它的底角?
等腰三角形和等 边三角形课件
汇报人: 202X-12-26
目录
• 等腰三角形的定义与性质 • 等边三角形的定义与性质 • 等腰三角形与等边三角形的异同
点 • 等腰三角形和等边三角形的实际
应用 • 练习题与答案解析
01
等腰三角形定义与性质
定义
01
等腰三角形是两边相等的三角形 ,记作$bigtriangleup ABC$, 其中$AB = AC$。
题目2
一个等腰三角形的底角是 45度,求它的顶角?
题目3
一个等腰三角形的两条腰 长为5厘米,求它的周长?
进阶练习题
题目4
一个等边三角形的边长为6厘米,求它的面积?
题目5
一个等边三角形的面积为15平方厘米,求它的边长?
题目6
一个等腰三角形的一个底角是60度,求它的顶角?
等腰三角形和等边三角形的判定PPT课件
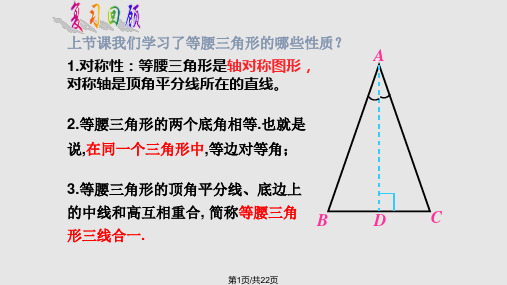
∴ ∠ADE=∠B,∠AED=∠C. (两直线平行,同位角相等)
∴ ∠ADE=∠AED(. 等量代换)
∴ △ADE为等腰三角形. (有两个角相等的三角形是等腰三角形)
第8页/共22页
动脑筋
有一个角是60°的等腰三角 形是等边三角形吗?为什么?
第9页/共22页
如图,在等腰三角形ABC中,
性质
判定
等
A 有两边 1.两腰相等
1.两边相等
腰
相等的
三
三角形 2.两底角相等 2.两角相等
角
是等腰
形 B
C 三角形 3. “三线合一”
4.是轴对称图形
第20页/共22页
等边三角形
名称 图 形 定 义
性质
判定
等
A 三边相 1.三边相等
1.三边相等
边
等的三
三
角形是 2.三角相等
2.三角相等
角 形B
等边三
由此得到等腰三角形的判定定理:
结论
有两个角相等的三角形是等腰三角形 (简称“等角对等边”).
注意:“等边对等角”的前提条件是在同一个三角形中。
A
几何语言表示如下:
在∆ABC中,
∵∠B=∠C
∴AB=AC
第5页/共22页
B
C
巩固练习:下列两个图形是否是等腰三角形?
300
400
400
750
第6页/共22页
结论
由此并且结合三角形内角和定理, 还可以得到等边三角形的判定定理: 三个角都是60°的三角形是等边三角 形。
第7页/共22页
例2 已知:如图,在△ABC中,AB=AC,点D, E分别是AB,AC上的点,且DE∥BC.
等腰三角形与等边三角形的性质知识点总结
等腰三角形与等边三角形的性质知识点总结等腰三角形和等边三角形是我们在初中数学学习中经常遇到的两种特殊三角形。
它们具有一些独特的性质,这些性质对于我们理解三角形的性质和解题都有很大的帮助。
下面将对等腰三角形和等边三角形的性质进行总结和归纳,帮助大家更好地理解和应用这些知识点。
一、等腰三角形的性质1. 定义:等腰三角形是指两边长度相等的三角形。
2. 底角和顶角:等腰三角形的两个底角(底边两侧的角)是相等的,称为底角;顶角是等腰三角形的顶点所对的角,也是两个底角。
3. 对称性质:等腰三角形具有对称性,即等腰三角形可以通过一条对称轴分成两个对称部分。
4. 高度:等腰三角形的高度是从顶点到底边的垂直距离,高度所在的线段与底边垂直,并且把底边分为两个相等的线段。
5. 角平分线:等腰三角形的顶角所在的角平分线同时也是底边的中线和高线。
6. 等腰定理:等腰三角形的两个底角相等。
7. 等腰三角形的面积:等腰三角形的面积可以通过高度和底边的长度来计算,公式为:面积 = 底边长度 ×高度 ÷ 2。
8. 等腰三角形的判定:当我们知道一个三角形的两边相等时,可以判断它是否为等腰三角形。
二、等边三角形的性质1. 定义:等边三角形是指三条边长度都相等的三角形。
2. 角度:等边三角形的三个角都是60度。
3. 高度:等边三角形的高度是从顶点到底边的垂直距离,高度所在的线段与底边垂直。
4. 三角形内角和:等边三角形的三个角的和为180度,因为每个角都是60度,所以三角形的三个角相加为180度。
5. 等边定理:如果一个三角形的三边相等,则它是等边三角形。
6. 等边三角形的面积:等边三角形的面积可以通过边长来计算,公式为:面积 = 边长的平方× √3 ÷ 4。
7. 等边三角形的判定:当我们知道一个三角形的三边相等时,可以判断它是否为等边三角形。
三、等腰三角形与等边三角形的关系1. 等腰三角形也可以是等边三角形:当等腰三角形的两个底角为60度时,它就是等边三角形。
等腰三角形的判定及等边三角形
等腰三角形【知识要点】知识点1 等腰三角形的概念有两条边相等的三角形,叫做等腰三角形,相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.知识点2 等腰三角形的性质性质1:“等边对等角”――等腰三角形的两个底角相等性质2:“三线合一”――等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.知识点3 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).【典型例题】一、等腰三角形的性质例1.已知等腰三角形的一个内角是110°,求另外两个角的度数 . 例2.(1)若等腰三角形的一个内角为40°,则它的顶角为;(2)若等腰三角形的两个内角和为100°,则它的顶角为 .(3)等腰三角形的一个内角是80°,则它的另外两个角为 .例3.等腰三角形的底角与顶角的度数之比为2∶1,则顶角为( )A.72°B.36°C.36°或72°D.18°例4.若等腰三角形的底边长是8cm,腰长是5cm,则这个等腰三角形的周长是( )A.21cmB.18cmC.18cm或21cmD.13cm或26cm例5.如果等腰三角形的三边长均为整数,且它的周长为10cm,那么它的三边长分别为 . 例6.若等腰三角形一腰上的高和另一腰的夹角为25°,则三角形的一个底角是例7.如图所示,在△ABC中,AB=AC=CD,AD=DB,求∠BAC的度数.性质练习1、等腰三角形的两边长分别为6,8,则周长为2、等腰三角形的周长为14,其中一边长为6,则另两边分别为3、等腰三角形的一个角为70°,则另外两个角的度数是4、等腰三角形的一个角为120°则另外两个角的度数是5、如图,在△ABC中,AB=AC,(1)若AD平分∠BAC,那么、(2)若BD=CD,那么、(3)若AD⊥BC,那么、二、等腰三角形的判定例1.如图所示,在△ABC中,AB=AC,AD⊥BC于点D,E是AD延长线上一点,连接BE,CE.求证:等腰△BEC.例2.如图,在△ABC中,AB=AC,AE是∠BAC外角∠DAC的平分线.试判断AE与BC的位置关系.例3.如图,在△ABC中.AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.例4.已知:如图,OA 平分BAC ∠,12 ∠∠.求证:ABC △是等腰三角形.例5.如图,已知点O 是∠ABC ,∠ACB 的平分线的交点,且OD ∥AB ,OE ∥AC. (1)图形中共有哪几个等腰三角形?选一者证明; (2)试说明△ODE 的周长与BC 的关系; (3)若BC=12cm ,则△ODE 的周长 .例6.如图:△ABC 的边AB 的延长线上有一个点D ,过点D 作DF ⊥AC 于F ,交BC 于E ,且BD =BE ,求证:△ABC 为等腰三角形。
等边三角形与等腰三角形
等边三角形与等腰三角形等边三角形和等腰三角形是几何学中常见的两种特殊三角形。
它们具有独特的性质和特点,对于几何学的研究和应用都具有重要意义。
本文将从定义、性质、示例等方面探讨等边三角形与等腰三角形的关系和区别。
一、等边三角形的定义与性质等边三角形是指三个边都相等的三角形。
根据等边三角形的定义,我们可以得出以下性质:1. 三条边相等:在等边三角形中,三条边的长度相等,即AB = BC = CA。
2. 三个内角相等:由于等边三角形的三边相等,按照三角形内角和定理可知,等边三角形的三个内角相等,均为60度。
3. 三个外角相等:等边三角形的三个外角相等,均为120度。
4. 对称性:等边三角形具有对称性,即以任意边为对称轴,可以得到完全相同的图形。
二、等腰三角形的定义与性质等腰三角形是指两边边长相等的三角形。
我们可以从以下角度了解等腰三角形的定义和性质:1. 两边相等:在等腰三角形中,两个边的长度相等,即AB = AC。
2. 两个底角相等:等腰三角形的两个底角(即底边所对的角)相等,可表示为∠B = ∠C。
3. 对称轴:等腰三角形中线对称轴是指通过顶点和底边的中点构成的直线。
等腰三角形具有一条中线对称轴。
4. 高度:等腰三角形的高边是底边的中线,高度刚好将等腰三角形分成两个全等的直角三角形。
三、等边三角形和等腰三角形的关系与区别1. 关系:等边三角形是等腰三角形中的一种特殊情况,即所有等边三角形也是等腰三角形,但不是所有等腰三角形都是等边三角形。
2. 区别:等边三角形的三边边长均相等,而等腰三角形只有两边边长相等;等边三角形的三个内角均相等为60度,而等腰三角形两个底角相等;等边三角形具有三个外角均相等为120度,而等腰三角形没有特定的外角性质。
四、示例1. 等边三角形示例:图1展示了一个等边三角形ABC,其中AB = BC = CA。
[图片]2. 等腰三角形示例:图2展示了一个等腰三角形DEF,其中DE = DF,且∠D = ∠E。
等腰三角形性质和判定怎么判定等腰三角形
等腰三角形性质和判定怎么判定等腰三角形等腰三角形的性质:1.等腰三角形的两个底角相等(简写成“等边对等角”)。
2.等腰三角形的顶角的平分线,底边上的中线,底边上的高的重合。
3.等腰三角形的两底角的平分线相等。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
等腰三角形的性质1.等腰三角形的两个底角相等(简写成“等边对等角”)。
2.等腰三角形的顶角的平分线,底边上的中线,底边上的高的重合。
3.等腰三角形的两底角的平分线相等。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
等腰三角形的判定1.两边相等的三角形为等腰三角形。
2.两底角相等的三角形为等腰三角形。
3.中线和高合一的三角形为等腰三角形。
4.角平分线和高合一的三角形为等腰三角形。
5.一个三角形,底边上的中垂线是同一条线,可以判定是此三角形是等腰三角形。
等腰三角形的公式(1)已知三角形底a,高h,则S=ah/2。
(2)已知三角形三边a,b,c,则(海伦公式)(p=(a+b+c)/2),S=sqrt=sqrt=1/4sqrt(3)已知三角形两边a,b,这两边夹角C,则S=1/2absinC,即两夹边之积乘夹角的正弦值。
(4)设三角形三边分别为a、b、c,内切圆半径为r,则三角形面积=(a+b+c)r/2。
(5)设三角形三边分别为a、b、c,外接圆半径为R,则三角形面积=abc/4R。
等腰三角形的性质的相关例题下列关于等腰三角形的性质叙述错误的是___A.等腰三角形两底角相等B.等腰三角形底边上的高、底边上的中线,顶角的平分线互相重合C.等腰三角形是中心对称图形D.等腰三角形是轴对称图形答案:C解析:A.等腰三角形两底角相等,故本选项正确;B.等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合,故本选项正确;C.等腰三角形不是中心对称图形,故本选项错误;D.等腰三角形是轴对称图形,故本选项正确。
故选C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1,事实上,如图,在△ABC中,∠B=∠C. 沿过点A的直线把∠BAC 对折 , 得∠BAC的平分线AD交BC于点D, 则∠1= . 又∠B=∠C, 由三角形内角和的性质得 ∠ADB=∠ . 1 2 沿AD所在直线折叠, 由于∠ADB=∠ ,∠1=∠ , 所以射线DB与射线 重合, 射线AB与射线 重合. D 从而点B与点 重合, 于是AB=AC.
澧斓中学八年级数学备课组
等腰三角形、等边三角形的 判定
激情导入
我们知道: 等腰三角形的两底角相等. 这是等腰三角形很重要的一条性质. 你知道这个命题的逆命题怎么说吗? 它的逆命题是真命题吗?
学习目标
1、了解等腰三角形和等边三角形的判定方法. 2、会阐述、推证判定方法. 3、经历判定方法的过程.
自 学 提 示
A E B O
5 2 1 43 6
F D
C
当堂测评:
教材65页练习1、2、3
合作探究 例1 已知:如图,在△ABC中,AB=AC,点D,E分别 是AB,AC上的点,且DE∥BC. 求证:△ADE为等腰三角形.
例2 已知:如图,△ABC是等边三角形,点D,E分别在BA,CA的延长 线上,且AD=AE. 求证:△ADE是等边三角形.
合作探究
合作探究 例3 如图,⊿ABC中,∠ACB的平分线交AB于点E,过点E作 FE//BC,交AC于点O,交∠ACD的平分线于点F,求证:EO=FO.
自学提示 2,如图, △ABC中, ∠A= ∠B= ∠C. 求证: △ABC是等边三角形.
3,如图, △ABC中,AB=AC,且∠B=60 °. 求证: △: 1、等腰三角形的判定方法:(1)定义:有 相等 的三角形是等腰三角形;(2)有 相等的三角 形是等腰三角形. 2、等边三角形的判定方法:(1)定义: 相等的 三角形是等边三角形;(2)三个角都是 的三角 形是等边三角形;(3)有一个角是 的 三角 形是等边三角形.
