一种新型的Lagrange非线性规划神经网络
基于Lagrange乘子法神经网络求解弹塑性力学有限元问题

求解线性规划问题 的神经 网络一
T H线性优 化网络 . 它可
-
收稿 E期 :0 ̄ 2 5 t 2 0 一1 —1
Ab ta t s c :Acodn eb sco t zt npicpeo r f i e rl ew r h erl ew r d — r c rigt t ai p miai r il f t ca n ua tok,ten ua tokmo oh i o n ai l i n n e b sdo l ae nL rn mut l ri ue ov eea t pat c a i nt me t rbe ,I i o a lpi sd t slet ls ls cme hncf i de n o l i e s o h  ̄ i i e p ms t sn ln e  ̄ f8yt o vr ie u ly cnt it it q a t n y s c aibe ,w i e u e h o g rn i x o cn et n q a t osr ns no e u ly o e b l k vr ls hc rd c te 8 i a i s a a h s
L i i ,W A n , HA a - u , UA h-i I Ha- n b NG Ha g S NG F h a D N Z i n n x
(col f i c ,ne M no a n e i f Tcnl y oht 10 1 C i ) Sho o S e e Inr ogl U i rt c n i v syo eho g,H ho 005 , h a o n
一种非线性凸优化的神经网络算法

一种非线性凸优化的神经网络算法作者:吴炎翰来源:《科学与财富》2019年第01期摘要:在日常生活、工程应用和研宄数学中,优化问题普遍存在。
对于优化问题的高效求解一直为学者探究,自1986年Hopfield 和Tank 提出优化问题可以利用神经网络求解之后,人们广泛关注并不断研究这样一种高效的优化求解方法[1][4]。
本文在凸优化理论,Lyapunov 稳定性理论的背景前提下,利用Karush-Kuhn-Tucker (KKT)条件转换并构造了一个递归神经网络模型,研究了如何利用神经网络求解含等式与不等式约束条件的凸优化问题。
关键词:递归神经网络;非线性凸优化;KKT条件1 论述凸优化问题和Karush-Kuhn-Tucker(KKT)条件1.1 凸优化,由于其已经证明的性质——局部最优解即为全局最优解——以及拉格朗日对偶性[2]被广泛用于线性回归、插值拟合等问题。
将无法求解或难以求解的优化问题(如Linear-Fractional规划,整数规划)转化为凸优化问题是近年来学者和业界工程师广泛研究并使用的解决手段。
接下来,我们看如下带有等式和不等式(非线性)约束条件的凸优化问题:其中,f(x)是可微凸函数, G(x)≤0 , Hx=0分别是凸优化问题的等式约束条件和不等式约束条件,不失一般性地,令H是一个行满秩矩阵( rank(H)=m1.2 Karush-Kuhn-Tucker(KKT)条件,是非线性优化问题下对Lagrange乘数法的推广。
可以将含等式约束优化问题扩展至含有不等式约束条件的问题。
那么,对于上述凸优化问题,其KKT条件为:定义拉格朗日函数L(x)=f(x)+g(x)Ta+h(x)Tb,若x是该优化问题的一个最优解,那么存在a∈Rm, b∈Rl,使得下面的式子成立:1)aTg(x)=02)L(a,b,x)对x求导为零3)h(x)=02 针对上述凸优化,欲通过神经网络求解,我们需要将其转换为一个动力系统,通过对KKT条件的推导,我们构造了递归神经网络模型:其中y=[y+g(x)]+易证该神经网络动力系统是李雅普诺夫(Lyapunov)稳定的,且可以从任意初始点收敛于上述凸优化的最优解。
拉格朗日神经网络解决带等式和不等式约束的非光滑非凸优化问题

拉格朗日神经网络解决带等式和不等式约束的非光滑非凸优化问题喻昕;许治健;陈昭蓉;徐辰华【摘要】Nonconvex nonsmooth optimization problems are related to many fields of science and engineering applications, which are research hotspots. For the lack of neural network based on early penalty function for nonsmooth optimization problems, a recurrent neural network model is proposed using Lagrange multiplier penalty function to solve the nonconvex nonsmooth optimization problems with equality and inequality constrains. Since the penalty factor in this network model is variable, without calculating initial penalty factor value, the network can still guarantee convergence to the optimal solution, which is more convenient for network computing. Compared with the traditional Lagrange method, the network model adds an equality constraint penalty term, which can improve the convergence ability of the network. Through the detailed analysis, it is proved that the trajectory of the network model can reach the feasible region in finite time and finally converge to the critical point set. In the end, numerical experiments are given to verify the effectiveness of the theoretic results.%非凸非光滑优化问题涉及科学与工程应用的诸多领域,是目前国际上的研究热点.该文针对已有基于早期罚函数神经网络解决非光滑优化问题的不足,借鉴Lagrange乘子罚函数的思想提出一种有效解决带等式和不等式约束的非凸非光滑优化问题的递归神经网络模型.由于该网络模型的罚因子是变量,无需计算罚因子的初始值仍能保证神经网络收敛到优化问题的最优解,因此更加便于网络计算.此外,与传统Lagrange方法不同,该网络模型增加了一个等式约束惩罚项,可以提高网络的收敛能力.通过详细的分析证明了该网络模型的轨迹在有限时间内必进入可行域,且最终收敛于关键点集.最后通过数值实验验证了所提出理论的有效性.【期刊名称】《电子与信息学报》【年(卷),期】2017(039)008【总页数】6页(P1950-1955)【关键词】拉格朗日神经网络;收敛;非凸非光滑优化【作者】喻昕;许治健;陈昭蓉;徐辰华【作者单位】广西大学计算机与电子信息学院南宁 530004;广西大学计算机与电子信息学院南宁 530004;广西大学计算机与电子信息学院南宁 530004;广西大学电气工程学院南宁 530004【正文语种】中文【中图分类】TP183作为解决优化问题的并行计算模型,递归神经网络在过去的几十年里受到了极大的关注,不少神经网络模型被提出。
第5章 非线性规划

(水力约束) (水力摩阻系数约束)
KD GC
L (热力约束)
(粘温关系约束)
(工艺要求约束) (管道强度约束)
在目标函数中,f1(TR)、f2(Pd)一般为非线性函数,约束条 件中亦存在不少非线性函数,显然是一个NLP问题。
非线性规划的基本概念和定理
例3:最小二乘问题:该问题大量存在于工业生产和科学 实验的数据处理中。例如原油的粘度可以表示为:
凹函数的几何意义:
对 于 一 元 函 数 f(x) , 若
函数曲线上任意两点之 间的连线永远不在曲线
的 上 方 , 则 f(x) 为 凹 函
数(参见右图) 。
非线性规划的基本概念和定理 f(X)
f [X 1 (1 ) X 2 ]
对于二元函数 f(x1,x2), 若函数曲面上任意两点 之间的连线永远不在曲 面的上方,则f(x1,x2)为 凹函数(参见右图)。
1、一元函数:
①必要条件:f(x)在x*处取得极值的必要条件是f'(x*)=0;
②充分条件:若f"(x*)<0,则x*为极大点; 若f"(x*)>0,则x*为极小点。 2、多元函数: ①必要条件: f(X)在D域内存在极值点X*的必要条件为 * f ( X ) 0 (即f(X)在X*处的所有一阶偏导数等于0)。
非线性规划的基本概念和定理
根据定义,线性函数既是凸函数,又是凹函数。 凸函数的几何意义: 对 于 一 元 函 在曲线的下方, 则 f(x) 为 凸 函 数 ( 参 见 右
图) 。
非线性规划的基本概念和定理 f(X)
f ( X 1 ) (1 ) f ( X 2 )
§5.1 非线性规划的基本概念和定理
一、什么是非线性规划?
【国家自然科学基金】_非线性lagrange函数_基金支持热词逐年推荐_【万方软件创新助手】_20140801
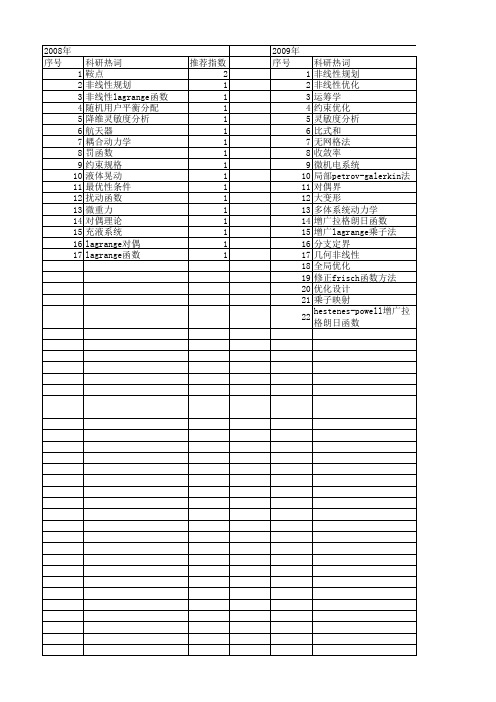
科研热词 高维函数优化算法 非线性边界 非线性规划 隶玻色子 轴向应变 组合激励 约束凝聚 神经网络 相对转动 混沌 模式搜索法 李雅普诺夫稳定 曲率 拉格朗日代价函数法 弹性曲线 平方根容积卡尔曼滤波 姿态估计 奇异非线性凸优化 四元数 分岔 几何非线性 不变性原理 k-s函数 hubbard模型 euler-bernoulli梁
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
科研热词 鞍点 非线性规划 非线性lagrange函数 随机用户平衡分配 降维灵敏度分析 航天器 耦合动力学 罚函数 约束规格 液体晃动 最优性条件 扰动函数 微重力 对偶理论 充液系统 lagrange对偶 lagrange函数
2011年 科研热词 推荐指数 高压直流输电 1 风电 1 频率分析 1 面向对象程序设计 1 非线性拉格朗日函数 1 非线性优化 1 非线性lagrange函数 1 非线性 1 雷达网 1 集中质量 1 逆散射 1 色散介质 1 自由振动 1 翘曲 1 空间钢框架 1 正则化方法 1 横向弯曲振动 1 最大熵 1 时域有限差分法 1 无源性 1 收敛性 1 控制 1 拉格朗日乘子 1 悬臂梁 1 归一化约束最小二乘 1 对偶性 1 定位精度 1 多目标优化 1 基于电压源变流器的柔性直流输电1 四边固定 1 变流器 1 变尺度法 1 加劲板 1 剪切变形 1 刚柔耦合 1 几何刚度矩阵 1 先验信息 1 ncp函数 1 lagrange方程 1
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
非线性规划

非线性规划什么是非线性规划?非线性规划(Nonlinear Programming,简称NLP)是一种数学优化方法,用于求解包含非线性约束条件的优化问题。
与线性规划不同,非线性规划中的目标函数和约束条件都可以是非线性的。
非线性规划的数学表达式一般来说,非线性规划可以表示为以下数学模型:minimize f(x)subject to g_i(x) <= 0, i = 1, 2, ..., mh_j(x) = 0, j = 1, 2, ..., px ∈ R^n其中,f(x)是目标函数,g_i(x)和h_j(x)分别是m个不等式约束和p个等式约束,x是优化变量,属于n维实数空间。
非线性规划的解法由于非线性规划问题比线性规划问题更为复杂,因此解决非线性规划问题的方法也更多样。
以下列举了几种常用的非线性规划求解方法:1. 数值方法数值方法是最常用的非线性规划求解方法之一。
它基于迭代的思想,通过不断优化目标函数的近似解来逼近问题的最优解。
常见的数值方法有梯度下降法、牛顿法、拟牛顿法等。
2. 优化软件优化软件是一类针对非线性规划问题开发的专用软件,它集成了各种求解算法和优化工具,可以方便地求解各种类型的非线性规划问题。
常见的优化软件有MATLAB、GAMS、AMPL等。
3. 线性化方法线性化方法是一种将非线性规划问题转化为等价的线性规划问题的求解方法。
它通过线性化目标函数和约束条件,将非线性规划问题转化为线性规划问题,然后利用线性规划的求解方法求解得到最优解。
4. 分类方法分类方法是一种将非线性规划问题分解为若干个子问题求解的方法。
它将原始的非线性规划问题分解为多个子问题,然后将每个子问题分别求解,并逐步逼近原始问题的最优解。
以上仅是非线性规划求解方法的一小部分,实际上还有很多其他的方法和技巧可供选择。
在实际应用中,选择合适的方法和工具是非常重要的。
非线性规划的应用非线性规划在实际生活和工程中有着广泛的应用。
求解非线性规划的Hopfield网络方法
求解非线性规划的Hopfield网络方法
刘劲涛;刘铁男;周忠波
【期刊名称】《东北石油大学学报》
【年(卷),期】2006(030)002
【摘要】根据求解非线性规划的连续Hopfield网络技术的发展,利用网络模型所依据的最优化方法,对Hopfield神经网络(HNN)模型进行了分类:求解无约束化的HNN和求解约束化的HNN.后者又可分为基于罚函数的HNN和基于Lagrange 乘子法的HNN.阐述了神经最优化技术所涉及的前沿问题,并指出今后的发展方向为开发智能优化求解系统.
【总页数】3页(P90-92)
【作者】刘劲涛;刘铁男;周忠波
【作者单位】天津大学,管理学院,天津,300072;大庆石油学院,电气信息工程学院,黑龙江,大庆,163318;大庆石化公司,塑料厂,黑龙江,大庆,163714
【正文语种】中文
【中图分类】TP183
【相关文献】
1.一种基于聚类技术的Hopfield网络求解TSP方法 [J], 龚安;张敏
2.基于连续Hopfield网络求解TSP的新方法 [J], 费春国;韩正之;唐厚君
3.一种基于粒子群算法和Hopfield网络求解TSP问题的方法 [J], 龚淑蕾;张煜东;吴含前;韦耿
4.电磁场数值分析中的人工神经网络方法--利用Hopfield网络求解二维静电场问
题 [J], 王彦保;纪玉良
5.基于遗传算法和非线性规划求解信息交互的光伏阵列模型鲁棒参数辨识方法 [J], 郑银燕;胡桂廷;张正江;闫正兵;朱志亮
因版权原因,仅展示原文概要,查看原文内容请购买。
snopt算法的原理
snopt算法的原理SNOPT(Sequential Nonlinear Programming Technique)是一种常用的求解非线性优化问题的算法。
它采用序列化的方法解决非线性规划问题,并在每个序列点上使用全局算法来逼近最优解。
以下是关于SNOPT算法的原理的参考内容:SNOPT算法是基于逐次二次规划(Sequential Quadratic Programming,SQP)的优化算法。
它以信赖域方法为基础,结合了内点法和激励函数的思想。
SNOPT算法的核心思想是通过构造一系列的信赖域子问题来逐步逼近最优解。
它以初始点开始迭代,并通过求解信赖域子问题来对搜索方向进行调整,使目标函数逐渐收敛。
在每一次迭代中,SNOPT算法首先通过求解一个线性化模型来计算搜索方向。
然后,它通过信赖域控制来确保搜索方向在信赖域内。
信赖域控制是指在每次迭代中限制搜索的步长,以保证每一步的目标函数值都能实现减少。
SNOPT算法使用了一种广义的Lagrange函数来描述非线性优化问题。
这个Lagrange函数被分为两部分:主问题和子问题。
主问题是将非线性优化问题转化成一系列子问题,通过求解这些子问题来逼近最优解。
子问题是对应于信赖域模型的最小化问题。
SNOPT算法的求解过程可以分为以下几个步骤:1. 初始化:设置初始点和信赖域半径,准备迭代过程。
2. 计算搜索方向:通过求解线性化模型来计算搜索方向。
3. 信赖域控制:在搜索方向上进行信赖域控制,以确保步长在信赖域内。
4. 更新迭代点:根据得到的搜索方向来更新迭代点,并计算目标函数的值。
5. 判断停止准则:根据预设的停止准则来判断是否达到最优解。
6. 迭代调整:如果停止准则不满足,则调整信赖域半径,并重新执行第2-5步,直到满足停止准则。
SNOPT算法使用了一些高效的数值算法来求解信赖域子问题和线性化模型,如线性化模型的求解采用了广义矩阵求逆技术,信赖域子问题的求解采用了凸二次规划等方法。
基于Log-Sigmoid函数的非线性Lagrange函数的开题报告
基于Log-Sigmoid函数的非线性Lagrange函数的开题报告1. 研究背景及意义非线性Lagrange函数是一种特殊的非线性优化技术,在现代控制理论、信号处理、计算机视觉等领域中广泛应用。
在实际应用中,不同的问题需要采用不同的非线性Lagrange函数进行建模和求解。
本文将研究基于Log-Sigmoid函数的非线性Lagrange函数,旨在探究其在优化问题中的应用。
Log-Sigmoid函数是一种常用的非线性函数,其形式如下:f(x) = 1 / (1+exp(-x))该函数常用于神经网络中,可通过调整参数实现不同程度的抑制或增强,使其具有很好的非线性表示能力。
在本文中,我们将研究基于Log-Sigmoid函数的非线性Lagrange函数,分析其建模能力和求解效率,探究其在优化问题中的应用价值。
2. 研究内容本文将对基于Log-Sigmoid函数的非线性Lagrange函数进行研究,主要包括以下方面:(1)非线性Lagrange函数的概念及相关理论知识的介绍;(2)Log-Sigmoid函数的基本特性分析;(3)利用Log-Sigmoid函数构建非线性Lagrange函数,并分析其在不同优化问题中的应用效果;(4)实验验证和对比分析。
3. 研究方法和步骤本文将采用数学建模和实验验证相结合的研究方法,具体步骤如下:(1)进行相关理论知识的文献调研;(2)对Log-Sigmoid函数进行基本特性分析;(3)探究Log-Sigmoid函数在非线性Lagrange函数中的应用,建立相应的数学模型;(4)采用数值计算方法对模型进行求解,并分析结果;(5)设计实验验证,对所建模型进行对比分析。
4. 研究预期结果及意义通过本文的研究,我们将得到以下预期结果:(1)对基于Log-Sigmoid函数的非线性Lagrange函数进行了详细的分析和研究,为今后优化问题的求解提供了一种新的思路和方法;(2)利用Log-Sigmoid函数构建的非线性Lagrange函数具有很好的建模能力和求解效率,在实际问题中具有广阔的应用前景;(3)实验验证和对比分析结果将进一步证明所提方法的优越性和可行性,为相应领域的研究和应用提供了借鉴和参考价值。
基于极限学习机的非平稳下击暴流风速预测
基于极限学习机的非平稳下击暴流风速预测钟旺;李春祥【摘要】分别运用经验模态分解(empirical mode decomposition, EMD)法和快速集合经验模态分解(fast ensemble empirical mode decomposition, FEEMD)法将非平稳下击暴流风速分解为一系列稳态序列集, 即固有模态分量. 建立极限学习机(extreme learning machines, ELM)风速预测模型(EMD-ELM)和快速EMD-ELM(FEEMD-ELM),分别对分解后的非平稳脉动风速训练集和测试集进行预测. 同时,将EMD和FEEMD与基于粒子群优化(particle swarm optimization, PSO)最小二乘支持向量机(least squares support vector machine, LSSVM)进行混合, 形成EMD-PSO-LSSVM和FEEMD-PSO-LSSVM混合模型算法. 通过比较这4种预测算法的结果发现, 基于EMD-ELM和FEEMD-ELM的非平稳下击暴流风速预测模型更为准确高效,其中FEEMD-ELM模型预测最佳.%Using the empirical mode decomposition (EMD) and fast ensemble empiri-cal mode decomposition (FEEMD), respectively, a nonstationary downburst wind velocity sample can be decomposed into a series of stationary sequence sets, namely, intrinsic mode functions. Extreme learning machines based on EMD and FEEMD, referred to as the EMD-ELM and FEEMD-ELM, are proposed to forecast the training and testing sets, both partitioned to stationary sequence sets. Meanwhile, combining EMD and FEEMD with a least squares support vector machine (SVM) based on particle swarm optimization, EMD-PSO-LSSVM and FEEMD-PSO-LSSVM algorithms are obtained. Comparison of these four prediction algorithms shows thatEMD-ELM and FEEMD-ELM are more accurate and efficient in predicting nonstationary downburst wind velocity, while FEEMD-ELM is the best.【期刊名称】《上海大学学报(自然科学版)》【年(卷),期】2018(024)003【总页数】10页(P446-455)【关键词】极限学习机;下击暴流;非平稳风速预测;经验模态分解;最小二乘支持向量机【作者】钟旺;李春祥【作者单位】上海大学土木工程系,上海200444;上海大学土木工程系,上海200444【正文语种】中文【中图分类】TU311非平稳脉动风速是一种具有非线性和非平稳性的特殊序列信号,其中的非平稳下击暴流风速是强非平稳过程.尽管极限学习机(extreme learning machine,ELM)能够较好地拟合风速的非线性部分,但风速非平稳部分将对预测效果造成较大的影响,因此降低风速非平稳性就显得尤为重要[1].降低非平稳性的主要方法有小波变换和经验模态分解(empirical mode decomposition,EMD).EMD将复杂非平稳性信号分解成不同频率段的信号,从而降低序列的非平稳性;集合经验模态分解(ensemble empirical mode decomposition,EEMD)将白噪声序列加入到原始序列,这样尽可能地得到数据信号的真实形态,然后再对数据信号进行EMD分解;快速集合经验模态分解(fast ensemble EMD,FEEMD)是EEMD的快速实现形式.目前,预测模型主要有时间序列模型、人工神经网络(artif i cial neural network,ANN)模型、支持向量机(support vector machine,SVM)模型和最近的ELM.ELM是Huang等[2-3]于2004年提出的一种性能优良的新型单隐层前馈神经网络(single-hidden layer feed forward neural networks,SLFNs),其基本思想是训练前设置合适的隐层节点数,在执行过程中只需要输入权值和为隐层偏置随机赋值,整个过程无需迭代,一次性产生唯一的最优解.与ANN相比,ELM显著提高了网络的泛化能力和学习速度,具有强非线性拟合能力.因此,当前国内外研究人员非常重视极限学习机的发展.鉴于ELM优势,本工作试图建立基于ELM的非平稳下击暴流风速预测算法.将EMD和FEEMD与基于粒子群优化(particle swarm optimization,PSO)的最小二乘支持向量机(least squares support vector machines,LSSVM)进行混合,形成EMD-PSO-LSSVM和FEEMD-PSO-LSSVM混合模型算法.1 非平稳下击暴流脉动风速的分解1.1 经验模态分解法EMD是Huang等[4]于1998年提出的数据处理方法,将非平稳信号按不同尺度的波动或趋势逐级分解成若干个固有模态分量(intrinsic mode function,IMF).每个IMF需满足2个条件:①数据集的极值点个数与穿0点个数相等或至多相差一个;②在任一点,由所有极大值点所形成包络和由所有极小值点所形成包络的均值等于0. 设U(t)为待分解的非平稳风速样本,先找出其所有极大、极小值,接着使用3次样条函数拟合出上、下极值包络线,计算出上、下包络线的平均值m1(t).于是,去除均值后的第1分量为第1次筛分所得分量h1(t)通常并不满足IMF的要求,故将h1(t)作为新的待筛分序列,再进行k次筛分,直到h1k(t)满足IMF的要求为止.于是,把h1k(t)当作IMF1,记为c1(t)=h1k(t).第1个IMF1[c1(t)]包含了非平稳风速U(t)的最短周期分量,将c1(t)从U(t)中分离后的余量为但是,r1(t)仍然包含较长周期分量,再将r1(t)作为新的待筛分序列,筛分得第2个IMF2[c2(t)];继续进行这样的筛分过程,直到余量变得很小为止.最终余量为那么,非平稳风速U(t)被分解成IMFs之和再加上最终余量:1.2 快速集合经验模态分解法EMD常常出现模态混叠现象,造成IMF物理意义上的缺失.为此,Huang[5]通过将白噪声加入待分解信号提出了EEMD.当将在整个时-频空间分布一致的零均值白噪声加到待分解信号时,不同时间尺度信号将自动分布到合适的参考尺度上,经多次平均噪声将相互抵消,集成均值结果.与EMD相同,EEMD将非平稳风速U(t)分解成IMFs之和再加上最终余量rn(t),即式(4).而FEEMD则是EEMD的快速实现方式,其原理与EEMD相同[6].2 下击暴流脉动风速智能预测模型2.1 基于粒子群优化最小二乘SVM的风速预测Suykens[7]用误差的二次平方来代替SVM的不敏感损失函数,将不等式约束转变为等式约束,进而将求解二次规划问题转化成求解如下的线性方程组,即形成LSSVM:式中,ω为权向量,b为偏置项,C为惩罚参数,ei∈R为误差,ei∈Rl×l为误差向量.为解决式(5)的优化问题,构造Lagrange函数:对式(6)求偏导,并根据最优化理论中的KKT(Karush-Kuhn-Tucher)条件,得到如下方程组:设α =(α1,α2,···,αl)T,Q=(1,1,···,1)T,Y=(Y1,Y2,···,Yl)T,I 为单位矩阵. 联立求解方程组,消去ω和ei,则式(7)的解为于是得到LSSVM的回归模型:式中,K为核函数矩阵,其元素k(xi,xj)=ψ(xi)ψ(xj).本工作采用径向基(radial basis function,RBF)核函数,其表达式为采用PSO算法对LSSVM中的核参数进行优化,形成基于粒子群优化的最小二乘SVM(PSO-LSSVM).2.2 基于极限学习机的风速预测ELM是一种快速的单隐层前馈神经网络训练算法[8].针对训练数据样本(x,t),隐含层节点数为L、激发函数为g(x)的ELM模型输出函数表达式为式中,β =[βi1,βi2,···,βin]T 为第 i隐层节点和输出节点间的连接权向量;ω=[ωi1,ωi2,···,ωin]T为连接第i隐层节点和输入节点的权重;bi为第i隐层节点的偏置;tj为第j个节点的输出值,ωixj为ωi和xj的内积.激发函数g(x)可以为Sigmoid,Sine或Hardlim等.式(11)的矩阵表达式可表示为式中,H=式中,H为隐层输出矩阵,其第i列表示为第i个隐层节点对应于输入x1,x2,···,xN的第i个隐层神经元的输出向量.运用式(12),将数据样本集映射到隐含层的特征空间中.设E(W)为ELM网络输出值与实际值之间的误差平方和,问题的求解转化为求解最优权值W=(ω,b,β),使E(W)最小:式中,εj=(εj1,εj2,···,εjm)T 是第 j 个样本的误差.当激发函数无限可微时,并不需要将网络参数全部进行调整,输入连接权值ω和隐含层节点偏置b在训练时可以随机选择.当隐含层节点数目足够多时,输入权随机取值,ELM可逼近任何连续函数.为使ELM具有较好的泛化能力,通常使L≪N.因此,连接隐层和输出节点的权值β可通过求解线性方程组Hβ=T的最小二乘解获得,其解为式中,H+为输出矩阵H的Moore-Penrose广义逆矩阵.至此,基于ELM风速预测算法的步骤如下:(1)随机赋值隐层节点和输入节点的权重ωi、隐层节点偏置bi(i=1,2,···,L);(2)计算隐含层输出矩阵H=(3)通过求解线性方程组(13)的最小二乘解计算输出层权重β.图1给出了基于ELM和PSO-LSSVM的非平稳下击暴流风速预测算法流程.图1 基于ELM和PSO-LSSVM的非平稳下击暴流风速预测算法流程Fig.1 Flowchart of ELM and PSO-LSSVM based on non-stationary downburst wind velocity prediction algorithms3 风速智能预测算法的数值验证3.1 非平稳下击暴流风速模拟下击暴流为雷暴天气中强烈的下沉气流猛烈撞击地面,并由撞击点向四周沿地表传播的极具突发性和破坏性的一种高强风[9].运用时变自回归滑动平均模型(auto-regressive moving average model,TARMA)[10-12]模拟m维非平稳脉动风速的表达式为式中,U(t)为非平稳随机过程向量,Ai(t)为回归系数矩阵,B(t)为时变滑动回归系数矩阵,p为自回归阶数,q为滑动回归阶数,X(t)是方差为1、正态分布的白噪声序列. TARMA模型p=4,q=1,模拟点位于沿下击暴流移动方向且距离下击暴流雷暴中心3 500 m处.下击暴流的平均风速模型采用Oseguera和Bowles模型;竖向分布模型采用Vicroy模型,其中竖向分布风速中最大风速Vmax=80 m/s,所处高度Zmax=67 m;风速场中某高度处径向最大风速Vr,max=47 m/s,与下击暴流中心水平距离rmax=1000 m,径向长度比例系数Rr=700 m.雷暴强度随时间变化的函数为下击暴流平移速度V0=8 m/s.当运用TARMA模型模拟时,上限截止频率为2πrad,N=211,Δω =同时,考虑下击暴流自身移动,模拟时间间隔Δt=0.5 s,模拟时长为1 000 s,共2 000个样本点.图2给出了运用TARMA模型模拟出的高度在20 m处的非平稳下击暴流脉动风速结果.图2 运用TARMA模型模拟出的高度在20 m处的非平稳下击暴流脉动风速Fig.2 Non-stationary downburst f l uctuating wind velocity at 20 m height simulated by TARMA3.2 预测算法数值验证ELM模型的隐层节点L=20,激发函数为Sigmoid;PSO-LSSVM采用RBF核函数,模型核参数2σ2∈[0.01,100],q=3,惩罚参数c∈[0.1,1 000].将非平稳下击暴流脉动风速的分解模型和预测模型两两组合,产生组合预测模型:EMD-ELM,EMD-PSO-LSSVM,FEEMD-ELM和FEEMD-PSO-LSSVM.运用TARMA模型模拟出的1 000 s非平稳下击暴流脉动风速样本是以0.5 s为时间单位,则样本中有2 000个风速点.取前1 000个风速点(500 s)构成训练集,后1 000个风速点(500 s)作为测试集.对1 000 s非平稳下击暴流脉动风速分别进行EMD和FEEMD分解,得到如图3所示的结果,其中的Signal为原始(模拟)非平稳风速,imf 1~8为分解后的固有模态函数,res为筛分后余量很小的剩余分量.在FEEMD分解时,白噪声方差α取为0.25,噪声组的数值取为100.当α取为0,噪声组数值取为1时,FEEMD就转化为EMD.将IMFs进行相空间重构,选取时间延迟τ=1,嵌入维数m=10,于是产生的训练集为990个10维向量,测试集为1 000个10维向量.使用上述4种组合预测模型对该非平稳下击暴流脉动风速样本进行预测,将各个IMF分量的预测结果进行叠加,得到非平稳下击暴流脉动风速的预测结果.图3 非平稳下击暴流脉动风速的分解Fig.3 Decompositions of the non-stationary downburst f l uctuating wind velocity图4 基于ELM和PSO-LSSVM的预测风速与模拟风速比较Fig.4 Comparisons of predicted wind velocity using ELM and PSO-LSSVM with the simulated wind velocity图5 基于ELM和PSO-LSSVM预测风速与模拟风速自相关函数的对比Fig.5 Auto-correlation function comparisons of predicted wind velocity using ELM and PSO-LSSVM with the simulated wind velocity图6 基于ELM和PSO-LSSVM预测风速与模拟风速功率谱函数的对比Fig.6 Power spectral function comparisons of predicted wind velocity using ELM and PSOLSSVM with the simulated wind velocity运用EMD-ELM,EMD-PSO-LSSVM,FEEMD-ELM和FEEMD-PSO-LSSVM预测模型对非平稳下击暴流脉动风速进行预测.图4~6分别给出了预测与模拟的非平稳下击暴流风速、自相关函数以及功率谱函数.由图4~6可知,在非平稳风速、自相关函数和功率谱3个方面,4种预测模型的预测结果均与TARMA模型的模拟值(原始值)较好地吻合,其中FEEMD-ELM的吻合度最高.4 风速智能预测算法的预测性能根据训练集和测试集,分别计算了预测风速与模拟风速的平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE)和相关系数(R),以比较这4种组合预测模型的预测精度.表1给出了4种预测模型对训练集和测试(预测)集的预测性能指标.由表1可以看出,无论是对训练集还是测试集,使用FEEMD分解的各IMF分量来进行预测,其精度均高于EMD;采用ELM预测模型进行预测的效果优于PSO-LSSVM.显然,采用FEEMD-ELM的预测精度是4种预测模型中最好的.综上所述,EMD-ELM和FEEMD-ELM是非平稳下击暴流风速预测的高精度算法.表1 训练集和测试集的预测性能指标Table 1 Prediction performance indexes for training and testing sets预测模型训练集测试集MAE RMSE R MAE RMSE R EMD-ELM 0.688 1 1.201 1 0.997 3 0.561 7 0.937 4 0.997 7 FEEMD-ELM 0.528 6 0.532 3 0.998 8 0.453 4 0.399 0 0.999 0 EMD-PSO-LSSVM 0.701 6 1.476 5 0.996 9 0.770 1 1.536 1 0.996 0 FEEMD-PSO-LSSVM 0.540 8 0.633 5 0.998 6 0.608 9 0.991 5 0.998 0表1中,平均误差为目标值(原始样本数据),^yn为预测值,N为预测样本数;均方根误差RMSE=相关系数R=5 风速智能预测算法的计算速度通过比较计算时间可以发现,运用EMD对非平稳下击暴流脉动风速进行分解的耗时较短;由于EEMD需要向信号中添加白噪声平滑脉冲干扰,因此耗时相对较长;FEEMD则有效改善了EEMD耗时较长的缺点,显著提高了EEMD的分解速度.不过,相对于预测的耗时,脉动风速分解的耗时是可以忽略的.更为重要的是,ELM预测模型的计算耗时约为28 s,而PSO-LSSVM预测模型的计算耗时则约为821 s,PSO-LSSVM耗时约为ELM的30倍.可见,EMD-ELM和FEEMD-ELM是非平稳下击暴流风速预测的高速算法.6 结束语经训练集和测试集非平稳下击暴流脉动风速时间序列、自相关函数和功率谱模拟值与预测值以及预测性能指标的比较后发现,对于EMD-ELM和FEEMD-ELM算法,训练集和测试集的预测精度均高于EMD-PSO-LSSVM和FEEMD-PSO-LSSVM 算法.相对于PSO-LSSVM算法,ELM预测算法的参数选取更容易、简单,在训练过程中不需要调整输入权值和偏置,训练速度显著提高;而且,该算法只需设定合适的隐层节点和激发函数便可以获得唯一的最优解,故EMD-ELM和FEEMD-ELM是非平稳下击暴流风速预测的高精度、高计算速度的算法,其中FEEMD-ELM是更为优秀的算法.参考文献:[1]张翌晖,王贺,胡志坚.基于集合经验模态分解和改进极限学习机的短期风速组合预测[J].电力系统保护与控制,2014,42(10):29-34.[2]HUANG G B,ZHU Q Y,SIEW C K.Extreme learning machine:a new learning scheme of feedforward neural networks[C]//Proceedings of International Joint Conference on Neural Networks.2004:985-990.[3]WANG D,HUANG G B.Protein sequence classif i cation using extreme learning machine[C]//Proceedings of International Joint Conference on Neural Networks.2005:1406-1411.[4]HUANG N E,SHEN Z,LONG S R.The empirical mode decomposition andHilbert spectrum for nonlinear and non-stationary time seriesanalysis[J].Proc Roy Soc,1998,454(17):903-905.[5]WU Z,HUANG N E.Ensemble empirical mode decomposition:a noise-assisted data analysis method[J].Advances in Adaptive DataAnalysis,2009,1(1):1-41.[6]WANG Y H,YEH C H.On the computational complexity of the empirical mode decomposition algorithm[J].Physica A,2014,1:159-167.[7]SUYKENS J A K,VAN DEWALLE J.Least squares support vector machine classif i ers[J].Neural Processing Letters,1999,9:293-300.[8]HUANG G B,ZHU Q Y,SIEW C K.Extreme learning machine:theory and application[J].Neurocomputing,2006,70(1/2/3):489-501.[9]李锦华,吴春鹏,陈水生.下击暴流非平稳脉动风速数值模拟[J].振动与冲击,2014,33(14):54-60.[10]LI J H,LI C X,HE L,et al.Extended modulating functions for simulation of wind velocities with weak and strong nonstationarity[J].Renewable Energy,2015,5:384-397.[11]何亮.基于时变ARMA的非平稳风速模拟与预测[D].上海:上海大学,2015.[12]李春祥,迟恩楠,何亮,等.基于时变ARMA和EMD-PSO-LSSVM算法的非平稳下击暴流风速预测[J].振动与冲击,2016,35(17):33-38.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
te a p o d: fa dn e p t y h p r a o d ig t e h mh
1 引 言
自从 H p e of l i d提出 神经 优化 的思 想 以来_ , l 有很 多人列
式 中 . . : R, : 一 ∈ ,R 一 h
和 g: 一 是 给 定 的 函
数 m 且
. 设 h ) g ) 假 ( 和 ( 二次连 续可 微.
这个 问题 进行 了深人研 究 . 文献 : , ] 34 卉绍 了用 神经 网 络求解
线性 规划 和非线性 规划 同题的方法 以及 电路实 现 然 而. 文献
定义 1 设 满 足 约 束条 件 , , 1 是 由 g( ) : 且 (- =0
的 i 成 的 指 标 集 即 组
[] 4 H讨论 丁不等 式约 束的非线 性规划 问题 尽 管在 数学 上等
, ) i ( ) . =12 … . } ( =; =0 i , . r 如果梯 度向量 h( ) 茎, . ’ 1 茎m, &( ) ∈ j ) 性 , ( 线
ie e tp fL r n i ,ie rpm 删 d a a H w y e o 哪 a  ̄ ln a n e r ln t r sc ntu td, ndt tbit nd c nv g n u a ewo k i o sr c e a he sa l ya 0 e i 0 h e r l fte n u a
维普资讯
第 1 期
2O O 2年 1月
电
于
学
报
3 0 jn a
№ m
ACr EL C RON A I I A A E T SNC
一
种 新 型 的 L ga g arn e非 线 性 规 划 神 经 网 络
黄 远 灿
f t 理 工 上 学 自 动 控 制 系 ,七 L08 J京 』 京 00 1
[] 5 提出用 Lgag ar e乘子 法 构造 神 经 网 络解 决 一般 非线 眭规  ̄ 划问题 文献 : 过政造 I舯 r 乘 子的 方法直 接 处理 不 等 6通 J a
t ̄ u } , , nSto ,t e t f m【 &帆
1 01 m ) 0 8, 0
A la t B , iigt a 硼 mL l r,oheulyadieul = ml a etae et ay B sd0  ̄ rc: Y. d( n eL o v h d i sbt q ai n qat 0 @ e t n i r “ cnb etdi n cl . ae n  ̄( b r d i l
取罚 田 f 和 韧 始 点 的 信 息 , 函 数 法 在 理 论 上 必 须 通 过 极 小 罚 化一 系列 罚 因 子 逐 渐 增 加 的 无 约 束 问 题 来 求 问 题 的 解 . 采 或 用 试 凑 法 确 定 罚 因 子 和 初 始 . 两 种 方 洼 在 实 际 中 都 不 可 这 行 . 且 . 函 数 法 总 会 碰 到 病 态 问 题 【 . 对 这 些 缺 氨 , 献 而 罚 针 文
摘
件.
要 : 通过 改造 L
・ 乘 子 项 , 不 等 式 约 束 和 等 式 约 束 用 同 样 的方 法 处 理 . 造 出 一 种 新 型 的 hga 非 对 构 rr
线性 规划 神经 网络 , 对 网络的稳 定性和收敛 性进 行严格 的理论分 析 而且 , 井 用增 加惩罚项 的方 法 , 放宽 网络 收敛 的条 关键词 : 神经优化 ;非线性 规划 ;稳定性 T I3 P 8 文献 标识码 : A 文章 编号 : 0 7-12(0 2 1 0 70 3 22 1 20 )0 . 2 - 0 3
中 围分 类号 :
A Ne T p fL g a g mmig Neu a t r l a o a n n r lNe wo k
HUA C L l CM YI l  ̄q l - a
t e t  ̄ A tm t o l Dp t m o u f &C ̄w , an f o ̄
t w r z n lz d r o o s u h r r .h o v re c o [ o te n t o k i r l e  ̄t o k ae a a e g ru l F a e mo e t e c n e g t ec l i n h ew r ea d y i y 3  ̄f i s x t ms i h a I n f e n te L r r a mwt n i o K y wo d e rs: v u a 0 mia ' n n n a rg a , r/ e zb n; o / e  ̄p o r mmi s bi . o i n t iB g; a i
定 义 2 L舯 r 函数 L … :a :
L 尺定 义为
( , = , ) ) ( : ( + ) g ) () 2 式中, ∈ 和 ∈ 是l 乘子 . +=( }2 / , /, 2 i
…
/1 2
这里需要说 明的 是 , 我们 定义 的 L 皆 丑 e函数 与经 典 优
无 关 则 称 是 正 则 . .
式约 束可用两 个耦台 的不等式 代替 . 应用文献 [l 但 4 的方法 处 J
理等式约 束 问题 , 电路 由两个反 向的二极 管耦 台而成 . 能 其 不
正常 工作 . 另外 . 文献 : ] 4 中的方 洼基于罚 函数 法 . 如果段 有 选
