基于二阶滑模观测器的永磁同步电机无位置传感器控制
基于滑模观测器的永磁同步电动机无传感器控制研究

R e e r h o ns re sCo r l o r a ntM a n tS nc o us s a c n Se o ls nto rPe m ne g e y hr no f M o orBa e n S i i o t s d o ld ng M de Obs r e ev r
Ke r s ema e t g e y c r n u t r P M) e s r s o tol g l igmo e ywo d :p r n n n t n h o o smoo ( MS ;sn ol s nr ln :si n d ma s e c i d
o e v r s t r to u c i n bs r e : a u a i n f n to
p r a e tm a n ts n h o o sm o o. d tep r a e tma e y c r no sm oo a e n d b g e , e em n n g e y c r n u trAn e h m n n g ts n h o u t rh sb e e u g d t n h r s t h w h tc n b c iv db l i gm o eo s r e fs n o ls e a e tma n ts n h o o sm oo e ul s o ta a ea h e e y si n d b ev ro s re sp r n n g e y c r n u t r s d e m r t r o i o si ain t o to em oo . o o st n etm t , c n r l t r p i o o h t
co elo p e n e ec re t otg eee c in l fe h Ir g lt rAp lc t n o ii l i a ls -o p s e d a d g t o rc l er fr n esg a trt eP e u ao . p iai fdgt g l h t v a a o a sn p o e s r TM S 2 LF 4 7 p o r mm e a g t he l n mo e o s r e si t n n a c nr l r c so 3 0 2 0 A r g a d c n e t si g di d b ev r e t mai ,a d c n o to o
基于新型滑模观测器的永磁同步电机无传感器控制策略

电动汽车
智
能
机
器
人
新兴产业
轨道交通
无传感器控制研究背景
旋转变压器
获取转子信息
添加标题内容
单击此处输入你的正文,文字是您思
想的提炼,为了最终演示发布的良好
果,请尽量言简意赅的阐述观点
增加成本
占用空间大
增加轴承的惯量
光电编码器
永磁同步电机无传感器控制策略研究具有重要意义!
无传感器控制研究背景
添加标题内容
为滑模观测器控制律。
永磁同步电机新型滑模控制
由式(2-3)减式(2-1)得到定子电流误差系统
i iˆ i , i iˆ i
电流 i i i
误差
向量
T
iˆ i iˆ i
T
v v v 控制输入向量
T
T
e e e 反电动势向量
n / r min 1
500
40
20
0
-20
0.8
-40
100
0
0
-60
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
-80
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
t /s
传统滑模观测器的转速估算误差
t /s
传统滑模观测器的转速
7
6
实时值
估算值
/ rad
5
转速抖振较大
PART
TWO
永磁同步电机新型滑模控制
永磁同步电机新型滑模控制
基于滑模观测器的无位置传感器永磁同步电机研究资料

s cx1 x2
c>0
直线s=0是切换线,在这个切换线上,u是不连续的。
设t=0时,状态x在s>0一侧,在u=u+作用下,在某个时限后到达s=0, 并进入s<0一侧,u=u-,又往s=0控制。……
当系统在滑模状态时,s 0, s 0
滑模观测器在无位置观测器系统中的应用
PMSM在 坐标系下的数学模型
u R 1 i e i L L L u R 1 i i e L L L
e 0e sin e e 0e cos e
假设 e 0 即转速变化很慢时,电机的反电动势模型:
e e
2. 国内外研究现状
电力电子器件的发展为电机调速奠定了物质基础。高速数字信号处理器 (DsP)的 高速处理能力使无位置传感器电机控制技术的复杂算法得到实现,近10年来, 各国学者致力于无位置传感器控制系统的研究,并且提出了几种切实可行的方 法,目前,适用于永磁同步电机位置估算的主要策略有: (1)利用定子端电压和电流直接计算ω和θ (2)基于观测器基础上的估算 (3)模型参考自适应 (4)人工智能理论基础上的估算
基于滑模观测器的无位置传感器 永磁同步电机研究
黎永华 08.12.16
1. 研究意义
永磁同步电机调速系统是以永磁同步电机为控制对象,采用变压变频技术对电机 进行调速的控制系统。因其具有能耗低、可靠性高、控制精确等优点,在许多领 域得到广泛的应用。PMSM控制系统稳定运行是建立在闭环控制基础之上的,如何 获取转子位置和速度信号是整个系统中相当重要的一个环节。当前,在大多数调速 驱动系统中,最常用的方法是在转子轴上安装位置传感器,不过传感器增加了系统 的成本,降低了系统的可靠性和耐用性。因此,无位置传感器的控制系统有着广泛 的应用前景。它通过测量电动机的电流、电压等可测量的物理量,通过特定的观测 器策略估算转子位置,提取永磁转子的位置和速度信息,完成闭环控制。 主要优点: 1、减少成本 2、减小电机体积 3、提高系统可靠性 4、减少系统维护量
基于滑模观测器的永磁同步电机无传感器控制

基于滑模观测器的永磁同步电机无传感器控制
永磁同步电机具有高效节能、响应速度快等优良性能,因此在工业控制中被广泛应用。
传统的永磁同步电机控制往往需要采用传感器进行位置和速度测量,这不仅增加了成本,
还会降低系统可靠性。
因此,研究无传感器控制策略,对于降低系统成本和提高系统性能
至关重要。
本文基于滑模观测器提出了一种永磁同步电机无传感器控制策略。
首先,对永磁同步
电机进行建模,并采用励磁电流转子磁链定向控制(FOC)技术进行电机控制。
在此基础上,通过引入滑模观测器,实现了无传感器的位置测量和速度测量功能。
滑模观测器通过构造一个滑动面实现对电机状态量的估计。
具体来说,滑动面的设计
需要满足两个条件:一是系统状态变化率与滑动面法向的内积小于等于零;二是系统状态
变量在滑动面上的变化率能够表示系统运动的特征。
通过不断调节滑动面参数,使得滑动
面法向趋于零,进而实现对系统状态量的精确估计。
本文在MATLAB/Simulink仿真环境下,对提出的无传感器控制策略进行了验证。
仿真
结果表明,该策略能够有效地实现对永磁同步电机的位置和速度测量,同时具有抗扰性强、动态响应快等优良特性。
与传统的基于位置传感器的控制方法相比,所提出的无传感器控
制策略能够降低系统成本,提高系统性能。
总之,本文提出了一种基于滑模观测器的永磁同步电机无传感器控制策略。
该策略可
以实现对电机位置和速度的精确估计,具有抗扰性强、动态响应快等优良特性。
未来,可
以进一步研究如何将该策略应用到实际的永磁同步电机控制中,并进行实际测试和验证。
基于滑模观测器的永磁同步电机无传感器控制

基于滑模观测器的永磁同步电机无传感器控制【摘要】本文针对永磁同步电机无传感器控制问题展开研究,通过引入滑模观测器原理,提出一种新的控制方法。
文章首先介绍了永磁同步电机的基本原理,然后概述了传感器控制方法,并详细解释了滑模观测器的工作原理。
接着,提出了基于滑模观测器的永磁同步电机控制方法,并通过实验结果进行分析。
结论部分探讨了这种控制方法的优势,同时提出了未来研究方向。
通过本研究,可以为无传感器控制的永磁同步电机提供新的解决方案,具有一定的实际应用价值。
【关键词】永磁同步电机、无传感器控制、滑模观测器、控制方法、实验结果、优势、未来研究方向1. 引言1.1 研究背景在控制系统领域,永磁同步电机因其高效率、高功率密度和低惯量等优点,被广泛应用于各种工业领域。
传统的永磁同步电机控制方法需要准确测量电机转子位置和速度,以实现精准的控制。
传统的传感器控制方法存在成本高、可靠性差、体积大等缺点,尤其在一些特殊环境下难以应用。
开展基于滑模观测器的永磁同步电机无传感器控制研究具有重要的理论和应用意义。
通过深入研究和分析,可以为永磁同步电机的控制与应用提供新的思路和方法,推动永磁同步电机技术的进一步发展和应用。
1.2 研究意义永磁同步电机是一种性能优越的电机,在各种领域广泛应用。
传统的永磁同步电机控制方法需要使用传感器来获取电机的转子位置信息,这不仅增加了系统构建的复杂度,还增加了系统成本。
基于滑模观测器的永磁同步电机无传感器控制方法备受研究关注。
研究意义主要体现在以下几个方面:采用无传感器控制方法可以减少系统构建的复杂度,降低系统成本。
基于滑模观测器的控制方法具有较好的鲁棒性,对参数变化和外部干扰具有一定的容忍性。
通过无传感器控制方法,可以提高系统的可靠性和稳定性,减少系统的维护成本。
最重要的是,这种控制方法能够提高永磁同步电机的性能表现,提高其控制精度和效率,从而更好地满足现代工业对电机控制精度和效率的要求。
基于Super-Twisting滑模观测器的永磁同步电机无传感器控制

Journal of Northeastern University( Natural Science)
第41 卷 第5 期
2020 年 5 月
Vo l. 41ꎬNo. 5
May 2 0 2 0
doi: 10. 12068 / j. issn. 1005 - 3026. 2020. 05. 022
control is used to control the motor speed so as to realize the sensorless control of PMSM. According
to the Lyapunov stability theoryꎬ the convergence property of the observer is proved. In additionꎬ
鲁棒性和动态响应能力.
关 键 词: 永磁同步电机ꎻsuper ̄twisting 滑模观测器ꎻ Lyapunov 稳定性ꎻ无传感器控制ꎻ矢量控制
中图分类号: TM 30 文献标志码: A 开放科学( 资源服务) 标识码( OSID) :
文章编号: 1005 - 3026(2020)05 - 0741 - 06
compared with the traditional first ̄order sliding mode algorithmꎬ the super ̄twisting algorithm greatly
weakens the chattering of the systemꎬ and reduces the overshoot adjustment time of the system. The
基于滑模观测器的永磁同步电机无传感器控制

基于滑模观测器的永磁同步电机无传感器控制永磁同步电机无传感器控制技术是近年来电机控制领域的研究热点之一,它不依赖于传感器的反馈信号,可以实现简单、实用、高效的电机控制。
其中,基于滑模观测器的控制方法可以实现对永磁同步电机的高性能控制,本文就基于滑模观测器的永磁同步电机无传感器控制进行了详细探讨。
首先,我们需要知道滑模控制是一种通过引入滑模面使得系统的状态在该面上特性改变的控制方法。
滑模控制具有简单、鲁棒性好等优点,但是其实际应用往往受到模型不确定性、参数变化等因素的影响,因此需要引入滑模观测器对系统状态进行观测和估计,以提高控制系统的性能和鲁棒性。
在永磁同步电机无传感器控制中,我们需要设计一个滑模观测器来估计电机转子位置和速度。
其中,滑模面通过选取适当的表达式可以使得观测器具有较好的鲁棒性。
具体地,我们可以将滑模面选为:$$s = y - \hat{y} - L(\hat{y})\dot{x}$$其中,$y$是电机的输出信号,$\hat{y}$是估计输出信号,$x$是系统状态向量,$L(\hat{y})$是一个对称正定的矩阵,满足$L(\hat{y}) = L^T(\hat{y})$。
观测器的状态方程可以表示为:$$\dot{\hat{x}} = f(\hat{x},u) + g(\hat{x})u + h(\hat{x})\textbf{w}(t)$$$$\hat{y} = h^T(\hat{x})\hat{x}$$$$\textbf{w}(t) = \textbf{w}(t - \tau)$$其中,$u$是系统的输入信号,$\textbf{w}(t)$是输入的不确定性误差,$\tau$是时间延迟常数。
滑模观测器的目标是使得滑模面$s$趋于零,从而估计出电机的状态变量,然后利用估计的状态变量来设计控制器。
具体地,我们可以利用反电动势进行电机位置估计,和斜坡函数法得到电机速度估计。
接下来,利用PI控制器进行速度控制和电流控制,其中,电流控制采用矢量控制方法,可以实现对电机转矩和磁通的控制。
基于滑模观测器的永磁同步电机无传感器控制
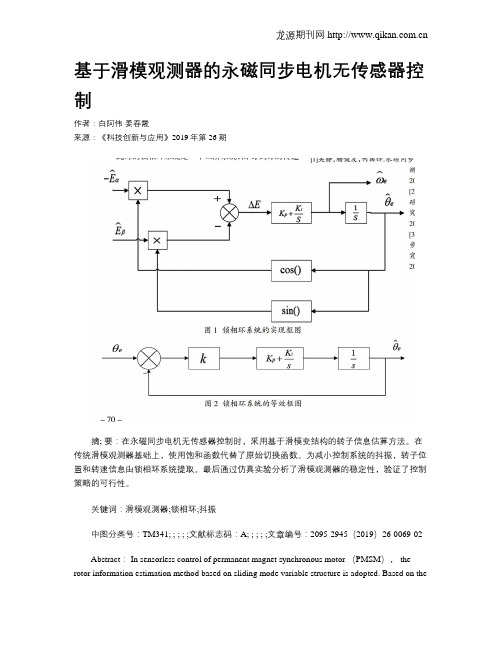
基于滑模观测器的永磁同步电机无传感器控制作者:白阿伟姜春霞来源:《科技创新与应用》2019年第26期摘; 要:在永磁同步电机无传感器控制时,采用基于滑模变结构的转子信息估算方法。
在传统滑模观测器基础上,使用饱和函数代替了原始切换函数。
为减小控制系统的抖振,转子位置和转速信息由锁相环系统提取。
最后通过仿真实验分析了滑模观测器的稳定性,验证了控制策略的可行性。
关键词:滑模观测器;锁相环;抖振中图分类号:TM341; ; ; ; ;文献标志码:A; ; ; ; ;文章编号:2095-2945(2019)26-0069-02Abstract: In sensorless control of permanent magnet synchronous motor (PMSM), the rotor information estimation method based on sliding mode variable structure is adopted. Based on thetraditional sliding mode observer, the original switching function is replaced by the saturation function. In order to reduce the chattering of the control system, the position and speed information of the rotor are extracted from the PLL system. Finally, the stability of the sliding mode observer is analyzed through simulation experiments, and the feasibility of the control strategy is verified.Keywords: sliding mode observer; phase-locked loop; chattering引言实现对永磁同步电机高性能控制离不开对转子位置和转速信息的精确测量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于二阶滑模观测器的永磁同步电机无位置传感器控制张晓光;孙力;陈小龙;安群涛【摘要】A kind of second-order sliding mode observer 1s proposed to estimate the rotor position and speed of PMSM(Permanent Magnet Synchronous Motor),which combines the linear sliding mode with the hybrid non-singular terminal sliding mode to avoid the phase lag caused by the low-pass filter in conventional sliding mode observer and to improve the precision of rotor position and speed estimation.The sliding mode control law is designed to restrain the inherent chattering and to guarantee the stability of observer.The tracking algorithm with phase-lock function is employed to demodulate rotor position and speed from the observed back electromotive force.Simulative and experimental results demonstrate the validity of the proposed observer.%为了准确估计永磁同步电机的转子位置与速度,提出一种二阶滑模观测器.该观测器在传统线性滑模面基础上引入了混合非奇异终端滑模面,避免了常规滑模观测器由于低通滤波所产生的相位滞后问题,同时可以提高转子位置与速度的估算精度.为了保证观测器的稳定并抑制滑模固有的抖振现象,设计了滑模控制律.最后,采用具有锁相功能的转子位置与速度跟踪算法从观测的反电动势中解调出转子位置和速度信息.仿真和实验证明了所提观测器的正确性.【期刊名称】《电力自动化设备》【年(卷),期】2013(033)008【总页数】6页(P36-41)【关键词】二阶滑模观测器;滑模控制;锁相环;永磁同步电机;控制【作者】张晓光;孙力;陈小龙;安群涛【作者单位】哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨150001;哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨150001;哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨150001;哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨150001【正文语种】中文【中图分类】TM3410 引言永磁同步电机PMSM(Permanent Magnet Synchronous Motor)的转子位置与速度是进行矢量解耦控制的必要条件,通常采用位置传感器进行检测,其中光电编码器、磁编码器以及旋转变压器等最常见。
采用传感器可以准确、方便地获得转子位置与速度信息,是电机控制系统设计的首选方案。
但在航空航天等一些特殊应用场合,位置传感器的应用将受到一定的限制,主要问题有:在恶劣环境下,由于温度、湿度以及机械振动等影响,使得传感器受到干扰,导致其精度降低,性能不稳定甚至无法工作;高精度、高响应的传感器价格昂贵,对于低成本控制系统而言,增加系统成本;传感器的应用增加了电机轴向尺寸和体积,在空间受限系统中无法使用。
为了解决位置传感器在一些特殊场合应用受限问题,国内外学者做了大量研究,一些无位置传感器控制方法已经被广泛研究,包括高频注入法、扩展卡尔曼滤波器、滑模观测器、全阶/降阶观测器、磁链估计法等[1-6]。
其中滑模观测器具有鲁棒性强、动态响应快、易于工程实现等诸多优点而得到了广泛关注[7-10]。
然而滑模观测器中抖振现象的存在会直接影响观测精度,为了解决抖振问题,文献[11]在滑模边界层内采用连续函数取代符号函数,从而抑制了抖振现象,但在滑模边界层内观测器的鲁棒性将无法得到保证。
文献[12]和[13]分别设计了具有变截止频率的低通滤波器和具有扩展卡尔曼滤波器结构的滤波器对观测的电机反电动势进行滤波,但在抑制抖振的同时,被观测量也将产生相位滞后与幅值的减小,因此需要对估计的转子角度进行相位和幅值补偿。
本文在分析传统滑模观测器的基础上,提出一种基于线性滑模与混合非奇异终端滑模的新型二阶滑模观测器,并对滑模控制律进行了设计,抑制了滑模固有的抖振现象。
该观测器能够避免常规滑模观测器由于低通滤波所产生的相位滞后,提高了转子位置与速度的估算精度。
利用Lyapunov方法证明了观测器的稳定性,并给出了滑模控制律参数的自适应律。
最后通过仿真和实验结果验证了该观测器的正确性和有效性。
1 永磁同步电机数学模型对于表贴式永磁同步电机,假设转子永磁磁场在气隙空间分布为正弦波,定子电枢绕组中的感应电动势也为正弦波,不计铁芯涡流与磁滞损耗,其在静止参考坐标系下的电压方程如下:其中,R 为定子电阻;L 为定子电感;eα、eβ,iα、iβ,uα、uβ分别为αβ坐标系下的绕组反电势、定子电流和定子电压。
由式(1)可得表贴式永磁同步电机在静止αβ坐标系下状态方程为:其中,。
2 二阶滑模观测器2.1 常规滑模观测器由于电机转子位置与速度信息包含在电机反电动势中,因此可构建滑模观测器对反电动势进行观测,进而估计电机转子位置与速度。
根据式(2)所示永磁同步电机的状态方程,构建常规滑模观测器如下:其中,“^”表示观测值;K= [-k1-k1]T为滑模增益矩阵,k1>0;sgn(·)为符号函数。
将式(3)与式(2)相减得到观测误差方程:其中,为定子电流观测误差,并将其作为滑模切换面,如式(5)所示。
当系统状态达到滑模切换面以后,由等效控制理论可知滑模切换面满足,则观测误差方程可简化为:由式(6)可知,电机的反电势信息被包含在符号函数中,但符号函数为不连续变化量,含有大量高频干扰,因此需要对其进行低通滤波才能得到平滑的反电势信号,经过滤波处理后的估算反电势为:其中,ωc为低通滤波器的截止频率。
通过低通滤波的反电动势将会产生相位延迟,该延迟与低通滤波器的截止频率直接相关,截止频率越低,对应固定频率的相延迟越大,实际应用中需对其进行相位补偿。
补偿后的转子位置与速度估计值为:其中,为补偿角度。
2.2 二阶滑模观测器的构建与稳定性分析对常规滑模观测器的分析可知,为了得到平滑的反电势信息,采用了低通滤波器对符号函数中抖振信号进行滤波处理,从而导致了估算转子位置的相位延迟,需要进行相位补偿。
同时由式(9)可知,估算速度由转子位置微分计算得到,将会引入大量干扰,从而影响观测精度。
为了解决常规观测器的上述问题,本文提出二阶混合非奇异终端滑模观测器,该观测器在本质上抑制了滑模固有的抖振现象,省去了低通滤波器,从而避免了观测转子位置的相位滞后,提高了观测精度。
构建新型滑模观测器如下:其中,v=[vα vβ]T为观测器控制律。
将式(10)与式(2)相减得到新型观测器的观测误差方程:由滑模控制理论可知,滑模切换面的设计将直接影响系统状态的收敛特性[14-15]。
而对于滑模观测器而言,滑模切换面是观测器设计的关键,它将决定观测值收敛到实际值的速度与方式。
因此本文基于线性滑模与混合非奇异终端滑模设计了如式(12)所示的滑模切换面。
其中,c、γ、p、q 为滑模参数,且 c>0,γ>0,p/q>1,p、q均为奇数;为定子电流观测误差,将其作为一阶线性滑模切换面;s为二阶混合非奇异终端滑模切换面。
滑模切换面确定之后,需要进一步对新型观测器(式(10))中的滑模控制律v进行设计,以保证该观测器的稳定。
本文设计滑模观测器控制律v为:其中,η、u、lg均为滑模控制律参数,且η>0,u>0。
选择Lyapunov函数为对滑模观测器的稳定性进行分析。
由Lyapunov稳定性理论可知,当式成立时满足滑模到达条件,即观测器稳定。
因此对求微分,并根据式(12)可得:其中,,且 F >0。
结合误差方程式(11),可得:进一步根据滑模控制律式(13),可得:当滑模控制律参数lg取值满足:则式(16)可进一步简化为:显然在参数lg的选取范围内所设计的滑模控制律满足滑模到达条件,能够保证该滑模观测器的稳定。
而根据滑模控制律参数lg的选取范围可设计参数自适应律如式(19)所示,其中 g>1。
2.3 转子位置与速度信息获取根据滑模控制理论可知,在控制律式(13)作用下,二阶滑模切换面s将会在有限时间内收敛于平衡点,此时滑模切换面方程式(12)为:当s收敛于平衡点以后,线性滑模变量f与进入混合非奇异终端滑模运动状态,并最终收敛到零,即满足,则新型观测器误差方程式(11)可简化为:式(21)表明电机的反电动势信息可通过滑模控制律进行观测。
同时与式(6)进行对比可知,常规滑模观测器的反电动势信息包含在引起抖振现象的符号函数中,而新型滑模观测器的反电动势信息包含在滑模控制律式(13)中,虽然滑模控制律中同样包含符号函数,但该符号函数经过了积分器的滤波环节,使得抖振现象得到有效抑制,因此,转子位置可以直接由观测的反电动势信息计算得到,不需要再进行低通滤波处理,避免了常规滑模观测器的相位滞后问题。
常规滑模观测器计算转子位置与转速的方法通常采用如式(8)和(9)所示的反正切与微分计算方法,这种方法精度不高且微分运算容易引入干扰。
为了克服上述缺点提高观测精度,本文采用如图1所示的转子位置与速度跟踪算法从观测的反电动势中解调出转子位置和速度。
图中,分别为估算转子位置与速度。
图1 转子位置与速度跟踪算法Fig.1 Rotor position and speed tracking algorithm对图1算法进行分析可知:其中,θ*re为观测反电势的相位角,k为反电势系数。
而当角度误差满足的时候,有,则式(22)可简化为:此时图1所示的跟踪算法结构等效于图2所示的锁相环结构。
转子位置误差Δθre 经过PI调节后得到估算转速,而估算转速经过积分环节得到估算转子位置。
某一时刻,若估算转子位置小于实际转子位置,则位置误差增大,经PI调节输出后的估算转速增大,进而调节估算转子位置逐渐增大,最终使其与实际转子位置相接近;若估算转子位置大于实际转子位置,分析类似。
图2 锁相环结构框图Fig.2 Structure of PLL图3为二阶混合非奇异终端滑模观测器结构框图。
