选修2-1第一章《充分必要条件、简单的逻辑联结词》

合集下载

高中数学选修2系列知识点

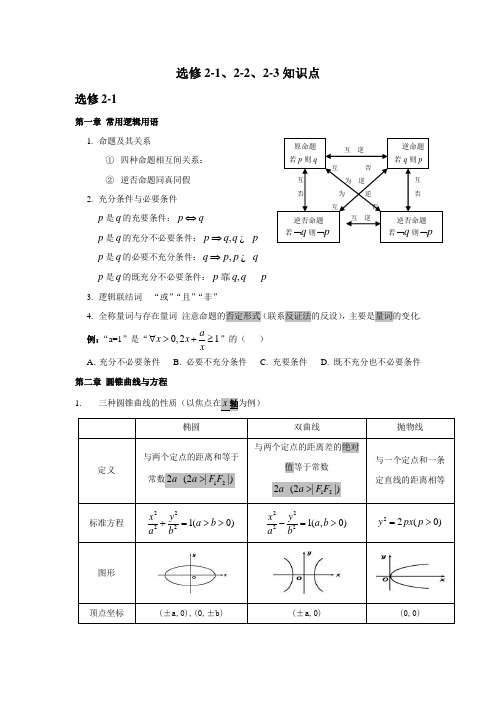
选修2-1、2-2、2-3知识点选修2-1第一章常用逻辑用语 1. 命题及其关系① 四种命题相互间关系： ② 逆否命题同真同假 2. 充分条件与必要条件p 是q 的充要条件：p q ⇔p 是q 的充分不必要条件：,p q q p ⇒¿ p 是q 的必要不充分条件：,q p p q ⇒¿ p 是q 的既充分不必要条件：,p q qp 靠3. 逻辑联结词 “或”“且”“非”4. 全称量词与存在量词注意命题的否定形式（联系反证法的反设），主要是量词的变化. 例：“a=1”是“0,21ax x x∀>+≥”的（） A ．充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件第二章圆锥曲线与方程 1.2.“回归定义” 是一种重要的解题策略。

如：（1）在求轨迹时，若所求的轨迹符合某种圆锥曲线的定义，则根据圆锥曲线的方程，写出所求的轨迹方程；（2）涉及椭圆、双曲线上的点与两个焦点构成的焦点三角形问题时，常用定义结合解三角形（一般是余弦定理）的知识来解决；（3）在求有关抛物线的最值问题时，常利用定义把到焦点的距离转化为到准线的距离，结合几何图形利用几何意义去解决。

3. 直线与圆锥曲线的位置关系（1）有关直线与圆锥曲线的公共点的个数问题，直线与圆锥曲线的位置关系有三种情况：相交、相切、相离.联立直线与圆锥曲线方程,经过消元得到一个一元二次方程（注意在和双曲线和抛物线方程联立时二次项系数是否为0）,直线和圆锥曲线相交、相切、相离的充分必要条件分别是0∆>、0∆=、0∆<.应注意数形结合(例如双曲线中，利用直线斜率与渐近线的斜率之间的关系考查直线与双曲线的位置关系)常见方法：①联立直线与圆锥曲线方程，利用韦达定理等；②点差法（主要适用中点问题，设而不求，注意需检验，化简依据：12122100212,2,22x x y y y y x y k x x ++-===-）（2）有关弦长问题，应注意运用弦长公式及韦达定理来解决；（注意斜率是否存在）① 直线具有斜率k ，两个交点坐标分别为1122(,),(,)A x y B x y1212AB x y =-=- ② 直线斜率不存在,则12AB y y =-.（3）有关对称垂直问题，要注意运用斜率关系及韦达定理，设而不求，简化运算。

选修2-1数学课后习题答案(全)

新课程标准数学选修2—1第一章课后习题解答第一章常用逻辑用语1．1命题及其关系练习（P4）1、略.2、（1）真；（2）假；（3）真；（4）真.3、（1）若一个三角形是等腰三角形，则这个三角形两边上的中线相等. 这是真命题.（2）若一个函数是偶函数，则这个函数的图象关于y轴对称. 这是真命题.（3）若两个平面垂直于同一个平面，则这两个平面平行. 这是假命题.练习（P6）1、逆命题：若一个整数能被5整除，则这个整数的末位数字是0. 这是假命题.否命题：若一个整数的末位数字不是0，则这个整数不能被5整除. 这是假命题.逆否命题：若一个整数不能被5整除，则这个整数的末位数字不是0. 这是真命题.2、逆命题：若一个三角形有两个角相等，则这个三角形有两条边相等. 这是真命题.否命题：若一个三角形有两条边不相等，这个三角形有两个角也不相等. 这是真命题.逆否命题：若一个三角形有两个角不相等，则这个三角形有两条边也不相等.这是真命题.3、逆命题：图象关于原点对称的函数是奇函数. 这是真命题.否命题：不是奇函数的函数的图象不关于原点对称. 这是真命题. 逆否命题：图象不关于原点对称的函数不是奇函数. 这是真命题. 练习（P8）证明：若1a b -=，则22243a b a b -+--()()2()2322310a b a b a b b a b b a b =+-+---=++--=--=所以，原命题的逆否命题是真命题，从而原命题也是真命题. 习题1.1 A 组（P8）1、（1）是；（2）是；（3）不是；（4）不是.2、（1）逆命题：若两个整数a 与b 的和a b +是偶数，则,a b 都是偶数. 这是假命题.否命题：若两个整数,a b 不都是偶数，则a b +不是偶数. 这是假命题. 逆否命题：若两个整数a 与b 的和a b +不是偶数，则,a b 不都是偶数. 这是真命题.（2）逆命题：若方程20x x m +-=有实数根，则0m >. 这是假命题. 否命题：若0m ≤，则方程20x x m +-=没有实数根. 这是假命题. 逆否命题：若方程20x x m +-=没有实数根，则0m ≤. 这是真命题.3、（1）命题可以改写成：若一个点在线段的垂直平分线上，则这个点到线段的两个端点的距离相等.逆命题：若一个点到线段的两个端点的距离相等，则这个点在线段的垂直平分线上.这是真命题.否命题：若一个点到不在线段的垂直平分线上，则这个点到线段的两个端点的距离不相等. 这是真命题.逆否命题：若一个点到线段的两个端点的距离不相等，则这个点不在线段的垂直平分线上. 这是真命题.（2）命题可以改写成：若一个四边形是矩形，则四边形的对角线相等.逆命题：若四边形的对角线相等，则这个四边形是矩形. 这是假命题. 否命题：若一个四边形不是矩形，则四边形的对角线不相等. 这是假命题.逆否命题：若四边形的对角线不相等，则这个四边形不是矩形. 这是真命题.4、证明：如果一个三角形的两边所对的角相等，根据等腰三角形的判定定理，这个三角形是等腰三角形，且这两条边是等腰三角形，也就是说这两条边相等. 这就证明了原命题的逆否命题，表明原命题的逆否命题为真命题. 所以，原命题也是真命题.习题 B 组（P8）证明：要证的命题可以改写成“若p ，则q ”的形式：若圆的两条弦不是直径，则它们不能互相平分.此命题的逆否命题是：若圆的两条相交弦互相平分，则这两条相交弦是圆的两条直径.可以先证明此逆否命题：设,AB CD 是O 的两条互相平分的相交弦，交点是E ，若E 和圆心O 重合，则,AB CD 是经过圆心O 的弦，,AB CD 是两条直径. 若E 和圆心O 不重合，连结,,AO BO CO 和DO ，则OE 是等腰AOB ∆，COD ∆的底边上中线，所以，OE AB ⊥，OE CD ⊥. AB 和CD 都经过点E ，且与OE 垂直，这是不可能的. 所以，E 和O 必然重合. 即AB 和CD 是圆的两条直径.原命题的逆否命题得证，由互为逆否命题的相同真假性，知原命题是真命题.1．2充分条件与必要条件练习（P10）1、（1）⇒；（2）⇒；（3）⇒；（4）⇒.2、（1）. 3（1）.4、（1）真；（2）真；（3）假；（4）真.练习（P12）1、（1）原命题和它的逆命题都是真命题，p是q的充要条件；（2）原命题和它的逆命题都是真命题，p是q的充要条件；（3）原命题是假命题，逆命题是真命题，p是q的必要条件.2、（1）p是q的必要条件；（2）p是q的充分条件；（3）p是q的充要条件；（4）p是q的充要条件.习题1.2 A组（P12）1、略.2、（1）假；（2）真；（3）真.3、（1）充分条件，或充分不必要条件；（2）充要条件；（3）既不是充分条件，也不是必要条件；（4）充分条件，或充分不必要条件.4、充要条件是222+=.a b r习题 B组（P13）1、（1）充分条件；（2）必要条件；（3）充要条件.2、证明：（1）充分性：如果222++=++，那么a b c ab ac bc2220a b c ab ac bc++---=.所以222-+-+-=a b a c b c()()()0所以，0b c-=.-=，0a b-=，0a c即a b c∆是等边三角形.==，所以，ABC（2）必要性：如果ABC==∆是等边三角形，那么a b c所以222-+-+-=()()()0a b a c b c所以2220++---=a b c ab ac bc所以222++=++a b c ab ac bc1．3简单的逻辑联结词练习（P18）1、（1）真；（2）假.2、（1）真；（2）假.3、（1）225x-=的根，假命题；+≠，真命题；（2）3不是方程290（31≠-，真命题.习题1.3 A组（P18）1、（1）4{2,3}∈或2{2,3}∈且2{2,3}∈，假命题；∈，真命题；（2）4{2,3}（3）2是偶数或3不是素数，真命题；（4）2是偶数且3不是素数，假命题.2、（1）真命题；（2）真命题；（3）假命题.3、（1不是有理数，真命题；（2）5是15的约数，真命题；（3）23+=，真命题；≥，假命题；（4）8715（5）空集不是任何集合的真子集，真命题.习题 B组（P18）（1）真命题. 因为p为真命题，q为真命题，所以p q∨为真命题；（2）真命题. 因为p为真命题，q为真命题，所以p q∧为真命题；（3）假命题. 因为p为假命题，q为假命题，所以p q∨为假命题；（4）假命题. 因为p为假命题，q为假命题，所以p q∧为假命题.1．4全称量词与存在量词练习（P23）1、（1）真命题；（2）假命题；（3）假命题.2、（1）真命题；（2）真命题；（3）真命题.练习（P26）1、（1）00,n Z n Q ∃∈∉；（2）存在一个素数，它不是奇数；（3）存在一个指数函数，它不是单调函数.2、（1）所有三角形都不是直角三角形；（2）每个梯形都不是等腰梯形；（3）所有实数的绝对值都是正数.习题1.4 A 组（P26）1、（1）真命题；（2）真命题；（3）真命题；（4）假命题.2、（1）真命题；（2）真命题；（3）真命题.3、（1）32000,x N x x ∃∈≤；（2）存在一个可以被5整除的整数，末位数字不是0；（3）2,10x R x x ∀∈-+>；（4）所有四边形的对角线不互相垂直. 习题 B 组（P27）（1）假命题. 存在一条直线，它在y 轴上没有截距；（2）假命题. 存在一个二次函数，它的图象与x 轴不相交；（3）假命题. 每个三角形的内角和不小于180︒；（4）真命题. 每个四边形都有外接圆.第一章复习参考题A 组（P30）1、原命题可以写为：若一个三角形是等边三角形，则此三角形的三个内角相等.逆命题：若一个三角形的三个内角相等，则此三角形是等边三角形. 是真命题；否命题：若一个三角形不是等边三角形，则此三角形的三个内角不全相等. 是真命题；逆否命题：若一个三角形的三个内角不全相等，则此三角形不是等边三角形. 是真命题.2、略.3、（1）假；（2）假；（3）假；（4）假.4、（1）真；（2）真；（3）假；（4）真；（5）真.5、（1）2,0n N n ∀∈>；（2）{P P P ∀∈在圆222x y r +=上}，(OP r O =为圆心)；（3）(,){(,),x y x y x y ∃∈是整数}，243x y +=；（4）0{x x x ∃∈是无理数}，30{x q q ∈是有理数}.6、（1）32≠，真命题；（2）54≤，假命题；（3）00,0x R x ∃∈≤，真命题；（4）存在一个正方形，它不是平行四边形，假命题.第一章复习参考题B 组（P31）1、（1）p q ∧；（2）()()p q ⌝∧⌝，或()p q ⌝∨.2、（1）Rt ABC ∀∆，90C ∠=︒，,,A B C ∠∠∠的对边分别是,,a b c ，则222c a b =+；（2）ABC ∀∆，,,A B C ∠∠∠的对边分别是,,a b c ，则sin sin sin a b c A B C==.新课程标准数学选修2—1第二章课后习题解答第二章圆锥曲线与方程2．1曲线与方程练习（P37）1、是. 容易求出等腰三角形ABC 的边BC 上的中线AO 所在直线的方程是0x =.2、3218,2525a b ==. 3、解：设点,A M 的坐标分别为(,0)t ，(,)x y .（1）当2t ≠时，直线CA 斜率 20222CA k t t-==-- 所以，122CB CA t k k -=-= 由直线的点斜式方程，得直线CB 的方程为 22(2)2t y x --=-. 令0x =，得4y t =-，即点B 的坐标为(0,4)t -.由于点M 是线段AB 的中点，由中点坐标公式得4,22t tx y -==. 由2t x =得2t x =，代入42ty -=，得422xy -=，即20x y +-=……① （2）当2t =时，可得点,A B 的坐标分别为(2,0)，(0,2) 此时点M 的坐标为(1,1)，它仍然适合方程①由（1）（2）可知，方程①是点M 的轨迹方程，它表示一条直线. 习题2.1 A 组（P37）1、解：点(1,2)A -、(3,10)C 在方程2210x xy y -++=表示的曲线上；点(2,3)B -不在此曲线上2、解：当0c ≠时，轨迹方程为12c x +=；当0c =时，轨迹为整个坐标平面. 3、以两定点所在直线为x 轴，线段AB 垂直平分线为y 轴，建立直角坐标系，得点M 的轨迹方程为224x y +=.4、解法一：设圆22650x y x +-+=的圆心为C ，则点C 的坐标是(3,0). 由题意，得CM AB ⊥，则有1CM AB k k =-. 所以，13y yx x⨯=--(3,0)x x ≠≠ 化简得2230x y x +-=(3,0)x x ≠≠当3x =时，0y =，点(3,0)适合题意；当0x =时，0y =，点(0,0)不合题意.解方程组 222230650x y x x y x ⎧+-=⎪⎨+-+=⎪⎩，得5,3x y ==所以，点M 的轨迹方程是2230x y x +-=，533x ≤≤. 解法二：注意到OCM ∆是直角三角形，利用勾股定理，得2222(3)9x y x y ++-+=，即2230x y x +-=. 其他同解法一. 习题 B 组（P37）1、解：由题意，设经过点P 的直线l 的方程为1x y ab+=. 因为直线l 经过点(3,4)P ，所以341ab+= 因此，430ab a b --=由已知点M 的坐标为(,)a b ，所以点M 的轨迹方程为430xy x y --=.2、解：如图，设动圆圆心M 的坐标为(,)x y .由于动圆截直线30x y -=和30x y +=所得弦分别为AB ，CD ，所以，8AB =，4CD =. 过点M 分别作直线30x y -=和30x y +=的垂线，垂足分别为E ，F ，则4AE =，2CF =.ME =，MF =.连接MA ，MC ，因为MA MC =，则有，2222AE ME CF MF+=+所以，22(3)(3)1641010x y x y -++=+，化简得，10xy =. 因此，动圆圆心的轨迹方程是10xy =.2．2椭圆练习（P42）1、14. 提示：根据椭圆的定义，1220PF PF +=，因为16PF =，所以214PF =.2、（1）22116x y +=；（2）22116y x +=；（3）2213616x y +=，或2213616y x +=.3、解：由已知，5a =，4b =，所以3c ==.（1）1AF B ∆的周长1212AF AF BF BF =+++.由椭圆的定义，得122AF AF a +=，122BF BF a +=. 所以，1AF B ∆的周长420a ==.（2）如果AB 不垂直于x 轴，1AF B ∆的周长不变化.这是因为①②两式仍然成立，1AF B ∆的周长20=，这是定值. 4、解：设点M 的坐标为(,)x y ，由已知，得直线AM 的斜率 1AM yk x =+(1)x ≠-；直线BM 的斜率 1BM yk x =-(1)x ≠；由题意，得2AM BM k k =，所以211y yx x =⨯+-(1,0)x y ≠±≠ 化简，得3x =-(0)y ≠因此，点M 的轨迹是直线3x =-，并去掉点(3,0)-.练习（P48）1、以点2B （或1B ）为圆心，以线段2OA 为半径画圆，圆与x 轴的两个交点分别为点12,F F 就是椭圆的两个焦点.这是因为，在22Rt B OF ∆中，2OB b =，222B F OA a ==，所以，2OF c =. 同样有1OF c =. 2、（1）焦点坐标为(8,0)-，(8,0)；（2）焦点坐标为(0,2)，(0,2)-.3、（1）2213632x y +=；（2）2212516y x +=.4、（1）22194x y += （2）22110064x y +=，或22110064y x +=.5、（1）椭圆22936x y +=，椭圆2211612x y +=的离心率是12，因为132>，所以，椭圆2211612x y +=更圆，椭圆22936x y +=更扁；（2）椭圆22936x y +=的离心率是3，椭圆221610x y +=的离心率是5，因为3>221610x y +=更圆，椭圆22936x y +=更扁.6、（1）8(3,)5；（2）(0,2)；（3）4870(,)3737--. 7、7. 习题2.2 A 组（P49）1、解：由点(,)M x y 10=以及椭圆的定义得，点M 的轨迹是以1(0,3)F -，2(0,3)F 为焦点，长轴长为10的椭圆.它的方程是2212516y x +=.2、（1）2213632x y +=；（2）221259y x +=；（3）2214940x y +=，或2214940y x +=.3、（1）不等式22x -≤≤，44y -≤≤表示的区域的公共部分；（2）不等式x -≤≤，101033y -≤≤表示的区域的公共部分. 图略.4、（1）长轴长28a =，短轴长24b =，离心率e =，焦点坐标分别是(-，，顶点坐标分别为(4,0)-，(4,0)，(0,2)-，(0,2)；（2）长轴长218a =，短轴长26b =，离心率e =，焦点坐标分别是(0,-，，顶点坐标分别为(0,9)-，(0,9)，(3,0)-，(3,0).5、（1）22185x y +=；（2）2219x y +=，或221819y x +=；（3）221259x y +=，或221259y x +=.6、解：由已知，椭圆的焦距122F F =.因为12PF F ∆的面积等于1，所以，12112P F F y ⨯⨯=，解得1P y =.代入椭圆的方程，得21154x +=，解得x =所以，点P 的坐标是(1)2±±，共有4个7、解：如图，连接QA . 由已知，得QA QP =. 所以，QO QA QO QP OP r +=+==. 又因为点A 在圆内，所以OA OP <根据椭圆的定义，点Q 的轨迹是以,O A 为焦点，r 为长轴长的椭圆. 8、解：设这组平行线的方程为32y x m =+.把32y x m =+代入椭圆方程22149x y +=，得22962180x mx m ++-=.这个方程根的判别式 223636(218)m m ∆=-- （1）由0∆>，得m -<<当这组直线在y 轴上的截距的取值范围是(-时，直线与椭圆相交.（2）设直线与椭圆相交得到线段AB ，并设线段AB 的中点为(,)M x y . 则 1223x x mx +==-. 因为点M 在直线32y x m =+上，与3m x =-联立，消去m ，得320x y +=.这说明点M 的轨迹是这条直线被椭圆截下的弦（不包括端点），这些弦的中点在一条直线上.9、222213.525 2.875x y +=. 10、地球到太阳的最大距离为81.528810⨯km ，最下距离为81.471210⨯km. 习题 B 组（P50）1、解：设点M 的坐标为(,)x y ，点P 的坐标为00(,)x y ，则0x x =，032y y =. 所以0x x =，023y y = ……①. 因为点00(,)P x y 在圆上，所以22004x y += ……②.将①代入②，得点M 的轨迹方程为22449x y +=，即22149x y +=所以，点M 的轨迹是一个椭圆与例2相比可见，椭圆也可以看作是由圆沿某个方向压缩或拉伸得到.2、解法一：设动圆圆心为(,)P x y ，半径为R ，两已知圆的圆心分别为12,O O .分别将两已知圆的方程 22650x y x +++=，226910x y x +--= 配方，得 22(3)4x y ++=， 22(3)100x y -+=当P 与1O ：22(3)4x y ++=外切时，有12O P R =+ ……①当P 与2O ：22(3)100x y -+=内切时，有210O P R =- ……② ①②两式的两边分别相加，得1212O P O P +=12= ……③ 化简方程③.先移项，再两边分别平方，并整理，得 12x =+ ……④ 将④两边分别平方，并整理，得 22341080x y +-= ……⑤将常数项移至方程的右边，两边分别除以108，得 2213627x y += ……⑥由方程⑥可知，动圆圆心的轨迹是椭圆，它的长轴和短轴长分别为12，12= ……①由方程①可知，动圆圆心(,)P x y 到点1(3,0)O -和点2(3,0)O 距离的和是常数12，所以点P 的轨迹方程是焦点为(3,0)-、(3,0)，长轴长等于12的椭圆. 并且这个椭圆的中心与坐标原点重合，焦点在x 轴上，于是可求出它的标准方程.因为 26c =，212a =，所以3c =，6a =所以236927b =-=.于是，动圆圆心的轨迹方程为2213627x y +=.3、解：设d 是点M 到直线8x =的距离，根据题意，所求轨迹就是集合12MF P M d ⎧⎫==⎨⎬⎩⎭由此得12= 将上式两边平方，并化简，得 223448x y +=，即2211612x y +=所以，点M 的轨迹是长轴、短轴长分别为8，. 4、解：如图，由已知，得(0,3)E - 因为,,R S T 是线段OF ,,R S T '''是线段CF 所以，(1,0),(2,0),(3,0)R S T ；933(4,),(4,),(4,)424R S T '''.直线ER 的方程是33y x =-；直线GR '的方程是3316y x =-+. 联立这两个方程，解得 3245,1717x y ==.所以，点L 的坐标是3245(,)1717. 同样，点M 的坐标是169(,)55，点N 的坐标是9621(,)2525. 由作图可见，可以设椭圆的方程为22221x y m n+=(0,0)m n >> ……①把点,L M 的坐标代入方程①，并解方程组，得22114m =，22113n =. 所以经过点,L M 的椭圆方程为221169x y +=.把点N 的坐标代入22169x y +，得22196121()()11625925⨯+⨯=，所以，点N 在221169x y +=上.因此，点,,L M N 都在椭圆221169x y +=上.2．3双曲线练习（P55）1、（1）221169x y -=. （2）2213y x -=.（3）解法一：因为双曲线的焦点在y 轴上所以，可设它的标准方程为22221y x a b-=(0,0)a b >>将点(2,5)-代入方程，得222541a b-=，即22224250a b a b +-=又 2236a b +=解方程组 222222425036a b a b a b ⎧+-=⎪⎨+=⎪⎩令22,m a n b ==，代入方程组，得425036mn m n m n +-=⎧⎨+=⎩解得 2016m n =⎧⎨=⎩，或459m n =⎧⎨=-⎩第二组不合题意，舍去，得2220,16a b ==所求双曲线的标准方程为2212016y x -=解法二：根据双曲线的定义，有2a ==.所以，a = 又6c =，所以2362016b =-=由已知，双曲线的焦点在y 轴上，所以所求双曲线的标准方程为2212016y x -=.2、提示：根据椭圆中222a b c -=和双曲线中222a b c +=的关系式分别求出椭圆、双曲线的焦点坐标.3、由(2)(1)0m m ++>，解得2m <-，或1m >- 练习（P61）1、（1）实轴长2a =，虚轴长24b =；顶点坐标为-；焦点坐标为(6,0),(6,0)-；离心率e =（2）实轴长26a =，虚轴长218b =；顶点坐标为(3,0),(3,0)-；焦点坐标为-；离心率e =（3）实轴长24a =，虚轴长24b =；顶点坐标为(0,2),(0,2)-；焦点坐标为-；离心率e =（4）实轴长210a =，虚轴长214b =；顶点坐标为(0,5),(0,5)-；焦点坐标为；离心率5e =2、（1）221169x y -=；（2）2213628y x -=.3、22135x y -=4、2211818x y -=，渐近线方程为y x =±.5、（1）142(6,2),(,)33-；（2）25(,3)4习题2.3 A 组（P61）1、把方程化为标准方程，得2216416y x -=. 因为8a =，由双曲线定义可知，点P 到两焦点距离的差的绝对值等于16. 因此点P 到另一焦点的距离是17.2、（1）2212016x y -=. （2）2212575x y -=3、（1）焦点坐标为12(5,0),(5,0)F F -，离心率53e =；（2）焦点坐标为12(0,5),(0,5)F F -，离心率54e =；4、（1）2212516x y -=. （2）221916y x -=（3）解：因为ce a==，所以222c a =，因此2222222b c a a a a =-=-=.设双曲线的标准方程为 22221x y a a -=，或22221y x a a-=.将(5,3)-代入上面的两个方程，得222591a a -=，或229251a a-=. 解得 216a = （后一个方程无解）.所以，所求的双曲线方程为2211616x y -=.5、解：连接QA ，由已知，得QA QP =. 所以，QA QO QP QO OP r -=-==. 又因为点A 在圆外，所以OA OP >.根据双曲线的定义，点Q 的轨迹是以,O A 为焦点，r 为实轴长的双曲线.6、22188x y -=.习题 B 组（P62）1、221169x y -=2、解：由声速及,A B 两处听到爆炸声的时间差，可知,A B 两处与爆炸点的距离的差，因此爆炸点应位于以,A B 为焦点的双曲线上.使,A B 两点在x 轴上，并且原点O 与线段AB 的中点重合，建立直角坐标系xOy .设爆炸点P 的坐标为(,)x y ，则 34031020PA PB -=⨯=. 即 21020a =，510a =.又1400AB =，所以21400c =，700c =，222229900b c a =-=.因此，所求双曲线的方程为221260100229900x y -=. 3、22221x y a b-=4、解：设点11(,)A x y ，22(,)B x y 在双曲线上，且线段AB 的中点为(,)M x y .设经过点P 的直线l 的方程为1(1)y k x -=-，即1y kx k =+-把1y kx k =+-代入双曲线的方程2212y x -=得222(2)2(1)(1)20k x k k x k ------=（220k -≠） ……① 所以，122(1)22x x k k x k +-==- 由题意，得2(1)12k k k -=-，解得 2k =.当2k =时，方程①成为22430x x -+=.根的判别式162480∆=-=-<，方程①没有实数解.所以，不能作一条直线l 与双曲线交于,A B 两点，且点P 是线段AB 的中点.2．4抛物线练习（P67）1、（1）212y x =；（2）2y x =；（3）22224,4,4,4y x y x x y x y ==-==-.2、（1）焦点坐标(5,0)F ，准线方程5x =-；（2）焦点坐标1(0,)8F ，准线方程18y =-；（3）焦点坐标5(,0)8F -，准线方程58x =；（4）焦点坐标(0,2)F -，准线方程2y =；3、（1）a ，2pa -. （2），(6,- 提示：由抛物线的标准方程求出准线方程. 由抛物线的定义，点M 到准线的距离等于9，所以 39x +=，6x =，y =±练习（P72） 1、（1）2165y x =；（2）220x y =；（3）216y x =-；（4）232x y =-. 2、图形见右，x3、解：过点(2,0)M 且斜率为1的直线l 的方程为2y x =-与抛物线的方程24y x =联立 224y x y x=-⎧⎨=⎩解得 1142x y ⎧=+⎪⎨=+⎪⎩2242x y ⎧=-⎪⎨=-⎪⎩ 设11(,)A x y ，22(,)B x y ，则AB ===.4、解：设直线AB 的方程为x a =(0)a >.将x a =代入抛物线方程24y x =，得24y a =，即y =± 因为 22AB y ==⨯== 所以，3a = 因此，直线AB 的方程为3x =.习题2.4 A 组（P73）1、（1）焦点坐标1(0,)2F ，准线方程12y =-；（2）焦点坐标3(0,)16F -，准线方程316y =；（3）焦点坐标1(,0)8F -，准线方程18x =；（4）焦点坐标3(,0)2F ，准线方程32x =-. 2、（1）28y x =-；（2），或(4,-3、解：由抛物线的方程22y px =(0)p >，得它的准线方程为2px =-.根据抛物线的定义，由2MF p =，可知，点M 的准线的距离为2p . 设点M 的坐标为(,)x y ，则 22p x p +=，解得32px =. 将32px =代入22y px =中，得y =. 因此，点M的坐标为3()2p，3(,)2p. 4、（1）224y x =，224y x =-；（2）212x y =-（图略）5、解：因为60xFM ∠=︒，所以线段FM所在直线的斜率tan 60k =︒= 因此，直线FM 的方程为1)y x =-与抛物线24y x =联立，得21)142y x y x ⎧=-⎪⎨=⎪⎩将1代入2得，231030x x -+=，解得，113x =，23x =把113x =，23x =分别代入①得1y =，2y = 由第5题图知1(,33-不合题意，所以点M的坐标为.因此，4FM ==6、证明：将2y x =-代入22y x =中，得2(2)2x x -=，化简得 2640x x -+=，解得3x =± 则321y =±=±因为OB k =，OA k所以15195OB OA k k -⋅===--所以 OA OB ⊥7、这条抛物线的方程是217.5x y =8、解：建立如图所示的直角坐标系，设拱桥抛物线的方程为22x py =-，因为拱桥离水面2 m ，水面宽4 m 所以 222(2)p =--，1p =因此，抛物线方程为22x y =- ……①水面下降1 m ，则3y =-，代入①式，得22(3)x =-⨯-，x =.这时水面宽为 m.习题 B 组（P74）1、解：设垂线段的中点坐标为(,)x y ，抛物线上相应点的坐标为11(,)x y .根据题意，1x x =，12y y =，代入2112y px =，得轨迹方程为212y px =. 由方程可知，轨迹为顶点在原点、焦点坐标为(,0)8p 的抛物线.2、解：设这个等边三角形OAB 的顶点,A B 在抛物线上，且坐标分别为11(,)x y ，22(,)x y ，则 2112y px =，2222y px =.又OA OB =，所以 22221122x y x y +=+即221212220x x px px -+-=，221212()2()0x x p x x -+-= 因此，1212()(2)0x x x x p -++= 因为120,0,20x x p >>>，所以12x x =由此可得12y y =，即线段AB 关于x 轴对称.因为x 轴垂直于AB ，且30AOx ∠=︒，所以11tan303y x =︒=. 因为2112y x p=，所以1y =，因此12AB y ==.3、解：设点M 的坐标为(,)x y由已知，得直线AM 的斜率 (1)1AM yk x x =≠-+. 直线BM 的斜率 (1)1BM yk x x =≠-. 由题意，得2AM BM k k -=，所以，2(1)11y y x x x -=≠±+-，化简，得2(1)(1)x y x =--≠±第二章复习参考题A 组（P80）1、解：如图，建立直角坐标系，使点2,,A B F 在x 轴上，2F 为椭圆的右焦点（记1F 为左焦点）.因为椭圆的焦点在x 轴上，所以设它的标准方程为22221(0)x y a b+=>>.则 22a c OA OF F A -=-=63714396810=+=22a c OB OF F B +=+=637123848755=+=，解得 7782.5a =，8755c =所以 b ==用计算器算得 7722b ≈因此，卫星的轨道方程是2222177837722x y +=.2、解：由题意，得 12a c R r a c R r -=+⎧⎨+=+⎩，解此方程组，得1221222R r r a r r c ++⎧=⎪⎪⎨-⎪=⎪⎩因此卫星轨道的离心率21122cr r e aR r r -==++.3、（1）D ；（2）B .4、（1）当0α=︒时，方程表示圆.（2）当090α︒<<︒时，方程化成2211cos y x α+=. 方程表示焦点在y 轴上的椭圆.（3）当90α=︒时，21x =，即1x =±，方程表示平行于y 轴的两条直线. （4）当90180α︒<≤︒时，因为cos 0α<，所以22cos 1x y α+=表示双曲线，其焦点在x 轴上. 而当180α=︒时，方程表示等轴双曲线.5、解：将1y kx =-代入方程224x y -=得 2222140x k x kx -+--= 即 22(1)250k x kx -+-= ……①222420(1)2016k k k ∆=+-=-令 0∆<，解得k >，或k <因为0∆<，方程①无解，即直线与双曲线没有公共点，所以，k 的取值范围为k >，或k <6、提示：设抛物线方程为22y px =，则点B 的坐标为(,)2p p ，点C 的坐标为(,)2pp - 设点P 的坐标为(,)x y ，则点Q 的坐标为(,0)x .因为，PQ y ==2BC p =，OQ x =.所以，2PQ BC OQ =，即PQ 是BC 和OQ 的比例中项.7、解：设等边三角形的另外两个顶点分别是,A B ，其中点A 在x 轴上方.直线FA 的方程为 )2p y x =-与22y px =联立，消去x ，得 220y p --=解方程，得 12)y p =+，22)y p =-把12)y p =+代入)2p y x =-，得 17(2x p =+.把22)y p =代入)2p y x =-，得 27(2x p =-.所以，满足条件的点A 有两个17((2))2A p p +，27((2))2A p p -.根据图形的对称性，可得满足条件的点B 也有两个17((,2))2B p p +-，27((,2))2B p p --所以，等边三角形的边长是112)A B p =+，或者222(2A B p =. 8、解：设直线l 的方程为2y x m =+.把2y x m =+代入双曲线的方程222360x y --=，得221012360x mx m +++=.1265mx x +=-，2123610m x x += ……①由已知，得 21212(14)[()4]16x x x x ++-= ……②把①代入②，解得 m =所以，直线l 的方程为2y x =±9、解：设点A 的坐标为11(,)x y ，点B 的坐标为22(,)x y ，点M 的坐标为(,)x y .并设经过点M 的直线l 的方程为1(2)y k x -=-，即12y kx k =+-.把12y kx k =+-代入双曲线的方程2212y x -=，得222(2)2(12)(12)20k x k k x k ------=2(20)k -≠. ……① 所以，122(12)22x x k k x k+-==-由题意，得2(12)22k k k -=-，解得4k =当4k =时，方程①成为 21456510x x -+=根的判别式25656512800∆=-⨯=>，方程①有实数解. 所以，直线l 的方程为47y x =-.10、解：设点C 的坐标为(,)x y .由已知，得直线AC 的斜率 (5)5AC yk x x =≠-+ 直线BC 的斜率 (5)5BC yk x x =≠- 由题意，得AC BC k k m =. 所以，(5)55y y m x x x ⨯=≠±+- 化简得，221(5)2525x y x m-=≠± 当0m <时，点C 的轨迹是椭圆(1)m ≠-，或者圆(1)m =-，并除去两点(5,0),(5,0)-；当0m >时，点C 的轨迹是双曲线，并除去两点(5,0),(5,0)-；11、解：设抛物线24y x =上的点P 的坐标为(,)x y ，则24y x =.点P 到直线3y x =+的距离d ===.当2y =时，d. 此时1x =，点P 的坐标是(1,2).12顶为原点、拱高所在直线为y 轴（向上），建立直角坐标系.设隧道顶部所在抛物线的方程为22x py =-因为点(4,4)C -在抛物线上所以 242(4)p =-- 解得 24p =-所以，隧道顶部所在抛物线的方程为24x y =-.设0.5EF h =+. 则(3, 5.5)F h -把点F 的坐标代入方程24x y =-，解得 3.25h =. 答：车辆通过隧道的限制高度为3.2 m.第二章复习参考题B 组（P81）1、12PF F S ∆=2、解：由题意，得1PF x ⊥轴.把x c =-代入椭圆方程，解得 2b y a=±. 所以，点P 的坐标是2(,)b c a -直线OP 的斜率21b k ac =-. 直线AB 的斜率2bk a=-.由题意，得2b bac a=，所以，b c =，a =.由已知及1F A a c =+，得 a c +=所以 (1c += c =所以，a =，b =因此，椭圆的方程为221105x y +=.3、解：设点A 的坐标11(,)x y ，点B 的坐标22(,)x y .由OA OB ⊥，得12120x x y y +=.由已知，得直线AB 的方程为25y x =-+. 则有 12125()250y y y y -++= ……①由25y x =-+与22y px =消去x ，得250y py p +-= ……② 12y y p +=-，125y y p =- ……③ 把③代入①，解得54p =当54p =时，方程②成为245250y y +-=，显然此方程有实数根. 所以，54p =4、解：如图，以连接12,F F 的直线为x 轴，线段12F F 的中点为原点，建立直角坐标系.对于抛物线，有176352922922p =+=，所以，4584p =，29168p =.对于双曲线，有2080529c a c a +=⎧⎨-=⎩解此方程组，得775.5a =，1304.5c = 因此，2221100320b c a =-=.所以，所求双曲线的方程是221601400.31100320x y -=(775.5)x ≥. 因为抛物线的顶点横坐标是 (1763)(1763775.5)987.5a --=--=- 所以，所求抛物线的方程是 29168(987.5)y x =+ 答：抛物线的方程为29168(987.5)y x =+，双曲线的方程是221601400.31100320x y -=(775.5)x ≥. 5、解：设点M 的坐标为(,)x y由已知，得直线AM 的斜率 (1)1AM yk x x =≠-+ 直线BM 的斜率 (1)1BM yk x x =≠-由题意，得2AM BM k k +=，所以2(1)11y y x x x +=≠±-+，化简，得21(1)xy x x =-≠±所以，点M 轨迹方程是21(1)xy x x =-≠±.6、解：（1）当1m =时，方程表示x 轴；（2）当3m =时，方程表示y 轴；（3）当1,3m m ≠≠时，把方程写成22131x y m m +=--. ①当13,2m m <<≠时，方程表示椭圆； ②2m =时，方程表示圆；③当1m <，或3m >时，方程表示双曲线.7、以AB 为直径的圆与抛物线的准线l 相切.证明：如图，过点,A B 分别作抛物线22(0)y px p =>的准线l 的垂线，垂足分别为,D E .由抛物线的定义，得 AD AF =，BE BF =.所以，AB AF BF AD BE =+=+.设AB 的中点为M ，且过点M 作抛物线22(0)y px p =>的准线l 的垂线，垂足为C .显然MC ∥x 轴，所以，MC 是直角梯形ADEB 的中位线. 于是，11()22MC AD BE AB =+=.因此，点C 在以AB 为直径的圆上.又MC l ⊥，所以，以AB 为直径的圆与抛物线的准线l 相切. 类似地，可以证明：对于椭圆，以经过焦点的弦为直径的圆与相应的准线相离；对于双曲线，以经过焦点的弦为直径的圆与相应的准线相交.新课程标准数学选修2—1第三章课后习题解答第三章空间向量与立体几何 3．1空间向量及其运算练习（P86）1、略.2、略.3、A C AB AD AA ''=+-，BD AB AD AA ''=-+，DB AA AB AD ''=--.练习（P89）1、（1）AD ；（2）AG ；（3）MG .2、（1）1x =；（2）12x y ==；（3）12x y ==. 3练习（P92） 1、B .2、解：因为AC AB AD AA ''=++，所以22()AC AB AD AA ''=++2222222()4352(0107.5)85AB AD AA AB AD AB AA AD AA '''=+++⋅+⋅+⋅=+++⨯++=所以85AC '=3、解：因为AC α⊥所以AC BD ⊥，AC AB ⊥，又知BD AB ⊥. 所以0AC BD ⋅=，0AC AB ⋅=，又知0BD AB ⋅=.2CD CD CD =⋅222222()()CA AB BD CA AB BD CA AB BDa b c =++⋅++=++=++所以CD .练习（P94）1、向量c 与a b +，a b -一定构成空间的一个基底. 否则c 与a b +，a b -共面，于是c 与a ，b 共面，这与已知矛盾. 2、共面 2、（1）解：OB OB BB OA AB BB OA OC OO a b c ''''=+=++=++=++；BA BA BB OC OO c b '''=+=-+=-CA CA AA OA OC OO a b c '''=+=-+=-+（2）1111()2222OG OC CG OC CB b a c a b c '=+=+=++=++. 练习（P97）1、（1）(2,7,4)-；（2）(10,1,16)-；（3）(18,12,30)-；（4）2.2、略.3、解：分别以1,,DA DC DD 所在的直线为x 轴、y 轴、z 轴，建立空间直角坐标系.则(0,0,0)D ，1(1,1,1)B ，1(1,,0)2M ，(0,1,0)C 所以，1(1,1,1)DB =，1(1,,0)2CM =-.所以，111110cos ,3DB CM DB CM DB CM-+⋅<>===⋅习题3.1 A 组（P97）1、解：如图，（1）AB BC AC +=；（2）AB AD AA AC AA AC CC AC ''''++=+=+=；（3）设点M 是线段CC '的中点，则12AB AD CC AC CM AM '++=+=；（4）设点G 是线段AC '的三等分点，则11()33AB AD AA AC AG ''++==. 向量,,,AC AC AM AG '如图所示. 2、A .3、解：22()AC AB AD AA ''=++2222222()15372(53573722298AB AD AA AB AD AB AA AD AA '''=+++⋅+⋅+⋅=+++⨯⨯+⨯⨯+⨯⨯=+所以，13.3AC '≈.4、（1）21cos602AB AC AB AC a ⋅=⋅︒=；（2）21cos1202AD DB AD DB a ⋅=⋅︒=-；（3）21cos1802GF AC GF AC a ⋅=⋅︒=- 11()22GF AC a ==；（4）21cos604EF BC EF BC a ⋅=⋅︒= 11()22EF BD a ==；（5）21cos1204FG BA FG BA a ⋅=⋅︒=- 11()22FG AC a ==；（6）11()22GE GF GC CB BA CA ⋅=++⋅2111()222111424111cos120cos60cos6042414DC CB BA CA DC CA CB CA BA CA DC CA CB CA BA CA a =++⋅=⋅+⋅+⋅=⋅︒+⋅︒+⋅︒=5、（1）60︒；（2）略.6、向量a 的横坐标不为0，其余均为0；向量b 的纵坐标不为0，其余均为0；向量c 的竖坐标不为0，其余均为0.7、（1）9；（2）(14,3,3)-.8、解：因为a b ⊥，所以0a b ⋅=，即8230x --+=，解得103x =. 9、解：(5,1,10)AB =--，(5,1,10)BA =-设AB 的中点为M ，119()(,,2)222OM OA OB =+=-，所以，点M 的坐标为19(,,2)22-，(AB =-=10、解：以1,,DA DC DD 分别作为x 轴、y 轴、z 轴建立空间直角坐标系O xyz -.则1,,,C M D N 的坐标分别为：(0,1,0)C ，1(1,0,)2M ，1(0,0,1)D ，1(1,1,)2N . 1(1,1,)2CM =-，11(1,1,)2D N =-所以2312CM ==，21312D N ==111114cos ,994CM D N --<>==- 由于异面直线CM 和1D N 所成的角的范围是[0,]2π因此，CM 和1D N 所成的角的余弦值为19.11、31(,,3)22- 习题 B 组（P99）1、证明：由已知可知，OA BC ⊥，OB AC ⊥∴ 0OA BC ⋅=，0OB AC ⋅=，所以()0OA OC OB ⋅-=，()0OB OC OA ⋅-=. ∴ OA OC OA OB ⋅=⋅，OB OC OB OA ⋅=⋅.∴ 0OA OC OB OC ⋅-⋅=，()0OA OB OC -⋅=，0BA OC ⋅=. ∴ OC AB ⊥.2、证明：∵ 点,,,E F G H 分别是,,,OA OB BC CA 的中点.∴ 12EF AB =，12HG AB =，所以EF HG = ∴四边形EFGH 是平行四边形.1122EF EH AB OC ⋅=⋅11()()44OB OA OC OB OC OA OC =-⋅=⋅-⋅ ∵ OA OB =，CA CB =（已知），OC OC =.∴ BOC ∆≌AOC ∆（SSS ） ∴ BOC AOC ∠=∠ ∴ OB OC OA OC ⋅=⋅ ∴ 0EF EH ⋅= ∴ EF EH ⊥∴ 平行四边形□EFGH 是矩形.3、已知：如图，直线OA ⊥平面α，直线BD ⊥平面α，,O B 为垂足. 求证：OA ∥BD证明：以点O 为原点，以射线OA 方向为z 轴正方向，建立空间直角坐标系O xyz -，,,i j k 分别为沿x 轴、y 轴、z 轴的坐标向量，且设(,,)BD x y z =.∵ BD α⊥.∴ BD i ⊥，BD j ⊥.∴ (,,)(1,0,0)0BD i x y z x ⋅=⋅==，(,,)(0,1,0)0BD j x y z y ⋅=⋅==. ∴ (0,0,)BD z =. ∴ BD zk =.∴ BD ∥k ，又知,O B 为两个不同的点. ∴ BD ∥OA .3．2立体几何中的向量方法练习（P104）1、（1）3b a =，1l ∥2l ；（2）0a b ⋅=，1l ⊥2l ；（3）3b a =-，1l ∥2l .2、（1）0u v ⋅=，αβ⊥；（2）2v u =-，α∥β；（3）2247u v u v⋅=-α与β.练习（P107）1、证明：设正方形的棱长为1.11D F DF DD =-，AE BE BA =-.因为11()000D F AD DF DD AD ⋅=-⋅=-=，所以1D F AD ⊥.因为1111()()00022D F AE DF DD BE BA ⋅=-⋅-=+-+=，所以1D F AE ⊥. 因此1D F ⊥平面ADE .2、解：22()CD CD CA AB BD ==++222222361664268cos(18060)68CA AB BD CA AB CA BD AB BD=+++⋅+⋅+⋅=+++⨯⨯⨯︒-︒=∴CD =练习（P111）1、证明：1()()2MN AB MB BC CN AB MB BC CD AB ⋅=++⋅=++⋅222211()22111cos120cos60cos600222MB BC AD AC AB a a a a =++-⋅=+︒+︒-︒=∴ MN AB ⊥. 同理可证MN CD ⊥.2、解：222222()2cos l EF EA A A AF m d n mn θ''==++=+++（或2cos()mn πθ-）22222cos d l m n mn θ=--，所以AA d '==.3、证明：以点D 为原点，,,DA DC DD '的方向分别为x 轴、y 轴、z 轴正方向，建立坐标系，得下列坐标：(0,0,0)D ，(0,1,0)C ，(1,1,0)B ，(0,1,1)C '，11(,1,)22O . ∵ 11(,1,)(1,0,1)022DO BC '⋅=---⋅-= ∴DO BC '⊥ 习题3.2 A 组（P111） 1、解：设正方形的棱长为1（1）1()()2MN CD MB B N CC C D ''''''⋅=+⋅+=，21MN CD '⋅== 112cos 12θ==，60θ=︒.（2）1()2MN AD MB B N AD ''⋅=+⋅=，21MN AD ⋅==1cos 22θ==，45θ=︒.2、证明：设正方体的棱长为1因为11()000DB AC DB BB AC ⋅=+⋅=+=，所以1DB AC ⊥.因为111111()000DB AD DA AB AD ⋅=+⋅=+=，所以11DB AD ⊥. 因此，1DB ⊥平面1ACD .3、证明：∵()cos cos 0OA BC OC OB OA OC OA OB OA θθ⋅=-⋅=-=，∴OA BC ⊥.4、证明：（1）因为11()000AC LE A A AC LE ⋅=+⋅=+=，所以1AC LE ⊥. 因为11()000AC EF A B BC EF ⋅=+⋅=+=，所以1AC EF ⊥. 因此，1AC ⊥平面EFGHLK . （2）设正方体的棱长为1因为1111()()1AC DB A A AC DB DB ⋅=+⋅+=-，211(3)3ACDB ⋅== 所以 1cos 3θ=-.因此1DB 与平面EFGHLK 的所成角α的余弦cos 3α=. 5、解：（1）222211111()()22222DE DE DE DE DA AB AC AB OA AC AB ==⋅=++-=++11(111111)42=++-+-=所以，2DE =（2）11111()()22222AE AO AC AB AO ⋅=+⋅=+=，32AE AO ⋅=1cos2θ===sin 3θ=点O 到平面ABC的距离sin 1OH OA θ=== 6、解：（1）设1AB =，作AO BC ⊥于点O ，连接DO .以点O 为原点，,,OD OC OA 的方向分别为x 轴、y 轴、z 轴正方向，建立坐标系，得下列坐标：(0,0,0)O ，D ，1(0,,0)2B ，3(0,,0)2C ，A .∴3((4DO DA ⋅=-⋅=，18DODA ⋅=，cos 2θ=. ∴ AD 与平面BCD所成角等于45︒.（2）(0,1,0)(0BC DA ⋅=⋅=. 所以，AD 与BC 所成角等于90︒.（3）设平面ABD 的法向量为(,,1)x y ，。

高二数学 (新课标人教A版)选修2-1《1.3简单的逻辑联结词》教案

1.3简单的逻辑联结词1.3.1且 1.3.2或学生探究过程：1、引入在当今社会中，人们从事任何工作、学习，都离不开逻辑．具有一定逻辑知识是构成一个公民的文化素质的重要方面．数学的特点是逻辑性强，特别是进入高中以后，所学的数学比初中更强调逻辑性．如果不学习一定的逻辑知识，将会在我们学习的过程中不知不觉地经常犯逻辑性的错误．其实，同学们在初中已经开始接触一些简易逻辑的知识．在数学中，有时会使用一些联结词，如“且”“或”“非”。

在生活用语中，我们也使用这些联结词，但表达的含义和用法与数学中的含义和用法不尽相同。

下面介绍数学中使用联结词“且”“或”“非”联结命题时的含义和用法。

为叙述简便，今后常用小写字母p，q，r，s，…表示命题。

（注意与上节学习命题的条件p 与结论q的区别）2、思考、分析问题1：下列各组命题中，三个命题间有什么关系？（1）①12能被3整除；②12能被4整除；③12能被3整除且能被4整除。

（2）①27是7的倍数；②27是9的倍数；③27是7的倍数或是9的倍数。

学生很容易看到，在第（1）组命题中，命题③是由命题①②使用联结词“且”联结得到的新命题，在第（2）组命题中，命题③是由命题①②使用联结词“或”联结得到的新命题，。

问题2：以前我们有没有学习过象这样用联结词“且”或“或”联结的命题呢？你能否举一些例子？例如：命题p：菱形的对角线相等且菱形的对角线互相平分。

命题q：三条边对应成比例的两个三角形相似或两个角相等的两个三角形相似。

3、归纳定义一般地，用联结词“且”把命题p和命题q联结起来，就得到一个新命题，记作p∧q读作“p且q”。

一般地，用联结词“或”把命题p和命题q联结起来，就得到一个新命题，记作p∨q,读作“p或q”。

命题“p∧q”与命题“p∨q”即，命题“p且q”与命题“p或q”中的“且”字与“或”字与下面两个命题中的“且”字与“或”字的含义相同吗？（1）若 x∈A且x∈B，则x∈A∩B。

选修2-1数学课后习题答案(全)

新课程标准数学选修2—1第一章课后习题解答第一章常用逻辑用语1．1命题及其关系练习（P4）1、略.2、（1）真；（2）假；（3）真；（4）真.3、（1）若一个三角形是等腰三角形，则这个三角形两边上的中线相等. 这是真命题.（2）若一个函数是偶函数，则这个函数的图象关于y 轴对称. 这是真命题.（3）若两个平面垂直于同一个平面，则这两个平面平行. 这是假命题.练习（P6）1、逆命题：若一个整数能被5整除，则这个整数的末位数字是0. 这是假命题.否命题：若一个整数的末位数字不是0，则这个整数不能被5整除. 这是假命题.逆否命题：若一个整数不能被5整除，则这个整数的末位数字不是0. 这是真命题.2、逆命题：若一个三角形有两个角相等，则这个三角形有两条边相等. 这是真命题.否命题：若一个三角形有两条边不相等，这个三角形有两个角也不相等. 这是真命题.逆否命题：若一个三角形有两个角不相等，则这个三角形有两条边也不相等.这是真命题.3、逆命题：图象关于原点对称的函数是奇函数. 这是真命题.否命题：不是奇函数的函数的图象不关于原点对称. 这是真命题.逆否命题：图象不关于原点对称的函数不是奇函数. 这是真命题.练习（P8）证明：若1a b -=，则22243a b a b -+-- ()()2()2322310a b a b a b b a b b a b =+-+---=++--=--=所以，原命题的逆否命题是真命题，从而原命题也是真命题.习题1.1 A 组（P8）1、（1）是；（2）是；（3）不是；（4）不是.2、（1）逆命题：若两个整数a 与b 的和a b +是偶数，则,a b 都是偶数. 这是假命题.否命题：若两个整数,a b 不都是偶数，则a b +不是偶数. 这是假命题.逆否命题：若两个整数a 与b 的和a b +不是偶数，则,a b 不都是偶数. 这是真命题.（2）逆命题：若方程20x x m +-=有实数根，则0m >. 这是假命题.否命题：若0m ≤，则方程20x x m +-=没有实数根. 这是假命题.逆否命题：若方程20x x m +-=没有实数根，则0m ≤. 这是真命题.3、（1）命题可以改写成：若一个点在线段的垂直平分线上，则这个点到线段的两个端点的距离相等. 逆命题：若一个点到线段的两个端点的距离相等，则这个点在线段的垂直平分线上.这是真命题.否命题：若一个点到不在线段的垂直平分线上，则这个点到线段的两个端点的距离不相等.这是真命题.逆否命题：若一个点到线段的两个端点的距离不相等，则这个点不在线段的垂直平分线上.这是真命题.（2）命题可以改写成：若一个四边形是矩形，则四边形的对角线相等.逆命题：若四边形的对角线相等，则这个四边形是矩形. 这是假命题.否命题：若一个四边形不是矩形，则四边形的对角线不相等. 这是假命题.逆否命题：若四边形的对角线不相等，则这个四边形不是矩形. 这是真命题.4、证明：如果一个三角形的两边所对的角相等，根据等腰三角形的判定定理，这个三角形是等腰三角形，且这两条边是等腰三角形，也就是说这两条边相等. 这就证明了原命题的逆否命题，表明原命题的逆否命题为真命题. 所以，原命题也是真命题.习题1.1 B 组（P8）证明：要证的命题可以改写成“若p ，则q ”的形式：若圆的两条弦不是直径，则它们不能互相平分.此命题的逆否命题是：若圆的两条相交弦互相平分，则这两条相交弦是圆的两条直径.可以先证明此逆否命题：设,AB CD 是O 的两条互相平分的相交弦，交点是E ，若E 和圆心O 重合，则,AB CD 是经过圆心O 的弦，,AB CD 是两条直径. 若E 和圆心O 不重合，连结,,AO BO CO 和DO ，则OE 是等腰AOB ∆，COD ∆的底边上中线，所以，OE AB ⊥，OE CD ⊥. AB 和CD 都经过点E ，且与OE 垂直，这是不可能的. 所以，E 和O 必然重合. 即AB 和CD 是圆的两条直径. 原命题的逆否命题得证，由互为逆否命题的相同真假性，知原命题是真命题.1．2充分条件与必要条件练习（P10）1、（1）⇒；（2）⇒；（3）⇒；（4）⇒.2、（1）. 3（1）.4、（1）真；（2）真；（3）假；（4）真.练习（P12）1、（1）原命题和它的逆命题都是真命题，p 是q 的充要条件；（2）原命题和它的逆命题都是真命题，p 是q 的充要条件；（3）原命题是假命题，逆命题是真命题，p 是q 的必要条件.2、（1）p 是q 的必要条件；（2）p 是q 的充分条件；（3）p 是q 的充要条件；（4）p 是q 的充要条件.习题1.2 A 组（P12）1、略.2、（1）假；（2）真；（3）真.3、（1）充分条件，或充分不必要条件；（2）充要条件；（3）既不是充分条件，也不是必要条件；（4）充分条件，或充分不必要条件.4、充要条件是222a b r +=.习题1.2 B 组（P13）1、（1）充分条件；（2）必要条件；（3）充要条件.2、证明：（1）充分性：如果222a b c ab ac bc ++=++，那么2220a b c ab ac bc ++---=. 所以222()()()0a b a c b c -+-+-=所以，0a b -=，0a c -=，0b c -=.即 a b c ==，所以，ABC ∆是等边三角形.（2）必要性：如果ABC ∆是等边三角形，那么a b c ==所以222()()()0a b a c b c -+-+-=所以2220a b c ab ac bc ++---=所以222a b c ab ac bc ++=++1．3简单的逻辑联结词练习（P18）1、（1）真；（2）假.2、（1）真；（2）假.3、（1）225+≠，真命题；（2）3不是方程290x -=的根，假命题；（31≠-，真命题.习题1.3 A 组（P18）1、（1）4{2,3}∈或2{2,3}∈，真命题；（2）4{2,3}∈且2{2,3}∈，假命题；（3）2是偶数或3不是素数，真命题；（4）2是偶数且3不是素数，假命题.2、（1）真命题；（2）真命题；（3）假命题.3、（1不是有理数，真命题；（2）5是15的约数，真命题；（3）23≥，假命题；（4）8715+=，真命题；（5）空集不是任何集合的真子集，真命题.习题1.3 B 组（P18）（1）真命题. 因为p 为真命题，q 为真命题，所以p q ∨为真命题；（2）真命题. 因为p 为真命题，q 为真命题，所以p q ∧为真命题；（3）假命题. 因为p 为假命题，q 为假命题，所以p q ∨为假命题；（4）假命题. 因为p 为假命题，q 为假命题，所以p q ∧为假命题.1．4全称量词与存在量词练习（P23）1、（1）真命题；（2）假命题；（3）假命题.2、（1）真命题；（2）真命题；（3）真命题.练习（P26）1、（1）00,n Z n Q ∃∈∉；（2）存在一个素数，它不是奇数；（3）存在一个指数函数，它不是单调函数.2、（1）所有三角形都不是直角三角形；（2）每个梯形都不是等腰梯形；（3）所有实数的绝对值都是正数.习题1.4 A 组（P26）1、（1）真命题；（2）真命题；（3）真命题；（4）假命题.2、（1）真命题；（2）真命题；（3）真命题.3、（1）32000,x N x x ∃∈≤；（2）存在一个可以被5整除的整数，末位数字不是0；（3）2,10x R x x ∀∈-+>；（4）所有四边形的对角线不互相垂直.习题1.4 B 组（P27）（1）假命题. 存在一条直线，它在y 轴上没有截距；（2）假命题. 存在一个二次函数，它的图象与x 轴不相交；（3）假命题. 每个三角形的内角和不小于180︒；（4）真命题. 每个四边形都有外接圆.第一章复习参考题A 组（P30）1、原命题可以写为：若一个三角形是等边三角形，则此三角形的三个内角相等.逆命题：若一个三角形的三个内角相等，则此三角形是等边三角形. 是真命题；否命题：若一个三角形不是等边三角形，则此三角形的三个内角不全相等. 是真命题；逆否命题：若一个三角形的三个内角不全相等，则此三角形不是等边三角形. 是真命题.2、略.3、（1）假；（2）假；（3）假；（4）假.4、（1）真；（2）真；（3）假；（4）真；（5）真.5、（1）2,0n N n ∀∈>；（2）{P P P ∀∈在圆222x y r +=上}，(OP r O =为圆心)；（3）(,){(,),x y x y x y ∃∈是整数}，243x y +=；（4）0{x x x ∃∈是无理数}，30{x q q ∈是有理数}. 6、（1）32≠，真命题；（2）54≤，假命题；（3）00,0x R x ∃∈≤，真命题；（4）存在一个正方形，它不是平行四边形，假命题.第一章复习参考题B 组（P31）1、（1）p q ∧；（2）()()p q ⌝∧⌝，或()p q ⌝∨.2、（1）Rt ABC ∀∆，90C ∠=︒，,,A B C ∠∠∠的对边分别是,,a b c ，则222c a b =+；（2）ABC ∀∆，,,A B C ∠∠∠的对边分别是,,a b c ，则sin sin sin a b c A B C ==.新课程标准数学选修2—1第二章课后习题解答第二章圆锥曲线与方程2．1曲线与方程练习（P37）1、是. 容易求出等腰三角形ABC 的边BC 上的中线AO 所在直线的方程是0x =.2、3218,2525a b ==. 3、解：设点,A M 的坐标分别为(,0)t ，(,)x y .（1）当2t ≠时，直线CA 斜率 20222CA k t t -==-- 所以，122CB CA t k k -=-= 由直线的点斜式方程，得直线CB 的方程为 22(2)2t y x --=-. 令0x =，得4y t =-，即点B 的坐标为(0,4)t -.由于点M 是线段AB 的中点，由中点坐标公式得4,22t t x y -==. 由2t x =得2t x =，代入42t y -=，得422x y -=，即20x y +-=……① （2）当2t =时，可得点,A B 的坐标分别为(2,0)，(0,2)此时点M 的坐标为(1,1)，它仍然适合方程①由（1）（2）可知，方程①是点M 的轨迹方程，它表示一条直线.习题2.1 A 组（P37）1、解：点(1,2)A -、(3,10)C 在方程2210x xy y -++=表示的曲线上；点(2,3)B -不在此曲线上2、解：当0c ≠时，轨迹方程为12c x +=；当0c =时，轨迹为整个坐标平面. 3、以两定点所在直线为x 轴，线段AB 垂直平分线为y 轴，建立直角坐标系，得点M 的轨迹方程为224x y +=.4、解法一：设圆22650x y x +-+=的圆心为C ，则点C 的坐标是(3,0).由题意，得CM AB ⊥，则有1CM AB k k =-.所以，13y y x x⨯=--(3,0)x x ≠≠ 化简得2230x y x +-=(3,0)x x ≠≠当3x =时，0y =，点(3,0)适合题意；当0x =时，0y =，点(0,0)不合题意.解方程组 222230650x y x x y x ⎧+-=⎪⎨+-+=⎪⎩，得5,3x y == 所以，点M 的轨迹方程是2230x y x +-=，533x ≤≤. 解法二：注意到OCM ∆是直角三角形，利用勾股定理，得2222(3)9x y x y ++-+=，即2230x y x +-=. 其他同解法一.习题2.1 B 组（P37）1、解：由题意，设经过点P 的直线l 的方程为1x y a b+=.因为直线l 经过点(3,4)P ，所以341a b+= 因此，430ab a b --= 由已知点M 的坐标为(,)a b ，所以点M 的轨迹方程为430xy x y --=.2、解：如图，设动圆圆心M 的坐标为(,)x y . 由于动圆截直线30x y -=和30x y +=所得弦分别为 AB ，CD ，所以，8AB =，4CD =. 过点M 分别作直线30x y -=和30x y +=的垂线，垂足分别为E ，F ，则4AE =，2CF =.ME =，MF =. 连接MA ，MC ，因为MA MC =，则有，2222AE ME CF MF +=+ 所以，22(3)(3)1641010x y x y -++=+，化简得，10xy =. 因此，动圆圆心的轨迹方程是10xy =.2．2椭圆练习（P42）1、14. 提示：根据椭圆的定义，1220PF PF +=，因为16PF =，所以214PF=. 2、（1）22116x y +=；（2）22116y x +=；（3）2213616x y +=，或2213616y x +=. 3、解：由已知，5a =，4b =，所以3c .（1）1AF B ∆的周长1212AF AF BF BF =+++. 由椭圆的定义，得122AF AF a +=，122BF BF a +=.所以，1AF B ∆的周长420a ==.（2）如果AB 不垂直于x 轴，1AF B ∆的周长不变化.这是因为①②两式仍然成立，1AF B ∆的周长20=，这是定值.4、解：设点M 的坐标为(,)x y ，由已知，得直线AM 的斜率 1AM y k x =+(1)x ≠-；直线BM 的斜率 1BMy k x =-(1)x ≠；由题意，得2AM BM k k =，所以211y y x x =⨯+-(1,0)x y ≠±≠ 化简，得3x =-(0)y ≠因此，点M 的轨迹是直线3x =-，并去掉点(3,0)-.练习（P48）1、以点2B （或1B）为圆心，以线段2OA （或1OA ）为半径画圆，圆与x 轴的两个交点分别为12,F F .点12,F F 就是椭圆的两个焦点.这是因为，在22Rt B OF ∆中，2OB b =，22B F OA =所以，2OF c =. 同样有1OF c =.2、（1）焦点坐标为(8,0)-，(8,0)；（2）焦点坐标为(0,2)，(0,2)-. 3、（1）2213632x y +=；（2）2212516y x+=. 4、（1）22194x y += （2）22110064x y +=，或22110064y x +=. 5、（1）椭圆22936x y +=的离心率是3，椭圆2211612x y +=的离心率是12， 12>，所以，椭圆2211612x y +=更圆，椭圆22936x y +=更扁；（2）椭圆22936x y +=的离心率是3，椭圆221610x y +=的离心率是5，因为35>，所以，椭圆221610x y +=更圆，椭圆22936x y +=更扁.6、（1）8(3,)5；（2）(0,2)；（3）4870(,)3737--. 7、7. 习题2.2 A 组（P49） 1、解：由点(,)M x y10=以及椭圆的定义得，点M 的轨迹是以1(0,3)F -，2(0,3)F 为焦点，长轴长为10的椭圆. 它的方程是2212516y x +=. 2、（1）2213632x y +=；（2）221259y x +=；（3）2214940x y +=，或2214940y x +=. 3、（1）不等式22x -≤≤，44y -≤≤表示的区域的公共部分；（2）不等式x -≤≤101033y -≤≤表示的区域的公共部分. 图略. 4、（1）长轴长28a =，短轴长24b =，离心率2e =，焦点坐标分别是(-，，顶点坐标分别为(4,0)-，(4,0)，(0,2)-，(0,2)；（2）长轴长218a =，短轴长26b =，离心率3e =，焦点坐标分别是(0,-，，顶点坐标分别为(0,9)-，(0,9)，(3,0)-，(3,0).5、（1）22185x y +=；（2）2219x y +=，或221819y x +=；（3）221259x y +=，或221259y x +=. 6、解：由已知，椭圆的焦距122F F =.因为12PF F ∆的面积等于1，所以，12112P F F y ⨯⨯=，解得1P y =. 代入椭圆的方程，得21154x +=，解得2x =±. 所以，点P的坐标是(1)2±±，共有4个. 7、解：如图，连接QA . 由已知，得QA QP =.所以，QO QA QO QP OP r +=+==.又因为点A 在圆内，所以OA OP <根据椭圆的定义，点Q 的轨迹是以,O A 为焦点，r 为长轴长的椭圆.8、解：设这组平行线的方程为32y x m =+. 把32y x m =+代入椭圆方程22149x y +=，得22962180x mx m ++-=. 这个方程根的判别式 223636(218)m m ∆=--（1）由0∆>，得m -<<当这组直线在y 轴上的截距的取值范围是(-时，直线与椭圆相交.（2）设直线与椭圆相交得到线段AB ，并设线段AB 的中点为(,)M x y . 则 1223x x m x +==-. 因为点M 在直线32y x m =+上，与3m x =-联立，消去m ，得320x y +=. 这说明点M 的轨迹是这条直线被椭圆截下的弦（不包括端点），这些弦的中点在一条直线上. 9、222213.525 2.875x y +=. 10、地球到太阳的最大距离为81.528810⨯km ，最下距离为81.471210⨯km.习题2.2 B 组（P50）1、解：设点M 的坐标为(,)x y ，点P 的坐标为00(,)x y ，则0x x =，032y y =. 所以0x x =，023y y = ……①. 因为点00(,)P x y 在圆上，所以22004x y += ……②.将①代入②，得点M 的轨迹方程为22449x y +=，即22149x y += 所以，点M 的轨迹是一个椭圆与例2相比可见，椭圆也可以看作是由圆沿某个方向压缩或拉伸得到.2、解法一：设动圆圆心为(,)P x y ，半径为R ，两已知圆的圆心分别为12,O O .分别将两已知圆的方程 22650x y x +++=，226910x y x +--=配方，得 22(3)4x y ++=， 22(3)100x y -+=当P 与1O ：22(3)4x y ++=外切时，有12O P R =+……① 当P 与2O ：22(3)100x y -+=内切时，有210O P R =- ……② ①②两式的两边分别相加，得1212O P O P +=12……③化简方程③.先移项，再两边分别平方，并整理，得 12x =+ ……④ 将④两边分别平方，并整理，得 22341080x y +-= ……⑤ 将常数项移至方程的右边，两边分别除以108，得 2213627x y += ……⑥ 由方程⑥可知，动圆圆心的轨迹是椭圆，它的长轴和短轴长分别为12，. 12= ……①由方程①可知，动圆圆心(,)P x y 到点1(3,0)O -和点2(3,0)O 距离的和是常数12，所以点P 的轨迹方程是焦点为(3,0)-、(3,0)，长轴长等于12的椭圆.并且这个椭圆的中心与坐标原点重合，焦点在x轴上，于是可求出它的标准方程. 因为 26c =，212a =，所以3c =，6a =所以236927b =-=. 于是，动圆圆心的轨迹方程为2213627x y +=. 3、解：设d 是点M 到直线8x =的距离，根据题意，所求轨迹就是集合12MF PM d ⎧⎫==⎨⎬⎩⎭由此得 12= 将上式两边平方，并化简，得 223448x y +=，即2211612x y += 所以，点M 的轨迹是长轴、短轴长分别为8，.4、解：如图，由已知，得(0,3)E -，(4,0)F 因为,,R S T 是线段OF 的四等分点，,,R S T '''是线段CF 的四等分点，所以，(1,0),(2,0),(3,0)R S T ；933(4,),(4,),(4,)424R S T '''. 直线ER 的方程是33y x =-；直线GR '的方程是3316y x =-+. 联立这两个方程，解得 3245,1717x y ==. 所以，点L 的坐标是3245(,)1717.同样，点M 的坐标是169(,)55，点N 的坐标是9621(,)2525.由作图可见，可以设椭圆的方程为22221x y m n+=(0,0)m n >> ……①把点,L M 的坐标代入方程①，并解方程组，得22114m =，22113n =. 所以经过点,L M 的椭圆方程为221169x y +=. 把点N 的坐标代入22169x y +，得22196121()()11625925⨯+⨯=，所以，点N 在221169x y +=上. 因此，点,,L M N 都在椭圆221169x y +=上. 2．3双曲线练习（P55）1、（1）221169x y -=. （2）2213y x -=. （3）解法一：因为双曲线的焦点在y 轴上所以，可设它的标准方程为22221y x a b-=(0,0)a b >>将点(2,5)-代入方程，得222541a b-=，即22224250a b a b +-= 又 2236a b +=解方程组 222222425036a b a b a b ⎧+-=⎪⎨+=⎪⎩令22,m a n b ==，代入方程组，得425036mn m n m n +-=⎧⎨+=⎩解得 2016m n =⎧⎨=⎩，或459m n =⎧⎨=-⎩第二组不合题意，舍去，得2220,16a b ==所求双曲线的标准方程为2212016y x -=解法二：根据双曲线的定义，有2a ==.所以，a = 又6c =，所以2362016b =-=由已知，双曲线的焦点在y 轴上，所以所求双曲线的标准方程为2212016y x -=. 2、提示：根据椭圆中222a b c -=和双曲线中222a b c +=的关系式分别求出椭圆、双曲线的焦点坐标.3、由(2)(1)0m m ++>，解得2m <-，或1m >- 练习（P61）1、（1）实轴长2a =，虚轴长24b =；顶点坐标为-；焦点坐标为(6,0),(6,0)-；离心率4e =. （2）实轴长26a =，虚轴长218b =；顶点坐标为(3,0),(3,0)-；焦点坐标为-；离心率e =（3）实轴长24a =，虚轴长24b =；顶点坐标为(0,2),(0,2)-；焦点坐标为-；离心率e =（4）实轴长210a =，虚轴长214b =；顶点坐标为(0,5),(0,5)-；焦点坐标为；离心率e =2、（1）221169x y -=；（2）2213628y x -=. 3、22135x y -= 4、2211818x y -=，渐近线方程为y x =±. 5、（1）142(6,2),(,)33-；（2）25(,3)4习题2.3 A 组（P61）1、把方程化为标准方程，得2216416y x -=. 因为8a =，由双曲线定义可知，点P 到两焦点距离的差的绝对值等于16. 因此点P 到另一焦点的距离是17.2、（1）2212016x y -=. （2）2212575x y -= 3、（1）焦点坐标为12(5,0),(5,0)F F -，离心率53e =；（2）焦点坐标为12(0,5),(0,5)F F -，离心率54e =；4、（1）2212516x y -=. （2）221916y x -=（3）解：因为ce a==，所以222c a =，因此2222222b c a a a a =-=-=. 设双曲线的标准方程为 22221x y a a -=，或22221y x a a-=.将(5,3)-代入上面的两个方程，得222591a a -=，或229251a a -=.解得 216a = （后一个方程无解）.所以，所求的双曲线方程为2211616x y -=. 5、解：连接QA ，由已知，得QA QP =.所以，QA QO QP QO OP r -=-==. 又因为点A 在圆外，所以OA OP >.根据双曲线的定义，点Q 的轨迹是以,O A 为焦点，r 为实轴长的双曲线.6、22188x y -=.习题2.3 B 组（P62）1、221169x y -= 2、解：由声速及,A B 两处听到爆炸声的时间差，可知,A B 两处与爆炸点的距离的差，因此爆炸点应位于以,A B 为焦点的双曲线上.使,A B 两点在x 轴上，并且原点O 与线段AB 的中点重合，建立直角坐标系xOy . 设爆炸点P 的坐标为(,)x y ，则 34031020PA PB -=⨯=. 即 21020a =，510a =.又1400AB =，所以21400c =，700c =，222229900b c a =-=.因此，所求双曲线的方程为221260100229900x y -=. 3、22221x y a b-=4、解：设点11(,)A x y ，22(,)B x y 在双曲线上，且线段AB 的中点为(,)M x y .设经过点P 的直线l 的方程为1(1)y k x -=-，即1y kx k =+-把1y kx k =+-代入双曲线的方程2212y x -=得 222(2)2(1)(1)20k x k k x k ------=（220k -≠） ……①所以，122(1)22x x k k x k +-==- 由题意，得2(1)12k k k-=-，解得 2k =. 当2k =时，方程①成为22430x x -+=.根的判别式162480∆=-=-<，方程①没有实数解.所以，不能作一条直线l 与双曲线交于,A B 两点，且点P 是线段AB 的中点.2．4抛物线练习（P67）1、（1）212y x =；（2）2y x =；（3）22224,4,4,4y x y x x y x y ==-==-.2、（1）焦点坐标(5,0)F ，准线方程5x =-；（2）焦点坐标1(0,)8F ，准线方程18y =-；（3）焦点坐标5(,0)8F -，准线方程58x =；（4）焦点坐标(0,2)F -，准线方程2y =； 3、（1）a ，2pa -. （2），(6,- 提示：由抛物线的标准方程求出准线方程. 由抛物线的定义，点M 到准线的距离等于9，所以 39x +=，6x =，y =±练习（P72）1、（1）2165y x =；（2）220x y =；（3）216y x =-；（4）232x y =-. 2、图形见右，x 的系数越大，抛物线的开口越大. 3、解：过点(2,0)M 且斜率为1的直线l 的方程为2y x =-与抛物线的方程24y x =联立 224y x y x=-⎧⎨=⎩解得1142x y ⎧=+⎪⎨=+⎪⎩2242x y ⎧=-⎪⎨=-⎪⎩ 设11(,)A x y ，22(,)B x y，则AB ===4、解：设直线AB 的方程为x a =(0)a >.将x a =代入抛物线方程24y x =，得24y a =，即y =±因为22AB y ==⨯== 所以，3a =因此，直线AB 的方程为3x =.习题2.4 A 组（P73）1、（1）焦点坐标1(0,)2F ，准线方程12y =-；（2）焦点坐标3(0,)16F -，准线方程316y =；（3）焦点坐标1(,0)8F -，准线方程18x =；（4）焦点坐标3(,0)2F ，准线方程32x =-.2、（1）28y x =-；（2），或(4,-3、解：由抛物线的方程22y px =(0)p >，得它的准线方程为2px =-. 根据抛物线的定义，由2MF p =，可知，点M 的准线的距离为2p .设点M 的坐标为(,)x y ，则 22p x p +=，解得32px =. 将32p x =代入22y px =中，得y =. 因此，点M的坐标为3()2p，3(,)2p.4、（1）224y x =，224y x =-；（2）212x y =-（图略）5、解：因为60xFM ∠=︒，所以线段FM所在直线的斜率tan 60k =︒=. 因此，直线FM 的方程为1)y x =-与抛物线24y x =联立，得21)142y x y x ⎧=-⎪⎨=⎪⎩将1代入2得，231030x x -+=，解得，113x =，23x =把113x =，23x =分别代入①得1y =，2y =由第5题图知1(,33-不合题意，所以点M 的坐标为.因此，4FM ==6、证明：将2y x =-代入22y x =中，得2(2)2x x -=，化简得 2640x x -+=，解得 3x=±则 321y ==±因为OB k ，OA k=所以15195OB OA k k -⋅===--所以 OA OB ⊥7、这条抛物线的方程是217.5x y = 8、解：建立如图所示的直角坐标系，设拱桥抛物线的方程为22x py =-，因为拱桥离水面2 m ，水面宽4 m 所以 222(2)p =--，1p =因此，抛物线方程为22x y =- ……①水面下降1 m ，则3y =-，代入①式，得22(3)x =-⨯-，x =这时水面宽为 m.习题2.2 B 组（P74）1、解：设垂线段的中点坐标为(,)x y ，抛物线上相应点的坐标为11(,)x y .根据题意，1x x =，12y y =，代入2112y px =，得轨迹方程为212y px =. 由方程可知，轨迹为顶点在原点、焦点坐标为(,0)8p的抛物线. 2、解：设这个等边三角形OAB 的顶点,A B 在抛物线上，且坐标分别为11(,)x y ，22(,)x y ，则 2112y px =，2222y px =.又OA OB =，所以 22221122x y x y +=+即221212220x x px px -+-=，221212()2()0x x p x x -+-=因此，1212()(2)0x x x x p -++= 因为120,0,20x x p >>>，所以12x x = 由此可得12y y =，即线段AB 关于x 轴对称. 因为x 轴垂直于AB ，且30AOx ∠=︒，所以11tan30y x =︒=. 因为2112y x p=，所以1y =，因此12AB y ==.3、解：设点M 的坐标为(,)x y由已知，得直线AM 的斜率 (1)1AM yk x x =≠-+. 直线BM 的斜率 (1)1BM yk x x =≠-. 由题意，得2AM BM k k -=，所以，2(1)11y y x x x -=≠±+-，化简，得2(1)(1)x y x =--≠± 第二章复习参考题A 组（P80）1、解：如图，建立直角坐标系，使点2,,A B F 在x 轴上，2F 为椭圆的右焦点（记1F 为左焦点）.因为椭圆的焦点在x 轴上，所以设它的标准方程为22221(0)x y a b a +=>>.则 22a c OA OF F A -=-=63714396810=+=，22a c OB OF F B +=+=637123848755=+=，解得 7782.5a =，8755c =所以b ===用计算器算得 7722b ≈因此，卫星的轨道方程是2222177837722x y +=. 2、解：由题意，得 12a c R r a c R r -=+⎧⎨+=+⎩，解此方程组，得1221222R r r a r r c ++⎧=⎪⎪⎨-⎪=⎪⎩因此卫星轨道的离心率21122c r r e a R r r -==++. 3、（1）D ；（2）B .4、（1）当0α=︒时，方程表示圆.（2）当090α︒<<︒时，方程化成2211cos y x α+=. 方程表示焦点在y 轴上的椭圆. （3）当90α=︒时，21x =，即1x =±，方程表示平行于y 轴的两条直线.（4）当90180α︒<≤︒时，因为cos 0α<，所以22cos 1x y α+=表示双曲线，其焦点在x 轴上.而当180α=︒时，方程表示等轴双曲线. 5、解：将1y kx =-代入方程224x y -=得 2222140x k x kx -+--= 即 22(1)250k x kx -+-= ……① 222420(1)2016k k k ∆=+-=-令 0∆<，解得2k >，或2k <- 因为0∆<，方程①无解，即直线与双曲线没有公共点，所以，k的取值范围为k >k <6、提示：设抛物线方程为22y px =，则点B 的坐标为(,)2p p ，点C 的坐标为(,)2pp - 设点P 的坐标为(,)x y ，则点Q 的坐标为(,0)x .因为，PQ y ==2BC p =，OQ x =.所以，2PQ BC OQ =，即PQ 是BC 和OQ 的比例中项.7、解：设等边三角形的另外两个顶点分别是,A B ，其中点A 在x 轴上方.直线FA 的方程为 )32py x =-与22y px =联立，消去x ，得 220y p --=解方程，得 12)y p =，22)y p =把12)y p =代入)2p y x =-，得 17(2x p =+.把22)y p =代入)32p y x =-，得 27(2x p =-.所以，满足条件的点A 有两个17((2))2A p p +，27((2))2A p p -.根据图形的对称性，可得满足条件的点B 也有两个17((,2))2B p p +-，27((,2))2B p p --所以，等边三角形的边长是112)A B p =，或者222(2A B p =. 8、解：设直线l 的方程为2y x m =+.把2y x m =+代入双曲线的方程222360x y --=，得221012360x mx m +++=.1265mx x +=-，2123610m x x += ……①由已知，得 21212(14)[()4]16x x x x ++-= ……②把①代入②，解得 3m =±所以，直线l 的方程为23y x =±9、解：设点A的坐标为11(,)x y，点B的坐标为22(,)x y，点M的坐标为(,)x y.并设经过点M的直线l的方程为1(2)y k x-=-，即12y kx k=+-.把12y kx k=+-代入双曲线的方程2212yx-=，得222(2)2(12)(12)20k x k k x k------=2(20)k-≠. ……①所以，122(12)22x x k kxk+-==-由题意，得2(12)22k kk-=-，解得4k=当4k=时，方程①成为21456510x x-+=根的判别式25656512800∆=-⨯=>，方程①有实数解.所以，直线l的方程为47y x=-.10、解：设点C的坐标为(,)x y.由已知，得直线AC的斜率(5)5ACyk xx=≠-+直线BC的斜率(5)5BCyk xx=≠-由题意，得AC BCk k m=. 所以，(5)55y ym xx x⨯=≠±+-化简得，221(5)2525x yxm-=≠±当0m<时，点C的轨迹是椭圆(1)m≠-，或者圆(1)m=-，并除去两点(5,0),(5,0)-；当0m>时，点C的轨迹是双曲线，并除去两点(5,0),(5,0)-；11、解：设抛物线24y x=上的点P的坐标为(,)x y，则24y x=.点P到直线3y x=+的距离d===当2y=时，d. 此时1x=，点P的坐标是(1,2).12、解：如图，在隧道的横断面上，以拱顶为原点、拱高所在直线为y轴（向上），建立直角坐标系.设隧道顶部所在抛物线的方程为22x py=-因为点(4,4)C -在抛物线上所以 242(4)p =-- 解得 24p =-所以，隧道顶部所在抛物线的方程为24x y =-.设0.5EF h =+. 则(3, 5.5)F h -把点F 的坐标代入方程24x y =-，解得 3.25h =. 答：车辆通过隧道的限制高度为3.2 m.第二章复习参考题B 组（P81）1、12PF F S ∆=.2、解：由题意，得1PF x ⊥轴.把x c =-代入椭圆方程，解得 2b y a=±. 所以，点P 的坐标是2(,)b c a -直线OP 的斜率21b k ac =-. 直线AB 的斜率2bk a =-.由题意，得2b bac a =，所以，b c =，a =.由已知及1F A a c =+，得a c +=所以 (1c +=+ c =所以，a =，b =因此，椭圆的方程为221105x y +=. 3、解：设点A 的坐标11(,)x y ，点B 的坐标22(,)x y .由OA OB ⊥，得12120x x y y +=. 由已知，得直线AB 的方程为25y x =-+. 则有 12125()250y y y y -++= ……①由25y x =-+与22y px =消去x ，得250y py p +-= ……②（第4题）12y y p +=-，125y y p =- ……③ 把③代入①，解得54p = 当54p =时，方程②成为245250y y +-=，显然此方程有实数根. 所以，54p = 4、解：如图，以连接12,F F 的直线为x 轴，线段12F F 的中点为原点，建立直角坐标系.对于抛物线，有176352922922p=+=，所以，4584p =，29168p =.对于双曲线，有2080529c a c a +=⎧⎨-=⎩解此方程组，得775.5a =，1304.5c = 因此，2221100320b c a =-=.所以，所求双曲线的方程是221601400.31100320x y -=(775.5)x ≥. 因为抛物线的顶点横坐标是 (1763)(1763775.5)987.5a --=--=- 所以，所求抛物线的方程是 29168(987.5)y x =+ 答：抛物线的方程为29168(987.5)y x =+，双曲线的方程是221601400.31100320x y -=(775.5)x ≥. 5、解：设点M 的坐标为(,)x y由已知，得直线AM 的斜率 (1)1AM yk x x =≠-+ 直线BM 的斜率 (1)1BM yk x x =≠-由题意，得2AM BM k k +=，所以2(1)11y y x x x +=≠±-+，化简，得21(1)xy x x =-≠± 所以，点M 轨迹方程是21(1)xy x x =-≠±.6、解：（1）当1m =时，方程表示x 轴；（2）当3m =时，方程表示y 轴；（3）当1,3m m ≠≠时，把方程写成22131x y m m +=--. ①当13,2m m <<≠时，方程表示椭圆； ②2m =时，方程表示圆；③当1m <，或3m >时，方程表示双曲线.7、以AB 为直径的圆与抛物线的准线l 相切.证明：如图，过点,A B 分别作抛物线22(0)y px p =>的准线l 的垂线，垂足分别为,D E .由抛物线的定义，得 AD AF =，BE BF =.所以，AB AF BF AD BE =+=+.设AB 的中点为M ，且过点M 作抛物线22(0)y px p =>的准线l 的垂线，垂足为C .显然MC ∥x 轴，所以，MC 是直角梯形ADEB 的中位线. 于是，11()22MC AD BE AB =+=. 因此，点C 在以AB 为直径的圆上.又MC l ⊥，所以，以AB 为直径的圆与抛物线的准线l 相切. 类似地，可以证明：对于椭圆，以经过焦点的弦为直径的圆与相应的准线相离；对于双曲线，以经过焦点的弦为直径的圆与相应的准线相交.新课程标准数学选修2—1第三章课后习题解答第三章空间向量与立体几何 3．1空间向量及其运算练习（P86）1、略.2、略.3、A C AB AD AA ''=+-，BD AB AD AA ''=-+，DB AA AB AD ''=--. 练习（P89）1、（1）AD ；（2）AG ；（3）MG .2、（1）1x =；（2）12x y ==；（3）12x y ==. 3.练习（P92） 1、B .2、解：因为AC AB AD AA ''=++，所以22()AC AB AD AA ''=++2222222()4352(0107.5)85AB AD AA AB AD AB AA AD AA '''=+++⋅+⋅+⋅=+++⨯++=（第7题）PRS B CAQ O（第3题）所以85AC '=3、解：因为AC α⊥所以AC BD ⊥，AC AB ⊥，又知BD AB ⊥.所以0AC BD ⋅=，0AC AB ⋅=，又知0BD AB ⋅=. 2CD CD CD =⋅222222()()CA AB BD CA AB BD CA AB BDa b c =++⋅++=++=++所以CD .练习（P94）1、向量c 与a b +，a b -一定构成空间的一个基底. 否则c 与a b +，a b -共面，于是c 与a ，b 共面，这与已知矛盾.2、共面2、（1）解：OB OB BB OA AB BB OA OC OO a b c ''''=+=++=++=++；BA BA BB OC OO c b '''=+=-+=-CA CA AA OA OC OO a b c '''=+=-+=-+（2）1111()2222OG OC CG OC CB b a c a b c '=+=+=++=++. 练习（P97）1、（1）(2,7,4)-；（2）(10,1,16)-；（3）(18,12,30)-；（4）2.2、略.3、解：分别以1,,DA DC DD 所在的直线为x 轴、y 轴、z 轴，建立空间直角坐标系.则(0,0,0)D ，1(1,1,1)B ，1(1,,0)2M ，(0,1,0)C 所以，1(1,1,1)DB =，1(1,,0)2CM =-.所以，111110cos ,153DB CM DB CM DB CM-+⋅<>===⋅.习题3.1 A 组（P97）1、解：如图，（1）AB BC AC +=；（2）AB AD AA AC AA AC CC AC ''''++=+=+=；（3）设点M 是线段CC '的中点，则12AB AD CC AC CM AM '++=+=；（4）设点G 是线段AC '的三等分点，则11()33AB AD AA AC AG ''++==.向量,,,AC AC AM AG '如图所示. 2、A .3、解：22()AC AB AD AA ''=++2222222()15372(53573722298AB AD AA AB AD AB AA AD AA '''=+++⋅+⋅+⋅=+++⨯⨯+⨯⨯+⨯⨯=+所以，13.3AC '≈.4、（1）21cos602AB AC AB AC a ⋅=⋅︒=；（2）21cos1202AD DB AD DB a ⋅=⋅︒=-；（3）21cos1802GF AC GF AC a ⋅=⋅︒=- 11()22GF AC a ==；（4）21cos604EF BC EF BC a ⋅=⋅︒= 11()22EF BD a ==；（5）21cos1204FG BA FG BA a ⋅=⋅︒=- 11()22FG AC a ==；（6）11()22GE GF GC CB BA CA ⋅=++⋅2111()222111424111cos120cos60cos6042414DC CB BA CA DC CA CB CA BA CA DC CA CB CA BA CA a =++⋅=⋅+⋅+⋅=⋅︒+⋅︒+⋅︒=5、（1）60︒；（2）略.6、向量a 的横坐标不为0，其余均为0；向量b 的纵坐标不为0，其余均为0；向量c 的竖坐标不为0，其余均为0.7、（1）9；（2）(14,3,3)-.8、解：因为a b ⊥，所以0a b ⋅=，即8230x --+=，解得103x =.9、解：(5,1,10)AB =--，(5,1,10)BA =-设AB 的中点为M ，119()(,,2)222OM OA OB =+=-，所以，点M 的坐标为19(,,2)22-，(AB =-10、解：以1,,DA DC DD 分别作为x 轴、y 轴、z 轴建立空间直角坐标系O xyz -.则1,,,C M D N 的坐标分别为：(0,1,0)C ，1(1,0,)2M ，1(0,0,1)D ，1(1,1,)2N . 1(1,1,)2CM =-，11(1,1,)2D N =- 所以2312CM ==，21312D N == 111114cos ,994CM D N --<>==- 由于异面直线CM 和1D N 所成的角的范围是[0,]2π因此，CM 和1D N 所成的角的余弦值为19. 11、31(,,3)22- 习题3.1 B 组（P99）1、证明：由已知可知，OA BC ⊥，OB AC ⊥∴ 0OA BC ⋅=，0OB AC ⋅=，所以()0OA OC OB ⋅-=，()0OB OC OA ⋅-=. ∴ OA OC OA OB ⋅=⋅，OB OC OB OA ⋅=⋅.∴ 0OA OC OB OC ⋅-⋅=，()0OA OB OC -⋅=，0BA OC ⋅=. ∴ OC AB ⊥.2、证明：∵ 点,,,E F G H 分别是,,,OA OB BC CA 的中点.∴ 12EF AB =，12HG AB =，所以EF HG = ∴四边形EFGH 是平行四边形.1122EF EH AB OC ⋅=⋅11()()44OB OA OC OB OC OA OC =-⋅=⋅-⋅∵ OA OB =，CA CB =（已知），OC OC =. ∴ BOC ∆≌AOC ∆（SSS ） ∴ BOC AOC ∠=∠∴ OB OC OA OC ⋅=⋅∴ 0EF EH ⋅= ∴ EF EH ⊥∴ 平行四边形□EFGH 是矩形.3、已知：如图，直线OA ⊥平面α，直线BD ⊥平面α，,O B 为垂足. 求证：OA ∥BD证明：以点O 为原点，以射线OA 方向为z 轴正方向，建立空间直角坐标系O xyz -，,,i j k 分别为沿x 轴、y 轴、z 轴的坐标向量，且设(,,)BD x y z =.∵ BD α⊥.∴ BD i ⊥，BD j ⊥.∴ (,,)(1,0,0)0BD i x y z x ⋅=⋅==，(,,)(0,1,0)0BD j x y z y ⋅=⋅==. ∴ (0,0,)BD z =. ∴ BD zk =.∴ BD ∥k ，又知,O B 为两个不同的点.∴ BD ∥OA .3．2立体几何中的向量方法练习（P104）1、（1）3b a =，1l ∥2l ；（2）0a b ⋅=，1l ⊥2l ；（3）3b a =-，1l ∥2l .2、（1）0u v ⋅=，αβ⊥；（2）2v u =-，α∥β；（3）292247u v u v⋅=-，α与β相交，交角的余弦等于292247.练习（P107）1、证明：设正方形的棱长为1.11D F DF DD =-，AE BE BA =-.因为11()000D F AD DF DD AD ⋅=-⋅=-=，所以1D F AD ⊥. 因为1111()()00022D F AE DF DD BE BA ⋅=-⋅-=+-+=，所以1D F AE ⊥. 因此1D F ⊥平面ADE .2、解：22()CD CD CA AB BD ==++（第3题）222222361664268cos(18060)68CA AB BD CA AB CA BD AB BD =+++⋅+⋅+⋅=+++⨯⨯⨯︒-︒=∴CD =练习（P111）1、证明：1()()2MN AB MB BC CN AB MB BC CD AB ⋅=++⋅=++⋅ 222211()22111cos120cos60cos600222MB BC AD AC AB a a a a =++-⋅=+︒+︒-︒=∴ MN AB ⊥. 同理可证MN CD ⊥.2、解：222222()2cos l EF EA A A AF m d n mn θ''==++=+++（或2cos()mn πθ-）22222cos d l m n mn θ=--，所以 22cos AA d mn θ'=.3、证明：以点D 为原点，,,DA DC DD '的方向分别为x 轴、y 轴、z 轴正方向，建立坐标系，得下列坐标：(0,0,0)D ，(0,1,0)C ，(1,1,0)B ，(0,1,1)C '，11(,1,)22O . ∵ 11(,1,)(1,0,1)022DO BC '⋅=---⋅-= ∴DO BC '⊥ 习题3.2 A 组（P111）1、解：设正方形的棱长为1（1）1()()2MN CD MB B N CC C D ''''''⋅=+⋅+=，212MN CD '⋅== 112cos 12θ==，60θ=︒.（2）1()2MN AD MB B N AD ''⋅=+⋅=，212MN AD ⋅==1cos 2θ==，45θ=︒.2、证明：设正方体的棱长为1因为11()000DB AC DB BB AC ⋅=+⋅=+=，所以1DB AC ⊥.因为111111()000DB AD DA AB AD ⋅=+⋅=+=，所以11DB AD ⊥. 因此，1DB ⊥平面1ACD .3、证明：∵()cos cos 0OA BC OC OB OA OC OA OB OA θθ⋅=-⋅=-=，∴OA BC ⊥.4、证明：（1）因为11()000AC LE A A AC LE ⋅=+⋅=+=，所以1AC LE ⊥. 因为11()000AC EF A B BC EF ⋅=+⋅=+=，所以1AC EF ⊥. 因此，1AC ⊥平面EFGHLK . （2）设正方体的棱长为1因为1111()()1AC DB A A AC DB DB ⋅=+⋅+=-，211(3)3AC DB ⋅== 所以 1cos 3θ=-. 因此1DB 与平面EFGHLK 的所成角α的余弦cos 3α=. 5、解：（1）222211111()()22222DE DE DE DE DA AB AC AB OA AC AB ==⋅=++-=++11(111111)42=++-+-= 所以，2DE =（2）11111()()22222AE AO AC AB AO ⋅=+⋅=+=，32AE AO ⋅=1cos 2θ===sin θ=点O 到平面ABC 的距离sin 1OH OA θ===. 6、解：（1）设1AB =，作AO BC ⊥于点O ，连接DO .以点O 为原点，,,OD OC OA 的方向分别为x 轴、y 轴、z 轴正方向，建立坐标系，得下列坐标：(0,0,0)O，D ，1(0,,0)2B，3(0,,0)2C，A . ∴3((4DO DA ⋅=-⋅=，184DO DA ⋅=，cos 2θ=. ∴ AD 与平面BCD 所成角等于45︒. （2）(0,1,0)(0BC DA ⋅=⋅=. 所以，AD 与BC 所成角等于90︒.（3）设平面ABD 的法向量为(,,1)x y ，则1(,,1)(,,1)(0,,02x y AB x y ⋅=⋅=，(,,1)(,,1)0x y AD x y ⋅=⋅=. 解得 1x =，y =显然(0,0,1)为平面BCD 的法向量.(0,0,1)1⋅=，cos θ==因此，二面角A BD C --的余弦cos cos()απθ=-=7、解：设点B 的坐标为(,,)x y z ，则(1,2,)AB x y z =-+.因为AB ∥α，所以123412x y z-+==-. 因为226AB α==26=.解得5x =-，6y =，24z =，或7x =，10y =-，24z =-.8、解：以点O 为原点建立坐标系，得下列坐标：(,,0)A a a -，(,,0)B a a ，(,,0)C a a -，(,,0)D a a --，(0,0,)V h ，(,,)222a a hE -.（1）222233(,,)(,,)6222222cos ,10a a h a a h h a BE DE h a BE DE--⋅-<>==+.（2）223(,,)(,,)02222a a h h VC BE a a h a ⋅=--⋅--=-=，222h a = 222222641cos ,10123h a a BE DE h a a --<>===-+9、解：以点A 为原点建立坐标系，得下列坐标：(0,0,0)A ，(0,1,0)B ，111(,,)222O -，1(0,0,1)A ，1(1,0,1)D -，1(0,0,)2M .因为10OM AA ⋅=，10OM BD ⋅=，所以1OM AA ⊥，1OM BD ⊥，2OM ==. 10、解：以点A 为原点建立坐标系，得下列坐标：(0,0,0)A ，(0,7,0)B ，(0,0,24)C ，(,,)D x y z .因为(,7,)(0,7,0)0BD AB x y z ⋅=-⋅=，所以7y =.由24BD ==，25CD ==解得12z =，x =1cos 2BD AC BD ACθ⋅==⋅，60θ=︒ 因此，线段BD 与平面α所成的角等于9030θ︒-=︒.11、解：以点O 为原点建立坐标系，得下列坐标：(0,0,0)O ，(4,0,0)A ，(0,3,0)B ，(0,0,4)O '，(4,0,4)A '，(0,3,4)B '，3(2,,4)2D ，(0,3,)P z .由3(0,3,)(2,,4)02OP BD z ⋅=⋅-=，解得98z =. 所以，938tan 38PB OB θ===.12、解：不妨设这条线段MN 长为2，则点M 到二面角的棱的距离1MP =，点N 到二面角的棱的距离1NQ =，QM PN ==PQ =22cos 2PQ MNPQ PQ MNθ⋅====⋅， 45θ=︒. 习题3.2 B 组（P113） 1、解：12222ABC S ∆=⨯⨯=， ()224502AD BE AB BD BE ⋅=+⋅=︒+=，202cos AD BE AD AD θ⋅==，20AD =，204BD ==. 184233ABCD V =⨯⨯=2、解：（1）以点B 为原点建立坐标系，得下列坐标：(0,0,0)B ，(1,0,0)A ，(0,0,1)C ，(1,1,0)F，,0,1)M -，,0)N .。

2018版高中数学选修2-1课件：第一章常用逻辑用语 1-2

解析答案
(3)p： 3是无理数，q： 3是实数；
解 p∧q： 3是无理数且是实数；
∵p真，q真，∴p∧q为真.
p∨q： 3是无理数或是实数； ∵p真，q真，∴p∨q为真.
(4)p：方程x2＋2x＋1＝0有两个相等的实数根，q：方程x2＋2x＋1＝0两
根的绝对值相等. 解 p∧q：方程x2＋2x＋1＝0有两个相等的实数根且两根的绝对值相等；
第1章常用逻辑用语
1.2 简单的逻辑联结词
学习目标
1.了解联结词“且”“或”“非”的含义. 2.会用联结词“且”“或”“非”联结或改写某些数学命题，并判断新命题的真假. 3.通过学习，明白对条件的判定应该归结为判断命题的真假.
栏目索引
知识梳理
题型探究当堂检测
自主学习
重点突破自查自纠
知识梳理
a>2或a<－2， ∴a<－2或a≥6； ①若 p 真 q 假，则有 a≤2或a≥6，－2≤a≤2， ②若 p 假 q 真，则有通过分析可知不存在这样的 a. 2<a<6，
综上，a<－2或a≥6.
解析答案
返回
当堂检测
1
2
3
4
5
1.命题p ： “x>0” 是 “x2>0” 的必要不充分条件，命题 q ：△ABC 中，
(2)命题的否定与否命题有什么区别？
答案命题的否定只否定命题的结论，而否命题既否定命题的条件，又否定命题的结论.
答案
返回
题型探究
重点突破
题型一 p∧q命题及p∨q命题
例1 分别写出下列命题构成的“p∧q”“p∨q”的形式，并判断它们
的真假.
(1)p：函数y＝3x2是偶函数，q：函数y＝3x2是增函数；解 p∧q：函数y＝3x2是偶函数且是增函数；

数学高二选修2-1 第1章常用逻辑用语第2讲简单的逻辑联结词

高二选修2-1 第1章常用逻辑用语第2讲简单的逻辑联结词【基础知识】1．简单的逻辑联结词 (1)逻辑联结词命题中的“且”、“或”、“非”叫做逻辑联结词． (2)命题p ∧q ，p ∨q ，綈p 的真假判断p q p ∧q p ∨q 綈p 真真真真假真假假真假假真假真真假假假假真2.全称量词与存在量词(1)常见的全称量词有：“任意一个”“一切”“每一个”“任给”“所有的”等．(2)常见的存在量词有：“存在一个”“至少有一个”“有些”“有一个”“某个”“有的”等． (3)全称量词用符号“∀”表示；存在量词用符号“∃”表示． 3．全称命题与特称命题(1)含有全称量词的命题叫全称命题． (2)含有存在量词的命题叫特称命题． 4．命题的否定(1)全称命题的否定是特称命题；特称命题的否定是全称命题． (2)p 或q 的否定为：非p 且非q ；p 且q 的否定为：非p 或非q .【典型例题】考点一含有逻辑联结词命题的真假判断【例1】设命题p ：函数y ＝sin 2x 的最小正周期为π2；命题q ：函数y ＝cos x 的图象关于直线x ＝π2对称．则下列判断正确的是( )．A ．p 为真B ．綈q 为假C ．p ∧q 为假D ．p ∨q 为真【例2】(2013·湖北卷)在一次跳伞训练中，甲、乙两位学员各跳一次．设命题p 是“甲降落在指定范围”，q 是“乙降落在指定范围”，则命题“至少有一位学员没有降落在指定范围”可表示为()．A．(綈p)∨(綈q) B．p∨(綈q)C．(綈p)∧(綈q) D．p∨q【训练1】若命题p：关于x的不等式ax＋b＞0的解集是{x|x＞－ba}，命题q：关于x的不等式(x－a)(x－b)＜0的解集是{x|a＜x＜b}，则在命题“p∧q”、“p∨q”、“綈p”、“綈q”中，是真命题的有________．【训练2】已知命题p1：y＝ln[(1－x)·(1＋x)]为偶函数；命题p2：y＝ln 1－x1＋x为奇函数，则下列命题是假命题的是()A.p1且p2B.p1或(綈p2)C.p1或p2D.p1且(綈p2)【训练3】已知命题p：若x>y，则－x<－y；命题q：若x>y，则x2>y2.在命题①p且q；②p或q；③p且(綈q)；④(綈p)或q中，真命题是()A.①③B.①④C.②③D.②④【训练4】已知命题p：对任意x∈R，总有2x>0；q：“x>1”是“x>2”的充分不必要条件，则下列命题为真命题的是()A.p且qB.(綈p)且(綈q)C.(綈p)且qD.p且(綈q)考点二含有量词的命题的真假判断【例3】下列四个命题p 1：∃x 0∈(0，＋∞)，012x ⎛⎫⎪⎝⎭＜013x ⎛⎫ ⎪⎝⎭；p 2：∃x 0∈(0,1)，12logx 0＞13log x 0；p 3：∀x ∈(0，＋∞)，12x⎛⎫ ⎪⎝⎭＞12logx ；p 4：∀x ∈⎝⎛⎭⎫0，13，12x⎛⎫ ⎪⎝⎭＜13log x . 其中真命题是( D )． A ．p 1，p 3 B ．p 1，p 4 C ．p 2，p 3 D ．p 2，p 4【训练1】下列命题中，为真命题的是( ) A.任意x ∈R ，x 2>0 B.任意x ∈R ，－1<sin x <1 C.存在x 0∈R,2x 0<0D.存在x 0∈R ，tan x 0＝2解析 (1)任意x ∈R ，x 2≥0，故A 错；任意x ∈R ，－1≤sin x ≤1，故B 错；任意x ∈R,2x >0，故C 错，故选D.【训练2】判断下列命题的真假． (1)∀x ∈R ，都有x 2－x ＋1>12.(2)∃α，β使cos(α－β)＝cos α－cos β. (3)∀x ，y ∈N ，都有x －y ∈N . (4)∃x 0，y 0∈Z ，使得2x 0＋y 0＝3.【训练3】(2010·江苏苏州中学阶段性测试一)若命题“∃x ∈R ，使得x 2＋(1－a )x ＋1<0”是真命题，则实数a 的取值范围为__________________．考点三全称命题与存在性命题的否定【例4】写出下列命题的否定，并判断其真假： (1)p ：∀x ∈R ，x 2－x ＋14≥0；(2)q ：所有的正方形都是矩形； (3)r ：∃x 0∈R ，x 20＋2x 0＋2≤0； (4)s ：至少有一个实数x 0，使x 30＋1＝0.【训练1】命题“存在实数x ，使x >1”的否定是( ) A.对任意实数x ，都有x >1 B.不存在实数x ，使x ≤1 C.对任意实数x ，都有x ≤1 D.存在实数x ，使x ≤1【训练2】设x ∈Z ，集合A 是奇数集，集合B 是偶数集.若命题p ：任意x ∈A,2x ∈B ，则綈p 为：______.【训练3】下列命题中的真命题是( ) A.存在x ∈R ，使得sin x ＋cos x ＝32B.任意x ∈(0，＋∞)，e x >x ＋1C.存在x ∈(－∞，0)，2x <3xD.任意x ∈(0，π)，sin x >cos x【训练4】 (2010·深圳一模)已知命题p ：∃x ∈R ，x 2＋2ax ＋a ≤0.若命题p 是假命题，则实数a 的取值范围为________．考点四借助逻辑联结词求解参数范围问题【例题 5】 (12分)已知a ＞0，设命题p ：函数y ＝a x 在R 上单调递增；命题q ：不等式ax 2－ax ＋1＞0对∀x ∈R 恒成立．若“p ∧q ”为假，“p ∨q ”为真，求a 的取值范围．【训练1】(2014·锦州月考)命题p：关于x的不等式x2＋2ax＋4＞0对一切x∈R恒成立，q：函数f(x)＝(3－2a)x 是增函数，若p或q为真，p且q为假，求实数a的取值范围．【训练2】已知p：存在x∈R，mx2＋1≤0，q：任意x∈R，x2＋mx＋1>0，若p或q为假命题，则实数m的取值范围为()A.m≥2B.m≤－2C.m≤－2或m≥2D.－2≤m≤2【训练3】(1)已知命题p：“任意x∈[1,2]，x2－a≥0”，命题q：“存在x∈R，使x2＋2ax＋2－a＝0”，若命题“p且q”是真命题，则实数a的取值范围是()A.{a|a≤－2或a＝1}B.{a|a≥1}C.{a|a≤－2或1≤a≤2}D.{a|－2≤a≤1}1．逻辑联结词“或”“且”“非”的含义的理解．(1)“或”与日常生活用语中的“或”意义有所不同，日常用语“或”带有“不可兼有”的意思，如工作或休息，而逻辑联结词“或”含有“同时兼有”的意思，如x<6或x>9.(2)命题“非p”就是对命题“p”的否定，即对命题结论的否定；否命题是四种命题中的一种，是对原命题条件和结论的同时否定．2．判断复合命题的真假，要首先确定复合命题的构成形式，再指出其中简单命题的真假，最后根据真值表判断．3．全称命题“∀x∈M，p(x)”的否定是一个存在性命题“∃x∈M，綈p(x)”，存在性命题“∃x∈M，p(x)”的否定是一个全称命题“∀x∈M，綈p(x)”.【课堂练习】1.常用逻辑用语及其应用一、命题的真假判断典例已知命题p：存在x∈R，x2＋1<2x；命题q：若mx2－mx－1<0恒成立，则－4<m<0，那么()A.“綈p”是假命题B.q是真命题C.“p或q”为假命题D.“p且q”为真命题二、求参数的取值范围典例已知命题p：“任意x∈[0,1]，a≥e x”；命题q：“存在x∈R，使得x2＋4x＋a＝0”.若命题“p且q”是真命题，则实数a的取值范围是________.三、利用逻辑推理解决实际问题典例(1)甲、乙、丙三位同学被问到是否去过A，B，C三个城市时，甲说：我去过的城市比乙多，但没去过B城市；乙说：我没去过C城市；丙说：我们三人去过同一城市.由此可判断乙去过的城市为________.(2)对于中国足球参与的某次大型赛事，有三名观众对结果作如下猜测：甲：中国非第一名，也非第二名；乙：中国非第一名，而是第三名；丙：中国非第三名，而是第一名.竞赛结束后发现，一人全猜对，一人猜对一半，一人全猜错，则中国足球队得了第________名.【课后练习】1．(2014·湖南五市十校联考)下列命题中是假命题的是()．A．∃α，β∈R，使sin(α＋β)＝sin α＋sin βB．∀φ∈R，函数f(x)＝sin(2x＋φ)都不是偶函数C．∃m∈R，使f(x)＝(m－1)·x m2－4m＋3是幂函数，且在(0，＋∞)上单调递减D．∀a＞0，函数f(x)＝ln2x＋ln x－a有零点2．(2013·衡水二模)已知命题p：“∃x0∈R，使得x20＋2ax0＋1＜0成立”为真命题，则实数a满足()．A．[－1,1) B．(－∞，－1)∪(1，＋∞)C．(1，＋∞) D．(－∞，－1)3．(2014·宿州检测)给出如下四个命题：①若“p∧q”为假命题，则p，q均为假命题；②命题“若a＞b，则2a＞2b－1”的否命题为“若a≤b，则2a≤ 2b－1”；③“∀x∈R，x2＋1≥1”的否定是“∃x0∈R，x20＋1≤1”；④在△ABC中，“A＞B”是“sin A＞sin B”的充要条件．其中不正确的命题的序号是________．4．已知命题p：方程x2＋mx＋1＝0有两个不等的负根；命题q：方程4x2＋4(m－2)x＋1＝0无实根．若“p∨q”为真，“p∧q”为假，求实数m的取值范围．5.已知命题p：存在x∈R，x－2>lg x，命题q：任意x∈R，x2>0，则()A.p或q是假命题B.p且q是真命题C.p且(綈q)是真命题D.p或(綈q)是假命题6.四个命题：①任意x∈R，x2－3x＋2>0恒成立；②存在x∈Q，x2＝2；③存在x∈R，x2＋1＝0；④任意x∈R,4x2>2x－1＋3x2.其中真命题的个数为()A.0B.1C.2D.47.下列结论正确的是()A.若p：存在x∈R，x2＋x＋1<0，则綈p：任意x∈R，x2＋x＋1<0B.若p或q为真命题，则p且q也为真命题C.“函数f(x)为奇函数”是“f(0)＝0”的充分不必要条件D.命题“若x2－3x＋2＝0，则x＝1”的否命题为真命题8.已知命题p：“任意x∈R，存在m∈R,4x－2x＋1＋m＝0”，若命题綈p是假命题，则实数m的取值范围是________.9.设p ：方程x 2＋2mx ＋1＝0有两个不相等的正根；q ：方程x 2＋2(m －2)x －3m ＋10＝0无实根.则使p 或q 为真，p 且q 为假的实数m 的取值范围是________________________.10.有下列命题：①在函数y ＝cos ⎝⎛⎭⎫x －π4cos ⎝⎛⎭⎫x ＋π4的图像中，相邻两个对称中心的距离为π； ②函数y ＝x ＋3x －1的图像关于点(－1,1)对称；③已知命题p ：对任意的x ∈R ，都有sin x ≤1，则綈p ：存在x 0∈R ，使得sin x 0>1； ④在△ABC 中，若3sin A ＋4cos B ＝6,4sin B ＋3cos A ＝1，则角C 等于30°或150°. 其中的真命题是________.。

2014年人教A版选修2-1课件 1.3 简单的逻辑联结词

∴ (2) 中的命题是真命题.
例3. 判断下列命题的真假: (1) 2≤2; (2) 集合A是A∩B的子集或是A∪B的子集; (3) 周长相等的两个三角形全等或面积相等的两个三角形全等.
解: (3) 题设中的命题是 p∨q 的形式, p: 周长相等的两个三角形全等, 这是假命题;
q: 面积相等的两个三角形全等, 这也是假命题. ∴ 题设中的命题是假命题.
∴ p∨q 是真命题.
练习: (补充) 将下列命题写成 p∨q 的形式, 并判断其真假: (1) 若直线 l 不在平面 a 内, 则 l 就在平面 a 外; (2) a{a, b, c}∪{c, d, e}. 解: (2) p: a{a, b, c}. q: a{c, d, e}. p∨q: a{a, b, c} 或 a{c, d, e}. ∵ 命题 p 是真命题,
2. 用逻辑联结词联结命题后得到的新命题与原命题的真假性有什么关系? 怎样判断新命题的真假?
1.3.1 且 (and)
问题1. “12 能被 3 整除且能被 4 整除” 是命题吗? 它是由哪两个命题联结起来的? 是用什么词联结成的? 如果是命题, 它的真假性如何? (1) 12 能被 3 整除. (2) 12 能被 4 整除. 将上面两命题用逻辑联结词 “且” 联结起来即得 12 能被 3 整除且能被 4 整除. 这也是命题.
本章内容
1.1 命题及其关系 1.2 充分条件与必要条件
1.3 简单的逻辑联结词 1.4 全称量词与存在量词第一章小结
1.3 简单的逻辑联结词
1.3.t)
1. 本节教材中有哪几个简单的逻辑联结词? 它们用在命题中各自的含义是什么?
例1. 将下列命题用 “且” 联结成新命题, 并判断它们的真假: (1) p: 平行四边形的对角线互相平分, q: 平行四边形的对角线相等; (2) p: 菱形的对角线互相垂直, q: 菱形的对角线互相平分; (3) p: 35 是 15 的倍数, q: 35 是 7 的倍数. 解: (1) p˄ q: 平行四边形的对角线相等且互相平分. 因为命题 q 是假命题, 所以 p˄ q 是假命题. (2) p˄ q: 菱形的对角线互相垂直且平分. 因为 p, q 都是真命题, 所以 p˄ q 是真命题. (3) p˄ q: 35 是 15 的倍数且是 7 的倍数. 因为命题 p 是假命题, 所以 p˄ q 是假命题.

选修2-1第一章《充分必要条件、简单的逻辑联结词》

高中数学选修2系列知识点

选修2-1数学课后习题答案(全)

高二数学 (新课标人教A版)选修2-1《1.3简单的逻辑联结词》教案

选修2-1数学课后习题答案(全)

2018版高中数学选修2-1课件：第一章 常用逻辑用语 1-2

数学 高二 选修2-1 第1章常用逻辑用语 第2讲 简单的逻辑联结词

2014年人教A版选修2-1课件 1.3 简单的逻辑联结词

最新人教版高二数学选修2-1电子课本课件【全册】

2018版高中数学选修2-1课件：第一章常用逻辑用语 1-2

数学高二选修2-1 第1章常用逻辑用语第2讲简单的逻辑联结词