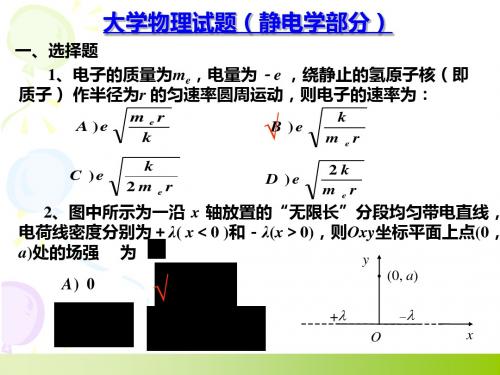
11年重庆大学电磁场原理考题及题解
重庆大学大学物理历年期末考试试题
8、电流从 a 点分两路通过对称的圆环形分路,汇合于b点.若ca、
bd都沿环的径向,则在环形分路的环心处的磁感应强度
A)方向垂直环形分路所在平面且指向纸内。
B)方向垂直环形分路所在平面且指向纸外。
C)方向在环形分路所在平面,且指向b。
D)方向在环形分路所在平面内,且指向a。
√E)为零。
1
[分析]
I
q (d t)
0S
由此得 C q 0S
UAUB dt
因C 值仅与d、t 有关,与d1、d2无关,故金属片的安放位置对 电容值无影响.
2、一内半径为a、外半径为b的金属球壳,带有电量Q,在球壳 空 腔内距离球心r 处有一点电荷q。设无限远处为电势零点,试求:l)球 壳内、外表面上的电荷。2)球心O点处,由球壳内表面上电荷产生的 电势。 3)球心O点处的总电势。
3、若空间存在两根无限长直载流导线,空间的磁场分布就不具 有简单的对称性,则该磁场分布
A)不能用安培环路定理计算。B)可以直接用安培环路定理求出。 C)只能用毕奥—萨伐尔定律求出。
√D)可以用安培环路定理和磁感应强度的叠加原理求出。
4、两根载流直导线相互正交放置,I1 沿Y 轴的正方向流动,I2 沿Z 轴负方向流动。若载流I1 的导线不能动,载流I2 的导线 可以自由运动, 则载流I2 的导线开始运动的趋势是
A) E 0,U Q/(4 0r)
√B) E 0,U Q/(4 0R)
C) E Q/(4 0r2),U Q/(4 0r) D) E Q/(4 0r2),U Q/(4 0R)
Q
Or
R
p
6、一平行板电容器中充满相对介电常量为εr 的各向同性均匀 电介质。已知介质表面极化电荷面密度为±σ′,则极化电荷在电容
大学电磁场考试题及答案

大学电磁场考试题及答案一、选择题(每题2分,共20分)1. 电磁场中,电场与磁场的相互作用遵循以下哪个定律?A. 高斯定律B. 法拉第电磁感应定律C. 安培环路定律D. 洛伦兹力定律答案:D2. 在真空中,电磁波的传播速度是多少?A. 100,000 km/sB. 300,000 km/sC. 1,000,000 km/sD. 3,000,000 km/s答案:B3. 一个点电荷产生的电场强度与距离的平方成什么关系?A. 正比B. 反比C. 对数关系D. 线性关系答案:B4. 以下哪种介质不能支持电磁波的传播?A. 真空B. 空气C. 玻璃D. 金属答案:D5. 麦克斯韦方程组中描述变化电场产生磁场的方程是?A. 高斯定律B. 高斯磁定律C. 法拉第电磁感应定律D. 安培环路定律答案:C6. 一个均匀带电球壳内部的电场强度是多少?A. 零B. 与球壳内的电荷分布有关C. 与球壳外的电荷分布有关D. 与球壳的总电荷量成正比答案:A7. 电磁波的频率和波长之间有什么关系?A. 频率与波长成正比B. 频率与波长成反比C. 频率与波长无关D. 频率越大,波长越小答案:B8. 根据洛伦兹力公式,一个带电粒子在磁场中运动时,其受到的力的方向与什么因素有关?A. 粒子的速度B. 磁场的方向C. 粒子的电荷D. 所有上述因素答案:D9. 电磁波的偏振现象说明电磁波是横波,这是因为?A. 电磁波的振动方向与传播方向垂直B. 电磁波的振动方向与传播方向平行C. 电磁波的传播不需要介质D. 电磁波在真空中传播速度最快答案:A10. 一个闭合电路中的感应电动势遵循以下哪个定律?A. 欧姆定律B. 基尔霍夫电压定律C. 法拉第电磁感应定律D. 安培环路定律答案:C二、填空题(每题2分,共20分)11. 电磁波的传播不需要______,因此它可以在真空中传播。
答案:介质12. 根据麦克斯韦方程组,电荷守恒定律可以表示为:∇⋅ E =______。
重庆大学电磁场复习资料【包含习题和答案】

期末复习基本概念和理论1. Maxwell 方程组积分形式 微分形式⎰⎰⎰⎰⋅∂∂+⋅+⋅=⋅S DS v S E l H d d d d S S S l t ργ t c ∂∂+=⨯∇D J H(tv ∂∂+=DJ ) S Bl E d d ⋅∂∂-=⋅⎰⎰S l t t ∂∂-=⨯∇B E0d =⋅⎰S B S 0=⋅∇B q S =⋅⎰S D d ρ=⋅∇D明了各基本方程的意义,方程的基本特点。
2. 导出静态场的基本方程微分形式:()0=∂∂tc J H =⨯∇ 0=⨯∇E 0=⨯∇=⨯∇⨯∇c J H0=⋅∇B ρ=⋅∇D 0=⨯∇E积分形式:⎰∑⎰=⋅=⋅I S c l S J l H d d 0d =⋅⎰l E l 0d =⋅⎰l E l 0d =⋅⎰S B S q S =⋅⎰S D d 0d =⋅⎰S J S c3. 正弦电磁场中微分形式Maxwell 方程组的相量表达式D J Hωj c +=⨯∇ B Eωj -=⨯∇0=⋅∇Bρ=⋅∇D 4. 准静态场(1)电准静态场 (2)磁准静态场tc ∂∂+=⨯∇DJ H c J H ≈⨯∇ 0≈⨯∇E t ∂∂-=⨯∇BE0=⋅∇B 0=⋅∇B ρ=⋅∇D ρ=⋅∇D循环图的闭环已被断开。
5. 媒质的影响P E D +=0ε, ()M H B +=0μ, ()E J J =,各向同性、线性媒质E E D εεε==r 0,H H B μμμ==r 0, E J γ=6. 媒质分界面衔接条件k )H (H e =-⨯12n 012=-⨯)E (E e n 012=-⋅)B (B e n σ=-⋅)D (D e 12n应用矢量形式7. 波动特性和能量传输(1)动态位波动方程和动态位解答:ερϕμεϕ-=∂∂-∇222t , c tJ AA μμε-=∂∂-∇222V d R v R t t V '⎪⎭⎫ ⎝⎛-'=⎰',r )(r,ρπεϕ41 , ()V Rv R t T c V '⎪⎭⎫ ⎝⎛-'⎰='d 4,r J r,A πμ 动态位解答的波动特点,推迟效应,似稳条件 (2)坡印廷定律和坡印廷矢量:()⎰⎰⎰⎰⋅+--∂∂-=⋅⨯V V e V c S V v V t Wd d d 2E J J S H E ργH E s ⨯= , ()t TTav d 10⎰⨯=H E s (3)电磁场能量密度在各向同性、线性媒质中2221212121H E m eμεωωω+=⋅+⋅='+'='H B D E 8. 均匀平面电磁波的传播9. 基本问题(1)何谓标量场?何谓矢量场?(2)“ ”算符的微分特性和矢量特性?(3)电场强度是怎样定义的?其物理意义如何?(4)电位的定义式和它的物理意义。
电磁场期末考试题及答案

电磁场期末考试题及答案一、选择题(每题2分,共20分)1. 电磁波在真空中的传播速度是()。
A. 3×10^8 m/sB. 2×10^8 m/sC. 1×10^8 m/sD. 4×10^8 m/s答案:A2. 电场强度的定义式为E=()。
A. F/qB. F/QC. Q/FD. F/C答案:A3. 磁场强度的定义式为B=()。
A. F/IB. F/iC. F/qD. F/Q答案:B4. 根据麦克斯韦方程组,变化的磁场会产生()。
A. 电场B. 磁场C. 电势D. 电势差答案:A5. 电磁波的波长、频率和波速之间的关系是()。
B. λ = f/cC. λ = c*fD. λ = f^2/c答案:A6. 两个点电荷之间的静电力与它们之间的距离的平方成()。
A. 正比B. 反比C. 无关D. 一次方答案:B7. 根据洛伦兹力公式,带电粒子在磁场中运动时,受到的力与磁场强度的关系是()。
A. 正比C. 无关D. 一次方答案:A8. 电容器的电容与两极板之间的距离成()。
A. 正比B. 反比C. 无关D. 一次方答案:B9. 根据楞次定律,当线圈中的磁通量增加时,感应电流产生的磁场方向是()。
A. 增加磁通量B. 减少磁通量D. 增加或减少磁通量答案:B10. 根据法拉第电磁感应定律,感应电动势的大小与磁通量变化率的关系是()。
A. 正比B. 反比C. 无关D. 一次方答案:A二、填空题(每题2分,共20分)1. 电场中某点的电势为V,将单位正电荷从该点移到无穷远处,电场力做的功为________。
2. 两个点电荷q1和q2之间的静电力常数为k,它们之间的距离为r,则它们之间的静电力大小为________。
答案:k*q1*q2/r^23. 磁场中某点的磁感应强度为B,将单位电流元i放置在该点,电流元与磁场方向垂直时,受到的磁力大小为________。
答案:B*i4. 根据麦克斯韦方程组,变化的电场会产生________。
重庆大学电磁场习题答案习题(第4章)

重庆大学电磁场习题答案习题(第4章)第四章习题答案4-4 设磁矢量位的参考点为无穷远处,计算一段长为2m 的直线电流I 在其中垂线上距线电流1m 的磁矢量位值。
解:选圆柱坐标,在z '处取元电流段z e I l I'dz d =,元电流段产生的元磁矢量位为z 0e R4z Id A d πμ'=整个线电流产生的磁矢量位:C e R z Id 4A z 2l 2l 0+'=-//πμ 其中 22z R '+=ρ,电流有限分布,参考点选在无穷远处,所以积分常数C 为零。
()()2222ln 44z 2222022220e l l l l I e z z Id A z l l //////++-++=?'+'=-ρρπμρπμ 将 l =2 ,1=ρ 带入上式,得z e I A1212ln π40-+=μ4.5解:由恒定磁场的基本方程,磁感应强度一定要满足0B ?=,因此,此方程可以作为判断一个矢量是否为磁感应强度B 的条件。
4-6 相距为d 的平行无限大平面电流,两个平面分别在2d z -=和2d z =且平行与xO y 平面。
相应的面电流密度分别为x e k 和y e k,求由两个无限大平面分割出来的三个空间区域的磁感应强度。
解:由例题4-7结果,分别求出面电流x e k 和y e k产生的磁场,然后应用叠加原理,x e k产生的磁场为:ρy图4-4-<->-2d z e 2K 2d z e 2K B y 0y 01,,)()(μμ= y e k产生的磁场为><-2),(22),(2002d z e K d z e K B x xμμ=由叠加原理知:>+-<<-+--<-=2),(222,)(22),(2000d z e e K d z d e e K d z e e K B xy x y x yμμμ4-7 参见教材例4.84-8 如题图4-8所示,同轴电缆通以电流I ,求各处的磁感应强度。
(完整版)大学物理电磁场练习题含答案

前面是答案和后面是题目,大家认真对对. 三、稳恒磁场答案1-5 CADBC 6-8 CBC 三、稳恒磁场习题1. 有一个圆形回路1及一个正方形回路2,圆直径和正方形的边长相等,二者中通有大小相等的电流,它们在各自中心产生的磁感强度的大小之比B 1 / B 2为 (A) 0.90. (B) 1.00.(C) 1.11. (D) 1.22. [ ]2.边长为l 的正方形线圈中通有电流I ,此线圈在A 点(见图)产生的磁感强度B 为(A) l I π420μ. (B) l Iπ220μ.(C)l Iπ02μ. (D) 以上均不对. [ ]3.通有电流I 的无限长直导线有如图三种形状,则P ,Q ,O 各点磁感强度的大小B P ,B Q ,B O 间的关系为:(A) B P > B Q > B O . (B) B Q > B P > B O .(C) B Q > B O > B P . (D) B O > B Q > B P .[ ]4.无限长载流空心圆柱导体的内外半径分别为a 、b ,电流在导体截面上均匀分布,则空间各处的B ϖ的大小与场点到圆柱中心轴线的距离r 的关系定性地如图所示.正确的图是 [ ]5.电流I 由长直导线1沿平行bc 边方向经a 点流入由电阻均匀的导线构成的正三角形线框,再由b 点沿垂直ac 边方向流出,经长直导线2返回电源(如图).若载流直导线1、2和三角形框中的电流在框中心O 点产生的磁感强度分别用1B ϖ、2B ϖ和3Bϖ表示,则O 点的磁感强度大小(A) B = 0,因为B 1 = B 2 = B 3 = 0.(B) B = 0,因为虽然B 1≠ 0、B 2≠ 0,但021=+B B ϖϖ,B 3 = 0.(C) B ≠ 0,因为虽然B 2 = 0、B 3= 0,但B 1≠ 0.(D) B ≠ 0,因为虽然021≠+B B ϖϖ,但B 3≠ 0. [ ]6.电流由长直导线1沿半径方向经a 点流入一电阻均匀的圆环,再由b 点沿切向从圆环流出,经长导线2返回电源(如图).已知直导线上电流强度为I ,圆环的半径为R ,且a 、b 与圆心O 三点在同一直线上.设直电流1、2及圆环电流分别在O 点产生的磁感强度为1B ϖ、2B ϖ及3Bϖ,则O 点的磁感强度的大小(A) B = 0,因为B 1 = B 2 = B 3 = 0.(B) B = 0,因为021=+B B ϖϖ,B 3= 0.(C) B ≠ 0,因为虽然B 1 = B 3 = 0,但B 2≠ 0. (D) B ≠ 0,因为虽然B 1 = B 2 = 0,但B 3≠ 0.(E) B ≠ 0,因为虽然B 2 = B 3 = 0,但B 1≠ 0. [ ] v7.电流由长直导线1沿切向经a 点流入一个电阻均匀的圆环,再由b 点沿切向从圆环流出,经长直导线2返回电源(如图).已知直导线上电流强度为I ,圆环的半径为R ,且a 、b 和圆心O 在同一直线上.设长直载流导线1、2和圆环中的电流分别在O 点产生的磁感强度为1B ϖ、2B ϖ、3Bϖ,则圆心处磁感强度的大小(A) B = 0,因为B 1 = B 2 = B 3 = 0.(B) B = 0,因为虽然B 1≠ 0、B 2≠ 0,但021=+B B ϖϖ,B 3 = 0.(C) B ≠ 0,因为B 1≠ 0、B 2≠ 0,B 3≠ 0.(D) B ≠ 0,因为虽然B 3= 0,但021≠+B B ϖϖ. [ ]8.a R r OO ′I在半径为R 的长直金属圆柱体内部挖去一个半径为r 的长直圆柱体,两柱体轴线平行,其间距为a ,如图.今在此导体上通以电流I ,电流在截面上均匀分布,则空心部分轴线上O ′点的磁感强度的大小为(A) 2202R a a I ⋅πμ (B)22202R r a a I -⋅πμ(C) 22202r R a a I-⋅πμ (D) )(222220a r Ra a I -πμ [ ]参考解:导体中电流密度)(/22r R I J -π=.设想在导体的挖空部分同时有电流密度为J 和-J 的流向相反的电流.这样,空心部分轴线上的磁感强度可以看成是电流密度为J 的实心圆柱体在挖空部分轴线上的磁感强度1B ϖ和占据挖空部分的电流密度-J 的实心圆柱在轴线上的磁感强度2B ϖ的矢量和.由安培环路定理可以求得02=B , )(222201r R a Ia B -π=μ 所以挖空部分轴线上一点的磁感强度的大小就等于)(22201r R IaB -π=μ 9. πR 2c3分10.221R B π-3分11. 6.67×10-7 T 3分7.20×10-7 A ·m 2 2分12. 减小 2分在2/R x <区域减小;在2/R x >区域增大.(x 为离圆心的距离) 3分13. 0 1分I 0μ- 2分14. 4×10-6 T 2分 5 A 2分15. I0μ 1分 0 2分2I0μ 2分16. 解:①电子绕原子核运动的向心力是库仑力提供的.即∶ 02202041a m a e v =πε,由此得 002a m e επ=v 2分②电子单位时间绕原子核的周数即频率000142a m a e a ενππ=π=v 2分 由于电子的运动所形成的圆电流00214a m a e e i ενππ== 因为电子带负电,电流i 的流向与 v ϖ方向相反 2分 ③i 在圆心处产生的磁感强度002a i B μ=00202018a m a eεμππ= 其方向垂直纸面向外 2分17.1 234 R ROI a β2解:将导线分成1、2、3、4四部份,各部分在O 点产生的磁感强度设为B 1、B 2、B 3、B 4.根据叠加原理O 点的磁感强度为:4321B B B B B ϖϖϖϖϖ+++= ∵ 1B ϖ、4B ϖ均为0,故32B B B ϖϖϖ+= 2分)2(4102R I B μ= 方向⊗ 2分 242)sin (sin 401203R I a I B π=-π=μββμ)2/(0R I π=μ 方向 ⊗ 2分其中 2/R a =, 2/2)4/sin(sin 2=π=β 2/2)4/sin(sin 1-=π-=β∴ R I R I B π+=2800μμ)141(20π+=R I μ 方向 ⊗ 2分 18. 解:电流元1d l I ϖ在O 点产生1d B ϖ的方向为↓(-z 方向) 电流元2d l I ϖ在O 点产生2d B ϖ的方向为⊗(-x 方向) 电流元3d l I ϖ在O 点产生3d B ϖ的方向为⊗ (-x 方向) 3分kR I i R IB ϖϖϖπ-+ππ-=4)1(400μμ 2分 19. 解:设x 为假想平面里面的一边与对称中心轴线距离,⎰⎰⎰++==Rx RRxrl B r l B S B d d d 21Φ, 2分d S = l d r2012R IrB π=μ (导线内) 2分r I B π=202μ (导线外) 2分)(42220x R R Il -π=μΦR R x Il +π+ln20μ 2分 令 d Φ / d x = 0, 得Φ 最大时 Rx )15(21-= 2分20. 解:洛伦兹力的大小 B q f v = 1分对质子:1211/R m B q v v = 1分 对电子: 2222/R m B q v v = 1分∵ 21q q = 1分 ∴ 2121//m m R R = 1分21.解:电子在磁场中作半径为)/(eB m R v =的圆周运动. 2分连接入射和出射点的线段将是圆周的一条弦,如图所示.所以入射和出射点间的距离为:)/(3360sin 2eB m R R l v ==︒= 3分2解:在任一根导线上(例如导线2)取一线元d l ,该线元距O 点为l .该处的磁感强度为θμsin 20l I B π=2分 方向垂直于纸面向里. 1分电流元I d l 受到的磁力为 B l I F ϖϖϖ⨯=d d 2分其大小θμsin 2d d d 20l lI l IB F π== 2分 方向垂直于导线2,如图所示.该力对O 点的力矩为 1分θμsin 2d d d 20π==lI F l M 2分 任一段单位长度导线所受磁力对O 点的力矩⎰⎰+π==120d sin 2d l l l I M M θμθμsin 220π=I 2分 导线2所受力矩方向垂直图面向上,导线1所受力矩方向与此相反.23. (C) 24. (B)25. 解: ===l NI nI H /200 A/m3分===H H B r μμμ0 1.06 T 2分26. 解: B = Φ /S=2.0×10-2 T 2分===l NI nI H /32 A/m 2分 ==H B /μ 6.25×10-4 T ·m/A 2分=-=1/0μμχm 496 2分9. 一磁场的磁感强度为k c j b i a B ϖϖϖϖ++= (SI),则通过一半径为R ,开口向z 轴正方向的半球壳表面的磁通量的大小为____________Wb .10.任意曲面在匀强磁场B ϖ中,取一半径为R 的圆,圆面的法线n ϖ与B ϖ成60°角,如图所示,则通过以该圆周为边线的如图所示的任意曲面S 的磁通量==⎰⎰⋅Sm S B ϖϖd Φ_______________________.11. 一质点带有电荷q =8.0×10-10 C ,以速度v =3.0×105 m ·s -1在半径为R =6.00×10-3 m 的圆周上,作匀速圆周运动.该带电质点在轨道中心所产生的磁感强度B =__________________,该带电质点轨道运动的磁矩p m =___________________.(μ0 =4π×10-7 H ·m -1)12. 载有一定电流的圆线圈在周围空间产生的磁场与圆线圈半径R 有关,当圆线圈半径增大时,(1) 圆线圈中心点(即圆心)的磁场__________________________.(2) 圆线圈轴线上各点的磁场________如图,平行的无限长直载流导线A 和B ,电流强度均为I ,垂直纸面向外,两根载流导线之间相距为a ,则(1) AB 中点(P 点)的磁感强度=p B ϖ_____________.(2) 磁感强度B ϖ沿图中环路L 的线积分 =⎰⋅L l B ϖϖd ______________________.14. 一条无限长直导线载有10 A 的电流.在离它 0.5 m 远的地方它产生的磁感强度B 为______________________.一条长直载流导线,在离它 1 cm 处产生的磁感强度是10-4 T ,它所载的电流为__________________________.两根长直导线通有电流I ,图示有三种环路;在每种情况下,⎰⋅lB ϖϖd 等于:____________________________________(对环路a ).____________________________________(对环路b ).____________________________________(对环路c ).设氢原子基态的电子轨道半径为a 0,求由于电子的轨道运动(如图)在原子核处(圆心处)产生的磁感强度的大小和方向.17.一根无限长导线弯成如图形状,设各线段都在同一平面内(纸面内),其中第二段是半径为R 的四分之一圆弧,其余为直线.导线中通有电流I ,求图中O 点处的磁感强度.18.z y xR 1 321d l I ϖ2d l I ϖ3d l I ϖO如图,1、3为半无限长直载流导线,它们与半圆形载流导线2相连.导线1在xOy平面内,导线2、3在Oyz 平面内.试指出电流元1d l I ϖ、2d l I ϖ、3d l I ϖ在O 点产生的Bϖd 的方向,并写出此载流导线在O 点总磁感强度(包括大小与方向).19.一根半径为R 的长直导线载有电流I ,作一宽为R 、长为l 的假想平面S ,如图所示。
电磁场考试试题及答案

电磁场考试试题及答案一、选择题(每题5分,共20分)1. 麦克斯韦方程组描述了电磁场的基本规律,下列哪一项不是麦克斯韦方程组中的方程?A. 高斯定律B. 法拉第电磁感应定律C. 欧姆定律D. 安培环路定律答案:C2. 在电磁波传播过程中,电场和磁场的相位关系是:A. 相位相同B. 相位相反C. 相位相差90度D. 相位相差180度答案:C3. 根据洛伦兹力定律,带电粒子在磁场中运动时受到的力的方向是:A. 与速度方向相同B. 与速度方向相反C. 与速度方向垂直D. 与磁场方向垂直答案:C4. 以下哪种介质的磁导率不是常数?A. 真空B. 铁C. 铜D. 空气答案:B二、填空题(每题5分,共20分)1. 根据高斯定律,通过任何闭合表面的电通量与该闭合表面所包围的总电荷量成正比,比例常数为____。
答案:\(\frac{1}{\varepsilon_0}\)2. 法拉第电磁感应定律表明,闭合回路中的感应电动势等于通过该回路的磁通量变化率的负值,其数学表达式为 \(\mathcal{E} = -\frac{d\Phi_B}{dt}\),其中 \(\Phi_B\) 表示____。
答案:磁通量3. 根据安培环路定律,磁场 \(\vec{B}\) 在闭合回路上的线积分等于该回路所包围的总电流乘以比例常数 \(\mu_0\),其数学表达式为\(\oint \vec{B} \cdot d\vec{l} = \mu_0 I_{\text{enc}}\),其中\(I_{\text{enc}}\) 表示____。
答案:回路所包围的总电流4. 电磁波在真空中的传播速度为 \(c\),其值为 \(3 \times 10^8\) 米/秒,该速度也是光速,其物理意义是____。
答案:电磁波在真空中传播的速度三、简答题(每题15分,共40分)1. 简述电磁波的产生机制。
答案:电磁波是由变化的电场和磁场相互作用产生的。
当电场变化时,会在周围空间产生磁场;同样,变化的磁场也会在周围空间产生电场。
(完整版)电磁场理论试题

《电磁场理论》考试试卷(A 卷)(时间120分钟)1. 关于有限区域内的矢量场的亥姆霍兹定理,下列说法中正确的是 (A )任意矢量场可以由其散度和旋度唯一地确定; (B )任意矢量场可以由其散度和边界条件唯一地确定; (C ) 任意矢量场可以由其旋度和边界条件唯一地确定; (D ) 任意矢量场可以由其散度、旋度和边界条件唯一地确定。
2. 谐变电磁场所满足的麦克斯韦方程组中,能反映“变化的电场产生磁场”和“变化的磁场产生电场” 这一物理思想的两个方程是 (B5关于高斯定理的理解有下面几种说法, 其中正确的是、选择题(每小题2分,共20 分)(A)H 0, E —(B ) H J E, E(C H J,E 0(D )H 0, E -3.—圆极化电磁波从媒质参数为分量不产生反射,入射角应为 3 r 1的介质斜入射到空气中,要使电场的平行极化(B )(A) 15°(B ) 30°(C ) 45(D) 604.在电磁场与电磁波的理论中分析中,常引入矢量位函数A ,并令B A ,其依据是(C )(A)B 0 ;(C ) B 0;(B)B J ;(D) B J电磁学》试卷 第 2 页 共 7 页(A) 如果高斯面内无电荷,则高斯面上 E 处处为零; (B) 如果高斯面上 E 处处不为零,则该面内必有电荷; (C) 如果高斯面内有净电荷,则通过该面的电通量必不为零; (D) 如果高斯面上 E 处处为零,则该面内必无电荷。
6.若在某区域已知电位移矢量 ( A)2( B ) 2D xe x( C )ye y ,则该区域的电何体密度为 ( B )2( D )27. 两个载流线圈之间存在互感,对互感没有影响的是( C )(A )线圈的尺寸(B ) 两个线圈的相对位置(C )线圈上的电流 (D )线圈中的介质8 . 以下关于时变电磁场的叙述中,正确的是( B )(A )电场是无旋场 (B )电场和磁场相互激发(C)电场和磁场无关 (D )磁场是有源场9. 两个相互平行的导体平板构成一个电容器, 与电容无关的是10. 用镜像法求解静电场边值问题时, 判断镜像电荷设置是否正确的依据是 ( C )(A) 镜像电荷的位置是否与原电荷对称 (B) 镜像电荷是否与原电荷等值异号(C) 待求区域内的电位函数所满足的方程与边界条件是否保持不变 (D) 同时满足A 和B(A )导体板上的电荷(C )导体板的几何形状 (B) 平板间的介质(D) 两个导体板的相对位1 •电磁波在波导中传播的条件是波导管只能让频率 __________ 一特定值的电磁波通过,该特 定频率称为 _____________ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10、单元偶极子的远区电场相量形式为 E
2Il sin j
4 0 r
e j
r
,因此该电磁波为(
c )。
(a) 均匀平面波; (b) 均匀球面波; (c) 非均匀球面波
二、(10 分)求曲面 x2 y2 z2 9 和 z x2 y2 3 在点(2,-1,2)处的夹
角。
题解:将这两个曲面分别看做是两个标量场的等值面,对应的两个标量场函数分别为:
一、(10 分)单选题,将你选择的答案序号填入各题括弧内。
1、下面哪一个矢量恒等式是正确的?( c
(a) F 0 ; ( b ) F 0 ;
) ( c ) f 0 。
2、介质极化的影响是由下面哪种等效极化电荷的分布来描述的?( c )
(a) p P,
P
P
e
;
(b ) p M,
(c)在时变磁场中处于静止状态。
5、导电媒质中的时谐均匀平面波,电场和磁场的幅值是( a )衰减的。
(a)按指数规律;
(b) 线性;
(c) 不。
6、下面的说法不正确的是( a );
(a) 相速代表信号的能量传播的速度;(b) 在导电媒质中,相速与频率有关;
(c) 相速是指等相面移动的速度。
7.在自由空间传播的电磁波电场有两个分量分别为 Ey Emcos( t x) 和
1 x2 y2 z2 ,2 x2 y2 z
曲面 x2 y2 z2 9 上任意一点处的法线为:
1 =( x 2
y2
z2
)
2xex
2
yey
2zez
----------------------------------------------(2 分)
曲面 x2 y2 z2 9 在点(2,-1,2)处的法线为
H *
1 2
Em H mez
1 2
Z 0 H m2 ez
1 40 2
0.022 0.012
ez
0.01ez (W/m2)
Sav
Re E H
1 2
Em H mex
1 2
Z
0
H
2 m1 2Fra bibliotek400.022
0.012
ex
0.01
w/m2
dS
l
Edl
S
B t
dS
S BdS 0
S DdS q
电磁场基本方程的微分形式为:
H
JC
D t
JV
D t
E
B
t
B 0
D
基本方程组中的第一方程为全电流定律,说明除运动的电荷之外,变化的电场
也产生磁场,
D
为其矢量源密度,时变磁场是有旋场,
H
线可以闭合;第二
t
方程电磁感应定律指出变化的磁场产生电场, B 为其矢量场源密度,时变电
E1
q 4r 2
er
a r b
S2 0E2dS2 0E2 4r 2 Q q
E2
Qq 40r 2
er
c r
内球壳电位
a
Edr
a
b a
E1dr
b
E2dr
b a
q 4r
2
dr
b
Qq 40r 2
dr
q 4
1 a
1 b
Qq 40c
又由于內球体接地,故a 0
曲面 z x2 y2 3 在点(2,-1,2)处的法线为
2
(2,-1,2)
=4ex
2ey
ez
--
---------------------------------------(1 分)
(1) (2 ) 1 2 cos
cos (1) (2 ) 1 2
----------------------------------------------(3 分)
b
Qq 40r 2
dr
Qq 40r
c r
a r b
E2
Qq 40r 2
er
c r
(3) 内、外导体与大地组成了三导体静电独立系统,静电独立系统的能量
| | We
1 2
k qk
1 2
q
1
ra
1 2
Q
2
rc
Qq Q
8 0 c
(3 分)
(4) 系统的等值电容
C
Q2 2We
4 0 cQ Qq
NI 2
(1)
气隙中的磁感应强度大小为:
B
0H
0 NI 2
磁通: BS 0NI dD 2
磁场能量:Wm
1 2
BHV
1 2
0H 2 (2dD )
0
NI 2
2
dD
0 N 2I 2dD 4
(2)
与线圈铰链的磁链: N 0N 2I dD 2
因此线圈自感为: L 0 N 2 dD I 2
(3)在恒电流系统中,广义坐标为 ,应用虚功原理可得可动部件的受力为:
于是:
q
0c
ab Q
b a
ab
(2) 两个介质区间中的电位函数与电场强度
1 r
Edr
r
b r
E1dr
b
E2dr
b q dr a 4r2
Qq dr
b 40r 2
q 1 1 Q q 4 r b 40c
E1
q 4r 2
er
a r b
2r
r
E2dr
Ez Emsin( t x) ,该电磁波为( b )。
(a) 左旋波;
(b) 右旋波; (c) 椭圆极化波
8. 在矩形波导中传输电磁波的工作波长应( b )截止波长。
(a)大于;
(b)小于;
(c) 等于。
9、单元偶极子的远区场的条件是( c ):
(a) r << λ, r << 1; (b) r << λ, r >> 1; (c) r >> λ, r >> 1
H1n B1n B2n 0 H2n 。
又由于 ,所以有 H1n 0 。
应用安培环路定律有:
lH dl l1 H1ndl1 l1 H2ndl2 2H2n NI
H dl l
H1ndl1
H2ndl2 2 H2n NI
l1
l2
有:
H2n
NI 2
所以:故
H
H2
H2n
H dl
l
S JcdS 得:
2 H E 2
H
U 0 2d
e
所以
S
EH
U0 d
ez
2d
U0
e
U
2 0
2d 2
-eρ
进入电容的功率为
S
ds
s
S
a
e 0
2 0
ez
ae
ddz
aU
2 0
2d 2
2ad
a
2U
2 0
d
GU
2 0
S
ds
S
d 0
Fm
Wm g
Wm
0 N 2I 2dD 4 2
方向指向使广义坐标 变小的方向,即为竖直向上。
六、(15 分)正确写出电磁场基本方程的积分和微分形式,并说明各基本方程
的物理意义。并由基本方程组导出磁准静态电磁场基本方程的微分形式。
解答:
电磁场基本方程的积分形式为:
l
Hdl
S
EdS
S
vdS
S
D t
2
aU
2 0
0 2d2
e
edzd
a
2U
2 0
d
GU 2
五、(15 分)对于附图所示厚度为 D(垂直纸面方向)的磁路,试求:
(1) 磁感应强度、磁通和磁场能量; (2) 线圈的自感; (3) 可动部件所受的力。 (提示:忽略边缘效应,气隙磁场可视为均匀场)
I
N
d
题五图
解:由恒定磁场的分界面衔接条件知,磁场由高磁导率媒质进入低磁导率媒质 时,磁力线垂直分界面。因此,分界面处仅有法向磁场且
三、(15 分)半径为 a 的导体球,被内半径为 b(b>a)、外半径为 c(c >b)的
同心导体球壳所包围,两导体间填充介质,其介电系数为 ε(常数),外球壳之 外为空气。设外导体带有电荷 Q,内球接地(假定大地在无限远处)。 试求:
(1)内球上的电荷;
(2)球壳内外的电场强度 E 和电位函数 ;
JC
此时,时变场为磁准静态场,其磁场可按照恒定磁场处理。于是,磁准静态电
磁场基本方程的微分形式为:
H JC
E
B
t
B 0
D
七、(10 分)有一无限长直螺线管,半径为 a ,单位长度上绕有 n 匝线圈,螺管
的铁心磁导率为 。假设线圈中通有电流 i Im sin t ,计算铁心内的电场强
1
(2,-1,2)
=4ex
2ey
4ez
----------------------------------------------(1 分)
曲面 z x2 y2 3 上任意一点处的法线为:
2
=( x 2
y2
z)
2xex
2
yey
ez
----------------------------------------------(2 分)
t
场是有旋场, E 线也可闭合;第三方程磁通连续性原理说明时变磁场是无散
场,这一结论符合迄今为止尚未发现有单独的磁荷存在这一基本事实;第四方
