中考几何证明练习题复习及的答案.doc

合集下载

中考数学专题复习八几何证明题

专题八：几何证明题问题解析几何证明题重在训练学生应用数学语言合情推理能力;几何证明题和计算题在中考中占有重要地位．根据新的课程标准;对几何证明题证明的方法技巧上要降低;繁琐性、难度方面要降低．但是注重考查学生的基础把握推理能力;所以几何证明题是目前常考的题型．热点探究类型一：关于三角形的综合证明题例题12016·四川南充已知△ABN和△ACM位置如图所示;AB=AC;AD=AE;∠1=∠2．1求证：BD=CE；2求证：∠M=∠N．分析1由SAS证明△ABD≌△ACE;得出对应边相等即可2证出∠BAN=∠CAM;由全等三角形的性质得出∠B=∠C;由AAS证明△ACM≌△ABN;得出对应角相等即可．解答1证明：在△ABD和△ACE中;;∴△ABD≌△ACESAS;∴BD=CE；2证明：∵∠1=∠2;∴∠1+∠DAE=∠2+∠DAE;即∠BAN=∠CAM;由1得：△ABD≌△ACE;∴∠B=∠C;在△ACM和△ABN中;;∴△ACM≌△ABNASA;∴∠M=∠N．点评本题考查了全等三角形的判定与性质；证明三角形全等是解决问题的关键．同步练2016·山东省菏泽市·3分如图;△ACB和△DCE均为等腰三角形;点A;D;E在同一直线上;连接BE．1如图1;若∠CAB=∠CBA=∠CDE=∠CED=50°①求证：AD=BE；②求∠AEB的度数．2如图2;若∠ACB=∠DCE=120°;CM为△DCE中DE边上的高;BN为△ABE中AE边上的高;试证明：AE=2CM+BN．类型二：关于四边形的综合证明题例题22016·山东省滨州市·10分如图;BD是△ABC的角平分线;它的垂直平分线分别交AB;BD;BC 于点E;F;G;连接ED;DG．1请判断四边形EBGD的形状;并说明理由；2若∠ABC=30°;∠C=45°;ED=2;点H是BD上的一个动点;求HG+HC的最小值．考点平行四边形的判定与性质；角平分线的性质．分析1结论四边形EBGD是菱形．只要证明BE=ED=DG=GB即可．2作EM⊥BC于M;DN⊥BC于N;连接EC交BD于点H;此时HG+HC最小;在RT△EMC中;求出EM、MC即可解决问题．解答解：1四边形EBGD是菱形．理由：∵EG垂直平分BD;∴EB=ED;GB=GD;∴∠EBD=∠EDB;∵∠EBD=∠DBC;∴∠EDF=∠GBF;在△EFD和△GFB中;;∴△EFD≌△GFB;∴ED=BG;∴BE=ED=DG=GB;∴四边形EBGD是菱形．2作EM⊥BC于M;DN⊥BC于N;连接EC交BD于点H;此时HG+HC最小;在RT△EBM中;∵∠EMB=90°;∠EBM=30°;EB=ED=2;∴EM=BE=;∵DE∥BC;EM⊥BC;DN⊥BC;∴EM∥DN;EM=DN=;MN=DE=2;在RT△DNC中;∵∠DNC=90°;∠DCN=45°;∴∠NDC=∠NCD=45°;∴DN=NC=;∴MC=3;在RT△EMC中;∵∠EMC=90°;EM=．MC=3;∴EC===10．∵HG+HC=EH+HC=EC;∴HG+HC的最小值为10．点评本题考查平行四边形的判定和性质、菱形的判定和性质、角平分线的性质、垂直平分线的性质、勾股定理等知识;解题的关键是利用对称找到点H的位置;属于中考常考题型．同步练2016·山东省济宁市·3分如图;正方形ABCD的对角线AC;BD相交于点O;延长CB至点F;使CF=CA;连接AF;∠ACF的平分线分别交AF;AB;BD于点E;N;M;连接EO．1已知BD=;求正方形ABCD的边长；2猜想线段EM与CN的数量关系并加以证明．类型三：关于圆的综合证明题例题32016·山东潍坊正方形ABCD内接于⊙O;如图所示;在劣弧上取一点E;连接DE、BE;过点D作DF∥BE交⊙O于点F;连接BF、AF;且AF与DE相交于点G;求证：1四边形EBFD是矩形；2DG=BE．考点正方形的性质；矩形的判定；圆周角定理．分析1直接利用正方形的性质、圆周角定理结合平行线的性质得出∠BED=∠BAD=90°;∠BFD=∠BCD=90°;∠EDF=90°;进而得出答案；2直接利用正方形的性质的度数是90°;进而得出BE=DF;则BE=DG．解答证明：1∵正方形ABCD内接于⊙O;∴∠BED=∠BAD=90°;∠BFD=∠BCD=90°;又∵DF∥BE;∴∠EDF+∠BED=180°;∴∠EDF=90°;∴四边形EBFD是矩形；2∵正方形ABCD内接于⊙O;∴的度数是90°;∴∠AFD=45°;又∵∠GDF=90°;∴∠DGF=∠DFC=45°;∴DG=DF;又∵在矩形EBFD中;BE=D同步练枣庄市 2015 中考 -24如图;在△ABC中;∠ABC=90°;以AB的中点O为圆心、OA为半径的圆交AC于点D;E是BC的中点;连接DE;OE．1判断DE与⊙O的位置关系;并说明理由；2求证：BC2=CD 2OE；3若cos∠BAD=35;BE=6;求OE的长．类型四：关于相似三角形的证明问题例题42016·黑龙江齐齐哈尔·8分如图;在△ABC中;AD⊥BC;BE⊥AC;垂足分别为D;E;AD与BE 相交于点F．1求证：△ACD∽△BFD；2当tan∠ABD=1;AC=3时;求BF的长．考点相似三角形的判定与性质．分析1由∠C+∠DBF=90°;∠C+∠DAC=90°;推出∠DBF=∠DAC;由此即可证明．2先证明AD=BD;由△ACD∽△BFD;得==1;即可解决问题．解答1证明：∵AD⊥BC;BE⊥AC;∴∠BDF=∠ADC=∠BEC=90°;∴∠C+∠DBF=90°;∠C+∠DAC=90°;∴∠DBF=∠DAC;∴△ACD∽△BFD．2∵tan∠ABD=1;∠ADB=90°∴=1;∴AD=BD;∵△ACD∽△BFD;∴==1;∴BF=AC=3．同步练2016·湖北武汉·10分在△ABC中;P为边AB上一点．1 如图1;若∠ACP＝∠B;求证：AC2＝AP·AB；2 若M为CP的中点;AC＝2;① 如图2;若∠PBM＝∠ACP;AB＝3;求BP的长；② 如图3;若∠ABC＝45°;∠A＝∠BMP＝60°;直接写出BP的长．达标检测1. 2016·黑龙江哈尔滨·8分已知：如图;在正方形ABCD 中;点E 在边CD 上;AQ⊥BE 于点Q;DP⊥AQ 于点P ．1求证：AP=BQ ；2在不添加任何辅助线的情况下;请直接写出图中四对线段;使每对中较长线段与较短线段长度的差等于PQ 的长．2. 2016·四川内江9分如图6所示;△ABC 中;D 是BC 边上一点;E 是AD 的中点;过点A 作BC 的平行线交CE 的延长线于F;且AF ＝BD;连接BF ．1求证：D 是BC 的中点；2若AB ＝AC;试判断四边形AFBD 的形状;并证明你的结论．3. 烟台市 2015 中考 -23如图;以△ABC 的一边AB 为直径的半圆与其它两边AC;BC 的交点分别为D 、E;且=．1试判断△ABC 的形状;并说明理由．2已知半圆的半径为5;BC=12;求sin∠ABD 的值．4. 2015 内蒙古呼伦贝尔兴安盟;第22题7分如图;在平行四边形ABCD 中;E 、F 分别为边AB 、CD 的中点;BD 是对角线．1求证：△ADE ≌△CBF ；2若∠ADB 是直角;则四边形BEDF 是什么四边形证明你的结论．5. 烟台市 2014 中考 -24如图;AB 是⊙O 的直径;延长AB 至P;使BP=OB;BD 垂直于弦BC;垂足为点B;点D 在PC 上．设∠PCB=α;∠POC=β．求证：tanα tan=．DCEF B A 图66. 2015 梧州;第25题12分如图;在正方形ABCD中;点P在AD上;且不与A、D重合;BP的垂直平分线分别交CD、AB于E、F两点;垂足为Q;过E作EH⊥AB于H．1求证：HF=AP；2若正方形ABCD的边长为12;AP=4;求线段EQ的长．7. 2015 北海;第25题12分如图;AB、CD为⊙O的直径;弦AE∥CD;连接BE 交CD于点F;过点E作直线EP与CD的延长线交于点P;使∠PED=∠C．1求证：PE是⊙O的切线；2求证：ED平分∠BEP；3若⊙O的半径为5;CF=2EF;求PD的长．参考答案类型一：关于三角形的综合证明题同步练2016·山东省菏泽市·3分如图;△ACB和△DCE均为等腰三角形;点A;D;E在同一直线上;连接BE．1如图1;若∠CAB=∠CBA=∠CDE=∠CED=50°①求证：AD=BE；②求∠AEB的度数．2如图2;若∠ACB=∠DCE=120°;CM为△DCE中DE边上的高;BN为△ABE中AE边上的高;试证明：AE=2CM+BN．考点等腰三角形的性质．分析1①通过角的计算找出∠ACD=∠BCE;再结合△ACB和△DCE均为等腰三角形可得出“AC=BC;DC=EC”;利用全等三角形的判定SAS即可证出△ACD≌△BCE;由此即可得出结论AD=BE；②结合①中的△ACD≌△BCE可得出∠ADC=∠BEC;再通过角的计算即可算出∠AEB的度数；2根据等腰三角形的性质结合顶角的度数;即可得出底角的度数;利用1的结论;通过解直角三角形即可求出线段AD、DE的长度;二者相加即可证出结论．解答1①证明：∵∠CAB=∠CBA=∠CDE=∠CED=50°;∴∠ACB=∠DCE=180°﹣2×50°=80°．∵∠ACB=∠ACD+∠DCB;∠DCE=∠DCB+∠BCE;∴∠ACD=∠BCE．∵△AC B和△DCE均为等腰三角形;∴AC=BC;DC=EC．在△ACD和△BCE中;有;∴△ACD≌△BCESAS;∴AD=BE．②解：∵△ACD≌△BCE;∴∠ADC=∠BEC．∵点A;D;E在同一直线上;且∠CDE=50°;∴∠ADC=180°﹣∠CDE=130°;∴∠BEC=130°．∵∠BEC=∠CED+∠AEB;且∠CED=50°;∴∠AEB=∠BEC﹣∠CED=130°﹣50°=80°．2证明：∵△ACB和△DCE均为等腰三角形;且∠ACB=∠DCE=120°;∴∠CDM=∠CEM=×180°﹣120°=30°．∵CM⊥DE;∴∠CMD=90°;DM=EM．在Rt△CMD中;∠CMD=90°;∠CDM=30°;∴DE=2DM=2×=2CM．∵∠BEC=∠ADC=180°﹣30°=150°;∠BEC=∠CEM+∠AEB;∴∠AEB=∠BEC﹣∠CEM=150°﹣30°=120°;∴∠BEN=180°﹣120°=60°．在Rt△BNE中;∠BNE=90°;∠BEN=60°;∴BE==BN．∵AD=BE;AE=AD+DE;∴AE=BE+DE=BN+2CM．点评本题考查了等腰三角形的性质、全等三角形的判定及性质、解直角三角形以及角的计算;解题的关键是：1通过角的计算结合等腰三角形的性质证出△ACD≌△BCE；2找出线段AD、DE的长．本题属于中档题;难度不大;但稍显繁琐;解决该题型题目时;利用角的计算找出相等的角;再利用等腰三角形的性质找出相等的边或角;最后根据全等三角形的判定定理证出三角形全是关键．类型二：关于四边形的综合证明题同步练2016·山东省济宁市·3分如图;正方形ABCD的对角线AC;BD相交于点O;延长CB至点F;使CF=CA;连接AF;∠ACF的平分线分别交AF;AB;BD于点E;N;M;连接EO．1已知BD=;求正方形ABCD的边长；2猜想线段EM与CN的数量关系并加以证明．考点正方形的性质．分析1根据正方形的性质以及勾股定理即可求得；2根据等腰三角形三线合一的性质证得CE⊥AF;进一步得出∠BAF=∠BCN;然后通过证得△ABF≌△CBN得出AF=CN;进而证得△ABF∽△COM;根据相似三角形的性质和正方形的性质即可证得CN= CM．解答解：1∵四边形ABCD是正方形;∴△ABD是等腰直角三角形;∴2AB2=BD2;∵BD=;∴AB=1;∴正方形ABCD的边长为1；2CN=CM．证明：∵CF=CA;AF是∠ACF的平分线;∴CE⊥AF;∴∠AEN=∠CBN=90°;∵∠ANE=∠CNB;∴∠BAF=∠BCN;在△ABF和△CBN中;;∴△ABF≌△CBNAAS;∴AF=CN;∵∠BAF=∠BCN;∠ACN=∠BCN;∴∠BAF=∠OCM;∵四边形ABCD是正方形;∴AC⊥BD;∴∠ABF=∠COM=90°;∴△ABF∽△COM;∴=;∴==;即CN=CM．类型三：关于圆的综合证明题同步练枣庄市 2015 中考 -24如图;在△ABC中;∠ABC=90°;以AB的中点O为圆心、OA为半径的圆交AC于点D;E是BC的中点;连接DE;OE．1判断DE与⊙O的位置关系;并说明理由；2求证：BC2=CD 2OE；3若cos∠BAD=35;BE=6;求OE的长．思路分析：本题考查了切线的判定;垂径定理以及相似三角形的判定与性质等知识点．故对于题1可以连接OD;BD;由AB为圆O的直径;得到∠ADB为直角;从而得出三角形BCD为直角三角形;E为斜边BC 的中点;利用斜边上的中线等于斜边的一半;得到CE=DE;利用等边对等角得到一对角相等;再由OA=OD;利用等边对等角得到一对角相等;由直角三角形ABC中两锐角互余;利用等角的余角相等得到∠ADO与∠CDE互余;可得出∠ODE为直角;即DE垂直于半径OD;可得出DE为圆O的切线；对于题2首先可证明OE是△ABC的中位线;则AC=2OE;然后证明△ABC∽△BDC;根据相似三角形的对应边的比相等;即可证得；对于题3在直角△ABC中;利用勾股定理求得AC的长;之后根据三角形中位线定理OE的长即可求得．解题过程：1证明：连接OD;BD;∵AB为圆O的直径;∴∠ADB=90°;在Rt△BDC中;E为斜边BC的中点;∴CE=DE=BE=12 BC;∴∠C=∠CDE;∵OA=OD;∴∠A=∠ADO;∵∠ABC=90°;即∠C+∠A=90°;∴∠ADO+∠CDE=90°;即∠ODE=90°;∴DE⊥OD;又OD为圆的半径;∴DE为⊙O的切线；2证明：∵E是BC的中点;O点是AB的中点; ∴OE是△ABC的中位线;∴AC=2OE;∵∠C=∠C;∠ABC=∠BDC;∴△ABC∽△BDC;∴BC ACCD BC=;即BC2=AC CD．∴BC2=2CD OE；3解：∵cos∠BAD=35;∴sin∠BAC=45 BCAC=;又∵BE=6;E是BC的中点;即BC=12;∴AC=15．又∵AC=2OE;∴OE=12AC=152．规律总结：熟练把握切线的判定;垂径定理以及相似三角形的判定与性质等知识点是解决本题的关键．要证某线是圆的切线;已知此线过圆上某点;连接圆心与这点即为半径;再证垂直即可．类型四：关于相似三角形的证明问题同步练2016·湖北武汉·10分在△ABC中;P为边AB上一点．1 如图1;若∠ACP＝∠B;求证：AC2＝AP·AB；2 若M为CP的中点;AC＝2;① 如图2;若∠PBM＝∠ACP;AB＝3;求BP的长；② 如图3;若∠ABC＝45°;∠A＝∠BMP＝60°;直接写出BP的长．考点相似形综合;考查相似三角形的判定和性质;平行线的性质;三角形中位线性质;勾股定理..答案 1证△ACP∽△ABC即可；2①BP＝5；②71解析1证明：∵∠ACP＝∠B;∠BAC＝∠CAP;∴△ACP∽△ABC;∴AC：AB＝AP：AC;∴AC2＝AP·AB；2①如图;作CQ∥BM交AB延长线于Q;设BP＝x;则P Q＝2x∵∠PBM＝∠ACP;∠PAC＝∠CAQ;∴△APC∽△ACQ;由AC2＝AP·AQ得：22＝3－x35即BP②如图：作CQ⊥AB 于点Q;作CP 0＝CP 交AB 于点P 0;∵AC ＝2;∴AQ＝1;CQ ＝BQ; 设P0Q ＝PQ ＝1－x;BP －1＋x;∵∠BPM＝∠CP 0A ;∠BMP＝∠CAP 0;∴△AP 0C∽△MPB;∴00AP P C MP BP =;∴MP P0C ＝2012P C ==AP 0 BP ＝1＋x;解得x ∴BP ＝－11-．达标检测1. 2016·黑龙江哈尔滨·8分已知：如图;在正方形ABCD 中;点E 在边CD 上;AQ⊥BE 于点Q;DP⊥AQ 于点P ．1求证：AP=BQ ；2在不添加任何辅助线的情况下;请直接写出图中四对线段;使每对中较长线段与较短线段长度的差等于PQ 的长．考点正方形的性质；全等三角形的判定与性质．分析1根据正方形的性质得出AD=BA;∠BAQ=∠ADP;再根据已知条件得到∠AQB=∠DPA;判定△AQB≌△DPA 并得出结论；2根据AQ ﹣AP=PQ 和全等三角形的对应边相等进行判断分析．解答解：1∵正方形ABCD∴AD=BA;∠BAD=90°;即∠BAQ+∠DAP=90°∵DP⊥AQ∴∠ADP+∠DAP=90°∴∠BAQ=∠ADP∵AQ⊥BE 于点Q;DP⊥AQ 于点P∴∠AQB=∠DPA=90°∴△AQB≌△DPAAAS∴AP=BQ2①AQ﹣AP=PQ②AQ﹣BQ=PQ③DP﹣AP=PQ④DP﹣BQ=PQ2. 2016·四川内江9分如图6所示;△ABC 中;D 是BC 边上一点;E 是AD 的中点;过点A 作BC 的平行线交CE 的延长线于F;且AF ＝BD;连接BF ．1求证：D 是BC 的中点；2若AB ＝AC;试判断四边形AFBD 的形状;并证明你的结论．考点三角形例行;特殊四边形的性质与判定..1证明：∵点E 是AD 的中点;∴AE ＝DE ．∵AF ∥BC;∴∠AFE ＝∠DCE;∠FAE ＝∠CDE ．∴△EAF ≌△EDC ．∴AF ＝DC ．∵AF ＝BD;∴BD ＝DC;即D 是BC 的中点．2四边形AFBD 是矩形．证明如下：∵AF ∥BD;AF ＝BD;∴四边形AFBD 是平行四边形．∵AB ＝AC;又由1可知D 是BC 的中点;∴AD ⊥BC ．DC EF B A图6∴□AFBD是矩形．3. 烟台市 2015 中考 -23如图;以△ABC的一边AB为直径的半圆与其它两边AC;BC的交点分别为D、E;且=．1试判断△ABC的形状;并说明理由．2已知半圆的半径为5;BC=12;求sin∠ABD的值．思路分析：1连结AE;如图;根据圆周角定理;由=得∠DAE=∠BAE;由AB为直径得∠AEB=90°;根据等腰三角形的判定方法即可得△ABC为等腰三角形；2由等腰三角形的性质得BE=CE=BC=6;再在Rt△ABE中利用勾股定理计算出AE=8;接着由AB为直径得到∠ADB=90°;则可利用面积法计算出BD=;然后在Rt△ABD中利用勾股定理计算出AD=;再根据正弦的定义求解．解题过程：解：1△ABC为等腰三角形．理由如下：连结AE;如图;∵=;∴∠DAE=∠BAE;即AE平分∠BAC;∵AB为直径;∴∠AEB=90°;∴AE⊥BC;∴△ABC为等腰三角形；2∵△ABC为等腰三角形;AE⊥BC;∴BE=CE=BC=×12=6;在Rt△ABE中;∵AB=10;BE=6;∴AE==8;∵AB为直径;∴∠ADB=90°;∴AE BC=BD AC;∴BD==;在Rt△ABD中;∵AB=10;BD=;∴AD==;∴sin∠ABD===．规律总结：本题考查了圆周角定理：在同圆或等圆中;同弧或等弧所对的圆周角相等;都等于这条弧所对的圆心角的一半．推论：半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径．也考查了等腰三角形的判定与性质和勾股定理．4. 2015 内蒙古呼伦贝尔兴安盟;第22题7分如图;在平行四边形ABCD中;E、F分别为边AB、CD的中点;BD是对角线．1求证：△ADE≌△CBF；2若∠ADB是直角;则四边形BEDF是什么四边形证明你的结论．考点：平行四边形的性质；全等三角形的判定与性质；菱形的判定．分析：1由四边形ABCD是平行四边形;即可得AD=BC;AB=CD;∠A=∠C;又由E、F分别为边AB、CD的中点;可证得AE=CF;然后由SAS;即可判定△ADE≌△CBF；2先证明BE与DF平行且相等;然后根据一组对边平行且相等的四边形是平行四边形;再连接EF;可以证明四边形AEFD是平行四边形;所以AD∥EF;又AD⊥BD;所以BD⊥EF;根据菱形的判定可以得到四边形是菱形．解答：1证明：∵四边形ABCD是平行四边形;∴AD=BC;AB=CD;∠A=∠C;∵E、F分别为边AB、CD的中点;∴AE=AB;CF=CD;∴AE=CF;在△ADE和△CBF中;∵;∴△ADE≌△CBFSAS；2若∠ADB是直角;则四边形BEDF是菱形;理由如下：解：由1可得BE=DF;又∵AB∥C D;∴BE∥DF;BE=DF;∴四边形BEDF是平行四边形;连接EF;在 ABCD中;E、F分别为边AB、CD的中点;∴DF∥AE;DF=AE;∴四边形AEFD是平行四边形;∴EF∥AD;∵∠ADB是直角;∴AD⊥BD;∴EF⊥BD;又∵四边形BFDE是平行四边形;∴四边形BFDE是菱形．点评：本题主要考查了平行四边形的性质;全等三角形的判定以及菱形的判定;利用好E、F 是中点是解题的关键．5. 烟台市 2014 中考 -24如图;AB是⊙O的直径;延长AB至P;使BP=OB;BD垂直于弦BC;垂足为点B;点D在PC上．设∠PCB=α;∠POC=β．求证：tanα tan=．解析：连接AC先求出△PBD∽△PAC;再求出=;最后得到tanα tan=．解答：证明：连接AC;则∠A=∠POC=;∵AB是⊙O的直径;∴∠ACB=90°;∴tanα=;BD∥AC;∴∠PBD=∠A;∵∠P=∠P;∴△PBD∽△PAC;∴=;∵PB=0B=OA;∴=;∴tana tan===．点评：本题主要考查了相似三角形的判定与性质及圆周角的知识;本题解题的关键是求出△PBD∽△PAC;再求出tanα tan=．6. 2015 梧州;第25题12分如图;在正方形ABCD中;点P在AD上;且不与A、D重合;BP的垂直平分线分别交CD、AB于E、F两点;垂足为Q;过E作EH⊥AB于H．1求证：HF=AP；2若正方形ABCD的边长为12;AP=4;求线段EQ的长．考点：正方形的性质；全等三角形的判定与性质；勾股定理．所有分析： 1先根据EQ⊥BO;EH⊥AB得出∠EQN=∠BHM=90°．根据∠EMQ=∠BMH得出△EMQ∽△BMH;故∠QEM=∠HBM．由ASA定理得出△APB≌△HFE;故可得出结论；2由勾股定理求出BP的长;根据EF是BP的垂直平分线可知BQ=BP;再根据锐角三角函数的定义得出QF=BQ的长;由1知;△APB≌△HFE;故EF=BP=4;再根据EQ=EF﹣QF即可得出结论．解答： 1证明：∵EQ⊥BO;EH⊥AB;∴∠EQN=∠BHM=90°．∵∠EMQ=∠BMH;∴△EMQ∽△BMH;∴∠QEM=∠HBM．在Rt△APB与Rt△HFE中;;∴△APB≌△HFE;∴HF=AP；2解：由勾股定理得;BP===4．∵EF是BP的垂直平分线;∴BQ=BP=2;∴QF=BQ tan∠FBQ=BQ tan∠ABP=2×=．由1知;△APB≌△HFE;∴EF=BP=4;∴EQ=EF﹣QF=4﹣=．点评：本题考查的是正方形的性质;熟知正方形的性质及全等三角形的判定与性质是解答此题的关键．7.8. 2015 北海;第25题12分如图;AB、CD为⊙O的直径;弦AE∥CD;连接BE交CD于点F;过点E作直线EP与CD的延长线交于点P;使∠PED=∠C．1求证：PE是⊙O的切线；2求证：ED平分∠BEP；3若⊙O的半径为5;CF=2EF;求PD的长．考点：切线的判定．分析： 1如图;连接OE．欲证明PE是⊙O的切线;只需推知OE⊥PE即可；2由圆周角定理得到∠AEB=∠CED=90°;根据“同角的余角相等”推知∠3=∠4;结合已知条件证得结论；3设EF=x;则CF=2x;在RT△OEF中;根据勾股定理得出52=x2+2x﹣52;求得EF=4;进而求得BE=8;CF=8;在RT△AEB中;根据勾股定理求得AE=6;然后根据△AEB∽△EFP;得出=;求得PF=;即可求得PD的长．解答： 1证明：如图;连接OE．∵CD是圆O的直径;∴∠CED=90°．∵OC=OE;∴∠1=∠2．又∵∠PED=∠C;即∠PED=∠1;∴∠PED=∠2;∴∠PED+∠OED=∠2+∠OED=90°;即∠OEP=90°; ∴OE⊥EP;又∵点E在圆上;∴PE是⊙O的切线；2证明：∵AB、CD为⊙O的直径;∴∠AEB=∠CED=90°;∴∠3=∠4同角的余角相等．又∵∠PED=∠1;∴∠PED=∠4;即ED平分∠BEP；3解：设EF=x;则CF=2x;∵⊙O的半径为5;∴OF=2x﹣5;在RT△OEF中;OE2=OF2+EF2;即52=x2+2x﹣52;解得x=4;∴EF=4;∴BE=2EF=8;CF=2EF=8;∴DF=CD﹣CF=10﹣8=2;∵AB为⊙O的直径;∴∠AEB=90°;∵AB=10;BE=8;∴AE=6;∵∠BEP=∠A;∠EFP=∠AEB=90°;∴△AEB∽△EFP;∴=;即=;∴PF=;∴PD=PF﹣DF=﹣2=．点评：本题考查了切线的判定和性质;圆周角定理的应用;勾股定理的应用;三角形相似的判定和性质;熟练掌握性质定理是解题的关键．。

中考几何证明专项练习题一

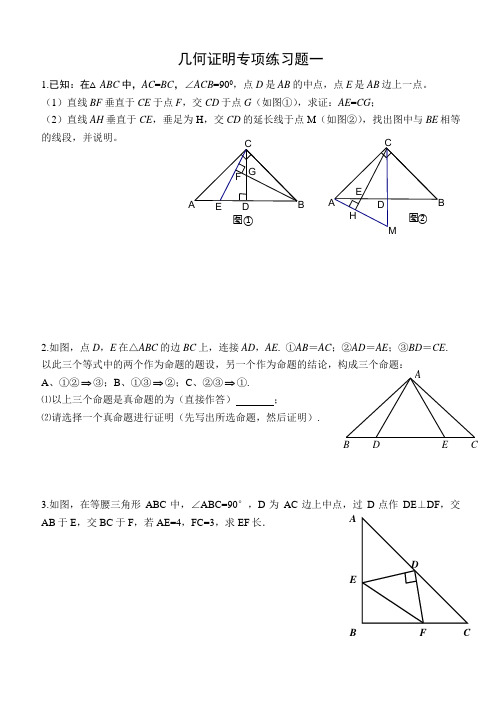
图①GF EDC BAHM图②ED CB A几何证明专项练习题一1.已知：在△ABC 中，AC =BC ，∠ACB =900，点D 是AB 的中点，点E 是AB 边上一点。

（1）直线BF 垂直于CE 于点F ，交CD 于点G （如图①），求证：AE =CG ；（2）直线AH 垂直于CE ，垂足为H ，交CD 的延长线于点M （如图②），找出图中与BE 相等的线段，并说明。

2.如图，点D ，E 在△ABC 的边BC 上，连接AD ，AE . ①AB ＝AC ；②AD ＝AE ；③BD ＝CE .以此三个等式中的两个作为命题的题设，另一个作为命题的结论，构成三个命题： A 、①②⇒③；B 、①③⇒②；C 、②③⇒①. ⑴以上三个命题是真命题的为（直接作答）； ⑵请选择一个真命题进行证明（先写出所选命题，然后证明）.3.如图，在等腰三角形ABC 中，∠ABC=90°，D 为AC 边上中点，过D 点作DE ⊥DF ，交AB 于E ，交BC 于F ，若AE=4，FC=3，求EF 长． E DCB ABA EDFC4. 已知：如图，锐角△ABC 的两条高BE 、CD 相交于点O ，且OB=OC ，（1）求证：△ABC 是等腰三角形；（2）判断点O 是否在∠B AC 的角平分线上，并说明理由。

5.如图， △ABC 中，AB=AC ，∠A=36°，AC 的垂直平分线交AB 于E ，D 为垂足，连结EC ．（1）求∠ECD 的度数；（2）若CE=5，求BC 长．6.数学课上，李老师出示了如下框中的题目.在等边三角形ABC 中，点E 在AB 上，点D 在CB 的延长线上，且ED=EC ，如图.试确定线段AE 与DB 的大小关系，并说明理由.EABCD小敏与同桌小聪讨论后，进行了如下解答：（1）特殊情况，探索结论:当点E 为AB 的中点时，如图1，确定线段AE 与DB 的大小关系，请你直接写出结论：AE DB （填“>”,“<”或“=”）.（2）特例启发，解答题目解：题目中，AE 与DB 的大小关系是：AE DB （填“>”,“<”或“=”）.理由如下：如图2，过点E 作//EF BC ，交AC 于点F .（请你完成以下解答过程） EAB CD6题图2EA BCD6题图1EBD A C F AF DE BC7.如图，在△ABC 和△ADE 中，点E 在BC 边上，∠BAC=∠DAE ，∠B=∠D ，AB=AD. ⑴求证：△ABC ≌△ADE ；⑵如果∠AEC=75°，将△ADE 绕着点A 旋转一个锐角后与△ABC 重合，求这个旋转角的大小.8.在正方形ABCD 中，AC 为对角线，E 为AC 上一点，连接EB 、ED ．（1）求证：△BEC ≌△DEC ；（2）延长BE 交AD 于F ，当∠BED =120°时，求∠EFD 的度数．9.如图,四边形ABCD 是边长为2的正方形，点G 是BC 延长线上一点，连结AG ，点E 、F 分别在AG 上，连接BE 、DF ，∠1=∠2，∠3=∠4． ⑴证明：△ABE ≌△DAF ； ⑵若∠AGB=30°，求EF 的长．10.如图，等边△ABC 中，AO 是∠BAC 的角平分线，D 为AO 上一点，以CD 为一边且在CD 下方作等边△CDE ,连结BE . ⑴求证：△ACD ≌△BCE ；⑵延长BE 至Q, P 为BQ 上一点，连结CP 、CQ 使CP ＝CQ ＝5, 若BC ＝8时，求PQ 的长.11.如图，正方形ABCD 的对角线交于点0，点E 是线段0D 上一点，连接EC ，作BF ⊥CE 于点F ，交0C 于点G ． (1)求证：BG=CE;(2)若AB=4 BF 是∠DBC 的角平分线，求OG 的长．12.已知：如图，在直角梯形ABCD 中，AD∥BC，∠ABC=90º，DE⊥AC 于点F ，交BC 于点G ，交AB 的延长线于点E ，且AE=AC 。

2019届中考数学复习《几何证明与计算》专题训练含答案

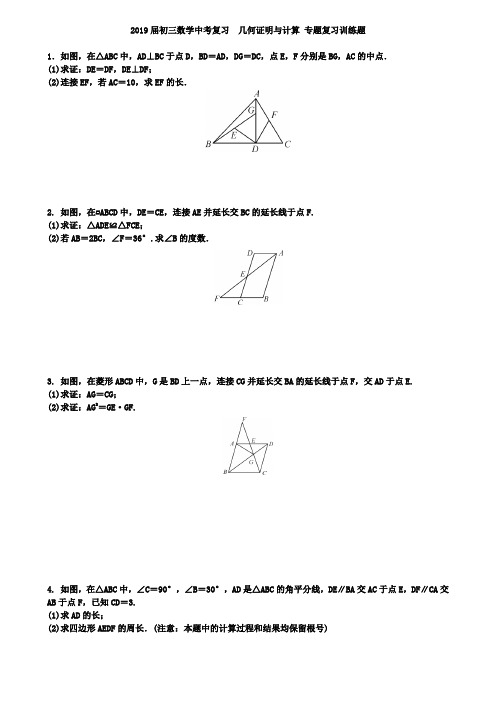
2019届初三数学中考复习几何证明与计算专题复习训练题1．如图，在△ABC中，AD⊥BC于点D，BD＝AD，DG＝DC，点E，F分别是BG，AC的中点．(1)求证：DE＝DF，DE⊥DF；(2)连接EF，若AC＝10，求EF的长．2. 如图，在▱ABCD中，DE＝CE，连接AE并延长交BC的延长线于点F.(1)求证：△ADE≌△FCE；(2)若AB＝2BC，∠F＝36°.求∠B的度数．3. 如图，在菱形ABCD中，G是BD上一点，连接CG并延长交BA的延长线于点F，交AD于点E.(1)求证：AG＝CG；(2)求证：AG2＝GE·GF.4. 如图，在△ABC中，∠C＝90°，∠B＝30°，AD是△ABC的角平分线，DE∥BA交AC于点E，DF∥CA交AB于点F，已知CD＝3.(1)求AD的长；(2)求四边形AEDF的周长．(注意：本题中的计算过程和结果均保留根号)5. 如图，在菱形ABCD中，点E，O，F分别为AB，AC，AD的中点，连接CE，CF，OE，OF.(1)求证：△BCE≌△DCF；(2)当AB与BC满足什么关系时，四边形AEOF是正方形？请说明理由．6. 如图，点E是正方形ABCD的边BC延长线上一点，连接DE，过顶点B作BF⊥DE，垂足为F，BF分别交AC于点H，交CD于点G.(1)求证：BG＝DE；(2)若点G为CD的中点，求HGGF的值．7. 如图，在正方形ABCD中，点G在对角线BD上(不与点B，D重合)，GE⊥DC于点E，GF⊥BC于点F，连接AG.(1)写出线段AG，GE，GF长度之间的数量关系，并说明理由；(2)若正方形ABCD的边长为1，∠AGF＝105°，求线段BG的长．8. 如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为D，E，AD与BE相交于点F.(1)求证：△ACD∽△BFD；(2)当tan∠ABD＝1，AC＝3时，求BF的长．9. 如图，在菱形ABCD中，G是BD上一点，连接CG并延长交BA的延长线于点F，交AD于点E.(1)求证：AG＝CG；(2)求证：AG2＝GE·GF.10. 如图，在△ABC和△BCD中，∠BAC＝∠BCD＝90°，AB＝AC，CB＝CD.延长CA至点E，使AE＝AC；延长CB至点F，使BF＝BC.连接AD，AF，DF，EF，延长DB交EF于点N.(1)求证：AD＝AF；(2)求证：BD＝EF；(3)试判断四边形ABNE的形状，并说明理由．11. 在△ABC中，∠ABM＝45°，AM⊥BM，垂足为M，点C是BM延长线上一点，连接AC.(1)如图①，若AB＝32，BC＝5，求AC的长；(2)如图②，点D是线段AM上一点，MD＝MC，点E是△ABC外一点，EC＝AC，连接ED并延长交BC于点F，且点F是线段BC的中点，求证：∠BDF＝∠CEF.12. 如图，正方形ABCD中，M为BC上一点，F是AM的中点，EF⊥AM，垂足为F，交AD的延长线于点E，交DC于点N.(1)求证：△ABM∽△EFA；(2)若AB＝12，BM＝5，求DE的长．参考答案：1. 解：(1)证明：∵AD⊥BC，∴∠ADB＝∠ADC＝90°.在△BDG和△ADC中，⎩⎪⎨⎪⎧BD ＝AD ，∠BDG ＝∠ADC DG ＝DC ，，∴△BDG ≌△ADC. ∴BG ＝AC ，∠BGD ＝∠C.∵∠ADB＝∠ADC＝90°， E ，F 分别是BG ，AC 的中点，∴DE ＝12BG ＝EG ，DF ＝12AC ＝AF.∴DE＝DF ，∠EDG ＝∠EGD，∠FDA ＝∠FAD.∴∠EDG＋∠FDA＝90°，∴DE ⊥DF.(2)∵AC＝10，∴DE ＝DF ＝5，由勾股定理，得EF ＝DE 2＋DF 2＝5 2. 2. 解：(1)证明：∵四边形ABCD 是平行四边形，∴AD ∥BC ，AD ＝BC.∴∠D＝∠ECF.在△ADE 和△FCE 中，⎩⎪⎨⎪⎧∠D＝∠ECF，DE ＝CE ，∠AED ＝∠FEC，∴△ADE ≌△FCE(ASA)．(2)∵△ADE≌△FCE，∴AD＝FC.∵AD＝BC ，AB ＝2BC ，∴AB＝FB.∴∠BAF＝∠F＝36°.∴∠B＝180°－2×36°＝108°. 3. 证明：(1)∵四边形ABCD 是菱形，∴AB ∥CD ，AD ＝CD ，∠ADB ＝∠CDB.又GD 为公共边，∴△ADG ≌△CDG(SAS)，∴AG ＝CG. (2)∵△ADG≌△CDG，∴∠EAG ＝∠DCG.∵AB∥CD，∴∠DCG ＝∠F.∴∠EAG＝∠F.∵∠AGE＝∠AGE，∴△AGE ∽△FGA.∴AG FG ＝EG AG.∴AG 2＝GE·GF. 4. 解：(1)∵∠C＝90°，∠B ＝30°，∴∠CAB ＝60°.∵AD 平分∠CAB ，∴∠CAD ＝12∠CAB＝30°.在Rt △ACD 中，∵∠ACD ＝90°，∠CAD ＝30°，∴AD ＝2CD ＝6. (2)∵DE∥BA 交AC 于点E ，DF ∥CA 交AB 于点F ， ∴四边形AEDF 是平行四边形，∠EAD ＝∠ADF＝∠DAF. ∴AF＝DF.∴四边形AEDF 是菱形．∴AE＝DE ＝DF ＝AF. 在Rt △CED 中，∵DE ∥AB ，∴∠CDE ＝∠B＝30°. ∴DE ＝CDcos30°＝2 3.∴四边形AEDF 的周长为8 3.5. 解：(1)证明：∵四边形ABCD 是菱形，∴∠B ＝∠D，AB ＝BC ＝DC ＝AD.∵点E ，O ，F 分别为AB ，AC ，AD 的中点，∴AE ＝BE ＝DF ＝AF ，OF ＝12DC ，OE ＝12BC ，OE ∥BC.在△BCE 和△DCF 中，⎩⎪⎨⎪⎧BE ＝DF ，∠B ＝∠D，BC ＝DC ，∴△BCE ≌△DCF(SAS)． (2)当AB⊥BC 时，四边形AEOF 是正方形，理由如下：由(1)得AE ＝OE ＝OF ＝AF ，∴四边形AEOF 是菱形．∵AB⊥BC，OE∥BC，∴OE⊥AB.∴∠AEO＝90°.∴四边形AEOF 是正方形．6. 解：(1)证明：∵BF⊥DE，∴∠GFD ＝90°.∵∠BCG ＝90°，∠BGC ＝∠DGF，∴∠CBG ＝∠CDE. 在△BCG 与△DCE 中.⎩⎪⎨⎪⎧∠CBG＝∠CDE，BC ＝CD ，∠BCG ＝∠DCE，∴△BCG ≌△DCE(ASA)，∴BG ＝DE.(2)设CG ＝x ，∵G 为CD 的中点，∴GD ＝CG ＝x ，由(1)可知△BCG≌△DCE(ASA)，∴CG ＝CE ＝x.由勾股定理可知DE ＝BG ＝5x ，∵sin ∠CDE ＝CE DE ＝GFGD ，∴GF＝55x.∵AB∥CG，∴△ABH ∽△CGH.∴AB CG ＝BH GH ＝21. ∴BH＝253x ，GH ＝53x.∴HG GF ＝53.7. 解：(1)结论：AG 2＝GE 2＋GF 2.理由：连接CG.∵四边形ABCD 是正方形，∴点A ，C 关于对角线BD 对称． ∵点G 在BD 上，∴GA＝GC.∵GE⊥DC 于点E ，GF⊥BC 于点F ， ∴∠GEC＝∠ECF＝∠CFG＝90°.∴四边形EGFC 是矩形．∴CF＝GE.在Rt △GFC 中，∵CG 2＝GF 2＋CF 2，∴AG 2＝GF 2＋GE 2.(2)过点B 作BN⊥AG 于点N ，在BN 上取一点M ，使得AM ＝BM.设AN ＝x.∵∠AGF＝105°，∠FBG ＝∠FGB＝∠ABG＝45°， ∴∠AGB ＝60°，∠GBN ＝30°，∠ABM ＝∠MAB＝15°.∴∠AMN ＝30°.∴AM ＝BM ＝2x ，MN ＝3x.在Rt △ABN 中，∵AB 2＝AN 2＋BN 2，∴1＝x 2＋(2x ＋3x)2，解得x ＝6－24，∴BN ＝6＋24.∴BG＝BN cos30°＝32＋66. 8. 解：(1)∵AD⊥BC，BE ⊥AC ，∴∠BDF ＝∠ADC＝∠BEC＝90°，∴∠C ＋∠DBF＝90°，∠C ＋∠DAC＝90°，∴∠DBF ＝∠DAC，∴△ACD ∽△BFD(2)∵tan ∠ABD ＝1，∠ADB ＝90°，∴AD BD ＝1，∵△ACD ∽△BFD ，∴AC BF ＝ADBD＝1，∴BF ＝AC ＝39. 解：(1)∵四边形ABCD 是菱形，∴AB ∥CD ，AD ＝CD ，∠ADB ＝∠CDB，可证△ADG≌△CDG(SAS)，∴AG ＝CG(2)∵△ADG≌△CDG，∴∠EAG ＝∠DCG，∵AB ∥CD ，∴∠DCG ＝∠F，∴∠EAG ＝∠F，∵∠AGE ＝∠AGE，∴△AGE ∽△FGA ，∴AG FG ＝EG AG，∴AG 2＝GE·GF10. 解：(1)∵AB＝AC ，∠BAC ＝90°，∴∠ABC ＝∠ACB ＝45°，∴∠ABF ＝135°，∵∠BCD ＝90°，∴∠ACD ＝∠ACB＋∠BCD＝135°，∴∠ABF ＝∠ACD，∵CB ＝CD ，CB ＝BF ，∴BF ＝CD ，可证△ABF≌△ACD(SAS)，∴AD ＝AF(2)由(1)知AF ＝AD ，△ABF ≌△ACD ，∴∠FAB ＝∠DAC，∵∠BAC ＝90°，∴∠EAB ＝∠BAC＝90°，∴∠EAF ＝∠BAD，可证△AEF≌△ABD(SAS)，∴BD ＝EF(3)四边形ABNE 是正方形．理由如下：∵CD＝CB ，∠BCD ＝90°，∴∠CBD ＝45°，又∵∠ABC＝45°，∴∠ABD ＝∠ABC＋∠CBD＝90°，由(2)知∠EAB＝90°，△AEF ≌△ABD ，∴∠AEF ＝∠ABD＝90°，∴四边形ABNE 是矩形，又∵AE＝AB ，∴四边形ABNE 是正方形 11. 解：(1)∵∠ABM＝45°，AM ⊥BM ，∴AM ＝BM ＝ABcos45°＝32×22＝3. 则CM ＝BC －BM ＝5－3＝2，∴AC ＝AM 2＋CM 2＝22＋32＝13.(2)证明：延长EF 到点G ，使得FG ＝EF ，连接BG.∵DM ＝MC ，∠BMD ＝∠AMC ，BM ＝AM ，∴△BMD≌△AMC(SAS)．∴AC ＝BD.又CE ＝AC ，∴BD ＝CE.∵BF ＝FC ，∠BFG ＝∠EFC ，FG ＝FE ，∴△BFG≌△CFE.∴BG＝CE ，∠G＝∠E.∴BD＝CE ＝BG ，∴∠BDG＝∠G＝∠E. 12. 解：(1)证明：∵四边形ABCD 是正方形， ∴AB＝AD ，∠B＝90°，AD∥BC.∴∠AMB＝∠EA F.又∵EF⊥AM，∴∠AFE＝90°.∴∠B＝∠AFE.∴△ABM∽△EFA. (2)∵∠B＝90°，AB ＝AD ＝12，BM ＝5，∴AM ＝122＋52＝13.∵F 是AM 的中点，∴AF ＝12AM ＝6.5.∵△ABM∽△EFA，∴BM AF ＝AM AE ，即56.5＝13AE.∴AE ＝16.9，∴DE ＝AE －AD ＝4.9.2019-2020学年数学中考模拟试卷一、选择题1．已知二次函数y ＝ax 2+bx+c （a≠0），过（1，y 1）、（2，y 2）．下列结论：①若y 1＞0时，则a+b+c ＞0； ②若a ＝2b 时，则y 1＜y 2；③若y 1＜0，y 2＞0，且a+b ＜0，则a ＞0．其中正确的结论个数为（） A ．0个B ．1个C ．2个D ．3个2．已知直线a ∥b ，将一块含45o角的直角三角板(∠C=90o)按如图所示的位置摆放，若∠1=55o，则∠2 的度数为( )A ．85oB ．70oC ．80oD ．75o3．如图，⊙O 与BC 相切于点B ，弦AB ∥OC ，若∠C ＝40°，则∠AOB 的度数是（）A.60B.70°C.80°D.90°4．如图，点P(-a,2a)是反比例函数与的一个交点，图中阴影部分的面积为5π，则反比例函数的解析是为（）A. B. C. D.5．如图，等边三角形ABC ，B 点在坐标原点，C 点的坐标为（4，0），则点A 的坐标为（）A ．（2，3）B ．（2，）C ．（，2）D ．（2，6．如图，在平面直角坐标系中，四边形OABC 是菱形，点C 的坐标为(4,0)，60AOC ∠=︒，垂直于x 轴的直线l 从y 轴出发，沿x 轴正方向以每秒1个单位长度的速度向右平移，设直线l 与菱形OABC 的两边分别交于点M ，N(点M 在点N 的上方)，若OMN ∆的面积为S ，直线l 的运动时间为t 秒(04)t ≤≤，则能大致反映S 与t 的函数关系的图象是( )A. B.C. D.7．如果a+b ＝12，那么a b a b b a+--22的值是（） A ．12B ．14C ．2D ．48．《九章算术》中记载：“今有甲乙二人持钱不知其数，甲得乙半而钱五十，乙得甲太半而亦钱五十.问甲乙持钱各几何？”其大意是：今有甲、乙两人各带了若干钱.如果甲得到乙所有钱的一半，那么甲共有钱；如果乙得到甲所有钱的三分之二，那么乙也共有.问甲、乙两人各带了多少钱？设甲带钱为，乙带钱为，根据题意，可列方程组为（）A.B.C.D.9．如图，在矩形ABCD 中，AB=8，BC=6，点E 在边AB 上，点F 在边CD 上，点G ，H 在对角线AC 上，若四边形GEHF 是菱形，则AE 的长是（）A.5B.254C. D.10．正比例函数y ＝kx(k≠0)的图象上一点A 到x 轴的距离与到y 轴的距离之比为2 : 3，且y 随x 的增大而减小，则k 的值是 ( ) A ．23B ．32C ．32-D ．23-11．如图，在四边形ABCD 中，AC 与BD 相交于点O ，∠BAD ＝90°，BO ＝DO ，那么添加下列一个条件后，仍不能判定四边形ABCD 是矩形的是( )A ．∠ABC ＝90°B ．∠BCD ＝90°C ．AB ＝CD D ．AB ∥CD12．如图，在矩形ABCD 中，6AB =，4BC =，动点E 从点A 出发，沿A B C →→的路线运动,当点E 到达点C 时停止运动，过点E 作FE AE ⊥,交CD 于点F ，设点E 运动的路程为x ,FC y =.则y 关于x 的图象大致为（）A ．B ．C ．D ．二、填空题13．如图，将边长为3的正方形纸片ABCD 对折，使AB 与DC 重合，折痕为EF ，展平后，再将点B 折到边CD 上，使边AB 经过点E ，折痕为GH ，点B 的对应点为M ，点A 的对应点为N ，那么折痕GH 的长为_____．14．计算：①232n m ⎛⎫= ⎪⎝⎭_____；②b a a b a b -=-- _____． 15．如图是23名射击运动员的一次测试成绩的频数分布折线图，则射击成绩的中位数_____。

2023年中考数学几何培优专题：线段等量关系的证明(含答案)

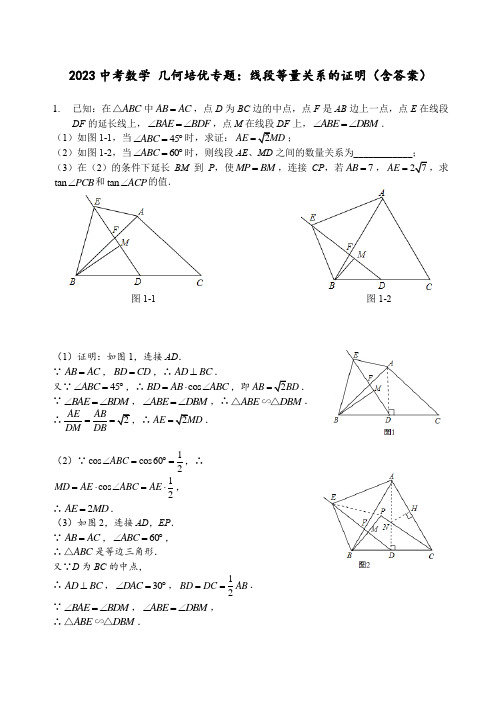
2023中考数学几何培优专题：线段等量关系的证明（含答案）1. 已知：在ABC △中AB AC =，点D 为BC 边的中点，点F 是AB 边上一点，点E 在线段DF 的延长线上，BAE BDF ∠=∠，点M 在线段DF 上，ABE DBM ∠=∠．（1）如图1-1，当45ABC ∠=︒时，求证：2AE MD =；（2）如图1-2，当60ABC ∠=︒时，则线段AE 、MD 之间的数量关系为____________；（3）在（2）的条件下延长BM 到P ，使MP BM =，连接CP ，若7AB =，27AE =，求tan PCB ∠和tan ACP ∠的值．图1-1 图1-2（1）证明：如图1，连接AD ．∵AB AC =，BD CD =，∴AD BC ⊥．又∵45ABC ∠=︒，∴cos BD AB ABC =⋅∠，即2AB BD =． ∵BAE BDM ∠=∠，ABE DBM ∠=∠，∴ABE DBM ∽△△．∴2AE AB DM DB ==，∴2AE MD =．（2）∵1cos cos602ABC ∠=︒=，∴1cos 2MD AE ABC AE =⋅∠=⋅，∴2AE MD =．（3）如图2，连接AD ，EP ． ∵AB AC =，60ABC ∠=︒， ∴ABC △是等边三角形．又∵D 为BC 的中点，∴AD BC ⊥，30DAC ∠=︒，12BD DC AB ==．∵BAE BDM ∠=∠，ABE DBM ∠=∠， ∴ABE DBM ∽△△．∴2BE ABBM DB ==，AEB DMB ∠=∠． ∴2EB BM =．又∵BM MP =， ∴EB BP =．∵60EBM ABC ∠=∠=︒， ∴BEP △为等边三角形， ∴EM BP ⊥， ∴90BMD ∠=︒， ∴90AEB ∠=︒，在Rt AEB △中，AE =7AB =，∴BE∴tan EAB ∠． ∵D 为BC 中点，M 为BP 中点，∴DM//PC ．∴MDB PCB ∠=∠，∴EAB PCB ∠=∠．∴tan PCB ∠=．在Rt ABD △中，sin AD AB ABD =⋅∠在Rt NDC △中，tan ND DC NCD =⋅∠，∴NA AD ND =-．过N 作NH AC ⊥，垂足为H ．在Rt ANH △中，12NH AN ==，21cos 8AH AN NAH =⋅∠=，∴358CH AC AH =-=，∴tan ACP ∠=．2.如图，在Rt ABC△中，90ACB∠=︒，1AC=，7BC=，点D是边CA延长线的一点，AE BD⊥，垂足为点E，AE的延长线交CA的平行线BF于点F，连结CE交AB于点G．（1）当点E是BD的中点时，求tan AFB∠的值；（2）CE AF⋅的值是否随线段AD长度的改变而变化？如果不变，求出CE AF⋅的值；如果变化，请说明理由；（3）当BGE△和BAF△相似时，求线段AF的长．（1）过点E作EH CD⊥于H，如图1，则有90EHA EHD∠=∠=︒．∵90BCD∠=︒，BE DE=，∴CE DE=．∴CH DH=，∴1722 EH BC==．设AH x=，则1DH CH x==+．∵AE BD⊥，∴90 AEH DEH AED∠+∠=∠=︒．∵90AEH EAH∠+∠=︒，∴EAH DEH∠=∠，∴AHE EHD∽△△，∴AH EH EH DH=，∴2EH AH DH=⋅，∴27(1)2x x⎛⎫=+⎪⎝⎭，解得5212x-=（舍负），∴75212tan75212EHEAHAH+∠===-．∵BF//CD，∴AFB EAH∠=∠，∴521tan 7AFB +∠=；（2）CE AF ⋅的值不变．取AB 的中点O ，连接OC 、OE ，如图2， ∵90BCA BEA ∠=∠=︒， ∴OC OA OB OE ===， ∴点A 、C 、B 、E 共圆，∴BCE BAF ∠=∠，180CBE CAE ∠+∠=︒． ∵BF//CD ，∴180BFA CAE ∠+∠=︒， ∴CBE BFA ∠=∠，∴BCE FAB ∽△△， ∴BC CE FA AB=，∴CE FA BC AB ⋅=⋅． ∵90BCA ∠=︒，7BC =，1AC =，∴52AB =，∴752=352CE FA ⋅=⨯；（3）过点E 作EH CD ⊥于H ，作EM BC ⊥于M ，如图3， ∴90EMC MCH CHE ∠=∠=∠=︒， ∴四边形EMCH 是矩形．∵BCE FAB ∽△△，BGE △与FAB △相似， ∴BGE △与BCE △相似， ∴EBG ECB ∠=∠．∵点A 、C 、B 、E 共圆， ∴ECA EBG ∠=∠，∴ECB ECA ∠=∠，∴EM EH =， ∴矩形EMCH 是正方形， ∴CM CH =．∵1452ECB ECA BCA ∠=∠=∠=︒，∴45EBA EAB ∠=∠=︒， ∴EB EA =，∴Rt Rt (HL)BME AHE ≌△△，∴BM AH =．设AH x =，则BM x =，7CM x =-，1CH x =+， ∴71x x -=+，∴3x =，∴4CH =．在Rt CHE △中，42cos 2CH ECH CE CE ∠===， ∴42CE =．由（2）可得352CE FA ⋅=，∴35235=442AF =．3. 已知：ACB △与DCE △为两个有公共顶点C 的等腰直角三角形，且90ACB DCE ∠=∠=︒，AC BC =，DC EC =．把DCE △绕点C 旋转，在整个旋转过程中，设BD 的中点为N ，连接CN ．（1）如图3-1，当点D 在BA 的延长线上时，连接AE ，求证：2AE CN =；（2）如图3-2，当DE 经过点A 时，过点C 作CH BD ⊥，垂足为H ，设AC 、BD 相交于F ，若4NH =，16BH =，求CF 的长．（1）证明：延长CN 至点K ，使NK CN =，连接DK ， ∵90DCA ACE ∠+∠=︒，90BCE ACE ∠+∠=︒， ∴180DCB ACE ∠+∠=︒，∴KDN CBN ∠=∠，∴DK//BC ，∵DN NB =，CN NK =，DNK BNC ∠=∠， ∴DNK BNC ≌△△，∴DK BC AC ==，∴180KDC DCB ∠+∠=︒，∵KDC ACE ∠=∠，又∵DK AC =，CD CE =，∵KDC ACE ≌△△， ∴AE CK =，∴2AE CN =；（2）延长CN 交DE 于点P ，延长CH 交DE 于点M ，图3-1D A NB EC图① 图② 备用图D A N BE DF A N H C C B ED B EF A N H KP M C备用图BF AN H CE图3-2A F N H DC B E4. 已知：在ABC △中，90ACB ∠=︒，点P 是线段AC 上一点，过点A 作AB 的垂线，交BP的延长线于点M ，MN AC ⊥于点N ，PQ AB ⊥于点Q ，AQ MN =．（1）如图4-1，求证：PC AN =；（2）如图4-2，点E 是MN 上一点，连接EP 并延长交BC 于点K ，点D 是AB 上一点，连接DK ，DKE ABC ∠=∠，EF PM ⊥于点H ，交BC 延长线于点F ，若2NP =，3PC =，:2:3CK CF =，求DQ 的长．图4-1 图4-2AQNPMAMQDNEPHAQ NPM B CAMQDNEPHB KC F GT图①图②5. 在ABC △中，90ACB ∠=︒．经过点B 的直线l （l 不与直线AB 重合）与直线BC 的夹角等于ABC ∠，分别过点C 、点A 作直线l 的垂线，垂足分别为点D 、点E ．（1）若45ABC ∠=︒，1CD =（如图），则AE 的长为_______；（2）写出线段AE 、CD 之间的数量关系，并加以证明；（3）若直线CE 、AB 交于点F ，56CF EF =，4CD =，求BD 的长．（1）2AE =.（2）线段AE 、CD 之间的数量关系为2AE CD =. 证明：如图1，延长AC 与直线l 交于点G ．依题意，可得12∠=∠． ∵90ACB ∠=︒，∴34∠=∠. ∴BA BG =，∴CA CG =．∵AE l ⊥，CD l ⊥，∴CD //AE ． ∵C 为AG 的中点，∴2AE CD =．（3）解：当点F 在线段AB 上时，如图2，过点C 作CG //l 交AB 于点H ，交AE 于点G ． ∴2HCB ∠=∠．∵12∠=∠，∴1HCB ∠=∠． ∴CH BH =．∵90ACB ∠=︒，∴34901HCB ∠+∠∠+∠=︒＝． ∴34∠∠＝．∴CH AH BH ==． ∵CG //l ，∴FCH △∽FEB △． ∴56CF CH EF EB =＝．设5CH x =，6BE x =，则10AB x =． ∴在AEB △中，90AEB ∠=︒，8AE x =．由（2）得，2AE CD =．∵4CD =，∴8AE =．∴1x =． ∴10AB =，6BE =，5CH =． ∵CG //l ，∴AGH AEB △△∽． ∴12HG AH BE AB ==．∴3HG =． ∴8CG CH HG =+=． ∵CG //l ，CD //AE ，A C()D B E l图1A C3124G D B E l图2AC124D B El3GHF∴四边形CDEG 为平行四边形. ∴8DE CG ==.∴2BD DE BE =-=．当点F 在线段BA 的延长线上时，如图3，同理可得5CH =，3GH =，6BE =. ∴2DE CG CH HG ==-=． ∴8BD DE BE =+=． ∴2BD =或8．6. 如图，在平面直角坐标系中，直线l 平行x 轴，交y 轴于点A ，第一象限内的点B 在l 上，连结OB ，动点P 满足90APQ ∠=︒，PQ 交x 轴于点C ．（1）当动点P 与点B 重合时，若点B 的坐标是(2,1)，求P A 的长．（2）当动点P 在线段OB 的延长线上时，若点A 的纵坐标与点B 的横坐标相等，求:PA PC 的值．（3）当动点P 在直线OB 上时，点D 是直线OB 与直线CA 的交点，点E 是直线CP 与y 轴的交点，若ACE AEC ∠=∠，2PD OD =，求:PA PC 的值．（1）∵点P 与点B 重合，点B 的坐标是(2,1)， ∴点P 的坐标是(2,1)．∴P A 的长为2．（2）过点P 作PM x ⊥轴，垂足为M ，过点P 作PN y ⊥轴，垂足为N ，如图1所示．∵点A 的纵坐标与点B 的横坐标相等， ∴OA AB =．∵90OAB ∠=︒，∴45AOB ABO ∠=∠=︒． ∵90AOC ∠=︒，∴45POC ∠=︒． ∵PM x ⊥轴，PN y ⊥轴，∴PM PN =，90ANP CMP ∠=∠=︒． ∴90NPM ∠=︒．∵90APC ∠=︒． ∵APN CPM ∠=∠，PN PM =，ANP CMP ∠=∠， ∴ANP CMP ≌△△．∴PA PC =． ∴:PA PC 的值为1:1．（3）①若点P 在线段OB 的延长线上，过点P 作PM x ⊥轴，垂足为M ，过点P 作PN y ⊥轴，垂足为N ，PM 与直线AC 的交点为F ，如图2所示． ∵APN CPM ∠=∠，ANP CMP ∠=∠，∴ANP CMP ∽△△．∴PA PNPC PM=． ∵ACE AEC ∠=∠，∴AC AE =． ∵AP PC ⊥，∴EP CP =．∵PM//y 轴，∴AF CF =，OM CM =．∴12FM OA =．设OA x =，∵PF//OA ，∴PDF ODA ∽△△．∴PF PDOA OD=∵2PD OD =，∴22PF OA x ==，12FM x =．∴52PM x =．∵90APC ∠=︒，AF CF =， ∴24AC PF x ==． ∵90AOC ∠=︒，∴OC =．∵90PNO NOM OMP ∠=∠=∠=︒， ∴四边形PMON 是矩形．∴PN OM =．∴5:::2PA PC PN PM x ===． ②点P 在BO 延长线上时，同理可得：32PM x =，24CA PF x ==，OC =．∴12PN OM OC ==．∴3:::PA PC PN PM x ===．综上所述：:PA PC．7. 正方形ABCD 和等腰直角DEF △有公共点D ，点E 在AD 边上，点F 在CD 的延长线上，连接CE ，AF ．（1）试判断线段CE 和AF 的数量关系和位置关系，并证明你的结论；（2）将DEF △绕点D 按顺时针方向旋转，当点E 落在AC 上时，设EF 与AD 交于点M ． ①求证：AEM CDE ∽△△；②当34AE EC =时，求AM MD的值．（1）CE AF ⊥，CE AF =．证明略（2）①∵AC 为正方形ABCD 的对角线 ∴45DAC ACD ∠=∠=︒，∵45FED ∠=︒，180FED AEM CED ∠+∠+∠=︒，180MAE AME AEM ∠+∠+∠=︒， ∴CED AME ∠=∠，∴AEM CDE ∽△△，②∵AEM CDE ∽△△，∴AE AMDC=， ∴设3AE a =，4EC a =，则DC =，4AMa=，∴AM ，∴MD =， ∴2425AM MD =． A B C E A BF D CEM8. 已知：在菱形ABCD 中，O 是对角线BD 上的一动点．（1）如图2-1，P 为线段BC 上一点，连接PO 并延长交AD 于点Q ，当O 是BD 的中点时，求证：OP OQ =；（2）如图2-2，连接AO 并延长，与DC 交于点R ，与BC 的延长线交于点S ．若4AD =，60DCB ∠=︒，10BS =，求AS 和OR 的长．图2-1 图2-2（1）证明：∵ABCD 为菱形，∴AD//BC ，∴OBP ODQ ∠=∠，∵O 是是BD 的中点，∴OB OD =，在BOP △和DOQ △中，∵OBP ODQ ∠=∠，OB OD =，BOP DOQ ∠=∠，∴(ASA)BOP DOQ ≌△△，∴OP OQ =. （2）解：如图，过A 作AT BC ⊥，与CB 的延长线交于T .∵ABCD 是菱形，60DCB ∠=︒，∴4AB AD ==，60ABT ∠=︒，∴sin 60AT AB =︒=，cos602TB AB =︒=， ∵10BS =，∴12TS TB BS =+=，∴AS = ∵AD//BS ，∴AOD SOB △△∽. ∴42105AO AD OS SB ===，则25AS OS OS -=，∴75AS OS =，∵AS =75OS AS ==. 同理可得ARD SRC △△∽，∴4263AR AD RS SC ===,则23AS SR RS -=，∴5AS =，∴3RS AS ==∴OR OS RS =-=-=.A DB C S O R TA QDOBP CA DB C SOR9. 在矩形ABCD 中，点P 在AD 上，2AB =，1AP =．将直角尺的顶点放在P 处，直角尺的两边分别交AB ，BC 于点E ，F ，连接EF （如图3-1）. （1）当点E 与点B 重合时，点F 恰好与点C 重合（如图3-2），求PC 的长；（2）探究：将直尺从图3-2中的位置开始，绕点P 顺时针旋转，当点E 和点A 重合时停止．在这个过程中，请你观察、猜想，并解答：①tan ∠PEF 的值是否发生变化？请说明理由；②直接写出从开始到停止，线段EF 的中点经过的路线长．图3-1 图3-2（1）在矩形ABCD 中，90A D ∠=∠=︒，1AP =，2CD AB ==，则PB =， ∴90ABP APB ∠+∠=︒，又∵90BPC ∠=︒，∴90APB DPC ∠+∠=︒，∴ABP DPC ∠=∠，∴APB DCP ∽△△，∴AP PBCD PC=，即12=PC =故答案为：（2）①PF PE的值不变，理由为：证明：过F 作FG AD ⊥，垂足为G ，则四边形ABFG 是矩形，∴90A PGF ∠=∠=︒，2GF AB ==， ∴90AEP APE ∠+∠=︒，又∵90EPF ∠=︒， ∴90APE GPF ∠+∠=︒，∴AEP GPF ∠=∠，∴APE GFP ∽△△，∴2PF GFPE AP==，∴Rt EPF △中，tan 2PFPEF PE∠==，∴PF PE的值不变． ②线段EF.A P DEB F CGA P DE BF C A P D ()()B E C F10. 已知：ABC △中，2ACB ABC ∠=∠，AD 为BAC ∠的平分线，E 为线段AC 上一点，过E作AD 的垂线交直线AB 于F ．（1）当E 点与C 点重合时（如图4-1），求证：BF DE =；（2）连接BE 交AD 于点N ，M 是BF 的中点，连接DM （如图4-2），若DM BF ⊥，4DC =，:3:2ABD ACD S S =△△，求DN 的长．图4-1 图4-2（1）连接DF ，设AD 与EF 交于点K ，∵AD 是BAC ∠的平分线，∴BAD CAD ∠=∠， ∵EF AD ⊥，∴90AKF AKE ∠=∠=︒，∴AFK AEK ∠=∠，∴AF AE =，∴AFD AED ≌△△， ∴DF DE =，AFD AED ∠=∠，又∵2ACB ABC ∠=∠，∴FBD FDB ∠=∠，∴BF DF =，∴DE BF =；（2）过A 作AP ⊥BC 于点P ，过D 作DQ ⊥AC 于点Q ．连接DF ，∵:3:2ABD ACD S S =△△，即132122BD APDC AP ⋅=⋅， ∴32BD DC =，∵4DC =，∴6BD =， AF()BD CE BD CFAMEN图1 图2 A F ()B D C E B D C F A M E N K Q P∵AD 是BAC ∠的平分线，DM AB ⊥，DQ AC ⊥，∴DM DQ =，∴132122AB DMAC DQ ⋅=⋅，∴32AB AC =由（1）可得：AQ AM =，DC BM =，∴AB AC DC =+， ∴32AC DC AC +=，∴8AC =，12AB =，设PC x =，则10BP x =-，又勾股定理得：22222AB BP AC PC AP -=-=，即22122(10)82x x --=-，解得：1x =，∴3DP =，又22222AD DP AC PC AP -=-=， ∴272AD =，AD =EF AD ⊥， ∴90AKF AKE ∠=∠=︒． ∵DA 平分BAC ∠， ∴FAD EAD ∠=∠，∴AFE AEF ∠=∠，∴AF AE =， ∴AFD AED ≌△△，∴AFD AED ∠=∠，DF DE =，又∵DB DF =， ∴6DB DE ==，∴BFD DEC DBF ∠=∠=∠，∴180180C DEC C DBF ︒-∠-∠=︒-∠-∠， ∴2EDC BAC DAE ∠=∠=∠，又∵2EDC NED ∠=∠， ∴DAE NED ∠=∠， ∵ADE EDN ∠=∠， ∴DAE DEN ∽△△， ∴DA DE DE DN=， ∴2DE DN DA =⋅，即36DN =⋅，∴DN =。

中考复习初中数学几何证明试题(含答案)

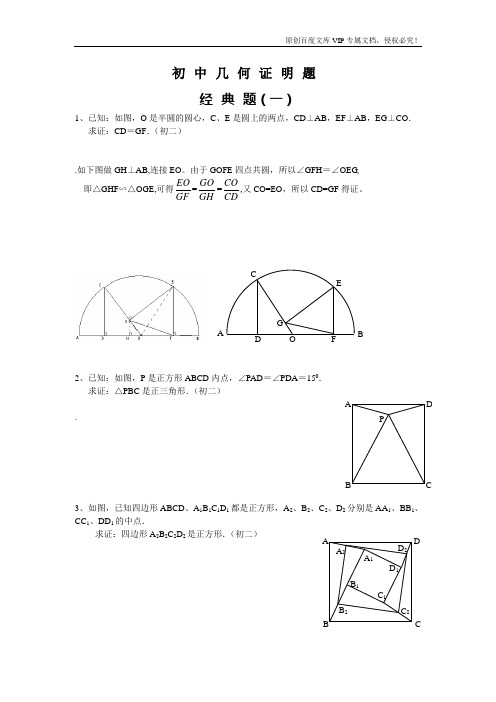
初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）.如下图做GH ⊥AB,连接EO 。

由于GOFE 四点共圆，所以∠GFH ＝∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ，所以CD=GF 得证。

2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）.3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）APCDB D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 AFGCEBOD4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．BF求证：点P 到边AB 的距离等于AB 的一半．经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEFB 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）经典题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值． A P CB P A D CB C B D A F PD E CB A APCB3、P为正方形ABCD内的一点，并且PA＝a，PB＝2a，PC＝3a，求正方形的边长．4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典题（一）1.如下图做GH⊥AB,连接EO。

中考几何证明题专项练习(A)

几何证明题专项练习（A ）
1．如图，已知：□ABCD 中，BCD ∠的平分线CE 交边AD 于E ，ABC ∠的平分线BG 交CE
于F ，交AD 于G ．求证：AE=DG ．
2.如图，在△ABC 中，点D 、E 分别在边AC 、AB 上，BD=CE ，∠DBC=∠ECB 。

求证：AB=AC 。

3.如图，C 是线段AB 的中点，CD 平分∠ACE ，CE 平分∠BCD ，CD=CE ． ⑴求证：△ACD≌△BCE；
⑵若∠D=50°，求∠B 的度数．
4.如图，在△ABC 中，D 是BC 边上的点（不与B ，C 重合），F ，E 分别是AD 及其延长线上的点，CF ∥BE . 请你添加一个条件，使△BDE ≌△CDF (不再添加其它线段，不再标注或使用其他
字母)，并给出证明．
（1）你添加的条件是：；
（2）证明：
.
A B C
D
E F G A C
B
D F E
5.如图，请在下列四个关系中，选出两个恰当．．．．的关系作为条件，推出四边形ABCD 是平行四边形，并予以证明．（写出一种即可）关系：①AD ∥BC ，②CD AB =，③C A ∠=∠，④︒=∠+∠180C B ．已知：在四边形ABCD 中，，；求证：四边形ABCD 是平行四边形．
6.如图，在
ABCD 中，点E 、F 是对角线AC 上两点，且CF AE =．求证：FDE EBF =∠．
7.如图，点B ，F ，C ，E 在同一条直线上，点A ，D 在直线BE 的两侧，AB ∥DE ，AC ∥DF ，BF=CE ．求证：AC=DF ．
A
B
C
D
F
E
D
C
B
A。

2020年数学中考复习：压轴几何证明题的解法(含答案)

2020年数学中考复习：压轴几何证明题的解法1.(2019.葫芦岛)如图，△ABC 是等腰直角三角形，∠ACB =900，D 是射线CB 上一点（点D 不与点B 重合），以AD 为斜边作等腰直角三角形ADE （点E 和点C 在AB 的同侧），连接CE 。

（1）如图①，当点D 与点C 重合时，直接写出CE 与AB 的位置关系；（2）如图②，当点D 与点C 不重合时，（1）的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；（3）当∠EAC =150时，请直接写出AB CE 的值。

解析：（1）由∠ECA =∠CAB =450,可得EC ∥AB 。

（2）由22=AB AC =AD AE ,且∠EAC =∠DAB ,可得△EAC ∽△DAB 进而得出∠ECA =∠DBA =450=∠CAB ,所以CE ∥AB .(3)此问分两种情况点D 在BC 上，点D 在CB 延长线上。

①当点D 在BC 上时，如图（2），此时∠CAB =150能得出∠CAD =300，这样就有33=AC CD ,也就是BC -DB =33AC ,BC =AC ,所以BD =333－AC 。

又由△EAC ∽△DAB 得21=BD CE ,因此有BD =2CE ，所以可得CE =6623－AC ，又AB =2AC ，因此ABCE =６３－3.当D 点在CB 延长线上时，∠CDA =300,解三角形得3AC =3CD 。

CD =BC +BD ,由△AEC ∽△ABD ,可得BD =2AC ，就能得到CE =ＡＣ２－１3,AB =2AC ，所以２－１3=AB CE . 2.(2019.沈阳）思维启迪：（1）如图1，A ，B 两点分别位于一个池塘的两端，小亮想用绳子测量A ，B 间的距离，但绳子不够长，聪明的小亮想出一个办法：先在地上取一个可以直接到达B 点的点C ，连接BC ，取BC 的中点P （点P 可以直接到达A 点），利用工具过点C 作CD ∥AB 交AP 的延长线于点D ，此时测得CD =200米，那么A ,B 间的距离是_200_米。

中考数学-几何证明

2020年-春季-初三下-【入学考试】1.(初2020级BZ初三下入学测试)如图，正方形ABCD中，对角线AC, BD交于点。

，点E.点OB ,线段AB上，且AF OE ,连接AE交OF于G , 连接DG交AO于H.F分别在线段⑴如图1,若点E为线段BO中点，AE J5,求BF的长：(2)如图2,若AE平分BAC,求证：FG HG;(3)如图3,点E在线段BO (含端点)上运动，连接HE，当线段HE长度取得最大值时，直接写出cos HDO的值.2.(初2020级BS初三下入学测试)如图，平行四边形ABCD中，AB=2BC, B 60 . 曲 DC中点，连接AE . F为AD上一点，连接CF交AE与点G , CM平分FCB交AB于点M .(1)如图1,若BC 3,AF 1 求sin DCF 的值.(2)求证：EG BM CG(3)如图2, CN AB于点N ,若AG=4, MN : BN=3: 5.求CG 的长度.3.(初2020级YZ初三下入学测试)在0ABCD中BAC=90 , AB=AE,延长BE交CD 于点F . AG BE交BE于点H点，M是BC边上的点.(1)如图1,若点M与点G重合，AH 5, AD 显26 ,求CF的长：2(2)如图2.若AM是BAD的角平分线，连接MH , HMG MAH ,求证：AM 2 .2HM(3)如图3,若点M为BC的中点，作点B关于AM的对称点N，连接AN、MN、EN,请直接写出AMH、NAE、MNE之间的角度关系.4.(初2020级YZ 初三下入学测试)在正方形 ABCD 中，E 为边CD 上一点(不与点 C 、D 第4页共34重合)，垂直于BE 的一条直线 MN 分别交BC 、BE 、AD 于点M 、P 、N,正方形ABCD 的边长为6.(1)如图1,当点M 和点C 重合时，若AN =4,求线段PM 的长度;(2)如图2,当点M 在边BC 上时，判断线段AN 、MB 、EC 之间的数量关系，并说明理由;(3)如图3,当垂足P 在正方形 ABCD 的对角线 AC 上运动时，连接 NB,将^ BPN 沿着BN 翻折，点P 落在点P 处，AB 的中点为Q,直接写出PQ 的最小值.5.(万二中初2020级初三下入学测试)在4ABC与4ADF中，/BAC=/DAF=90° ,AB=AC,AD=AF, DF的延长线交BC于点E,连接DB、CF.(1)如图1,当点C、A、D三点在同一直线上，且AC=g AF, AF=超时，求CE的长；(2)如图2,当/ AFC = 90°时，求证：E是BC的中点；(3)如图3,若CF平分/ ACB,且CF的延长线与DB交于点G,请直接写出BG、DG、FG之间的数量关系.[ D6.(万中初2020级初三下入学测试) 如图，在？ABCD中，/ACB = 45° , AEXBC于点E, 过点C 作CFLAB于点F,交AE于点M.点N在边BC上，且AM = CN ,连结DN .(1)若AB= 10Q , AC = 4,求BC 的长；(2)求证：AD+AM= 22DN .(3)如图，连接EF、探究AF、EF、CF之间存在的数量关系，直接写出数量关系不需要证明.2020年-春季-初三下-【第一次诊断】1.(初2020级YW初三下第一次诊断)如图，在平行四边形ABCD中，AC为对角线，过点D作DELDC交直线AB于点E,过点E作EHXAD于点H,过点B作BFXAD于点F.(1)如图，若/ BAD=60° , AF=3, AH=2,求AC 的长.(2)如图，若BF=DH,在AC上取一点G,连接DG、GE, 若/ DGE=75° ,/CDG=45° -/CAB,求证：DG 立CG22.如图，已知ABCD中，/ B=45° , CE^AD于G,交BA延长线E, CF平分/ DCE ,连接EF, ED.(1)如果AB=5, AD = 372,求线段DE的长.(2)如果/ CFE=90° ,求证：CD 2DF 版AG .(3)如图，在(2)的条件下，若FG J5,点M、N是线段CF、CD上的动点，DM+MN 是否存在最小值，若存在，求出这个最小值；若不存在，请说明理由 ^3.(初2020级BZ初三下第一次诊断)已知△ ABC是等边三角形，CD，AB交AB于M, DBXBC, E是AC上一点，EHXBC,垂足为H, EH与CD交于点F,连接BE.(1)如图，若EC=-AC , EH=6,求BE 的长. 5(2)如图，连接AF,将AF绕点A顺时针旋转，使F点落在BD边上的G点处，AG交CD 于Q,求证：BG=CF.(3)如图，在(2)的条件下，连接FG,交BE于N,连接MN,若竺勺，4AGF的面QG 3积为49户，求MN的长.3.(万州国本中学初三下期中考试)已知，在0ABCD中，AB BD, AB BD, E为射线BC上一点，连接AE交BD于点F .(1)如图1,若点E与点C重合，且AF 2胫，求AD的长；(2)如图2,当点E在BC边上时，过点D作DG AE于G ,延长DG交BC于H ,连接FH ,求证：AF DH FH ；(3)如图3,当点E在射线BC上运动时，过点D作DG AE于G , M为AG的中点，点N在BC边上且BN 1 ,已知AB 4 J2 ,请直接写出MN的最小值.4 .（万州国本中学初三下第一次诊断）【问题背景】如图1所示，在gABC 中，AB= BC, ABC=90，点D 为直线BC 上的一个动点（不与 B 、C 重合），连结AD,将线段AD 绕点D 按顺时针方向旋转90。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

精品文档
【题4】已知：如图，点B、F、C、E在同一直线上，BF=CE，AB ∥ED，AC∥FD，证明AB=DE，AC=DF.
【题5】已知：如图，△ABC是正三角形，P是三角形内一点，PA＝3，PB＝4，PC＝5．
求：∠APB的度数．
【题6】如图：△ABC中，∠ACB=90°，AC=BC，AE是BC边上的中
线，过C作CF⊥AE，垂足是F，过B作BD⊥BC交CF的延长线于D。

（1）求证：AE=CD;
（2）若AC=12㎝，求BD的长.
【题7】等边三角形CEF于菱形ABCD边长相等.
求证：（1）∠AEF=∠AFE
(2)角B的度数
【题8】如图，在△ABC中，∠C=2∠B，AD是△ABC的角平分线，∠1=∠B，求证：AB=AC+CD.
【题9】如图，在三角形ABC 中，AD 是BC 边上的中线，E 是AD 的中点，BE 的延长线交AC 于点F. 求证：AF=2
1FC
【题10】如图，将边长为1的正方形ABCD 绕点C 旋转到A'B'CD'的位置，若∠B'CB=30度，求AE 的长.
【题11】AD,BE分别是等边△ABC中BC,AC上的高。

M,N分别在AD,BE 的延长线上，∠CBM=∠ACN.求证AM=BN.
【题12】已知：如图，AD、BC相交于点O，OA=OD，OB=OC，点E、F在AD上，且AE=DF，∠ABE＝∠DCF.
求证：BE‖CF.
【巩固练习】
【练1】如图，已知BE垂直于AD，CF垂直于AD，且BE=CF. （1）请你判断AD是三角形ABC的中线还是角平分线？请证明你的结论。

（2）链接BF,CE，若四边形BFCE是菱形，则三角形ABC中应添加一个什么条件？
【练2】在等腰直角三角形ABC中，O是斜边AC的中点，P是斜边上的一个动点，且PB=PD，DE垂直AC，垂足为E。

（1）求证：PE=BO
（2）设AC=3a，AP=x，四边形PBDE的面积为y，求y与x之间的函数关系式。

【练3】已知：如图，在四边形ABCD中，AD＝BC，M、N分别是AB、CD的中点，AD，BC的延长线叫MN与E、F
求证∠DEN=∠F.
【练4】如图，若C在直线OB上，试判断△CDM形状。

【练5】已知△ABC，AD是BC边上的中线，分别以AB边、AC边为直角边向形外作等腰直角三角形。

求证：EF=2AD
1、【练6】如图，等边三角形ABC的边长为2，点P和点Q分别是从
A和C两点同时出发，做匀速运动，且他们的速度相同，点P沿射线AB运动，Q点沿点C在BC延长线上运动。

设PQ与直线AC相交于点D，作PE⊥AC于点E，当P和Q运动时，线段DE的长度是否改变？证明你的结论。

【提示】
【题1】分析：在ＢＣ上截取ＢＥ＝ＢＡ，连接ＤＥ．可得ΔBAD ≌
ΔBED ．由已知可得：，，
．∴，∴CD ＝CE ，∴BC ＝AB ＋CD ．
【题2】分析：将ΔABF 视为ΔADE 绕Ａ顺时针旋转即可．
∵．∴．
又∵，ＡＢ＝ＡＤ．∴ΔABF ≌ΔADE ．（ＡＳＡ）∴ＤＥ＝ＤＦ．【题3】分析：延长ＡＤ到Ｅ使得ＡＤ＝ＥＤ．易证ΔABD ≌ΔECD ．∴ＥＣ＝ＡＢ．
∵．∴．∴ＡＣ＝ＥＣ＝ＡＢ．
【题4】本题比较简单，难点在BF+CF=CE+CF 这，一般刚接触三角形证明的人会在这失手。

证明：∵BF=CE 又∵BF+CF=BC CE+CF=EF ∴BC=EF
∵AB ∥DE ，AC ∥FD ∴∠B=∠E ，∠DFE=∠BCA
18ABD DBE ∠=∠=o
108A BED ∠=∠=o
36C ABC ∠=∠=o
72DEC EDC ∠=∠=o
90o
90FAB BAE EAD BAE ∠+∠=∠+∠=o
FBA EDA ∠=∠90FBA EDA ∠=∠=o
BAD CAD ∠=∠E CAD ∠=∠
又∵BF=CE
∴△DEF≌△ABC（ASA）
∴AB=DE，AC=DF
【题5】顺时针旋转△ABP 600，连接PQ ，则△PBQ是正三角形。

可得△PQC是直角三角形。

所以∠APB=1500。

【题6】解析：如果遇到这类题，有时在图形中隐藏着一些不明显的条件，你就先试试一个角加公共角等于90°，再试其它角加这个公共角是否能等于90°，能说明它俩相等。

证明：（1）∵BD⊥BC，CF⊥AE
∴∠DBC=∠ACB=∠EFC=90°
∵∠D+∠BCD=90°
∠FEC+∠BCD=90°
∴∠D=∠FEC
又∵∠DBC=∠ACE=90°，AC=BC
∴△DBC ≌△ACE （HL ） ∴AE=CD
（2）由（1）可知 △BDC ≌△ACE
∴BC=AC=12㎝，BD=CE ∵AE 是BC 边上的中线 ∴BE=EC=1
2BC=6㎝ ∵BD=CE ∴BD=6㎝【题7】解：
∵CB=CE,CD=CF
∴∠B=∠CEB ，∠D=∠CFD ∵∠B=∠D(菱形的对角相等） ∴∠CEB=∠CFD ∵∠CEF=∠CFE=60° ∠CEB+∠CEF+∠AEF=180° ∠CED+∠CFE+∠AFE=180° ∴∠AEF=∠AFE
(2)设∠B=X,则∠A=180°—X ，∠CEB=X ∵∠AEF=∠AFE,∠A=∠AEF+∠AFE=180° ∴ (180°－X ) +2∠AEF=180° ∴∠AEF=X/2
∵∠CEB+∠CEF+∠AEF=180°
∴X+60°+X/2=180°
∴X=80°
∴∠B=80°
【题8】解析：这种类型的题，一般是一条长的线段被分为两段，只能证AC、CD这两条线段与AB这条线段平分的两条线段AE、BE 相等，从而证明出来。

证明：∵∠AED是△EDB的一个外角
又∵∠1=∠B
∴∠AED=2∠B
∴∠AED=∠C=2∠B
∵AD是△ABC的角平分线
∴∠CAD=∠DAE
又∵∠AED=∠C，AD=DA
∴△ACD≌△AED（AAS）
∴AC=AE，CD=DE
∵∠1=∠B
∴DE=BE
∴CD=BE
∵AB=AE+BE
又∵AC=AE，CD=BE
∴AB=AC+CD
【题9】解析：作CF的中点G，连接DG，则FG=GC
∴DG ∥BF
∴AE ∶ED=AF ∶FG
∵AE=ED
∴AF=FG
∴FC AF =21
∴即AF=2
1FC 【题10】提示：证明三角形ABD 和三角形CAF 全等。

AEBD 四点共圆。

四边形EDCF 是平行四边形。

（一组对边平行且相等的四边形是平行四边形）
【题11】
证明：因为△ABC 为等边三角形，AD 垂直于BC 、BE 垂直于AC ，
所以 ∠BAM=∠CBN ，又因为∠CBM=∠ACN 所以∠ABM=∠BCN
在△ABM 和△BCN 中，有AB=BC
∠BAM=∠CBN
由三角形全等的判定ASA得
△ABM和△BCN全等
所以 AM=BN
【题12】分析：要证明BE‖CF，只要证明∠E＝∠F；已知∠ABE ＝∠DCF，又由三角形的外角性质可知∠E＝∠BAO﹣∠ABE，∠F＝∠CDO﹣∠DCF，因此只要证明∠BAO＝∠CDO.
资料。