正余弦函数图像及性质的应用
合集下载
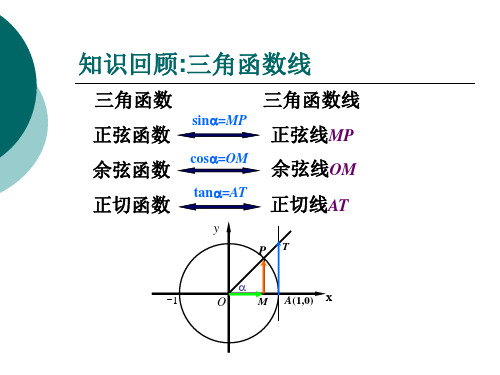
正弦函数和余弦函数的图像与性质

x 10, 3 2 , 0, 2 , 3
3. 求最小正周期: (1) f ( x) 3sin x 4cos x (2) f ( x) sin 2 x (3) f ( x) sin 2 x cos 2 x
y cos x , x R 的值域是 [1,1],最大值是 1,最小值是 1.
当 cos x 1时,x 2k (k Z). 当 cos x 1 时,x (2k 1) (k Z).
(2)周期性
一般地,对于函数 f ( x),如果存在一个常数 T (T 0), 使得当 x 取定义域 D 内的任意值时,都有 f ( x T ) f ( x) 成立,那么函数 f ( x) 叫做周期函数,常数 T 叫做函数 f ( x) 的周期。对于一个周期函数 f ( x) 来说,如果在所有的周期中 存在一个最小正数,那么这个最小正数叫做函数 f ( x) 的 最小正周期。
解: 偶函数; (1)
(2) f ( x) cos 2 x,偶函数;
2 (k Z)
(3)sin x 1 x 2k
x
,但 x 可以取 ,即 f ( x)的定义域不关于原点对称, 2 2
f ( x) 是非奇非偶函数。
(4) f ( x)
1 sin 2 x sin x 1 1 sin 2 x sin x 1
5 3 增:k , k (k Z), 减:k , k (k Z) 8 8 8 8
(4) y log 1 2cos x 3
2
3 解: x cos x 2 k , 2 k 2 6 6
3. 求最小正周期: (1) f ( x) 3sin x 4cos x (2) f ( x) sin 2 x (3) f ( x) sin 2 x cos 2 x
y cos x , x R 的值域是 [1,1],最大值是 1,最小值是 1.
当 cos x 1时,x 2k (k Z). 当 cos x 1 时,x (2k 1) (k Z).
(2)周期性
一般地,对于函数 f ( x),如果存在一个常数 T (T 0), 使得当 x 取定义域 D 内的任意值时,都有 f ( x T ) f ( x) 成立,那么函数 f ( x) 叫做周期函数,常数 T 叫做函数 f ( x) 的周期。对于一个周期函数 f ( x) 来说,如果在所有的周期中 存在一个最小正数,那么这个最小正数叫做函数 f ( x) 的 最小正周期。
解: 偶函数; (1)
(2) f ( x) cos 2 x,偶函数;
2 (k Z)
(3)sin x 1 x 2k
x
,但 x 可以取 ,即 f ( x)的定义域不关于原点对称, 2 2
f ( x) 是非奇非偶函数。
(4) f ( x)
1 sin 2 x sin x 1 1 sin 2 x sin x 1
5 3 增:k , k (k Z), 减:k , k (k Z) 8 8 8 8
(4) y log 1 2cos x 3
2
3 解: x cos x 2 k , 2 k 2 6 6
正弦函数、余弦函数的图像课件(第一课时)

总结词
正弦函数和余弦函数的图像在极值点处达到最大或最小值。
详细描述
正弦函数和余弦函数的图像在极值点处呈现出明显的拐点,即函数值从增加变为减少或从减少变为增 加的点。这些极值点的位置与函数的周期性有关,它们通常出现在周期的中点和结束处。在数学上, 这些极值点可以通过求导数或观察函数图像来确定。
05
总结与回顾
正弦函数具有周期性、单调性、奇偶性等性质。在区间[0,π]上,正弦函数是单 调递增的;在区间[π,2π]上,正弦函数是单调递减的。正弦函数是奇函数,满 足sin(-x) = -sin(x)。
余弦函数的定义与性质
定义
余弦函数是三角函数的另一种形式,定义为直角三角形中锐角的邻边与斜边的比 值,记作cos(x)。
绘制图像
使用与绘制正弦函数相同的方 法来绘制余弦函数的图像。
显示图像
同样使用matplotlib的show 函数来显示绘制的图像。
04
图像分析
正弦函数和余弦函数的图像对比
总结词
正弦函数和余弦函数的图像在形状上非常相似,但在相位上存在差异。
详细描述
正弦函数和余弦函数都是周期函数,它们的图像呈现出规律性的波动。在直角坐标系中,正弦函数的图像是一个 连续的波形,而余弦函数的图像同样是连续的波形,但相对于正弦函数,它有一个相位偏移。在极坐标系中,正 弦函数和余弦函数的图像分别呈现出正弦曲线和余弦曲线的形状。
课程目标
掌握正弦函数和余弦 函数的图像特点。
能够运用正弦函数和 余弦函数的图像解决 一些实际问题。
理解正弦函数和余弦 函数的周期性和对称 性。
02
正弦函数和余弦函数的定 义与性质
正弦函数的定义与性质
定义
正弦函数是三角函数的一种,定义为直角三角形中锐角的对边与斜边的比值, 记作sin(x)。
正弦函数和余弦函数的图像在极值点处达到最大或最小值。
详细描述
正弦函数和余弦函数的图像在极值点处呈现出明显的拐点,即函数值从增加变为减少或从减少变为增 加的点。这些极值点的位置与函数的周期性有关,它们通常出现在周期的中点和结束处。在数学上, 这些极值点可以通过求导数或观察函数图像来确定。
05
总结与回顾
正弦函数具有周期性、单调性、奇偶性等性质。在区间[0,π]上,正弦函数是单 调递增的;在区间[π,2π]上,正弦函数是单调递减的。正弦函数是奇函数,满 足sin(-x) = -sin(x)。
余弦函数的定义与性质
定义
余弦函数是三角函数的另一种形式,定义为直角三角形中锐角的邻边与斜边的比 值,记作cos(x)。
绘制图像
使用与绘制正弦函数相同的方 法来绘制余弦函数的图像。
显示图像
同样使用matplotlib的show 函数来显示绘制的图像。
04
图像分析
正弦函数和余弦函数的图像对比
总结词
正弦函数和余弦函数的图像在形状上非常相似,但在相位上存在差异。
详细描述
正弦函数和余弦函数都是周期函数,它们的图像呈现出规律性的波动。在直角坐标系中,正弦函数的图像是一个 连续的波形,而余弦函数的图像同样是连续的波形,但相对于正弦函数,它有一个相位偏移。在极坐标系中,正 弦函数和余弦函数的图像分别呈现出正弦曲线和余弦曲线的形状。
课程目标
掌握正弦函数和余弦 函数的图像特点。
能够运用正弦函数和 余弦函数的图像解决 一些实际问题。
理解正弦函数和余弦 函数的周期性和对称 性。
02
正弦函数和余弦函数的定 义与性质
正弦函数的定义与性质
定义
正弦函数是三角函数的一种,定义为直角三角形中锐角的对边与斜边的比值, 记作sin(x)。
正弦和余弦的图像和性质
其定义域为R,值域为[-1,1],周期为2
y sin x, x [0, 2 ]的图象 作法: (1) 等分
(2) 作正弦线
问题:如何作出比较精确的正弦函数图象? (3) 平移
途径:利用单位圆中正弦线来解决。
(4) 连线
y
B
1
用光滑曲线将这些正弦线 的终点连结起来!
A
O1
O 2 5 7 4 3 5 11 22
2
(
,1)
(
2 ,1)
(
2
,1)
(
2
,1)
( 2( ,21),1) ( 2 ,1)
,0) 3
(
2
( ,0) 2
(
((((((,,0,00),)0,),(003)2))(32,(-312,(1)32),1(33,)(212(3(323)2,21-,1,-),-1)-11)))
2 ,0) x
2 ,0)
解: x
3
0
2
2
2
sinx
0
1
0
-1
0
1+sinx
1
2
1
0
1
y
2
y=1+sinx,x[0, 2]
1
o
2
-1
2
3
2
x
2
典型例题:
例1(2) 画出函数y= -cosx,x[0, 2]的简图:
x
0
2
3
2
2
cosx
1
0
-1 0
1
-cosx
-1
0
1
0
-1
y
1
y=-cosx,x[0, 2]
y sin x, x [0, 2 ]的图象 作法: (1) 等分
(2) 作正弦线
问题:如何作出比较精确的正弦函数图象? (3) 平移
途径:利用单位圆中正弦线来解决。
(4) 连线
y
B
1
用光滑曲线将这些正弦线 的终点连结起来!
A
O1
O 2 5 7 4 3 5 11 22
2
(
,1)
(
2 ,1)
(
2
,1)
(
2
,1)
( 2( ,21),1) ( 2 ,1)
,0) 3
(
2
( ,0) 2
(
((((((,,0,00),)0,),(003)2))(32,(-312,(1)32),1(33,)(212(3(323)2,21-,1,-),-1)-11)))
2 ,0) x
2 ,0)
解: x
3
0
2
2
2
sinx
0
1
0
-1
0
1+sinx
1
2
1
0
1
y
2
y=1+sinx,x[0, 2]
1
o
2
-1
2
3
2
x
2
典型例题:
例1(2) 画出函数y= -cosx,x[0, 2]的简图:
x
0
2
3
2
2
cosx
1
0
-1 0
1
-cosx
-1
0
1
0
-1
y
1
y=-cosx,x[0, 2]
正弦函数、余弦函数的性质(全)

当且仅当 x 2k, ( k Z) 时 , (cos x)min 1.
y
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
ycox(sxR)
例题
求使函数
y3cos2x( )
取得最大值、最小值的
2
自变量的集合,并写出最大值、最小值。
y
1
3 5 2
而在每个闭区间[ 2k , 3 2k ](k Z )上都是
2
2
减函数,其值从1减小到-1。
探究:余弦函数的单调性 y
1
3 5 2
2 3
2
2
O 3 2 5 3 x
2
2
2
1
当x在区间 [3 , 2 ]、[,0]、[,2 ][3 , 4 ] 上时,
4
5 6 x
y=cosx (xR)
y
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
一.周期性
对于函数f (x),如果存在一个非零常数T,使得 当x取定义域内的每一个值时,都有 f (x+T)=f (x)
那么函数f (x)就叫做周期函数,非零常数T叫做这个 函数的周期。
注:1正、T弦要是函非数零常是数周期函数,2k(kZ且 k0),最小
其值从 1减至-1
五、余弦函数的单调性
y
1
-3 5 -2 3
2
2
o - 2
2
-1
x - … …
2
cosx -1
0
正弦函数和余弦函数的图像与性质.ppt

, 0), (2 ,1)
2
2
并注意-4 曲线的“凹凸”变化.
课堂练习
1.作函数 y sin x 与 y sin x 1在 [0, 2 ]
上的大致图像. 2.指出1.中各图像与正弦函数图像的位置关系.
3.作函数 y cos x, x [ , ]的大致图像.
4.利用3.解不等式:cos x sin x, x [ , ]
-2
五个关键点:(0, 0), ( ,1), ( , 0), (3 , 1), (2 , 0)
2
2
利用五个关-4键点作简图的方法称为“五点法”
10
三、余弦函数的图像
根据诱导公式
cos
8
x
sin(
x) 可知余弦函数
y
cos
6
x的图像可由
y
2 sin
x
的图像向左平移
2
4
个单位得到.
1
2
2
-10
3-5
0
2
1
-2
余弦函数的值域是[1,1] -4
当且仅当 x 2k , k Z 时, -6
余弦函数取得最大值1;-8
5
2
35
x10
2
yP
OM x
当且仅当 x 2k , k-10 Z 时,
余弦函数取得最小值-1-1.2例1.求下列函数的源自大值与最小值,及取到最值6
课堂练习答案
12
1. y sin x, x [0, 2 ] y4
10
x
0
2
3 2
2
2 8
5
-10
正弦函数、余弦函数的图象_优质课件

3) y 3sin(1 x ), x R 一般
35
结论:
函数y Asin(x )及y Acos(x ), x R
( A,,为常数, A 0, 0)的周期T 2
新课讲解. 正弦函数、余弦函数的性质 (三)关于奇偶性(复习)
一般地, •如果对于函数f( x )的定义域内任意一个x, 都有f(- x )= f( x ),那么就说f( x )是偶函数 •如果对于函数f( x )的定义域内任意一个x, 都有f(- x )= -f( x ),那么就说f( x )是奇函数
小结回顾
正切函数的基本性质
4 5
应用提升
练习1:试着画出y | tan x | 和y tan | x |
并讨论它们的单调性,周期性和奇偶性.
练习2.如果、
(
,
)且
tan
cot
,
2
那么必有( )
A.
B.
C. 3 D. 3
2
2
应用提升
例3.求函数y tan x 1 的定义域 3 tan x
例4.试讨论函数y loga tan x的单调性
2
2
y=cosx
y cos x : 定义域为R,值域[1,1]
1
最-6大 值1,此-5时 x
2-k4; 最小值-3-1,
此时x
-2
2k
-;
-1
2 3 2 3
4 5 4 5
6 x 6 x
五.定义域 、值域及取到最值时相应的x的集合:
-6 -5
-4 -3
复习回顾
-2 -
y y=sinx
1 o
-1
2 3
(2) y sin x, y cosx与y Asin(x ), y Acos(x )间的换元思想
正弦函数余弦函数的图像与性质

三角函数在物理学中的应用
振动与波动
正弦和余弦函数是描述简谐振动和波动的基本函 数,广泛应用于声学、光学等领域。
交流电
交流电的电压和电流是时间的正弦或余弦函数, 用于驱动各种电器设备。
磁场与电场
在电磁学中,正弦和余弦函数用于描述磁场和电 场的分布和变工程中的许多振动问题都可以用 正弦和余弦函数来描述,如桥梁 振动、车辆振动等。
周期性
正弦函数具有周期性, 其周期为2π。
奇偶性
正弦函数是奇函数,满 足sin(-x) = -sin(x)。
余弦函数的定义
定义
余弦函数是三角函数的另一种形式,定义为直角三角形中锐角的邻边与斜边的比值,记作 cos(x)。
周期性
余弦函数也具有周期性,其周期为2π。
奇偶性
余弦函数是偶函数,满足cos(-x) = cos(x)。
奇偶性
总结词
正弦函数是奇函数,而余弦函数是偶 函数。
详细描述
奇函数满足$f(-x) = -f(x)$,偶函数满 足$f(-x) = f(x)$。对于正弦函数, $sin(-x) = -sin(x)$;对于余弦函数, $cos(-x) = cos(x)$。
最值与振幅
总结词
正弦函数和余弦函数都具有最大值和最小值,这取决于它们的振幅。
正弦函数余弦函数的图像与性质
目录
• 正弦函数与余弦函数的定义 • 正弦函数与余弦函数的图像 • 正弦函数与余弦函数的性质 • 正弦函数与余弦函数的应用 • 正弦函数与余弦函数的扩展知识
01 正弦函数与余弦函数的定 义
正弦函数的定义
定义
正弦函数是三角函数的 一种,定义为直角三角 形中锐角的对边与斜边 的比值,记作sin(x)。
正弦函数、余弦函数的图像和性质

-
图象的最高点 图象的最高点 与x轴的交点 轴的交点
x
1-
( 0 ,1 ) (2π ,1)
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
π ( π ,0 ) (32 ,0) 2π 2 图象的最低点 (π ,−1) 图象的最低点
-
应用“ 例1.应用“五点法”作图。 应用 五点法”作图。
π
π
例2.分别利用函数的图像和三角函数 先两种方法,求下列不等式的解集:
1 (1) sin x ≥ ; 2 1 5π (2) cos x ≤ (0 < x ≤ ); 2 2
例3.判断y = cos x + 1, x ∈ [0,2π ]与下列 直线交点的个数: 3 ( )y = 2; (2) y = ; (3) y = 0. 1 2
图
y
1-
数、 图
数
图象的最高点 ( ,1) 图象的最高点 2 与x轴的交点 轴的交点
( 0 , 0 ) (π , 0 ) (2π ,0)
x
π
-
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
2π
图象的最低点 (32 ,−1 图象的最低点 π )
简图作法 (1) 列表 列出对图象形状起关键作用的五点坐标) 列表( (2) 描点 定出五个关键点) 描点( y (3) 连线 用光滑的曲线顺次连结五个点) 连线(
图象的最高点 图象的最高点 与x轴的交点 轴的交点
x
1-
( 0 ,1 ) (2π ,1)
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
π ( π ,0 ) (32 ,0) 2π 2 图象的最低点 (π ,−1) 图象的最低点
-
应用“ 例1.应用“五点法”作图。 应用 五点法”作图。
π
π
例2.分别利用函数的图像和三角函数 先两种方法,求下列不等式的解集:
1 (1) sin x ≥ ; 2 1 5π (2) cos x ≤ (0 < x ≤ ); 2 2
例3.判断y = cos x + 1, x ∈ [0,2π ]与下列 直线交点的个数: 3 ( )y = 2; (2) y = ; (3) y = 0. 1 2
图
y
1-
数、 图
数
图象的最高点 ( ,1) 图象的最高点 2 与x轴的交点 轴的交点
( 0 , 0 ) (π , 0 ) (2π ,0)
x
π
-
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
2π
图象的最低点 (32 ,−1 图象的最低点 π )
简图作法 (1) 列表 列出对图象形状起关键作用的五点坐标) 列表( (2) 描点 定出五个关键点) 描点( y (3) 连线 用光滑的曲线顺次连结五个点) 连线(
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 sinx cosx 1 sinx cosx
思考(2): 能否借助上面作点C的方法, 在直角坐标系中作出正弦函数
y sinx,x R 的图象呢?
作正弦函数的图象
y
1
x
o1
o
2 5
7
4
3
5 11
2
6
3
2
36
6
3
2
3
6
-1
y=sinx, x [ 0, 2 ]
作正弦函数的图象
y
1
x
6 求出它的周期。
变式:求函数f x cos x 的单调增区
3 间并求出它的周期。
巩固练习
求下列函数的单调减区间。
1y cos 2x 2y log 1cos2x
2
3y cos x
4
题型五:怎样判断三角函数的奇偶性?
判断下列函数的奇偶性:
1y 2cos2x
(2)y cosx1
y=sinx x[0,2]
f (x 2k ) f (x) 利用图象平移
y=sinx xR
y
-4 -3
-2
1
- o
-1
正弦曲 线
2
3
4
5 6 x
y
(五点作图法)
图象的最高点 ( ,1)
1-
与x轴的交点 2
(0,0) ( ,0) (2 ,0)
-
-1
o
6
3
2
2 3
5 6
7 6
4 3
3 2
5 3
11 6
2
x
图象的最低点
(
3 2
,1)
-1 -
简图作法
(1) 列表(列出对图象形状起关键作用的五点坐标) (2) 描点(定出五个关键点) (3) 连线(用光滑的曲线顺次连结五个点)
例1.分别作出下列函数简图(五点法作图)
(1)y=2sinx , x∈[0,2π]
x
3
0 2 2 2
y=2sinx 0 2 0 -2 0
o1
o
2 5 7 4 3 5 11 2
632
36
6
3
23
6
-1
y=sinx, x [ 0, 2 ]
作正弦函数的图象
y
1
x
o1
o
2 5 7 4 3 5 11 2
632
36
6
3
23
6
-1
y=sinx, x [ 0, 2 ]
终边相同角的三角函数值相等
即: sin(x+2k)=sinx, kZ
一.正弦函数的性质 y
1
-4 -3
-2
- o
-1
二.余弦函数的性质
y
1
-4 -3
-2
- o
-1
三.正余弦函数的图像画法
1.五点法
2.图像变换
2
3
4
2
3
4
5 6 x 5 6 x
一、知识回顾:正、余弦函数的图像和性质
y sinx
y cosx
图像
3
2
o
2
2
0
2
2
定义域 值域
性
周期
定义域为 R; 值域为[1,1]
5
题型七:综合应用
1.若cosx
1 m 2m 3
,
且x
6
,
6
, 则m的
取值范围______.
2.方程 cosx 1 x 在区间0,100 内解的
2 个数 _______.
3.已知f x ax b sin3 x 1且f x 7求f 5 ____
4.已知函数y f x为奇函数,在其定义域 1 , 1
4
变式: 有两个实根?
7.求函数y cos x 的图像的对称轴的方程和对称中心。
4
8.若-cos2 2mcos 2m 1 0恒成立。试求实数m的取值
范围。
题型七:综合应用
9.已知sinx cosy 1 ,求t sinx cos2x的最值。 3
10.求函数的最小正周期:y 1 sinx cosx 1 sinx cosx
最小正周期T 2
单 增区间
[2k ,2k ],k Z
2
2
调 性
减区间
[2k
,2k
3
],k
Z
2
2
质对
奇函数
称
对称中心:( k ,0)
性
对称轴: x k
2
[2k ,2k ],k Z
[2k ,2k ],k Z
偶函数
对称中心:(k ,0)
2
对称轴:x k
题型一:怎样画函数的图像
2 2
上是减函数,且f (1 sin ) f (sin2 1) 0,求的
取值范围.
题型七:综合应用
5.已知定义在 ,3上的单调减函数f x
使得f a2 cosx f a 2 cos2x 对于一切
实数都成立, 求a的取值范围。
6.方程2cos x a在0, 上有实根求a的取值范围.
(4)y cosx- 2 cosx-1
变式1:已知函数f x 2acos 2x b的定义域为
3
0,2 ,函数的最大值为1,最小值为-5,求a, b
变式:求函数f x cos2x - 2acosx1的最值。
题型四:怎样求三角函数的单调区间?
1.求函数f x cos 2x 单调区间并
3y 1 cosx cosx1
题型六:利用单调性比较大小
1 不求值,比较下列各对正弦值的大小:
(1) cos( )与cos( )
18
10
(2)cos 2 与cos3
3
4
练习: 1.比较cos1, cos1.2, cos1.5大小. 2.cos 3 , cos 1 ,cos 7 的大小.
2 10 4 3.cos1 ,sin5的大小.
3
4 x
正弦函数y=sinx的性质:
y 1
(1)定义域 实数集R
(2)值域
当x=__2__2_k__,_k___Z_____时, ymax ___1__
当x=___2___2_k__, k___Z____时, ymin ___1_值_ 域是: 1,1
(3)周期性
T 2
y
解: (1)列表(2)描点作图Yy=2sinx
2
y=sinx
1
0
2 X
2、五点作图法
(2)y=sin2x , x∈[0,π]
解: (1)列表 (2)描点作图
2x
x
3 0 24 2 24 2
yy==ssinin2xx 0 1 0 -1 0
Y
y=sin2x
1
0
X
2
y
1
y 1
2
2
O
1 2
3 2
2
(2)2cos 2x 3 0
12
3.求下列函数的定义域。
1y lg3 4cos2x
2y lg cos2x 9 x2
题型三:怎样求三角函数的值域或最值?
1.求下列函数的值域。
1y 3 4sinx, x R
(2)y sinx sinx
3y cos2x 2cosx-1
1.画出下列函数y cosx的图像.并指出其性质。
学生巩固练习
1.方程lg x cosx有多少个解? 2.用两种方法画出函数y 1 3cosx的 图像,并指出它的性质。
题型二:怎样解三角方程和不等式?
1. 求下列方程中的角x的集合
12cosx1 0 22cos 2x 3
12
2.解不等式 (1)2cosx1 0
思考(2): 能否借助上面作点C的方法, 在直角坐标系中作出正弦函数
y sinx,x R 的图象呢?
作正弦函数的图象
y
1
x
o1
o
2 5
7
4
3
5 11
2
6
3
2
36
6
3
2
3
6
-1
y=sinx, x [ 0, 2 ]
作正弦函数的图象
y
1
x
6 求出它的周期。
变式:求函数f x cos x 的单调增区
3 间并求出它的周期。
巩固练习
求下列函数的单调减区间。
1y cos 2x 2y log 1cos2x
2
3y cos x
4
题型五:怎样判断三角函数的奇偶性?
判断下列函数的奇偶性:
1y 2cos2x
(2)y cosx1
y=sinx x[0,2]
f (x 2k ) f (x) 利用图象平移
y=sinx xR
y
-4 -3
-2
1
- o
-1
正弦曲 线
2
3
4
5 6 x
y
(五点作图法)
图象的最高点 ( ,1)
1-
与x轴的交点 2
(0,0) ( ,0) (2 ,0)
-
-1
o
6
3
2
2 3
5 6
7 6
4 3
3 2
5 3
11 6
2
x
图象的最低点
(
3 2
,1)
-1 -
简图作法
(1) 列表(列出对图象形状起关键作用的五点坐标) (2) 描点(定出五个关键点) (3) 连线(用光滑的曲线顺次连结五个点)
例1.分别作出下列函数简图(五点法作图)
(1)y=2sinx , x∈[0,2π]
x
3
0 2 2 2
y=2sinx 0 2 0 -2 0
o1
o
2 5 7 4 3 5 11 2
632
36
6
3
23
6
-1
y=sinx, x [ 0, 2 ]
作正弦函数的图象
y
1
x
o1
o
2 5 7 4 3 5 11 2
632
36
6
3
23
6
-1
y=sinx, x [ 0, 2 ]
终边相同角的三角函数值相等
即: sin(x+2k)=sinx, kZ
一.正弦函数的性质 y
1
-4 -3
-2
- o
-1
二.余弦函数的性质
y
1
-4 -3
-2
- o
-1
三.正余弦函数的图像画法
1.五点法
2.图像变换
2
3
4
2
3
4
5 6 x 5 6 x
一、知识回顾:正、余弦函数的图像和性质
y sinx
y cosx
图像
3
2
o
2
2
0
2
2
定义域 值域
性
周期
定义域为 R; 值域为[1,1]
5
题型七:综合应用
1.若cosx
1 m 2m 3
,
且x
6
,
6
, 则m的
取值范围______.
2.方程 cosx 1 x 在区间0,100 内解的
2 个数 _______.
3.已知f x ax b sin3 x 1且f x 7求f 5 ____
4.已知函数y f x为奇函数,在其定义域 1 , 1
4
变式: 有两个实根?
7.求函数y cos x 的图像的对称轴的方程和对称中心。
4
8.若-cos2 2mcos 2m 1 0恒成立。试求实数m的取值
范围。
题型七:综合应用
9.已知sinx cosy 1 ,求t sinx cos2x的最值。 3
10.求函数的最小正周期:y 1 sinx cosx 1 sinx cosx
最小正周期T 2
单 增区间
[2k ,2k ],k Z
2
2
调 性
减区间
[2k
,2k
3
],k
Z
2
2
质对
奇函数
称
对称中心:( k ,0)
性
对称轴: x k
2
[2k ,2k ],k Z
[2k ,2k ],k Z
偶函数
对称中心:(k ,0)
2
对称轴:x k
题型一:怎样画函数的图像
2 2
上是减函数,且f (1 sin ) f (sin2 1) 0,求的
取值范围.
题型七:综合应用
5.已知定义在 ,3上的单调减函数f x
使得f a2 cosx f a 2 cos2x 对于一切
实数都成立, 求a的取值范围。
6.方程2cos x a在0, 上有实根求a的取值范围.
(4)y cosx- 2 cosx-1
变式1:已知函数f x 2acos 2x b的定义域为
3
0,2 ,函数的最大值为1,最小值为-5,求a, b
变式:求函数f x cos2x - 2acosx1的最值。
题型四:怎样求三角函数的单调区间?
1.求函数f x cos 2x 单调区间并
3y 1 cosx cosx1
题型六:利用单调性比较大小
1 不求值,比较下列各对正弦值的大小:
(1) cos( )与cos( )
18
10
(2)cos 2 与cos3
3
4
练习: 1.比较cos1, cos1.2, cos1.5大小. 2.cos 3 , cos 1 ,cos 7 的大小.
2 10 4 3.cos1 ,sin5的大小.
3
4 x
正弦函数y=sinx的性质:
y 1
(1)定义域 实数集R
(2)值域
当x=__2__2_k__,_k___Z_____时, ymax ___1__
当x=___2___2_k__, k___Z____时, ymin ___1_值_ 域是: 1,1
(3)周期性
T 2
y
解: (1)列表(2)描点作图Yy=2sinx
2
y=sinx
1
0
2 X
2、五点作图法
(2)y=sin2x , x∈[0,π]
解: (1)列表 (2)描点作图
2x
x
3 0 24 2 24 2
yy==ssinin2xx 0 1 0 -1 0
Y
y=sin2x
1
0
X
2
y
1
y 1
2
2
O
1 2
3 2
2
(2)2cos 2x 3 0
12
3.求下列函数的定义域。
1y lg3 4cos2x
2y lg cos2x 9 x2
题型三:怎样求三角函数的值域或最值?
1.求下列函数的值域。
1y 3 4sinx, x R
(2)y sinx sinx
3y cos2x 2cosx-1
1.画出下列函数y cosx的图像.并指出其性质。
学生巩固练习
1.方程lg x cosx有多少个解? 2.用两种方法画出函数y 1 3cosx的 图像,并指出它的性质。
题型二:怎样解三角方程和不等式?
1. 求下列方程中的角x的集合
12cosx1 0 22cos 2x 3
12
2.解不等式 (1)2cosx1 0
