《管理运筹学》第四版课后习题
《管理运筹学》第4版课后习题解析(韩伯棠)
10 x1 2 x2 s1 20 3x1 3x2 s2 18 4 x1 9 x2 s3 36 x1 , x2 , s1 , s2 , s3 ≥ 0
2
《管理运筹学》第四版课后习题解析
韩伯棠
剩余变量（0, 0, 13） 最优解为 x1=1，x2=5。 6．解： （1）最优解为 x1=3，x2=7。 （2） 1 c1 3 。 （3） 2 c2 6 。 （4）
x1 6。 x2 4。
（5）最优解为 x1=8，x2=0。 （6）不变化。因为当斜率 1 ≤
c1 1 ≤ ，最优解不变，变化后斜率为 1，所以最优解不变。 c2 3
7.解： 设 x，y 分别为甲、乙两种柜的日产量， 目标函数 z=200x＋240y， 线性约束条件： 6 x 12 y 120 8 x 4 y 64 x 0 y 0 x 2 y 20 2 x y 16 x 0 y 0
作直线 960x＋360y=0． 即 8x＋3y=0，向上平移至过点 B(10，8)时，z=960x ＋360y 取到最小值． z 最小=960×10＋360×8=12480 答：大卡车租 10 辆，农用车租 8 辆时运费最低，最低运费为 12480 元． 11．解： 设圆桌和衣柜的生产件数分别为 x、y，所获利润为 z，则 z=6x＋10y． 0.18 x 0.09 y 72 2 x y 800 0.08 x 0.28 y 56 2 x 7 y 1400 即 x 0 x 0 y 0 y 0
． 但 E 不是可行域内的整点，在可行域的整点中，点 ( 4,8) 使 z 取得最小值。 答：应截第一种钢板 4 张，第二种钢板 8 张，能得所需三种规格的钢板，且使所 用钢板的面积最小． 9．解： 设用甲种规格原料 x 张，乙种规格原料 y 张，所用原料的总面积是 zm2，目标函 x 2 y 2 2 x y 3 数 z=3x＋2y，线性约束条件 作出可行域．作一组平等直线 3x＋ x 0 y 0 x 2 y 2 2y=t． 解 得 C ( 4 / 3,1 / 3) 2 x y 3
《管理运筹学》第四版 第2章 线性规划的图解法 课后习题解析
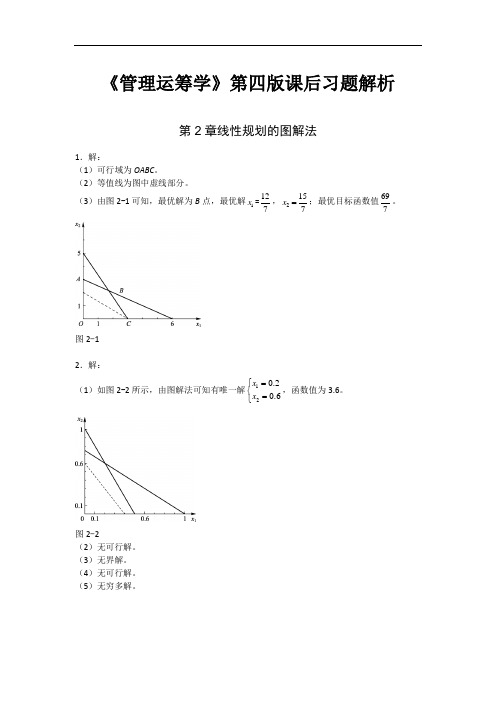
《管理运筹学》第四版课后习题解析第2章线性规划的图解法1．解：（1）可行域为OABC 。
（2）等值线为图中虚线部分。
（3）由图2-1可知，最优解为B 点，最优解1x =127，2157x =；最优目标函数值697。
图2-12．解：（1）如图2-2所示，由图解法可知有唯一解120.20.6x x =⎧⎨=⎩，函数值为3.6。
图2-2（2）无可行解。
（3）无界解。
（4）无可行解。
（5）无穷多解。
（6）有唯一解1220383x x ⎧=⎪⎪⎨⎪=⎪⎩，函数值为923。
3．解：（1）标准形式12123max 32000f x x s s s =++++1211221231212392303213229,,,,0x x s x x s x x s x x s s s ++=++=++=≥（2）标准形式1212min 4600f x x s s =+++12112212121236210764,,,0x x s x x s x x x x s s --=++=-=≥（3）标准形式12212min 2200f x x x s s ''''=-+++ 1221122122212212355702555032230,,,,0x x x s x x x x x x s x x x s s '''-+-+=''''-+=''''+--=''''≥4．解： 标准形式1212max 10500z x x s s =+++1211221212349528,,,0x x s x x s x x s s ++=++=≥ 松弛变量（0，0） 最优解为1x =1，x 2=3/2。
5．解：标准形式12123min 118000f x x s s s =++++121122123121231022033184936,,,,0x x s x x s x x s x x s s s +-=+-=+-=≥剩余变量（0, 0, 13） 最优解为x 1=1，x 2=5。
《管理运筹学》第四版课后习题答案
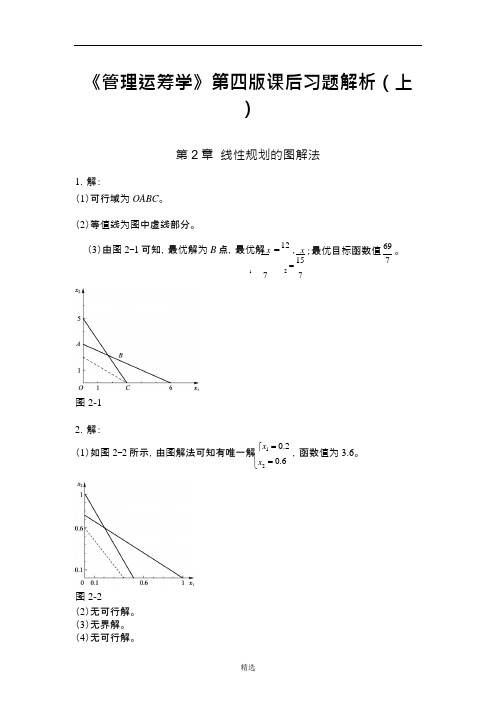
精选⎨= 0.6《管理运筹学》第四版课后习题解析（上）第2章 线性规划的图解法1．解：（1）可行域为OABC 。
（2）等值线为图中虚线部分。
（3）由图2-1可知，最优解为B 点，最优解 x =12， x = 15 1727图2-1；最优目标函数值 69。
72．解：（1）如图2-2所示，由图解法可知有唯一解 ⎧x 1 = 0.2，函数值为3.6。
⎩x 2图2-2（2）无可行解。
（3）无界解。
（4）无可行解。
⎨ （5）无穷多解。
⎧x = （6）有唯一解 ⎪ 1⎪ 203 ，函数值为 92 。
8 3 x = ⎪⎩ 2 33．解： （1）标准形式max f = 3x 1 + 2x 2 + 0s 1 + 0s 2 + 0s 39x 1 + 2x 2 + s 1 = 303x 1 + 2x 2 + s 2 = 13 2x 1 + 2x 2 + s 3 = 9x 1, x 2 , s 1, s 2 , s 3 ≥ 0（2）标准形式min f = 4x 1 + 6x 2 + 0s 1 + 0s 23x 1 - x 2 - s 1 = 6 x 1 + 2x 2 + s 2 = 10 7x 1 - 6x 2 = 4x 1, x 2 , s 1, s 2 ≥ 0（3）标准形式min f = x 1' - 2x 2' + 2x 2'' + 0s 1 + 0s 2-3x 1 + 5x 2' - 5x 2'' + s 1 = 70 2x 1' - 5x 2' + 5x 2'' = 50 3x 1' + 2x 2' - 2x 2'' - s 2 = 30 x 1', x 2' , x 2'' , s 1, s 2 ≥4．解： 标准形式max z = 10x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4x 2 + s 1 = 9 5x 1 + 2x 2 + s 2 = 8 x 1, x 2 , s 1, s 2 ≥ 0≤松弛变量（0，0）最优解为 x 1 =1，x 2=3/2。
《管理运筹学》第四版课后习题解析(下)
《管理运筹学》第四版课后习题解析（下）第9章 目 标 规 划 1、解：设工厂生产A 产品1x 件，生产B 产品2x 件。
按照生产要求，建立如下目标规划模型。
由管理运筹学软件求解得12121211.25,0,0,10, 6.25,0x x d d d d --++====== 由图解法或进一步计算可知，本题在求解结果未要求整数解的情况下，满意解有无穷多个，为线段(135/14,15/7)(1)(45/4,0),[0,1]ααα+-∈上的任一点。
2、解：设该公司生产A 型混凝土x 1吨，生产B 型混凝土x 2吨，按照要求建立如下的目标规划模型。
由管理运筹学软件求解得.0,0,20,0,0,0,0,35,40,0,120,120554433221121============+-+-+-+-+-d d d d d d d d d d x x3、解：设x 1,x 2分别表示购买两种基金的数量，按要求建立如下的目标规划模型。
用管理运筹学软件求解得，所以，该人可以投资A 基金113.636份，投资B 基金159.091份。
4、解：设食品厂商在电视上发布广告1x 次，在报纸上发布广告2x 次，在广播中发布广告3x 次。
目标规划模型为 用管理运筹学软件先求下述问题。
得10d -=，将其作为约束条件求解下述问题。
得最优值20-=d ，将其作为约束条件计算下述问题。
得最优值30d +=，将其作为约束条件计算下述问题。
得123112233449.474,20, 2.105,0,0,0,00, 4.211,14.316,0+-+-+-+-===========x x x d d d d d d d d ,。
所以，食品厂商为了依次达到4个活动目标，需在电视上发布广告9.474次，报纸上发布广告20次，广播中发布广告2.105次。
（使用管理运筹学软件可一次求解上述问题） 5、解：（1）设该化工厂生产1x 升粘合剂A 和2x 升粘合剂B 。
管理运筹学第四课后习题答案
《管理运筹学》第四版课后习题解析（上）第2章 线性规划的图解法1．解：（1）可行域为OABC 。
（2）等值线为图中虚线部分。
（3）由图2-1可知，最优解为B 点，最优解 x = 12 ， x 15 1 7 2 7图2-1；最优目标函数值 69 。
72．解：（1）如图2-2所示，由图解法可知有唯一解 x 1 ，函数值为。
x 2图2-2（2）无可行解。
（3）无界解。
（4）无可行解。
（5）无穷多解。
x （6）有唯一解 1203 ，函数值为 92 。
83 x 2 33．解：（1）标准形式max f 3x 1 2x 2 0s 10s 2 0s 3 9x 1 2x 2 s 1 30 3x 1 2x 2 s 2 132x 1 2x 2 s 3 9x 1, x 2 , s 1, s 2 , s 3 ≥ 0（2）标准形式min f 4x 1 6x 2 0s 10s 2 3x 1 x 2s 1 6x 1 2x 2s 2 107x 1 6x 2 4x 1, x 2 , s 1, s 2 ≥ 0（3）标准形式min f x 12x 22x 20s10s 23x 15x 25x2s1 702x 15x 25x2503x 12x 22x 2s 2 30 x 1, x 2, x 2, s 1, s 2 ≥ 04．解：标准形式max z 10x 1 5x 2 0s 10s 23x1 4x2s915x1 2x2 s2 8 x, x2 , s1, s2 ≥01≤松弛变量（0，0）最优解为 x 1 =1，x 2=3/2。
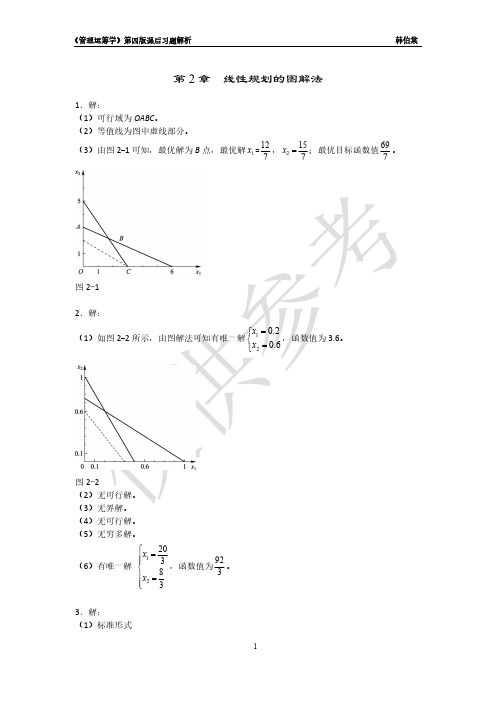
5．解：标准形式min f 11x 1 8x 2 0s 1 0s 2 0s 310x 12x 2 s 1 20 3x 13x 2 s 2 18 4x 1 9x 2 s 3 36x 1, x 2 , s 1, s 2 , s 3 ≥ 0剩余变量（0, 0, 13）最优解为 x 1=1，x 2=5。
6．解：（1）最优解为 x 1=3，x 2=7。
最新《运筹学》第四版课后习题答案
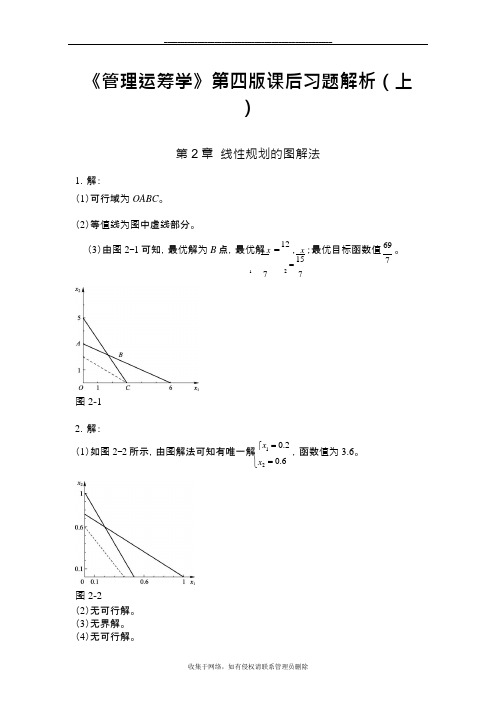
作出可行域．
x2y20
2xy16
得Q(4,8)
z最大200424082720
答：该公司安排甲、乙两种柜的日产量分别为4台和8台，可获最大利润2720元．
8．解：
设需截第一种钢板x张，第二种钢板y张，所用钢板面积zm2． 目标函数z=x＋2y，线性约束条件：
xy12
2xy15
x3y27
x0
y0
x3y27
（4）x16。
x24。
（5）最优解为x1=8，x2=0。
（6）不变化。因为当斜率1≤c1
c2
1，最优解不变，变化后斜率为1，所以最优解3
不变。
7.解：
设x，y分别为甲、乙两种柜的日产量， 目标函数z=200x＋240y，线性约束条件：
6x12y120
8x4y64
即
x0
y0
x2y20
2xy16
x0
y0
x350
得ቤተ መጻሕፍቲ ባይዱ
y100
即C(350，100)．当直线6x＋10y=0即3x＋5y=0平移到
经过点C(350，100)时，z=6x＋10y最大
12．解：
模型maxz500x1400x2
2x1≤300
3x2≤540
2x12x1≤440
1.2x11.5x2≤300
x1,x2≥0
（1）x1150，x270，即目标函数最优值是103000。
《管理运筹学》第四版课后习题解析（上
）
第
1．解：
（1）可行域为OABC。
（2）等值线为图中虚线部分。
（3）由图2-1可知，最优解为B点，最优解x=12，x15
最新《运筹学》第四版课后习题答案
收集于网络，如有侵权请联系管理员删除⎨= 0.6《管理运筹学》第四版课后习题解析（上）第2章 线性规划的图解法1．解：（1）可行域为OABC 。
（2）等值线为图中虚线部分。
（3）由图2-1可知，最优解为B 点，最优解 x =12， x = 15 1727图2-1；最优目标函数值 69。
72．解：（1）如图2-2所示，由图解法可知有唯一解 ⎧x 1 = 0.2，函数值为3.6。
⎩x 2图2-2（2）无可行解。
（3）无界解。
（4）无可行解。
⎨ （5）无穷多解。
⎧x = （6）有唯一解 ⎪ 1⎪ 203 ，函数值为 92 。
8 3 x = ⎪⎩ 2 33．解： （1）标准形式max f = 3x 1 + 2x 2 + 0s 1 + 0s 2 + 0s 39x 1 + 2x 2 + s 1 = 303x 1 + 2x 2 + s 2 = 13 2x 1 + 2x 2 + s 3 = 9x 1, x 2 , s 1, s 2 , s 3 ≥ 0（2）标准形式min f = 4x 1 + 6x 2 + 0s 1 + 0s 23x 1 - x 2 - s 1 = 6 x 1 + 2x 2 + s 2 = 10 7x 1 - 6x 2 = 4x 1, x 2 , s 1, s 2 ≥ 0（3）标准形式min f = x 1' - 2x 2' + 2x 2'' + 0s 1 + 0s 2-3x 1 + 5x 2' - 5x 2'' + s 1 = 70 2x 1' - 5x 2' + 5x 2'' = 50 3x 1' + 2x 2' - 2x 2'' - s 2 = 30 x 1', x 2' , x 2'' , s 1, s 2 ≥4．解： 标准形式max z = 10x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4x 2 + s 1 = 9 5x 1 + 2x 2 + s 2 = 8 x 1, x 2 , s 1, s 2 ≥ 0≤松弛变量（0，0）最优解为 x 1 =1，x 2=3/2。
《管理运筹学》第四版课后习题解析[下]
![《管理运筹学》第四版课后习题解析[下]](https://img.taocdn.com/s3/m/97cbd28969dc5022aaea006f.png)
给 标号 ，同理 标号 。得到最短路线为 ,最短时间为1.35小时。
4．解：
以 为起始点， 标号为 ；
，
边集为 =
且有
所以， 标号（4,1）。
则 ，
边集为
且有
所以， 标号（5,1）。
则 ，
边集为
且有
所以， 标号（7,2）。
则 ，
边集为
且有
所以， 、 标号（8,2）。
则 ，
边集为
且有
所以， 标号（9,4）。
则 ，
边集为
且有
所以， 标号（11.5,6）。
则 ，
边集为
且有
所以， 标号（12,7）。
， 为空集。
所以，最短路径为
5．解：
（1）从 出发，令 ={ }，其余点为 ，给 标号 。 的所有边为 ，
累计距离最小为 ，给 标号为 ，令 。
（2） 的所有边为 ，累计距离最小为 ，令 。
（2）
图解法求解如图9-1所示，目标1，2可以达到，目标3达不到，所以有满意解为A点（150，120）。
6、解：
假设甲乙两种产品量为x1,x2,建立数学规划模型如下。
用管理运筹学软件求解得：
所以，甲乙两种产品量分别为8.333吨，3.333吨，该计划内的总利润为250元。
7、解：
设该汽车装配厂为达到目标要求生产产品A 件，生产产品B 件。
图解法略，求解得 。
（2）目标规划模型如下。
图解法略，求解得 。
由此可见，所得结果与（1）中的解是不相同的。
（3）加权目标规划模型如下，
求解得 。
9、解：
假设甲乙两种洗衣机的装配量分别是x1,x2,建立数学规划模型如下。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
推导出 ， ,故基金A投资90万元，基金B投资30万元。
第3章线性规划问题的计算机求解
1.解:
⑴甲、乙两种柜的日产量是分别是４和8，这时最大利润是27２０
⑵每多生产一件乙柜，可以使总利润提高1３.33３元
⑶常数项的上下限是指常数项在指定的范围内变化时,与其对应的约束条件的对偶价格不变。比如油漆时间变为１00，因为100在40和１６0之间，所以其对偶价格不变仍为13．33３
(3）５0，０,200,０。
含义:1车间每增加１工时,总利润增加50元；3车间每增加１工时,总利润增加2００元；２车间与4车间每增加一个工时,总利润不增加。
(４）３车间，因为增加的利润最大。
(5）在4０0到正无穷的范围内变化,最优产品的组合不变。
(6）不变,因为在 的范围内。
（7）所谓的上限和下限值指当约束条件的右边值在给定范围内变化时,约束条件1的右边值在 变化,对偶价格仍为50(同理解释其他约束条件）。
z最小=96０×10+36０×８＝１2480
答：大卡车租10辆,农用车租8辆时运费最低,最低运费为12480元.
11．解:
设圆桌和衣柜的生产件数分别为x、y,所获利润为z，则z=6x＋１0y．
即 作出可行域．平移6ｘ+１０y=0 ，如图
得 即C（3５0，1０0)．当直线6x＋10y=０即3x+5ｙ=0平移到经过点C（3５0,10０）时，z＝6ｘ+１０y最大
图２-１
2.解:
(1）如图２－2所示,由图解法可知有唯一解 ,函数值为3．6。
图2－2
（2)无可行解。
（3）无界解。
（4)无可行解。
（5）无穷多解。
（6)有唯一解 ，函数值为 。
3．解:
（1）标准形式
(２)标准形式
（3）标准形式
４．解:
标准形式
松弛变量(0，0）
最优解为 =1,x2=3／2。
5.解：
《管理运筹学》第四版课后习题
————————————————————————————————作者:
————————————————————————————————日期:
《管理运筹学》第四版课后习题答案
第2章线性规划的图解法
1．解:
(１)可行域为ＯABＣ。
（2）等值线为图中虚线部分。
(3）由图2-１可知，最优解为B点,最优解 = , ;最优目标函数值 。
答：应截第一种钢板4张,第二种钢板8张，能得所需三种规格的钢板，且使所用钢板的面积最小．
9.解:
设用甲种规格原料x张，乙种规格原料y张，所用原料的总面积是ｚm2，目标函数z＝3x＋2y，线性约束条件 作出可行域．作一组平等直线３x+2ｙ=ｔ. 解 得
Ｃ不是整点,Ｃ不是最优解．在可行域内的整点中，点B(1,1）使ｚ取得最小值． ｚ最小=3×1＋2×1＝5,
⑷不变,因为还在12０和480之间。
２.解:
⑴不是，因为上ቤተ መጻሕፍቲ ባይዱ得到的最优解不为整数解,而本题需要的是整数解⑵最优解为（４,8)
３.解：
⑴农用车有12辆剩余
⑵大于30０
⑶每增加一辆大卡车，总运费降低192元
４．解：
计算机得出的解不为整数解，平移取点得整数最优解为(10，８）
5．解：
圆桌和衣柜的生产件数分别是350和100件，这时最大利润是３10０元
（8）总利润增加了100×5０＝５０００，最优产品组合不变。
(9)不能，因为对偶价格发生变化。
(10）不发生变化,因为允许增加的百分比与允许减少的百分比之和
(11）不发生变化，因为允许增加的百分比与允许减少的百分比之和 ,其最大利润为103000+５0×50−6０×200＝93500元。
7．解：
（1)４0０0,10000,６200０。
(2）约束条件1:总投资额增加1个单位,风险系数则降低0.057;
约束条件2：年回报额增加1个单位，风险系数升高2.16７;
约束条件3:基金Ｂ的投资额增加１个单位，风险系数不变。
(3）约束条件1的松弛变量是０,表示投资额正好为１20０00０；约束条件2的剩余变量是0，表示投资回报额正好是6０0０0；约束条件３的松弛变量为700００0,表示投资B基金的投资额为３7００00。
标准形式
剩余变量(0, 0, 13）
最优解为x1＝1，x2=5。
６.解:
(1)最优解为ｘ1＝3，x2＝7。
（２) 。
(３) 。
(4）
(5)最优解为ｘ１＝８，x2＝0。
(6）不变化。因为当斜率 ,最优解不变,变化后斜率为1，所以最优解不变。
7.解:
设x,y分别为甲、乙两种柜的日产量，
目标函数z＝20０x＋２4０y, 线性约束条件:
即 作出可行域.
解 得
答:该公司安排甲、乙两种柜的日产量分别为４台和8台,可获最大利润２７2０元.
8.解：
设需截第一种钢板x张,第二种钢板y张,所用钢板面积zｍ2．
目标函数z=x＋2ｙ， 线性约束条件:
作出可行域，并做一组一组平行直线x+2y=ｔ．解 得
.
但Ｅ不是可行域内的整点,在可行域的整点中,点 使z取得最小值。
相差值为0代表,不需要对相应的目标系数进行改进就可以生产该产品。
最优解不变，因为C1允许增加量２0-６=14;Ｃ2允许减少量为10-３=7，所有允许增加百分比和允许减少百分比之和（7.５-6）／14＋(１0-9）/7〈100%,所以最优解不变。
6．解：
（１） , ;目标函数最优值1０3000。
(2）１、3车间的加工工时数已使用完；２、4车间的加工工时数没用完；没用完的加工工时数为２车间330小时，4车间1５小时。
答：用甲种规格的原料1张,乙种原料的原料1张，可使所用原料的总面积最小为５ｍ2.
10.解:
设租用大卡车x辆,农用车ｙ辆，最低运费为z元．目标函数为z=96０x＋360y.
线性约束条件是 作出可行域，并作直线９60ｘ+３60y＝０. 即8ｘ＋3ｙ=0,向上平移
由 得最佳点为
作直线9６0x+36０y＝0. 即8ｘ+３y=0,向上平移至过点B(1０,8)时,z＝9６0x＋3６0ｙ取到最小值．
12.解:
模型
（1） ， ，即目标函数最优值是１03０00。
(2)2，４有剩余,分别是33０，15,均为松弛变量。
（3）5０，0,200,0。
（4）在 变化，最优解不变；在４00到正无穷变化,最优解不变。
(5)因为 ,所以原来的最优产品组合不变。
１3．解：
（１）模型
基金A,Ｂ分别为40００元，1０000元,回报额为62０００元。