matlab与统计回归分析 (1)
用MATLAB求解回归分析
估
F值、与F对应的概率p
计
相关系数 r2 越接近 1，说明回归方程越显著；
.
（
缺
省显
时著
为性
0
水 平
05
）
F > F1-α（k，n-k-1）时拒绝 H0，F 越大，说明回归方程越显著；
与 F 对应的概率 p 时拒绝 H0，回归模型成立.
3、画出残差及其置信区间： rcoplot（r，rint）
例1 解：1、输入数据：
stats = 0.9702 40.6656
0.0005
1、回归：
非线性回 归
是事先用m-文件定 义的非线性函数
（1）确定回归系数的命令： [beta，r，J]=nlinfit（x，y，’model’, beta0）
估计出的 回归系数
残差 Jacobian矩阵
输入数据x、y分别为 n m矩阵和n维列向 量，对一元非线性回 归，x为n维列向量。
r2=0.9282, F=180.9531, p=0.0000
p<0.05, 可知回归模型 y=-16.073+0.7194x 成立.
3、残差分析，作残差图： rcoplot(r,rint)
从残差图可以看出，除第二个数据外，其余数据的残
差离零点均较近，且残差的置信区间均包含零点，这说明 回归模型 y=-16.073+0.7194x能较好的符合原始数据，而第 二个数据可视为异常点.
2、预测和预测误差估计：
（1）Y=polyval（p，x）求polyfit所得的回归多项式在 x处 的预测值Y； （2）[Y，DELTA]=polyconf（p，x，S，alpha）求 polyfit所得的回归多项式在x处的预测值Y及预测值的 显著性为 1-alpha的置信区间Y DELTA；alpha缺省时为0.5
在MATLAB中进行分类和回归分析
在MATLAB中进行分类和回归分析在科学和工程领域，分类和回归分析是常见的数据分析方法。
而MATLAB作为一种功能强大的数据分析软件，提供了丰富的工具和函数，使得分类和回归分析变得更加简单和高效。
本文将介绍在MATLAB中进行分类和回归分析的方法和技巧，帮助读者更好地理解和应用这些技术。
一、背景介绍分类和回归分析是基于已知数据的模式进行预测和分类的统计方法。
分类分析用于将数据分为不同的类别，而回归分析则试图通过已知数据的模式预测未知数据的数值。
这些方法在各个领域都有广泛的应用，如金融、医疗、市场营销等。
二、数据准备在进行分类和回归分析之前，需要准备好相应的数据。
一般来说，数据应当包含自变量（也称为特征或输入）和因变量（也称为标签或输出）。
自变量是用来作为预测或分类的输入变量，而因变量是要预测或分类的目标变量。
通常情况下，数据应当是数值型的，如果包含分类变量，需要进行相应的编码或处理。
三、分类分析在MATLAB中进行分类分析，有多种方法和技术可供选择。
其中最常见的方法包括K最近邻算法（K-nearest neighbors）和支持向量机（Support Vector Machines）等。
这些方法都有相应的函数，可以用于在MATLAB中实现分类分析。
K最近邻算法基于训练样本和测试样本之间的距离，将测试样本分类为与其最近的K个训练样本所属的类别。
而支持向量机则试图找到一个超平面，将不同类别的样本分开，并使得分类误差最小化。
在MATLAB中，我们可以使用fitcknn和fitcsvm函数来实现K最近邻算法和支持向量机。
除了上述方法，还有其他的分类算法可以在MATLAB中使用，如决策树、随机森林等。
根据数据的具体情况和需求，选择适合的分类算法非常重要。
四、回归分析在进行回归分析时，我们需要首先选择适当的回归模型。
常用的回归模型包括线性回归、多项式回归、岭回归等。
根据数据的分布和特点，选择合适的回归模型能够提高分析的准确性。
matlab回归分析一例
问题：新筹建的东方人大学，规划的在校生人数为4900人，现根据调查统计，不同规模的学校的学生人数与教师人数如下表1，试用回归分析法，依据调查数据测算应该招聘的教师人数。
表1 学生人数与教师人数小席你好：应招聘人数为1958人，解答如下：解：1、输入数据，作散点图在matlab命令窗口中键入如下命令：x=100*[10 20 30 40 50]';y=100*[3 8 11 16 20]';plot(x,y,'+')绘图结果见下面的散点图：2、回归分析及其检验：在matlab命令窗口中输入如下命令：X=[ ones(5,1) x];Y=y;[b,bint,r,rint,stats]=regress(Y ,X);b,bint,stats运行结果为：b =-100.00000.4200bint =-272.3621 72.36210.3680 0.4720stats =1.0e+03 *0.0010 0.6615 0.0000 2.6667即42.0ˆ,100ˆ10=-=ββ；0ˆβ的置信区间为[-272.3621，72.3621], 1ˆβ的置信区间为[0.3680，0.4720]; r 2=1, F=661.5, p=0.0000p<0.05, 可知回归模型 y=-100+0.42x 成立.3、残差分析，作残差图在matlab 命令窗口中键入如下命令：rcoplot(r,rint)残差图如下：从残差图可以看出，所有数据的残差离零点均较近，且残差的置信区间均包含零点，这说明回归模型y=-100+0.42x能较好地符合原始数据.4、预测及作图：z=b(1)+b(2)*xplot(x,Y,'k+',x,z,'r')上图再次直观地说明回归模型y=-100+0.42x能较好地符合原始数据.5、测算应该招聘的教师人数在matlab窗口中键入如下命令：zprs=b(1)+b(2)*4900运行结果为：zprs =1.9580e+03即应招聘人数为1958人.。
MATLAB回归分析
MATLAB回归分析回归分析是统计学中常用的一种方法，用于建立一个依赖于自变量（独立变量）的因变量（依赖变量）的关系模型。
在MATLAB环境下，回归分析可以实现简单线性回归、多元线性回归以及非线性回归等。
简单线性回归是一种最简单的回归分析方法，它假设自变量和因变量之间存在线性关系。
在MATLAB中，可以通过`polyfit`函数进行简单线性回归分析。
该函数可以拟合一元数据点集和一维多项式，返回回归系数和截距。
例如：```matlabx=[1,2,3,4,5];y=[2,3,4,5,6];p = polyfit(x, y, 1);slope = p(1);intercept = p(2);```上述代码中，`x`是自变量的数据点，`y`是因变量的数据点。
函数`polyfit`的第三个参数指定了回归的阶数，这里是1，即一次线性回归。
返回的`p(1)`和`p(2)`分别是回归系数和截距。
返回的`p`可以通过`polyval`函数进行预测。
例如：```matlabx_new = 6;y_pred = polyval(p, x_new);```多元线性回归是在有多个自变量的情况下进行的回归分析。
在MATLAB中，可以使用`fitlm`函数进行多元线性回归分析。
例如：```matlabx1=[1,2,3,4,5];x2=[2,4,6,8,10];y=[2,5,7,8,10];X=[x1',x2'];model = fitlm(X, y);coefficients = model.Coefficients.Estimate;```上述代码中，`x1`和`x2`是两个自变量的数据点，`y`是因变量的数据点。
通过将两个自变量放在`X`矩阵中，可以利用`fitlm`函数进行多元线性回归分析。
返回值`model`是回归模型对象，可以通过`model.Coefficients.Estimate`获得回归系数。
Matlab中的样本分类和回归分析技巧
Matlab中的样本分类和回归分析技巧引言：在现代科学和工程领域中，对于数据的分类和回归分析是非常重要的技能。
Matlab作为一种功能强大的数值计算和编程环境，提供了丰富的工具和函数来处理这些任务。
本文将介绍Matlab中常用的样本分类和回归分析技巧，帮助读者更好地应用这些方法。
一、数据预处理与可视化在进行样本分类和回归分析之前，首先需要对数据进行预处理和可视化。
Matlab中提供了一些实用的函数和工具箱来处理这些任务。
例如，可以使用importdata函数导入各种格式的数据文件，并使用preprocessing工具箱进行数据清洗，例如去除异常值或缺失数据。
此外，Matlab还提供了强大的绘图功能，可以使用plot和scatter函数绘制数据的散点图、箱线图和直方图，以便更好地理解数据的分布和特征。
二、特征选择与提取在样本分类和回归分析中，选择合适的特征对于模型的性能至关重要。
在Matlab中，可以使用特征选择算法来从原始数据中选择最相关的特征。
Matlab提供了一些功能强大的特征选择工具箱，例如ReliefF、Lasso和稀疏正则化算法等。
此外，Matlab还提供了一些特征提取算法，例如主成分分析（PCA）和独立成分分析（ICA），可以从原始数据中提取出最重要的特征。
三、样本分类算法Matlab中提供了许多常用的样本分类算法，包括支持向量机（SVM）、K最近邻（K-Nearest Neighbors，KNN）和决策树等。
这些算法在Matlab中都有相应的函数和工具箱，可以方便地进行模型训练和测试。
例如，使用fitcsvm函数可以训练支持向量机模型，并使用predict函数对新样本进行分类。
在选择分类算法时，需要根据数据的属性和目标来选择合适的算法，并使用交叉验证等方法评估模型的性能。
四、回归分析算法与样本分类类似，Matlab中也提供了多种用于回归分析的算法，例如线性回归、岭回归和支持向量回归等。
第三讲 MATLAB预测(1)回归分析
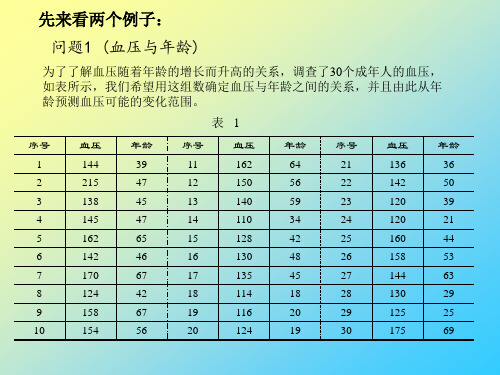
ˆ 489.2946 s t 2 65.8896 t 9.1329
方法二
化为多元线性回归：
t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
3
1
模型：记血压为 y ，年龄为 x1 ，体重指数为 x2 ，吸烟习惯为 x3 ， 用Matlab将 y 与 x2 的数据做散点图，看出大致也呈线性关系，建立 模型： y 0 1 x1 2 x2 3 x3 由数据估计系数 0，2，3，4 ，也可看做曲面拟合（其实为 超平面）
T=[ones(14,1) t‘ (t.^2)'];
[b,bint,r,rint,stats]=regress(s',T); b,stats
得回归模型为 ：
ˆ 9.1329 65.8896 s t 489.2946 t2
预测及作图
Y=polyconf(p,t,S) plot(t,s,'k+',t,Y,'r')
（二）多元二项式回归
命令：rstool（x，y，’model’, alpha）
nm矩阵
n维列向量
显著性水平
（缺省时为0.05）
由下列 4 个模型中选择 1 个（用字符串输入，缺省时为线性模型）： linear（线性）： y 0 1 x1 m xm purequadratic（纯二次）： interaction（交叉）： y
其中 x=（x1，x2，„，xn） ，y=（y1，y2 ，„，yn） ； m m-1 p=（a1，a2，„，am+1）是多项式 y=a1x +a2x +„+amx+am+1 的系数；S 是一个矩阵，用来估计预测误差.
Matlab回归分析：详解+实例
姚明女儿的身高
问 建立父母身高和女儿身高的模型 题 姚明2.26米，叶莉1.90米，预测姚明女儿身高
女孩身高y(cm) 156 172 162 158 164 166 160 155 174 165
父母平均身高 x(cm)
158.5
170.5
166
163.5
166
168.5 165.5
自变量X：用来解释Y的变量，通常有多个。
Y：薪资收入 X:学历、年龄、性别...
注意：（1）自变量可以是定量数据，也可以是定
性数据，它不决定回归模型的类型，决定回归模型 类型的是因变量；
（2）确定自变量的方法可以头脑风暴，但同时也 要看数据的可获得性，有时候可能头脑风暴想的很 好，但是没办法获取这个指标的数据也是不行的， 所以自变量的选取往往看一个数据的可获取性。
1 n
(x0 x)2 Lxx
小结
1.回归分析的任务 研究变量之间的相关关系
2.线性回归的步骤
(1) 推测回归函数; (3) 估计未知参数; (5) 预测.
(2) 建立回归模型; (4) 进行假设检验;
MATLAB中回归分析的实现
多元线性回归
1.确定回归系数的点估计值,用命令:
b=regress(Y,X)
女孩身高y(cm) 156 172 162 158 164 166 160 155 174 165
父母平均身高 x(cm)
158.5
170.5
166
163.5
166
168.5 165.5
159
180.5
169
基本模型
y 0 1x
y ~女孩身高
0, 1 ~回归系数
如何在MATLAB中进行统计回归分析
如何在MATLAB中进行统计回归分析统计回归分析是一种被广泛应用于数据科学和统计学领域的技术。
它被用来分析变量之间的关系，并预测一个或多个自变量对因变量的影响。
在MATLAB中，有许多强大的工具和函数可以帮助我们进行统计回归分析。
本文将讨论如何在MATLAB中使用这些功能进行统计回归分析。
1. 数据导入与预处理在进行回归分析之前，首先需要将数据导入到MATLAB中。
MATLAB支持多种数据格式，如CSV、Excel、文本文件等。
可以使用readmatrix或readtable等函数读取数据，根据数据的特点选择合适的函数。
在导入数据之后，通常需要对数据进行预处理。
这包括处理缺失值、异常值以及数据的标准化。
MATLAB提供了一系列函数来处理这些问题，如isnan、isoutlier和zscore等。
2. 单变量回归分析单变量回归分析是最基本的回归分析方法。
它用于分析一个自变量对一个因变量的影响。
在MATLAB中，可以使用fitlm函数进行单变量回归分析。
fitlm函数需要输入自变量和因变量的数据，然后可以对回归模型进行拟合，并得到回归系数、残差等统计信息。
使用plot函数可以绘制回归模型的拟合曲线，以及残差的散点图。
通过观察残差的分布，可以评估拟合模型的合理性。
3. 多变量回归分析多变量回归分析是在一个或多个自变量对一个因变量的影响进行分析。
在MATLAB中，可以使用fitlm函数或者fitlmulti函数实现多变量回归分析。
fitlm函数可以处理多个自变量，但是需要手动选择自变量，并提供自变量和因变量的数据。
fitlmulti函数则可以自动选择最佳的自变量组合，并进行回归拟合。
它需要提供自变量和因变量的数据矩阵。
多变量回归分析的结果可以通过查看回归系数和残差来解释。
还可以使用plot函数绘制回归模型的拟合曲面或曲线，以便更好地理解自变量对因变量的影响。
4. 方差分析方差分析是一种常用的统计方法，用于比较两个或多个因素对因变量的影响。
MATLAB回归分析工具箱使用方法
MATLAB回归分析工具箱使用方法回归分析是一种用于探索变量之间关系的统计方法。
它可以通过分析一个或多个自变量（也称为预测变量或解释变量）与一个因变量（也称为响应变量或预测变量）之间的关系来进行预测和解释。
在MATLAB中，进行回归分析需要使用统计和机器学习工具箱。
下面是使用MATLAB回归分析工具箱的一般步骤：1.准备数据：首先，你需要准备你要进行回归分析的数据。
数据应包括自变量和因变量。
你可以将数据存储在MATLAB的工作空间中。
2. 导入数据：如果你的数据存储在外部文件中，如Excel文件或CSV文件，你可以使用MATLAB的导入工具将数据导入到MATLAB中。
3.拟合模型：在回归分析中，你需要选择适当的模型来拟合你的数据。
MATLAB提供了多种回归模型，如线性回归、多项式回归、广义线性模型等。
你可以根据你的数据类型和需求选择适当的模型。
4. 拟合模型参数：一旦你选择了合适的模型，你需要拟合模型参数。
在MATLAB中，你可以使用"fitlm"函数来拟合线性模型，使用"fitrgp"函数来拟合高斯过程回归模型。
这些函数将返回一个拟合模型的对象。
5.模型评估：拟合模型后，你可以对模型进行评估。
MATLAB提供了一些工具来评估模型的好坏，如决定系数（R²）、均方根误差（RMSE）等。
你可以使用这些指标来判断你的模型是否满足你的需求。
6. 预测：一旦你拟合了你的模型并评估了模型的好坏，你可以使用模型来进行预测。
你可以使用"predict"函数来预测新的自变量对应的因变量。
除了上述步骤外，MATLAB还提供了一些其他的回归分析工具箱的功能，如特征选择、模型比较、交叉验证等。
你可以根据你的需求来选择适当的功能和方法。
总结起来，使用MATLAB回归分析工具箱进行回归分析的一般步骤包括数据准备、数据导入、选择模型、拟合模型参数、模型评估和预测。
在Matlab中进行回归分析和预测模型的技术
在Matlab中进行回归分析和预测模型的技术在当今数据驱动的社会中，回归分析和预测模型成为了数据科学领域中不可或缺的技术。
在这方面，Matlab作为一个功能强大且广泛应用的数学软件包，为进行回归分析和预测模型提供了丰富的工具和函数。
本文将探讨在Matlab中使用回归分析进行数据建模和预测的技术。
首先，回归分析是一种通过建立一个数学方程来描述变量之间关系的统计方法。
它常用于研究自变量（也称为预测变量）与因变量之间的关系。
在Matlab中，回归分析主要通过线性回归模型来实现。
线性回归模型假设因变量与自变量之间存在线性关系。
在Matlab中，可以使用regress函数来拟合线性回归模型。
该函数可以通过最小二乘法估计回归系数，使得预测变量与实际观测值之间的残差平方和最小化。
除了线性回归模型，Matlab还提供了其他类型的回归模型，如多项式回归模型、岭回归模型和弹性网络回归模型等。
多项式回归模型通过增加自变量的多项式项来处理非线性关系。
岭回归模型和弹性网络回归模型则通过引入正则化项来解决多重共线性问题，提高模型的鲁棒性和预测能力。
在进行回归分析时，特征工程是一个重要的环节。
特征工程涉及到对原始数据进行处理和转换，以提取对模型建立和预测有用的特征。
在Matlab中，可以利用数据预处理工具箱来进行特征工程。
数据预处理工具箱提供了一系列函数和工具来处理数据中的缺失值、异常值和重复值，进行特征选择和降维，并进行数据标准化和归一化等操作。
通过合理的特征工程，可以提高模型的性能和准确度。
除了回归分析，预测模型在许多实际应用中也起着重要的作用。
预测模型可以根据历史数据和趋势来预测未来的趋势和行为。
在Matlab中，可以利用时间序列分析和神经网络等方法进行预测建模。
时间序列分析是一种用于预测未来数值的统计方法，广泛应用于经济学、金融学和气象学等领域。
在Matlab中，时间序列分析主要通过自回归（AR）模型和移动平均（MA）模型来实现。
MATLAB 回归分析regress,nlinfit,stepwise函数
MATLAB 回归分析regress,nlinfit,stepwise函数matlab回归分析regress,nlinfit,stepwise函数回归分析1．多元线性重回在matlab统计工具箱中使用命令regress()实现多元线性回归，调用格式为b=regress(y，x)或[b，bint，r，rint，statsl=regess(y，x，alpha)其中因变量数据向量y和自变量数据矩阵x按以下排列方式输入对一元线性重回，挑k=1即可。
alpha为显著性水平(缺省时预设为0.05)，输入向量b，bint为回归系数估计值和它们的置信区间，r，rint为残差及其置信区间，stats就是用作检验重回模型的统计数据量，存有三个数值，第一个就是r2，其中r就是相关系数，第二个就是f统计数据量值，第三个就是与统计数据量f对应的概率p，当p拒绝h0，回归模型成立。
图画出来残差及其置信区间，用命令rcoplot(r，rint)实例1：已知某湖八年来湖水中cod浓度实测值(y)与影响因素湖区工业产值(x1)、总人口数(x2)、捕鱼量(x3)、降水量(x4)资料，建立污染物y的水质分析模型。
(1)输出数据x1=[1.376,1.375,1.387,1.401,1.412,1.428,1.445,1.477]x2=[0.450,0.475,0.485,0.50 0,0.535,0.545,0.550,0.575]x3=[2.170,2.554,2.676,2.713,2.823,3.088,3.122,3.262]x4=[0.8922,1.1610,0.5346,0.9589,1.0239,1.0499,1.1065,1.1387]y=[5.19,5.30,5.60，5.82，6.00,6.06，6.45，6.95](2)留存数据(以数据文件.mat形式留存，易于以后调用)savedatax1x2x3x4yloaddata(抽出数据)(3)继续执行重回命令x=[ones(8,1)，]；[b，bint，r，rint，stats]=regress得结果：b=(-16.5283，15.7206，2.0327，-0.2106，-0.1991)’stats=(0.9908，80.9530，0.0022)即为=-16.5283+15.7206xl+2.0327x2-0.2106x3+0.1991x4r2=0.9908，f=80.9530，p=0.00222．非线性重回非线性回归可由命令nlinfit来实现，调用格式为[beta,r,j]=nlinfit(x，y，'model’，beta0)其中，输人数据x，y分别为n×m矩阵和n维列向量，对一元非线性回归，x为n维列向量model是事先用m-文件定义的非线性函数，beta0是回归系数的初值，beta是估计出的回归系数，r是残差，j是jacobian矩阵，它们是估计预测误差需要的数据。
MATLAB 回归分析regress,nlinfit,stepwise函数
回归分析1．多元线性回归在Matlab统计工具箱中使用命令regress()实现多元线性回归，调用格式为b=regress(y，x)或[b，bint，r，rint，statsl = regess(y，x，alpha)其中因变量数据向量y和自变量数据矩阵x按以下排列方式输入对一元线性回归，取k=1即可。
alpha为显著性水平(缺省时设定为0.05)，输出向量b，bint为回归系数估计值和它们的置信区间，r，rint为残差及其置信区间，stats是用于检验回归模型的统计量，有三个数值，第一个是R2，其中R是相关系数，第二个是F统计量值，第三个是与统计量F对应的概率P，当P<α时拒绝H0，回归模型成立。
画出残差及其置信区间，用命令rcoplot(r，rint)实例1：已知某湖八年来湖水中COD浓度实测值(y)与影响因素湖区工业产值(x1)、总人口数(x2)、捕鱼量(x3)、降水量(x4)资料，建立污染物y的水质分析模型。
(1)输入数据x1=[1.376, 1.375, 1.387, 1.401, 1.412, 1.428, 1.445, 1.477]x2=[0.450, 0.475, 0.485, 0.500, 0.535, 0.545, 0.550, 0.575]x3=[2.170 ,2.554, 2.676, 2.713, 2.823, 3.088, 3.122, 3.262]x4=[0.8922, 1.1610 ,0.5346, 0.9589, 1.0239, 1.0499, 1.1065, 1.1387]y=[5.19, 5.30, 5.60，5.82，6.00, 6.06，6.45，6.95](2)保存数据(以数据文件.mat形式保存，便于以后调用)save data x1 x2 x3 x4 yload data (取出数据)(3)执行回归命令x =[ones(8,1)，]；[b，bint，r，rint，stats] = regress得结果：b = (-16.5283，15.7206，2.0327，-0.2106，-0.1991)’stats = (0.9908，80.9530，0.0022)即= -16.5283 + 15.7206xl + 2.0327x2 - 0.2106x3 + 0.1991x4R2 = 0.9908，F = 80.9530，P = 0.00222．非线性回归非线性回归可由命令nlinfit来实现，调用格式为[beta,r,j] = nlinfit(x，y，'model’，beta0)其中，输人数据x，y分别为n×m矩阵和n维列向量，对一元非线性回归，x 为n维列向量model是事先用m-文件定义的非线性函数，beta0是回归系数的初值，beta是估计出的回归系数，r是残差，j是Jacobian矩阵，它们是估计预测误差需要的数据。
在MATLAB中使用高斯过程进行回归分析
在MATLAB中使用高斯过程进行回归分析随着数据科学和机器学习的发展，回归分析成为了一种非常常见和有用的数据分析工具。
而高斯过程作为一种统计建模工具，在回归分析中具有广泛的应用。
在本文中，我们将介绍如何在MATLAB中使用高斯过程进行回归分析。
高斯过程，也被称为基于核函数的回归（Kriging）或者高斯过程回归（Gaussian Process Regression，简称GPR），是一种概率模型，广泛应用于回归分析中。
它通过对数据进行建模，将数据与潜在函数之间的关系进行学习和预测。
在MATLAB中，可以使用Statistics and Machine Learning Toolbox来进行高斯过程回归分析。
首先，我们需要准备一些数据来进行回归分析。
假设我们想要预测一个物体的重量，我们可以将物体的尺寸作为输入变量，将物体的重量作为输出变量。
我们可以通过测量一系列物体的尺寸和重量来获得这些数据。
在MATLAB中，我们可以使用`fitrgp`函数来进行高斯过程回归的建模和预测。
首先，我们需要将数据拆分成输入变量和输出变量。
假设我们的输入变量存储在一个名为`X`的矩阵中，输出变量存储在一个名为`Y`的向量中。
我们可以使用以下代码进行拆分：```matlabX = [尺寸1; 尺寸2; 尺寸3; ...; 尺寸n];Y = [重量1; 重量2; 重量3; ...; 重量n];```接下来，我们可以使用`fitrgp`函数来建立高斯过程回归模型：```matlabmodel = fitrgp(X, Y);```在这个过程中，`fitrgp`函数将自动选择核函数和其他参数，来对输入变量和输出变量之间的关系进行建模。
但是，我们也可以通过指定自定义的核函数和参数来调整建模的过程。
建立了模型之后，我们可以使用`predict`函数来对新的数据进行预测。
假设我们想要预测一个新物体的重量，我们可以将其尺寸作为输入变量传递给`predict`函数：```matlabnew_size = [新物体的尺寸];predicted_weight = predict(model, new_size);````predict`函数将返回一个预测的重量值，这个值可以帮助我们了解新物体的重量。
matlab回归分析方法
当然，也可以利用直线拟合得到同一方程。只不过不能得到参数置信区间和对模型进行检验。拟合程序如下：
y=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164];
8.2多元线性回归分析
8.2.1多元线性回归模型的建模步骤及其MATLAB实现
如果根据经验和有关知识认为与因变量有关联的自变量不止一个，那么就应该考虑用最小二乘准则建立多元线性回归模型。
设影响因变量 的主要因素（自变量）有m个，记 ，假设它们有如下的线性关系式：
，
如果对变量 与自变量 同时作n次观察（n>m）得n组观察值，采用最小二乘估计求得回归方程
（1）收集一组包含因变量和自变量的数据；
（2）选定因变量和自变量之间的模型，即一个数学式子，利用数据按照最小二乘准则计算模型中的系数；
（3）利用统计分析方法对不同的模型进行比较，找出与数据拟合得最好的模型；
（4）判断得到的模型是否适合于这组数据；
（5）利用模型对因变量作出预测或解释。
应用统计分析特别是多元统计分析方法一般都要处理大量数据，工作量非常大，所以在计算机普及以前，这些方法大都是停留在理论研究上。运用一般计算语言编程也要占用大量时间，而对于经济管理及社会学等对高级编程语言了解不深的人来说要应用这些统计方法更是不可能。MATLAB等软件的开发和普及大大减少了对计算机编程的要求，使数据分析方法的广泛应用成为可能。MATLAB统计工具箱几乎包括了数理统计方面主要的概念、理论、方法和算法。运用MATLAB统计工具箱，我们可以十分方便地在计算机上进行计算，从而进一步加深理解，同时，其强大的图形功能使得概念、过程和结果可以直观地展现在我们面前。本章内容通常先介绍有关回归分析的数学原理，主要说明建模过程中要做的工作及理由，如模型的假设检验、参数估计等，为了把主要精力集中在应用上，我们略去详细而繁杂的理论。在此基础上再介绍在建模过程中如何有效地使用MATLAB软件。没有学过这部分数学知识的读者可以不深究其数学原理，只要知道回归分析的目的，按照相应方法通过软件显示的图形或计算所得结果表示什么意思，那么，仍然可以学到用回归模型解决实际问题的基本方法。包括：一元线性回归、多元线性回归、非线性回归、逐步回归等方法以及如何利用MATLAB软件建立初步的数学模型，如何透过输出结果对模型进行分析和改进，回归模型的应用等。
如何使用MATLAB进行数据拟合与回归分析
如何使用MATLAB进行数据拟合与回归分析MATLAB是一种功能强大的数值计算和数据分析工具，可以用于数据拟合和回归分析。
下面将介绍如何使用MATLAB进行数据拟合和回归分析的步骤。
1. 导入数据：首先，将需要进行数据拟合和回归分析的数据导入到MATLAB中。
可以通过读取Excel文件、文本文件或直接将数据输入到MATLAB的工作空间中。
2. 数据预处理：在进行数据拟合和回归分析之前，通常需要对数据进行预处理。
这包括数据清洗、去除异常点、处理缺失值等。
MATLAB提供了许多数据预处理函数，如清除NaN值的函数“cleanData”和删除异常值的函数“outliers”。
3. 数据可视化：在进行数据拟合和回归分析之前，可以先对数据进行可视化，以便更好地了解数据的特征和分布。
MATLAB提供了丰富的绘图函数，可以绘制散点图、直方图、箱线图等。
例如，可以使用“scatter”函数绘制散点图，使用“histogram”函数绘制直方图。
4. 数据拟合：数据拟合是根据已有数据点，拟合出一个数学模型与函数，以揭示数据的内在规律。
在MATLAB中，可以使用“polyfit”函数进行多项式拟合，使用“fit”函数进行曲线拟合，也可以使用自定义函数进行拟合。
拟合过程可以使用最小二乘法等方法进行。
5. 回归分析：回归分析是通过对自变量和因变量之间的关系进行建模，预测因变量的值。
在MATLAB中，可以使用线性回归模型、多项式回归模型、逻辑回归模型等进行回归分析。
可以使用“fitlm”函数进行线性回归分析，使用“polyfit”函数进行多项式回归分析，使用“fitglm”函数进行逻辑回归分析。
6. 模型评估：在进行数据拟合和回归分析之后，需要对模型进行评估，以判断模型的合理性和预测能力。
在MATLAB中，可以使用均方误差（MSE）、决定系数（R-squared）、残差分析等方法对模型进行评价。
可以使用“mse”函数计算MSE，使用“rsquared”函数计算R-squared。
MATLAB回归分析
MATLAB回归分析回归分析是一种通过建立数学模型来研究变量之间的关系的统计方法。
在MATLAB中，我们可以使用回归分析工具箱来进行回归分析。
回归分析的目标是找到一个能够最好地描述自变量和因变量之间关系的数学模型。
在这篇文章中，我们将介绍回归分析的基本原理、MATLAB中的回归分析工具箱的使用以及如何解释回归分析的结果。
回归分析的基本原理回归分析建立在线性回归的基础上。
线性回归假设因变量与自变量之间存在一个线性关系。
回归分析通过找到最佳拟合线来描述这种关系。
最常用的回归方程是一元线性回归方程，它可以表示为：y=β0+β1x+ε，其中y是因变量，x是自变量，β0和β1是回归系数，ε是误差项。
- regress函数：用于计算多元线性回归模型，并返回回归系数、截距和残差。
例如，[B, BINT, R]=regress(y, X)用于计算因变量y和自变量矩阵X之间的回归模型。
- fitlm函数：用于拟合线性回归模型并返回拟合对象。
例如，mdl= fitlm(X, y)用于拟合因变量y和自变量矩阵X之间的线性回归模型，并返回mdl拟合对象。
- plot函数：用于绘制回归分析的结果。
例如，plot(mdl)用于绘制fitlm函数返回的拟合对象mdl的结果。
- coefCI函数：用于计算回归系数的置信区间。
例如，CI =coefCI(mdl)用于计算拟合对象mdl中回归系数的置信区间。
解释回归分析的结果回归分析的结果通常包括拟合曲线、回归系数以及模型的可靠性指标。
拟合曲线描述了自变量和因变量之间的关系。
回归系数可以用来解释自变量对因变量的影响。
模型的可靠性指标包括截距、回归系数的显著性检验以及相关系数等。
拟合曲线可以通过调用plot函数来绘制。
回归系数可以通过调用coef函数来获取。
对回归系数的显著性检验可以利用置信区间来判断，如果置信区间包含0，则说明回归系数不显著。
相关系数可以通过调用corrcoef函数来计算。
用MATLAB求解回归分析-文档资料
多元线性回归
y x ... x 0 1 1 p p
1、确定回归系数的点估计值：
b=regress( Y, X )
ˆ 0 ˆ b 1 .. ˆ p
Y1 Y Y 2 ... Y n
3、残差分析，作残差图： rcoplot(r,rint) 从残差图可以看出，除第二个数据外，其余数据的残 差离零点均较近，且残差的置信区间均包含零点，这说明 回归模型 y=-16.073+0.7194x能较好的符合原始数据，而第 二个数据可视为异常点.
Residual Case Order Plot 4
方法一
直接作二次多项式回归： t=1/30:1/30:14/30; s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48]; [p,S]=polyfit(t,s,2) 得回归模型为 ： 2 ˆ s 489 . 2946 t 65 . 8896 t 9 . 1329
1 x1 1 x1 2 1 x x2 2 21 X ... ... ... 1 xn1 xn2
... x1 p ... x2 p ... ... ... xn p
对一元线性回归，取p=1即可。
2、求回归系数的点估计和区间估计、并检验回归模型： [b, bint,r,rint,stats]=regress(Y,X,alpha)
法二 化为多元线性回归： t=1/30:1/30:14/30; s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48]; T=[ones(14,1) t' (t.^2)']; [b,bint,r,rint,stats]=regress(s',T); b,stats 得回归模型为 ： 2 ˆ s 9 . 1329 65 . 8896 t 489 . 2946 t
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一Matlab作方差分析方差分析是分析试验（或观测）数据的一种统计方法。
在工农业生产和科学研究中，经常要分析各种因素及因素之间的交互作用对研究对象某些指标值的影响。
在方差分析中，把试验数据的总波动（总变差或总方差）分解为由所考虑因素引起的波动（各因素的变差）和随机因素引起的波动（误差的变差），然后通过分析比较这些变差来推断哪些因素对所考察指标的影响是显著的，哪些是不显著的。
【例1】（单因素方差分析）一位教师想要检查3种不同的教学方法的效果，为此随机地选取水平相当的15位学生。
把他们分为3组，每组5人，每一组用一种方法教学，一段时间以后，这位教师给15位学生进行统考，成绩见下表1。
问这3种教学方法的效果有没有显著差异。
表1 学生统考成绩表方法成绩甲75 62 71 58 73乙71 85 68 92 90丙73 79 60 75 81Matlab中可用函数anova1(…)函数进行单因子方差分析。
调用格式：p=anova1(X)含义：比较样本m×n的矩阵X中两列或多列数据的均值。
其中，每一列表示一个具有m 个相互独立测量的独立样本。
返回：它返回X中所有样本取自同一总体（或者取自均值相等的不同总体）的零假设成立的概率p。
解释：若p值接近0（接近程度有解释这自己设定），则认为零假设可疑并认为至少有一个样本均值与其它样本均值存在显著差异。
Matlab程序：Score=[75 62 71 58 73;81 85 68 92 90;73 79 60 75 81]’;P=anova1(Score)输出结果：方差分析表和箱形图ANOVA TableSource SS df MS F Prob>FColumns 604.9333 2 302.4667 4.2561 0.040088Error 852.8 12 71.0667Total 1457.7333 14由于p值小于0.05，拒绝零假设，认为3种教学方法存在显著差异。
例2（双因素方差分析）为了考察4种不同燃料与3种不同型号的推进器对火箭射程（单位：海里）的影响，做了12次试验，得数据如表2所示。
表2 燃料-推进器-射程数据表推进器1 推进器2 推进器3燃料1 58.2 56.2 65.3燃料2 49.1 54.1 51.6燃料3 60.1 70.9 39.2燃料4 75.8 58.2 48.7在Matlab中利用函数anova2函数进行双因素方差分析。
调用格式：p=anova2(X,reps)含义：比较样本X中两列或两列以上和两行或两行以上数据的均值。
不同列的数据代表因素A的变化，不同行的数据代表因素B的变化。
若在每个行-列匹配点上有一个以上的观测量，则参数reps指示每个单元中观测量的个数。
返回：当reps=1（默认值）时，anova2将两个p值返回到向量p中。
H0A：因素A的所有样本（X中的所有列样本）取自相同的总体；H0B：因素B的所有样本（X中的所有行样本）取自相同的总体。
当reps>1时，anova2还返回第三个p值：H0AB：因素A与因素B没有交互效应。
解释：如果任意一个p值接近于0，则认为相关的零假设不成立。
Matlab程序：disp1=[58.2 56.2 65.3;49.1 54.1 51.6;60.1 70.9 39.2;75.8 58.2 48.7]’;p=anova2(disp1,1)输出结果：方差分析表ANOVA TableSource SS df MS F Prob>FColumns 157.59 3 52.53 0.43059 0.73875Rows 223.8467 2 111.9233 0.91743 0.44912Error 731.98 6 12 1.9967Total 1113.4167 11由于燃料和推进器对应的p值均大于0.05，所以可以接受零假设H0A和H0B，认为燃料和推进器对火箭的射程没有显著影响。
例3（双因素方差分析）设火箭的射程在其它条件基本相同时与燃料种类及推进器型号有关。
现在考虑4种不同的燃料及3种不同型号的推进器，对于每种搭配个发射了火箭两次，得数据见表3。
问各自变量和自变量的交互效应是否对火箭的射程有显著影响？表3 燃料-推进器-射程数据表推进器1 推进器2 推进器3燃料1 58.252.6 56.241.265.360.8燃料2 49.142.8 54.150.551.648.4燃料3 60.158.3 70.973.239.240.7燃料4 75.871.5 58.251.048.741.4Matlab程序：disp2=[58.2 52.6 49.1 42.8 60.1 58.3 75.8 71.5;56.2 41.2 54.1 50.5 70.9 73.2 58.2 51.0;65.3 60.8 51.6 48.4 39.2 40.7 48.7 41.4]’;p=anova2(disp2,2)输出结果：方差分析表ANOVA TableSource SS df MS F Prob>FColumns 370.9808 2 185.4904 9.3939 0.003506Rows 261.675 3 87.225 4.4174 0.025969Interaction 1768.6925 6 294.7821 14.9288 6.1511e-005Error 236.95 12 19.7458Total 2638.2983 23显著。
方差分析上机练习为研究广告的效果，考察4种广告方式：当地报纸（paper)、当地广播（radio）、店内销售员（people）和店内展示（display）的效果。
共设有144个销售点，每种广告随机抽取36个销售点记录销售额，分布在6个地区的144个销售点的销售情况生成的数据集ADS见下表。
数据集ADS中有3个变量：AD表示广告的类型、AREA表示地区、SALES表示销售额（单位：千元）。
请完成以下练习：(1) 概括下列数据：用箱形图、条形图直观地呈现四种广告方式下销售量的分布情况；计算四种广告方式下销售量的均值、方差、标准差、最大和最小值；(2) 进行单因素方差分析：检验四种广告方式下销售量数据是否服从正态分α=）；布，方差是否相等；检验四种广告方式下的销售量是否有显著差异（0.01若四种广告方式下的销售量有显著差异，指出哪些类型的广告效果有显著的不同？(3) 在设计广告效果的试验时，虽然地区差异对销售量的影响并不是我们感兴趣的，但希望排除这一因素的影响。
数据集ADS记录了各个销售点所在的地区AREA。
试用双因素方差分析方法分析销售数据，并指出广告方式和地区对销α=）？广告方式(AD)与地区(AREA)之间有无交售量是否有显著影响（0.01,0.1互效应？表ADS数据集中的数据广告方式（变量:AD）销售额（单位：千元）（变量SALES）地区1 地区2 地区3 地区4 地区5 地区6当地报纸(paper) 75 57 7668 75 8377 757266 667676 816370 866294 54 7088 56 8687 656584 777879 627580 6270当地广播(radio)69 5110054 78 7990 776083 746933 797368 7565100 616870 53 7368 638379 666576 737481 5765店内销售员（people）63 67 8558 82 7880 876287 707770 754068 615564 40 6776 70 7751 617542 716564 506278 3783店内展示（display）52 61 6141 44 8676 575275 756333 696052 614361 66 4169 43 5165 585060 525544 455852 4560参考答案（1）箱形图：boxplot(ads) 结果：有异常值。
（其它：略）（2）正态性检验Paper：Hist(X1,6)频数直方图分布的正态性检验：normplot(X1)均服从正态分布。
单因素方差分析ANOVA TableSource SS df MS F Prob>FColumns 5866.0833 3 1955.3611 13.4831 8.8495e-008 Error 20303.2222 140 145.023Total 26169.3056 143P=8.8495e-008<0.01，四种广告方式下的销售量是否有显著差异。
对应的箱形图为：当地媒体和电台广播与点内展示有显著不同。
（3）ANOVA TableSource SS df MS F Prob>FColumns 1444.2222 5 288.8444 1.9582 0.089763Rows 5866.0833 3 1955.3611 13.2559 1.5637e-007Interaction 1158 15 77.2 0.52336 0.92341Error 17701 120 147.5083Total 26169.3056 143从以上分析结果可知：0.05<P1=0.089763<0.1，地区对检验水平有一定影响，但不显著。
P2=1.5637e-007<0.01<0.1，无论哪种检验水平，广告方式对销售量都有显著影响；P3=0.92341>0.1，地区和广告方式对销售量无交互效应。
二Matlab作回归分析回归分析的相关数学理论可以参见《概率论与数理统计教程》，下面仅以示例说明如何利用matlab处理回归分析。
1.一元线性回归分析【例1】为了了解百货商店销售额x与流通费率（反映商业活动的一个质量指标，指每元商品流转额所分摊的流通费用）y之间的关系，收集了九个商店的有关数据，见下表1.试建立流通费率y与销售额x的回归方程。
样本点销售额x(万元) 流通费率y1 1.5 7.02 4.5 4.83 7.5 3.64 10.5 3.15 13.5 2.76 16.5 2.57 19.5 2.48 22.5 2.39 25.5 2.2【分析】域的知识和经验进行，有时可能需要多种尝试。
选定目标函数后进行线性化变换，针对变换后的线性目标函数进行回归建模与评价，然后还原为非线性回归方程。
【Matlab数据处理】：【Step1】：绘制散点图以直观地选择拟合曲线x=[1.5 4.5 7.5 10.5 13.5 16.5 19.5 22.5 25.5];y=[7.0 4.8 3.6 3.1 2.7 2.5 2.4 2.3 2.2];plot(x,y,'-o')输出图形见图1。