应用多元统计分析课后习题答案高惠璇第七章习题解答
应用多元统计分析答案详解汇总_高惠璇[1]
![应用多元统计分析答案详解汇总_高惠璇[1]](https://img.taocdn.com/s3/m/5f0eb38784868762caaed582.png)
e
1 2 ( x2 2 x1 x2 14 x2 ) 2
dx2
1 e 2
1 2 ( 2 x1 22 x1 65 ) 2
e
1 2 ( x2 2 x2 ( x1 7 ) ( x1 7 ) 2 ) 2
比较上下式相应的系数,可得:
1 2 1 12 2 2 2 12 1 1 2 1 2 2 2 22 1 2 1 2 2 2 2 2 1 2 1 2 1 14 2 2 2 2 2 1 2 1 2 1 2 1 2
x1 y2 (2)第二次配方.由于 x2 y1 y2
14
第二章
2 1 2 2 2 1 2 1 2 2
多元正态分布及参数的估计
2 x x 2 x1 x2 22 x1 14 x2 65 y y 22 y2 14( y1 y2 ) 65 y 14 y1 49 y 8 y2 16 ( y1 7) ( y2 4)
由定理2.3.1可知X1 +X2 和X1 - X2相互独立.
4
第二章
(2) 因
多元正态分布及参数的估计
1 2 2 2(1 ) 0 X1 X 2 ~ N2 , Y 2(1 ) 0 X1 X 2 1 2
O 2(1 2 ) O 2(1 2 )
由定理2.3.1可知X(1) +X(2)和X(1) -X(2) 相 互独立.
7
第二章
(2) 因
(1) (2)
应用多元统计分析课后题答案
c) c)2
2( x1
a)( x2
c)]
其中 a x1 b ， c x2 d 。求 （1）随机变量 X1 和 X 2 的边缘密度函数、均值和方差； （2）随机变量 X1 和 X 2 的协方差和相关系数； （3）判断 X1 和 X 2 是否相互独立。
（1）解：随机变量 X1 和 X 2 的边缘密度函数、均值和方差；
12
2 2
1/
2
exp
1 2
(x
μ)
12 21
12
2 2
1
(x
μ)
。
2.3 已知随机向量 ( X1 X 2 ) 的联合密度函数为
f
( x1 ,
x2 )
2[(d
c)( x1
a)
(b a)(x2 (b a)2 (d
μ)
1 n 1
n i 1
E(Xi
-
μ)(
X i
-
μ)
nE(X
μ)(X
μ)
Σ
。
故 S 为 Σ 的无偏估计。 n 1
2.9.设 X(1) , X(2) , ..., X(n) 是从多元正态分布 X ~ N p (μ, Σ) 抽出的一个简单随机样本，试求 S
c) 2(x1 a)(x2 a)2(d c)2
c)]
dx2
2(d c)(x1 a)x2 d dc 2[(b a)t 2(x1 a)t] dt
(b a)2 (d c)2
应用多元统计分析课后答案
应用多元统计分析课后答案第二章2.1.试叙述多元联合分布和边际分布之间的关系。
解：多元联合分布讨论多个随机变量联合到一起的概率分布状况，12(,,)p X X X X '=的联合分布密度函数是一个p 维的函数，而边际分布讨论是12(,,)p X X X X '=的子向量的概率分布，其概率密度函数的维数小于p 。
2.2设二维随机向量12()X X '服从二元正态分布，写出其联合分布。
解：设12()X X '的均值向量为()12μμ'=μ，协方差矩阵为21122212σσσσ⎛⎫ ⎪⎝⎭，则其联合分布密度函数为1/21222112112222122121()exp ()()2f σσσσσσσσ--⎧⎫⎛⎫⎛⎫⎪⎪'=---⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭x x μx μ。
2.3已知随机向量12()X X '的联合密度函数为121212222[()()()()2()()](,)()()d c x a b a x c x a x c f x x b a d c --+-----=--其中1a x b ≤≤，2c x d ≤≤。
求（1）随机变量1X 和2X 的边缘密度函数、均值和方差； （2）随机变量1X 和2X 的协方差和相关系数； （3）判断1X 和2X 是否相互独立。
（1）解：随机变量1X 和2X 的边缘密度函数、均值和方差；112121222[()()()()2()()]()()()dx cd c x a b a x c x a x c f x dx b a d c --+-----=--⎰12212222222()()2[()()2()()]()()()()dd c c d c x a x b a x c x a x c dx b a d c b a d c -------=+----⎰ 12122222()()2[()2()]()()()()dd cc d c x a x b a t x a t dt b a d c b a d c ------=+----⎰2212122222()()[()2()]1()()()()d cdcd c x a x b a t x a t b a d c b a d c b a------=+=----- 所以由于1X 服从均匀分布，则均值为2b a +，方差为()212b a -。
多元统计分析第七章主成分分析习题答案
7.1 设随机变量12X(X ,X )'=的协差阵为21,12⎡⎤∑=⎢⎥⎣⎦试求Ｘ的特征根和特征向量，并写出主成分。
解：先求Ｘ的特征根λ，λ满足方程：21012-λ=-λ，即2(2)10-λ-=，因此两个特征根分别为123, 1.λ=λ=设13λ=对应的单位特征向量为()1121a ,a '，则()1121a ,a '满足：1121a 110a 110-⎛⎫⎡⎤⎛⎫= ⎪ ⎪⎢⎥-⎣⎦⎝⎭⎝⎭，故可以取1121a a ⎛⎛⎫ = ⎪ ⎝⎭ ⎝，其对应主成分为：112F X X 22=+；设21λ=对应的单位特征向量为()1222a ,a '，则()1222a ,a '满足：1222a 110a 110⎛⎫⎡⎤⎛⎫=⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭，故可以取1222a a ⎛⎫⎛⎫ ⎪= ⎪ ⎝⎭- ⎝，其对应的主成分为：212F 22=-.7.2设随机变量123X (X ,X ,X )'=的协差阵为120250,002-⎡⎤⎢⎥∑=-⎢⎥⎢⎥⎣⎦试求Ｘ的主成分及主成分对变量Ｘ的贡献率。
解：先求Ｘ的特征根λ，λ满足方程：12025002-λ---λ=-λ，即()2(2)610-λλ-λ+=，因此三个特征根分别为1235.8284,2,0.1716λ=λ=λ=设1 5.8284λ=对应的单位特征向量为()112131a ,a ,a '，则它满足：1121314.828420a 020.82840a 000 3.8284a 0--⎡⎤⎛⎫⎛⎫⎪ ⎪⎢⎥--=⎪ ⎪⎢⎥ ⎪ ⎪⎢⎥-⎣⎦⎝⎭⎝⎭，故可以取 112131a 10.38271a 2.41420.92392.6131a 00⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，其对应主成分为： 112F 0.3827X 0.9239X =-，其贡献率为5.828472.86%5.828420.1716=++；设22λ=对应的单位特征向量为()122232a,a ,a '，则它满足：122232120a 0230a 0000a 0--⎡⎤⎛⎫⎛⎫ ⎪ ⎪⎢⎥-= ⎪ ⎪⎢⎥ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭，故可以取122232a 0a 0a 1⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，其对应主成分为： 23F X =，其贡献率为225%5.828420.1716=++；设30.1716λ=对应的单位特征向量为()132333a ,a ,a '，则它满足：1323330.828420a 02 4.82840a 000 1.8284a 0-⎡⎤⎛⎫⎛⎫⎪ ⎪⎢⎥-=⎪ ⎪⎢⎥ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭，故可以取132333a 10.92391a 0.41420.38271.0824a 00⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，其对应主成分为： 312F 0.9239X 0.3827X =+，其贡献率为0.17162.14%5.828420.1716=++.7.3 设随机变量12X (X ,X )'=的协差阵为14,4100⎡⎤∑=⎢⎥⎣⎦试从∑和相关阵Ｒ出发求出总体主成分，并加以比较。
应用多元统计分析_课后答案
图 2.1
Descriptives 对话框
2.
单击 Options 按钮，打开 Options 子对话框。在对话框中选择 Mean 复选框，即计 算样本均值向量，如图 2.2 所示。单击 Continue 按钮返回主对话框。
图 2.2 Options 子对话框 3. 单击 OK 按钮，执行操作。则在结果输出窗口中给出样本均值向量，如表 2.1，即 样本均值向量为（35.3333，12.3333，17.1667，1.5250E2） 。
2.5 解： 依据题意，X= 57000 40200 21450 21900 45000 28350
′
15 16 12 8 15 8
27000 18750 12000 13200 21000 12000
144 36 381 190 138 26
′ E(X)= ∑6 α=1 x(α) = (35650,12.33,17325,152.5) n σ1 σ2 ρ2 (x1 −μ1 )2 σ2 1
+
σ2 1
(x2 −μ2 )2 σ2 2 )2
= = [
(x1 −μ1 )2 σ2 1 ρ(x1 −μ1 ) σ1
− −
2ρ(x1 −μ1 )(x2 −μ2 ) σ1 σ2 (x2 −μ2 ) 2 ] σ2
+
E( X ) μ
n→∞
lim E(
1 1 ������） = lim E( ������） = Σ n→∞ ������ n−1
2.7 试证多元正态总体 的样本均值向量 ̅) = E ( ΣX 证明： E(������ （α） ) = E (ΣX （α） ) =
n n 1 1 nμ n 1 n2
exp[−
应用多元统计第七章实验题答案
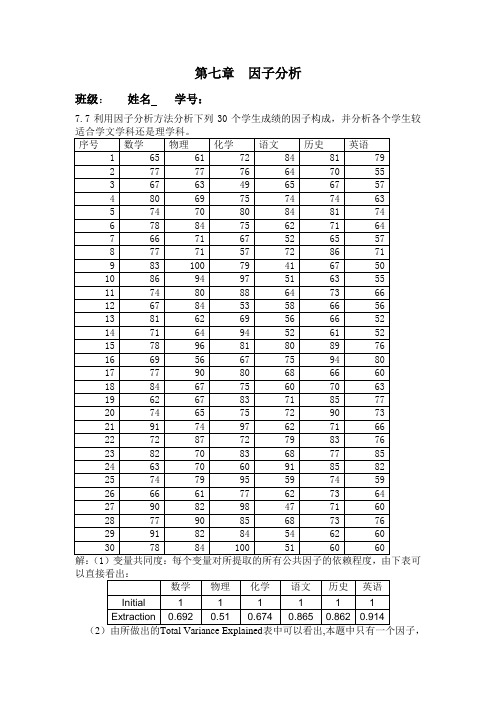
第七章因子分析班级：姓名学号：7.7利用因子分析方法分析下列30个学生成绩的因子构成，并分析各个学生较（2则由上表可写出每个原始变量的因子表达式：X1=-0.662F1+0.503F2；X2=-0.53F1+0.478F2；X6=0.816F1+0.498F2;（4）由Rotated Component Matrix表可以给出旋转后的因子载荷矩阵（见下表），第一个公共因子在指标语文、历史、英语上有较大的载荷，说明这三个指标有较强的相关性，可以归为一类，从分科情况来看，这三个指标属于学生较适合学文学科；第二个公共因子在指标为数学、物理、化学上有较大载荷，同样可以归为一类，这三个指标同属于学生较适合学理科。
（5）根据因子得分系数矩阵与原始变量的标准化值可以计算每个观测值的各F1=F2=0.439X1+0.4X2+0.484X3-0.01X4+0.073X5+0.169X6；则将学生成绩按顺序对应分别带入上面两个式子可以判定，当F1>F2时，该学生适合学文科，当F1<F2时，该学生适合学理科。
24、26的学生适合学文科；学生标号为：2、6、7、9、10、11、13、14、17、18、21、25、27、28、29、30的学生适合学理科。
7.8某汽车组织欲根据一系列指标来预测汽车的销售情况，为了避免有些指标之间的相关关系影响预测结果，须首先进行因子分析来简化系统。
下表是抽查欧洲某汽车市场7个品牌不同型号的汽车的各种指标数据，试用因子分析法找出其简X1=0.794F1；X2=0.879F1；X9=-0.893F1;（4）因为只有一个因子，因此不能被旋转。
（5）根据因子得分系数矩阵与原始变量的标准化值可以计算每个观测值的各因子的得分数，则根据下表可得出该题中的因子得分表达式即为所求的指标系统为：27X8-0.132X9。
7.10 根据习题5.11中2003年我国省会城市和计划单列城市的主要经济指标数据，利用因子分析法对其进行排序和分类，并与聚类分析的结果进行比较。
最新应用多元统计分析课后习题答案高惠璇PPT课件
(2) 考虑随机变量Y= X1-X2 ,显然有
YX 1X2 0 X 1X 1,当 估计
P{Y0}P{X11或 X11} P{X11}P{X11} (X1~N(0,1)) 2(1)0.317 04
若(X1 , X2 ) 是二元正态分布,则由性质4可知,
31
第三章 多元正态总体参数的检验
证明 记rk(A)=r.
若r=n,由AB＝O,知B＝ On×n,于是 X′AX与X′BX
若r=0时,则A＝0,则两个二次型也是独 立的.
以下设0＜r＜n.因A为n阶对称阵,存在正 交阵Γ,使得
32
第三章 多元正态总体参数的检验
其中λi≠0为A的特征值(i=1,…,r).于是
P { X 2 x } P { X 1 x } ( x )
当x≥1时, P{X2x}
P{X2 1}P{1X2 1}P{1X2 x}
P{X11}P{1X11}P{1X1x}
P{X1x}(x) 17
第二章 多元正态分布及参数的估计
当-1≤x≤1时,
P{X2 x}P{X2 1}P{1X2 x} P{X1 1}P{xX1 1} P{X1 1}P{1X1 x} P{X1 x}(x)
它的任意线性组合必为一元正态. 但Y= X1-X2 不是正态分布,故(X1 , X2 ) 不是二元正态分布.
19
第二章 多元正态分布及参数的估计
2-17 设X～Np(μ,Σ),Σ＞0,X的密度函数记为 f(x;μ,Σ).(1)任给a＞0,试证明概率密度等高面
f(x;μ,Σ)= a
是一个椭球面. (2) 当p=2且
比较上下式相应的系数,可得:
1
2 2
2
1 2
应用多元统计分析课后习题答案高惠璇第七章习题解答-20页PPT精选文档
解:
9
第七章 主成分分析
7-5 设3维总体X的协差阵为
试求总体主成分.
4 0 0
0 4 0
0 0 2
解:总体主成分为
Zi Xi(i1,2,3)
主成分向量为
Z ( X 1 ,X 2 ,X 3 ) 或 Z ( X 2 ,X 1 ,X 3 )
三个主成分的方差分别为4,4,2.
(01).
(1)
Z1 1p(X1X2Xp);
(2) 试求第一主成分的贡献率.
7
第七章 主成分分析
解:
1
8
第七章 主成分分析
7-4 设总体X＝(X1,…,Xp)′～Np(μ,Σ) (Σ＞0),等概率密度
椭球为
(X-μ)′Σ-1(X-μ)=C2(C为常数).
试问椭球的主轴方向是什么?
14 13
13 14 2
12
14
13
12 2
,
其中 1 21 31,421 4 21.3
试求X的主成分.
12
第七章 主成分分析
解:
13
第七章 主成分分析
7-8
14
第七章 主成分分析
15
第七章 主成分分析
7-9
16
其中ρ为X1和X2的相关系数(ρ>0). (1) 试从Σ出发求X
1
1
(2) 求X
(3) 试问当ρ取多大时才能使第一主成分的贡献率达95%以上.
解:
5
第七章 主成分分析
6
第七章 主成分分析
7-3 设p维总体X的协差阵为
21
1
应用多元统计分析课后习题答案详解北大高惠璇部分习题解答
可提成假设检验问题.因为
1 : 2 : 3 6 : 4 :1 C 0
其中
C
1 0
0 1
6 4
23
,
注意:
第24页/共46页
1 3
6 , 且 2 4
1
3 1
12
63 43
00.
24
第三章 多元正态总体参数的检验
或
C
2 1
3 0
0 6
~
Nr (0, 11),
X (2) ( )
~
N pr (0, 22 ),
记
X
n p
xij
X (1) | X (2) , nr n( pr)
则
W
X
X
X (1)X (1) X (2)X (1)
X X
(1) X (2) X
(2) (2)
WW1211
W12 W22
,
即 W11 X (1)X (1), W22 X (2)X (2)
样本，样本均值为X，样本离差阵为A.记μ＝(μ1,…,μp)′.为检验
H0:μ1=μ2=…=μp ,H1:μ1,μ2,…,μp至少有一对不相等.令
C 11
1 0
0 1
0 0
,
1 0 0 1( p1)p
则上面的假设等价于H0：Cμ=0p-1,H1：Cμ≠ 0p-1
试求检验H0 的似然比统计量和分布.
Tx2 n(n 1)(X ) Ax1( X )
~ T 2 ( p, n 1).
令 Y(i) CX (i) d (i 1,..., n)
其中C是pp非退化常数矩阵，d是p1常向量。
应用多元统计分析课后习题答案高惠璇第七章习题解答
04
习题4解答
题目
• 题目：在多元线性回归中，如果 一个自变量与其他自变量高度相 关，那么这个自变量是否应该被 包括在回归模型中？为什么？
解答
01
解答：在多元线性回归中，如果一个自变量与其他自变量 高度相关，那么这个自变量是否应该被包括在回归模型中 ，需要视具体情况而定。
解答
• 当$x < 0$时，$P(X \leq x) = \frac{1}{2}e^{x}$，所以$p(x) = \frac{1}{2}e^{x}$。
解答
• 接下来，我们计算期望值
• 当$x \geq 0$时，$E(X) = \int{0}^{\infty}xp(x)dx = \int{0}^{\infty}\frac{1}{2}xe^{-xdx} = \frac{1}{2}e^{-x}|_{0}^{\infty} = 0$。
• 因此，$E(X) = 0$。
01
03 02
解答
• 当$x \geq 0$时，$P(X^2 \leq x) = P(X \leq \sqrt{x}) = \frac{1}{2}e^{-\sqrt{x}}$，所以 $p_1(x) = \frac{1}{2}\sqrt{x}e^{\sqrt{x}}$。
答案
证明过程如上所述，结论 正确。
证明过程如上所述，结论 正确。
证明过程如上所述，结论 正确。
答案1
答案2
答案3
03
习题3解答
题目
题目：设随机变量$X$的 分布函数为$F(x) = begin{cases}
0 & x notin mathbf{R}
frac{1}{2}e^{-|x|} & x in mathbf{R}
(完整版)多元统计分析课后练习答案
第1章 多元正态分布1、在数据处理时，为什么通常要进行标准化处理？数据的标准化是将数据按比例缩放，使之落入一个小的特定区间。
在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。
其中最典型的就是0-1标准化和Z 标准化。
2、欧氏距离与马氏距离的优缺点是什么？欧氏距离也称欧几里得度量、欧几里得度量，是一个通常采用的距离定义，它是在m 维空间中两个点之间的真实距离。
在二维和三维空间中的欧氏距离的就是两点之间的距离。
缺点：就大部分统计问题而言，欧氏距离是不能令人满意的。
每个坐标对欧氏距离的贡献是同等的。
当坐标表示测量值时，它们往往带有大小不等的随机波动，在这种情况下，合理的方法是对坐标加权，使变化较大的坐标比变化较小的坐标有较小的权系数，这就产生了各种距离。
当各个分量为不同性质的量时，“距离”的大小与指标的单位有关。
它将样品的不同属性之间的差别等同看待，这一点有时不能满足实际要求。
没有考虑到总体变异对距离远近的影响。
马氏距离表示数据的协方差距离。
为两个服从同一分布并且其协方差矩阵为Σ的随机变量与的差异程度:如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧氏距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离。
优点：它不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关。
由标准化数据和中心化数据计算出的二点之间的马氏距离相同。
马氏距离还可以排除变量之间的相关性的干扰。
缺点：夸大了变化微小的变量的作用。
受协方差矩阵不稳定的影响，马氏距离并不总是能顺利计算出。
3、当变量X1和X2方向上的变差相等，且与互相独立时，采用欧氏距离与统计距离是否一致？统计距离区别于欧式距离，此距离要依赖样本的方差和协方差，能够体现各变量在变差大小上的不同，以及优势存在的相关性，还要求距离与各变量所用的单位无关。
如果各变量之间相互独立,即观测变量的协方差矩阵是对角矩阵, 则马氏距离就退化为用各个观测指标的标准差的倒数作为权数的加权欧氏距离。
应用多元统计分析课后习题答案高惠璇
2 1 2 2 2 (1)第一次配方: 2 x12 2 x1 x2 x2 ( x1 x2 ) 2 x12
2 1 x1 2 1 1 1 1 1 因2 x 2 x1 x2 x ( x1 , x2 ) , 而 BB, 1 1 x2 1 1 1 0 1 0 y1 1 1 x1 x1 x2 2 2 2 2 令y , 则 2 x 2 x x x y y 1 1 2 2 1 2 y x x 1 0 2 1 2
类似地有
1 2 2 ( 2 x1 22 x1 65 x1 14 x1 49 ) 2
f 2 ( x2 )
X 2 ~ N (3,2).
f (x , x )dx
1 2 1
1 2 2
e
1 ( x2 3) 2 4
10
第二章
多元正态分布及参数的估计
1 e 2
1 2 ( 2 x1 22 x1 65) 2
e
1 2 ( x2 2 x2 ( x1 7 ) ( x1 7 ) 2 ) 2
dx2 e
1 ( x1 7 ) 2 2
9
第二章
多元正态分布及参数的估计
1 ( x2 x1 7 ) 2 2
1 e e dx2 2 1 2 1 ( x 8 x 16 ) ( x2 x1 7 ) 2 1 1 1 1 2 e 2 e dx2 2 2 1 ( x1 4 ) 2 1 e 2 X1 ~ N (4,1). 2
u1 x1 4 令 u2 x2 3
高惠璇多元统计分析习题答案
第四章4-1 设⎪⎩⎪⎨⎧++=+-=+=,2,2,332211εεεb a y b a y a y ).,0(~323321I N σεεεε⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=（1）试求参数b a ,的最小二乘估计；（2）试导出检验b a H =:0的似然比统计量，并指出当假设成立时，这个统计量是分布是什么？解：（1）由题意可知.,,,211201321321⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=εεεεβ b a y y y Y C 则⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎪⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==--321'1''1'211201************)(ˆy y y Y C C C β.ˆˆ)2(51)2(6132321⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-++ba y y y y y（2）由题意知，检验b a H =:0的似然比统计量为2322ˆ⎪⎪⎭⎫ ⎝⎛=σσλ 其中，])ˆ2ˆ()ˆˆ2()ˆ[(31ˆ2322212b a y b a y a y --++-+-=σ。
当0H 成立时，设0a b a ==，则⎪⎩⎪⎨⎧+=+=+=,3,,303202101εεεa y a y a y ,311⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=C 可得,ˆ)3y (111311311311)(ˆ0321321'1''1'ay y y y y Y C C C =++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==--β ],)ˆ3()ˆ()ˆ[(31ˆ20320220120a y a y ay -+-+-=σ因此，当假设0H 成立时，与似然比统计量λ等价的F 统计量及其分布为).1,1(~ˆˆˆ2202F F σσσ-=4-3 设Y 与321,,x x x 有相关关系，其8组观测数据见表4.5.表 4.5 观测数据序号 1x2x3xY1 38 47.5 23 66.02 41 21.3 17 43.0 3 34 36.5 21 36.0 4 35 18.0 14 23.0 5 31 29.5 11 27.06 34 14.2 9 14.07 29 21.0 4 12.0 83210.087.6（1）设εββββ++++=3322110x x x Y ，试求回归方程及决定系数2R 和均方误差2s 。
应用多元统计分析课后习题答案高惠璇第七章习题解答共20页
第七章 主成分分析
17
第七章 主成分分析
7-10
18
第七章 主成分分析
77--1112
19
谢谢
解:
9
第七章 主成分分析
7-5 设3维总体X的协差阵为
试求总体主成分.
4 0 0
0 4 0
0 0 2
解:总体主成分为
Zi Xi(i1,2,3)
主成分向量为
Z ( X 1 ,X 2 ,X 3 ) 或 Z ( X 2 ,X 1 ,X 3 )
三个主成分的方差分别为4,4,2.
(01).
(1)
Z1 1p(X1X2Xp);
(2) 试求第一主成分的贡献率.
7
第七章 主成分分析
解:
1
8
第七章 主成分分析
7-4 设总体X＝(X1,…,Xp)′～Np(μ,Σ) (Σ＞0),等概率密度
椭球为
(X-μ)′Σ-1(X-μ)=C2(C为常数).
试问椭球的主轴方向是什么?
14 13
13 14 2
12
14
13
12 2
,
其中 1 21 31,421 4 21.3
试求X的主成分.
12
第七章 主成分分析
解:
13
第七章 主成分分析
7-8
14
第七章 主成分分析
15
第七章 主成分分析
7-9
16
10
第七章 主成分分析
7-6
设3维总体X的协差阵为
2 2
2 2
0
2
0 2 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
7-4 设总体X＝(X1,…,Xp)′～Np(μ,Σ) (Σ＞0),等概率密度
椭球为
(X-μ)′Σ-1(X-μ)=C2(C为常数).
试问椭球的主轴方成分分析
7-5 设3维总体X的协差阵为
试求总体主成分.
4 0 0
0 4 0
0 0 2
解:总体主成分为
Zi Xi(i1,2,3)
1
1
(2) 求X
(3) 试问当ρ取多大时才能使第一主成分的贡献率达95%以上.
解:
5
第七章 主成分分析
6
第七章 主成分分析
7-3 设p维总体X的协差阵为
21
1
1
(01).
(1)
Z1 1p(X1X2Xp);
(2) 试求第一主成分的贡献率.
7
第七章 主成分分析
解:
1
8
第七章 主成分分析
2
12
13 14
12 2
14 13
13 14 2
12
14
13
12 2
,
其中 1 21 31,421 4 21.3
试求X的主成分.
12
第七章 主成分分析
解:
13
第七章 主成分分析
7-8
14
第七章 主成分分析
15
第七章 主成分分析
7-9
16
第七章 主成分分析
主成分向量为
Z ( X 1 ,X 2 ,X 3 ) 或 Z ( X 2 ,X 1 ,X 3 )
三个主成分的方差分别为4,4,2.
10
第七章 主成分分析
7-6
设3维总体X的协差阵为
2 2
2 2
0
2
0 2 2
试求总体主成分，并计算每个主成分解释的方差比例
解:
11
第七章 主成分分析
7-7 设4维随机向量X的协差阵是
17
第七章 主成分分析
7-10
18
第七章 主成分分析
77--1112
19
应用多元统计分析
第七章习题解答
第七章 主成分分析
7-1 设X=(X1, X2)′的协方差阵 试从Σ和相关阵R出发求出总体主成分，
14
1040,
并加以比较.
解:
2
第七章 主成分分析
3
第七章 主成分分析
4
第七章 主成分分析
7-2 设X=(X1, X2)′～N2(0,Σ),协方差Σ＝
其中ρ为X1和X2的相关系数(ρ>0). (1) 试从Σ出发求X