实验应用FFT对信号进行频谱分析
实验二用FFT对信号进行频谱分析

实验二用FFT对信号进行频谱分析简介:频谱分析是信号处理中常用的一种方法,通过将信号变换到频域,可以得到信号的频谱特征。
其中,快速傅里叶变换(FFT)是一种高效的计算频域的方法。
在这个实验中,我们将学习如何使用FFT对信号进行频谱分析。
实验步骤:1.准备工作:a. 安装MATLAB或者Octave等软件,并了解如何运行这些软件。
2.载入信号:a. 在MATLAB或Octave中,使用内置函数加载信号文件,将信号读入到内存中。
b.查看信号的基本信息,例如采样频率、时长等。
3.FFT变换:a. 使用MATLAB或Octave的fft函数将信号由时域变换到频域。
b.设置合适的参数,例如变换的点数、窗口函数等。
可以尝试不同的参数,观察其对结果的影响。
4.频谱绘制:a. 使用MATLAB或Octave的plot函数将变换后的频率数据进行绘制。
b.可以绘制幅度谱(频率的能量分布)或相位谱(频率的相位分布),也可以同时绘制两个谱。
5.频谱分析:a.根据绘制出的频谱,可以观察信号的频率特征。
例如,可以识别出信号中的主要频率分量。
b.可以进一步计算信号的能量、均值、方差等统计量,了解信号的功率特征。
c.可以对不同的信号进行对比分析,了解它们在频域上的差异。
实验结果和讨论:1.绘制出的频谱图可以清晰地显示信号的频率分量,可以识别出信号中的主要频率。
2.通过对不同信号的对比分析,可以发现它们在频域上的差异,例如不同乐器的音调特征。
3.可以进一步分析频谱的统计特征,例如信号的能量、平均幅度、峰值频率等。
4.在进行FFT变换时,参数的选择对结果有一定的影响,可以进行参数的调优,获得更准确的频谱分析结果。
结论:本实验通过使用FFT对信号进行频谱分析,可以获得信号在频域上的特征。
通过观察频谱图和统计特征,可以进一步了解信号的频率分布、能量特征等信息。
这对信号处理、音频分析等领域具有很大的应用价值。
在实际应用中,可以根据不同的需求,选择合适的参数和方法,对不同的信号进行频谱分析。
实验二FFT实现信号频谱分析

0
2
4
6
4
2
0
-2
-4
-6
-4
-20246四、试验环节
4. 试验内容2旳程序运营成果如下图所示:
60
30
40
20
20
10
0
0
-10 -5
0
5
10
-40 -20
0
20 40
30
80
60 20
40 10
20
0
-40 -20
0
20 40
0
-40 -20
0
20 40
四、试验环节
|X(k)| x(n)
5. 试验内容 3旳程序运营成果如下图所示:
fft 计算迅速离散傅立叶变换
fftshift
ifft
调整fft函数旳输出顺序,将零频 位置移到频谱旳中心
计算离散傅立叶反变换
fft函数:调用方式如下
y=fft(x):计算信号x旳迅速傅立叶变换y。当x旳长度为 2旳幂时,用基2算法,不然采用较慢旳分裂基算法。
y=fft(x,n):计算n点FFT。当length(x)>n时,截断x,不 然补零。
【例2-11】产生一种正弦信号频率为60Hz,并用fft函数 计算并绘出其幅度谱。
fftshift函数:调用方式如下 y=fftshift(x):假如x为向量,fftshift(x)直接将x旳左右两 部分互换;假如x为矩阵(多通道信号),将x旳左上、右 下和右上、左下四个部分两两互换。 【例2-12】产生一种正弦信号频率为60Hz,采样率为1000Hz, 用fftshift将其零频位置搬到频谱中心。
以上就是按时间抽取旳迅速傅立叶变换
实验二的应用FFT对信号进行频谱分析

实验二的应用FFT对信号进行频谱分析引言:频谱分析是通过将连续信号转换为离散信号,根据信号在频域上的强度分布来分析信号的频谱特性。
其中,FFT(Fast Fourier Transform,快速傅里叶变换)是一种常见的频谱分析算法,可以高效地计算离散信号的傅里叶变换。
实验目的:本实验旨在使用FFT算法来对一个信号进行频谱分析,从而了解FFT 的原理和应用。
实验器材:-计算机-MATLAB软件实验步骤:1.准备信号数据:首先,需要准备一个信号数据用于进行频谱分析。
可以通过MATLAB 自带的函数生成一个简单的信号数据,例如生成一个正弦信号:```Fs=1000;%采样频率T=1/Fs;%采样时间间隔L=1000;%信号长度t=(0:L-1)*T;%时间向量S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); % 生成信号,包含50Hz和120Hz的正弦波成分```其中,Fs为采样频率,T为采样时间间隔,L为信号长度,t为时间向量,S为生成的信号数据。
2.进行FFT计算:利用MATLAB提供的fft函数,对准备好的信号数据进行FFT计算,得到信号的频谱:```Y = fft(S); % 对信号数据进行FFT计算P2 = abs(Y/L); % 取FFT结果的模值,并归一化P1=P2(1:L/2+1);%取模值前一半P1(2:end-1) = 2*P1(2:end-1); % 对非直流分量进行倍频处理f=Fs*(0:(L/2))/L;%计算对应的频率```其中,Y为FFT计算的结果,P2为对应结果的模值,并进行归一化处理,P1为P2的前一半,f为对应的频率。
3.绘制频谱图:使用MATLAB的plot函数,将频率和对应的功率谱绘制成频谱图:```plot(f,P1)title('Single-Sided Amplitude Spectrum of S(t)')xlabel('f (Hz)')ylabel(',P1(f),')```实验结果与分析:上述实验步骤通过MATLAB实现了对一个信号的频谱分析并绘制成频谱图。
实验四应用快速傅里叶变换对信号进行频谱分析

实验四应用快速傅里叶变换对信号进行频谱分析引言:频谱分析是信号处理领域中的重要技术之一,可以用于研究信号的频率特性和频域内的信号成分。
傅里叶变换是一种能将时域信号转换为频域信号的数学工具,通过将信号分解成一系列频率分量来分析信号。
快速傅里叶变换(FFT)是一种高效的计算傅里叶变换的方法,尤其适合实时信号处理。
实验目的:1.理解傅里叶变换在频谱分析中的应用;2.掌握使用FFT对信号进行频谱分析的方法;3.实现频谱分析并得出相应的频谱图。
实验器材和材料:1.信号源(例如信号发生器);2.电脑或数字信号处理器(DSP);3.音频线或数据线连接信号源和电脑或DSP。
实验步骤:1.确定实验所需信号源的类型和参数,例如正弦信号、方波信号或任意信号;2.连接信号源和电脑或DSP,确保信号源输出的信号能够被电脑或DSP接收;3. 在电脑或DSP上选择合适的软件或编程语言环境,例如MATLAB、Python或C;4.编写程序或命令以控制信号源产生相应的信号,并将信号输入到电脑或DSP中;5.读取信号,并使用FFT对信号进行傅里叶变换;6.分析得到的频谱数据,绘制频谱图;7.对得到的频谱图进行解读和分析。
实验注意事项:1.在选择信号源和连接电脑或DSP时,注意信号源的输出范围和电脑或DSP的输入范围,避免信号超出范围导致损坏设备;2.根据实际需要选择合适的采样率和采样点数,以保证能够对信号进行充分的频谱分析;3.在进行FFT计算时,注意选择适当的窗函数和重叠率,以克服频谱分析中的泄漏效应。
实验结果与讨论:通过对信号进行频谱分析,我们可以得到信号的频率特性和频域内的成分信息。
根据得到的频谱图,我们可以分析信号的主要频率分量、功率谱密度以及可能存在的干扰或噪声。
通过对频谱图的解读和分析,可以帮助我们理解信号的特征和变化规律,为后续的信号处理和应用提供有价值的信息。
结论:本实验通过应用快速傅里叶变换对信号进行频谱分析,从而得到信号在频域内的成分信息并绘制出频谱图。
实验三用FFT对信号进行频谱分析和MATLAB程序

实验三用FFT对信号进行频谱分析和MATLAB程序实验三中使用FFT对信号进行频谱分析的目的是通过将时域信号转换为频域信号,来获取信号的频谱信息。
MATLAB提供了方便易用的函数来实现FFT。
首先,我们需要了解FFT的原理。
FFT(快速傅里叶变换)是一种快速计算离散傅里叶变换(DFT)的算法,用于将离散的时间域信号转换为连续的频域信号。
FFT算法的主要思想是将问题划分为多个规模较小的子问题,并利用DFT的对称性质进行递归计算。
FFT算法能够帮助我们高效地进行频谱分析。
下面是一个使用MATLAB进行频谱分析的示例程序:```matlab%生成一个10秒钟的正弦波信号,频率为1Hz,采样率为100Hzfs = 100; % 采样率t = 0:1/fs:10-1/fs; % 时间范围f=1;%正弦波频率x = sin(2*pi*f*t);%进行FFT计算N = length(x); % 信号长度X = fft(x); % FFT计算magX = abs(X)/N; % 幅值谱frequencies = (0:N-1)*(fs/N); % 频率范围%绘制频谱图figure;plot(frequencies, magX);xlabel('频率(Hz)');ylabel('振幅');title('信号频谱');```上述代码生成了一个10秒钟的正弦波信号,频率为1 Hz,采样率为100 Hz。
通过调用MATLAB的fft函数计算信号的FFT,然后计算每个频率分量的幅值谱,并绘制出信号频谱图。
在频谱图中,横轴表示频率,纵轴表示振幅。
该实验需要注意以下几点:1.信号的采样率要与信号中最高频率成一定比例,以避免采样率不足导致的伪频谱。
2.FFT计算结果是一个复数数组,我们一般只关注其幅值谱。
3.频率范围是0到采样率之间的频率。
实验三的报告可以包含以下内容:1.实验目的和背景介绍。
应用FFT实现信号频谱分析

应用FFT实现信号频谱分析一、快速傅里叶变换(FFT)原理快速傅里叶变换是一种将时域信号转换为频域信号的算法,它通过将信号分解为不同频率的正弦波的和,来实现频谱分析。
FFT算法是一种高效的计算DFT(离散傅里叶变换)的方法,它的时间复杂度为O(nlogn),在实际应用中得到广泛使用。
二、FFT算法FFT算法中最基本的思想是将DFT进行分解,将一个长度为N的信号分解成长度为N/2的两个互为逆序的子信号,然后对这两个子信号再进行类似的分解,直到分解成长度为1的信号。
在这一过程中,可以通过频谱折叠的性质,减少计算的复杂度,从而提高计算效率。
三、FFT实现在实际应用中,可以使用Matlab等软件来实现FFT算法。
以Matlab 为例,实现FFT可以分为以下几个步骤:1.读取信号并进行预处理,如去除直流分量、归一化等。
2. 对信号进行FFT变换,可以调用Matlab中的fft函数,得到频域信号。
3.计算频谱,可以通过对频域信号进行幅度谱计算,即取频域信号的模值。
4.可选地,可以对频谱进行平滑处理,以降低噪音干扰。
5.可选地,可以对频谱进行归一化处理,以便于分析和比较不同信号的频谱特性。
四、应用1.音频处理:通过分析音频信号的频谱,可以实现音频特性的提取,如频率、振幅、共振等。
2.图像处理:通过分析图像信号的频谱,可以实现图像特征的提取,如纹理、边缘等。
3.通信系统:通过分析信号的频谱,可以实现信号的调制解调、频谱分配等功能。
4.电力系统:通过分析电力信号的频谱,可以实现电力质量分析、故障检测等。
总结:应用FFT实现信号频谱分析是一种高效的信号处理方法,通过将时域信号转换为频域信号,可以实现对信号频谱特性的提取和分析。
在实际应用中,我们可以利用FFT算法和相应的软件工具,对信号进行频谱分析,以便于进一步的研究和应用。
应用FFT对信号进行频谱分析

应用FFT对信号进行频谱分析FFT(快速傅里叶变换)是一种将时域信号转换为频域信号的有效算法。
它通过将信号分解成一系列频率成分来实现频谱分析。
频谱分析是对信号中不同频率分量的定性和定量分析。
它在许多领域中具有广泛的应用,例如通信、音频处理、图像处理等。
FFT算法通过将信号从时域转换到频域,将连续信号转化为以频率为参量的离散信号,在频率域中对信号进行分析。
FFT算法的核心思想是将一个N点的复数序列转换为具有相同N点的复数序列,该序列表示信号的频谱。
FFT算法具有快速计算的特点,可以大大提高计算效率。
在实际应用中,首先需要将信号进行采样。
采样是指以一定的频率对信号进行测量。
采样定律表明,为了准确恢复信号的频谱,采样频率必须大于信号中最高频率的两倍。
在采样完成后,就可以对采样信号应用FFT算法进行频谱分析。
首先,将采样信号与一个窗函数进行截断。
窗函数是用于减小采样信号端点带来的频谱泄漏的一种方法。
然后,使用FFT算法将截断的采样信号转换为频谱。
FFT计算的结果是一个具有幅度和相位的复数序列。
通常,我们只关心幅度谱,表示信号在不同频率上的强度。
可以通过取幅度谱的绝对值来获得幅度。
在频域中,可以对信号的频率成分进行分析和处理。
频谱分析可以帮助我们了解信号中的频率成分、频率分布和频率特征。
例如,通过FFT分析音频信号,可以获得不同频率的音调、音乐节奏等信息。
除了频谱分析,FFT还可以应用于其他信号处理任务,如滤波、信号压缩等。
在滤波中,可以通过将信号和一个滤波器的频谱进行乘法来实现频域滤波。
在信号压缩中,可以通过保留频域信号的主要频率成分来减小信号的数据量。
总结起来,FFT是一种常用的信号处理方法,可以通过将信号从时域转换到频域进行频谱分析。
通过FFT,可以获得信号在不同频率上的强度信息,并进行进一步的信号处理和分析。
实验二_应用FFT对信号进行频谱分析
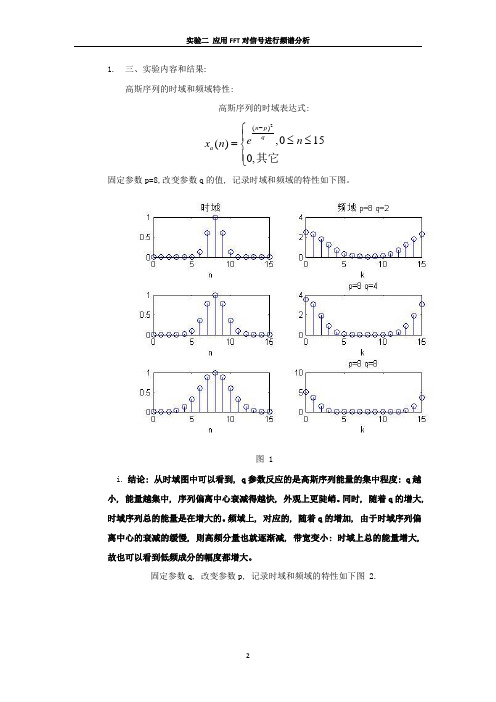
1. 三、实验内容和结果:高斯序列的时域和频域特性:高斯序列的时域表达式:2(),015()0,n p q a e n x n -⎧⎪≤≤=⎨⎪⎩其它固定参数p=8,改变参数q 的值, 记录时域和频域的特性如下图。
图 1i. 结论: 从时域图中可以看到, q 参数反应的是高斯序列能量的集中程度: q 越小, 能量越集中, 序列偏离中心衰减得越快, 外观上更陡峭。
同时, 随着q 的增大, 时域序列总的能量是在增大的。
频域上, 对应的, 随着q 的增加, 由于时域序列偏离中心的衰减的缓慢, 则高频分量也就逐渐减, 带宽变小: 时域上总的能量增大, 故也可以看到低频成分的幅度都增大。
固定参数q, 改变参数p, 记录时域和频域的特性如下图 2.图 22. 结论: p 是高斯序列的对称中心, p 的变化在时域表现为序列位置的变化。
由于选取的矩形窗函数一定, p 值过大时, 会带来高斯序列的截断。
并且随着p 的增大, 截断的越来越多。
对应地, 看频域上的变化: 截断的越多, 高频的成分也在增多, 以至发生谱间干扰, 泄露现象变得严重。
从图中可以看到, 在p=13时, 已经有混叠存在。
当p=14时, 混叠进一步加大, 泄露变得更明显。
衰减正弦序列的时域和幅频特性:sin(2),015()0,n b e fn n x n απ-⎧≤≤=⎨⎩其它改变参数f, 记录时域和幅频特性如下图3.图 33. 结论: 随着f 的增大, 时域上可以看到, 序列的变化明显快多了。
从幅度谱上看, 序列的高频分量逐渐增多, 低频分量逐渐减小, 以至于发生严重的频谱混叠。
当f 增大到一定的程度, 从图中可以看到, f=0.4375和f=0.5625时的幅度谱是非常相似的, 此时已经很难看出其幅度谱的区别。
三角序列的时域表达式和对应的时域和幅频特性如图 4:c 1,03()8,470,n n x n n n n +≤≤⎧⎪=-≤≤⎨⎪⎩其它图 4结论: 随着fft 取点数的增多, 能够看到的幅度谱的频率分量变得丰富, 得到的是高密度更高的谱, 也就是减轻了栅栏效应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
20090401310074 海南大学实验二 应用FFT 对信号进行频谱分析一、实验目的1、进一步加深DFT 算法原理和基本性质的理解(因为FFT 只是DFT 的一种快速算法, 所以FFT 的运算结果必然满足DFT 的基本性质)。
2、学习用FFT 对连续信号和时域离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT 。
二、实验原理i.模拟信号频率Ω和采样得到的数字信号频率ω的关系:/s T f ω=Ω=Ωii.DTFT 与对应的理想采样信号的频谱之间的对应关系为:|^()()jw a T X j X e ω=ΩΩ=即DTFT 与FT 的关系为:12()[()]j a r X e X j r T T Tωωπ∞=-∞=-∑就是说,只要知道了采样序列的频谱,就可以得到相应的连续信号的频谱。
(满足耐奎斯特采样定理)DFT 是对离散时间序列的频域采样,是对ZT 上单位圆上的均匀采样,或者是DTFT 上[0,2]π的等间距采样。
当满足频域的采样定理时,便可以由频域的采样值恢复ZT 或者是DTFT 。
所以能用DFT 对信号进行频谱分析。
当采样的点数足够时,便能用它的包络作为模拟信号的近似谱。
近似的过程中,可能会有混叠现象,泄露现象和栅栏效应这三种误差。
iv.离散傅立叶变换DFT :10()(),0,1,2...,1N nkN n X k x n W k N -===-∑[]11()()(),0,1,2...,1N nk Nn x n IDFT X k X k Wn N N--====-∑反变换与正变换的区别在于N W 变为1-N W ,并多了一个N 1的运算。
因为N W 和1-N W 对于推导按时间抽取的快速傅立叶变换算法并无实质性区别,因此借助FFT 来实现IFFT.三、实验内容和结果:1. 高斯序列的时域和频域特性:高斯序列的时域表达式:2(),015()0,n p q a e n x n -⎧⎪≤≤=⎨⎪⎩其它i. 固定参数p=8,改变参数q 的值,记录时域和频域的特性如下图。
图 1结论:从时域图中可以看到,q 参数反应的是高斯序列能量的集中程度:q 越小,能量越集中,序列偏离中心衰减得越快,外观上更陡峭。
同时,随着q 的增大,时域序列总的能量是在增大的。
频域上,对应的,随着q 的增加,由于时域序列偏离中心的衰减的缓慢,则高频分量也就逐渐减,带宽变小:时域上总的能量增大,故也可以看到低频成分的幅度都增大。
ii. 固定参数q ,改变参数p ,记录时域和频域的特性如下图 2.图 2结论:p 是高斯序列的对称中心,p 的变化在时域表现为序列位置的变化。
由于选取的矩形窗函数一定,p 值过大时,会带来高斯序列的截断。
并且随着p 的增大,截断的越来越多。
对应地,看频域上的变化:截断的越多,高频的成分也在增多,以至发生谱间干扰,泄露现象变得严重。
从图中可以看到,在p=13时,已经有混叠存在。
当p=14时,混叠进一步加大,泄露变得更明显。
2. 衰减正弦序列的时域和幅频特性:sin(2),015()0,n b e fn n x n απ-⎧≤≤=⎨⎩其它改变参数f ,记录时域和幅频特性如下图3.图 3结论:随着f 的增大,时域上可以看到,序列的变化明显快多了。
从幅度谱上看,序列的高频分量逐渐增多,低频分量逐渐减小,以至于发生严重的频谱混叠。
当f 增大到一定的程度,从图中可以看到,f=0.4375和f=0.5625时的幅度谱是非常相似的,此时已经很难看出其幅度谱的区别。
3. 三角序列的时域表达式和对应的时域和幅频特性如图 4:c 1,03()8,470,n n x n n n n +≤≤⎧⎪=-≤≤⎨⎪⎩其它图 4结论:随着fft 取点数的增多,能够看到的幅度谱的频率分量变得丰富,得到的是高密度更高的谱,也就是减轻了栅栏效应。
但是这种截断后补零的方法不能提高物理频率的分辨率。
因为截断已经使频谱变模糊,补零后使采样间隔减小,但得到的频谱采样的包络任然是已经变模糊的频谱,所以频谱的分辨率没有提高。
因此,要提到频率的分辨率,就必须对原始信号截取的长度加长,也就是增加采样时间0T 的长度。
另外,可以看到,三角序列的频谱几乎集中在低频区,旁瓣的幅度非常小。
4. 反三角序列的时域表达式和对应的时域和频域特性如图 5:4,03()3,470,d n n x n n n n -≤≤⎧⎪=-≤≤⎨⎪⎩其它图 5结论:同样,随着fft 取点数的增多,能够看到的幅度谱的频率分量变得丰富,得到的是高密度更高的谱,减轻了栅栏效应。
另外,可以看到,求8点的fft 时,三角序列和反三角序列的幅频特性是一样的。
原因在于:反三角序列()d x n 可以看成是三角序列x ()c n 的4点圆周移位,即x ()((4))()d c N N n x n R n =-,根据DFT 的圆周移位性质,则有4()()k d N c X k W X k =.由于=8N ,所以4k k W =-N (1),即()(1)()kd c X k X k =-,故()()d c X k X k =.不过,当补零之后,能够看到的频率成分增多,可以发现,反三角序列的频谱较宽,旁瓣的分量很多。
四、调用fft 函数计算ifft 的函数原理:11x()[(k)]()N nk Nk n ifft X X k WN--===∑变换上式有:1**01()[()]N nk N k x n X k W N -==∑于是,可以调用fft 模块,即**1()[(()]x n fft X k n=相应的程序清单如下:function [x]=myifft(y) N=length(y); y1=conj(y); x1=fft(y1); x=conj(x1)/N;验证:>> x=[1 2 3 5 7] x =1 2 3 5 7 >> y=fft(x,6) y =Columns 1 through 418.0000 -8.0000 + 1.7321i 0 - 5.1962i 4.0000Columns 5 through 60 + 5.1962i -8.0000 - 1.7321i >> a=myifft(y) a =1 2 3 5 7 0可以看到,a 只是在x 的末尾补了一个0,原因在于在y 是x 的6点fft,即在调用fft 的过程中有给x 的末尾补0的过程。
所以,在回调的过程中,补充的0还在。
五、思考题1、在N=8时, c ()x n 和d ()x n 的DFT 幅频特性会相同吗? 为什么? N=16呢? 在N=8时,c ()x n 和d ()x n 的幅频特性相同。
N=16时不同。
原因如下:当N=8时,}{c c 1,03()8,47()1,2,3,4,4,3,2,10,n n x n n n x n n +≤≤⎧⎪=-≤≤=⎨⎪⎩,即其它,}{d d 4,03()3,47,x n 4,3,2,1,1,2,3,40,n n x n n n n -≤≤⎧⎪=-≤≤⎨⎪⎩即()=其它,谱分析时,[]∑-===1)()()(N n knNWn x n x FFT k X ,其中NjN eW π2-=。
当N=8时,4πjN eW -=,此时∑∑-===7047)()()(kn j n kn Nen x Wn x k X π,代入,有:0123456744444444()12+3+4+4321j kj k j k j k j k j k j k j k c X k ee e e e e e eππππππππ--------=++++(1) 0123456744444444()43+2+1+1234j kj k j k j k j k j k j k j k d X k eeeeeeeeππππππππ--------=++++(2)调整顺序,有4567012344444444()1234+43+2+1j k j k j k j k j k j k j k j k d X k eeeeeeeeππππππππ--------=++++(3)(1)式和(3)式相对照,且21j k eπ±=,故有k k kd c X X ()=(-1)(),即有c k k d X X =()()。
故N=8时,x2(n)和x3(n)的幅频特性相同。
或者像在实验结论中运用DFT 圆周移位的性质来说明,不再重复。
而当N=16时,8πjNe W -=。
此时∑∑=-===7n 815)()()(kn j n knNen x Wn x k X π,易知)()(32k X k X ≠。
即N=16时,k c X ()和k d X ()的幅频特性不同。
2、实验中的信号序列c ()x n 和d ()x n ,在单位圆上的Z 变换频谱e j c X ω()和j d X ω(e )会相同吗?哪一个的低频分量多,说明原因?e j c X ω()和j d X ω(e )是不同的,三角序列e j c X ω()的低频分量更多。
可以这样解释: ()[]=()j j n n X e DTFT x x n e ωω+∞-=-∞=∑(n ),并且频谱的分布反映时域变化的快慢程度。
就是说,时域信号变化的越剧烈,频域的高频分量便较多,对应的,时域的信号较平缓,则频域的低频分量较多。
可以看到,在c ()x n 和d ()x n 的非零域内,c ()x n 和d ()x n 的变换程度是相当的,变化量都是1(增加1或者减小1)。
不过在零域和非零域的分界处,c ()x n 的变化量是1,而d ()x n 的变化量是4,要大得多,也就是变化的剧烈的多,就不奇怪d ()x n 的高频分量要多了。
3、对于一个有限长序列进行离散傅里叶变换(DFT )时,等价于将该序列周期延拓后进行傅里叶级数(DFS )展开。
因为DFS 也只是取一个周期来运算,所以FFT 在一定的条件下也可以用以分析周期信号序列。
如果实正信号sin(2),0.1fn f π=,用16点的FFT 来做DFS 运算,得到的频谱是信号的真实谱吗?不是的,该实正信号的周期N=10,只有当进行N 的整数倍的FFT 时,才能得到真实的频谱。
六、实验总结数字低频是0ω=,数字高频是ωπ=.当满足耐奎斯特采样定理: 2s c f f ≥时,c s 2/c f f ωππ=≤,当且仅当2s c f f =时, c ωπ=.也就是说,数字频率中的高频π对的是模拟频率1/2f s .当在DTFT 的e j X ω()的[0,2]π内采样N 个点时,第N/2条谱线就代表着数字最高频率π,也即代表着模拟频率1/2f s 。
