二重积分计算习题课
合集下载
二重积分的习题课(无解题过程)

Ik f ( x, y)d (k 1, 2, 3)
Dk
试比较I1, I2 , I3之大小。
y
2 D1 D2 1 D3
o
x
12
例2 设f (x, y)是有界闭域D : x2 y2 a2上的
连续函数,
试求极限
lim
a0
1
a
2
D
f (x, y)dxdy。
例3 把 f (x, y)d表为极坐标下的二次积分, D
2
D1
f
( x,
y)d ,
当f ( x, y) f ( x, y)时 当f ( x, y) f ( x, y)时
其中D1是D的右半区域 (奇零偶倍)
8
2、若D关于x轴对称
即当(x,y)∈D时,必有(x, y) ∈D,则
f ( x, y)d
D
0,
如D的边界是由直角坐标方 程:y =f (x) 给出,通常可从几何 意义去确定D的极坐标表示(图
形是重要的)或利用x=rcos, y=rsin 进行变换。
r 2( )
D
O
r 1( )
r x2( ) D
O
r 1( )
x
r ( )
oD
x
6
(3)坐标系的选取
D
D
1 [ f ( x, y) f ( y, x)]d
2D
(轮换对称)
(四)有关二重积分的一些证明题
中值定理、变上限积分、换元等
11
例1 设D1是以(0,1)为中心,边长为2的正方形,
D2, D3分别为D1的内切圆和外接圆 f ( x, y) (2 y x2 y2 )e x2 y2
Dk
试比较I1, I2 , I3之大小。
y
2 D1 D2 1 D3
o
x
12
例2 设f (x, y)是有界闭域D : x2 y2 a2上的
连续函数,
试求极限
lim
a0
1
a
2
D
f (x, y)dxdy。
例3 把 f (x, y)d表为极坐标下的二次积分, D
2
D1
f
( x,
y)d ,
当f ( x, y) f ( x, y)时 当f ( x, y) f ( x, y)时
其中D1是D的右半区域 (奇零偶倍)
8
2、若D关于x轴对称
即当(x,y)∈D时,必有(x, y) ∈D,则
f ( x, y)d
D
0,
如D的边界是由直角坐标方 程:y =f (x) 给出,通常可从几何 意义去确定D的极坐标表示(图
形是重要的)或利用x=rcos, y=rsin 进行变换。
r 2( )
D
O
r 1( )
r x2( ) D
O
r 1( )
x
r ( )
oD
x
6
(3)坐标系的选取
D
D
1 [ f ( x, y) f ( y, x)]d
2D
(轮换对称)
(四)有关二重积分的一些证明题
中值定理、变上限积分、换元等
11
例1 设D1是以(0,1)为中心,边长为2的正方形,
D2, D3分别为D1的内切圆和外接圆 f ( x, y) (2 y x2 y2 )e x2 y2
二重积分的计算习题课
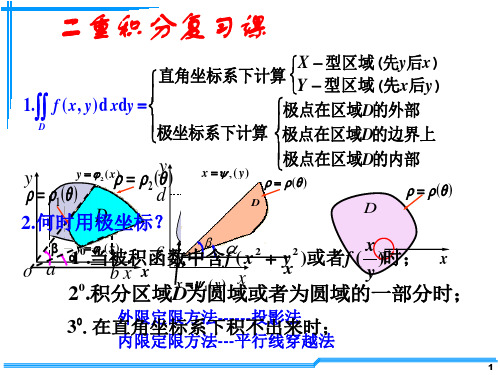
y= x
x x = ∫1 (− ) 1 dx y x
2
2
x
1
o
D
1
x=2
9 = ∫1 ( x − x)dx = . 4
2 3
2
x
型区域计算可以吗? 按Y-型区域计算可以吗 型区域计算可以吗
6
P155:15(2) P155:15(2)
∫∫
D
π 2 1 1− ρ 1 − x2 − y2 dxdy = ∫ 2 dθ ∫ ρ dρ 2 2 2 0 0 1+ x + y 1+ ρ
• 确定积分序
• 写出积分限
• 计算要简便 (充分利用对称性,几何意义和性质等 充分利用对称性, 充分利用对称性 几何意义和性质等)
2
P154:2(3) P154:2(3)
e x + y d σ , 其 中 D = {( x , y ) x + y ≤ 1 ∫∫
D
}.
1
0 ≤ x ≤1 解: X-型 D1: 型 x − 1 ≤ y ≤ 1 − x
12
6. (10分)计算二重积分 ∫∫ r 2 sin θ 1 − r 2 sin 2θ drdθ ,
D
π 其中D = ( r ,θ ) 0 ≤ r ≤ sec θ , 0 ≤ θ ≤ . 4
(10数学二 数学二) 数学二
7. (10分)计算二重积分 ∫∫ ( x + y )3 dxdy , 其中D由曲线x = 1 + y 2
二重积分复习课
1.∫∫ f ( x, y)d xdy = 极点在区域D的外部 D 极坐标系下计算 极点在区域D的边界上 极点在区域D的内部 y x =ψ ( y) y = ϕ ( x) y ρ = ρ2(θ) ρ = ρ(θ ) ρ = ρ(θ) d ρ=ρ (θ)
二重积分计算习题省公开课一等奖全国示范课微课金奖PPT课件

1
x2
2 (1
3
x2)2
]dx
0
0
0
3
4
2
(cos2
t
2
cos4
t)dt
0
3
4(1 2 3 1 ) 3
22 3422 2 第7页
解法2:(极坐标系下解)
在极坐标系中,闭区域D可表示为
D {(r, ) | 0 r 1, 0 2} 于是
V
2
d
1(2 r2 )rdr
于是
D
arctan
y x
d
4
x
2
rdrd
4 d 0
1
rdr
D
1 ( )2 1 (22 1) 3 2
24 2
64
第2页
[知识整理]
(1) 直角坐标系下二重积分计算 I、 x 型区域(先y后x)
V
f (x, y)dxdy
b
dx
2 (x) f (x, y)dy
D
a
1 ( x)
II、 y 型区域(先x后y)
1
0
e e1
D1
D2
-1
1x
第11页
【相关练习】
① sin x2 y2 D D (x, y) | 2 x2 y2 4 2
②
1 x2 y2 d D为圆域 x2 y2 4
D
③
D
1 1 x2
xy y2
d
D为半圆域
x2 y2 1, x 0
第12页
例4
把以下二重积分 f (x, y)dxdy 化为二次积分
P(x, y) (x 200)2 ( y 100)2 5000 现已知一周内甲商品销售量在150~200之间 改变,乙商品销售量在80~100之间改变, 试求销售这两种商品一周平均利润。
二重积分习题课(简)

1
错误点:大多同学都做错了, 错误点:大多同学都做错了,可能是正切函数的导数 不清楚了。 不清楚了。
11
目录 上页 下页 返回
第三次作业共有2 第三次作业共有2题 P13) 多元函数微分法 习题课二 (习题册第一本 P13) 填空 1. f ( x, y )在 ( x0 , y0 ) 处有极值,则 D 处有极值, (A) f x ( x0 , y0 ) = 0, f y ( x0 , y0 ) = 0 ) 内唯一驻点, (B) ( x0 , y0 ) 是D内唯一驻点,则必为最大值点;且 ) 内唯一驻点 则必为最大值点;
1 2 1 2 −0 ≤ x + y < × 2ε = ε 2 2 x2 + y2 xy
即
( x , y ) →(0,0)
lim
f ( x, y ) = 0 = f (0, 0).
处连续。 因此函数 f ( x, y ) 在点 (0, 0) 处连续。 错误作法: 取极限, 错误作法: 有的同学令 y = kx 取极限,得到
∆y →0
= lim
∆y ∆y
∆y →0
g (0, 0),
存在, 因为 f x (0, 0) 和 f y (0, 0) 存在,并且
∆x → 0
lim
∆x ∆x
不存在, 不存在,所以 g (0, 0) = 0.
错误:多数同学做得不好,从偏导数的形式得不到 错误:多数同学做得不好,
g (0, 0) = 0
x →0, y = kx →0
lim
f ( x, y ) = 0 = f (0, 0) 从而得到结论。 从而得到结论。
3
目录 上页 下页 返回
第二节:( :(习题册第一本 P4) (2)第二节:(习题册第一本 P4)四 四、设 f ( x, y ) = x − y g ( x, y ), 其中 g ( x, y ) 在点 (0, 0) 的邻域内连续。 应满足什么条件, 的邻域内连续。问:g ( x, y ) 应满足什么条件,使
二重积分的计算习题课

2 x 1
d y d x
0 x y 1 x
e x y d y
d x e x 1 1
)dx (e
1 0
(e e
D D1
2 x 1
x y x y 问: e d 4 e d ?
1 e )d x e . e
1
3
0
2 d
2 0
3!! 3 4 a 4a cos d 4a 4!! 2 4
4 4
4
4
P155:13(1)(3)
(1) dx
0 2a 2 ax x 2 0
把下列积分化为极坐标形式,并计算积分值.
2 2
( x y )d y
(3) dx 2 ( x 2 y 2 ) d y
• 确定积分序
积分域分块要少.
累次积分好算为妙(首先内积分易积). “平行线穿越法” “射线穿越法”
• 写出积分限
• 计算要简便 (充分利用对称性,几何意义和性质等)
2
P154:2(3)
x y e d , 其中D ( x , y ) x y 1 D
.
1
0 x 1 解: X-型 D1: x 1 y 1 x
V 2 x y d x y d
2 2
D
2
2
D
D
o x
y
d
0
2
1
0
2 2 ρd d ρd
0 0
2
1
y
x2 y2 1
1
o D
x
9
P155:10
计算曲面z x 2 2 y 2及z 6 2 x 2 y 2所围成的立体的体积.
d y d x
0 x y 1 x
e x y d y
d x e x 1 1
)dx (e
1 0
(e e
D D1
2 x 1
x y x y 问: e d 4 e d ?
1 e )d x e . e
1
3
0
2 d
2 0
3!! 3 4 a 4a cos d 4a 4!! 2 4
4 4
4
4
P155:13(1)(3)
(1) dx
0 2a 2 ax x 2 0
把下列积分化为极坐标形式,并计算积分值.
2 2
( x y )d y
(3) dx 2 ( x 2 y 2 ) d y
• 确定积分序
积分域分块要少.
累次积分好算为妙(首先内积分易积). “平行线穿越法” “射线穿越法”
• 写出积分限
• 计算要简便 (充分利用对称性,几何意义和性质等)
2
P154:2(3)
x y e d , 其中D ( x , y ) x y 1 D
.
1
0 x 1 解: X-型 D1: x 1 y 1 x
V 2 x y d x y d
2 2
D
2
2
D
D
o x
y
d
0
2
1
0
2 2 ρd d ρd
0 0
2
1
y
x2 y2 1
1
o D
x
9
P155:10
计算曲面z x 2 2 y 2及z 6 2 x 2 y 2所围成的立体的体积.
二重积分习题课

D
几何意义
设f ( x , y ) ≥ 0, ( x , y ) ∈ D , 则曲顶
为高和以M为高的 为高和以 柱体的体积介于以D为底 柱体的体积介于以 为底,以m为高和以 为高的 为底 两个平顶柱体体积之间. 两个平顶柱体体积之间
6
在闭区 性质6(二重积分中值定理) 性质6(二重积分中值定理) 设f (x, y)在闭区 6(二重积分中值定理 的面积, 上连续, 域D上连续 σ为D的面积 则在 上至少存在一点 上连续 为 的面积 则在D上至少存在一点 (ξ ,η ), 使得
ψ1( y)
f ( x, y)dx
c
O
x
先对x 后对y的二次积分 的二次积分. 先对 后对 的二次积分
11
三、在极坐标系中化二重积分为累次积分
(1)设f (x, y)在平面有界平面闭区域 上连续 设 在平面有界平面闭区域D上连续 在平面有界平面闭区域 上连续.
D = {( x, y)α ≤ θ ≤ β ,ϕ1(θ ) ≤ r ≤ ϕ2(θ )}
β
ϕ(θ )
f (r cosθ , r sinθ )rdr;
r = ϕ (θ )
D β θα
O
A
13
(3)设f (x, y)在平面有界平面闭区域 上连续 设 在平面有界平面闭区域D上连续 在平面有界平面闭区域 上连续.
D = {( x, y) 0 ≤ θ ≤ 2π,0 ≤ r ≤ ϕ(θ )}
其中函数 ϕ(θ )在区间[α, β ]上连续.
则
∫∫ f ( x, y)dxdy = 0, D
f (x, y)对x为偶函数 即 为偶函数, 对 为偶函数
f ( − x , y ) = f ( x , y ), ∀( x , y ) ∈ D ,
几何意义
设f ( x , y ) ≥ 0, ( x , y ) ∈ D , 则曲顶
为高和以M为高的 为高和以 柱体的体积介于以D为底 柱体的体积介于以 为底,以m为高和以 为高的 为底 两个平顶柱体体积之间. 两个平顶柱体体积之间
6
在闭区 性质6(二重积分中值定理) 性质6(二重积分中值定理) 设f (x, y)在闭区 6(二重积分中值定理 的面积, 上连续, 域D上连续 σ为D的面积 则在 上至少存在一点 上连续 为 的面积 则在D上至少存在一点 (ξ ,η ), 使得
ψ1( y)
f ( x, y)dx
c
O
x
先对x 后对y的二次积分 的二次积分. 先对 后对 的二次积分
11
三、在极坐标系中化二重积分为累次积分
(1)设f (x, y)在平面有界平面闭区域 上连续 设 在平面有界平面闭区域D上连续 在平面有界平面闭区域 上连续.
D = {( x, y)α ≤ θ ≤ β ,ϕ1(θ ) ≤ r ≤ ϕ2(θ )}
β
ϕ(θ )
f (r cosθ , r sinθ )rdr;
r = ϕ (θ )
D β θα
O
A
13
(3)设f (x, y)在平面有界平面闭区域 上连续 设 在平面有界平面闭区域D上连续 在平面有界平面闭区域 上连续.
D = {( x, y) 0 ≤ θ ≤ 2π,0 ≤ r ≤ ϕ(θ )}
其中函数 ϕ(θ )在区间[α, β ]上连续.
则
∫∫ f ( x, y)dxdy = 0, D
f (x, y)对x为偶函数 即 为偶函数, 对 为偶函数
f ( − x , y ) = f ( x , y ), ∀( x , y ) ∈ D ,
习题课 二重积分的计算共28页文档

▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
28
▪
26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
习题课 二重Leabharlann 分的计算11、获得的成功越大,就越令人高兴 。野心 是使人 勤奋的 原因, 节制使 人枯萎 。 12、不问收获,只问耕耘。如同种树 ,先有 根茎, 再有枝 叶,尔 后花实 ,好好 劳动, 不要想 太多, 那样只 会使人 胆孝懒 惰,因 为不实 践,甚 至不接 触社会 ,难道 你是野 人。(名 言网) 13、不怕,不悔(虽然只有四个字,但 常看常 新。 14、我在心里默默地为每一个人祝福 。我爱 自己, 我用清 洁与节 制来珍 惜我的 身体, 我用智 慧和知 识充实 我的头 脑。 15、这世上的一切都借希望而完成。 农夫不 会播下 一粒玉 米,如 果他不 曾希望 它长成 种籽; 单身汉 不会娶 妻,如 果他不 曾希望 有小孩 ;商人 或手艺 人不会 工作, 如果他 不曾希 望因此 而有收 益。-- 马钉路 德。
高数二重积分习题加答案
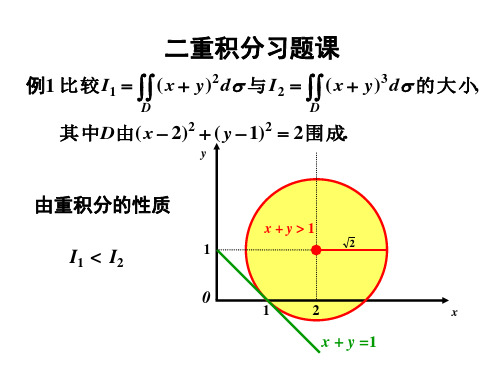
0 3a2 r 2
2a a2 r 2 d (a2 r 2 )
a0
6
3
4
2 3
6
2 3
a2.
练习题
交换下列二次积分的次序:
1 2y
3 3 y
1. 0 dy0 f ( x, y)dx 1 dy0 f ( x, y)dx;
1
1 1 x2
2. 0 dx x f ( x, y)dy;
计算下列二次积分:
D
D: x + y =1 , x – y = 1,x = 0 所围.
1y
先对 y 积分
y =1– x
x
I dx f ( x, y)dy
x
0
1x
y = x –1 –1
先对 x 积分
1y
D1
0
D2
x =1– y
I
D1 D2
y
dy f ( x, y)dx
1x
y
dy f ( x, y)dx
y x2 d D
( x2 y)d ( y x2 )d
D1 D2
D3
D3
D1
D2
1
dx
x2
( x2 y)dy
1
dx
1 ( y x2 )dy 11.
1 0
1
x2
15
例7 证明
b
dx
x
(x
y)n2
f
(
y)dy
1
b
(b
y)n1
f
( y)dy.
aa
n1 a
证
b
dx
x
D ( x)D ( y) D
2
其中a, b为常数, D {( x, y) 0 x, y 1}.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本要求:变换后定限简便,求积容易. 基本要求:变换后定限简便,求积容易.
∂( x, y) 1 2. J = . = ∂(u,v) ∂(u,v) ∂( x, y)
二、例题分析
(x2 + y2 )dσ D: 2x − x2 ≤ y ≤ 4− x2 例1 计算 ∫∫
D
解
积分区域由不等式给出 在不等式中取等号所得的曲线是两个半圆 但它们围不成区域 要使 2 x − x , 4 − x 都有意义 必须限制 x ∈ [0,2]
∫ f (r)rdr 0
4
D1 D
π
⇒ I = 4∫ dr ∫ rf (r )dθ + 4 ∫ dr
0
1
1
π
2
0
2
1
1 = π ∫ rf ( r )dr + ∫ (π − 4 arccos )rf ( r )dr r 0 1
arccos r
∫ rf (r )dθ 1
4
1 = π ∫ rf (r )dr − 4 ∫ rf (r ) arccos dr r 0 1
2
2
注
依题意, 依题意,要化为定积分首先应设法将二元函数 f ( x 2 + y 2 ) 化为一元函数 自然想到用极坐标 其次, 其次,若先对 r 后对 θ 不可进一步化为定积分 又想到换序 例8 连续, 设 f(x) 连续,证明
A
A A ∫∫ f (x − y)dxdy = −∫Af (t)[A− | t |]dt D:| x |≤ 2 ,| y |≤ 2 D
证一 令 u = x − y, v = x + y 则
v + u = 2x, v − u = 2 y
D → D′ : − A ≤ u + v ≤ A,− A ≤ v − u ≤ A ∂( x, y) 1 J= = ≠0 ∂ ( u, v ) 2
化累次积分后 外限是常数 内限是外层积分变量的函数或常数 极坐标系下勿忘
r
4。关于对称性 。
利用对称性来简化重积分的计算是十分有效的, 利用对称性来简化重积分的计算是十分有效的, 它与利用奇偶性来简化定积分的计算是一样的, 它与利用奇偶性来简化定积分的计算是一样的,不 过重积分的情况比较复杂,在运用对称性是要兼顾 过重积分的情况比较复杂,在运用对称性是要兼顾 被积分函数和积分区域两个方面, 被积分函数和积分区域两个方面,不可误用 对 I = f ( x , y )dxdy ∫∫ ①若D关于 x 轴对称 关于
D D
D2 D1
xyf ( x2 + y2 )dσ = 0 ∫∫
D
0
1
∫∫ xdσ = ∫∫ xdσ = ∫ xdx ∫ dy D D
−1 x
3
−x
3
2 =− 5
2 I =− 5
1
例6 设 f (x) 在 [0,1] 上连续
1 1
求
∫ dx∫ f (x) f ( y)dy 0 x
1 1
∫ f (x)dx = A 0
(2)当f (− x, y) = f ( x, y)时 I = 2∫∫ f ( x , y )dxdy
D1 = {( x, y)( x, y) ∈ D, x ≥ 0}
D1
当 (1) f(− x, y) = − f( x, y) I = 0 − 时 (2)当f (− x,− y) = f ( x, y)时 I = 2∫∫ f ( x, y)dxdy
π
0
0
π
2
0
π
= ∫ [sin
0
2
π
2
−x
=π −2
− sin x ]dx − ∫ [cos x − sin ]dx 2 2 0
π
D2 D1
∫∫ sin(x + y) dxdy= 2π D : 0 ≤ x ≤ π ,0 ≤ y ≤ π
D
x+ y =
π
2
( x + y)dxdy, D: x2 + y2 ≤ x + y 例4 计算 ∫∫
确定积分限时一定要保证下限小于上限
定限
看图定限 —穿越法定限 和不等式定限 穿越法定限 先选序, 先选序,后定限
①直角坐标系 ⅰ。先 y 后 x , 过任一x ∈ [ a , b ],作平行于 y 轴的直线 作平行于 穿过D的内部 穿过 的内部 内层积分的下限 从D的下边界曲线 y = ϕ1 ( x) 穿入 —内层积分的下限 的下边界曲线 内层积分的上限 从上边界曲线 y = ϕ2 ( x) 穿出 —内层积分的上限 ⅱ。先 x 后 y 过任一 y ∈[ c , d ] 作平行于 x 轴的直线
关于原点 ③若D关于原点对称 关于原点对称
D3 = {( x, y)∈ D, x ≥ 0, y ≥ 0}
D3
关于直线 ④若 D 关于直线
y=x
对称
∫∫ f ( x, y)dxdy= ∫∫ f ( y, x)dxdy D D
——称为关于积分变量的轮换对称性 称为关于积分变量的轮换对称性 是多元积分所独有的性质 ①、②、③简单地说就是 奇函数关于对称域的积分等于0, 奇函数关于对称域的积分等于 ,偶函数关 于对称域的积分等于对称的部分区域上积分的两 倍,完全类似于 对称区间上奇偶函数的定积分的 性质 简述为“ 对称, 奇偶” 简述为“你对称,我奇偶”
r1 (θ ) ——内下限 内下限 r2 (θ ) 具体可分为三种情况
⑴极点在D的外部 极点在 的外部
—内上限 内上限
α ≤ θ ≤ β , r1 (θ ) ≤ r ≤ r2 (θ ) 极点在D的边界上 ⑵极点在 的边界上 α ≤ θ ≤ β , r1 (θ ) ≤ r ≤ r2 (θ )
α, β 是边界在极点处的切线的极角 r (θ ) 绝大多数情况下为 绝大多数情况下为0 1 极点在D的内部 ⑶极点在 的内部 0 ≤ θ ≤ 2π ,0 ≤ r ≤ r (θ )
2 以原点为起点作射线 这射线和两个半圆相交
从
θ ∈ [ 0, ]
π
r = 2cos θ
穿入
从
r =2
穿出
尽管极点在D的边界上 尽管极点在 的边界上 但极角为 θ (∈ [0, ]) 2 的射线并不是从极点穿入 域D的极坐标表示为 的极坐标表示为 而不是
π
0 ≤θ ≤ π ,0 ≤ r ≤ 2 2 π
1
y
解 I = dx f ( x) f ( y)dy = dy f ( x) f ( y)dx
1 x
∫ ∫ 0 x
x
∫ ∫ 0 0
1
= ∫ dx∫ f ( x) f ( y)dy
1
0
0
1
⇒ 2I = ∫ dx∫ f ( x) f ( y)dy + ∫ dx∫ f ( x) f ( y)dy
0 0 0 x
12 12 1 解 D的边界 ( x − ) + ( y − ) = 的边界 2 2 2
极点在D的边界上 极点在 的边界上 圆周在(0, 的切线斜率为 圆周在 0)的切线斜率为 y′ = −1 π 3π 故 α = − ,β = 4 4 3π
D
I=
−
∫π (cosθ + sinθ )dθ ∫ r dr 0
∂x ∂( x, y) ∂u J (u, v ) = = ∂(u, v ) ∂y ∂u
∂x ∂v ≠ 0 ∂y ∂v
∫∫ f ( x, y)dxdy = ∫∫ f [ x(u, v), y(u, v)]J (u, v)dudv D D
1
注意
1.作什么变换主要取决 于积分区域 D 的形状, 的形状, 同时也兼顾被积函数 f ( x , y ) 的形式. 的形式.
2 2
因此D只能在 因此 只能在x=0 , x=2 之间 确定了积分区域后, 确定了积分区域后,再看被积函数结合积 分区域的特点, 分区域的特点,化成极坐标计算较为简单
显然 r 呢? 0 ≤θ ≤π 2 极点在D的边界上 的边界上, 极点在 的边界上,所以 0 ≤ r ≤ 2 那就错了 积分限如何确定 不能以为极点O在区域的边界上 不能以为极点 在区域的边界上 积分的下限为0 就误以为对 r 积分的下限为 的积分限, 定 r 的积分限,应先固定
D
1
1
1
1
= ∫ dx∫ f ( x) f ( y)dy = ∫ f ( x)dx∫ f ( y)dy
0 0 0 0
A = [∫ f ( x)dx] = A ⇒I = 2 0 f ( 连 例7 设 ( x)在 −∞,+∞)上 续 试将二重积分
2 2
1
2
I = ∫∫ f ( x2 + y2 )dσ
D
4 3π 4 4
4
cosθ + sinθ 2
π 1 4 4 4 = ∫ (cosθ + sinθ ) dθ = ∫ sin (θ + )dθ 3 −π 3 −π 4
4
3π 4
(和差化积) 和差化积)
π 4 4 = ∫ sin tdt = 2 30
D
π
( 令t = θ + ) 4
π
例5 计算 ∫∫ x[1+ yf ( x2 + y2 )]dσ D: y = x3, y = 1, x = −1 解 2 2 I = ∫∫ xdσ + ∫∫ xyf ( x + y )dσ
5 关于二重积分的换元法
f(x,y)在D上连续 变换 : x=x(u,v),y=y(u,v) 在 上连续 变换T: 平面的闭区域D 平面上的闭区域D 将 uov 平面上的闭区域 1 变成 xoy 平面的闭区域
(1) x=x(u,v),y=y(u,v)在D1上具有连续的一阶偏导数 ) 在 (2)在D1上 )
∂( x, y) 1 2. J = . = ∂(u,v) ∂(u,v) ∂( x, y)
二、例题分析
(x2 + y2 )dσ D: 2x − x2 ≤ y ≤ 4− x2 例1 计算 ∫∫
D
解
积分区域由不等式给出 在不等式中取等号所得的曲线是两个半圆 但它们围不成区域 要使 2 x − x , 4 − x 都有意义 必须限制 x ∈ [0,2]
∫ f (r)rdr 0
4
D1 D
π
⇒ I = 4∫ dr ∫ rf (r )dθ + 4 ∫ dr
0
1
1
π
2
0
2
1
1 = π ∫ rf ( r )dr + ∫ (π − 4 arccos )rf ( r )dr r 0 1
arccos r
∫ rf (r )dθ 1
4
1 = π ∫ rf (r )dr − 4 ∫ rf (r ) arccos dr r 0 1
2
2
注
依题意, 依题意,要化为定积分首先应设法将二元函数 f ( x 2 + y 2 ) 化为一元函数 自然想到用极坐标 其次, 其次,若先对 r 后对 θ 不可进一步化为定积分 又想到换序 例8 连续, 设 f(x) 连续,证明
A
A A ∫∫ f (x − y)dxdy = −∫Af (t)[A− | t |]dt D:| x |≤ 2 ,| y |≤ 2 D
证一 令 u = x − y, v = x + y 则
v + u = 2x, v − u = 2 y
D → D′ : − A ≤ u + v ≤ A,− A ≤ v − u ≤ A ∂( x, y) 1 J= = ≠0 ∂ ( u, v ) 2
化累次积分后 外限是常数 内限是外层积分变量的函数或常数 极坐标系下勿忘
r
4。关于对称性 。
利用对称性来简化重积分的计算是十分有效的, 利用对称性来简化重积分的计算是十分有效的, 它与利用奇偶性来简化定积分的计算是一样的, 它与利用奇偶性来简化定积分的计算是一样的,不 过重积分的情况比较复杂,在运用对称性是要兼顾 过重积分的情况比较复杂,在运用对称性是要兼顾 被积分函数和积分区域两个方面, 被积分函数和积分区域两个方面,不可误用 对 I = f ( x , y )dxdy ∫∫ ①若D关于 x 轴对称 关于
D D
D2 D1
xyf ( x2 + y2 )dσ = 0 ∫∫
D
0
1
∫∫ xdσ = ∫∫ xdσ = ∫ xdx ∫ dy D D
−1 x
3
−x
3
2 =− 5
2 I =− 5
1
例6 设 f (x) 在 [0,1] 上连续
1 1
求
∫ dx∫ f (x) f ( y)dy 0 x
1 1
∫ f (x)dx = A 0
(2)当f (− x, y) = f ( x, y)时 I = 2∫∫ f ( x , y )dxdy
D1 = {( x, y)( x, y) ∈ D, x ≥ 0}
D1
当 (1) f(− x, y) = − f( x, y) I = 0 − 时 (2)当f (− x,− y) = f ( x, y)时 I = 2∫∫ f ( x, y)dxdy
π
0
0
π
2
0
π
= ∫ [sin
0
2
π
2
−x
=π −2
− sin x ]dx − ∫ [cos x − sin ]dx 2 2 0
π
D2 D1
∫∫ sin(x + y) dxdy= 2π D : 0 ≤ x ≤ π ,0 ≤ y ≤ π
D
x+ y =
π
2
( x + y)dxdy, D: x2 + y2 ≤ x + y 例4 计算 ∫∫
确定积分限时一定要保证下限小于上限
定限
看图定限 —穿越法定限 和不等式定限 穿越法定限 先选序, 先选序,后定限
①直角坐标系 ⅰ。先 y 后 x , 过任一x ∈ [ a , b ],作平行于 y 轴的直线 作平行于 穿过D的内部 穿过 的内部 内层积分的下限 从D的下边界曲线 y = ϕ1 ( x) 穿入 —内层积分的下限 的下边界曲线 内层积分的上限 从上边界曲线 y = ϕ2 ( x) 穿出 —内层积分的上限 ⅱ。先 x 后 y 过任一 y ∈[ c , d ] 作平行于 x 轴的直线
关于原点 ③若D关于原点对称 关于原点对称
D3 = {( x, y)∈ D, x ≥ 0, y ≥ 0}
D3
关于直线 ④若 D 关于直线
y=x
对称
∫∫ f ( x, y)dxdy= ∫∫ f ( y, x)dxdy D D
——称为关于积分变量的轮换对称性 称为关于积分变量的轮换对称性 是多元积分所独有的性质 ①、②、③简单地说就是 奇函数关于对称域的积分等于0, 奇函数关于对称域的积分等于 ,偶函数关 于对称域的积分等于对称的部分区域上积分的两 倍,完全类似于 对称区间上奇偶函数的定积分的 性质 简述为“ 对称, 奇偶” 简述为“你对称,我奇偶”
r1 (θ ) ——内下限 内下限 r2 (θ ) 具体可分为三种情况
⑴极点在D的外部 极点在 的外部
—内上限 内上限
α ≤ θ ≤ β , r1 (θ ) ≤ r ≤ r2 (θ ) 极点在D的边界上 ⑵极点在 的边界上 α ≤ θ ≤ β , r1 (θ ) ≤ r ≤ r2 (θ )
α, β 是边界在极点处的切线的极角 r (θ ) 绝大多数情况下为 绝大多数情况下为0 1 极点在D的内部 ⑶极点在 的内部 0 ≤ θ ≤ 2π ,0 ≤ r ≤ r (θ )
2 以原点为起点作射线 这射线和两个半圆相交
从
θ ∈ [ 0, ]
π
r = 2cos θ
穿入
从
r =2
穿出
尽管极点在D的边界上 尽管极点在 的边界上 但极角为 θ (∈ [0, ]) 2 的射线并不是从极点穿入 域D的极坐标表示为 的极坐标表示为 而不是
π
0 ≤θ ≤ π ,0 ≤ r ≤ 2 2 π
1
y
解 I = dx f ( x) f ( y)dy = dy f ( x) f ( y)dx
1 x
∫ ∫ 0 x
x
∫ ∫ 0 0
1
= ∫ dx∫ f ( x) f ( y)dy
1
0
0
1
⇒ 2I = ∫ dx∫ f ( x) f ( y)dy + ∫ dx∫ f ( x) f ( y)dy
0 0 0 x
12 12 1 解 D的边界 ( x − ) + ( y − ) = 的边界 2 2 2
极点在D的边界上 极点在 的边界上 圆周在(0, 的切线斜率为 圆周在 0)的切线斜率为 y′ = −1 π 3π 故 α = − ,β = 4 4 3π
D
I=
−
∫π (cosθ + sinθ )dθ ∫ r dr 0
∂x ∂( x, y) ∂u J (u, v ) = = ∂(u, v ) ∂y ∂u
∂x ∂v ≠ 0 ∂y ∂v
∫∫ f ( x, y)dxdy = ∫∫ f [ x(u, v), y(u, v)]J (u, v)dudv D D
1
注意
1.作什么变换主要取决 于积分区域 D 的形状, 的形状, 同时也兼顾被积函数 f ( x , y ) 的形式. 的形式.
2 2
因此D只能在 因此 只能在x=0 , x=2 之间 确定了积分区域后, 确定了积分区域后,再看被积函数结合积 分区域的特点, 分区域的特点,化成极坐标计算较为简单
显然 r 呢? 0 ≤θ ≤π 2 极点在D的边界上 的边界上, 极点在 的边界上,所以 0 ≤ r ≤ 2 那就错了 积分限如何确定 不能以为极点O在区域的边界上 不能以为极点 在区域的边界上 积分的下限为0 就误以为对 r 积分的下限为 的积分限, 定 r 的积分限,应先固定
D
1
1
1
1
= ∫ dx∫ f ( x) f ( y)dy = ∫ f ( x)dx∫ f ( y)dy
0 0 0 0
A = [∫ f ( x)dx] = A ⇒I = 2 0 f ( 连 例7 设 ( x)在 −∞,+∞)上 续 试将二重积分
2 2
1
2
I = ∫∫ f ( x2 + y2 )dσ
D
4 3π 4 4
4
cosθ + sinθ 2
π 1 4 4 4 = ∫ (cosθ + sinθ ) dθ = ∫ sin (θ + )dθ 3 −π 3 −π 4
4
3π 4
(和差化积) 和差化积)
π 4 4 = ∫ sin tdt = 2 30
D
π
( 令t = θ + ) 4
π
例5 计算 ∫∫ x[1+ yf ( x2 + y2 )]dσ D: y = x3, y = 1, x = −1 解 2 2 I = ∫∫ xdσ + ∫∫ xyf ( x + y )dσ
5 关于二重积分的换元法
f(x,y)在D上连续 变换 : x=x(u,v),y=y(u,v) 在 上连续 变换T: 平面的闭区域D 平面上的闭区域D 将 uov 平面上的闭区域 1 变成 xoy 平面的闭区域
(1) x=x(u,v),y=y(u,v)在D1上具有连续的一阶偏导数 ) 在 (2)在D1上 )
