概率论期末复习2015-2016
华中科技大学概率论复习资料

多个事件的独立性 P(AB)=P(A)P(B);P(BC)=P(B)P(C);P(CA)=P(C)P(A) 并且同时满足 P(ABC)=P(A)P(B)P(C),那么 A、B、C 相互独立。 对于 n 个事件类似。
P(A)= (1 ) ( 2 ) ( m ) = P(1 ) P( 2 ) P( m )
·密度函数具有下面 2 个性质: 1°
x
f ( x) 0 。
2°
f ( x)dx 1
。
四年生活,为华科人打造的大学生成长服务平台。
( 3)离散与连续型随机变量 的关系
· P ( X x ) P ( x X x dx ) f ( x ) dx 积分元 f ( x ) dx 在连续型随机变量理论中所起的作用与 P( X xk ) pk 在离散型随机变量理 论中所起的作用相类似。
随机变量 X 服从参数为 p 的几何分布,记为 G(p)。 设随机变量 X 的值只落在[a F (b) F (a ) 可以得到 X 落入区间 ( a , b ] 的概率。 分布函数 F ( x ) 表示随机变量
f ( x) 在[a,b]上为常数
落入区间(– ∞,x]内的概率。 ·分布函数具有如下性质: 1° 0 F ( x ) 1, x ; 2° F ( x ) 是单调不减的函数,即 x1 x 2 时,有 F ( x1) F ( x 2 ) ; 3° 4° 5° ( 4)分布函数 ( 5)八大分布 泊松分布 超几何分布
A Bi
i 1 n
第二章 随机变量及其分布
( 1)离散型随机变量的分布律 。 ·设离散型随机变量 X 的可能取值为 Xk(k=1,2,…) 且取各个值的概率,即事件 (X=Xk) 的概率为
概率论期末试题及答案

概率论期末试题及答案一、选择题(每题2分,共20分)1. 随机事件A的概率为P(A),则其对立事件的概率为:A. P(A) + 1B. 1 - P(A)C. P(A) - 1D. P(A) / 22. 某校有男女生比例为3:2,随机抽取1名学生,该学生是男生的概率为:A. 1/5B. 3/5C. 2/5D. 5/73. 抛一枚均匀硬币两次,至少出现一次正面的概率是:A. 1/2B. 1/4C. 3/4D. 5/84. 设随机变量X服从二项分布B(n, p),若n=15,p=0.4,则P(X=7)是:A. C^7_15 * 0.4^7 * 0.6^8B. C^7_15 * 0.6^7 * 0.4^8C. C^7_15 * 0.4^15D. C^8_15 * 0.4^7 * 0.6^85. 若随机变量Y服从泊松分布,λ=2,则P(Y=1)是:A. e^(-2) * 2B. e^(-2) * 2^2C. e^(-2) * 2^1D. e^(-2) * 2^06. 设随机变量Z服从标准正态分布,则P(Z ≤ 0)是:A. 0.5B. 0.25C. 0.75D. 0.337. 若两个事件A和B相互独立,P(A)=0.6,P(B)=0.7,则P(A∩B)是:A. 0.42B. 0.35C. 0.6D. 0.78. 随机变量X服从均匀分布U(0, 4),则E(X)是:A. 2B. 4C. 0D. 19. 设随机变量X和Y的协方差Cov(X, Y)=-2,则X和Y:A. 正相关B. 负相关C. 独立D. 不相关10. 若随机变量X服从指数分布,λ=0.5,则P(X > 1)是:A. e^(-0.5)B. e^(-1)C. 1 - e^(-0.5)D. 2 - e^(-1)二、填空题(每题3分,共30分)11. 若随机变量X服从参数为θ的概率分布,且P(X=θ)=0.3,P(X=2θ)=0.4,则P(X=3θ)=________。
概率论与数理统计期末考试复习资料
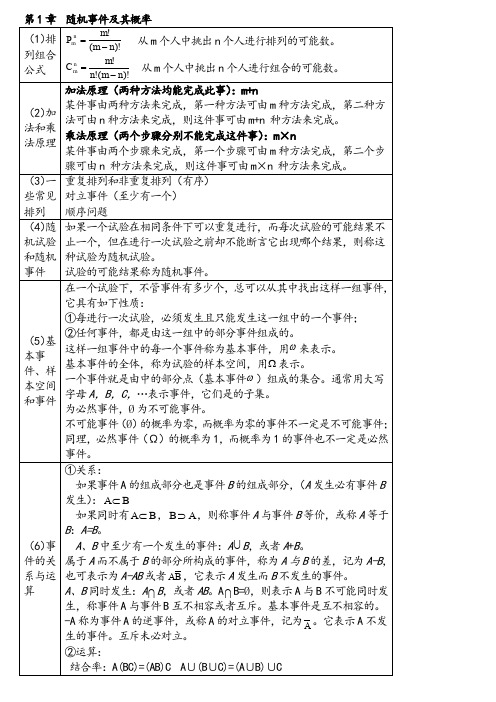
F (x) x f (x)dx ,
则称 X 为连续型随机变量。f (x) 称为 X 的概率密度函数或密度函 数,简称概率密度。 密度函数具有下面 4 个性质: 1° f (x) 0 。
2° f (x)dx 1。
X
| x1, x2,, xk, 。
P( X xk) p1, p2,, pk,
显然分布律应满足下列条件:
(2)连 续型随 机变量 的分布 密度
(3)离 散与连 续型随 机变量 的关系 (4)分 布函数
(5)八 大分布
(1) pk 0 ,k 1,2,, (2) pk 1。 k 1
ba
f
(x)
b
1
a
,
0,
a≤x≤b
其他,
则称随机变量 X 在[a,b]上服从均匀分布,记为 X~U(a,b)。
分布函数为
0,
xa, ba
x<a, a≤x≤b
x
F (x) f (x)dx
1,
x>b。
当 a≤x1<x2≤b 时,X 落在区间(x1, x2 )内的概率为
P( A)
条件概
下,事件 B 发生的条件概率,记为P(B / A) P(AB) 。
P( A)
率
条件概率是概率的一种,所有概率的性质都适合于条件概率。
例如 P(Ω/B)=1P( B /A)=1-P(B/A)
(13) 乘法公式:P(AB) P(A)P(B / A)
乘法公 更一般地,对事件 A1,A2,…An,若 P(A1A2…An-1)>0,则有
概率论期末复习题库答案

概率论期末复习题库答案一、选择题1. 某随机事件的概率为0.6,那么它的对立事件的概率为:A. 0.4B. 0.5C. 0.6D. 无法确定答案:A2. 假设事件A和事件B是互斥的,且P(A) = 0.3,P(B) = 0.2,那么P(A∪B)等于:A. 0.5B. 0.4C. 0.3D. 0.2答案:B3. 如果一个骰子连续投掷两次,求至少出现一次6的概率:A. 1/6B. 5/6C. 2/3D. 1/3答案:B二、填空题1. 随机变量X服从标准正态分布,那么P(X ≤ 0) = _______。
答案:0.52. 如果随机变量X的期望值为2,方差为4,那么P(X = 4) =_______。
答案:无法直接给出,需要更多信息3. 事件A发生的概率为0.3,事件B发生的概率为0.4,且P(A∩B) = 0.1,那么事件A和B是________。
答案:既不互斥也不独立三、简答题1. 什么是条件概率?请给出条件概率的公式。
答案:条件概率是指在已知一个事件已经发生的条件下,另一个事件发生的概率。
条件概率的公式为:\[ P(A|B) = \frac{P(A \cap B)}{P(B)} \]其中,\( P(A|B) \) 是在事件B发生的条件下事件A发生的条件概率,\( P(A \cap B) \) 是事件A和事件B同时发生的概率,\( P(B) \) 是事件B发生的概率。
2. 什么是大数定律?请简要说明其含义。
答案:大数定律是概率论中的一个基本概念,它描述了随机事件在大量重复试验中表现出的稳定性。
具体来说,大数定律指出,随着试验次数的增加,随机事件的相对频率会越来越接近其真实概率。
四、计算题1. 假设有一个装有红球和蓝球的袋子,其中红球有5个,蓝球有3个。
如果从袋子中随机抽取一个球,求抽到红球的概率。
答案:抽到红球的概率 \( P(\text{红球}) \) 可以通过以下公式计算:\[ P(\text{红球}) = \frac{\text{红球的数量}}{\text{总球数}} = \frac{5}{5+3} = \frac{5}{8} \]2. 假设随机变量X服从参数为λ的泊松分布,求X=2的概率。
概率总复习 期末考试必备 考题及答案

P( A B )P( B )
j 1 j j
n
, i 1, 2, , n.
称为贝叶斯公式.
事件的相互独立性
(1)两事件相互独立
设 A, B 是两事件 , 如果满足等式 P ( AB ) P ( A) P ( B ). 则称事件 A, B 相互独立, 简称 A, B 独立.
说明 事件 A 与 B 相互独立是指事件 A 出现的 概率与事件 B 是否出现无关.
为在事件 B 发生的条件下事件 A 发生的条件概率.
(2) 条件概率的性质
1 非负性 : P( A B) ≥ 0;
0
2 正则性 : P( B) 1, P( B) 0;
0
30 P ( A1 A2 B) P ( A1 B) P ( A2 B) P ( A1 A2 B);
4 0 P (列可加性 : 设 B1 , B2 , 是两两不相容的事件, 则有
P Bi A P ( Bi A). i 1 i 1
乘法公式
设 P ( A) 0, 则有 P ( AB) P ( B A) P ( A).
设 A, B, C 为事件, 且 P ( AB) 0, 则有
n重伯努利概型的计算公式 设n重伯努利试验中,事件A发生的概率为 p,则A出现k次的概率为:
k P( A) Cn pk (1 p)nk
随机变量
定义 设 E 是随机试验, 其样本空间为 {e }. 若对于每一个 e , 都有一个实数 X (e ) 与之 对应 , 这样得到定义在上的一个单值实值函 数 X (e ), 称X (e )为随机变量 .
说明 全概率公式的主要用处在于它可以将 一个复杂事件的概率计算问题分解为若干个简单 事件的概率计算问题, 最后应用概率的可加性求出 最终结果.
概率论期末复习

(6)两个相互独立的正态分布,期望未知,对方差的检验(F检验)
15)
根据双边检验和单边检验,给出的显著性水平,找出分位点,确定拒绝域。
16)
看检验统计量是否在拒绝域内判断原假设是否正确。
[10]
原假设为“=”时,为双边检验,其他为单边检验。
[2]
作图步骤:
(1)找出最小值和最大值;
(2)将选定区间分为k个小区间;
(3)算出每个区间的频率,在区间上做高度为频率的小矩形。
[3]
1)
样本(X1,X2,...,Xn)的不含有未知参数的连续函数g(X1,X2,...,Xn)称为统计量。(统计量是随机变量)
2)
样本均值
样本方差
样本标准差(标准偏差)
内容:参数估计、假设检验(重要)
目的:对总体特征作出推断
2.样本分析
[1]
总体——研究对象全体元素组成的集合。研究的对象的某个(或某些)数量指标的全体,它是一个随机变量(或多维随机变量),记为X。X的分布函数和数字特征称为总体的分布函数和数字特征。
个体——组成总体的每一个元素即总体的每个数量指标,可看作随机变量X的某个取值,可记作Xi
8)
定义:设 和 是θ的无偏估计量,且 ,则称 比 有效。
9)
定义:设 是θ的无偏估计量,当n(样本容量)→∞时, 收敛于θ。
[7]
10)
选取枢轴量
由分位点定义建立不等式
解出不等式
11)
定义:
正态分布的枢轴量选取:
(1)样本均值的置信区间(已知σ)
(2)样本均值的置信区间(未知σ)
(3)样本方差的置信区间(μ未知)
概率论期末考试题及答案
概率论期末考试题及答案一、选择题(每题4分,共40分)1. 随机变量X服从标准正态分布,则P(-1 < X < 1)的值是()。
A. 0.6827B. 0.9545C. 0.9772D. 0.5000答案:B2. 设随机变量X服从参数为λ的泊松分布,那么E(X)等于()。
A. λB. λ^2C. 1/λD. 1答案:A3. 两个相互独立的随机事件A和B,P(A)=0.3,P(B)=0.5,则P(A∪B)等于()。
A. 0.2B. 0.5C. 0.8D. 0.6答案:D4. 设随机变量X服从二项分布B(n,p),则X的方差Var(X)等于()。
A. npB. np(1-p)C. n(1-p)D. p(1-p)答案:B5. 随机变量X服从均匀分布U(a,b),则其概率密度函数f(x)为()。
A. 1/(b-a), a≤x≤bB. 1/(b-a), x≤a 或x≥bC. 1/(b-a), x<a 或 x>bD. 1/(b-a), x<b答案:A6. 设随机变量X服从正态分布N(μ,σ^2),则X的期望E(X)等于()。
A. σB. μC. 0D. 1答案:B7. 设随机变量X服从正态分布N(μ,σ^2),则X的均值μ和方差σ^2的关系是()。
A. μ = σ^2B. μ^2 = σ^2C. μ = 0D. μ ≠ σ^2答案:D8. 随机变量X服从二项分布B(n,p),当n趋于无穷大时,X的分布趋近于()。
A. 泊松分布B. 正态分布C. 均匀分布D. 指数分布答案:B9. 设随机变量X服从指数分布,其概率密度函数为f(x) = λe^(-λx) (x≥0),则其均值E(X)等于()。
A. λB. 1/λC. 0D. 1答案:B10. 随机变量X和Y相互独立,且X和Y都服从标准正态分布N(0,1),则Z=X+Y服从()。
A. N(0,2)B. N(0,1)C. N(2,1)D. N(1,2)答案:A二、填空题(每题4分,共20分)1. 设随机变量X服从二项分布B(10,0.5),则P(X=5) = _______。
15概率统计期末复习要点.doc
概率统计期末复习要点第十六章1、利用古典概型求解概率。
书p323 页例3; p325~326 页2、6补1:掷两颗骰子,已知两颗骰子点数之和为7,求其中有一颗为1点的概率。
补2:在A箱中,有8台录像机,其中3台是高档品牌;在B箱中,有5台录像机,其中2台是高档品牌。
现从两箱中各取一台录像机,求:(1)取出的两台都不是高档品牌的概率;(2)取出的两台只有一台是高档品牌的概率;(3)取出的两台有一台是高档品牌,求此台是从A箱中取出的概率。
2、古典概型中的两类典型问题:箱中摸球、分球入箱。
326页10、12、ppt中补充的箱中摸球问题:将n只不同的球随机地放入N (n<N)个盒子中去,试求每个盒子恰有一只球的概率(设盒子的容量不限)。
3、有关事件的运算。
332页,3.4、两事件和的概率公式。
A,3互不相容时公式;P332-334公式(1) (3) (5) 若A, 3相互独立时,公式又如何?(P(AB) = P(A)P(3))补:设P(3)=0.5, P(AUB) = 0.8,若(1)A、3互不相容,则P(A)是多少?(2)A、B相互独立,则P(A)是多少?5、条件概率的计算公式。
书355页,3, 66、两事件乘积概率的公式,两事件独立的相关应用。
书338页例3, 343页,2、3一盒子装有4只产品,其中有3只一等品,1只二等品。
从中取产品两次,每次任取一只,作不放回抽样。
求已知第一次取得的是一等品,第二次取到的也是一等品的概率。
7、在一次试验中,事件A发生的概率为p,现进行"次独立试验,则A至少发生一次的概率是什么,而事件A至多发生一次的概率是什么。
8、全概率公式、贝叶斯公式。
书352页,1;书355页,7, 8, ppt 5-6 p349、相容、互斥、独立三者关系,PPT上结论:若A、B互斥,且P(A)>0, P(B)>0,则A与B不独立.若A与B独立,且P(A)>0,P(B)>0,则A、B不互斥.独立、互斥的区别和联系:设A、3为互斥事件,且P(A)>0,P(B)>0,下面四个结论中,正确的是:A.P(5|A)>0B. P(A|5)=P(A)C. P(A|B)=OD. P(AB)=P(A)P(B)设A、3为独立事件,且P(A)>0,P(B)>0,下面四个结论中,不正确的是:l.P(B|A)>0 2. P(A|5)=P(A)3. P(A|5)=04. P(AB)=P(A)P(B)第十七章:1、离散型随机变量的概率分布性质。
概率论期末考试题及答案
概率论期末考试题及答案一、选择题(每题4分,共20分)1. 以下哪个事件是必然事件?A. 抛一枚硬币,正面朝上B. 抛一枚硬币,反面朝上C. 抛一枚硬币,正面或反面朝上D. 抛一枚硬币,硬币立起来答案:C2. 假设随机变量X服从正态分布N(μ, σ^2),则以下哪个选项是正确的?A. μ是X的中位数B. μ是X的众数C. μ是X的期望值D. μ是X的方差答案:C3. 假设随机变量X和Y独立,以下哪个选项是正确的?A. P(X=x, Y=y) = P(X=x)P(Y=y)B. P(X=x, Y=y) = P(X=x) + P(Y=y)C. P(X=x, Y=y) = P(X=x) - P(Y=y)D. P(X=x, Y=y) = P(X=x) / P(Y=y)答案:A4. 假设随机变量X服从二项分布B(n, p),以下哪个选项是正确的?A. E(X) = npB. E(X) = n/2C. Var(X) = np(1-p)D. Var(X) = np答案:A5. 假设随机变量X服从泊松分布P(λ),以下哪个选项是正确的?A. E(X) = λB. E(X) = λ^2C. Var(X) = λ^2D. Var(X) = λ答案:A二、填空题(每题5分,共20分)6. 如果随机变量X服从均匀分布U(a, b),则其概率密度函数为:f(x) = ________,其中x∈(a, b)。
答案:1/(b-a)7. 假设随机变量X服从正态分布N(μ, σ^2),其标准正态分布的累积分布函数记为Φ(z),则P(X ≤ x) = Φ((x - μ) / σ)。
答案:Φ((x - μ) / σ)8. 假设随机变量X服从指数分布Exp(λ),其概率密度函数为:f(x) = ________,其中x≥0。
答案:λe^(-λx)9. 假设随机变量X服从几何分布Geo(p),其概率质量函数为:P(X = k) = ________,其中k = 1, 2, 3, ...答案:(1-p)^(k-1)p三、计算题(每题15分,共30分)10. 假设随机变量X服从正态分布N(0, 1),求P(-1 ≤ X ≤ 1)。
2015-2016学年第一学期概率论与数理统计阶段测验(一)试卷及答案
因此,有
P(C ) = P(A1 ∪ A1B2 A3 ∪ A1B2 A3 B4 A5 ∪ A1B2 A3 B4 A5 B6 A7 ) = P( A1 ) + P (A1B2 A3 ) + P(A1B2 A3 B4 A5 ) + P(A1B2 A3 B4 A5 B6 A7 ) 3 7 6 3 7 6 5 4 3 7 6 5 4 3 2 3 + ⋅ ⋅ + ⋅ ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ 10 10 9 8 10 9 8 7 6 10 9 8 7 6 5 4 7 = = 0.58333333 . 12 =
1 1 + +0−0−0−0+0 12 16 7 = = 0.145833333333 . 48 =
⑵ 由于 {随机事件 A,B,C 都不发生 } = A B C = A ∪ B ∪ C ,
所以,
P{随机事件 A,B,C 都不发生 } = P A ∪ B ∪ C
= 1 − P( A ∪ B ∪ C ) = 1 − P( A) − P(B ) − P (C ) + P ( AB ) + P (BC ) + P( AC ) − P( ABC )
⑵ 将 5 颗骰子分成两组,一组 2 颗,一组 3 颗,有分法 C52 种.再将 6 个点数取 2 个, 分别分给两个组,有 P62 不同的分法.因此随机事件 B 含有 C52 ⋅ P62 个样本点.故
P (B ) =
C52 ⋅ P62 25 = = 0.03858024691 . 65 648
二. (本题满分 8 分) 设随机事件 A 、 B 、 C 满足: P ( A) = P (B ) = P (C ) =
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P ( A发 生 不 多 于 k次 ) p0 p1 pk P ( A发 生 不 少 于 k次 ) p k p k ( 8 ) 多 个 独 立 事 件 的 和设 :A1 , , An 相 互 独 立 , 则 他 们 至 少 发 生 一 个概 的率 是 P ( A1 An ) 1 P ( A1 An ) 1 P ( A1 An ) 1 [1 P ( A1 )][1 P ( A2 )][1 P(An )]
x2 pk
k
xn pn
(0 k n).
二项分布: P{ X k} C n p k (1 p ) n k ,
泊松分布: P{ X k}
k
k!
e , k 0,1,2, 其中 0 是常数。
(2)X为连续型随机变量,其中f (x)称为X的概率密度
2 2 y 1 2 y 1 2 2 y 1 1; 2
d y 1 1 ( y 1 ) / 4 1 1 1 故f ( y ) 2 1 2 e e ( y 1 ) / 4 dy 2 2 2( y 1) 2 ( y 1) 2
求 (1) 常 数 k; ( 2) 分 布 函 数 F ( x ); ( 3) P{0.3 X 0.7}; ( 4 )E ( X ), D( X )
( 5 )Y X 2求Y 的分布密度fY ( y) 1 (1) f ( x )dx 1 kxdx 1 k 2 解:
1、事件(随机变量)间的关系
AB A B; A B AB; A A; A B AB; A A S
A B A AB A AB AB
(互斥分解)
A B S , A B , A与B对立, 即A与B构成S的一个划分
AB : A与B互 不 相 容 AB , P ( AB ) 0, P ( A B ) P ( A) P ( B ) (注 意A 与B ; A 与B 等 不 一 定 也 互 不 相 容 ) P ( AB ) P ( A) P ( B ) : A, B相 互 独 立 (注 意A 与B ; A 与B 等 相 互 独 立 )
( 1 ) 求 他 最 后 可 能 迟 到概 的率 。 ( 2 ) 结 果 他 迟 到 了 , 求坐 是轮 船 来 的 概 率 。
(1) p P ( B ) 0.3 0.25 0.2 0.3 0.1 0.1 0.145 P ( A2 ) P ( B | A2 ) 0.2 0.3 0.06 ( 2) P ( A2 | B ) 0.41 P( B) 0.145 0.145
练习题
1.设 事 件 A, B互 不 相 容 P ( A) 0.6, P ( B ) 0.7, 则P ( A B )
2.设 事 件 A, B独 立, P ( A) 0.6, P ( B ) 0.7, 则 P ( AB ) , P( A B ) , P( A B) ,P ( A B ) 3.随 机 变 量 X服 从 二 项 分 布 B(100,0.2), 则P ( X 1)
x0 0 x1 x1
求 (1)k及概率密度f ( x ) (2) P{0.3 X 0.7}; ( 3 )E ( X ), D( X )
( 4 )Y X 2求Y 的概率密度fY ( y)
2 x , 0 x 1 解: (1)1 lim F ( x ) limkx k , f ( x ) F ( x ) x x1 0, 其他
二、一维随机变量 离散型随机变量分布律与分布函数的关系 连续型随机变量概率密度与分布函数的关系 由密度求随机变量的分布函数 几个常用的一维随机变量 求随机变量函数的分布律或概率密度 求数字特征:期望,方差
1、一维随机变量及其分布
(1)离散型随机变量X的分布律可以用表格形式给出:
X pk
x1 pk
函数 g( x )可导, 反函数有两单值枝 h1 ( y),h2 ( y) 则
( y ) | f X [h2 ( y )] | h2 ( y) | f X [h1 ( y )] | h1 fY ( y ) 0
y
其它
例.设连续性随机变量X的概率密度为 kx 0 x 1 f ( x) 其它 0
0 x2 1
x0 0 x 1 x 1
( 3) P{0.3 X 0.7}
0.7 0.3
f ( x )dx 0.72 x dx x 2 0.7 0.4
0.3
0.3
( 4 )E ( X )
xf ( x )dx ;
D( X ) ( x EX ) 2 f ( x )dx E ( X 2 ) E 2 ( X )
(5) B1 Bk , A A AB1 ABk,Bi B j P ( A) P ( ABk( ) 全概率)
k
P ( ABk ) ( 6 )P ( Bk | A) (逆 概 率) P ( ABk )
k
k k n k ( 7 )二项分布 pk P ( A 恰 好 发 生 k次 ) C n p q
( 2) P ( AB ) P ( A) P ( B | A) P ( B ) P ( A | B )独 立 P ( A) P ( B ) ( 3) P ( A ) 1 P ( A); P ( B | A) 1 P ( B | A( ) 条件概率)
(4) P ( A B) P ( A) P ( AB )
有 朋 友 至 远 方 来 参 加会 聚, 他 坐 火 车 、 轮 船汽 、车 、 飞 机 来 的 概 率 分别为 0.3,0.2,0.1,0.4; 若 坐 火 车 迟 到 的 概 是 率0.25 ,若坐船迟到的概 率 是0.3, 坐 汽 车 迟 到 的 概 率 0 是 .1, 坐 飞 机 则 不 会 迟 到 。
例 已知有10件产品,其中有2件为不合格品,现从中任 取5件,问 (1)所取5件恰好有1件为不合格品的概率; (2)取出5件产品恰好有2件为不合格品的概率, (3)取出5件产品有不合格品的概率。
解:设A:恰有1件是不合格,B:恰有2件不合格,C:有不合格
4 1 3 2 C8 C2 C8 C2 P ( A) , P ( B) ; 5 5 C10 C10
(2) P{0.3 X 0.7} F (0.7) - F (0.3) 0.72 - 0.32 0.4
(3)(4)同上例
例、设 X~N(0,1) (1)求 Y=e 的概率密度 (2)求 Y=2X2+1 的概率密度。
解: (1) y e x 是 单 调 的 。 y 0, 则f ( y ) 0; d d y 0, f ( y ) F ( y) ( x ) x ( y ) dy dx x ln y 1 2
a xb 其它
x0 其它
0 xa F ( x) ba 1
xa a xb xb
x
3.正态分布f ( x )
1 2
e
( x )2 22
,
x
例
X pk 1 1/ 4 2 1/ 2 3 1/ 4
x 1 1 x 2 2 x 3 x3
1 1 [ f ( y ) f ( y )] ; y 0 [ f Y ( y ) 2 y 2 y 0 ; y0 ;y 0 0
0 2 例:设 X的 分 布 函 数 为 F(x) kx 1
2 x f ( x) 0
0 x 1
0
其它 0 x f ( t )dt ( 2) F ( x ) P{ X x } 0 1 0 f ( t )dt
x0 0 x 1
x 1
x0 0 x x ( 2) F ( x ) P { X x } f ( t )dt 2tdt,0 x 0 0 1 2tdt , x 0 0
C A B, AB , P(C ) P ( A) P ( B)
例、玻璃杯成箱出售, 每箱10只. 已知各箱中残次品个数为0,1,2 的概率分别为0.8;0.15;0.05,现有一顾客欲购一箱玻璃杯, 售货员 任意取一箱, 顾客开箱随机地检验一只, 若不是残次品, 顾客则买 下该箱玻璃杯. 试求: 1. 顾客买下该箱玻璃杯的概率; 2. 在顾客买下的一箱玻璃杯中, 确实无残次品的概率.
,
P( A B) 1 P( A) P( B)
0.42 ;( 1 0.6 ) (1 0.7 ) ; 0.6 0.6 0.7; 0.6 0.7 0.42
P( X 0) P( X 1) 0.20 (1 0.2)100 0.2 (1 0.2)99
分布函数: F ( x )
x
f ( t )dt
概率密度: f ( x ) F ( x )
1 1.均 匀 分 布 f ( x ) b a 0
1 e 2.指数分布f ( x ) 0
P{ x1 X x2 }
x2 x1
f ( x )dx
1 (ln y ) 2 e 2
X
1 y
( 2 )y 2 x 2 1不 单 调 。 y [1, ), 当y 1时, f ( y ) 0; y 1时 F( y ) P (Y y ) P (2 X 2 1 y ) p y 1 X y 1
0 1 / 4 分 布 函 数F ( x ) 3 / 4 1
