高中数学选修双曲线的简单性质(基础)知识点巩固练习
2020-2021学年高中数学人教A版选修1-1习题:2.2.2 双曲线的简单几何性质 Word版含

2.2.2双曲线的简单几何性质课后篇巩固提升基础巩固1.双曲线=1的左焦点与右顶点之间的距离等于()A.6B.8C.9D.10(-5,0),右顶点(3,0),所以左焦点与右顶点之间的距离等于8.2.中心在原点,焦点在x轴上的双曲线的实轴与虚轴相等,一个焦点到一条渐近线的距离为,则双曲线方程为()A.x2-y2=1B.x2-y2=2C.x2-y2=D.x2-y2=,设双曲线方程为=1(a>0),则c=a,一条渐近线为y=x,∴,∴a2=2.∴双曲线方程为x2-y2=2.3.若实数k满足0<k<9,则曲线=1与曲线=1的()A.焦距相同B.实半轴长相等C.虚半轴长相等D.离心率相等0<k<9,则9-k>0,即曲线=1为焦点在x轴上的双曲线,焦点坐标为(,0);25-k>0,即曲线=1为焦点在x轴上的双曲线,焦点坐标为(,0),故两曲线的焦距相同,故选A.4.下列双曲线中,不是以2x±3y=0为渐近线的是()A.=1B.=1C.=1D.=1项中的双曲线=1,焦点在x轴上,渐近线方程为y=±x,不是2x±3y=0.5.两正数a,b的等差中项为,等比中项为,且a>b,则双曲线=1的离心率e为()A. B. C. D.a,b的等差中项为,等比中项为,所以解得因为a>b,所以所以e=.故选D.6.(2019江苏高考)在平面直角坐标系xOy中,若双曲线x2-=1(b>0)经过点(3,4),则该双曲线的渐近线方程是.双曲线x2-=1(b>0)过点(3,4),∴32-=1,解得b2=2,即b=或b=-(舍去).∵a=1,且双曲线的焦点在x轴上,∴双曲线的渐近线方程为y=±x.±x7.已知双曲线=1(a>0,b>0)的一条渐近线平行于直线l:y=2x+10,双曲线的一个焦点在直线l上,则双曲线的标准方程为.=2,c=5,所以c2=a2+b2=5a2=25,解得a2=5,b2=20,所以所求双曲线的方程为=1.18.若一条双曲线与-y2=1有共同渐近线,且与椭圆=1有相同的焦点,则此双曲线的方程为.=1得a2=20,b2=2,所以c2=20-2=18,得c=3.设与双曲线-y2=1有相同渐近线的双曲线方程为-y2=λ(λ≠0),因为所求双曲线的焦点在x轴上,则λ>0,双曲线方程化为=1,根据椭圆和双曲线共焦点,所以有8λ+λ=18,解得λ=2,所以所求双曲线的方程为=1.19.椭圆与双曲线有共同的焦点F1(0,-5),F2(0,5),点P(3,4)是双曲线的渐近线与椭圆的一个交点,试求椭圆的方程与双曲线的方程.F1(0,-5),F2(0,5),可设椭圆方程为=1(a2>25),双曲线方程为=1(0<b<5),点P(3,4)在椭圆上,所以=1,得a2=40,双曲线过点P(3,4)的渐近线为y=x,即4=×3,所以b2=16,故椭圆方程为=1,双曲线方程为=1.10.已知双曲线=1的右焦点为(2,0).(1)求双曲线的方程;(2)求双曲线的渐近线与直线x=-2围成的三角形的面积.∵双曲线的右焦点的坐标为(2,0),且双曲线的方程为=1,∴c2=a2+b2=3+b2=4,∴b2=1,∴双曲线的方程为-y2=1.(2)∵a=,b=1,∴双曲线的渐近线方程为y=±x.令x=-2,则y=±,设直线x=-2与双曲线的渐近线的交点为A,B,则|AB|=.记双曲线的渐近线与直线x=-2围成的三角形的面积为S,则S=×2=.能力提升1.我们把离心率之差的绝对值小于的两条双曲线称为“相近双曲线”.已知双曲线C:=1,则下列双曲线中与C是“相近双曲线”的是()A.x2-y2=1B.x2-=1C.y2-2x2=1D.=1C的离心率为2,对于A,其离心率为,不符合题意;对于B,其离心率为,符合题意;对于C,其离心率为,不符合题意;对于D,其离心率为3,不符合题意.故选B.2.若在双曲线=1(a>0,b>0)的右支上,到原点O和右焦点F的距离相等的点有两个,则双曲线的离心率的取值范围是()A.e>B.1<e<C.e>2D.1<e<2O和右焦点F距离相等的点在线段OF的垂直平分线上,其方程为x=.依题意,在双曲线=1(a>0,b>0)的右支上到原点O和右焦点F距离相等的点有两个,所以直线x=与右支有两个交点,故应满足>a,即>2,得e>2,故选C.3.已知a>b>0,若椭圆=1与双曲线=1的离心率之积为,则双曲线的渐近线方程为.,得,解得,所以双曲线的渐近线方程为y=±x,即x±y=0.±y=04.若中心在原点,焦点在坐标轴上的双曲线的一条渐近线经过点(8,-6),则其离心率等于.y=kx,由-6=8k,得k=-,所以渐近线方程为y=±x.若焦点在x轴上,则,于是离心率e=;若焦点在y轴上,则,于是离心率e=.5.求适合下列条件的双曲线的标准方程:(1)焦点在y轴上,虚轴长为8,离心率为e=;(2)经过点C(-),且与双曲线=1有共同的渐近线.设所求双曲线的标准方程为=1(a>0,b>0),则2b=8,e=,从而b=4,,代入c2=a2+b2,得a2=9,故方程为=1.(2)由题意可设所求双曲线方程为=λ(λ≠0),将点C(-)的坐标代入,得=λ,解得λ=,所以所求双曲线的标准方程为=1.6.已知椭圆C1的中心在原点,离心率为,焦点在x轴上且长轴长为10.过双曲线C2:=1(a>0,b>0)的右焦点F2作垂直于x轴的直线交双曲线C2于M,N两点.(1)求椭圆C1的标准方程;(2)若双曲线C2与椭圆C1有公共的焦点,且以MN为直径的圆恰好过双曲线的左顶点A,求双曲线C2的标准方程.设椭圆C1的标准方程为=1(a1>b1>0),根据题意得2a1=10,则a1=5.又e1=,∴c1=4,b1=3,∴椭圆C1的标准方程为=1.(2)设双曲线的右焦点F2(c,0),将x=c代入双曲线方程,得y=±,∴|MN|=.∵以MN为直径的圆恰好过双曲线的左顶点A,且|AF2|=a+c,∴a+c=,即a2+ac=b2=c2-a2,整理得2a2+ac-c2=0,即有e2-e-2=0.又e>1,∴e=2.又双曲线C2与椭圆C1有公共的焦点,∴c=4,∴a2=4,b2=12,∴双曲线C2的标准方程为=1.莘莘学子,最重要的就是不要去看远方模糊的,而要做手边清楚的事。
2020-2021高中数学人教版1-1配套作业:2.2.2 双曲线的简单几何性质含解析

2020-2021学年高中数学人教A版选修1-1配套作业:2.2.2 双曲线的简单几何性质含解析第二章2。
22。
2.2A级基础巩固一、选择题1.以椭圆错误!+错误!=1的顶点为顶点,离心率为2的双曲线方程为(C)A.错误!-错误!=1B.错误!-错误!=1C.错误!-错误!=1或错误!-错误!=1D.以上都不对[解析]当顶点为(±4,0)时,a=4,c=8,b=43,双曲线方程为错误!-错误!=1;当顶点为(0,±3)时,a=3,c=6,b=3错误!,双曲线方程为错误!-错误!=1。
2.双曲线2x2-y2=8的实轴长是(C)A.2B.2错误!C.4D.42[解析]双曲线2x2-y2=8化为标准形式为x24-y28=1,∴a=2,∴实轴长为2a=4。
3.(全国Ⅱ文,5)若a〉1,则双曲线x2a2-y2=1的离心率的取值范围是(C)A.(错误!,+∞) B.(错误!,2 )C.(1,错误!) D.(1,2)[解析]由题意得双曲线的离心率e=错误!.∴c2=a2+1a2=1+错误!.∵a>1,∴0〈错误!<1,∴1<1+错误!〈2,∴1〈e〈错误!.故选C.4.(2018·全国Ⅲ文,10)已知双曲线C:错误!-错误!=1(a>0,b>0)的离心率为错误!,则点(4,0)到C的渐近线的距离为(D) A. 2 B.2C.错误!D.2错误![解析]由题意,得e=错误!=错误!,c2=a2+b2,得a2=b2。
又因为a〉0,b>0,所以a=b,渐近线方程为x±y=0,点(4,0)到渐近线的距离为错误!=2错误!,故选D.5.(2019·全国Ⅲ卷理,10)双曲线C:错误!-错误!=1的右焦点为F,点P在C的一条渐近线上,O为坐标原点,若|PO|=|PF|,则△PFO的面积为(A)A.错误!B.错误!C.2错误!D.3错误![解析]双曲线错误!-错误!=1的右焦点坐标为(错误!,0),一条渐近线的方程为y=错误!x,不妨设点P在第一象限,由于|PO|=|PF|,则点P的横坐标为错误!,纵坐标为错误!×错误!=错误!,即△PFO 的底边长为错误!,高为错误!,所以它的面积为错误!×错误!×错误!=错误!。
高中数学 第二章 圆锥曲线与方程 2.2 双曲线(1)练习 新人教A版高二选修1-1数学试题

2.2 双曲线(1)A 级 基础巩固一、选择题1.已知M (-2,0)、N (2,0),|PM |-|PN |=4,则动点P 的轨迹是导学号 03624438( C )A .双曲线B .双曲线左支C .一条射线D .双曲线右支[解析]∵|PM |-|PN |=|MN |=4,∴动点P 的轨迹是一条射线. 2.双曲线3x 2-4y 2=-12的焦点坐标为导学号 03624439( D ) A .(±5,0) B .(0,±5) C .(±7,0)D .(0,±7)[解析] 双曲线3x 2-4y 2=-12化为标准方程为y 23-x 24=1,∴a 2=3,b 2=4,c 2=a 2+b 2=7,∴c =7,又∵焦点在y 轴上,故选D .3.已知方程x 21+k -y 21-k =1表示双曲线,则k 的取值X 围是导学号 03624440( A )A .-1<k <1B .k >0C .k ≥0D .k >1或k <-1[解析] 由题意得(1+k )(1-k )>0,∴(k -1)(k +1)<0,∴-1<k <1.4.(2016·某某某某高二检测)已知双曲线2mx 2-my =4的一个焦点为(0,6),则m 的值为导学号 03624441( B )A .1B .-1C .73D .-73[解析] 将双曲线方程化为x 22m-y 24m=1.因为一个焦点是(0,6),所以焦点在y 轴上,所以c =6,a 2=-4m ,b 2=-2m ,所以a 2+b 2=-4m -2m =-6k=c 2=6.所以m =-1.5.双曲线x 210-y 22=1的焦距为导学号 03624442( D )A .3 2B .4 2C .3 3D .4 3[解析] 由双曲线的标准方程,知a 2=10,b 2=2,则c 2=a 2+b 2=10+2=12,因此2c =43,故选D .6.(2015·某某理)若双曲线E :x 29-y 216=1的左、右焦点分别为F 1、F 2,点P 在双曲线E 上,且|PF 1|=3,则|PF 2|等于导学号 03624443( B )A .11B .9C .5D .3[解析] 由题,|||PF 1|-|PF 2|=2a =6, 即||3-|PF 2|=2a =6,解得|PF 2|=9. 二、填空题7.已知双曲线C :x 29-y 216=1的左、右焦点分别为F 1、F 2,P 为C 右支上的一点,且|PF 2|=|F 1F 2|,则△PF 1F 2的面积等于__48__.导学号 03624444[解析] 依题意得|PF 2|=|F 1F 2|=10,由双曲线的定义得|PF 1|-|PF 2|=6,∴|PF 1|=16.∴S △PF 1F 2=12×16×102-1622=48.8.已知双曲线x 225-y 29=1的两个焦点分别为F 1、F 2,若双曲线上的点P 到点F 1的距离为12,则点P 到点F 2的距离为__2或22__.导学号 03624445[解析] 设F 1为左焦点,F 2为右焦点,当点P 在双曲线左支上时,|PF 2|-|PF 1|=10,|PF 2|=22;当点P 在双曲线右支上时, |PF 1|-|PF 2|=10,|PF 2|=2. 三、解答题9.求满足下列条件的双曲线的标准方程.导学号 03624446 (1)焦点在x 轴上,c =6且经过点(-5,2); (2)过P (3,154)和Q (-163,5)两点.[解析] (1)设双曲线方程为x 2a 2-y 2b2=1(a >0,b >0),由题意得⎩⎪⎨⎪⎧25a 2-4b2=1a 2+b 2=6,解之得a 2=5,b 2=1, 故所求双曲线方程为x 25-y 2=1.(2)设双曲线方程为Ax 2+By 2=1(AB <0),由题意得 ⎩⎪⎨⎪⎧9A +22516B =12569A +25B =1,解之得⎩⎪⎨⎪⎧A =-116B =19.∴所求双曲线方程为y 29-x 216=1.B 级 素养提升一、选择题1.已知双曲线中心在原点,一个焦点为F 1(-5,0),点P 在该双曲线上,线段PF 1的中点坐标为(0,2),则双曲线的方程是导学号 03624447( B )A .x 24-y 2=1B .x 2-y 24=1C .x 22-y 23=1D .x 23-y 22=1[解析] 由条件知P (5,4)在双曲线x 2a 2-y 2b2=1上,∴5a 2-16b2=1,又a2+b 2=5,∴⎩⎪⎨⎪⎧a 2=1b 2=4,故选B .2.(2017·全国Ⅰ文,5)已知F 是双曲线C :x 2-y 23=1的右焦点,P 是C 上一点,且PF与x 轴垂直,点A 的坐标是(1,3),则△APF 的面积为导学号 03624448( D )A .13B .12C .23D .32[解析] 因为F 是双曲线C :x 2-y 23=1的右焦点,所以F (2,0).因为PF ⊥x 轴,所以可设P 的坐标为(2,y P ). 因为P 是C 上一点,所以4-y 2P3=1,解得y P =±3,所以P (2,±3),|PF |=3.又因为A (1,3),所以点A 到直线PF 的距离为1, 所以S △APF =12×|PF |×1=12×3×1=32.故选D .3.已知m 、n 为两个不相等的非零实数,则方程mx -y +n =0与nx 2+my 2=mn 所表示的曲线可能是导学号 03624449( C )[解析] 把直线方程和曲线方程分别化为y =mx +n ,x 2m +y 2n=1.根据图形中直线的位置,判定斜率m 和截距n 的正负,从而断定曲线的形状.4.已知双曲线的左、右焦点分别为F 1、F 2,过F 1的直线与双曲线的左支交于A 、B 两点,线段AB 的长为5,若2a =8,那么△ABF 2的周长是导学号 03624450( D )A .16B .18C .21D .26[解析] |AF 2|-|AF 1|=2a =8,|BF 2|-|BF 1|=2a =8, ∴|AF 2|+|BF 2|-(|AF 1|+|BF 1|)=16, ∴|AF 2|+|BF 2|=16+5=21,∴△ABF 2的周长为|AF 2|+|BF 2|+|AB |=21+5=26. 5.若方程x 2m -1+y 2m 2-4=3表示焦点在y 轴上的双曲线,则m 的取值X 围是导学号 03624451( C )A .(-∞,1)B .(2,+∞)C .(-∞,-2)D .(-2,1)[解析] 由题意,方程可化为y 2m 2-4-x 21-m=3,∴⎩⎪⎨⎪⎧m 2-4>01-m >0,解得m <-2.故选C .二、填空题6.(2016·某某某某高二检测)设双曲线与椭圆x 227+y 236=1有共同的焦点,且与椭圆相交,有一个交点的坐标为(15,4),则此双曲线的方程为y 24-x 25=1 .导学号 03624452[解析] 解法一:椭圆x 227+y 236=1的焦点坐标是(0,±3),根据双曲线的定义,知2a=|152+12-152+72|=4,故a =2.又b 2=c 2-a 2=5,故所求双曲线的方程为y 24-x 25=1. 解法二:椭圆x 227+y 236=1的焦点坐标是(0,±3).设双曲线方程为y 2a 2-x 2b2=1(a >0,b >0),则a 2+b 2=9,16a 2-15b 2=1,解得a 2=4,b 2=5.故所求双曲线的方程为y 24-x 25=1.解法三:设双曲线方程为x 227-λ+y 236-λ=1(27<λ<36),由于双曲线过点(15,4),故1527-λ+1636-λ=1,解得λ1=32,λ2=0(舍去).故所求双曲线方程为y 24-x 25=1. 7.已知F 1、F 2为双曲线C :x 2-y 2=1的左、右焦点,点P 在C 上,∠F 1PF 2=60°,则|PF 1|·|PF 2|等于__4__.导学号 03624453[解析] 在△PF 1F 2中,|F 1F 2|2=|PF 1|2+|PF 2|2-2|PF 1|·|PF 2|·cos60°=(|PF 1|-|PF 2|)2+|PF 1|·|PF 2|, 即(22)2=22+|PF 1|·|PF 2|, 解得|PF 1|·|PF 2|=4. 三、解答题8.已知双曲线方程为2x 2-y 2=k ,焦距为6,求k 的值.导学号 03624454 [解析] 由题意知c =3,若焦点在x 轴上,则方程可化为x 2k 2-y 2k =1,∴k 2+k =32,即k =6.若焦点在y 轴上,则方程可化为y 2-k -x 2-k2=1.∴-k +(-k2)=32,即k =-6.综上,k 的值为6或-6.C 级 能力提高1.双曲线8kx 2-ky 2=8的一个焦点坐标为(0,3),则k 的值为__-1__.导学号 03624455[解析] 将双曲线的方程化为x 21k-y 28k=1,因为双曲线的一个焦点坐标是(0,3), 所以焦点在y 轴上,且c =3. 所以a 2=-8k ,b 2=-1k.所以-8k -1k=9,解得k =-1.2.当0°≤α≤180°时,方程x 2cos α+y 2sin α=1表示的曲线如何变化?导学号 03624456[解析] (1)当α=0°时,方程为x 2=1,它表示两条平行直线x =±1. (2)当0°<α<90°时,方程为x 21cos α+y 21sin α=1. ①当0°<α<45°时,0<1cos α<1sin α,它表示焦点在y 轴上的椭圆.②当α=45°时,它表示圆x 2+y 2= 2.③当45<α<90°时,1cos α>1sin α>0,它表示焦点在x 轴上的椭圆.(3)当α=90°时,方程为y 2=1,它表示两条平行直线y =±1. (4)当90°<α<180°时,方程为y 21sin α-x 21-cos α=1,它表示焦点在y 轴上的双曲线.(5)当α=180°时,方程为x 2=-1,它不表示任何曲线.。
高中数学高考几何解析(椭圆双曲线抛物线)课本知识讲解及练习(含答案)
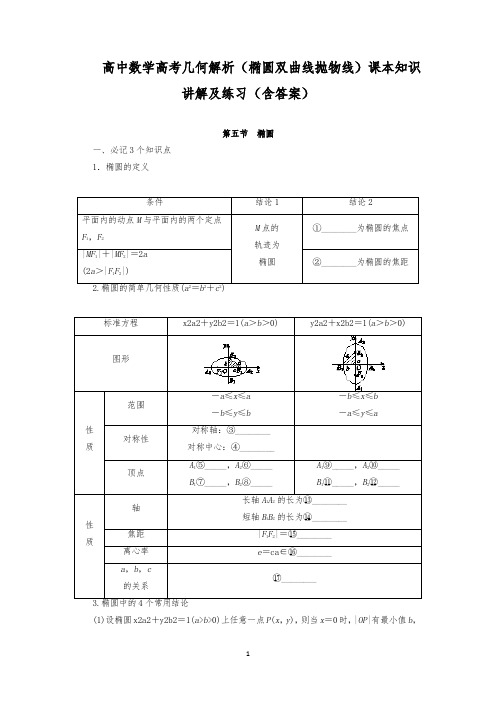
高中数学高考几何解析(椭圆双曲线抛物线)课本知识讲解及练习(含答案)第五节椭圆一、必记3个知识点1.椭圆的定义(1)设椭圆x2a2+y2b2=1(a>b>0)上任意一点P(x,y),则当x=0时,|OP|有最小值b,这时,P在短轴端点处;当x=±a时,|OP|有最大值a,这时,P在长轴端点处.(2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形,其中a是斜边长,a2=b2+c2.(3)已知过焦点F1的弦AB,则△ABF2的周长为4a.(4)若P为椭圆上任一点,F为其焦点,则a-c≤|PF|≤a+c.二、必明3个易误点1.椭圆的定义中易忽视2a>|F1F2|这一条件,当2a=|F1F2|其轨迹为线段F1F2,当2a<|F1F2|不存在轨迹.2.求椭圆的标准方程时易忽视判断焦点的位置,而直接设方程为x2a2+y2b2=1(a>b>0).3.注意椭圆的范围,在设椭圆x2a2+y2b2=1(a>b>0)上点的坐标为P(x,y)时,则|x|≤a,这往往在求与点P有关的最值问题中特别有用,也是容易被忽略而导致求最值错误的原因.三、技法1.求椭圆标准方程的2种常用方法(1)直接求出a,c来求解e.通过已知条件列方程组,解出a,c的值.(2)构造a,c的齐次式,解出e.由已知条件得出关于a,c的二元齐次方程,然后转化为关于离心率e的一元二次方程求解.(3)通过取特殊值或特殊位置,求出离心率.提醒:在解关于离心率e的二次方程时,要注意利用椭圆的离心率e∈(0,1)进行根的取舍,否则将产生增根.3.求解最值、取值范围问题的技巧(1)与椭圆几何性质有关的问题要结合图形进行分析,即使画不出图形,思考时也要联想到一个图形.(2)椭圆的范围或最值问题常常涉及一些不等式.例如,-a≤x≤a,-b≤y≤b,0<e<1,在求椭圆的相关量的范围时,要注意应用这些不等关系.(3)最值问题,将所求列出表达式,构造基本不等式或利用函数单调性求解.4.判断直线与椭圆位置关系的四个步骤第一步:确定直线与椭圆的方程.第二步:联立直线方程与椭圆方程.第三步:消元得出关于x(或y)的一元二次方程.第四步:当Δ>0时,直线与椭圆相交;当Δ=0时,直线与椭圆相切;当Δ<0时,直线与椭圆相离.5.直线被椭圆截得的弦长公式设直线与椭圆的交点坐标为A(x1,y1),B(x2,y2),则|AB|=(1+k2)[(x1+x2)2-4x1x2])=(y1+y2)2-4y1y2])(k为直线斜率).参考答案①F1,F2②|F1F2|③x轴,y轴④坐标原点⑤(-a,0)⑥(a,0)⑦(0,-b)⑧(0,b)⑨(0,-a)⑩(0,a)⑪(-b,0)⑫(b,0)⑬2a⑭2b⑮2c⑯(0,1)⑰c2=a2-b2第六节双曲线一、必记3个知识点1.双曲线的定义(1)平面内与两个定点F1、F2(|F1F2|=2c>0)的距离①________________为非零常数2a(2a<2c)的点的轨迹叫做双曲线.这两个定点叫做双曲线的②________,两焦点间的距离叫做③________.(2)集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a,c为常数且a>0,c>0.(ⅰ)当④________________时,M点的轨迹是双曲线;(ⅱ)当⑤________________时,M点的轨迹是两条射线;(ⅲ)当⑥________________时,M点不存在.2.双曲线的标准方程和几何性质⑧________x ∈对称轴:⑪________对称中心:⑫________顶点坐标:A 1⑮______,A 2⑯________⑱____________c =⑳________|=21________;线段________;a 叫做双曲线的虚半轴长>b >0)(1)双曲线为等轴双曲线⇔双曲线的离心率e =2⇔双曲线的两条渐近线互相垂直.(2)渐近线的斜率与双曲线的焦点位置的关系:当焦点在x 轴上时,渐近线斜率为±ba,当焦点在y 轴上时,渐近线斜率为±ab.(3)渐近线与离心率.x2a2-y2b2=1(a >0,b >0)的一条渐近线的斜率为ba=e2-1.(4)若P 为双曲线上一点,F 为其对应焦点,则|PF |≥c -a .二、必明4个易误点1.双曲线的定义中易忽视2a <|F 1F 2|这一条件.若2a =|F 1F 2|,则轨迹是以F 1,F 2为端点的两条射线,若2a >|F 1F 2|则轨迹不存在.2.双曲线的标准方程中对a ,b 的要求只是a >0,b >0,易误认为与椭圆标准方程中a ,b 的要求相同.若a >b >0,则双曲线的离心率e ∈(1,2);若a =b >0,则双曲线的离心率e =2;若0<a <b ,则双曲线的离心率e >2.3.注意区分双曲线中的a ,b ,c 大小关系与椭圆a ,b ,c 关系,在椭圆中a 2=b 2+c 2,而在双曲线中c2=a2+b2.4.易忽视渐近线的斜率与双曲线的焦点位置关系.当焦点在x轴上,渐近线斜率为±ba,当焦点在y轴上,渐近线斜率为±ab.三、技法1.双曲线定义的应用(1)判定满足某条件的平面内动点的轨迹是否为双曲线,进而根据要求可求出曲线方程;(2)在“焦点三角形”中,常利用正弦定理、余弦定理,经常结合||PF1|-|PF2||=2a,运用平方的方法,建立|PF1|与|PF2|的关系.[注意]在应用双曲线定义时,要注意定义中的条件,搞清所求轨迹是双曲线,还是双曲线的一支,若是双曲线的一支,则需确定是哪一支.2.求双曲线标准方程的一般方法(1)待定系数法:设出双曲线方程的标准形式,根据已知条件,列出参数a,b,c的方程并求出a,b,c的值.与双曲线x2a2-y2b2=1有相同渐近线时,可设所求双曲线方程为:x2a2-y2b2=λ(λ≠0).(2)定义法:依定义得出距离之差的等量关系式,求出a的值,由定点位置确定c的值.3.求双曲线离心率或其范围的方法(1)求a,b,c的值,由c2a2=a2+b2a2=1+b2a2直接求e.(2)列出含有a,b,c的齐次方程(或不等式),借助于b2=c2-a2消去b,然后转化成关于e的方程(或不等式)求解.4.求双曲线的渐近线方程的方法求双曲线x2a2-y2b2=1(a>0,b>0)的渐近线的方法是令x2a2-y2b2=0,即得两渐近线方程为:xa±yb=0.参考答案①之差的绝对值②焦点③焦距④2a<|F1F2|⑤2a=|F1F2|⑥2a>|F1F2|⑦x≥a或x≤-a⑧y≥a或y≤-a⑨x轴,y轴⑩坐标原点⑪x轴,y轴⑫坐标原点⑬(-a,0)⑭(a,0)⑮(0,-a)⑯(0,a)⑰y=±ba x⑱y=±ab x⑲ca⑳a2+b2212a222b23a2+b2第七节抛物线一、必记2个知识点1.抛物线定义、标准方程及几何性质x轴⑤________y轴⑥________O(0,0)O(0,0)O(0,0)O(0,0)F⑦________⑧________⑨________设AB是过抛物线y2=2px(p>0)的焦点F的弦,若A(x1,y1),B(x2,y2),则(1)x1x2=p24,y1y2=-p2.(2)弦长|AB|=x1+x2+p=2psin2α(α为弦AB的倾斜角).(3)以弦AB为直径的圆与准线相切.(4)通径:过焦点且垂直于对称轴的弦,长等于2p.二、必明2个易误点1.抛物线的定义中易忽视“定点不在定直线上”这一条件,当定点在定直线上时,动点的轨迹是过定点且与直线垂直的直线.2.抛物线标准方程中参数p易忽视,只有p>0,才能证明其几何意义是焦点F到准线l 的距离,否则无几何意义.三、技法1.应用抛物线定义的2个关键点(1)由抛物线定义,把抛物线上点到焦点距离与到准线距离相互转化.(2)注意灵活运用抛物线上一点P(x,y)到焦点F的距离|PF|=|x|+p2或|PF|=|y|+p2.2.求抛物线的标准方程的方法(1)求抛物线的标准方程常用待定系数法,因为未知数只有p,所以只需一个条件确定p值即可.(2)因为抛物线方程有四种标准形式,因此求抛物线方程时,需先定位,再定量.3.确定及应用抛物线性质的技巧(1)利用抛物线方程确定及应用其焦点、准线等性质时,关键是将抛物线方程化为标准方程.(2)要结合图形分析,灵活运用平面几何的性质以图助解.4.解决直线与抛物线位置关系问题的常用方法(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系.(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用公式|AB|=x1+x2+p,若不过焦点,则必须用一般弦长公式.(3)涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”“整体代入”等解法.提醒:涉及弦的中点、斜率时,一般用“点差法”求解.参考答案①相等②y2=-2px(p>0)③x2=-2py(p>0)④x2=2py(p>0)⑤x轴⑥y轴⑦F(-p2,0)⑧F(0,-p2)⑨F(0,p2)⑩e=1⑪x=-p2⑫y=-p2⑬-y0+p2⑭y0+p2⑮y≤0⑯y≥0。
高二选修双曲线及简单性质课后巩固试题 (1)

§2.3.2双曲线的简单几何性质(1)学习目标1.理解并掌握双曲线的几何性质.P 56~ P 58,文P 49~ P 51找出疑惑之处) 复习1:写出满足下列条件的双曲线的标准方程: ①3,4a b ==,焦点在x 轴上;②焦点在y 轴上,焦距为8,2a =. 复习2:前面我们学习了椭圆的哪些几何性质?二、新课导学: ※ 学习探究问题1:由椭圆的哪些几何性质出发,类比探究双曲线22221x y ab-=的几何性质?范围:x : y :对称性:双曲线关于 轴、 轴及 都对称. 顶点:( ),( ).实轴,其长为 ;虚轴,其长为 . 离心率:1c e a=>.渐近线: 双曲线22221x y ab-=的渐近线方程为:0x y ab±=.问题2:双曲线22221y x ab-=的几何性质?图形: 范围:x : y :对称性:双曲线关于 轴、 轴及 都对称. 顶点:( ),( )实轴,其长为 ;虚轴,其长为 . 离心率:1c e a=>.渐近线:双曲线22221y x ab-=的渐近线方程为: .新知:实轴与虚轴等长的双曲线叫 双曲线.※ 典型例题例1求双曲线2214925xy-=的实半轴长、虚半轴的长、焦点坐标、离心率及渐近线的方程.变式:求双曲线22916144y x -=的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程. 例2求双曲线的标准方程:⑴实轴的长是10,虚轴长是8,焦点在x 轴上;⑵离心率e =(5,3)M -;⑶渐近线方程为23y x =±,经过点9(,1)2M -.※ 动手试试练1.求以椭圆22185xy+=的焦点为顶点,以椭圆的顶点为焦点的双曲线的方程.练2.对称轴都在坐标轴上的等到轴双曲线的一个焦点是1(6,0)F -,求它的标准方程和渐近线方程.三、总结提升: ※ 学习小结双曲线的图形、范围、顶点、对称性、离心率、渐近线.※ 当堂检测1. 双曲线221168xy-=实轴和虚轴长分别是( ).A .8、B .8、C .4、D .4、2.双曲线224x y -=-的顶点坐标是( ).A .(0,1)±B .(0,2)±C .(1,0)±D .(2,0±)3. 双曲线22148xy-=的离心率为( ).A .1 B . C D .24.双曲线2241x y -=的渐近线方程是 .5.经过点(3,1)A -,并且对称轴都在坐标轴上的等轴双曲线的方程是 .1.求焦点在y 轴上,焦距是16,43e =的双曲线的标准方程.2.求与椭圆2214924xy+=有公共焦点,且离心率54e =的双曲线的方程.§2.3.2双曲线的简单几何性质(2)学习目标1.从具体情境中抽象出椭圆的模型;2.掌握椭圆的定义;3.掌握椭圆的标准方程.P 58~ P 60,文P 51~ P 53找出疑惑之处) 复习1:说出双曲线的几何性质? 复习2:双曲线的方程为221914xy-=,其顶点坐标是( ),( );渐近线方程 . 二、新课导学 ※ 学习探究探究1:椭圆22464x y +=的焦点是?探究2:双曲线的一条渐近线方程是0x +=,则可设双曲线方程为?问题:若双曲线与22464x y +=有相同的焦点,它的一条渐近线方程是0x +=,则双曲线的方程是?※ 典型例题例1双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小半径为12m ,上口半径为13m ,下口半径为25m ,高为55m ,试选择适当的坐标系,求出此双曲线的方程.例2点(,)M x y 到定点(5,0)F 的距离和它到定直线l :165x =的距离的比是常数54,求点M 的轨迹.例3过双曲线22136xy-=的右焦点,倾斜角为30的直线交双曲线于,A B 两点,求,A B 两点的坐标.变式:求A B ? 思考:1AF B ∆的周长?※ 动手试试练1.若椭圆22214xy a+=与双曲线2212xya-=的焦点相同,则a =____.练2 .若双曲线2214xym-=的渐近线方程为2y =±,求双曲线的焦点坐标.三、总结提升1.双曲线的综合应用:与椭圆知识对比,结合; 2.双曲线的另一定义; 3.直线与双曲线的位置关系.※ 当堂检测1.若椭圆2212516xy+=和双曲线22145xy-=的共同焦点为F 1,F 2,P 是两曲线的一个交点,则12PF PF ∙的值为( ). A .212B .84C .3D .212.以椭圆2212516x y+=的焦点为顶点,离心率为2的双曲线的方程( ). A.2211648xy-= B.221927xy-= C.2211648xy-=或221927xy-= D. 以上都不对3.过双曲线的一个焦点2F 作垂直于实轴的直线,交双曲线于P 、Q ,1F 是另一焦点,若∠12PF Q π=,则双曲线的离心率e 等于( ).A.1B.C. 1D. 24.双曲线的渐近线方程为20x y ±=,焦距为10,这双曲线的方程为_______________. 5.方程221xy+=表示焦点在x 轴上的双曲线,则k 的取值范围 .1.已知双曲线的焦点在x 轴上,方程为22221x y ab-=,两顶点的距离为8,一渐近线上有点(8,6)A ,试求此双曲线的方程.双曲线的简单几何性质随堂巩固1.双曲线19422=-yx的渐进线方程为( )A .x y 32±= B .x y 94±= C .x y 23±= D .x y 49±=2.已知双曲线C 的两条渐进线方程为x y ±=,且过点)1,2(M ,则双曲线的方程为( ) A .122=-y x B .222=-y x C .122-=-yx D .222-=-y x3.双曲线的离心率为2,则双曲线的两条渐近线的夹角是4.已知双曲线1422=-ymx的一条渐近线方程为x y =,则实数m =5.已知P 是双曲线19222=-yax 右支上的一点,双曲线的一条渐近线方程为03=-y x ,设21F F 、分别为双曲线的左、右焦点.若32=PF ,则1PF = 6.已知双曲线与椭圆125922=+yx共焦点,它们离心率之和为514,则双曲线方程是强化训练1.已知双曲线12222=-by ax 和椭圆)0,0(12222>>>=+b m a by mx 的离心率互为倒数,那么以m b a 、、为边长的三角形是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形 2.已知双曲线13622=-yx的焦点21,F F ,点M 在双曲线上且x MF ⊥1轴,则1F 到直线2MF 的距离为( )A .563 B .665 C .56 D .653.双曲线192522=-yx和)259(192522<<-=+--k k ykx有( )A .相同焦点B .相同的渐进线C .相同顶点D .相等的离心率 4.已知双曲线)0(19222>=-m x m y 的一个顶点到它的一条渐近线的距离为51,则m 等于( ) A .1 B .2 C .3 D .4 5.设1>a ,则1)1(2222=+-a yax 的离心率e 的取值范围是( )A .)2,2(B .)5,2(C .)5,2(D .)5,2(6.已知双曲线)0,0(12222>>=-b a by ax 的一条渐近线为)0(>=k kx y ,离心率为k e 5=,则双曲线方程为( )A .142222=-a yax B .152222=-ayax C .142222=-by bxD .152222=-by bx7.双曲线1251622=-yx的两条渐进线的夹角为8.已知圆0846:22=+--+y x y x C ,以圆C 与坐标轴的交点分别作为双曲线的一个焦点和顶点,则适合上述条件的双曲线的标准方程为 9.已知双曲线的渐进线方程为x y 34±=,并且焦点都在圆10022=+yx 上,求双曲线的方程10.已知双曲线的离心率21,2F F e 、=是双曲线的两个焦点,P 在双曲线上且SPF F ,6021=∠△21FPF =123,求双曲线的方程11.已知双曲线的中心在原点,焦点21F F 、在坐标轴上,离心率为2,且过)10,4(-M (1)求双曲线的方程(2)若点),3(m N 在双曲线上,求证:021=⋅NF NF (3)求△21NF F 的面积12.双曲线14922=-yx与直线1-=kx y 只有一个公共点,求k 的值第二课时1.双曲线112422=-xy的准线方程为( )A .169±=x B .49±=x C .169±=y D .49±=y2.已知双曲线9322=-y x ,则双曲线右支上的点P 到右焦点的距离与点P 到右准线的距离之比等于( )A .4 B .332 C .2 D .23.若双曲线)0(116222>=-b by x的一条准线恰好为圆0222=++x y x 的一条切线,则b 的值为( ) A .4 B .8 C .42 D .434.若双曲线的两渐进线是x y 23±=,焦点)0,26()0,26(21F F 、-,那么它两准线间距离为( ) A .26138 B .26134 C .261318 D .261395.双曲线两准线间距离等于半焦距,则离心率为( ) A .2 B .3 C .2 D .36.与曲线1492422=+yx共焦点,且与曲线1643622=-yx共渐进线的双曲线方程为( )A .191622=-yxB .116922=-yxC .191622=-xyD .116922=-xy强化训练1.已知双曲线14:22=-yx C ,过点)1,1(P 作直线l ,使l 与C 有且只有一个公共点,则满足上述条件的直线l 共有( ) A .1 条 B .2条 C .3条 D .4条 2.双曲线191622=-yx的右准线与渐进线在第四象限的交点与右焦点连线的斜率( )A .35- B .53 C .34 D .433.已知双曲线1242522=-yx上一点M 到右准线的距离是10,2F 是右焦点,N 是2MF 的中点,O 坐标原点,则ON 等于( )A .2 B .2或7 C .7或12 D .2或124.设双曲线12222=-by ax 的右准线与渐进线交于B A 、两点,点F 为右焦点,若AB 以为直径的圆经过点F ,则该双曲线离心率为( )A .332 B .2 C .3 D .25.设双曲线12222=-by ax 与)0,0(12222>>=+-b a by ax 的离心率分别为21e e 、,则当b a 、在变化时,2221e e +的最小值是( )A .2B .42 C .22 D .46.若双曲线)0,0(12222>>=-b a by ax 的右支上存在一点,它到右焦点及左准线的距离相等,则双曲线离心率的取值范围为( ) A .(]2,1 B .[)+∞,2 C .(]12,1+ D .[)+∞+,127.双曲线两准线将实轴三等分,则双曲线的离心率为 8.已知:点)0,2(),0,3(F A ,在双曲线1322=-yx 上求一点P ,使PF PA 21+的值最小9.设双曲线C 的渐进线方程为034=±y x ,一条准线为516=y ,求双曲线C 的方程10.设双曲线中心在坐标原点,准线平行于x 轴,离心率为25,已知)5,0(P 到双曲线上的点最近距离为2,求此双曲线的方程 11.在双曲线1121322-=-yx的一支上有不同的三点),()6,(),(33211y x C x B y x A 、、,与焦点)5,0(F 成等差数列(1)求31y y +的值(2)求证:线段AC 的垂直平分线经过某一定点,并求出定点坐标12.已知双曲线的中心在原点,焦点21,F F 在坐标轴上,离心率为2,且过点)10,4(- (1)求此双曲线(2)若直线系03=+--m k y kx (其中k 为参数)所过定点M 恰好在双曲线上, 求证:M F M F 21⊥13.已知直线1+=ax y 与双曲线1322=-y x 交于B A ,两点 (1)若以AB 为直径的圆过坐标原点,求实数a 的值 (2)是否存在这样的实数a ,使B A ,两点关于直线x y 21=对称?若存在,请求出a 的值;若不存在,请说明理由 14.设双曲线)0(1:222>=-a yax C 与直线1:=+y x l 相交于不同的点B A 、(1)求双曲线C 的离心率e 的取值范围 (2)设直线l 与y 轴的交点为P ,且PB PA 125=,求a 的值。
人教版A版高中数学高二版选修2-1练习 2.3.2第2课时双曲线方程及性质的应用

第二章 圆锥曲线与方程2.3 双曲线2.3.2 双曲线的简单几何性质 第2课时 双曲线方程及性质的应用A 级 基础巩固一、选择题1.已知双曲线x 22-y 2a=1的一条渐近线为y =2x ,则实数a 的值为( )A.2 B .2 C.3 D .4解析:由题意,得2=a 2,所以a =4. 答案:D2.已知点P (3,-4)是双曲线x 2a 2-y 2b2=1(a >0,b >0)渐近线上的一点,E 、F 是左、右两个焦点,若EP →·FP →=0,则双曲线的方程为( )A.x 29-y 225=1 B.x 225-y 29=1 C.x 29-y 216=1 D.x 216-y 29=1解析:设E (-c ,0)、F (c ,0),于是有EP →·FP →=(3+c ,-4)·(3-c ,-4)=9-c 2+16=0.于是c 2=25.排除A ,B.又由D 中双曲线的渐近线方程为y =±34x ,点P 不在其上排除D.答案:C3.双曲线x 2-y 2=1的顶点到其渐近线的距离等于( )A.12B.22C .1 D. 2 答案:B4.已知△ABP 的顶点A ,B 分别为双曲线x 216-y 29=1的左、右焦点,顶点P 在双曲线上,则|sin A -sin B |sin P的值等于( ) A.45 B.74 C.54D.7 解析:在△ABP 中,由正弦定理知|sin A -sin B |sin P =||PB |-|PA |||AB |=2a 2c =810=45. 答案:A5.已知双曲线x 2a 2-y 2b2=1与直线y =2x 有交点,则双曲线离心率的取值范围为( )A .(1,5)B .(1,5]C .(5,+∞)D .[5,+∞)解析:因为双曲线的一条渐近线方程为y =b a x ,则由题意得b a>2.所以e =c a= 1+⎝ ⎛⎭⎪⎫b a 2>1+4= 5.答案:C二、填空题6.已知F 是双曲线x 24-y 212=1的左焦点,P 是双曲线右支上的动点,若A (1,4),则|PF |+|PA |的最小值是________.解析:因为A 点在双曲线的两支之间,且双曲线右焦点为F ′(4,0),于是由双曲线的定义得|PF |-|PF ′|=2a =4.而|PA |+|PF ′|≥|AF ′|=5.两式相加得|PF |+|PA |≥9,当且仅当A ,P ,F ′三点共线时,等号成立.由双曲线的图象可知当点A 、P 、F 1共线时,满足|PF 1|+|PA |最小,易求得最小值为|AF 1|=5, 故所求最小值为9.答案:97.设双曲线x 2a 2-y 2b2=1的左、右焦点分别为F 1,F 2,点P 在双曲线的右支上,且|PF 1|=4|PF 2|,则此双曲线离心率的最大值为________.解析:依据双曲线的定义得|PF 1|-|PF 2|=2a ,又|PF 1|=4|PF 2|,所以|PF 1|+|PF 2|=10a 3≥2c ,所以e =c a ≤53,e max =53. 答案:538.若双曲线E :x 2a 2-y 2=1(a >0)的离心率等于2,直线y =kx -1与双曲线E 的右支交于A ,B 两点.则k 的取值范围为________.答案:(1,2)三、解答题9.过双曲线x 23-y 26=1的右焦点F 2且倾斜角为30°的直线交双曲线于A 、B 两点,O 为坐标原点,F 1为左焦点.(1)求|AB |;(2)求△AOB 的面积.解:(1)由双曲线的方程得a =3,b =6,所以c =a 2+b 2=3,F 1(-3,0),F 2(3,0).直线AB 的方程为y =33(x -3). 设A (x 1,y 1),B (x 2,y 2),由⎩⎨⎧y =33(x -3)x 23-y 26=1,得5x 2+6x -27=0 所以x 1+x 2=-65,x 1x 2=-275, 所以|AB |=1+k 2|x 1-x 2|= 1+⎝ ⎛⎭⎪⎫332×(x 1+x 2)2-4x 1x 2= 43×3625+1085=1635. (2)直线AB 方程变形为3x -3y -33=0所以原点O 到直线AB 的距离为d =|-33|(3)2+(-3)2=32所以S △AOB =12|AB |·d =12×1635×32=1235. 10.已知双曲线的中心在原点,离心率为2,一个焦点为F (-2,0).(1)求双曲线方程;(2)设Q 是双曲线上一点,且过点F ,Q 的直线l 与y 轴交于点M ,若|MQ →|=2|QF →|,求直线l 的方程.解:(1)由题意可设所求的双曲线方程为x 2a 2-y 2b2=1(a >0,b >0), 则有e =c a=2,c =2,所以a =1,则b =3, 所以所求的双曲线方程为x 2-y 23=1. (2)因为直线l 与y 轴相交于M 且过焦点F (-2,0),所以l 的斜率一定存在,设为k ,则l :y =k (x +2),令x =0,得M (0,2k ),因为|MQ →|=2|QF →|且M ,Q ,F 共线于l ,所以MQ →=2QF →或MQ →=-2QF →.当MQ →=2QF →时,x Q =-43,y Q =23k , 所以Q 的坐标为⎝ ⎛⎭⎪⎫-43,23k , 因为Q 在双曲线x 2-y 23=1上, 所以169-4k 227=1,所以k =±212, 所以直线l 的方程为y =±212(x +2). 当MQ →=-2QF →时,同理求得Q (-4,-2k ),代入双曲线方程得,16-4k 23=1,所以k =±352, 所以直线l 的方程为y =±352(x +2), 综上,所求的直线l 的方程为y =±212(x +2)或y =±352(x +2). B 级 能力提升1.P 是双曲线x 2a 2-y 2b2=1上的点,F 1、F 2是其焦点,双曲线的离心率是54,且∠F 1PF 2=90°,若△F 1PF 2的面积是9,则a +b 的值(a >0,b >0)等于( )A .4B .7C .6D .5答案:B2.直线l 与双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)交于A ,B 两点,M 是线段AB 的中点,若l 与OM (O 是原点)的斜率的乘积等于1,则此双曲线的离心率为________.解析:设A (x 1,y 1),B (x 2,y 2),M (x 0,y 0),则x 21a 2-y 21b 2=1,① x 22a 2-y 22b 2=1,② 两式相减得(x 1+x 2)(x 1-x 2)a 2=(y 1+y 2)(y 1-y 2)b 2, 所以b 2a 2=(y 1+y 2)(y 1-y 2)(x 1+x 2)(x 1-x 2), 所以b 2a 2=2y 0(y 1-y 2)2x 0(x 1-x 2)=k 0·k 1=1, 所以a 2=b 2,即a =b ,所以e =c a =a 2+b 2a= 2. 答案: 23.设A ,B 分别为双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右顶点,双曲线的实轴长为43,焦点到渐近线的距离为 3.(1)求双曲线的方程;(2)已知直线y =33x -2与双曲线的右支交于M 、N 两点,且在双曲线的右支上存在点D ,使OM →+ON →=tOD →,求t 的值及点D 的坐标.解:(1)由题意知a =23,所以一条渐近线为y =b 23x ,即bx -23y =0, 所以|bc |b 2+12= 3. 所以b 2=3,所以双曲线的方程为x 212-y 23=1. (2)设M (x 1,y 1),N (x 2,y 2),D (x 0,y 0),则x 1+x 2=tx 0,y 1+y 2=ty 0.将直线方程代入双曲线方程得x 2-163x +84=0,则x 1+x 2=163,y 1+y 2=12.所以⎩⎨⎧x 0y 0=433,x 2012-y 203=1,所以⎩⎨⎧x 0=43,y 0=3.由OM →+ON →=tOD →,得 (163,12)=(43t ,3t ),所以t =4,点D 的坐标为(43,3).。
高中数学 2.2 第2课时 双曲线的简单几何性质练习 新人

【成才之路】2014-2015学年高中数学 2.2 第2课时 双曲线的简单几何性质练习 新人教A 版选修1-1一、选择题1.(2013·福建文,3)双曲线x 2-y 2=1的顶点到其渐近线的距离等于( ) A .12 B .22C .1D . 2[答案] B[解析] 双曲线x 2-y 2=1的一个顶点为A (1,0),一条渐近线为y =x ,则A (1,0)到y =x 距离为d =12=22. 2.椭圆x 234+y 2n 2=1和双曲线x 2n 2-y 216=1有共同的焦点,则实数n 的值是( )A .±5B .±3C .25D .9[答案] B[解析] 依题意,34-n 2=n 2+16,解得n =±3,故答案为B.3.(2013·北京理,6)若双曲线x 2a 2-y 2b2=1的离心率为3,则其渐近线方程为( )A .y =±2xB .y =±2xC .y =±12xD .y =±22x [答案] B[解析] 本题考查双曲线的离心率及渐近线方程等几何性质.因为离心率e =3,所以c =3a ,即b =2a ,由双曲线的焦点在x 轴上,所以渐近线方程为y =±b a=±2x .选B.4.(2013·湖北文,2)已知0<θ<π4,则双曲线C 1:x 2sin 2θ-y 2cos 2θ=1,与C 2:y2cos 2θ-x 2sin 2θ=1 ( ) A .实轴长相等 B .虚轴长相等 C .离心率相等 D .焦距相等[答案] D[解析] 本题考查双曲线的性质.由双曲线的性质c 2=a 2+b 2知,C 1:c 2=sin 2θ+cos 2θ=1,C 2:c 2=cos 2θ+sin 2θ=1.∴C 1与C 2的焦距相等,故选D.5.经过点M (26,-26)且与双曲线x 24-y 23=1有相同渐近线的双曲线方程是( )A .x 26-y 28=1B .y 28-x 26=1C .y 26-x 28=1D .x 28-y 26=1[答案] C[解析] 设双曲线方程为x 24-y 23=λ(λ≠0),把点M (26,-26)代入双曲线方程,得λ=244-243=-2,∴双曲线方程为:y 26-x 28=1.6.(2013·北京文,7)双曲线x 2-y 2m=1的离心率大于2的充分必要条件是( )A .m >12B .m ≥1C .m >1D .m >2[答案] C[解析] 本题考查双曲线离心率的概念,充分必要条件的理解. 双曲线离心率e =1+m >2,所以m >1,选C. 二、填空题7.(2013·泗阳县模拟)两个正数a 、b 的等差中项是92,等比中项是25,且a >b ,则双曲线x 2a 2-y 2b2=1的离心率为________.[答案]415[解析] ∵两个正数a 、b 的等差中项是92,等比中项是25,且a >b ,∴⎩⎪⎨⎪⎧a +b 2=92,ab =25,a >b ,解得a =5,b =4,∴双曲线方程为x 225-y 216=1,∴c =25+16=41,∴双曲线x 2a 2-y 2b 2=1的离心率e =c a =415.8.已知双曲线C 1:x 2a 2-y 2b 2=1(a >0,b >0)与双曲线C 2:x 24-y 216=1有相同的渐近线,且C 1的右焦点为F (5,0),则a =________,b =________.[答案] 1 2[解析] 利用共渐近线方程求解.与双曲线x 24-y 216=1有共同渐近线的双曲线的方程可设为x 24-y 216=λ,即x 24λ-y 216λ=1.由题意知c =5,则4λ+16λ=5⇒λ=14,则a 2=1,b 2=4.又a >0,b >0,故a =1,b =2.9.(2014·天津市六校联考)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)和椭圆x 216+y 29=1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为__________________.[答案]x 24-y 23=1[解析] 椭圆中,a 2=16,b 2=9,∴c 2=a 2-b 2=7, ∴离心率e 1=74,焦点(±7,0), ∴双曲线的离心率e 2=c a =72,焦点坐标为(±7,0), ∴c =7,a =2,从而b 2=c 2-a 2=3, ∴双曲线方程为x 24-y 23=1.三、解答题10.(1)求与椭圆x 29+y 24=1有公共焦点,且离心率e =52的双曲线的方程;(2)求虚轴长为12,离心率为54的双曲线的标准方程.[解析] (1)设双曲线的方程为x 29-λ-y 2λ-4=1(4<λ<9),则a 2=9-λ,b 2=λ-4,∴c 2=a 2+b 2=5,∵e =52,∴e 2=c 2a 2=59-λ=54,解得λ=5,∴所求双曲线的方程为x 24-y 2=1.(2)由于无法确定双曲线的焦点在x 轴上还是在y 轴上,所以可设双曲线标准方程为x 2a 2-y 2b 2=1(a >0,b >0)或y 2a 2-x 2b2=1(a >0,b >0). 由题设知2b =12,c a =54且c 2=a 2+b 2,∴b =6,c =10,a =8.∴双曲线的标准方程为x 264-y 236=1或y 264-x 236=1.一、选择题11.已知方程ax 2-ay 2=b ,且a 、b 异号,则方程表示( ) A .焦点在x 轴上的椭圆 B .焦点在y 轴上的椭圆 C .焦点在x 轴上的双曲线 D .焦点在y 轴上的双曲线[答案] D[解析] 方程变形为x 2b a -y 2b a=1,由a 、b 异号知ba <0,故方程表示焦点在y 轴上的双曲线,故答案为D.12.(2014·吉林延边州质检)已知双曲线x 29-y 2m=1的一个焦点在圆x 2+y 2-4x -5=0上,则双曲线的渐近线方程为( )A .y =±34xB .y =±43xC .y =±223xD .y =±324x[答案] B[解析] ∵方程表示双曲线,∴m >0,∵a 2=9,b 2=m , ∴c 2=a 2+b 2=9+m ,∴c =9+m ,∵双曲线的一个焦点在圆上,∴9+m 是方程x 2-4x -5=0的根,∴9+m =5,∴m =16,∴双曲线的渐近线方程为y =±43x ,故选B.13.已知椭圆x 2a 2+y 2b 2=1(a >b >0)的离心率为12,则双曲线x 2a 2-y 2b2=1的渐近线方程为( )A .y =±32x B .y =±12xC .y =±2xD .y =±233x[答案] A[解析] 由题意得a 2-b 2a =12,∴3a 2=4b 2,∴b a =32. ∴双曲线x 2a 2-y 2b 2=1的渐近线方程为y =±32x .14.(2014·天津理,5)已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的一条渐近线平行于直线l :y=2x +10,双曲线的一个焦点在直线l 上,则双曲线的方程为( )A .x 25-y 220=1B .x 220-y 25=1 C .3x 225-3y2100=1D .3x 2100-3y225=1 [答案] A[解析] 由于一个焦点在直线y =2x +10上,则一个焦点为(-5,0),又由渐近线平行于直线y =2x +10.则b a=2,结合a 2+b 2=c 2,c =5得,∴a 2=5,b 2=20,双曲线标准方程为x 25-y 220=1,选A.二、填空题15.(2014·三峡名校联盟联考)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的一条渐近线方程为x-2y =0,则椭圆x 2a 2+y 2b2=1的离心率e =________.[答案]32[解析] 由条件知b a =12,即a =2b ,∴c 2=a 2-b 2=3b 2,c =3b , ∴e =c a =3b 2b =32. 三、解答题16.焦点在x 轴上的双曲线过点P (42,-3),且点Q (0,5)与两焦点的连线互相垂直,求此双曲线的标准方程.[解析] 因为双曲线焦点在x 轴上,所以设双曲线的标准方程为x 2a 2-y 2b 2=1(a >0,b >0),F 1(-c,0),F 2(c,0).因为双曲线过点P (42,-3), 所以32a 2-9b2=1.①又因为点Q (0,5)与两焦点的连线互相垂直, 所以QF 1→·QF 2→=0,即-c 2+25=0. 所以c 2=25. ② 又c 2=a 2+b 2,③所以由①②③可解得a 2=16或a 2=50(舍去). 所以b 2=9,所以所求的双曲线的标准方程是x 216-y 29=1.17.设双曲线x 2a 2-y 2b2=1(0<a <b )的半焦距为c ,直线l 过(a,0)、(0,b )两点,且原点到直线l 的距离为34c ,求双曲线的离心率. [分析] 由截距式得直线l 的方程,再由双曲线中a 、b 、c 的关系及原点到直线l 的距离建立等式,从而求出c a.[解析] 由l 过两点(a,0)、(0,b ),得l 的方程为bx +ay -ab =0.由原点到l 的距离为34c ,得ab a 2+b2=34c . 将b =c 2-a 2代入,平方后整理,得16⎝ ⎛⎭⎪⎫a 2c 22-16×a 2c 2+3=0.令a 2c 2=x ,则16x 2-16x +3=0,解得x =34或x =14.由e =ca有e =1x .故e =233或e =2. 因0<a <b ,故e =c a =a 2+b 2a =1+b 2a2>2, 所以应舍去e =233,故所求离心率e =2.。
课时规范练70 双曲线的定义、方程与性质--2025高中数学一轮复习课件基础版(新高考新教材)

2
− 2 =1(a>0,b>0)的左、右焦点分别为
2
⊥ 1 , 2 =- 2 ,则 C 的离心率
3
.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
解析 (方法 1 坐标法)
设 A(x,y),B(0,m),不妨令点 A 在第一象限,则 m<0.
设 F1(-c,0),F2(c,0),其中 c>0,
则 F1(-2,0),F2(2,0).
因为|OP|=2,所以点 P 在以 O 为圆心,F1F2 为直径的圆上,故 PF1⊥PF2,
则|PF1|2+|PF2|2=(2c)2=16.由双曲线的定义可知Hale Waihona Puke |PF1|-|PF2||=2a=2,
所以|PF1|2+|PF2|2-2|PF1|·
|PF2|=4,
1
所以|PF1|·
好平分第一、三象限,若C的虚轴长为4,则C的实轴长为
解析 由题意可知,双曲线C的一条渐近线为直线y=x,故a=b,
故其实轴长为2a=2b=4.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
4
.
10.(2024·山西阳泉模拟)请写出一个焦点在y轴上,且与直线y=2x没有交点
2 2
2
2
1 2
2
2
2
42
20
将|yP|=4 代入16 − 9 =1 得16 − 9 =1,得|xP|= 3 .
20
由双曲线的对称性,不妨取点 P 的坐标为 3 ,4
13
37
由双曲线的定义得|PF1|=|PF2|+2a= +8= ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录双曲线的简单性质 (1)【学习目标】 (1)【要点梳理】 (1)【典型例题】 (5)【巩固练习】 (13)双曲线的简单性质编稿:武小煊审稿:柏兴增【学习目标】1.知识与技能理解双曲线的范围、对称性及对称轴,对称中心、离心率、顶点、渐近线的概念.2.过程与方法锻炼学生观察分析抽象概括的逻辑思维能力和运用数形结合思想解决实际问题的能力.3.情感态度与价值观通过数与形的辨证统一,对学生进行辩证唯物主义教育,通过对双曲线对称美的感受,激发学生对美好事物的追求.【要点梳理】【高清课堂:双曲线的性质356749 知识要点二】要点一:双曲线的简单几何性质双曲线22221x ya b-=(a>0,b>0)的简单几何性质范围221x a≥,即22x a ≥ ∴x a ≥,或x a ≤-.双曲线上所有的点都在两条平行直线x = -a 和x = a 的两侧,是无限延伸的.因此双曲线上点的横坐标满足∴x a ≥,或x a ≤-.对称性对于双曲线标准方程22221x y a b -=(a >0,b >0),把x 换成-x ,或把y 换成-y ,或把x 、y 同时换成-x 、-y ,方程都不变,所以双曲线22221x y a b -=(a >0,b >0)是以x 轴、y 轴为对称轴的轴对称图形,且是以原点为对称中心的中心对称图形,这个对称中心称为双曲线的中心.顶点①双曲线与它的对称轴的交点称为双曲线的顶点.②双曲线22221x y a b -=(a >0,b >0)与坐标轴的两个交点即为双曲线的两个顶点,坐标分别为A 1(-a ,0),A 2(a ,0),顶点是双曲线两支上的点中距离最近的点.③两个顶点间的线段A 1A 2叫作双曲线的实轴;设B 1(0,- b ),B 2(0,b )为y 轴上的两个点,则线段B 1B 2叫做双曲线的虚轴.实轴和虚轴的长度分别为|A 1A 2|=2a ,|B 1B 2|=2b .a 叫做双曲线的实半轴长,b 叫做双曲线的虚半轴长.①双曲线只有两个顶点,而椭圆有四个顶点,不能把双曲线的虚轴与椭圆的短轴混淆. ②双曲线的焦点总在实轴上.③实轴和虚轴等长的双曲线称为等轴双曲线. 离心率①双曲线的焦距与实轴长的比叫做双曲线的离心率,用e 表示,记作22c ce a a==. ②因为c >a >0,所以双曲线的离心率1ce a=>. 由c 2= a 2+b 2,可得22222()11b c a c e a a a -==-=-,所以b a 决定双曲线的开口大小,b a越大,e 也越大,双曲线开口就越开阔.所以离心率可以用来表示双曲线开口的大小程度.③等轴双曲线a b=,所以离心率2e=.渐近线经过点A2、A1作y轴的平行线x=±a,经过点B1、B2作x轴的平行线y=±b,四条直线围成一个矩形(如图),矩形的两条对角线所在直线的方程是by xa=±.我们把直线by xa=±叫做双曲线的渐近线;双曲线与它的渐近线无限接近,但永不相交.22||b bMN x a xa a=--2222bx a xaabx x a=--=→+-【高清课堂:双曲线的性质356749知识要点一、3】要点二:双曲线两个标准方程几何性质的比较标准方程22221x ya b-=(0,0)a b>>22221y xa b-=(0,0)a b>>图形性质焦点1(,0)F c-,2(,0)F c1(0,)F c-,2(0,)F c要点诠释:双曲线的焦点总在实轴上,因此已知标准方程,判断焦点位置的方法是:看x 2、y 2的系数,如果x 2项的系数是正的,那么焦点在x 轴上;如果y 2项的系数是正的,那么焦点在y 轴上.对于双曲线,a 不一定大于b ,因此不能像椭圆那样通过比较分母的大小来判定焦点在哪一条坐标轴上. 要点三:双曲线的渐近线(1)已知双曲线方程求渐近线方程:若双曲线方程为22221x y a b -=,则其渐近线方程为22220x y a b -=⇒0x y a b ±=⇒b y x a =±已知双曲线方程,将双曲线方程中的“常数”换成“0”,然后因式分解即得渐近线方程. (2)已知渐近线方程求双曲线方程:若双曲线渐近线方程为0mx ny ±=,则可设双曲线方程为2222m x n y λ-=,根据已知条件,求出λ即可.(3)与双曲线22221x y a b-=有公共渐近线的双曲线与双曲线22221x y a b -=有公共渐近线的双曲线方程可设为2222(0)x y a bλλ-=≠(0λ>,焦点在x 轴上,0λ<,焦点在y 轴上)(4)等轴双曲线的渐近线等轴双曲线的两条渐近线互相垂直,为y x =±,因此等轴双曲线可设为22(0)x y λλ-=≠. 要点四:双曲线中a ,b ,c 的几何意义及有关线段的几何特征双曲线标准方程中,a 、b 、c 三个量的大小与坐标系无关,是由双曲线本身的形状大小所确定的,分别表示双曲线的实半轴长、虚半轴长和半焦距长,均为正数,且三个量的大小关系为:c >b >0,c >a >0,且c 2=a 2+b 2.双曲线22221x y a b-=(0,0)a b >>,如图:(1)实轴长12||2A A a =,虚轴长2b ,焦距12||2F F c =;(2)离心率:21211222121122||||||||11||||||||PF PF A F A F c b e e PM PM A K A K a a======+>; (3)顶点到焦点的距离:11A F =22A F c a =-,12A F =21A F a c =+;(4)12PF F ∆中结合定义122PF PF a -=与余弦定理,将有关线段1PF 、2PF 、12F F 和角结合起来; (5)与焦点三角形12PF F ∆有关的计算问题时,常考虑到用双曲线的定义及余弦定理(或勾股定理)、三角形面积公式121211sin 2PF F S PF PF F PF ∆=⋅∠相结合的方法进行计算与解题,将有关线段1PF 、2PF 、12F F ,有关角12F PF ∠结合起来,建立12PF PF -、12PF PF ⋅之间的关系.要点五:直线与双曲线的位置关系 直线与双曲线的位置关系将直线的方程y kx m =+与双曲线的方程22221x y a b-=(0,0)a b >>联立成方程组,消元转化为关于x或y 的一元二次方程,其判别式为Δ.222222222()20b a k x a mkx a m a b ----=.若2220,b a k -=即bk a =±,直线与双曲线渐近线平行,直线与双曲线相交于一点(实质上是直线与渐近线平行时的两种情况,相交但不相切).若2220,b a k -≠即b k a≠±, ①Δ>0⇔直线和双曲线相交⇔直线和双曲线相交,有两个交点; ②Δ=0⇔直线和双曲线相切⇔直线和双曲线相切,有一个公共点; ③Δ<0⇔直线和双曲线相离⇔直线和双曲线相离,无公共点. 直线与双曲线的相交弦设直线y kx m =+交双曲线22221x y a b-=(0,0)a b >>于点111222(,),(,)P x y P x y 两点,则弦长12||PP12|x x -同理可得1212|||(0)PP y y k =-≠ 这里12||,x x -12||,y y -的求法通常使用韦达定理,需作以下变形:12||x x -=;12||y y -双曲线的中点弦问题遇到中点弦问题常用“韦达定理”或“点差法”求解.在双曲线22221x y a b-=(0,0)a b >>中,以00(,)P x y 为中点的弦所在直线的斜率2020b x k a y =-;涉及弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来相互转化,同时还应充分挖掘题目的隐含条件,寻找量与量间的关系灵活转化,往往就能事半功倍.解题的主要规律可以概括为“联立方程求交点,韦达定理求弦长,根的分布找范围,曲线定义不能忘”.【典型例题】类型一:双曲线的简单几何性质【高清课堂:双曲线的性质 356749例1】例1.求双曲线22169144x y -=的实轴长和虚轴长、顶点坐标、焦点坐标、渐近线方程与离心率.【思路点拨】本题的关键是将双曲线化为标准方程22221x y a b -=(0,0)a b >>.【解析】双曲线的方程可化为:221916y x -=,由此可知实半轴长3a =,虚半轴长4b =,∴5c ==∴实轴长26a =,虚轴长28b =,顶点坐标(0,3),(0,3)-,焦点坐标(0,5),(0,5)-,离心率53e =,渐近线方程34y x =±.【总结升华】在几何性质的讨论中要注意a 和2a ,b 和2b 的区别,另外也要注意焦点所在轴的不同,几何量也有不同的表示.举一反三:【变式1】双曲线mx 2+y 2=1的虚轴长是实轴长的2倍,则m 等于( )A .14-B .-4C .4D .14【答案】A【变式2】已知双曲线8kx 2-ky 2=2的一个焦点为3(0,)2-,则k 的值等于( )A .-2B .1C .-1D .32-【答案】C类型二:双曲线的渐近线例2.已知双曲线方程,求渐近线方程.(1)221916x y -=;(2)221916x y -=-.【解析】(1)双曲线221916x y -=-的渐近线方程为:220916x y -=,即43y x =±.(2)双曲线221916x y -=的渐近线方程为:220916x y -=,即43y x =±.【总结升华】不同形式双曲线的渐进线方程为:(1)双曲线22221(0,0)x y a b a b -=>>的渐近线方程为by x a =±;(2)双曲线22221y x a b -=的渐近线方程为b x y a =±,即ay x b=±;(3)若双曲线的方程为2222x y m n λ-=(00m n λ>>、,,焦点在x 轴上,0λ<,焦点在y 轴上),则其渐近线方程为22220x y m n -=⇒0x y m n ±=⇒ny x m=±.举一反三:【变式1】求下列双曲线方程的渐近线方程:(1)2211636x y -=;(2)2228x y -=; (3)22272y x -=.【答案】(1)32y x =±;(2)y x =;(3)y = 【变式2】中心在坐标原点,离心率为53的圆锥曲线的焦点在y 轴上,则它的渐近线方程为( )A .54y x =±B .45y x =±C .43y x =±D .34y x =±【答案】D例3. 根据下列条件,求双曲线方程.(1) 与双曲线221916x y -=有共同的渐近线,且过点(3,-;(2)一渐近线方程为320x y +=,且双曲线过点M .【思路点拨】求双曲线的方程,应先定型,再定量.本题中“定型”是顺利解题的关键:(1)与双曲线有221916x y -=有公共渐进线的双曲线方程可设为()220916x y λλ-=≠;(2)320023x y x y +=⇔±=,以023x y±=为渐进线的双曲线方程可设为2249x y λ-=()0λ≠.【解析】 (1)解法一:当焦点在x 轴上时,设双曲线的方程为22221x y a b -=由题意,得2243(3)1b a a ⎧=⎪⎪⎨-⎪=⎪⎩,解得294a =,24b = 所以双曲线的方程为224194x y -=.当焦点在y 轴上时,设双曲线的方程为22221y x a b-=由题意,得2243(3)1a b b ⎧=⎪⎪--=,解得24a =-,294b =-(舍去) 综上所得,双曲线的方程为224194x y -=解法二:设所求双曲线方程为22916x y λ-=(0λ≠),将点(3,-代入得14λ=,所以双曲线方程为2219164x y -=即224194x y -=(2)依题意知双曲线两渐近线的方程是023x y±=.故设双曲线方程为2249x y λ-=,∵点M 在双曲线上, ∴284λ=,解得4λ=,∴所求双曲线方程为2211636x y -=.【总结升华】求双曲线的方程,关键是求a 、b ,在解题过程中应熟悉各元素(a 、b 、c 、e 及准线)之间的关系,并注意方程思想的应用.若已知双曲线的渐近线方程0ax by ±=,可设双曲线方程为2222a x b y λ-=(0λ≠).举一反三:【变式1】中心在原点,一个焦点在(0,3),一条渐近线为23y x =的双曲线方程是( ) A .225513654x y -= B .225513654x y -+= C .22131318136x y -= D .22131318136x y -+=【答案】D【变式2】过点(2,-2)且与双曲线2212x y -=有公共渐近线的双曲线是 ( )A . 22124y x -=B . 22142x y -=C . 22142y x -=D . 22124x y -=【答案】A【变式3】设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=,则a 的值为A .4B .3C .2D .1 【答案】C【变式4】双曲线22221x y a b -=与2222(0)x y a b λλ-=≠有相同的( )A .实轴B .焦点C .渐近线D .以上都不对 【答案】C类型三:求双曲线的离心率或离心率的取值范围例4. 已知12,F F 是双曲线22221(0)x y a b a b -=>>的左、右焦点,过1F 且垂直于x 轴的直线与双曲线的左支交于A 、B 两点,若2ABF ∆是正三角形,求双曲线的离心率.【解析】∵12||2F F c =,2ABF ∆是正三角形,∴12||2tan30AF c ==,224||2tan30cos30c AF c ===,∴21||||2AF AF a -===,∴3ce a== 【总结升华】双曲线的离心率是双曲线几何性质的一个重要参数,求双曲线离心率的关键是由条件寻求a 、c 满足的关系式,从而求出c e a=举一反三:【高清课堂:双曲线的性质 356749例2】 【变式1】(1) 已知双曲线22221(0,0)x y a b a b-=>>的离心率23e =,过点A (0,-b )和B (a ,0)的直线与原点间的距3,求双曲线的方程. (2) 求过点(-1,3),且和双曲线22149x y -=有共同渐近线的双曲线方程.【答案】(1)2213x y -=; (2)2241273y x -=【变式2】 等轴双曲线的离心率为_________2【变式3】已知a 、b 、c 分别为双曲线的实半轴长、虚半轴长、半焦距,且方程ax 2+bx +c =0无实根,则双曲线离心率的取值范围是( )A .1<e 5-2B .1< e <2C .1< e <3D .1< e <25【答案】D类型五:双曲线的焦点三角形例5.已知双曲线实轴长6,过左焦点1F 的弦交左半支于A 、B 两点,且||8AB =,设右焦点2F ,求2ABF ∆的周长.【思路点拨】将2ABF ∆的周长分拆成2211|||||||AF BF AF BF ,,,的和,利用双曲线的定义及条件||8AB =可求得周长.【解析】由双曲线的定义有: 21||||6AF AF -=,21||||6BF BF -=,∴2211(||||)(||||)12AF BF AF BF +-+=. 即22(||||)||12AF BF AB +-= ∴22||||12||20AF BF AB +=+=.故2ABF ∆的周长22||||||28L AF BF AB =++=.【总结升华】双曲线的焦点三角形中涉及了双曲线的特征几何量,在双曲线的焦点三角形中,经常运用正弦定理、余弦定理、双曲线定义来解题,解题过程中,常对定义式两边平方探求关系.举一反三:【变式1】已知双曲线的方程22221x y a b -=,点A 、B 在双曲线的右支上,且线段AB 经过双曲线的右焦点F 2,|AB |=m ,F 1为另一焦点,则△ABF 1的周长为( )A .2a +2mB .4a +2mC .a +mD .2a +4m【答案】B【变式2】已知12F F 、是双曲线221916x y -=的两个焦点,P 在双曲线上且满足12||||32PF PF ⋅=,则12F PF ∠=______【答案】90类型六:直线和双曲线的位置关系例6. 已知双曲线x 2-y 2=4,直线l :y =k (x -1),讨论直线与双曲线公共点个数.【思路点拨】直线与曲线恰有一个交点,即由直线方程与曲线方程联立的方程组只有一组解.【解析】联立方程组⎩⎨⎧=--=4)1(22y x x k y 消去y ,并依x 项整理得:(1-k 2)·x 2+2k 2x -k 2-4=0 ①(1)当1-k 2=0即k =±1时,方程①可化为2x =5,x =25,方程组只有一组解,故直线与双曲线只有一个公共点(实质上是直线与渐近线平行时的两种情况,相交但不相切).(2)当1-k 2≠0时,即k ≠±1,此时有Δ=4·(4-3k 2)若4-3k 2>0(k 2≠1),则k ∈⎪⎪⎭⎫ ⎝⎛⋃-⋃⎪⎪⎭⎫ ⎝⎛--332,1)1,1(1,332,方程组有两解,故直线与双曲线有两交点. (3)若4-3k 2=0(k 2≠1),则k =±332,方程组有解,故直线与双曲线有一个公共点(相切的情况). (4)若4-3k 2<0且k 2≠1则k ∈⎪⎪⎭⎫ ⎝⎛+∞⋃⎪⎪⎭⎫ ⎝⎛-∞-,332432,,方程组无解,故直线与双曲线无交点. 综上所述,当k =±1或k =±332时,直线与双曲线有一个公共点; 当k ∈⎪⎪⎭⎫ ⎝⎛⋃-⋃⎪⎪⎭⎫ ⎝⎛--332,1)1,1(1,332时,直线与双曲线有两个公共点; 当k ∈⎪⎪⎭⎫ ⎝⎛+∞⋃⎪⎪⎭⎫ ⎝⎛-∞-,332332,时,直线与双曲线无公共点. 【总结升华】本题通过方程组解的个数来判断直线与双曲线交点的个数,具体操作时,运用了重要的数学方法——分类讨论,而且是“双向讨论”,既要讨论首项系数1——k 2是否为0,又要讨论Δ的三种情况,为理清讨论的思路,可画“树枝图”如图:举一反三:【变式1】过原点的直线l 与双曲线3422y x -=-1交于两点,则直线l 的斜率取值范围是 ( ) A .⎥⎥⎦⎤ ⎝⎛-23,23 B .⎪⎪⎭⎫ ⎝⎛+∞⋃⎪⎪⎭⎫ ⎝⎛-∞-,2323, C .⎥⎥⎦⎤⎢⎢⎣⎡-23,33 D .⎪⎪⎭⎫⎢⎢⎣⎡+∞⋃⎥⎥⎦⎤ ⎝⎛-∞-,2323, 【答案】B【变式2】直线y =x +3与曲线-x 1x ·|x |+91y 2=1的交点个数是 ( ) A .0 B .1 C .2 D .3【答案】D例7.(1)求直线1y x =+被双曲线2214y x -=截得的弦长; (2)求过定点(0,1)的直线被双曲线2214y x -=截得的弦中点轨迹方程. 【思路点拨】(1)题为直线与双曲线的弦长问题,可以考虑弦长公式,结合韦达定理进行求解.(2)题涉及到直线被双曲线截得弦的中点问题,可采用点差法或中点坐标公式,运算会更为简便.【解析】由22141y x y x ⎧-=⎪⎨⎪=+⎩得224(1)40x x -+-=得23250x x --=(*) 设方程(*)的解为12,x x ,则有121225,33x x x x +==- 得, 212121242082|2()422933d x x x x x x =-=+-=+=. (2)方法一:若该直线的斜率不存在时与双曲线无交点,则设直线的方程为1y kx =+,它被双曲线截得的弦为AB 对应的中点为(,)P x y ,由22114y kx y x =+⎧⎪⎨-=⎪⎩得22(4)250k x kx ---=(*) 设方程(*)的解为12,x x ,则22420(4)0k k ∆=+->∴21680,||k k << 且12122225,44k x x x x k k +==---, ∴121212221114(),()()124224k x x x y y y x x k k =+==+=++=--, 22444k x k y k ⎧=⎪⎪-⎨⎪=⎪-⎩得2240(4x y y y -+=<-或0)y >.方法二:设弦的两个端点坐标为1122(,),(,)A x y B x y ,弦中点为(,)P x y ,则221122224444x y x y ⎧-=⎪⎨-=⎪⎩得:121212124()()()()x x x x y y y y +-=+-, ∴121212124()y y x x x x y y +-=+-, 即41y x x y =-, 即2240x y y -+=(图象的一部分)【总结升华】(1)弦长公式1212||||AB x x y y =-=-; (2)注意上例中有关中点弦问题的两种处理方法.举一反三: 【变式】垂直于直线230x y +-=的直线l 被双曲线221205x y -=l 的方程 【答案】210y x =±【巩固练习】一、选择题1.焦点为(0,±6)且与双曲线2212x y -=有相同渐近线的双曲线方程是( )A.2211224x y -= B.2211224y x -= C.2212412y x -= D.2212412x y -= 2.双曲线2222ay b x -=1的两条渐近线互相垂直,那么该双曲线的离心率是( ) A. 2 B.3 C.2 D.23 3.双曲线与椭圆2211664x y +=有相同的焦点,它的一条渐近线方程为y x =-,则双曲线的离心率为( ) A.2296x y -= B. 22160y x -= C. 2280x y -= D. 2224y x -= 4.过双曲线2222by a x -=1的右焦点F 2作垂直于实轴的弦PQ ,F 1是左焦点,若∠PF 1Q=90︒,则双曲线的离心率是( ) A.2 B.1+2C.2+2D.35. 已知双曲线22221x y a b-=(a >0,b >0)的焦点到渐近线的距离是其顶点到渐近线距离的3倍,则双曲线的渐近线方程为( )A .y =xB .y =±xC .y =±4x D .y =±3x 6.与双曲线16922y x -=1有共同的渐近线,且经过点(-3,23)的双曲线的一个焦点到一条渐近线的距离是( ).A.8B.4C.2D.1二、填空题7.已知双曲线C :22221x y a b-=(a >0,b >0)的实轴长为2,离心率为2,则双曲线C 的焦点坐标是________. 8.椭圆22214x y a+=与双曲线2221x y a -=焦点相同,则a =________.9.双曲线以椭圆221925x y +=的焦点为焦点,它的离心率是椭圆离心率的2倍,求该双曲线的方程为________. 10.过点P (3,0)的直线l 与双曲线4x 2-9y 2=36只有一个公共点,则这样的直线l 共有________条.三、解答题11.设双曲线2222by a x -=1(0<a<b )的半焦距为c ,直线l 过(a,0),(0,b)两点.已知原点到直线l 的距离为43c ,求双曲线的离心率.12. 设双曲线C :1:)0(1222=+>=-y x l a y ax 与直线相交于两个不同的点A 、B ;求双曲线C 的离心率e 的取值范围:13.已知双曲线22221x y a b-=(a >0,b >0)过点(14,5)A ,且点A 到双曲线的两条渐近线的距离的积为43,求此双曲线方程. 14.已知双曲线2214x y -=的两个焦点分别为12F F 、,点P 在双曲线上且满足1290F PF ∠=,求12F PF ∆的面积.15.如下图,已知F 1,F 2是双曲线22221x y a b-=(a >0,b >0)的两焦点,以线段F 1F 2为边作正三角形MF 1F 2,若边MF 1的中点在双曲线上,求双曲线的离心率.【答案与解析】1.【答案】: B【解析】: 与双曲线2212x y -=有共同渐近线的双曲线方程可设为222x y λ-=(λ≠0), 又因为双曲线的焦点在y 轴上,∴方程可写为2212x λλλ-=--. 又∵双曲线方程的焦点为(0,±6),∴-λ-2λ=36.∴λ=-12. ∴双曲线方程为2211224y x -=. 2.【答案】C 【解析】双曲线的渐近线方程为a y x b=± ∵渐近线互相垂直,且关于坐标轴对称,∴1a b =,得a=b. 双曲线离心率222c a b e a +===. 3.【答案】 D【解析】 设双曲线方程为22(0)y x λλ-=≠∵焦点(0,43),±∴0,λ>又22(43)λ=,24λ=4. 【答案】B 【解析】因为|PF 2|=|F 2F 1|, P 点满足2222b y a c -=1,∴22b y c a a=-, ∴222b c c a a=-,即 2ac=b 2=c 2-a 2, ∴12e e =-,故e=1+2. 5. 【答案】 B【解析】如图,分别过双曲线的右顶点A ,右焦点F 作它的渐近线的垂线,B 、C 分别为垂足,则△OBA ∽△OCF , ∴13OA AB OF FC ==, ∴13a c =,∴22b a = 故渐近线方程为:22y x =±.6. 【答案】C【解析】设所求方程为22916x y k -=,代入(-3,23)得14k =, 52c =, ∵双曲线221916x y -=的渐近线为43y x =±, ∴焦点5(,0)2到渐近线43y x =±的距离d=2. 7. 【答案】(±2,0)【解析】由题意得:a =1,e =c a =2,所以c =2,又由标准方程可得焦点在x 轴上,所以焦点坐标为(±2,0).8.【答案】2【解析】; 由题意得4-a 2=a 2+1,∴2a 2=3,a=29.【答案】 221253944y x -= 【解析】 椭圆221925x y +=中,a =5,b =3,c 2=16, 焦点为(0,±4),离心率45c e a ==, ∴双曲线的离心率e 1=2e =85, ∴111485c a a ==,∴a 1=52, ∴22211125164b c a =-=-=394, ∴双曲线的方程为221253944y x -=. 10. 【答案】3【解析】已知双曲线方程为22194y x -=,故P (3,0)为双曲线的右顶点,所以过P 点且与双曲线只有一个公共点的直线共有三条(一条切线和两条与渐近线平行的直线).11.【解析】 由已知,l 的方程为ay+bx-ab=0,原点到l4c =,又c 2=a 2+b 2,∴24ab =,两边平方,得16a 2(c 2-a 2)=3c 4. 两边同除以a 4并整理得3e 4-16e 2+16=0,∴e 2=4或243e =. ∵ 0<a<b, 1b a>,221b a >,得22222212a b b e a a +==+>, ∴e 2=4,故e=2.12.【解析】由C 与t 相交于两个不同的点,故知方程组⎪⎩⎪⎨⎧=+=-.1,1222y x y a x 有两个不同的实数解.消去y 并整理得 (1-a 2)x 2+2a 2x -2a 2=0.242210.0 1.48(1)0.a a a a a a ⎧-≠⎪<≠⎨+->⎪⎩所以解得双曲线的离心率01,2(2,).2e a a e e e =<<≠∴>≠+∞即离心率的取值范围为13.【解析】双曲线22221x y a b-=的两渐近线的方程为bx ±ay =0. 点A 到两渐近线的距离分别为1d =2d =已知d 1d 2=43,故2222|145|43b a a b -=+ (ⅰ) 又A 在双曲线上,则14b 2-5a 2=a 2b 2(ⅱ)(ⅱ)代入(ⅰ),得3a 2b 2=4a 2+4b 2(ⅲ)联立(ⅱ)、(ⅲ)解得b 2=2,a 2=4.故所求双曲线方程为22142x y -=. 14. 【解析】解法一: 由双曲线的方程知a=2, b=1, ∴5c =. 因此12||225F F c ==.由于双曲线是对称图形,如图所示, 设P 点坐标为(x,142-x ), 由已知F 1P ⊥F 2P ,∴111F P F P k k ⋅=-, 即221144155x x x x --⋅=-+-, 得2245x =,∴1221211||12512425F PF x S F F ∆=⋅⋅-=⨯⨯= 解法二:∵(|PF 1|-|PF 2|)2=4a 2=16,又由勾股定理得|PF 1|2+|PF 1|2=(2c)2=20, ∴|PF 1||PF 2|=21[|PF 1|2+|PF 2|2-(|PF 1|-|PF 2|)2]=21(20-16)=2, ∴121F PF S ∆=.15.【解析】设MF 1的中点为P ,在Rt △PMF 2中,|PF 2|=|MF 2|·sin60°=2c ·32=3c .又由双曲线的定义得|PF 2|-|PF 1|=2a ,所以312a c -=,3131c e a ===+-.。
