北京四中2014届九年级数学总复习专练:《二次函数》全章复习与巩固—巩固练习(基础)
北京四中2014届九年级数学总复习专练:《二次函数》全章复习与巩固—知识讲解(基础)

《二次函数》全章复习与巩固—知识讲解(基础)撰稿:张晓新审稿:杜少波【学习目标】1.通过对实际问题情境的分析确定二次函数的表达式,并体会二次函数的意义;2.会用描点法画出二次函数的图象,能从图象上认识二次函数的性质;3.会根据公式确定图象的顶点、开口方向和对称轴(公式不要求记忆和推导),并能解决简单的实际问题;4.会利用二次函数的图象求一元二次方程的近似解.【知识网络】【要点梳理】要点一、二次函数的定义一般地,如果是常数,,那么叫做的二次函数.要点诠释:如果y=ax2+bx+c(a,b,c是常数,a≠0),那么y叫做x的二次函数.这里,当a=0时就不是二次函数了,但b、c可分别为零,也可以同时都为零.a 的绝对值越大,抛物线的开口越小.要点二、二次函数的图象与性质1.二次函数由特殊到一般,可分为以下几种形式:①;②;③;④,其中;⑤.(以上式子a≠0)几种特殊的二次函数的图象特征如下:函数解析式开口方向对称轴 顶点坐标当时开口向上 当时开口向下(轴) (0,0) (轴)(0,) (,0)(,)()2.抛物线的三要素:开口方向、对称轴、顶点.(1)的符号决定抛物线的开口方向:当时,开口向上;当时,开口向下;相等,抛物线的开口大小、形状相同. (2)平行于轴(或重合)的直线记作.特别地,轴记作直线.3.抛物线20()y ax bx c a =++≠中,,,a b c 的作用: (1)决定开口方向及开口大小,这与中的完全一样.(2)和共同决定抛物线对称轴的位置.由于抛物线的对称轴是直线,故:①时,对称轴为轴;②(即、同号)时,对称轴在轴左侧;③(即 、异号)时,对称轴在轴右侧.(3)的大小决定抛物线与轴交点的位置.当时,,∴抛物线与轴有且只有一个交点(0,):①,抛物线经过原点; ②,与轴交于正半轴;③,与轴交于负半轴.以上三点中,当结论和条件互换时,仍成立.如抛物线的对称轴在轴右侧,则 .4.用待定系数法求二次函数的解析式: (1)一般式:(a≠0).已知图象上三点或三对、的值,通常选择一般式. (2)顶点式:(a≠0).已知图象的顶点或对称轴,通常选择顶点式.(可以看成的图象平移后所对应的函数.)(3)“交点式”:已知图象与轴的交点坐标、,通常选用交点式:(a≠0).(由此得根与系数的关系:).要点诠释:求抛物线2y ax bx c =++(a≠0)的对称轴和顶点坐标通常用三种方法:配方法、公式法、代入法,这三种方法都有各自的优缺点,应根据实际灵活选择和运用.要点三、二次函数与一元二次方程的关系 函数,当时,得到一元二次方程,那么一元二次方程的解就是二次函数的图象与x 轴交点的横坐标,因此二次函数图象与x 轴的交点情况决定一元二次方程根的情况. (1)当二次函数的图象与x 轴有两个交点,这时,则方程有两个不相等实根;(2)当二次函数的图象与x 轴有且只有一个交点,这时,则方程有两个相等实根;(3)当二次函数的图象与x 轴没有交点,这时,则方程没有实根.通过下面表格可以直观地观察到二次函数图象和一元二次方程的关系:的图象的解方程有两个不等实数解方程有两个相等实数解方程没有实数解要点诠释:二次函数图象与x 轴的交点的个数由的值来确定.(1)当二次函数的图象与x 轴有两个交点,这时,则方程有两个不相等实根;(2)当二次函数的图象与x 轴有且只有一个交点,这时,则方程有两个相等实根;(3)当二次函数的图象与x 轴没有交点,这时,则方程没有实根.要点四、利用二次函数解决实际问题利用二次函数解决实际问题,要建立数学模型,即把实际问题转化为二次函数问题,利用题中存在的公式、内含的规律等相等关系,建立函数关系式,再利用函数的图象及性质去研究问题.在研究实际问题时要注意自变量的取值范围应具有实际意义. 利用二次函数解决实际问题的一般步骤是: (1)建立适当的平面直角坐标系;(2)把实际问题中的一些数据与点的坐标联系起来; (3)用待定系数法求出抛物线的关系式;(4)利用二次函数的图象及其性质去分析问题、解决问题. 要点诠释:常见的问题:求最大(小)值(如求最大利润、最大面积、最小周长等)、涵洞、桥梁、抛物体、抛物线的模型问题等.解决这些实际问题关键是找等量关系,把实际问题转化为函数问题,列出相关的函数关系式.【典型例题】类型一、求二次函数的解析式1.已知二次函数的图象经过原点及点11,24⎛⎫-- ⎪⎝⎭,且图象与x 轴的另一交点到原点的距离为1,则该二次函数的解析式为____ ____. 【答案】 21133y x x =-+或2y x x =+. 【解析】 正确找出图象与x 轴的另一交点坐标是解题关键.由题意知另一交点为(1,0)或(-1,0). 因此所求抛物线的解析式有两种. 设二次函数解析式为2y ax bx c =++.则有0,1114420c a b c a b c =⎧⎪⎪-=-+⎨⎪++=⎪⎩,或0,111,4420,c a b c a b c =⎧⎪⎪-=-+⎨⎪-+=⎪⎩解之13130a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩,或1,1,0.a b c =⎧⎪=⎨⎪=⎩因此所求二次函数解析式为21133y x x =-+或2y x x =+. 【点评] 此题容易出错漏解的错误.举一反三:【变式】已知:抛物线y=x 2+bx+c 的对称轴为x=1,交x 轴于点A 、B(A 在B 的左侧),且AB=4,交y 轴于点C.求此抛物线的函数解析式及其顶点M 的坐标. 【答案】∵对称轴x=1,且AB=4∴抛物线与x 轴的交点为:A(-1,0),B(3,0)bb=-212c=-31b c 0⎧-=⎧⎪∴∴⎨⎨⎩⎪-+=⎩∴y=x 2-2x-3为所求,∵x=1时y=-4 ∴M(1,-4) ∵对称轴x=1,且AB=4∴抛物线与x 轴的交点为:A(-1,0),B(3,0)bb=-212c=-31b c 0⎧-=⎧⎪∴∴⎨⎨⎩⎪-+=⎩∴y=x 2-2x-3为所求,∵x=1时y=-4 , ∴M(1,-4).类型二、根据二次函数图象及性质判断代数式的符号2.二次函数2y ax bx c =++的图象如图1所示,反比例函数ay x=与正比例函数y =(b+c)x 在同一坐标系中的大致图象可能是( ).【答案】B ;【解析】由2y ax bx c =++的图象开口向上得a >0,又02ba->,∴ b <0. 由抛物线与y 轴负半轴相交得c <0. ∵ a >0,∴ ay x=的图象在第一、三象限. ∵ b+c <0,∴ y =(b+c)x 的图象在第二、四象限. 同时满足ay x=和()y b c x =+图象的只有B . 【点评】由图1得到a 、b 、c 的符号及其相互关系,去判断选项的正误. 练习:1、(2012重庆市4分)已知二次函数)0(2≠++=a c bx ax y 的图象如图所示对称轴为21-=x 。
数学中考试题北京市第四中学总复习:实际问题与二次函数—巩固练习(提高)

实际问题与二次函数—巩固练习(提高)【巩固练习】一、选择题1.将进货单价为90元的某种商品按100元售出时,能卖出500个;价格每上涨1元,其销售量就减少10个,为了获得最大利润,售价应定为( )A.110元B.120元C.130元D.150元2.某旅行社有100张床位,每床每晚收费10元时,客床可全部租出,若每床每晚收费提高2元,则减少10张床位的租出;若每床每晚收费再提高2元,则再减少10张床位租出,以每次提高2元的这种方法变化下去,为了投资少而获利大,每床每晚应提高(• ) A.4元或6元 B.4元 C.6元 D.8元3.心理学家发现,学生对概念的接受能力y 和提出概念所用的时间x(单位:分)之间大致满足函数关系式:20.1 2.643y x x =-++(0≤x ≤30),y 的值越大,表示接受能力越强,那么学生的接受能力达到最强时,概念提出所用的时间是( ).A .10分B .30分C .13分D .15分4.某广场有一喷水池,水从地面喷出,如图所示,以水平地面为x 轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y =-x 2+4x(单位:米)的一部分,则水喷出的最大高度是( )A .4米B .3米C .2米D .1米第4题 第6题5.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下列函数关系式:h =-5(t-1)2+6,则小球距离地面的最大高度是( )A .1米B .5米C .6米D .7米6.2011年5月22日—29日在美丽的青岛市举行了苏迪曼杯羽毛球混合团体锦标赛,在比赛中,某次羽毛球的运动路线可以看作是抛物线214y x bx c =-++的一部分(如图所示),其中出球点B 离地面O 点的距离是1m ,球落地点A 到O 点的距离是4m ,那么这条抛物线的解析式是( )A .213144y x x =-++ B .213144y x x =-+- C .213144y x x =--+ D .213144y x x =---二、填空题7.一件工艺品进价为100元,标价135元售出,每天可售出100件.根据销售统计,一件工艺品每降价1元出售,则每天可多售出4件,要使每天获得的利润最大,每件需降价的钱数为________元.8.出售某种手工艺品,若每个获利x元,一天可售出(8-x)个,则当x=________元时,一天出售该种手工艺品的总利润y最大.9.在平面直角坐标系xOy中,二次函数C1:y=ax2+bx+c的图象与C2:y=2x2-4x+3的图象关于y轴对称,且C1与直线y=mx+2交与点A(n,1).则m的值为 .10.某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,抛物线形状如图所示,如图建立直角坐标系,水流喷出的高度与水平距离之间的关系式是.请回答下列问题:柱子OA的高度为米;喷出的水流距水平面的最大高度是米;若不计其它因素,水池的半径至少要米,才能喷出的水流不至于落在池外.11.如图所示,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为________米.第11题第12题12.如图所示,有一条双向公路隧道,其横断面由抛物线和矩形ABCO的三边组成,隧道的最大高度为4.9m,AB=10m,BC=2.4m,现把隧道横断面放在平面直角坐标系中,若有一辆高为4m,宽为2m的装有集装箱的汽车要通过隧道,问:如果不考虑其他因素,汽车的右侧离隧道右壁至少米才不至于碰到隧道顶部?(抛物线部分为隧道顶部,AO,BC为壁)三、解答题13.某人定制了一种地砖,每块地砖(如图①所示)是边长为0.4米的正方形ABCD,点E,F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格依次为30元、20元、10元,若将此种地砖按如图②所示的形式铺设,则能使中间的阴影部分组成四边形EFGH.(1)判断图②中的四边形EFGH 是何形状,并说明理由;(2)点E 、F 分别在什么位置时,定制这批地砖所需的材料费用最省?14. 国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求。
人教版数学九年级上学期课时练习-《二次函数》全章复习与巩固(巩固篇)(人教版)

专题22.37 《二次函数》全章复习与巩固(巩固篇)(专项练习)一、单选题1.已知函数:①y =2x ﹣1;①y =﹣2x 2﹣1;①y =3x 3﹣2x 2;①y=2(x+3)2-2x 2;①y =ax 2+bx +c ,其中二次函数的个数为( )A .1B .2C .3D .42.如图,点A ,点B 的坐标分别为()1,4-,()4,4-,抛物线()2y a x h k =-+的顶点在线段AB 上运动,与x 轴交于C ,D 两点(点C 在点D 的左侧).若点D 的横坐标的最大值为6,则点C 的横坐标的最小值为( )A .52B .1C .1-D .2-3.二次函数y =﹣12(x ﹣4)2+3图象的顶点坐标是( )A .(﹣4,3)B .(﹣2,﹣3)C .(4,3)D .(2,3)4.已知点A (-3,y 1),B (0,y 2),C (3,y 3)都在二次函数y =-(x +2)2+4的图象上,则y 1,y 2,y 3的大小关系是( )A .y 3<y 2<y 1B .y 1=y 3<y 2C .y 1<y 2<y 3D .y 1<y 3<y 25.已知二次函数2y ax bx c =++(a ,b ,c 是常数,且0a ≠)的自变量x 与函数值y 的部分对应值如下表:当12x =-时,与其对应的函数值0y >,给出下列四个结论:①0b <;①关于x 的方程2ax bx c n ++=的两个根是1-和2;①210m n +<;①()4at at b +≥-(t 为任意实数.)其中正确结论的个数是( )A .1B .2C .3D .46.如图,已知抛物线2y x bx c =++与直线y =x 交于()1,1和()3,3两点,有以下结论:①240b c ->;①3b +c +6=0;①当13x <<时,()210x b x c +-+<;①当2x >时,22x bx c x++>,其中正确的个数是( )A .1B .2C .3D .47.已知二次函数2y ax bx c =++(0a ≠)的图象如图所示,对称轴为直线1x =,与x 轴的一个交点为3,0.给出下列结论:①240b ac -<;①420a b c ++>;①图象与x 轴的另一个交点为1,0;①当0x >时,y 随x 的增大而减小;①不等式20ax bx c ++<的解集是13x .其中正确结论的个数是( )A .4个B .3个C .2个D .1个8.如图,抛物线2y ax bx c =++与直线y kx h =+交于A 、B 两点,下列是关于x 的不等式或方程,结论正确的是( )A .2()ax b k x c h +-+>的解集是24x <<B .2()ax b k x c h +-+>的解集是4x >C .2()ax b k x c h +-+>的解集是2x <D .2()ax b k x c h +-+=的解是2x =或4x = 9.已知,在菱形ABCD 中,AB =6,∠B =60°,矩形PQNM 的四个.顶点分别在菱形的四边上,则矩形PMNQ 的最大面积为( )A .B .C .D .10.如图,在平面直角坐标系中,点B 是抛物线()214y a x =-+的图象的顶点,点A ,C 的坐标分别为()0,3,()1,0,将ABC 沿y 轴向下平移使点A 平移到点O ,再绕点O 逆时针旋转90︒,若此时点B ,C 的对应点B ',C '恰好落在抛物线上,则a 的值为( )A .34-B .-1C .43-D .-2二、填空题11.当m =____________时,函数2m1y (m 1)x +=-是二次函数.12.在同一个平面直角坐标系xOy 中,二次函数211y a x =,222y a x =,233y a x 的图象如图所示,则123,,a a a 的大小关系为___________(用“>”连接).13.如图,在平面直角坐标系中,坐标原点为O ,抛物线y =a (x ﹣2)2+1(a >0)的顶点为A ,过点A 作y 轴的平行线交抛物线2124y x =--于点B ,连接AO 、BO ,则①AOB 的面积为________.14.抛物线21122y x x =+的图象如图所示,点A 1,A 2,A 3,A 4…,A 2022在抛物线第一象限的图象上,点B 1,B 2,B 3,B 4...,B 2022在y 轴的正半轴上,11OA B 、122B A B 、…、202120222022B A B 都是等腰直角三角形,则20212022B A =________.15.在平面直角坐标系xOy 中,二次函数()20y ax a =>的图象上两点A ,B 的横坐标分别为1-,2.若AOB 为直角三角形,则a 的值为______.16.如图,正方形OABC 的顶点B 在抛物线2y x 的第一象限的图象上,若点B 的横坐标与纵坐标之和等于6,则对角线AC 的长为______.17.在平面直角坐标系中,点A 是抛物线()24y a x k =-+与y 轴的交点,点B 是这条抛物线上的另一点,且//AB x 轴,则以AB 为边的等边三角形ABC 的周长为_____.18.平面直角坐标系中,将抛物线2y x =-平移得到抛物线C ,如图所示,且抛物线C 经过点()1,0A -和()0,3B ,点P 是抛物线C 上第一象限内一动点,过点P 作x 轴的垂线,垂足为Q ,则OQ PQ +的最大值为______.19.已知二次函数()20y ax bx c a =++≠的图象如图所示,下列结论中:03a >①;②是方程20ax bc c ++=的一个根;0a b c ++>③;④当1x <时,y 随x 的增大而减小;240b ac ->⑤;正确的是______(.把所有正确结论的序号都写在横线上)20.如图,抛物线221y x x =-+与图象l 关于直线y x =对称,则图象l 所对应的关于x 与y 的关系式为______.21.已知直线y 13-=x +b 经过点A (﹣1,2)和B (m ,1),则m =____,若抛物线y 12-=x 2﹣x +a 与线段AB 有交点,则a 的取值范围是____.22.如图,在ABC ∆中,30ABC ACB ∠=∠=︒,4AB AC ==,D 为边AB 上一动点(B 点除外),连接CD ,作ED CD ⊥,且ED CD =,连接BE ,则BDE ∆面积的最大值为 _________.三、解答题23.已知二次函数y =-x 2+4x.(1)用配方法把该函数化为y =a(x -h)2+k 的形式; (2)求该函数图象的对称轴和顶点坐标.24.如图,抛物线y =a (x ﹣2)2+3(a 为常数且a ≠0)与y 轴交于点A (0,53).(1)求该抛物线的解析式;(2)若直线y =kx 23+(k ≠0)与抛物线有两个交点,交点的横坐标分别为x 1,x 2,当x 12+x 22=10时,求k 的值;(3)当﹣4<x ≤m 时,y 有最大值43m,求m 的值.25.受“新冠”疫情的影响,某销售商在网上销售A 、B 两种型号的“手写板”,获利颇丰.已知A 型,B 型手写板进价、售价和每日销量如表格所示:根据市场行情,该销售商对A 手写板降价销售,同时对B 手写板提高售价,此时发现A 手写板每降低5就可多卖1,B 手写板每提高5就少卖1,要保持每天销售总量不变,设其中A 手写板每天多销售x ,每天总获利的利润为y(1)求y 、x 间的函数关系式并写出x 取值范围;(2)要使每天的利润不低于234000元,直接写出x 的取值范围;(3)该销售商决定每销售一个B 手写板,就捐a 元给)000(1a <≤因“新冠疫情”影响的困难家庭,当3040x ≤≤时,每天的最大利润为229200元,求a 的值.26.综合与探究如图1,在平面直角坐标系xOy 中,抛物线W 的函数表达式为y =﹣421x 2+1621x +4.抛物线W 与x 轴交于A ,B 两点(点B 在点A 的右侧,与y 轴交于点C ,它的对称轴与x 轴交于点D ,直线l经过C、D两点.(1)求A、B两点的坐标及直线l的函数表达式.(2)将抛物线W沿x轴向右平移得到抛物线W′,设抛物线W′的对称轴与直线l交于点F,当①ACF 为直角三角形时,求点F的坐标,并直接写出此时抛物线W′的函数表达式.(3)如图2,连接AC,CB,将①ACD沿x轴向右平移m个单位(0<m≤5),得到①A′C′D′.设A′C 交直线l于点M,C′D′交CB于点N,连接CC′,MN.求四边形CMNC′的面积(用含m的代数式表示).参考答案1.A【分析】根据二次函数的定义判断即可;解:y =2x ﹣1是一次函数;y =﹣2x 2﹣1是二次函数; y =3x 3﹣2x 2不是二次函数;①y=2(x+3)2-2x 2222121821218x x x x =++-=+,不是二次函数; y =ax 2+bx +c ,没告诉a 不为0,故不是二次函数; 故二次函数有1个; 故答案选A .【点拨】本题主要考查了二次函数的定义,准确判断是解题的关键. 2.C 【分析】当D 点横坐标最大值时,抛物线顶点必为(4,4)B -,可得此时抛物线的对称轴为直线4x =,求出CD 间的距离;当C 点横坐标最小时,抛物线顶点为(1,4)A -,再根据此时抛物线的对称轴及CD 的长,可判断C 点横坐标的最小值.解:当点D 横坐标为6时,抛物线顶点为(4,4)B -,①对称轴为直线4x =,4CD =;当抛物线顶点为(1,4)A -时,抛物线对称轴为直线1x =, ①11212CD-=-=-, ①(1,0)C -,①点C 的横坐标最小值为1-, 故选C .【点拨】本题考查了二次函数的性质和图象.明确CD 的长度是定长是解题的关键. 3.C 【分析】根据题目中二次函数的顶点式可以直接写出它的顶点坐标. 解:①y =﹣12(x ﹣4)2+3,①此函数的顶点坐标为(4,3), 故选:C .【点拨】此题主要考查了二次函数的性质,关键是熟记:顶点式y =a (x -h )2+k ,顶点坐标是(h ,k ),对称轴是直线x =h .4.A 【分析】先确定抛物线的对称轴,然后比较三个点到对称轴的距离,再利用二次函数的性质判断对应的函数值的大小.解:二次函数y =﹣(x +2)2+4图象的对称轴为直线x =﹣2, 又①a =-1,二次函数开口向下, ①点到对称轴越近,函数值越大;①点A (﹣3,y 1)到直线x =﹣2的距离最小,点C (3,y 3)到直线x =﹣2的距离最大, ①y 3<y 2<y 1. 故选:A .【点拨】本题考查二次函数的图象及性质;理解开口向上的函数,点到对称轴距离越远,其函数值越大,反之,开口向下,点到对称轴越近,函数值越大是解题的关键.5.C 【分析】利用抛物线的图象与性质逐一判断即可.解:由表格可知,该抛物线图象经过点()()()()12021,2m n ---,,,,,,, ①该抛物线的对称轴为122b x a =-=,2c =-; ①当12x =-时,与其对应的函数值0y >, ①抛物线开口向上, ①0a >,①0b a =-<,故①正确;由图象经过的点和抛物线对称性可知,m n =,故①正确; 由当12x =-时,与其对应的函数值0y >, 得到112042a b -->①83a >,当1x =-时,222m a b a =--=-,①()2332210m n m a +==->,故①错误;由对称轴为12x =,图象开口向上可得: 2112242at bt a b +-≥+-, ①()4a t atb +≥-,故①正确;故选:C .【点拨】本题考查了抛物线的图象与性质,解题十五关键是掌握抛物线的对称轴公式以及利用抛物线的对称性进行解决问题,并能正确利用点的坐标判断代数式的取值情况.6.B【分析】由函数2y x bx c =++与x 轴无交点,可得240b c -<来判断①;当3x =时,933y b c =++=来判断①;当13x <<时,二次函数值小于一次函数值,可得2x bx c x ++<来求解①;把()11,和()3,3两点代入2y x bx c =++求出抛物线解析式进行得用抛物线与双曲线的交点坐标,分第一象限内和第三象限内来求解①.解:①函数2y x bx c =++与x 轴无交点,①240b c -<,故①不正确;当x=3时,933y b c =++=,即360b c ++=,故①正确;①当13x <<时,二次函数值小于一次函数值,①2x bx c x ++<,①()210x b x c +-+<,故①正确;把()11,和()3,3两点代入2y x bx c =++得抛物线的解析式为233y x x =-+ , 当2x =时,2331y x x =-+=,21y x==, 抛物线和双曲线的交点坐标为21(,), 第一象限内,当2x >时,22x bx c x++>; 或第三象限内,当0x <时,22x bx c x ++>,故①错误. 综上所述,正确的有①①共2个.故选:B .【点拨】本题考查了一次函数与二次函数的综合应用,注意掌握数形结合思想的应用. 7.C【分析】根据二次函数的图象与性质即可求出答案.解:①由图象可知:抛物线与x 轴有两个交点,①240b ac ∆=->,故①错误;①当2x =时,42y a b c =++,由图象可知当2x =时,0y >,①420a b c ++>,故①正确;①3,0关于直线x =1的对称点为1,0,故①正确;①当0x >时,由图象可知y 先随x 的增大而增大,再随x 的增大而减小,故①错误; ①由图象及①可知,抛物线与x 轴的交点为3,0,1,0,①当20ax bx c ++<时,1x <-可3x >,故①错误;综上,有①,①是正确的,故有2个正确的,故选:C .【点拨】本题主要考查二次函数的图象和性质,掌握抛物线的位置与系数a ,b ,c 的关系是正确判断的关键.8.D【分析】根据函数图象可知,不等式ax 2+bx +c >kx +h ,即2()ax b k x c h +-+>的解集为:x <2或>4;方程ax 2+bx +c =x +h ,即2()ax b k x c h +-+=的解为2x =或4x =.据此即可求解.解:由函数图象可得,不等式ax 2+bx +c >kx +h ,即2()ax b k x c h +-+>的解集为:x <2或>4;故A 、B 、C 不符合题意;方程ax 2+bx +c =x +h ,即2()ax b k x c h +-+=的解为2x =或4x =,故D 符合题意; 故选:D .【点拨】本题考查二次函数与不等式,方程的联系,利用图象法求解,掌握数形结合思想是解题的关键.9.D【分析】连接AC,BD,得到ΔABC为等边三角形,设AP=a,AE=CF12=a,从而求出EF=6-a,求出PQ,即可得出S与a的函数关系式,即可得到答案.解:如图:连接AC,BD交于点O,AC分别交PQ,MN于点E,F.①菱形ABCD中,AB=6,①B=60°,①①ABC是等边三角形,①ABD=30°,①AC=AB=6.①矩形MNQP,①PQ①BD,PM=EF,PQ①AC.①①APE=①ABD=30°,设AP=a,AE=CF12=a,①EF=PM=6﹣a.由勾股定理得:PE=①PQ=2PE.①S矩形PMNQ=PM•PQ=×(6﹣a)=a2+6a)=a﹣3)2①0,①当a=3时,矩形面积有最大值故选:D.【点拨】本题考查了菱形的性质,矩形的性质以及二次函数的性质,正确利用a表示出矩形PMNQ的面积是关键.10.A【分析】先根据题意确定抛物线顶点B 的坐标,过A 作AD BC ⊥于D ,得到AD ,BD 的长,再根据题意,ABC 与OB C ''△重合,进而得到B D ''和OD '的长,于是得到B '的坐标,由于B '在抛物线()214y a x =-+上,进而求解.解:过A 作AD BC ⊥于D ,如图①抛物线的解析式:()214y a x =-+,①其顶点是()1,4B ,对称轴1x =①()0,3A①1AD =,1BD BC CD =-=根据题意,ABC 与OB C ''△重合,①AD BC ⊥①OD B C '''⊥①1OD AD '==,1B D BD ''==①()1,1B '-①B ',C '在抛物线()214y a x =-+上①()21114a =--+ ①34a =- 故选:A【点拨】本题考查了二次函数与几何图形的综合,几何图形的平移与旋转的性质,掌握数形结合的思想方法和灵活运用所学知识是解本题的关键.11.-1解:试题分析:根据二次函数的定义列出方程及不等式,解之即可.解:①函数()211m y m x +=-是二次函数①212m +=且10m -≠①1m =-故答案为-1.12.321a a a >>.【分析】抛物线的开口方向由a 的符号决定,开口大小由a 的绝对值决定,绝对值越大,开口越小. 解:①二次函数y 1=a 1x 2的开口最大,二次函数y 3=a 3x 2的开口最小,而抛物线的开口都是向上的,则二次项的系数都为正数,①321a a a >>,故答案为:321a a a >>.【点拨】本题主要考查二次函数的性质,掌握抛物线的开口方向和开口大小由a 的值决定是解题的关键.13.4【分析】先求得顶点A 的坐标,然后根据题意得出B 的横坐标,把横坐标代入抛物线2124y x =--,得出B 点坐标,从而求得A 、B 间的距离,最后计算面积即可.解:设AB 交x 轴于C①抛物线线y =a (x ﹣2)2+1(a >0)的顶点为A ,①A (2,1),①过点A 作y 轴的平行线交抛物线2124y x =--于点B , ①B 的横坐标为2,OC =2把x =2代入2124y x =--得y =-3, ①B (2,-3),①AB =1+3=4,11==24=422AOB OC A S B ⋅⨯⨯. 故答案为:4.【点拨】本题考查了二次函数图象上点的坐标特征,求得A 、B 的坐标是解题的关键. 14.【分析】先设第一个等腰直角三角形的直角边长为x ,表示出点A 1的坐标,代入二次函数的解析式,求出x ;设第二个等腰直角三角形的直角边长为m ,表示出A 2的坐标,代入二次函数的解析式,求出m ,同理求出第2022个等腰直角三角形的直角边长,即可求出斜边.解:设A 1B 1=x ,①①OA 1B 1 是等腰直角三角形,①OB 1=x ,则A 1的坐标为(x ,x ),代入二次函数y =12x 2+12x ,得x =12x 2+12x ,解得x =1或x =0(舍),设A 2B 2=m ,①①B 1A 2B 2腰是等腰直角三角形,①B 1B 2=m ,①A 2的坐标为(m ,1+m ),代入二次函数y =12x 2+12x , 得12m 2+12m =1+m ,解得m =2或m =-1(舍),同理可求出A 3B 3=3,A 4B 4=4,①B 2022A 2022=2022,根据勾股定理,得B 2021A 2022=,故答案为:【点拨】本题考查了二次函数图象与规律综合题,利用等腰直角三角形的性质和二次函数的点坐标特征是解决本题的关键.15.1a =或a =【分析】分两种情况讨论,如图,当90OAB ∠=︒时,利用2222,OB OA AQ BQ -=+ 建立方程求解即可;当90,AOB ∠=︒ 利用2222,OA OB AQ BQ +=+建立方程求解即可;从而可得答案.解:如图,当90OAB ∠=︒时,222,OA AB OB ∴+=A ,B 的横坐标分别为1-,2,()()1,,2,4A a B a ∴-,2222224161153,AB OB OA a a a ∴=-=+--=+过A 作AQ BM ⊥于,M 则,3,AE QM a AQ EM ====43,BQ a a a ∴=-=222299,AB AQ BQ a ∴=+=+2215399,a a ∴+=+解得:1a = (负根舍去)当90,AOB ∠=︒同理可得:()()1,,2,4A a B a -222141699,a a a ∴+++=+解得:2a =(负根舍去)综上:1a =或a =【点拨】本题考查的是勾股定理的应用,二次函数的性质,掌握“利用勾股定理求解两点之间的距离”是解题的关键.16.【分析】根据点B 在抛物线y =x 2的第一象限部分,可设B 点坐标为(x ,x 2),则x >0.根据B 点的横坐标与纵坐标之和等于6,列出方程x +x 2=6,解方程求出x 的值,再求出OB 的长即可得到结论.解:连接OB ,如图,①正方形OABC 的顶点B 在抛物线y =x 2的第一象限部分,①可设B 点坐标为(x ,x 2),且x >0.①B 点的横坐标与纵坐标之和等于6,①x +x 2=6,解得x 1=2,x 2=-3(不合题意舍去),①B (2,4),①OB 2=22+42=20,①OB =①四边形OABC 是正方形,①AC OB ==故答案为【点拨】本题考查了二次函数的性质,二次函数图象上点的坐标特征,正方形的性质,求出B 点坐标是解题的关键.17.24【分析】根据抛物线的解析式即可确定对称轴,则可以确定AB 的长度,然后根据等边三角形的周长公式即可求解.解:抛物线2(4)y a x k =-+的对称轴是4x =过C 点作CD AB ⊥于点D ,如下图所示则4=AD ,则28AB AD ==则以AB 为边的等边ABC 的周长为2483=⨯.故答案为24.【点拨】此题考查了二次函数的性质,根据抛物线的解析式确定对称轴,从而求得AB 的长是关键.18.214【分析】求得抛物线C 的解析式,设Q (x ,0),则P (x ,-x 2+2x +3),即可得出OQ +PQ ,根据二次函数的性质即可求得.解:设平移后的解析式为y =-x 2+bx +c ,①抛物线C 经过点A (-1,0)和B (0,3),①103b c c --+=⎧⎨=⎩,解得23b c =⎧⎨=⎩, ①抛物线C 的解析式为y =-x 2+2x +3,设Q (x ,0),则P (x ,-x 2+2x +3),①点P 是抛物线C 上第一象限内一动点,①OQ +PQ =x +(-x 2+2x +3)=-x 2+3x +32321()24x =--+ ①OQ +PQ 的最大值为214故答案为:214 【点拨】本题考查了二次函数的性质,平移,二次函数图象与几何变换,根据题意得出OQ +PQ =-x 2+3x +3是解题的关键.19.②③⑤【分析】由抛物线的开口方向判断a 与0的关系,由抛物线与y 轴的交点判断c 与0的关系,然后根据对称轴及抛物线与x 轴交点情况进行推理,进而对所得结论进行判断.解:①抛物线开口向下,故0a >错误,不符合题意;②方程的一个根是1-,函数对称轴为:1x =,则3是方程20ax bc c ++=的一个根,符合题意;③当1x =时,0y a b c =++>,正确,符合题意;④当1x <时,y 随x 的增大而减小错误,不符合题意;⑤抛物线和x 轴有两个交点,故240b ac ->,符合题意;故答案为:②③⑤.【点拨】主要考查图象与二次函数系数之间的关系,会利用函数图象确定字母系数的取值范围,以及二次函数与方程之间的转换是解题的关键.20.221x y y =-+【分析】设(x ,y )是图象l 上的任意点,则它关于直线y x =的对称点一定在抛物线221y x x =-+上,因此将对称点(y ,x )代入抛物线即可.解:设(x ,y )是图象l 上的任意点,则关于直线y x =的对称点是(y ,x ),∴把(y ,x )代入221y x x =-+得221x y y =-+,故答案为:221x y y =-+.【点拨】本题主要考查了二次函数图像与几何变换的知识,明确关于y x =的对称的点的坐标特征是解题的关键.21. 2139≤a ≤5##1359a ≥≥ 【分析】将点A 坐标代入直线解析式求出b ,再将点B 坐标代入解析式求m 的值.根据抛物线解析式可得抛物线开口方向及对称轴,顶点坐标,再根据点A ,B 坐标求解即可.解:将(﹣1,2)代入y 13=-x +b 得213=+b , 解得b 53=, ①y 13=-x 53+, 把(m ,1)代入y 13=-x 53+得113=-m 53+, 解得m =2,①点B 坐标为(2,1),①y 12=-x 2﹣x +a 12=-(x +1)212++a , ①抛物线开口向下,对称轴为直线x =﹣1,顶点坐标为(﹣1,12+a ), 当抛物线经过点A 时,12+a =2, 解得a 32=, 令12-x 2﹣x +a 13=-x 53+,整理得3x 2+4x +10﹣6a =0, 当Δ=42﹣4×3(10﹣6a )≥0时,139a ≥, 把(2,1)代入y 12=-x 2﹣x +a 得1=﹣2﹣2+a , 解得a =5,当139≤a ≤5时,满足题意. 故答案为:2;139≤a ≤5. 【点拨】本题考查一次函数与二次函数图象上点的坐标特征,解题关键是掌握函数与方程的关系,掌握二次函数的性质.22.4.5【分析】过点C 作CG ①BA 于点G ,作EH ①AB 于点H ,作AM ①BC 于点M .由30ABC ACB ∠=∠=︒,AB =AC =4,可得BC =BM =CM =GB =6,设BD =x ,则DG =6−x ,证①EDH ①①DCG ,EH =DG =6−x ,求得S △BDE ,根据二次函数的性质求得最大值即可.解:过点C 作CG ①BA 于点G ,作EH ①AB 于点H ,作AM ①BC 于点M .①30ABC ACB ∠=∠=︒,4AB AC ==,①BM =CM =①GB =12AB AG AB AC +=+=6, 设BD =x ,则DG =6−x ,①ED =DC ,①EDC =90°,①EDH +①GDC =90°,①EDH +①HED =90°,①①EHD =①DGC ,①HED =①GDC ,①①EDH ①①DCG (AAS ),①EH =DG =6−x ,①S △BDE =12BD •EH =12x (6−x )=12- (x −3)2+4.5, 当x =3时,①BDE 面积的最大值为4.5.故答案为4.5.【点拨】本题考查了含30度角的直角三角形的性质,二次函数的性质以及全等三角形的判定与性质,熟练运用以上知识是解题的关键.23.(1)y=-(x -2)2+4;(2) 对称轴为直线x =2,顶点坐标为(2,4)【分析】(1)利用配方法时注意要先提出二次项系数,在加上一次项系数的一半的平方来凑完全平方式,可把一般式转化为顶点式;(2)根据y =a(x -h)2+k 的形式直接得出其对称轴和顶点坐标.解:(1)y =-x 2+4x =-(x -2)2+4.(2)由(1)得,对称轴为直线x =2,顶点坐标为(2,4).【点拨】二次函数的解析式有三种形式:(1)一般式:y=ax 2+bx+c (a≠0,a 、b 、c 为常数);(2)顶点式:y=a (x -h )2+k ;(3)交点式(与x 轴):y=a (x -x 1)(x -x 2).24.(1)()21233y x =--+;(2)1222,,3k k ==;(3)9.4m = 【分析】(1)把50,3A ⎛⎫ ⎪⎝⎭代入抛物线的解析式,解方程求解即可; (2)联立两个函数的解析式,消去,y 得:()21223,33x kx --+=+再利用根与系数的关系与()222121212210,x x x x x x +=+-=可得关于k 的方程,解方程可得答案; (3)先求解抛物线的对称轴方程,分三种情况讨论,当2,m ≤ 2<m <8, 8,m ≥ 结合函数图象,利用函数的最大值列方程,再解方程即可得到答案.解:(1)把50,3A ⎛⎫ ⎪⎝⎭代入()223y a x =-+中, 543,3a ∴+= 1,3a ∴=- ∴ 抛物线的解析式为:()212 3.3y x =--+ (2)联立一次函数与抛物线的解析式得:()2231233y kx y x ⎧=+⎪⎪⎨⎪=--+⎪⎩()21223,33x kx ∴--+=+整理得:()24330,x k x ---=121243,3,x x k x x ∴+=-=-()222121212210,x x x x x x +=+-= ()()()22432343120,k k ∴--⨯-=-+> ①x 1+x 2=4-3k ,x 1•x 2=-3,①x 12+x 22=(4-3k )2+6=10, 解得:1222,,3k k == ①1222,,3k k == (3)①函数的对称轴为直线x=2,当m <2时,当x=m 时,y 有最大值,43m =-13(m -2)2+3,解得①m=当m≥2时,当x=2时,y 有最大值, ①43m =3, ①m=94,综上所述,m 的值为94. 【点拨】本题考查的是利用待定系数法求解抛物线的解析式,抛物线与x 轴的交点坐标,一元二次方程根与系数的关系,二次函数的增减性,掌握数形结合的方法与分类讨论是解题的关键.25.(1)210900220000y x x =-++(060x ≤≤),且x 为整数;(2)2060x ≤≤,且x 为整数;(3)a =30【分析】(1)根据题意列函数关系式和不等式组,于是得到结论;(2)根据题意列方程和不等式,于是得到结论;(3)根据题意列函数关系式,然后根据二次函数的性质即可得到结论.解:(1)由题意得,2(9006005)(200)(12008005)(400)10900220000y x x x x x x =--++-+-=-++,0,30050,4000,x x x ⎧⎪-⎨⎪-⎩解得060x ,故x 的取值范围为060x 且x 为整数;(2)x 的取值范围为2060x .理由如下:221090022000010(45)240250y x x x =-++=--+,当234000y =时,210(45)240250234000x --+=,2(45)625x -=,4525x -=±,解得:20x 或70x =.要使234000y ,得2070x ;060x ,2060x ∴;(3)设捐款后每天的利润为w 元,则2210900220000(400)10(900)220000400w x x x a x a x a =-++--=-+++-, 对称轴为900452020a a x +==+, 0100a <, ∴454520a +>, 抛物线开口向下,当3040x 时,w 随x 的增大而增大,当40x =时,w 最大,1600040(900)220000*********a a ∴-+++-=,解得30a =.【点拨】本题考查了二次函数的应用,一元一次不等式的应用,列函数关系式等等,最大销售利润的问题常利用函数的增减性来解答.26.(1)点A 坐标为(﹣3,0),点B 的坐标为(7,0),y =﹣2x +4;(2) 点F 的坐标为(5,﹣6),y =﹣421x 2+4021x ;(3) 四边形CMNC ′的面积为45m 2. 【分析】根据抛物线的解析式,令y =0即可求出两点的坐标.根据抛物线的解析式可分别求出C ,D 两点的坐标,再用待定系数法即可求出直线的表达式.根据题意,利用角的等量关系可以得到①1=①3,进而得到tan①1=tan①3,根据三角函数的计算方法列出等式,根据一次函数的解析式设点的坐标为(xF ,﹣2xF +4),将各线段的长度代入等式即可求出点F 的坐标,再根据平移的法则即可求出w ′的表达式.根据平移,可以得到点C ′,A ′,D ′的坐标,再根据待定系数法可以得到直线A ′C ′,BC ,C ′D ′的解析式,根据交点的计算方法列方程组可以求得点M ,N 的坐标,根据平移的定义和平行四边形的定义可知四边形CMNC ′是平行四边形,再根据平行四边形面积的计算方法可以得到平行四边形CMNC ′的面积.解:(1)当y =0时,﹣421x 2+1621+4=0,解得x 1=﹣3,x 2=7, ①点A 坐标为(﹣3,0),点B 的坐标为(7,0).①﹣2b a =162142()21-⨯- ①抛物线w 的对称轴为直线x =2,①点D 坐标为(2,0).当x =0时,y =4,①点C 的坐标为(0,4).设直线l 的表达式为y =kx +b ,420b k b =⎧⎨+=⎩解得k=-2b=4⎧⎨⎩①直线l 的解析式为y =﹣2x +4;(2)①抛物线w 向右平移,只有一种情况符合要求,即①F AC =90°,如图.此时抛物线w′的对称轴与x轴的交点为G,①①1+①2=90°①2+①3=90°,①①1=①3,①tan①1=tan①3,①FGAG=AOCO.设点F的坐标为(xF,﹣2xF+4),①(24)(3)FFxx---+=34,解得xF=5,﹣2xF+4=﹣6,①点F的坐标为(5,﹣6),此时抛物线w′的函数表达式为y=﹣421x2+4021x;(3)由平移可得:点C′,点A′,点D′的坐标分别为C′(m,4),A′(﹣3+m,0),D′(2+m,0),CC′①x轴,C′D′①CD,可用待定系数法求得直线A′C′的表达式为y=43x+4﹣43m,直线BC的表达式为y=﹣47x+4,直线C′D′的表达式为y=﹣2x+2m+4,分别解方程组4443324y x my x⎧=+-⎪⎨⎪=-+⎩和224447y x my x=-++⎧⎪⎨=-+⎪⎩解得25445x my m⎧=⎪⎪⎨⎪=-+⎪⎩和75445x my m⎧=⎪⎪⎨⎪=-+⎪⎩①点M的坐标为(25m,﹣45m+4),点N的坐标为(75m,﹣45m+4),①yM=yN①MN①x轴,①CC′①x轴,①CC′①MN.①C′D′①CD,①四边形CMNC′是平行四边形,①S=m[4﹣(﹣45m+4)]=45m2【点拨】本题主要考查二次函数的图象与性质、一次函数的解析式以及二次函数的应用,数形结合思想是关键.。
中考试题北京市第四中学总复习:《二次函数》全章复习与巩固—巩固练习(基础).docx

《二次函数》全章复习与巩固—巩固练习(基础)【巩固练习】 一、选择题1.将二次函数2y x =的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( ).A .2(1)2y x =-+B .2(1)2y x =++C .2(1)2y x =--D .2(1)2y x =+-2.二次函数2y ax bx c =++的图象如图所示,则一次函数24y bx b ac =+-与反比例函数a b cy x++=在同一坐标系内的图象大致为( ).3.抛物线2y x bx c =++图象向右平移2个单位长度,再向下平移3个单位长度,所得图象的解析式为223y x x =--,则b 、c 的值为( ).A .b =2,c =2B .b =2,c =0C .b =-2,c =-1D .b =-3,c =2 4. 抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是( )A .22y x x =-- B .211122y x x =-++ C .211122y x x =--+ D .22y x x =-++ 5.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,有下列结论:①240b ac ->;②abc >0;③8a+c >0;④9a+3b+c <0.其中,正确结论的个数是( ). A .1 B .2 C .3 D .4第4题 第5题6.已知点(1x ,1y ),(2x ,2y )(两点不重合)均在抛物线21y x =-上,则下列说法正确的是( ).A .若12y y =,则12x x =B .若12x x =-,则12y y =-C .若120x x <<,则12y y >D .若120x x <<,则12y y > 7.在反比例函数a y x=中,当0x >时,y 随x 的增大而减小,则二次函数2y ax ax =-的图象大致是图中的( ).8.已知二次函数2y ax bx c =++(其中0a >,0b >,0c <),关于这个二次函数的图象有如下说法:①图象的开口一定向上;②图象的顶点一定在第四象限;③图象与x 轴的交点至少有一个在y 轴的右侧. 以上说法正确的有( ).A .0个B .1个C .2个D .3个二、填空题9.已知抛物线2(0)y ax bx c a =++>的对称轴为直线1x =,且经过点1(1,)y -,2(2,)y ,试比较1y 和2y的大小:1y ________2y (填“>”,“<”或“=”).10.抛物线2y x bx c =-++的图象如图所示,则此抛物线的解析式为___ _____.11.抛物线22(2)6y x =--的顶点为C ,已知y =-kx+3的图象经过点C ,则这个一次函数图象与两坐标轴所围成的三角形面积为________.12.已知二次函数22y x x m =-++的部分图象如图所示,则关于x 的一元二次方程220x x m -++=的解为___ _____.第10题 第12题 第13题13.如图所示的抛物线是二次函数2231y ax x a =-+-的图象,那么a 的值是________.14.烟花厂为扬州“4·18”烟花三月经贸旅游节特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是252012h t t =-++,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为________.15.已知抛物线2y ax bx c =++经过点A(-1,4),B(5,4),C(3,-6),则该抛物线上纵坐标为-6的另一个点的坐标是________.16.若二次函数26y x x c =-+的图象过A(-1,y 1)、B(2,y 2)、C(32+,y 3)三点,则y 1、y 2、y 3大小关系是 .三、解答题17.杂技团进行杂技表演,演员从跷跷板右端A 处弹跳到人梯顶端椅子B 处,其身体运动(看成一点)的路线是抛物线23315y x x =-++的一部分,如图所示.(1)求演员弹跳离地面的最大高度;(2)已知人梯高BC =3.4米,在一次表演中,人梯到起跳点A 的水平距离是4米,问这次表演是否成功?请说明理由.18. 如图所示,要设计一个等腰梯形的花坛,花坛上底长120米,下底长180米,上、下底相距80米,在两腰中点连线(虚线)处有一条横向甬道,上、下底之间有两条纵向甬道,各甬道的宽度相等,设甬道的宽为x 米.(1)用含x 的式子表示横向甬道的面积;(2)当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;(3)根据设计的要求,甬道的宽不能超过6米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是5.7,花坛其余部分的绿化费用为每平方米0.02万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?19.为迎接第四届世界太阳城大会,德州市把主要路段路灯更换为太阳能路灯.已知太阳能路灯售价为5000元/个,目前两个商家有此产品.甲商家用如下方法促销:若购买路灯不超过100个,按原价付款;若一次购买100个以上,且购买的个数每增加一个,其价格减少10元,但太阳能路灯的售价不得低于3500元/个.乙店一律按原价的80%销售.现购买太阳能路灯x 个,如果全部在甲商家购买,则所需金额为y 1元;如果全部在乙商家购买,则所需金额为y 2元. (1)分别求出y 1、y 2与x 之间的函数关系式;(2)若市政府投资140万元,最多能购买多少个太阳能路灯?20. 王亮同学善于改进学习方法,他发现对解题过程进行回顾反思,效果会更好.某一天他利用了30分钟时间进行自主学习.假设他用于解题的时间x(单位:分钟)与学习收益量)y 的关系如图1所示,用于回顾反思的时间x(单位:分钟)与学习收益量y 的关系如图2所示(其中OA 是抛物线的一部分,A 为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.(1)求王亮解题的学习收益量y 与用于解题的时间x 之间的函数关系式,并写出自变量x 的取值范围; (2)求王亮回顾反思的学习收益量y 与用于回顾反思的时间x 之间的函数关系式; (3)王亮如何分配解题和回顾反思的时间,才能使这30分钟的学习收益总量最大? (注:学习收益总量=解题的学习收益量+回顾反思的学习收益量)【答案与解析】 一、选择题 1.【答案】A ;【解析】2y x =向右平移1个单位后,顶点为(1,0),再向上平移2个单位后,顶点为(1,2),开口方向及大小不变,所以1a =,即2(1)2y x =-=.2.【答案】D ;【解析】由上图可知0a >,0c <,02ba->,∴ 0b <.0a b c ++<.240b ac ->, ∴ 反比例函数图象在第二、四象限内,一次函数图象经过第一、二、四象限,因此选D .3.【答案】B ;【解析】2223(1)4y x x x =--=--,把抛物线2(1)4y x =--向左平移2个单位长度,再向上平移3个单位长度后得抛物线2(1)1y x =+-,∴ 222(1)12y x bx c x x x =++=+-=+,∴ b =2,c =0.因此选B .4.【答案】D ;【解析】由图象知,抛物线与x 轴两交点是(-1,0),(2,0),又开口方向向下,所以0a <,抛物线与y 轴交点纵坐标大于1.显然A 、B 、C 不合题意,故选D . 5.【答案】D ;【解析】抛物线与x 轴交于两点,则0b <. 由图象可知a >0,c <0, 则b <0,故abc >0.当x =-2时,y =4a-2b+c >0. ∵ 12bx a=-=,∴ b =-2a , ∴ 4a-(-2a)×2+c >0,即8a+c >0.当x =3时,y =9a+3b+c <0,故4个结论都正确. 6.【答案】D ;【解析】画出21y x =-的图象,对称轴为0x =,若12y y =,则12x x =-;若12x x =-,则12y y =;若120x x <<,则21y y >;若120x x <<,则12y y >.7.【答案】A ; 【解析】因为a y x=,当0x >时,y 随x 增大而减小,所以a >0,因此抛物线2(1)y ax ax a x x =-=- 开口向上,且与x 轴相交于(0,0)和(1,0).8.【答案】C ;【解析】∵ 0a >,0b >,∴ 抛物线开口向上,02bx a=-<,因此抛物线顶点在y 轴的左侧, 不可能在第四象限;又0c <, 120cx x a=<·,抛物线与x 轴交于原点的两侧, 因此①③是正确的.二、填空题 9.【答案】>;【解析】根据题意画出抛物线大致图象,找出x =-1,x =2时的函数值,比较其大小,易如12y y >.10.【答案】223y x x =-++;【解析】由题意和图象知抛物线与x 轴两交点为(3,0)、(-1,0),∴ 抛物线解析式为(3)(1)y x x =--+,即223y x x =-++.11.【答案】1; 【解析】92k =,932y x =-+,与坐标轴交点为(0,3),2,03⎛⎫⎪⎝⎭. 12.【答案】 x 1=3或x 2=-1 ;【解析】由二次函数22y x x m =-++部分图象知,与x 轴的一个交点为(3,0).代入方程得m =3,解方程得x 1=3或x 2=-1.13.【答案】-1;【解析】因为抛物线过原点,所以210a -=,即1a =±,又抛物线开口向下,所以a =-1. 14.【答案】4s ; 【解析】204(s)522t =-=⎛⎫⨯- ⎪⎝⎭.15.【答案】(1,-6);【解析】常规解法是先求出关系式,然后再求点的坐标,但此方法繁琐耗时易出错,仔细分析就会注意到:A 、B 两点纵坐标相同,它们关于抛物线对称轴对称,由A(-1,4),B(5,4)得,对称轴1522x -+==,而抛物线上纵坐标为-6的一点是(3,-6),所以它关于x =2的对称点是(1,-6).故抛物线上纵坐标为-6的另一点的坐标是(1,-6).16.【答案】y 1>y 3>y 2. 【解析】因为抛物线的对称轴为6323x -==⨯.而A 、B 在对称轴左侧,且y 随x 的增大而减小, ∵ -1<2,∴ y 1>y 2,又C 在对称轴右侧,且A 、B 、C 三点到对称轴的距离分别 为2,1,2,由对称性可知:y 1>y 3>y 2.三、解答题17.【答案与解析】(1)2233519315524y x x x ⎛⎫=-++=--+ ⎪⎝⎭.∵ 305-<,∴ 函数的最大值是194.∴ 演员弹跳离地面的最大高度是194米.(2)当x =4时,234341 3.45y BC =-⨯+⨯+==.∴ 这次表演成功.18.【答案与解析】 (1)横向甬道的面积为1201801502x +=(m 2). (2)依题意:2112018028015028082x x x +⨯+-=⨯⨯,整理得21557500x x -+=,解得x 1=5,x 2=150(不合题意,舍去).∴ 甬道的宽为5米.(3)设建花坛的总费用为y 万元,则21201800.0280(1601502) 5.72y x x x x +⎡⎤=⨯⨯-+-+⎢⎥⎣⎦. ∴ y =0.04x 2-0.5x+240. 当0.56.25220.04b x a =-==⨯时,y 的值最小. ∵ 根据设计的要求,甬道的宽不能超过6 m .∴ 当x =6m 时,总费用最少,为0.04×62-0.5×6+240=238.44(万元).19.【答案与解析】(1)由题意可知,当x ≥100时,因为购买个数每增加一个,其价格减少10元,但售价不得低于3500元/个,所以5000350010025010x -≤+=,即100≤x ≤250时,购买一个需5000-10(x-100)元.故y 1=6000x-10x 2;当x >250时,购买一个需3500元. 故y 1=3500x .所以215000(0100),600010(100250),3500(250),x x y x xx x x ≤≤⎧⎪=-<≤⎨⎪>⎩y 2=5000×80%x =4000x .(2)当0<x ≤100时,y 1=5000x ≤500000<1400000;当100<x ≤250时,y 1=6000x-10x 2=-10(x-300)2+900000<1400000; 所以,由3500x =1400000,得x =400. 由4000x =1400000,得x =350.故选择甲商家,最多能购买400个路灯.20.【答案与解析】(1)设y =kx ,把(2,4)代入,得k =2,所以y =2x ,自变量x 的取值范围是:0≤x ≤30.(2)当0≤x <5时,设y =a(x-5)2+25, 把(0,0)代入,得25a+25=0,a =-1,所以22(5)2510y x x x =--+=-+.当5≤x ≤15时,y =25.即210(05),25(515).x x x y x ⎧-+≤<=⎨≤≤⎩(3)设王亮用于回顾反思的时间为x(0≤x <5)分钟,学习收益总量为Z ,则他用于解题的时间为(30-x)分钟.当0≤x <5时,222102(30)860(4)76Z x x x x x x =-++-=-++=--+.所以当x =4时,76Z =最大.当5≤x ≤15时,Z =25+2(30-x)=-2x+85. 因为Z 随x 的增大而减小, 所以当x =5时,75Z =最大.综合所述,当x =4时,76Z =最大,此时30-x =26.即王亮用于解题的时间为26分钟,用于回顾反思的时间为4分钟时.学习收益总量最大.初中数学试卷鼎尚图文**整理制作。
人教版数学九年级上学期课时练习- 《二次函数》全章复习与巩固(基础篇)(人教版)
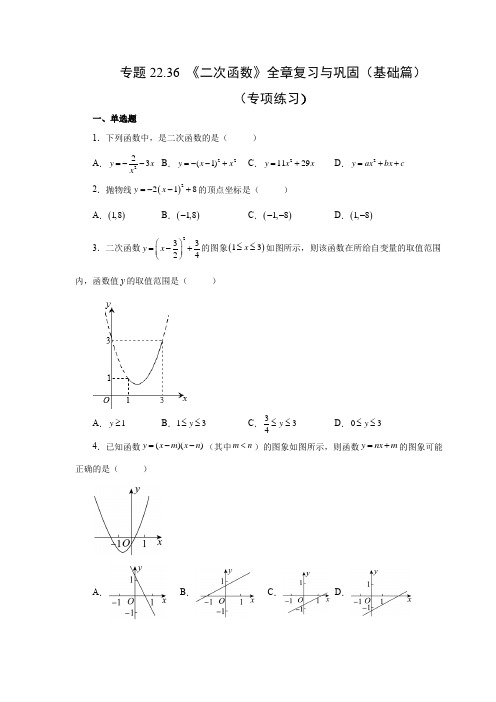
专题22.36 《二次函数》全章复习与巩固(基础篇)(专项练习)一、单选题1.下列函数中,是二次函数的是( ) A .223y x x=-- B .22(1)y x x =--+ C .21129y x x =+ D .2y ax bx c =++2.抛物线()2218y x =--+的顶点坐标是( ) A .()1,8B .()1,8-C .()1,8--D .()1,8-3.二次函数23324y x ⎛⎫=-+ ⎪⎝⎭的图象()13x ≤≤如图所示,则该函数在所给自变量的取值范围内,函数值y 的取值范围是( )A .1y ≥B .13y ≤≤C .334y ≤≤ D .03≤≤y4.已知函数()()y x m x n =--(其中m n <)的图象如图所示,则函数y nx m =+的图象可能正确的是( )A .B .C .D .5.如图,抛物线21y ax bx c =++与直线2y mx n =+相交于点()3,0和()0,3,若2ax bx c mx n ++>+,则x 的取值范围是( )A .03x <<B .13x <<C .0x <戓3x >D .1x <戓3x >6.如图,铅球运动员掷铅球的高度y (m )与水平距离x (m )之间的函数解析式是21251233y x x =-++,则该运动员此次掷铅球的成绩是( )A .6mB .12mC .8mD .10m7.在平面直角坐标系中,已知,点A (1,m )和点B (3,n )(其中mn <0)在抛物线y =ax 2+bx (a >0)上.若点(−1,y 1),(2,y 2),(4,y 3)也在该抛物线上,则y 1,y 2,y 3的大小关系是( )A .231y y y >>B .213y y y >>C .312y y y >>D .123y y y >>8.二次函数2(0)y ax bx c a =++≠的图象如图所示,下列说法中,错误的是( )A .对称轴是直线12x = B .当12x -<<时,0y < C .a c b +=D .a b c +>-9.如图,四边形ABCD 中,AB=AD ,CE ⊥BD ,CE =12BD .若△ABD 的周长为20cm ,则△BCD的面积S (cm 2)与AB 的长x (cm )之间的函数关系式可以是( )A .21101004S x x =-+ B .2240200S x x =-+ C .220100S x x =-+D .220100S x x =++10.如图,抛物线y =ax 2+bx +c 的对称轴为12x =-,经过点(﹣2,0),下列结论:①a =b ;②abc <0;③02a c +=;④点A (x 1,y 1),B (x 2,y 2)在抛物线y =ax 2+bx +c 上,当1212x x >≥-时,y 1<y 2;⑤若ax 12+bx 1=ax 22+bx 2且x 1≠x 2,则x 1+x 2=﹣1.其中正确结论的个数有( )A .2个B .3个C .4个D .5个二、填空题11.已知函数27(3)m y m x -=-是二次函数,则m =________. 12.抛物线()()y 2x 1x 3=+-的对称轴是______.13.二次函数y =12x 2—2x 一2的图象向右平移2个单位长度后,再向上平移5个单位长度,平移后的图象对应的二次函数解析式为_______.14.如图,抛物线()20y ax bx c a =++>的对称轴是过点(1,0)且平行于y 轴的直线,若点(4,0)P在该抛物线上,则42a b c -+的值为____.15.已知二次函数2(2)y a x b =++有最大值12,则a ,b 的大小关系为________.16.如图是二次函数21y ax bx c =++ 和一次函数y 2=kx +t 的图象,当y 1≥y 2时,x 的取值范围是_____.17.如图,在平面直角坐标系中,矩形OABC 的顶点O 落在坐标原点,点A 、点C 分别位于x 轴,y 轴的正半轴,G 为线段OA 上一点,将OCG ∆沿CG 翻折,O 点恰好落在对角线AC 上的点P 处,反比例函数12y x=经过点B .二次函数2(0)y ax bx c a =++≠的图象经过(0,3)C 、G 、A 三点,则该二次函数的解析式为_______.(填一般式)18.如图抛物线21322y x x =--+与x 轴相交于点A ,B ,与y 轴相交于点C ,则ABC 的面积为______.19.如图抛物线y =ax 2+bx+c 的对称轴是x =﹣1,与x 轴的一个交点为(﹣5,0),则一元二次方程ax 2+bx+c =0的另一根为______.20.如图,抛物线y=ax 2+bx+c 与直线y=mx+n 交于点A (﹣1.5,1),B (3,4),则关于x 、y 的方程组200ax bx c mx y n ⎧++=⎨-+=⎩的解为_____.21.2013年5月26日,中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y (米)与水平距离x (米)之间满足关系22810y x x 999=-++,则羽毛球飞出的水平距离为 米.22.下列说法中正确的序号是_____________ ⊥在函数y =﹣x 2中,当x =0时y 有最大值0; ⊥在函数y =2x 2中,当x >0时y 随x 的增大而增大⊥抛物线y =2x 2,y =﹣x 2,y =﹣212x 中,抛物线y =2x 2的开口最小,抛物线y =﹣x 2的开口最大⊥不论a 是正数还是负数,抛物线y =ax 2的顶点都是坐标原点 三、解答题23.如图,已知经过原点的抛物线22y x mx =+与x 轴交于另一点A (2,0). (1)求m 的值和抛物线顶点M 的坐标; (2)求直线AM 的解析式.24.已知二次函数的图象的顶点在原点O ,且经过点A (1,14).(1)求此函数的解析式;(2)将该抛物线沿着y 轴向上平移后顶点落在点P 处,直线x=2分别交原抛物和新抛物线于点M 和N ,且S △PMN =, 求:MN 的长以及平移后抛物线的解析式.25.如图,已知抛物线2y x bx c =++经过(10)A -,、(30)B ,两点,与y 轴相交于点C .(1)求抛物线的解析式;(2)点P 是对称轴上的一个动点,当PAC △的周长最小时,直接写出点P 的坐标和周长最小值;(3)点Q 为抛物线上一点,若8QABS=,求出此时点Q 的坐标.26.已知抛物线的解析式为21y x 4x 62=-+-()1求抛物线的顶点坐标;()2求出抛物线与x 轴的交点坐标; ()3当x 取何值时y 0>?27.某电商销售某种商品一段时间后,发现该商品每天的销售量y (单位:千克)和每千克的售价x (单位:元)满足一次函数关系(如图所示),其中5080x ≤≤,(1)求y关于x的函数解析式;(2)若该种商品的成本为每千克40元,该电商如何定价才能使每天获得的利润最大?最大利润是多少?参考答案1.C【分析】函数解析式中只含有一个未知数,并且未知数的最高次数是2的函数是二次函数,根据定义解答.解:A 、223y x x =--中含有分式,故不是二次函数; B 、22(1)y x x =--+=2x -1,不符合定义,故不是二次函数; C 、21129y x x =+符合定义,故是二次函数;D 、2y ax bx c =++中a 不确定不等于0,故不是二次函数; 故选:C .【点拨】此题考查二次函数的定义,熟记定义是解题的关键. 2.A 【分析】根据抛物线的顶点式()()20y a x m k a =++≠所对应的顶点坐标是(),m k -,可作出选择.解:对照抛物线的顶点式()()20y a x m k a =++≠可得1m =-,8k ,把1m =-,8k 代入顶点坐标公式(),m k -中,得此抛物线的顶点坐标为()1,8, 故选:A .【点拨】本题考查的是二次函数的基础知识:会根据顶点式写出顶点坐标.需要强调的是:公式要记清楚.顶点式()()20y a x m k a =++≠中的m 与顶点坐标(),m k -中的-m 是互为相反数的关系.3.C 【分析】先根据二次函数是顶点式,开口向上,可求出二次函数的最小值,然后结合函数图像求出最大值即可得到答案.解:⊥二次函数的解析式为23324y x ⎛⎫=-+ ⎪⎝⎭()13x ≤≤,1>0,⊥当32x =时,二次函数有最小值34, ⊥由函数图像可知,二次函数的最大值为3,⊥当13x ≤≤时,334y ≤≤, 故选C .【点拨】本题主要考查了二次函数图像的性质,解题的关键在于能够利用数形结合的思想进行求解.4.D 【分析】根据题意可得二次函数与x 轴的交点为(m ,0),(n ,0),从而得到1,01m n <-<<,进而得到函数y nx m =+经过第一三四象限,且与y 轴的交点位于点(0,-1)的下方,即可求解.解:令y =0,则()()0x m x n --=,解得:12,x m x n ==,⊥二次函数与x 轴的交点为(m ,0),(n ,0), ⊥m n <,⊥1,01m n <-<<,⊥函数y nx m =+经过第一、三、四象限,且与y 轴的交点位于点(0,-1)的下方. 故选:D【点拨】本题主要考查了二次函数和一次函数的图象和性质,熟练掌握二次函数和一次函数的图象和性质是解题的关键.5.C 【分析】根据函数图象写出抛物线在直线上方部分的x 的取值范围即可.解:抛物线21y ax bx c =++与直线2y mx n =+相交于点()3,0和()0,3,2ax bx c mx n ++>+则2ax bx c mx n ++>+的解集为:0x <戓3x >. 故选C .【点拨】本题考查了二次函数与不等式,数形结合是数学中的重要思想之一,解决函数问题更是如此.6.D 【分析】根据铅球落地时,高度y =0,把实际问题可理解为当y =0时,求x 的值即可.解:令21251233y x x =-++=0, 整理得:x 2−8x −20=0, (x −10)(x +2)=0, 解得x 1=10,x 2=−2(舍去), 故该运动员此次掷铅球的成绩是10m , 故选:D .【点拨】本题考查了二次函数的应用中函数式中自变量与函数表达的实际意义,需要结合题意,取函数或自变量的特殊值列方程求解是解题关键.7.C 【分析】分类讨论b 的正负情况,根据mn <0可得对称轴在x =32与直线x =12之间,再根据各点到对称轴的距离判断y 值大小.解:⊥y =ax 2+bx (a >0),⊥抛物线开口向上且经过原点,当b =0时,抛物线顶点为原点,x >0时y 随x 增大而增大,n >m >0不满足题意, 当b >0时,抛物线对称轴在y 轴左侧,同理,n >m >0不满足题意, ⊥b <0,抛物线对称轴在y 轴右侧,x =1时m <0,x =3时n >0, 即抛物线和x 轴的2个交点,一个为(0,0),另外一个在1和3之间, ⊥抛物线对称轴在直线x =32与直线x =12之间,即12<-2b a <32, ⊥点(2,y 2)与对称轴距离最近,点(4,y 3)与对称轴距离最远, ⊥y 2<y 1<y 3. 故选:C .【点拨】本题考查的是二次函数图象上点的坐标特征,熟知二次函数的性质是解题的关键. 8.D 【分析】由与x 轴的交点和中点公式求对称轴判断选项A ;结合函数图象判断选项B ;令x =-1,判断选项C ;令x =1,判断选项D ,即可解答.解:A 、对称轴为:直线12122x -+== ,故选项A 正确,不符合题意; B 、由函数图象知,当-1<x <2时,函数图象在x 轴的下方, ⊥当-1<x <2时,y <0,故选项B 正确,不符合题意; C 、由图可知:当x =-1时,y =a -b +c =0, ⊥a +c =b ,故选项C 正确,不符合题意; D 、由图可知:当x =1时,y =a +b +c <0 ⊥a +b <-c ,故选项D 错误,不符合题意; 故选:D .【点拨】本题主要考查了二次函数对称性、二次函数图象与系数之间的关系和二次函数图象上点的坐标特征,解题的关键理解函数图象与不等式之间以及方程的关系.9.C 【分析】先求解,BD CE 的长度,再利用三角形的面积公式列二次函数关系式即可. 解: AB=AD ,⊥ABD 的周长为20cm ,设,AB x =202,BD x1,2CE BD 120210,2CE x x,CEBD2112021020100,22BDCSBD CE x x x x故选:C【点拨】本题考查的是二次函数的几何应用,列二次函数关系式,掌握“利用图形面积公式列二次函数关系式”是解题的关键.10.C 【分析】 根据对称轴122b xa即可判断⊥,根据开口方向以及与y 轴的交点位置,即可判断⊥,根据经过点(﹣2,0)即可判断③,根据函数图象即可判断④,根据对称性即可判断⑤.解:⊥抛物线y =ax 2+bx +c 的对称轴为122b xa,则a b =, 故①正确;抛物线开口向上,与y 轴交点在y 轴的负半轴,则0a >,0c <, a b =,0b ∴>,0abc ∴<,故⊥正确;经过点(﹣2,0),420a b c ∴-+=,a b =,∴20a c +=,∴02a c+=, 故⊥正确;点A (x 1,y 1),B (x 2,y 2)在抛物线y =ax 2+bx +c 上,对称轴为12x =-, 当1212x x >≥-时,y 随x 的增大而增大,∴y 1>y 2;故④不正确,ax 12+bx 1+c =ax 22+bx 2+c 且x 1≠x 2, 对称轴为12x =-,即12122x x +=-, ∴x 1+x 2=﹣1.故⑤正确,其中正确结论的个数有4个. 故选C .【点拨】本题考查了二次函数图象与系数之间的关系,二次函数图象的性质,数形结合是解题的关键.11.3- 【分析】根据二次函数的定义得出30m -≠且272m -=,求出即可. 解:函数27(3)m y m x -=-是二次函数,30m ∴-≠且272m -=,解得:3m =-. 故答案为:3-.【点拨】本题考查了二次函数的定义,解题的关键是能熟记二次函数的定义即:表示形式为2(0)y ax bx c a =++≠.12.x 1= 【分析】函数与x 轴交点是()3,0,()1,0-,即可求解. 解:令y 0=,则:x 1=-或x 3=,即:函数与x 轴交点是()3,0,()1,0-, 故:对称轴是()1x 33112=-+= 答案是x 1=.【点拨】主要考查了对称点的特点和求抛物线的顶点坐标的方法. 13.y =12(x -4)2+1 【分析】先把抛物线化为顶点坐标式,再按照“左加右减,上加下减”的规律,即可求出平移后的函数表达式.解:⊥y =12x 2-2x -2=12(x -2)2-4,把其图象向右平移2个单位长度,再向上平移5个单位长度, 得抛物线y =12(x -2-2)2-4+5, 即为y =12(x -4)2+1.故答案为:y =12(x -4)2+1.【点拨】此题考查了二次函数图象与几何变换,同时考查了学生将一般式转化顶点式的能力,要求熟练掌握平移的规律:左加右减,上加下减.14.0 【分析】根据对称性确定抛物线与x 轴的另一个交点为(2,0)Q -,代入解析式求解即可; 解:如解图,设抛物线与x 轴的另一个交点是Q ,⊥抛物线的对称轴是过点(1,0)的直线,与x 轴的一个交点是(4,0)P , ⊥与x 轴的另一个交点(2,0)Q -,把(2-,0)代入解析式得:042a b c =-+, 420a b c ∴-+=.故答案为:0【点拨】本题主要考查了抛物线与坐标轴的交点,准确分析计算是解题的关键. 15.a b < 【分析】根据二次函数有最大值判断出a <0,并得到b 的值,然后比较大小即可. 解:⊥函数有最大值, ⊥a <0, ⊥函数的最值为12, ⊥b=12, 则a <b .【点拨】本题考查了二次函数的最值问题,属于基础题.当函数有最小值时则a >0;当函数有最大值时则a <0.16.﹣1≤x ≤2 【分析】根据图象可以直接回答,使得y 1≥y 2的自变量x 的取值范围就是直线y 1=kx+m 落在二次函数y 2=ax 2+bx+c 的图象上方的部分对应的自变量x 的取值范围.解:根据图象可得出:当y 1≥y 2时,x 的取值范围是:﹣1≤x ≤2. 故答案为:﹣1≤x ≤2.【点拨】本题考查了二次函数的性质.本题采用了“数形结合”的数学思想,使问题变得更形象、直观,降低了题的难度.17.2111324y x x =-+ 【分析】先由题意得到5AC =,再设设OG PG x ==,由勾股定理得到22(4)4x x -=+,解得x 的值,最后将点C 、G 、A 坐标代入二次函数表达式,即可得到答案.解:点(0,3)C ,反比例函数12y x=经过点B ,则点(4,3)B , 则3OC =,4OA =, ⊥5AC =,设OG PG x ==,则4GA x =-,532PA AC CP AC OC =-=-=-=, 由勾股定理得:22(4)4x x -=+, 解得:32x =,故点3(,0)2G ,将点C 、G 、A 坐标代入二次函数表达式得:3930421640c a b c a b c =⎧⎪⎪++=⎨⎪++=⎪⎩,解得:1a 211b 4c 3⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩,故答案为2111324y x x =-+. 【点拨】本题考查求二次函数解析式,解题的关键是熟练掌握待定系数法. 18.3 【分析】根据抛物线y =-12x 2-x +32,可以求得该抛物线与x 轴和y 轴的交点,从而可以得到点A 、B 、C的坐标,然后即可得到AB 和OC 的长,从而可以求得⊥ABC 的面积.解:⊥抛物线y =-12x 2-x +32,⊥当y =0时,x 1=-3,x 2=1,当x =0时,y =32,⊥点A 的坐标为(-3,0),点B 的坐标为(1,0),点C 的坐标为(0,32),⊥AB =1-(-3)=1+3=4,OC =32,⊥⊥ABC的面积为:12AB•OC=134322⨯⨯=.故答案为:3.【点拨】本题考查了抛物线与x轴的交点、二次函数图象上点的坐标特征、三角形的面积,解答本题的关键是求出点A、B、C的坐标,利用数形结合的思想解答.19.x=3【分析】根据抛物线的对称性知,抛物线与x轴的两个交点关于直线x=-1对称,据此可以求得抛物线与x轴的另一个交点,即可得出一元二次方程ax2+bx+c=0的另一个解.解:根据图示知,抛物线y=ax2+bx+c图象的对称轴是x=-1,与x轴的一个交点坐标为(-5,0),根据抛物线的对称性知,抛物线y=ax2+bx+c图象与x轴的两个交点关于直线x=-1对称,即抛物线y=ax2+bx+c图象与x轴的另一个交点与(-5,0)关于直线x=-1对称,⊥另一个交点的坐标为(3,0),⊥方程ax2+bx+c=0的另一个解是x=3;故答案是:x=3.【点拨】本题考查了抛物线与x轴的交点.解题的关键是掌握抛物线的对称性.20.1.51xy=-⎧⎨=⎩或34xy=⎧⎨=⎩.【分析】根据图像求解即可,方程组20ax bx cmx y n⎧++=⎨-+=⎩的解即为两个函数图像的交点坐标.解:⊥抛物线y=ax2+bx+c与直线y=mx+n交于点A(﹣1.5,1),B(3,4),⊥关于x、y的方程组20ax bx cmx y n⎧++=⎨-+=⎩的解为1.51xy=-⎧⎨=⎩或34xy=⎧⎨=⎩,故答案为1.51xy=-⎧⎨=⎩或34xy=⎧⎨=⎩.【点拨】本题考查了二次函数与一次函数解析式组成的方程组的解与两个函数图像交点的关系,两个解析式组成的方程组的解即为两函数图像交点的横纵坐标.21.5【分析】试题分析:根据羽毛球飞出的水平距离即为抛物线与x 轴正半轴交点到原点的距离求出即可. 解:当y=0时,22810x x 0999-++=,解得:x 1=﹣1(舍),x 2=5. ⊥羽毛球飞出的水平距离为5米. 22.⊥⊥⊥ 【分析】根据二次函数y =ax 2的图象与性质逐一判断即得答案解:由函数的解析式y =-x 2,可知a =﹣1<0,得到函数的开口向下,有最大值y =0,故⊥正确;由函数的解析式y =2x 2,可知其对称轴为y 轴,对称轴的左边(x <0),y 随x 增大而减小,对称轴的右边(x >0),y 随x 增大而增大,故⊥正确;根据二次函数的性质,系数a 决定抛物线的开口方向和开口大小,且a 越大开口越小,可知抛物线y =2x 2的开口最小,抛物线y =-x 2的开口第二小,而y 212x =-开口最大,故⊥不正确;不论a 是正数还是负数,抛物线y =ax 2的顶点都是坐标原点,故⊥正确. 综上,正确的结论是:⊥⊥⊥. 故答案为:⊥⊥⊥.【点拨】此题主要考查了二次函数的图象与性质,熟练掌握二次函数y =ax 2的与性质是解题的关键.23.(1)4m =-,M (1,-2);(2)24y x =- 【分析】(1)将A (2,0)代入抛物线的解析式,可求得m 的值,再配成顶点式即可求解; (2)利用待定系数法即可求得直线AM 的解析式.解:(1)⊥抛物线22y x mx =+过点A (2,0),22220m ∴⨯+=,解得4m =-, 224y x x ∴=-, 22(1)2x =--,⊥顶点M 的坐标是(1,-2);(2)设直线AM 的解析式为()0y kx b k =+≠,⊥图象过A (2,0),M (1,-2),202k b k b +=⎧∴⎨+=-⎩,解得24k b =⎧⎨=-⎩, ⊥直线AM 的解析式为24y x =-.【点拨】本题考查了待定系数法求函数解析式,二次函数的图象和性质,解题的关键是灵活运用所学知识解决问题.24.(1)y=14x 2;(2),y=14x 2【分析】(1)根据题意可直接设y =ax 2把点(1,﹣3)代入得a =﹣3,所以y =﹣3x 2;(2)设平移后y 14=x 2+d (d >0),则MN =d ,根据题意得出S 12=⨯2×d =,即可求得d的值,从而求得平移后的解析式.解:(1)∵抛物线顶点是原点,可设y =ax 2,把点A (1,14)代入,得:a =14,所以这个二次函数的关系式为y 14=x 2;(2)设平移后y 14=x 2+d (d >0),⊥MN =d ,S 12=⨯2×d =⊥d =⊥y 14=x 2+3.【点拨】本题考查了用待定系数法求函数解析式以及二次函数的图象与几何变换,熟练掌握待定系数法和平移的规律是解题的关键.25.(1)223y x x =--;(2)(1,2)P -(3)1(1Q - , 2(1Q + ,3(1,4)Q - 【分析】(1)把(10)A -,、(30)B ,代入抛物线2y x bx c =++即可求出b,c 即可求解; (2)根据A,B 关于对称轴对称,连接BC 交对称轴于P 点,即为所求,再求出坐标及PAC △的周长; (3)根据⊥QAB 的底边为4,故三角形的高为4,令y =4,求出对应的x 即可求解.解:(1)把(10)A -,、(30)B ,代入抛物线2y x bx c =++得01093b cb c =-+⎧⎨=++⎩解得23b c =-⎧⎨=-⎩⊥抛物线的解析式为:223y x x =--; (2)如图,连接BC 交对称轴于P 点,即为所求, ⊥223y x x =-- ⊥C(0,-3),对称轴x=1 设直线BC 为y=kx+b,把(30)B ,, C(0,-3)代入y=kx+b 求得k=1,b=-3, ⊥直线BC 为y=x -3 令x=1,得y=-2, ⊥P (1,-2),⊥PAC △的周长(3)⊥⊥QAB 的底边为AB=4, 182QABS AB H =⨯= ⊥三角形的高为4,令y =4,即2234x x --=±解得x 1=1-2=1+3=1故点Q 的坐标为1(1Q - , 2(1Q + ,3(1,4)Q -.【点拨】此题主要考查二次函数的图像与性质,解题的关键是熟知待定系数法与一次函数的求解.26.(1)抛物线顶点坐标为()4,2;()2 抛物线与x 轴的交点坐标为()()2,06,0,;()3当2x 6<<时,y 0>.【分析】(1)求抛物线的顶点坐标既可以利用公式,也可以利用配方法求解;(2)求抛物线与x 轴的交点坐标就是求函数值等于0时对应的x 的值即可解决问题;(3)y >0就是抛物线在x 轴上方的部分,所以利用抛物线的开口方向和与x 轴的交点坐标即可求解.解:(1)21y x 4x 62=-+- 21(x 4)22=--+, ⊥抛物线顶点坐标为()4,2;()2当y 0=时,即21y x 4x 602=-+-=, ⊥x 2=或x 6=, ⊥抛物线与x 轴的交点坐标为()()2,06,0;()3⊥抛物线的开口方向向下,且抛物线与x 轴的交点坐标为()()2,06,0,⊥当2x 6<<时,y 0>.【点拨】二次函数的性质,抛物线与x 轴的交点,二次函数与不等式(组).27.(1)y 关于x 的函数解析式为2200y x =-+;(2)该电商定价为70元时才能使每天获得的利润最大,最大利润是1800元.【分析】(1)由图象易得()50,100和()80,40,然后设y 关于x 的函数解析式为y kx b =+,进而代入求解即可;(2)设该电商每天所获利润为w 元,由(1)及题意易得222808000w x x =-+-,然后根据二次函数的性质可进行求解.解:(1)设y 关于x 的函数解析式为y kx b =+,则由图象可得()50,100和()80,40,代入得:501008040k b k b +=⎧⎨+=⎩,解得:2200k b =-⎧⎨=⎩, ⊥y 关于x 的函数解析式为2200y x =-+;(2)设该电商每天所获利润为w 元,由(1)及题意得:()()240220022808000w x x x x =--+=-+-,⊥-2<0,开口向下,对称轴为702b x a=-=, ⊥5080x ≤≤, ⊥当70x =时,w 有最大值,即为22702807080001800w =-⨯+⨯-=; 答:该电商定价为70元时才能使每天获得的利润最大,最大利润是1800元.【点拨】本题主要考查二次函数的应用,熟练掌握二次函数的应用是解题的关键.。
数学中考试题北京市第四中学总复习:《二次函数》全章复习与巩固—知识讲解(提高)

《二次函数》全章复习与巩固—知识讲解(提高)撰稿:张晓新审稿:杜少波【学习目标】1.通过对实际问题情境的分析确定二次函数的表达式,并体会二次函数的意义;2.会用描点法画出二次函数的图象,能从图象上认识二次函数的性质;3.会根据公式确定图象的顶点、开口方向和对称轴(公式不要求记忆和推导),并能解决简单的实际问题;4.会利用二次函数的图象求一元二次方程的近似解.【知识网络】【要点梳理】要点一、二次函数的定义一般地,如果是常数,,那么叫做的二次函数.要点诠释:如果y=ax2+bx+c(a,b,c是常数,a≠0),那么y叫做x的二次函数.这里,当a=0时就不是二次函数了,但b、c可分别为零,也可以同时都为零.a 的绝对值越大,抛物线的开口越小.要点二、二次函数的图象与性质1.二次函数由特殊到一般,可分为以下几种形式:①;②;③;④,其中;⑤.(以上式子a≠0)几种特殊的二次函数的图象特征如下:函数解析式开口方向对称轴顶点坐标当时开口向上当时开口向下(轴) (0,0)(轴) (0,)(,0)(,)()2.抛物线的三要素:开口方向、对称轴、顶点.(1)的符号决定抛物线的开口方向:当时,开口向上;当时,开口向下;相等,抛物线的开口大小、形状相同.(2)平行于轴(或重合)的直线记作.特别地,轴记作直线.3.抛物线20()y ax bx c a=++≠中,,,a b c的作用:(1)决定开口方向及开口大小,这与中的完全一样.(2)和共同决定抛物线对称轴的位置.由于抛物线的对称轴是直线,故:①时,对称轴为轴;②(即、同号)时,对称轴在轴左侧;③(即、异号)时,对称轴在轴右侧.(3)的大小决定抛物线与轴交点的位置.当时,,∴抛物线与轴有且只有一个交点(0,):①,抛物线经过原点;②,与轴交于正半轴;③,与轴交于负半轴.以上三点中,当结论和条件互换时,仍成立.如抛物线的对称轴在轴右侧,则 .4.用待定系数法求二次函数的解析式: (1)一般式:(a≠0).已知图象上三点或三对、的值,通常选择一般式.(2)顶点式:(a≠0).已知图象的顶点或对称轴,通常选择顶点式.(可以看成的图象平移后所对应的函数.)(3)“交点式”:已知图象与轴的交点坐标、,通常选用交点式:(a≠0).(由此得根与系数的关系:).要点诠释:求抛物线2y ax bx c =++(a≠0)的对称轴和顶点坐标通常用三种方法:配方法、公式法、代入法,这三种方法都有各自的优缺点,应根据实际灵活选择和运用.要点三、二次函数与一元二次方程的关系 函数,当时,得到一元二次方程,那么一元二次方程的解就是二次函数的图象与x 轴交点的横坐标,因此二次函数图象与x 轴的交点情况决定一元二次方程根的情况.(1)当二次函数的图象与x 轴有两个交点,这时,则方程有两个不相等实根;(2)当二次函数的图象与x 轴有且只有一个交点,这时,则方程有两个相等实根;(3)当二次函数的图象与x 轴没有交点,这时,则方程没有实根.通过下面表格可以直观地观察到二次函数图象和一元二次方程的关系:的图象的解方程有两个不等实数解方程有两个相等实数解方程没有实数解要点诠释:二次函数图象与x 轴的交点的个数由的值来确定.(1)当二次函数的图象与x 轴有两个交点,这时,则方程有两个不相等实根;(2)当二次函数的图象与x 轴有且只有一个交点,这时,则方程有两个相等实根;(3)当二次函数的图象与x 轴没有交点,这时,则方程没有实根.要点四、利用二次函数解决实际问题利用二次函数解决实际问题,要建立数学模型,即把实际问题转化为二次函数问题,利用题中存在的公式、内含的规律等相等关系,建立函数关系式,再利用函数的图象及性质去研究问题.在研究实际问题时要注意自变量的取值范围应具有实际意义. 利用二次函数解决实际问题的一般步骤是: (1)建立适当的平面直角坐标系;(2)把实际问题中的一些数据与点的坐标联系起来; (3)用待定系数法求出抛物线的关系式;(4)利用二次函数的图象及其性质去分析问题、解决问题. 要点诠释:常见的问题:求最大(小)值(如求最大利润、最大面积、最小周长等)、涵洞、桥梁、抛物体、抛物线的模型问题等.解决这些实际问题关键是找等量关系,把实际问题转化为函数问题,列出相关的函数关系式.【典型例题】类型一、求二次函数的解析式1. 已知抛物线的顶点是(3,-2),且在x 轴上截得的线段长为6,求抛物线的解析式. 【思路点拨】已知抛物线的顶点是(3,-2),可设抛物线解析式为顶点式,即2(3)2y a x =--,也就是2692y ax ax a =-+-,再由在x 轴上截得的线段长为6建立方程求出a .也可根据抛物线的对称轴是直线x =3,在x 轴上截得的线段长为6,则与x 轴的交点为(0,0)和(6,0),因此可设y =a(x-0)·(x-6).【答案与解析】解法一:∵ 抛物线的顶点是(3,-2),且与x 轴有交点,∴ 设解析式为y =a(x-3)2-2(a >0),即2692y ax ax a =-+-,设抛物线与x 轴两交点分别为(x 1,0),(x 2,0).则212364(92)||6||a a a x x a ---==,解得29a =.∴ 抛物线的解析式为22(3)29y x =--,即22493y x x =-. 解法二:∵ 抛物线的顶点为(3,-2), ∴ 设抛物线解析式为2(3)2y a x =--.∵ 对称轴为直线x =3,在x 轴上截得的线段长为6,∴ 抛物线与x 轴的交点为(0,0),(6,0).把(0,0)代入关系式,得0=a(0-3)2-2,解得29a =,∴ 抛物线的解析式为22(3)29y x =--, 即22493y x x =-.解法三:求出抛物线与x 轴的两个交点的坐标(0,0),(6,0)设抛物线解析式为y =a(x-0)(x-6),把(3,-2)代入得3(36)2a ⨯⨯-=-,解得29a =. ∴ 抛物线的解析式为2(6)9y x x =-,即22493y x x =-.【点评】求抛物线解析式时,根据题目条件,恰当选择关系式,可使问题变得简单. 举一反三:【高清课程名称:二次函数复习高清ID 号:357019 关联的位置名称(播放点名称):练习题精讲】 【变式】已知抛物线2442y mx mx m =-+-(m 是常数). (1)求抛物线的顶点坐标; (2)若155m <<,且抛物线与x 轴交于整数点,求此抛物线的解析式.【答案】(1)依题意,得0≠m ,∴2242=--=-=mm a b x , m m m m a b ac y 442444422)()(---=-=241681622-=--=m m m m∴抛物线的顶点坐标为)2,2(-.(2)∵抛物线与x 轴交于整数点,∴02442=-+-m mx mx 的根是整数.∴24164(42)22222m m m m m x m m±--==±. ∵0m >,∴22x m=±是整数.∴2m 是完全平方数.∵155m <<, ∴22105m<<,∴2m 取1,4,9,24164(42)22222m m m m mx m m±--==±. 当21m =时,2=m ;当24m =时,21=m ;当29m =时,29m =. ∴m 的值为2或21或29.∴抛物线的解析式为6822+-=x x y 或x x y 2212-=或22810999y x x =--.类型二、根据二次函数图象及性质判断代数式的符号2. 函数y ax b =+和2y ax bx c =++(0)a ≠在同一直角坐标系内的图象大致是( )【答案】C ;【解析】 ∵ a ≠0,∴ 分a >0,a <0两种情况来讨论两函数图象的分布情况.若a >0,则y =ax+b 的图象必经过第一、三象限,2y ax bx c =++的图象开口向上,可排除D . 若a >0,b >0,则y =ax+b 的图象与y 轴的交点在y 轴的正半轴上,2y ax bx c =++的图象的对称轴在y 轴的左侧,故B 不正确.若a >0,b <0,则y =ax+b 的图象与y 轴的交点在y 轴的负半轴上,2y ax bx c =++的图象的对称轴在y 轴的右侧,故C 正确.若a <0,则y =ax+b 的图象必经过第二、四象限,2y ax bx c =++的图象开口向下,故A 不正确.【点评】在同一直角坐标系中研究两种函数图象的分布情况,待定系数a ,b 满足一致性,因此讨论a ,b 符号的一致性成为解决本题的关键所在.事实上,a ,b 的符号既决定了一次函数图象的分布情况,又决定了抛物线的开口方向和对称轴的位置.类型三、数形结合3. 已知平面直角坐标系xOy(如图所示),一次函数334y x =+的图象与y 轴交于点A ,点M 在正比例函数32y x =的图象上,且MO =MA ,二次函数2y x bx c =++的图象经过点A 、M .(1)求线段AM 的长;(2)求这个二次函数的解析式;(3)如果点B 在y 轴上,且位于点A 下方,点C 在上述二次函数的图象上,点D 在一次函数334y x =+ 的图象上,且四边形ABCD 是菱形,求点C 的坐标. 【答案与解析】(1)一次函数334y x =+,当x =0时,y =3,所以点A 的坐标为(0,3), 又∵ MO =MA ,∴ M 在OA 的中垂线上,即M 的纵坐标为32,又M 在32y x =上,当32y =时,x =1, ∴ 点M 的坐标为31,2⎛⎫⎪⎝⎭.如图所示,22313122AM ⎛⎫=+= ⎪⎝⎭.(2)将点A(0,3),31,2M ⎛⎫ ⎪⎝⎭代入2y x bx c =++中,得3,31.2c b c =⎧⎪⎨++=⎪⎩ ∴ 5,23.b c ⎧=-⎪⎨⎪=⎩ 即这个二次函数的解析式为:2532y x x =-+. (3)如图所示,设B(0,m)(m <3),25(,3)2C n n n -+,3,34D n n ⎛⎫+ ⎪⎝⎭.则|AB|=3-m ,213||4D C DC y y n n =-=-,5||4AD n =.因为四边形ABCD 是菱形,所以||||||AB DC AD ==.所以2133,453.4m n n m n ⎧-=-⎪⎪⎨⎪-=⎪⎩ 解得113,0;m n =⎧⎨=⎩(舍去)221,22.m n ⎧=⎪⎨⎪=⎩将n =2代入2532y x x =-+,得2C y =,所以点C 的坐标为(2,2). 【点评】结合题意画出图形,再根据图形的特殊性求线段长或点的坐标,达到以“形”助“数”的目的.类型四、函数与方程4. 如图所示,把一张长10cm ,宽8 cm 的矩形硬纸板的四周各剪去一个同样大小的正方形,再折成一个无盖的长方体盒子(纸板的厚度忽略不计).(1)要使长方体盒子的底面积为48 cm 2,那么剪去的正方形的边长应为多少?(2)折成的长方体盒子的侧面积会不会有更大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请说明理由;(3)如果把矩形硬纸板的四周分别剪去两个同样大小的正方形和两个同样形状、同样大小的矩形,然后折成一个有盖的长方体盒子,是否有侧面积最大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由. 【答案与解析】(1)设剪去的正方形的边长为x cm ,则(10-2x)·(8-2x)=48,即x 2-9x+8=0. 解得x 1=8(不合题意,舍去),x 2=1.所以剪去的正方形的边长为1 cm .(2)有侧面积最大的情况.设此时剪去的正方形的边长为x cm ,盒子的侧面积为y cm 2, 则y 与x 的函数关系式为:y =2(10-2x)x+2(8-2x)x .即y =-8x 2+36x ,改写为2981842y x ⎛⎫=--+ ⎪⎝⎭,所以当x =2.25时,y =最大40.5.即当剪去的正方形的边长为2.25 cm 时,长方体盒子的侧面积最大为40.5 cm 2;(3)有侧面积最大的情况.设剪去的正方形的边长为x cm ,盒子的侧面积为y cm 2.若按图所示的方法剪折,则y 与x 的函数关系式为:1022(82)22x y x x x -=-+⨯,即213169666y x ⎛⎫=--+ ⎪⎝⎭.所以当136x =时,1696y =最大.若按图所示的方法剪折,则y 与x 的函数关系式为:822(102)22x y x x x -=-+⨯,即2798633y x ⎛⎫=--+ ⎪⎝⎭.所以当73x =时,983y =最大.比较以上两种剪折方法可以看出,按图所示的方法剪折得到的盒子侧面积最大, 即当剪去的正方形的边长为73cm 时,折成的有盖的长方体盒子的侧面积最大,最大面积为398cm 3.【点评】结合题意建立方程模型,注意到题目中剪去的正方形、矩形的边之间的关系:即正方形的边长应当与矩形的短边长度相同,这样才可以折成有盖的长方形盒子.用含字母的代数式表示长方体盒子的侧面积,联系所得出的侧面积与正方形的边长之间的关系式,根据函数的性质可以求出盒子侧面积的最大值,由于此题矩形的两边长度不同,所以剪切的方法有两种,应当注意分类,以免漏解. 举一反三: 【变式1】抛物线与直线只有一个公共点,则b=________.【答案】由题意得把②代入①得.∵抛物线与直线只有一个公共点,∴方程必有两个相等的实数根,∴,∴.【变式2】二次函数的图象如图所示,根据图象解答下列问题:(1)写出方程的两个根;(2)写出不等式的解集;(3)写出y随x的增大而减小的自变量x的取值范围;(4)若方程有两个不相等的实数根,求k的取值范围.【答案】(1)(2).(3).(4)方法1:方程的解,即为方程组中x的解也就是抛物线与直线的交点的横坐标,由图象可看出,当时,直线与抛物线有两个交点,∴.方法2:∵二次函数的图象过(1,0),(3,0),(2,2)三点,∴∴∴ ,即,∴ .∵ 方程有两个不相等的实数根,∴,∴ .类型五、分类讨论5.若函数22(2)2(2)x x y xx ⎧+≤=⎨>⎩,则当函数值y =8时,自变量x 的值是( ). A .6± B .4 C .6±或4 D .4或6-【思路点拨】此题函数是以分段函数的形式给出的,当y =8时,求x 的值时,注意分类讨论.【答案】D ;【解析】由题意知,当228x +=时,6x =±.而62>,∴ 6x =-.6x =(舍去).当2x =8时,x =4.综合上知,选D .【点评】正确的分类必须是周全的,既不重复、也不遗漏.类型六、与二次函数有关的动点问题6.如图所示,在直角坐标系中,点A ,B ,C 的坐标分别为(-1,0),(3,0),(0,3),过A ,B ,C 三点的抛物线的对称轴为直线l ,D 为对称轴l 上一动点.(1)求抛物线的解析式;(2)求当AD+CD 最小时点D 的坐标;(3)以点A 为圆心,以AD 为半径作⊙A .①证明:当AD+CD 最小时,直线BD 与⊙A 相切; ②写出直线BD 与⊙A 相切时,D 点的另一个坐标.【思路点拨】根据A 、B 两点在x 轴上,可设交点式求解析式.要AD+CD 最小,根据两点之间线段最短,可判定D 点位置,从而求出点D 坐标.要让BD 与⊙A 相切,只需证AD ⊥BD ,由圆的对称性, 可直接写出D 点另一个坐标.【答案与解析】(1)设抛物线的解析式为y =a(x+1)(x-3).将(0,3)代入上式,得3=a(0+1)(0-3).解得a =-1.∴ 抛物线的解析式为y =-(x+1)(x-3),即223y x x =-++.(2)连接BC ,交直线l 于点D ′.∵ 点B 与点A 关于直线l 对称,∴ AD ′=BD ′.∴ AD ′+CD ′=BD ′+CD ′=BC .由“两点之间,线段最短”的原理可知:此时AD ′+CD ′最小,点D ′的位置即为所求.设直线BC 的解析式为y =kx+b ,由直线BC 过点(3,0),(0,3),得03,3.k b b =+⎧⎨=⎩解这个方程组,得1,3.k b =-⎧⎨=⎩∴ 直线BC 的解析式为y =-x+3.∵ 对称轴l 为x =1.将x =1代入y =-x+3,得y =-1+3=2.∴ 点D 的坐标为(1,2).(3)①连接AD .设直线l 与x 轴的交点为点E .由(2)知:当AD+CD 最小时,点D 的坐标为(1,2).∵ DE =AE =BE =2,∴ ∠DAB =∠DBA =45°,∴ ∠ADB =90°. ∴ AD ⊥BD .∴ BD与⊙A相切.②(1,-2).【点评】动点问题分单点运动和双点运动,是中考的热点问题,在运动变化中发展空间想象能力和提高综合分析问题的能力,解决此类题要“以静制动”,即把动态问题变为静态的问题去解决,解题时用运动的眼光去观察研究问题,挖掘运动变化过程中的不变量、不变关系.。
中考总复习二次函数--巩固练习

中考总复习二次函数--巩固练习二次函数是高中数学中的重要内容,也是中考中常考的知识点。
通过对二次函数的巩固练习,可以帮助学生提高对二次函数的理解和运用能力,为中考做好准备。
下面是一些二次函数的巩固练习题,希望可以帮助你更好地掌握这个知识点。
1.判断以下函数是不是二次函数,并指出它的顶点、对称轴和开口方向:(1)y=4x²+3x-1(2)y=5x-1(3)y=-3x²+2x+4(4)y=-x²2.求以下函数的零点,并判断它的开口方向:(1)y=3x²-4x+1(2)y=-2x²+5(3)y=x²+2x-3(4)y=-4x²+4x3.求以下函数的顶点、对称轴和开口方向:(1)y=2x²-8x+6(2)y=-3x²+12x-9(3)y=x²+4x(4)y=-x²-5x-64.画出以下函数的图像,并指出它的顶点、对称轴和开口方向:(1)y=2(x-1)²+3(2)y=-3(x+2)²+4(3)y=(x+1)²-2(4)y=-2(x-3)²-55.求以下函数的最大值或最小值,并指出是在什么点取得:(1)y=-2x²+5x-3(2)y=3x²-6x+2(3)y=x²+4x+7(4)y=-4x²+2x-16.求以下函数的定义域和值域:(1)y=3x²-2x+1(2)y=-4x²+3x+2(3)y=x²+2x+3(4)y=-5x²-4x-17. 如果三次函数y = ax³ + bx² + cx + d的图像经过点(1,1),(2,4),(3,9),求它的解析式。
8.求以下函数的零点和解析式:(1)y = ax² + bx + c,已知它的图像与x轴有两个交点,且交点的横坐标分别为-1和2(2)y = ax² + bx + c,已知它的图像与x轴有一个交点,且该交点的横坐标为4这些是对二次函数的巩固练习题,希望可以帮助你更好地理解和运用二次函数。
初三数学中考专项练习 《二次函数》全章复习与巩固—知识讲解(提高)

《二次函数》全章复习与巩固—知识讲解(提高)【学习目标】1.通过对实际问题情境的分析确定二次函数的表达式,并体会二次函数的意义;2.会用描点法画出二次函数的图象,能从图象上认识二次函数的性质;3.会根据公式确定图象的顶点、开口方向和对称轴(公式不要求记忆和推导),并能解决简单的实际问题;4.会利用二次函数的图象求一元二次方程的近似解.【知识网络】【要点梳理】要点一、二次函数的定义一般地,如果是常数,,那么叫做的二次函数.要点诠释:如果y=ax2+bx+c(a,b,c是常数,a≠0),那么y叫做x的二次函数.这里,当a=0时就不是二次函数了,但b、c可分别为零,也可以同时都为零.a 的绝对值越大,抛物线的开口越小.要点二、二次函数的图象与性质1.二次函数由特殊到一般,可分为以下几种形式:①;②;③;④,其中;⑤.(以上式子a≠0)几种特殊的二次函数的图象特征如下:当(轴) (轴)(,)2.抛物线的三要素:开口方向、对称轴、顶点.(1)的符号决定抛物线的开口方向:当时,开口向上;当时,开口向下;相等,抛物线的开口大小、形状相同. (2)平行于轴(或重合)的直线记作.特别地,轴记作直线.3.抛物线20()y ax bx c a =++≠中,,,a b c 的作用: (1)决定开口方向及开口大小,这与中的完全一样.(2)和共同决定抛物线对称轴的位置.由于抛物线的对称轴是直线, 故:①时,对称轴为轴;②(即、同号)时,对称轴在轴左侧;③(即、异号)时,对称轴在轴右侧.(3)的大小决定抛物线与轴交点的位置.当时,,∴抛物线与轴有且只有一个交点(0,):①,抛物线经过原点; ②,与轴交于正半轴;③,与轴交于负半轴.以上三点中,当结论和条件互换时,仍成立.如抛物线的对称轴在轴右侧,则.4.用待定系数法求二次函数的解析式: (1)一般式:(a≠0).已知图象上三点或三对、的值,通常选择一般式.(2)顶点式:(a≠0).已知图象的顶点或对称轴,通常选择顶点式.(可以看成的图象平移后所对应的函数.)(3)“交点式”:已知图象与轴的交点坐标、,通常选用交点式:(a ≠0).(由此得根与系数的关系:).要点诠释:求抛物线2y ax bx c =++(a≠0)的对称轴和顶点坐标通常用三种方法:配方法、公式法、代入法,这三种方法都有各自的优缺点,应根据实际灵活选择和运用.要点三、二次函数与一元二次方程的关系 函数,当时,得到一元二次方程,那么一元二次方程的解就是二次函数的图象与x 轴交点的横坐标,因此二次函数图象与x 轴的交点情况决定一元二次方程根的情况.(1)当二次函数的图象与x 轴有两个交点,这时,则方程有两个不相等实根;(2)当二次函数的图象与x 轴有且只有一个交点,这时,则方程有两个相等实根;(3)当二次函数的图象与x 轴没有交点,这时,则方程没有实根.要点诠释:二次函数图象与x 轴的交点的个数由的值来确定.(1)当二次函数的图象与x 轴有两个交点,这时,则方程有两个不相等实根;(2)当二次函数的图象与x 轴有且只有一个交点,这时,则方程有两个相等实根;(3)当二次函数的图象与x 轴没有交点,这时,则方程没有实根.要点四、利用二次函数解决实际问题利用二次函数解决实际问题,要建立数学模型,即把实际问题转化为二次函数问题,利用题中存在的公式、内含的规律等相等关系,建立函数关系式,再利用函数的图象及性质去研究问题.在研究实际问题时要注意自变量的取值范围应具有实际意义. 利用二次函数解决实际问题的一般步骤是: (1)建立适当的平面直角坐标系;(2)把实际问题中的一些数据与点的坐标联系起来; (3)用待定系数法求出抛物线的关系式;(4)利用二次函数的图象及其性质去分析问题、解决问题. 要点诠释:常见的问题:求最大(小)值(如求最大利润、最大面积、最小周长等)、涵洞、桥梁、抛物体、抛物线的模型问题等.解决这些实际问题关键是找等量关系,把实际问题转化为函数问题,列出相关的函数关系式.【典型例题】类型一、求二次函数的解析式1. 已知抛物线的顶点是(3,-2),且在x 轴上截得的线段长为6,求抛物线的解析式. 【思路点拨】已知抛物线的顶点是(3,-2),可设抛物线解析式为顶点式,即2(3)2y a x =--,也就是2692y ax ax a =-+-,再由在x 轴上截得的线段长为6建立方程求出a .也可根据抛物线的对称轴是直线x =3,在x 轴上截得的线段长为6,则与x 轴的交点为(0,0)和(6,0),因此可设y =a(x-0)·(x-6).【答案与解析】解法一:∵ 抛物线的顶点是(3,-2),且与x 轴有交点,∴ 设解析式为y =a(x-3)2-2(a >0),即2692y ax ax a =-+-,设抛物线与x 轴两交点分别为(x 1,0),(x 2,0).则12||6x x -==,解得29a =.∴ 抛物线的解析式为22(3)29y x =--,即22493y x x =-. 解法二:∵ 抛物线的顶点为(3,-2), ∴ 设抛物线解析式为2(3)2y a x =--.∵ 对称轴为直线x =3,在x 轴上截得的线段长为6,∴ 抛物线与x 轴的交点为(0,0),(6,0).把(0,0)代入关系式,得0=a(0-3)2-2,解得29a =,∴ 抛物线的解析式为22(3)29y x =--, 即22493y x x =-.解法三:求出抛物线与x 轴的两个交点的坐标(0,0),(6,0)设抛物线解析式为y =a(x-0)(x-6),把(3,-2)代入得3(36)2a ⨯⨯-=-,解得29a =. ∴ 抛物线的解析式为2(6)9y x x =-,即22493y x x =-.【点评】求抛物线解析式时,根据题目条件,恰当选择关系式,可使问题变得简单. 举一反三:【变式】已知抛物线2442y mx mx m =-+-(m 是常数).(1)求抛物线的顶点坐标; (2)若155m <<,且抛物线与x 轴交于整数点,求此抛物线的解析式.【答案】(1)依题意,得0≠m ,∴2242=--=-=mma b x ,m m m m a b ac y 442444422)()(---=-=241681622-=--=m m m m∴抛物线的顶点坐标为)2,2(-. (2)∵抛物线与x 轴交于整数点,∴02442=-+-m mx mx 的根是整数.∴2x ==.∵0m >,∴2x =±2m是完全平方数.∵155m <<, ∴22105m <<,∴2m取1,4,9,2x ==. 当21m =时,2=m ;当24m =时,21=m ;当29m =时,29m =. ∴m 的值为2或21或29.∴抛物线的解析式为6822+-=x x y 或x x y 2212-=或22810999y x x =--.类型二、根据二次函数图象及性质判断代数式的符号2. (2016•鄂州)如图,二次函数y=ax 2+bx +c=0(a ≠0)的图象与x 轴正半轴相交于A 、B 两点,与y 轴相交于点C ,对称轴为直线x=2,且OA=OC ,则下列结论:①abc >0;②9a +3b +c <0;③c >﹣1;④关于x 的方程ax 2+bx +c=0(a ≠0)有一个根为﹣ 其中正确的结论个数有( )A.1个B.2个C.3个D.4个【思路点拨】由二次函数图象的开口方向、对称轴及与y轴的交点可分别判断出a、b、c的符号,从而可判断①;由图象可知当x=3时,y<0,可判断②;由OA=OC,且OA<1,可判断③;把﹣代入方程整理可得ac2﹣bc+c=0,结合③可判断④;从而可得出答案.【答案】C;【解析】解:由图象开口向下,可知a<0,与y轴的交点在x轴的下方,可知c<0,又对称轴方程为x=2,所以﹣>0,所以b>0,∴abc>0,故①正确;由图象可知当x=3时,y>0,∴9a+3b+c>,故②错误;由图象可知OA<1,∵OA=OC,∴OC<1,即﹣c<1,∴c>﹣1,故③正确;假设方程的一个根为x=﹣,把x=﹣代入方程可得﹣+c=0,整理可得ac﹣b+1=0,两边同时乘c可得ac2﹣bc+c=0,即方程有一个根为x=﹣c,由②可知﹣c=OA,而当x=OA是方程的根,∴x=﹣c是方程的根,即假设成立,故④正确;综上可知正确的结论有三个,故选C.【点评】本题主要考查二次函数的图象和性质.熟练掌握图象与系数的关系以及二次函数与方程、不等式的关系是解题的关键.特别是利用好题目中的OA=OC,是解题的关键.类型三、数形结合3. 已知平面直角坐标系xOy(如图所示),一次函数334y x=+的图象与y轴交于点A,点M在正比例函数32y x=的图象上,且MO=MA,二次函数2y x bx c=++的图象经过点A、M.(1)求线段AM 的长;(2)求这个二次函数的解析式;(3)如果点B 在y 轴上,且位于点A 下方,点C 在上述二次函数的图象上,点D 在一次函数334y x =+ 的图象上,且四边形ABCD 是菱形,求点C 的坐标. 【答案与解析】(1)一次函数334y x =+,当x =0时,y =3,所以点A 的坐标为(0,3), 又∵ MO =MA ,∴ M 在OA 的中垂线上,即M 的纵坐标为32,又M 在32y x =上,当32y =时,x =1,∴ 点M 的坐标为31,2⎛⎫⎪⎝⎭.如图所示,2AM ==.(2)将点A(0,3),31,2M ⎛⎫ ⎪⎝⎭代入2y x bx c =++中,得3,31.2c b c =⎧⎪⎨++=⎪⎩ ∴ 5,23.b c ⎧=-⎪⎨⎪=⎩ 即这个二次函数的解析式为:2532y x x =-+. (3)如图所示,设B(0,m)(m <3),25(,3)2C n n n -+,3,34D n n ⎛⎫+ ⎪⎝⎭.则|AB|=3-m ,213||4D C DC y y n n =-=-,5||4AD n =. 因为四边形ABCD 是菱形,所以||||||AB DC AD ==.所以2133,453.4m n n m n ⎧-=-⎪⎪⎨⎪-=⎪⎩ 解得113,0;m n =⎧⎨=⎩(舍去)221,22.m n ⎧=⎪⎨⎪=⎩将n =2代入2532y x x =-+,得2C y =,所以点C 的坐标为(2,2). 【点评】结合题意画出图形,再根据图形的特殊性求线段长或点的坐标,达到以“形”助“数”的目的.类型四、函数与方程4.(2015•本溪模拟)某体育用品店购进一批单件为40元的球服,如果按单价60元销售样,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套.设销售单价为x (x ≧60)元,销售量为y 套. (1)求出y 与x 的函数关系式;(2)当销售单件为多少元时,月销售额为14000元?(3)当销售单价为多少元时,才能在一个月内获得最大利润?最大利润是多少? 【答案与解析】解:(1)销售单价为x 元,则销售量减少×20,故销售量为y=240﹣×20=﹣4x+480(x ≥60);(2)根据题意可得,x (﹣4x+480)=14000, 解得x 1=70,x 2=50(不合题意舍去),故当销售价为70元时,月销售额为14000元; (3)设一个月内获得的利润为w 元,根据题意得: w=(x ﹣40)(﹣4x+480) =﹣4x2+640x ﹣19200 =﹣4(x ﹣80)2+6400.当x=80时,w 的最大值为6400.故当销售单价为80元时,才能在一个月内获得最大利润,最大利润是6400元.【点评】本题考查了函数模型的选择与应用,考查了数学建模思想方法,关键是对题意要正确理解. 举一反三:【变式1】抛物线与直线只有一个公共点,则b=________.【答案】由题意得把②代入①得.∵抛物线与直线只有一个公共点,∴方程必有两个相等的实数根,∴,∴.【变式2】二次函数的图象如图所示,根据图象解答下列问题:(1)写出方程的两个根;(2)写出不等式的解集;(3)写出y随x的增大而减小的自变量x的取值范围;(4)若方程有两个不相等的实数根,求k的取值范围.【答案】(1)(2).(3).(4)方法1:方程的解,即为方程组中x的解也就是抛物线与直线的交点的横坐标,由图象可看出,当时,直线与抛物线有两个交点,∴.方法2:∵ 二次函数的图象过(1,0),(3,0),(2,2)三点,∴ ∴∴ ,即,∴.∵ 方程有两个不相等的实数根,∴ ,∴.类型五、分类讨论5.若函数22(2)2(2)x x y xx ⎧+≤=⎨>⎩,则当函数值y =8时,自变量x 的值是( ).A .B .4C .或4D .4或【思路点拨】此题函数是以分段函数的形式给出的,当y =8时,求x 的值时,注意分类讨论. 【答案】D ; 【解析】由题意知,当228x +=时,x =2>,∴ x =x =舍去).当2x =8时,x =4.综合上知,选D .【点评】正确的分类必须是周全的,既不重复、也不遗漏.类型六、与二次函数有关的动点问题6.在平面直角坐标系xOy 中,二次函数y=mx 2-(m+n )x+n (m <0)的图象与y 轴正半轴交于A 点.(1)求证:该二次函数的图象与x 轴必有两个交点;(2)设该二次函数的图象与x 轴的两个交点中右侧的交点为点B ,若∠ABO=45°,将直线AB 向下平移2个单位得到直线l ,求直线l 的解析式;(3)在(2)的条件下,设M (p ,q )为二次函数图象上的一个动点,当-3<p <0时,点M 关于x 轴的对称点都在直线l 的下方,求m 的取值范围.【思路点拨】(1)直接利用根的判别式,结合完全平方公式求出△的符号进而得出答案;(2)首先求出B,A点坐标,进而求出直线AB的解析式,再利用平移规律得出答案;(3)根据当-3<p<0时,点M关于x轴的对称点都在直线l的下方,当p=0时,q=1;当p=-3时,q=12m+4;结合图象可知:-(12m+4)≤2,即可得出m的取值范围.【答案与解析】(3)由(2)得二次函数的解析式为:y=mx2-(m+1)x+1∵M(p,q)为二次函数图象上的一个动点,∴q=mp2-(m+1)p+1.∴点M关于轴的对称点M′的坐标为(p,-q).∴M′点在二次函数y=-m2+(m+1)x-1上.∵当-3<p<0时,点M关于x轴的对称点都在直线l的下方,当p=0时,q=1;当p=-3时,q=12m+4;结合图象可知:-(12m+4)≤2,【点评】此题主要考查了二次函数综合以及根的判别式和一次函数图象的平移等知识,利用数形结合得出是解题关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《二次函数》全章复习与巩固—巩固练习(基础)【巩固练习】一、选择题1.将二次函数2y x =的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( ).A .2(1)2y x =-+ B .2(1)2y x =++ C .2(1)2y x =-- D .2(1)2y x =+-2.二次函数2y ax bx c =++的图象如图所示,则一次函数24y bx b ac =+-与反比例函数a b cy x++=在同一坐标系内的图象大致为( ).3.抛物线2y x bx c =++图象向右平移2个单位长度,再向下平移3个单位长度,所得图象的解析式为223y x x =--,则b 、c 的值为( ).A .b =2,c =2B .b =2,c =0C .b =-2,c =-1D .b =-3,c =2 4. 抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是( )A .22y x x =-- B .211122y x x =-++ C .211122y x x =--+ D .22y x x =-++5.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,有下列结论:①240b ac ->;②abc >0;③8a+c >0;④9a+3b+c <0.其中,正确结论的个数是( ). A .1 B .2 C .3 D .4第4题 第5题6.已知点(1x ,1y ),(2x ,2y )(两点不重合)均在抛物线21y x =-上,则下列说法正确的是( ).A .若12y y =,则12x x =B .若12x x =-,则12y y =-C .若120x x <<,则12y y >D .若120x x <<,则12y y > 7.在反比例函数a y x=中,当0x >时,y 随x 的增大而减小,则二次函数2y ax ax =-的图象大致是图中的( ).8.已知二次函数2y ax bx c =++(其中0a >,0b >,0c <),关于这个二次函数的图象有如下说法:①图象的开口一定向上;②图象的顶点一定在第四象限;③图象与x 轴的交点至少有一个在y 轴的右侧. 以上说法正确的有( ).A .0个B .1个C .2个D .3个二、填空题9.已知抛物线2(0)y ax bx c a =++>的对称轴为直线1x =,且经过点1(1,)y -,2(2,)y ,试比较1y 和2y 的大小:1y ________2y (填“>”,“<”或“=”).10.抛物线2y x bx c =-++的图象如图所示,则此抛物线的解析式为___ _____. 11.抛物线22(2)6y x =--的顶点为C ,已知y =-kx+3的图象经过点C ,则这个一次函数图象与两坐标轴所围成的三角形面积为________.12.已知二次函数22y x x m =-++的部分图象如图所示,则关于x 的一元二次方程220x x m -++=的解为___ _____.第10题 第12题 第13题13.如图所示的抛物线是二次函数2231y ax x a =-+-的图象,那么a 的值是________.14.烟花厂为扬州“4·18”烟花三月经贸旅游节特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是252012h t t =-++,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为________.15.已知抛物线2y ax bx c =++经过点A(-1,4),B(5,4),C(3,-6),则该抛物线上纵坐标为-6的另一个点的坐标是________.16.若二次函数26y x x c =-+的图象过A(-1,y 1)、B(2,y 2)、C(32+,y 3)三点,则y 1、y 2、y 3大小关系是 .三、解答题 17.杂技团进行杂技表演,演员从跷跷板右端A 处弹跳到人梯顶端椅子B 处,其身体运动(看成一点)的路线是抛物线23315y x x =-++的一部分,如图所示.(1)求演员弹跳离地面的最大高度;(2)已知人梯高BC =3.4米,在一次表演中,人梯到起跳点A 的水平距离是4米,问这次表演是否成功?请说明理由.18. 如图所示,要设计一个等腰梯形的花坛,花坛上底长120米,下底长180米,上、下底相距80米,在两腰中点连线(虚线)处有一条横向甬道,上、下底之间有两条纵向甬道,各甬道的宽度相等,设甬道的宽为x 米.(1)用含x 的式子表示横向甬道的面积;(2)当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;(3)根据设计的要求,甬道的宽不能超过6米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是5.7,花坛其余部分的绿化费用为每平方米0.02万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?19.为迎接第四届世界太阳城大会,德州市把主要路段路灯更换为太阳能路灯.已知太阳能路灯售价为5000元/个,目前两个商家有此产品.甲商家用如下方法促销:若购买路灯不超过100个,按原价付款;若一次购买100个以上,且购买的个数每增加一个,其价格减少10元,但太阳能路灯的售价不得低于3500元/个.乙店一律按原价的80%销售.现购买太阳能路灯x 个,如果全部在甲商家购买,则所需金额为y 1元;如果全部在乙商家购买,则所需金额为y 2元.(1)分别求出y 1、y 2与x 之间的函数关系式;(2)若市政府投资140万元,最多能购买多少个太阳能路灯?20. 王亮同学善于改进学习方法,他发现对解题过程进行回顾反思,效果会更好.某一天他利用了30分钟时间进行自主学习.假设他用于解题的时间x(单位:分钟)与学习收益量)y 的关系如图1所示,用于回顾反思的时间x(单位:分钟)与学习收益量y 的关系如图2所示(其中OA 是抛物线的一部分,A 为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.(1)求王亮解题的学习收益量y 与用于解题的时间x 之间的函数关系式,并写出自变量x 的取值范围;(2)求王亮回顾反思的学习收益量y 与用于回顾反思的时间x 之间的函数关系式; (3)王亮如何分配解题和回顾反思的时间,才能使这30分钟的学习收益总量最大? (注:学习收益总量=解题的学习收益量+回顾反思的学习收益量)【答案与解析】 一、选择题 1.【答案】A ;【解析】2y x =向右平移1个单位后,顶点为(1,0),再向上平移2个单位后,顶点为(1,2),开口方向及大小不变,所以1a =,即2(1)2y x =-=.2.【答案】D ;【解析】由上图可知0a >,0c <,02b a->,∴ 0b <.0a b c ++<.240b ac ->, ∴ 反比例函数图象在第二、四象限内,一次函数图象经过第一、二、四象限,因此选D . 3.【答案】B ;【解析】2223(1)4y x x x =--=--,把抛物线2(1)4y x =--向左平移2个单位长度,再向上平移3个单位长度后得抛物线2(1)1y x =+-,∴222(1)12y x bx c x x x =++=+-=+,∴ b =2,c =0.因此选B .4.【答案】D ; 【解析】由图象知,抛物线与x 轴两交点是(-1,0),(2,0),又开口方向向下,所以0a <,抛物线与y 轴交点纵坐标大于1.显然A 、B 、C 不合题意,故选D . 5.【答案】D ;【解析】抛物线与x 轴交于两点,则0b <. 由图象可知a >0,c <0, 则b <0,故abc >0.当x =-2时,y =4a-2b+c >0. ∵ 12bx a=-=,∴ b =-2a , ∴ 4a-(-2a)×2+c >0,即8a+c >0.当x =3时,y =9a+3b+c <0,故4个结论都正确. 6.【答案】D ;【解析】画出21y x =-的图象,对称轴为0x =,若12y y =,则12x x =-;若12x x =-,则12y y =;若120x x <<,则21y y >;若120x x <<,则12y y >.7.【答案】A ; 【解析】因为ay x=,当0x >时,y 随x 增大而减小,所以a >0,因此抛物线2(1)y ax ax a x x =-=- 开口向上,且与x 轴相交于(0,0)和(1,0).8.【答案】C ;【解析】∵ 0a >,0b >,∴ 抛物线开口向上,02bx a=-<,因此抛物线顶点在y 轴的左侧,不可能在第四象限;又0c <, 120cx x a=<·,抛物线与x 轴交于原点的两侧,因此①③是正确的.二、填空题 9.【答案】>;【解析】根据题意画出抛物线大致图象,找出x =-1,x =2时的函数值,比较其大小,易如12y y >.10.【答案】223y x x =-++;【解析】由题意和图象知抛物线与x 轴两交点为(3,0)、(-1,0),∴ 抛物线解析式为(3)(1)y x x =--+,即223y x x =-++.11.【答案】1; 【解析】92k =,932y x =-+,与坐标轴交点为(0,3),2,03⎛⎫⎪⎝⎭.12.【答案】 x 1=3或x 2=-1 ;【解析】由二次函数22y x x m =-++部分图象知,与x 轴的一个交点为(3,0).代入方程得m =3,解方程得x 1=3或x 2=-1. 13.【答案】-1;【解析】因为抛物线过原点,所以210a -=,即1a =±,又抛物线开口向下,所以a =-1. 14.【答案】4s ; 【解析】204(s)522t =-=⎛⎫⨯- ⎪⎝⎭.15.【答案】(1,-6);【解析】常规解法是先求出关系式,然后再求点的坐标,但此方法繁琐耗时易出错,仔细分析就会注意到:A 、B 两点纵坐标相同,它们关于抛物线对称轴对称,由A(-1,4),B(5,4)得,对称轴1522x -+==,而抛物线上纵坐标为-6的一点是(3,-6),所以它关于x =2的对称点是(1,-6).故抛物线上纵坐标为-6的另一点的坐标是(1,-6).16.【答案】y 1>y 3>y 2. 【解析】因为抛物线的对称轴为6323x -==⨯.而A 、B 在对称轴左侧,且y 随x 的增大而减小,∵ -1<2,∴ y 1>y 2,又C 在对称轴右侧,且A 、B 、C 三点到对称轴的距离分别为2,1,2,由对称性可知:y 1>y 3>y 2.三、解答题17.【答案与解析】(1)2233519315524y x x x ⎛⎫=-++=--+ ⎪⎝⎭.∵ 305-<,∴ 函数的最大值是194. ∴ 演员弹跳离地面的最大高度是194米.(2)当x =4时,234341 3.45y BC =-⨯+⨯+==.∴ 这次表演成功.18.【答案与解析】(1)横向甬道的面积为1201801502x +=(m 2). (2)依题意:2112018028015028082x x x +⨯+-=⨯⨯,整理得21557500x x -+=,解得x 1=5,x 2=150(不合题意,舍去).∴ 甬道的宽为5米.(3)设建花坛的总费用为y 万元,则21201800.0280(1601502) 5.72y x x x x +⎡⎤=⨯⨯-+-+⎢⎥⎣⎦.∴ y =0.04x 2-0.5x+240. 当0.5 6.25220.04b x a =-==⨯时,y 的值最小. ∵ 根据设计的要求,甬道的宽不能超过6 m .∴ 当x =6m 时,总费用最少,为0.04×62-0.5×6+240=238.44(万元).19.【答案与解析】(1)由题意可知,当x ≥100时,因为购买个数每增加一个,其价格减少10元,但售价不得低于3500元/个,所以5000350010025010x -≤+=,即100≤x ≤250时,购买一个需5000-10(x-100)元.故y 1=6000x-10x 2;当x >250时,购买一个需3500元. 故y 1=3500x .所以215000(0100),600010(100250),3500(250),x x y x x x x x ≤≤⎧⎪=-<≤⎨⎪>⎩y 2=5000×80%x =4000x .(2)当0<x ≤100时,y 1=5000x ≤500000<1400000;当100<x ≤250时,y 1=6000x-10x 2=-10(x-300)2+900000<1400000; 所以,由3500x =1400000,得x =400. 由4000x =1400000,得x =350.故选择甲商家,最多能购买400个路灯.20.【答案与解析】(1)设y =kx ,把(2,4)代入,得k =2,所以y =2x ,自变量x 的取值范围是:0≤x ≤30.(2)当0≤x <5时,设y =a(x-5)2+25, 把(0,0)代入,得25a+25=0,a =-1, 所以22(5)2510y x x x =--+=-+. 当5≤x ≤15时,y =25.即210(05),25(515).x x x y x ⎧-+≤<=⎨≤≤⎩(3)设王亮用于回顾反思的时间为x(0≤x <5)分钟,学习收益总量为Z ,则他用于解题的时间为(30-x)分钟.当0≤x <5时,222102(30)860(4)76Z x x x x x x =-++-=-++=--+. 所以当x =4时,76Z =最大.当5≤x ≤15时,Z =25+2(30-x)=-2x+85. 因为Z 随x 的增大而减小, 所以当x =5时,75Z =最大.综合所述,当x =4时,76Z =最大,此时30-x =26.即王亮用于解题的时间为26分钟,用于回顾反思的时间为4分钟时.学习收益总量最大.。
