matlab-理想低通滤波算法
用 MATLAB 设计巴特沃斯低通滤波器
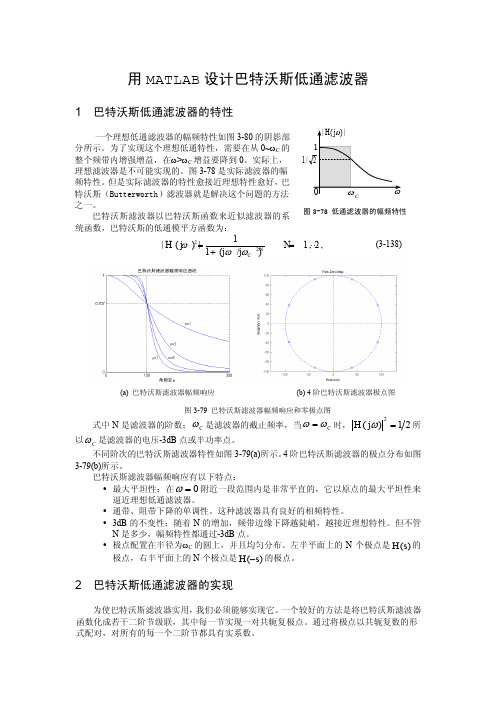
用MATLAB 设计巴特沃斯低通滤波器1 巴特沃斯低通滤波器的特性一个理想低通滤波器的幅频特性如图3-80的阴影部分所示。
为了实现这个理想低通特性，需要在从0~ωC 的整个频带内增强增益，在ω>ωC 增益要降到0。
实际上，理想滤波器是不可能实现的。
图3-78是实际滤波器的幅频特性。
但是实际滤波器的特性愈接近理想特性愈好，巴特沃斯（Butterworth ）滤波器就是解决这个问题的方法之一。
巴特沃斯滤波器以巴特沃斯函数来近似滤波器的系统函数，巴特沃斯的低通模平方函数为：221|()|1,2,,1(/)NC H j N j j ωωω==+ (3-138)式中以C ω是滤波器的电压-3dB 点或半功率点。
不同阶次的巴特沃斯滤波器特性如图3-79(a)所示。
4阶巴特沃斯滤波器的极点分布如图3-79(b)所示。
巴特沃斯滤波器幅频响应有以下特点：• 最大平坦性：在0=ω附近一段范围内是非常平直的，它以原点的最大平坦性来逼近理想低通滤波器。
• 通带、阻带下降的单调性。
这种滤波器具有良好的相频特性。
• 3dB 的不变性：随着N 的增加，频带边缘下降越陡峭，越接近理想特性。
但不管N 是多少，幅频特性都通过-3dB 点。
• 极点配置在半径为ωC 的圆上，并且均匀分布。
左半平面上的N 个极点是)(s H 的极点，右半平面上的N 个极点是)(s H -的极点。
2 巴特沃斯低通滤波器的实现为使巴特沃斯滤波器实用，我们必须能够实现它。
一个较好的方法是将巴特沃斯滤波器函数化成若干二阶节级联，其中每一节实现一对共轭复极点。
通过将极点以共轭复数的形式配对，对所有的每一个二阶节都具有实系数。
1图3-78 低通滤波器的幅频特性图3-80所示运算放大器电路为实现一对共轭极点提供了很好的方法。
电路的系统函数为202202121121122121)(1)11(1)(ωωω++=+++=s Qs C C R R s C R C R s C C R R s H (3-139)式中，ω0是S 平面原点与极点之间的距离，Q 被称为电路的“品质因数”，它提供了对响应峰值尖锐程度的一种度量。
matlab sinc函数用法 -回复
matlab sinc函数用法-回复Sinc函数是一种常用的数学函数，在数字信号处理、通信系统设计以及傅里叶分析等领域中广泛应用。
它定义为sin(x)/x，在数学上常用来表示理想低通滤波器的频率响应。
本文将以中括号内的内容为主题，详细介绍Matlab中sinc函数的用法和相关应用。
一、sinc函数概述Sinc函数是一种特殊的周期函数，其形式定义为：sinc(x) = sin(x)/x。
当x=0时，sinc(x)的值为1；而当x不等于0时，sinc(x)的值是sin(x)除以x的结果。
二、Matlab中的sinc函数Matlab作为一款强大的数学软件，提供了丰富的函数库，sinc函数也是其中之一。
Matlab中的sinc函数可以直接调用，使用方法非常简单。
可以通过help sinc命令来查询帮助文档，了解更多的使用细节。
三、sinc函数的基本用法使用Matlab中的sinc函数非常简单，只需使用函数名加参数的方式即可。
例如，要计算sinc函数在x=pi/4处的取值，可以在命令行窗口输入以下命令：y = sinc(pi/4)在这个例子中，sinc函数的参数为pi/4，运行结果将被存储在变量y中。
四、绘制sinc函数图像sinc函数的图像非常有趣，通常以钟形的形式展现。
在Matlab中，可以使用plot函数绘制sinc函数的图像。
以下是绘制sinc函数图像的代码示例：x = -10:0.1:10;y = sinc(x);plot(x, y)在这段代码中，首先定义了自变量x的取值范围（-10到10，步长为0.1）。
然后，通过sinc函数计算了因变量y的值。
最后，使用plot函数绘制了sinc函数的图像。
五、sinc函数的频域特性sinc函数在频域上有很多有趣的特性，尤其是在傅里叶变换中发挥着重要的作用。
例如，在频率为零的情况下，sinc函数的值是无穷大；而在频率越高的情况下，sinc函数的值越接近于零。
基于matlab对图像进行高通、低通、带通滤波
数字图像处理三级项目—高通、低通、带通滤波器摘要在图像处理的过程中,消除图像的噪声干扰是一个非常重要的问题。
利用matlab软件,采用频域滤波的方式,对图像进行低通和高通滤波处理。
低通滤波是要保留图像中的低频分量而除去高频分量，由于图像中的边缘和噪声都对应图像傅里叶频谱中的高频部分，所以低通滤波可以除去或消弱噪声的影响并模糊边缘轮廓；高通滤波是要保留图像中的高频分量而除去低频分量，所以高通滤波可以保留较多的边缘轮廓信息。
低通滤波器有巴特沃斯滤波器和高斯滤波器等等，本次设计使用的低通滤波器为****。
高通滤波器有巴特沃斯滤波器、高斯滤波器、Laplacian高通滤波器以及Unmask高通滤波器等等，本次设计使用巴特沃斯高通滤波器。
1、频域低通滤波器：设计低通滤波器包括 butterworth and Gaussian (选择合适的半径，计算功率谱比),平滑测试图像test1和2。
实验原理分析根据卷积定理，两个空间函数的卷积可以通过计算两个傅立叶变换函数的乘积的逆变换得到，如果f(x, y)和h(x, y)分别代表图像与空间滤波器，F(u, v)和H(u, v)分别为响应的傅立叶变换（H(u, v)又称为传递函数），那么我们可以利用卷积定理来进行频域滤波。
在频域空间，图像的信息表现为不同频率分量的组合。
如果能让某个范围内的分量或某些频率的分量受到抑制，而让其他分量不受影响，就可以改变输出图的频率分布，达到不同的增强目的。
频域空间的增强方法的步骤：（1）将图像从图像空间转换到频域空间；（2）在频域空间对图像进行增强；（3）将增强后的图像再从频域空间转换到图像空间。
低通滤波是要保留图像中的低频分量而除去高频分量。
图像中的边缘和噪声都对应图像傅里叶频谱中的高频部分，所以低通滤波可以除去或消弱噪声的影响并模糊边缘轮廓。
理想低通滤波器具有传递函数：其中D0为制定的非负数，D(u,v)为点(u,v)到滤波器中心的距离。
课程设计_低通滤波器设计(含matlab程序)
2010/2011学年第 2 学期学院：信息与通信工程学院专业：电子信息科学与技术学生姓名：学号：课程设计题目：低通滤波器设计起迄日期： 6 月 13 日～6月 24日课程设计地点：指导教师：系主任：下达任务书日期: 2011 年 6 月12 日课程设计任务书课程设计任务书目录1 设计目的及要 (5)1.1设计目的 (5)1.2设计内容和要求 (5)2设计原理 (5)2.1 FIR滤波器 (5)2.2窗函数 (6)2.3矩形窗 (7)3设计过程 (8)3.1设计流程图 (8)3.2 产生原始信号并分析频谱 (8)3.3 使用矩形窗设计不同特性的数字滤波器 (10)3.4 信号滤波处理 (11)4 实验结果及分析 (12)5 课程设计心得体会 (12)6 参考文献 (13)附录： (14)低通滤波器的设计1 设计目的及要求1.1设计目的设计一种低通滤波器并对信号进行滤波。
低通滤波器的作用是滤去信号中的中频和高频成分,增强低频成分。
要求做到:1.了解MATLAB的信号处理技术；2.使用MATLAB设计低通滤波器,掌握其滤波处理技术；3.对滤波前和滤波后的波形进行时域和频域比较。
1.2设计内容和要求1.熟悉有关采样,频谱分析的理论知识,对信号作频谱分析；2.熟悉有关滤波器设计理论知识,选择合适的滤波器技术指标,设计低通滤波器对信号进行滤波,对比分析滤波前后信号的频谱；3.实现信号频谱分析和滤波等有关MATLAB函数；2设计原理本次课程设计,我们主要是基于矩形窗的FIR滤波器来设计一个低通滤波器。
2.1 FIR滤波器FIR滤波器即有限抽样响应因果系统,其单位抽样响应h<n>是有限长的；极点皆位于z=0处；结构上不存在输出到输入的反馈,是非递归型的。
其系统函数表示为：普通的FIR滤波器系统的差分方程为：式中：N为FIR滤波器的抽头数；x<n>为第n时刻的输入样本；h<i>为FIR滤波器第i级抽头系数。
用Matlab设计的低通数字滤波器
指导教师评定成绩：审定成绩：重庆邮电大学自动化学院综合课程设计报告低通数字滤波器设计单位（二级学院）：自动化学生姓名：专业：自动化班级：0810902学号：指导教师：设计时间：2012 年11月重庆邮电大学自动化学院制摘要本次设计以AT89S52单片机为控制器件，利用AD/DA转换芯片构成低通数字滤波器。
首先利用MATLAB根据要求设计低通滤波器模型并在该平台进行初步仿真得到较为理想的效果。
接着利用proteus软件搭建硬件电路，并对编写的程序进行检测；程序检测无误后，再用Protel画出电路图。
首先利用ADC0809将模拟信号转换成数字信号输入单片机，正弦模拟信号由AD9850模块产生，是一般正常的低频正弦波；另一个噪声信号是通过单片机产生的高频脉冲信号。
然后通过滤波程序将采集的数据进行算法滤波，滤波后的数据通过DAC0832输出，将DA0832的输出信号通过一级运放（UA741）转换成电压输出。
最后将运放输出的结果接到示波器上进行显示。
关键字：AT89C51、DDS、ADC0809、DAC0832、UA741设计题目题目与要求低通滤波器是允许低频讯号通过，而不允许高频讯号通过的滤波器。
本题目要求用单片机（型号任选）制作一个低通数字滤波器，要求：1.根据确定的采样频率，用MATLAB设计低通滤波器模型以满足不同截止频率需求，并进行仿真；2.用单片机设计并制作一个低通数字滤波器，实现数据采集、滤波处理、信号输出等功能（包括软、硬件）；3.滤波器能与PC机通信，设计通信协议，实现截止频率参数的调节、原始信号采样数据与滤波后数据的上传；4.利用高级语言开发工具，设计PC机端的程序，可以调节滤波器参数，接收滤波器上传的原始信号采样数据与滤波后数据，并能绘图、保存；5.设计几种不同频率、类型的噪声，利用滤波器进行试验，记录实验情况并进行分析、总结；6.按规定的统一格式设计报告。
目录第一章 MATLAB仿真 (4)1.1方案论证 (4)1.2设计方法及原理介绍 (4)1.3 matlab编程实现 (5)1.4 Simulink仿真结构图 (5)第二章硬件设计方案 (6)2.1硬件功能整体设计 (6)2.2单片机最小系统 (7)2.3 ADC0809和74HC74 (7)2.4 DAC0832和UA741 (8)2.5 串口部分 (9)2.6 DDS部分 (9)第三章软件设计 (10)3.1 单片机软件设计 (10)3.2 PC机通信软件设计 (12)第四章心得体会 (13)参考文献 (14)附件1：方波源程序 (15)附件2：DDS正弦信号模块 (15)附件3：主单片机程序 (19)附录4：protues原理图 (21)附录5：protel电路图 (22)附录6：DDS原理图 (22)第一章 MATLAB 仿真1.1方案论证数字滤波器，按功能分类，可以分成低通、高通、带通、带阻、全通滤波器；按实现的网络结构或单位抽样响应分类：可以分成无限脉冲响应滤波器（IIR 滤波器）、有限脉冲响应滤波器（FIR 滤波器）。
利用MATLAB实现数字低通滤波器的设计
西南石油大学实验报告一实验目的：1学习用Matlab直接设计模拟滤波器和数字滤波器。
2学习用冲激响应不变法和双线性变换法的Matlab的实现。
二实验内容：设计满足下列指标的数字低通滤波器：Wp=0.2*pi, Rp=1db Ws=0.5*pi Rs=20db Fs=1khz1.利用B、C1型设计出模拟低通滤波器，采用冲激响应不变法、双线性发转换成数字低通滤波器。
2.直接设计出B、C1型数字低通滤波器。
三实验步骤：程序1Wp=2*pi*0.1*1000;Ws=2*pi*0.25*1000;Rp=1;Rs=20;[N,Wn]=buttord(Wp,Ws,Rp,Rs,'s');[z,p,k]=buttap(N);[B,A]=butter(N,Wn,'s');freq1=linspace(0,Wp,5);freq2=linspace(Wp,Ws,15);freq3=linspace(Ws,10*pi*2,25);h1=20*log10(abs(freqs(B,A,freq1)));h2=20*log10(abs(freqs(B,A,freq2)));h3=20*log10(abs(freqs(B,A,freq3)));plot([freq1 freq2 freq3]/(2*pi),[h1,h2,h3]);grid;Xlabel('Frequency in Hz');Ylabel('gain in DB');图一程序2wp=0.2*pi;ws=0.5*pi;rp=1;rs=20;fs=1000;omegap=wp*fs;omegas=ws*fs;[N,Wn]=buttord(omegap,omegas,rp,rs,'s');[B A]=butter(N,Wn,'s');[b,a]=impinvar(B,A,fs);[h,w]=freqz(b,a,256);h=20*log10(abs(h));plot(w/pi,h);图二程序3wp=0.2*pi;ws=0.5*pi;rp=1;rs=20;fs=1000;omegap=2*fs*tan(wp/2);omegas=2*fs*tan(ws/2);[N,Wn]=cheb1ord(omegap,omegas,rp,rs,'s');[B A]=cheby1(N,rp,Wn,'s');[b,a]=bilinear(B,A,fs);[h,w]=freqz(b,a,256);h=20*log10(abs(h));plot(w/pi,h);图三程序4wp=0.2*pi;ws=0.5*pi;rp=1;rs=20;[N,Wn]=buttord(wp/pi,ws/pi,rp,rs);[B A]=butter(N,Wn);[h,w]=freqz(B,A,256);h=20*log10(abs(h));plot(w/pi,h);图四程序5Wp=0.2*pi;Ws=0.5*pi;Rp=1;Rs=20;T=0.001;Fs=1000;omegap=(2/T)*tan(Wp/2);omegas=(2/T)*tan(Ws/2);[N,Wn]=cheb1ord(omegap,omegas,Rp,Rs,'s'); [B,A]=cheby1(N,Rp,Wn,'s');[b,a]=bilinear(B,A,Fs);[h,w]=freqz(b,a,256);h1=20*log10(abs(h));plot(w/pi,h1);grid;xlabel('Digital Frequency in pi units'); ylabel('Gain in DB');axis([0 1 -50 10]);图五Wp=0.2;Ws=0.5;Rp=1;Rs=20;disp('ÇбÈÑ©·òIÐÍ')[N,Wn]=cheb1ord(Wp,Ws,Rp,Rs)[B,A]=cheby1(N,Rp,Wn);disp('ÇбÈÑ©·òÐÍ·Ö×Ó¶àÏîʽ');fprintf('%.4e\n',B);disp('ÇбÈÑ©·ò·Öĸ¶àÏîʽ');fprintf('%.4e\n',A);w=linspace(0,0.8*pi,50);h1=20*log10(abs(freqz(B,A,w)));plot(w/pi,h1);grid;xlabel('Normalized frequency');ylabel('Gain in DB ');axis([0 0.8 -50 1]);图六四、实验小结通过本次实验,对MA TLAB软件有了进一步的了解,也在不断的实践中,更多的熟悉了MATLAB的编程，在编程方面一点点的有了进步。
matlab iir低通滤波器设计
I. 简介Matlab是一种非常常用的科学计算软件，它广泛用于信号处理、图像处理、控制系统等领域。
在信号处理中，IIR（Infinite Impulse Response）滤波器是一种常见的数字滤波器，常被用于模拟滤波、数字滤波等应用中。
这篇文章将介绍如何使用Matlab进行IIR低通滤波器的设计。
II. 什么是IIR低通滤波器1. IIR滤波器IIR滤波器是一种数字滤波器，其特点是其单位脉冲响应是无限长的。
它通常具有较为复杂的频率响应特性，且具有较小的阶数，能够更好地逼近某些复杂的频率响应曲线。
IIR滤波器分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器等。
2. 低通滤波器低通滤波器是一种常见的滤波器，其特点是只允许低频信号通过，而抑制高频信号。
在信号处理中，低通滤波器常被用于去除高频噪声、提取低频信号等应用中。
III. Matlab中的IIR低通滤波器设计1. 使用Matlab进行IIR低通滤波器设计Matlab提供了丰富的信号处理工具箱，包括了数字滤波器设计工具。
在Matlab中，可以使用函数butter、cheby1、cheby2、ellip等来设计IIR低通滤波器。
2. 设计步骤设计IIR低通滤波器的一般步骤如下：a. 确定通带和阻带的频率范围b. 选择滤波器的通带和阻带的最大允许衰减c. 选择滤波器的类型（Butterworth、Chebyshev等）以及阶数d. 使用Matlab中相应的函数设计滤波器e. 对设计的滤波器进行频率响应分析IV. 实例分析以下是一个在Matlab中设计IIR低通滤波器的简单实例：设计IIR低通滤波器fs = 1000; 采样频率fpass = 100; 通带截止频率fstop = 200; 阻带截止频率apass = 1; 通带最大允许衰减astop = 80; 阻带最小要求衰减[num, den] = butter(4, fpass/(fs/2), 'low');freqz(num, den, 512, fs); 绘制滤波器频率响应曲线V. 结论使用Matlab进行IIR低通滤波器设计是一种简单而有效的方法。
matlab低通滤波器函数
matlab低通滤波器函数
Matlab低通滤波器函数是Matlab中广泛使用的一种数字滤波器，它能够过滤掉频率超过一定阈值的信号频带，从而获取更加平滑的信号。
低通滤波器函数有两类。
一种是有限冲激响应（FIR）函数，它可以形
成有限长的滤波器，而且能够自动调整滤波器的形状来达到所需的滤
波效果。
另一种是无限冲激响应（IIR）函数，它可以创建一种动态的
滤波器，可以根据信号的变化而及时调整形状，从而获得更好的滤波
效果。
Matlab中还提供了各种滤波器函数，其中最常用的是低通滤波器函数。
它的使用方法如下：首先调用Matlab中的滤波器函数，然后将低通滤
波器函数的参数（边界频率、通带频率、增益等）设置为所需的值，
最后将输入的信号经过滤波器函数，即可得到滤波后的信号。
低通滤波器在诸多应用中都有着重要的作用，例如，在声音增强、图
像处理等领域，将低通滤波器用于去噪。
低通滤波器也可以用来减少
噪音，从而提高信号的稳定性和准确性。
此外，在信号处理过程中，低通滤波器还可以用于提取某一特定的信号，例如，假设想要提取一段语音中人类的声音，那么可以通过低通
滤波器来过滤掉多余的背景声音，从而使得最终提出来的语音更加清
晰易懂，实现更加精准的信息提取。
总之，Matlab低通滤波器函数是一种非常实用的数字滤波技术，具有
很多优点，包括低复杂度、极简的参数设置、动态复杂度等。
只要熟
练掌握使用方法，就可以在多个应用领域得到最大的效果。
基于matlab的低通滤波器的设计
基于matlab的低通滤波器的设计低通滤波器是一种能够过滤掉高频信号而保留低频信号的滤波器。
在信号处理领域中，低通滤波器是非常重要的一种滤波器，常见的应用包括：音频处理、图像处理、视频处理、通信领域、控制系统等。
在本篇文章中，我们将介绍如何使用matlab来设计低通滤波器。
设计的过程大致可以分为以下步骤：1. 确定滤波器类型2. 确定滤波器参数3. 执行滤波器设计4. 验证滤波器设计以下是详细的步骤：1. 确定滤波器类型低通滤波器的种类有很多，常见的包括Butterworth滤波器、Chebyshev滤波器、Elliptic滤波器等。
每种滤波器都有不同的特点，应该根据需要选择合适的滤波器类型。
在本篇文章中，我们介绍Butterworth滤波器。
这种滤波器是设计过程中最简单的一种，因为它的频率响应是平滑的、连续的，并且在通带中没有波纹和过渡带中没有振铃。
在设计Butterworth滤波器时，需要明确三个参数：通带截止频率、阻带截止频率和通带最大衰减。
通带截止频率：指在这个频率以下的信号将通过滤波器。
这个参数取决于应用，应根据需要进行选择。
阻带截止频率：指在这个频率以上的信号将被滤波器滤去。
这个参数的选择应该考虑到信号在该频率以上能够在处理方式下的好处。
通带最大衰减：指在通带截止频率处，滤波器对信号最大允许的衰减。
这个参数的选择应该是应用与滤波器频率响应上的折衷。
3. 执行滤波器设计当确定了滤波器类型和参数后，可以使用matlab执行滤波器设计。
在matlab中，可以使用“[b,a] = butter(n,Wn)”命令进行Butterworth滤波器设计。
其中，n是滤波器阶数，Wn是通带截止频率与Nyquist频率的比例。
这个命令将返回两个向量，b和a。
向量b代表数字滤波器分子多项式的系数，向量a 代表数字滤波器分母多项式的系数。
设计滤波器后，需要验证其设计是否正确，验证的方法包括频率响应的分析和信号滤波的实验。
matlab做低通滤波器设计思路
设计低通滤波器是数字信号处理领域中的一项关键任务，而Matlab 作为一款强大的数学建模与仿真软件，为我们提供了丰富的工具和函数来完成这一任务。
在本篇文章中，我们将介绍在Matlab中设计低通滤波器的思路和具体步骤。
设计低通滤波器主要涉及以下几个方面：1. 确定滤波器的规格要求在设计任何一种滤波器之前，我们首先需要明确滤波器的规格要求，包括截止频率、通带最大衰减、阻带最小衰减等。
这些规格要求将直接影响到滤波器的设计参数和性能。
在Matlab中，可以利用Signal Processing Toolbox提供的函数来帮助我们确定滤波器的规格要求。
2. 选择滤波器的类型根据实际的应用需求，我们需要选择合适的滤波器类型。
常见的低通滤波器包括巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器等。
每种类型的滤波器都有其适用的场景和特点。
在Matlab中，我们可以利用Filter Design and Analysis工具箱中的函数来选择合适的滤波器类型。
3. 根据规格要求设计滤波器一旦确定了滤波器的类型，我们就可以根据规格要求来设计滤波器。
在Matlab中，可以利用Filter Design and Analysis工具箱中的函数来实现滤波器设计，包括巴特沃斯滤波器设计函数butter()、切比雪夫滤波器设计函数cheby1()和cheby2()、椭圆滤波器设计函数ellip()等。
4. 分析和优化滤波器性能设计完成滤波器后，我们需要对滤波器的性能进行分析和优化。
在Matlab中，可以利用Filter Design and Analysis工具箱中的函数来对滤波器的频率响应、相位响应、裙延迟等进行分析，并根据实际需求对滤波器进行优化。
5. 验证滤波器的性能我们需要对设计完成的滤波器进行性能验证。
在Matlab中，可以利用Signal Processing Toolbox提供的函数来对设计的滤波器进行信号处理和性能评估，以确保滤波器能够满足实际需求。
基于matlab的低通滤波器
基于mat lab的低通滤波器摘要:调用MATLAB信号处理工具箱中滤波通过观察滤波器输入输出信号的时域波形及其频谱，建立数字滤波的概念。
应用最广泛的是双线性变换法。
基本设计过程是：①先将给定的数字滤波器的指标转换成过渡模拟滤波器的指标；②设计过渡模拟滤波器；③将过渡模拟滤波器系统函数转换成数字滤波器的系统函数。
MATLAB信号处理工具箱中的各种IIR数字滤波器设计函数都是采用双线性变换法。
关键词:滤波器，matlab，c语言，声音Abstract: call MATLAB signal processing toolbox filtering through the observation filter of input and output signals time domain waveform and spectrum, establish the concept of digital filter. One of the most widely applied is double linear transformation method. The basic design process is: (1) to a given digital filters index converted into analog filter transition index; (2) the design transition simulation filter; (3) transition simulation filter system function will be converted into digital filter system function. MATLAB signal processing toolbox digital filter function design of IIR is bilinear transformation method.Keywords: filter, matlab, the c language, the voice一.任务：用matlab软件设计IIR模拟、数字以及各种窗函数的FIR低通滤波器二.设计目的：（1）了解matlab软件的用途以及用法；（2）了解用冲激响应不变法设计模拟低通滤波器；（3）了解用脉冲响应不变法设计的巴特沃思数字低通滤波器；（4）了解基于汉明窗函数的FIR低通滤波器的设计。
F28335基于MATLAB的低通滤波器的实现
DSP28335基于MATLAB-FIR低通滤波器的实现1.任务目标：滤波器的截止频率为500HZ，采样频率为128000HZ，采样的点数为256，滤波器的阶数为32，输入信号如下：Sample[i]=511*(sin(2*pi*5*i/(a-1))+sin(2*pi*i*5*3/(a-1))/3+sin(2*pi*i*5*5/(a-1))/5)+5122.实现过程：由MAtlab的FDATOOL计算出滤波器的阶数，再由DSP程序进行卷积运算，最后由CCSV5的Graph功能进行输入前后的波形分析。
3.FIR(Finite Impulse Response)滤波器：有限长单位冲激响应滤波器，是数字信号处理系统中最基本的元件，它可以在保证任意幅频特性的同时具有严格的线性相频特性，同时其单位抽样响应是有限长的，因而滤波器是稳定的系统。
因此，FIR 滤波器在通信、图像处理、模式识别等领域都有着广泛的应用。
4.算法原理：离散信号序列通过一个离散滤波系统，得到离散输出信号，如果滤波系统的单位脉冲响应为h(n)，信号序列为x(n)，输出信号为y(n)，则使用运算关系式表达他们之间的关系如下：5.MATLAB---FDATOOL参数设置：然后在FILE-EXPORT-ASCII输出文件打开就有滤波器系数了。
6.各种情况下输出的波形图图一：matlab滤波器截止频率Fc设置为5000HZ得到的波形图二：程序自带滤波器参数得到的波形图三：截止频率设置为2000HZ得到的输出波形图四：Fc=1200HZ时的波形图五：Fc=600HZ时的波形图六：FC=2700HZ图七：FC=6000H图八：FC=3500HzFC=4000hzFC=4500HZ卷积算法如下：void LinearConvolution(Uint16 xn,Uint16 hn,float *x,float *h,float *y) {Uint16 i,j,k,l;Uint16 yn; //输出序列y的长度yn=xn+hn-1;for(i=0;i<yn;i++) y[i]=0; //输出数组初始化k=yn-1;for(i=hn-1;i>0;i--) //将*h作为被乘数{l=k;for(j=xn-1;j>0;j--) //数组x[n]的1~(xn-1)与h[i]逐一相乘 {y[l]+=h[i]*x[j];l--;}y[l]+=x[0]*h[i];k--;}l=k;for(j=xn-1;j>0;j--){y[l]+=h[0]*x[j];l--;}y[l]+=x[0]*h[0];}void main(void){Uint16 i;InitSysCtrl();InitPieCtrl();IER = 0x0000;IFR = 0x0000;for(i=0;i<a;i++) //产生一个a点的三次谐波叠加而成的方波{Sample[i]=511*(sin(2*pi*5*i/(a-1))+sin(2*pi*i*5*3/(a-1))/3+sin(2*pi*i*5*5/( a-1))/5)+512;//三个正弦波由5个15个25个包含在256个点的时间中// DELAY_US(10);+sin(2*pi*i*5*5/(a-1)) +sin(2*pi*i*5*3/(a-1))/4sin(2*pi*5*i/(a-1))/100+}LinearConvolution(a,b,Sample,h,y1);//线性卷积while(1){//sample=sin(2*pi*5*n/(N-1))+sin(2*pi*15*n/(N-1))/3+sin(2*pi*25*n/(N-1))/5;/* dly[0]=sample;yn=0;for(i=0;i<N;i++) yn+=h[i]*dly[i];for(i=N-1;i>0;i--) dly[i]=dly[i-1];output[n]=yn;if(n==(N-1)) n=0;else n++;*/}}。
低通滤波的matlab实现
四种低通滤波器：一、理想低通滤波器I=imread('bb.jpg');T=rgb2gray(I);figure(1);subplot(1,2,1),imshow(uint8(I));title('原图像');subplot(1,2,2),imshow(uint8(T));title('理想低通滤波所得图像');[f1,f2]=freqspace(size(T),'meshgrid');H=ones(size(T));r=sqrt(f1.^2+f2.^2);H(r>0.1)=0;Y=fft2(double(T));Y=fftshift(Y);Ya=Y.*H;Ya=ifftshift(Ya);I=ifft2(Ya);figure(2);surf(H,'Facecolor','interp','Edgecolor','none','Facelighting','phong'); title('频谱图');二、巴特沃斯低通滤波器I=imread('bb.jpg');T=rgb2gray(I);figure(1);subplot(1,2,1),imshow(uint8(I));title('原图像');subplot(1,2,2),imshow(uint8(T));title('巴特沃斯低通滤波所得图像');[f1,f2]=freqspace(size(T),'meshgrid');D=0.3;r=f1.^2+f2.^2;n=4;for i=1:size(T,1)for j=1:size(T,2)t=r(i,j)/(D*D);H(i,j)=1/(t^n+1);endendY=fft2(double(T));Y=fftshift(Y);Ya=Y.*H;Ya=ifftshift(Ya);I=real(ifft2(Ya));figure(2);surf(H,'Facecolor','interp','Edgecolor','none','Facelighting','phong'); title('频谱图');三、梯形滤波器I=imread('bb.jpg');T=rgb2gray(I);figure(1);subplot(1,2,1),imshow(uint8(I));title('原图像');subplot(1,2,2),imshow(uint8(T));title('梯形低通滤波所得图像');[f1,f2]=freqspace(size(T),'meshgrid');D=100/size(I,1);D0=0.1;D1=0.4;r=sqrt(f1.^2+f2.^2);H=zeros(size(T));H(r<D0)=1;for i=1:size(T,1)for j=1:size(I,2)if r(i,j)>=D0 & r(i,j)<=D1H(i,j)=(D1-r(i,j))/(D1-D0);endendendY=fft2(double(T));Y=fftshift(Y);Ya=Y.*H;Ya=ifftshift(Ya);I=real(ifft2(Ya));figure(2);surf(H,'Facecolor','interp','Edgecolor','none','Facelighting','phong'); title('频谱图');四、高斯低通滤波器I=imread('bb.jpg');T=rgb2gray(I);figure(1);subplot(1,2,1),imshow(uint8(I));title('原图像');subplot(1,2,2),imshow(uint8(T));title('高斯低通滤波所得图像');[f1,f2]=freqspace(size(T),'meshgrid');D=100/size(I,1);r=f1.^2+f2.^2;H=ones(size(T));for i=1:size(T,1)for j=1:size(T,2)t=r(i,j)/(D*D);H(i,j)=exp(-t);endendY=fft2(double(T));Y=fftshift(Y);Ya=Y.*H;Ya=ifftshift(Ya);I=real(ifft2(Ya));figure(2);surf(H,'Facecolor','interp','Edgecolor','none','Facelighting','phong'); title('频谱图');。
matlab中低通滤波器filter的用法
一、引言Matlab是一种强大的科学计算软件，广泛应用于工程、科学和数学领域。
在信号处理领域，滤波器是一种常用的工具，用于处理不同频率的信号。
低通滤波器是一种常见的滤波器类型，可以用于去除高频噪声或选择低频成分。
在Matlab中，可以使用filter函数来实现低通滤波器的功能。
本文将详细介绍Matlab中低通滤波器filter的用法，包括基本语法、参数设置以及实际应用。
二、基本语法在Matlab中，filter函数的基本语法如下：y = filter(b, a, x)其中，b和a分别是滤波器的分子和分母系数，x是输入信号，y是输出信号。
这里需要注意的是，b和a的长度通常是不相等的，分别对应于滤波器的分子和分母多项式系数。
三、参数设置1. 分子和分母系数的设置在使用filter函数时，需要首先设置滤波器的分子和分母系数。
这些系数可以通过滤波器的设计方法（如巴特沃斯滤波器、切比雪夫滤波器等）得到，也可以直接手动设置。
需要注意的是，分子和分母系数需要按照特定的格式输入，确保其正确性和合法性。
2. 输入信号的设置输入信号x可以是任何形式的信号数据，如数字信号、模拟信号、音频信号等。
在使用filter函数时，需要确保输入信号x的格式和长度与滤波器的要求相匹配，否则可能导致错误或不良效果。
3. 输出信号的获取在调用filter函数之后，会得到输出信号y。
可以将输出信号y保存到变量中，也可以通过绘图工具将其可视化显示。
在实际应用中，通常需要对输出信号y进行进一步的处理或分析，以满足具体的需求。
四、实际应用低通滤波器在实际应用中有着广泛的用途，如音频信号去噪、生物医学信号分析、通信系统等领域。
下面以音频信号去噪为例，介绍低通滤波器filter的实际应用。
```matlab读取音频文件[x, fs] = audioread('noisy_audio.wav');设计低通滤波器fc = 1000; 截止频率fs_new = 2 * fc; 采样频率设为截止频率的两倍[b, a] = butter(4, fc/fs_new);使用filter函数进行滤波y = filter(b, a, x);可视化输出信号t = (0:length(x)-1) / fs;t_new = (0:length(y)-1) / fs_new;figure;subplot(2,1,1);plot(t, x); title('原始音频信号');subplot(2,1,2);plot(t_new, y); title('滤波后的音频信号');保存滤波后的音频文件audiowrite('clean_audio.wav', y, fs_new);```在上述示例中，我们首先读取了一个存在噪声的音频文件，然后设计了一个低通滤波器，设置了截止频率为1000Hz，并使用了4阶巴特沃斯滤波器。
matlab设计低通滤波器
重庆邮电大学本科毕业设计（论文）摘要在当今的数字信息的世界里，数字信号处理已经演变成一门越来越重要的学科，并在通信、语音、图像、自动控制、雷达、军事、航空航天、医疗和家用电器等众多领域得到了广泛的应用。
其中数字滤波是数字信号处理的重要内容。
数字滤波器可分为IIR和FIR两大类，对于IIR滤波器的设计来说主要有脉冲响应不变法和双线性变换法，而对于FIR数字滤波器的设计来说主要有窗函数法和频率采样设计法。
本文应用MATLBA对数字低通滤波器进行仿真，并给出一定频率的信号通过所设计的滤波器来验证滤波器的性能，主要的研究工作主要包括以下几方面的内容:(1)介绍IIR滤波器和FIR滤波器的结构特点并比较两者之间的差别。
(2)在MATLAB中应用双线性变换法和脉冲响应不变法设计IIR滤波器，给出了滤波器的频率特性图和相位特性图。
(3)通过编写MATLAB程序用窗函数设计法和频率采样法来完成FIR低通滤波器的设计，并给出几个不同频率的信号通过所设定的滤波器来验证滤波器的性能。
(4)在MATLAB中应用Simulink模块来仿真FIR低通滤波器，并在示波器上同时显示输入信号的频率和输出信号的频率，最后对结果进行分析。
【关键字】FIR滤波器IIR滤波器, 双线性变换法脉冲响应不变法窗函数法频率采样法MATLABABSTRACTIn nowadays world of digital information, digital signal processing has become an increasingly important subject, and has been widely applied in all fields, such as medicine, communications, and other areas, digital filters are important elements of digital signal processing. Digital filters can be divided into two kinds of IIR and FIR, IIR filter design for pulse response method and bilinear transformation method, for FIR digital filter design, the main Windows function method and frequency of sampling design.In this paper simulation using MATLAB for digital low-pass filter, and to give a signal of a certain frequency through the filters designed to verify the performance of filter, the main research work mainly includes the following content:(1) Describes the structure of FIR and IIR filters filter characteristics and comparison of the differences between the two.(2) In MATLAB using bilinear transformation method and impulse response method design of IIR filters, to out of the filters of frequency response and phase characteristics.(3) Design method by writing MATLAB programs use the windows function and frequency sampling method to accomplish the design of FIR low-pass filters, and gives several different frequency signals passes through a set of filters to verify that the filter's performance.(4) In the MATLAB Simulink simulation FIR low-pass filter module to the application, and also on the scope displays the frequency of the input signal and the output signal frequency, final analysis of the results.【Key words】FIR digital IIR digital filter Bilinear transformation methodImpulse response method Windows functionFrequency sampling method MATLAB目录前言 (1)第一章数字滤波器 (2)第一节数字滤波器的简介 (2)第二节数字滤波器的应用 (3)第三节数字滤波器的实现方法分析及优点 (4)第四节MATLAB和Simulink简介 (5)第五节本章小结 (7)第二章数字滤波器的结构和设计原理 (8)第一节数字滤波器的基本结构 (8)一、IIR滤波器的基本结构 (8)二、FIR滤波器的基本结构 (10)第二节数字滤波器的设计原理 (12)一、滤波器的设计步奏 (12)二、滤波器的性能指标 (13)第三节IIR滤波器与FIR滤波器的分析比较 (13)第四节本章小结 (15)第三章IIR滤波器的设计 (16)第一节脉冲响应不变法的基本原理 (16)一、变化原理 (16)二、混叠失真 (16)三、主要特点 (17)四、MATLAB（脉冲响应不变法）设计滤波器 (18)第二节双线性不变法的基本原理 (19)一、变换原理 (19)二、主要优缺点 (19)三、MATLAB(双线性变化法)设计数字低通滤波器 (19)第三节本章小结 (21)第四章FIR滤波器的设计 (22)第一节线性相位FIR滤波器的特点 (22)第二节利用窗函数设计FIR低通滤波器 (24)一、窗函数的基本思想 (24)二、几种常用的窗函数 (24)第二节频率采样法设计FIR低通滤波器 (32)一、频率采样设计法的基本原理 (32)二、线性相位的约束 (32)三、逼近误差及其改进措施 (32)第三节FIR数字滤波器的优化设计 (35)第四节本章小结 (36)第五章仿真结果及分析 (37)第一节MATLAB(窗函数法)设计FIR数字低通滤波器 (37)第二节MATLAB(频率采样法)设计FIR数字低通滤波器 (39)第三节Simulink仿真FIR滤波器 (42)第四节本章小结 (44)结论 (45)致谢 (46)参考文献 (46)附录 (47)一、英文原文 (48)二、英文翻译 (55)三、仿真脚本 (62)重庆邮电大学本科毕业设计（论文）前言模拟滤波器与数字滤波器的设计对工程，应用数学及计算机科学都是非常重要的。
matlab低通滤波器设计
matlab低通滤波器设计
matlab低通滤波器设计：
1、使用matlab设计低通滤波器的方法
(1) 首先根据低通滤波器的频率响应要求，计算滤波器构成要素的参数；
(2) 确定滤波器所要采用的元件模型，选择常用的元件模型；
(3) 使用matlab构筑出低通滤波器的模型和原理图；
(4) 根据原理图推导出滤波器的传递函数，使用matlab计算滤波器的频率响应，绘制出滤波器的频率响应曲线；
(5) 分析滤波器的传递特性，观察是否符合要求，如果不符合要求，可以调整模型的参数，重新计算滤波器的频率响应，直到满足频率响应要求为止。
2、使用matlab构件低通滤波器所需要的工具
(1) matlab控制环境，用于控制滤波器的构筑和参数的设定；
(2) Matlab编程工具，用于实现计算滤波器构件的算法；
(3) Matlab图形操作工具，用于绘制滤波器的理论响应曲线；
(4) Matlab仿真工具，用于检查滤波器的理论分析结果。
3、低通滤波器的优势
(1) 低通滤波器对频率低于截止频率的信号又较低的衰减率，因此保证低频信号的精度；
(2) 滤波器设计简单，而且可以采用大量元件来实现；
(3) 低通滤波器的频率响应特性主要取决于滤波器的电路结构，使用matlab设计的低通滤波器可以很容易的设定符合自己要求的参数。
matlab 数据滤波算法
matlab 数据滤波算法MATLAB中有许多种数据滤波算法，根据不同的应用和需求可以选择合适的算法。
数据滤波的目标通常是去除噪声、平滑数据或者从数据中提取特定的信息。
以下是一些常见的数据滤波算法：1. 移动平均滤波，这是一种简单的滤波方法，通过计算数据点的移动平均值来平滑数据。
在MATLAB中，可以使用`smooth`函数来实现移动平均滤波。
2. 中值滤波，中值滤波是一种非线性滤波方法，它使用窗口中值来替换每个数据点，从而有效地去除噪声。
MATLAB中的`medfilt1`函数可以实现一维中值滤波。
3. 卡尔曼滤波，卡尔曼滤波是一种递归滤波方法，可以用于估计系统状态变量，特别适用于动态系统。
在MATLAB中，可以使用`kalman`函数来实现卡尔曼滤波。
4. 低通滤波，低通滤波器可以通过去除高频噪声来平滑信号。
MATLAB提供了许多滤波器设计函数，如`butter`、`cheby1`和`ellip`，可以用来设计和应用低通滤波器。
5. 高斯滤波，高斯滤波是一种线性平滑滤波方法，它通过应用高斯核来平滑数据。
在MATLAB中，可以使用`imgaussfilt`函数来实现一维或二维高斯滤波。
除了上述方法外，MATLAB还提供了许多其他滤波算法和工具箱，如信号处理工具箱和图像处理工具箱，这些工具箱中包含了丰富的滤波函数和工具，可以根据具体的需求选择合适的算法进行数据滤波。
在实际应用中，选择合适的滤波算法需要考虑数据特点、噪声类型、计算复杂度等因素，同时需要对滤波效果进行评估和调优。
希望以上信息能够帮助你更好地了解MATLAB中的数据滤波算法。
用MATLAB设计数字FIR低通滤波器(哈明窗)
用MATLAB设计数字FIR低通滤波器（哈明窗）设计数字FIR低通滤波器，技术指标如下：Wp=0.2pi.rp=0.25db;Ws=0.3pi,as=50db.求解，如下图：程序：wp=0.2*pi;ws=0.3*pi;trwidth=ws-wp;M=ceil(6.6*pi/trwidth)+1;%朝正无穷方向取整n=[0:1:M-1];wc=(ws+wp)/2%求的截止频率（弧度）hd=ideal_lp(wc,M) %调用计算理想低通滤波器的单位取样响应wham=(hamming(M))';%哈明窗函数h=hd.*wham;[H,w]=freqz(h,1,1000,'whole'); %求Z变换频率响应函数H=(H(1:1:501))';w=(w(1:1:501))'mag=abs(H);db=20*log10((mag+eps)/max(mag));pha=angle(H);grd=grpdelay(h,1,w);deltaw=2*pi/1000;Rp=-(min(db(1:1:wp/deltaw+1)))As=-round(max(db(ws/deltaw+1:1:501)))subplot(1,1,1)subplot(2,2,1),stem(n,hd);title('理想脉冲响应')axis([0 M-1 -0.1 0.3]);xlabel('N');ylabel('hd(n)');subplot(2,2,2),stem(n,wham);title('Hamming窗')axis([0 M-1 -0 1.1]);xlabel('N');ylabel('w(n)');subplot(2,2,3),stem(n,h);title('实际脉冲响应')axis([0 M-1 -0.1 0.3]);xlabel('N');ylabel('h(n)');subplot(2,2,4),plot(w/pi,db);title('相对标尺的幅度响应');grid on;axis([0 1 -100 10]);xlabel('frequency in pi units');ylabel('decibels');set(gca,'XTickMode','manual','XTick',[0,0.2,0.3,1])%设置或修改LTI对象的属性值set(gca,'XTickMode','manual','XTick',[-50,0])set(gca,'XTickLabelMode','manual','XTickLabels',['50';'0'])子程序：function hd=ideal_lp(wc,N);a=(N-1)/2;n=[0:1:(N-1)];m=n-a+eps;hd=sin(wc*m)./(pi*m);。