数学建模之报童收益最大期望问题(优选.)
报童模型

报童模型(Newsboy model)
问题:
报童出售报纸,零售价a>购进价b>退回价c。
因此,每售出一份报纸,赚a-b,每退回一份报纸赔b-c。
那么,报童每天要购进多少份报纸才能使收入最大?
分析:
如果购进太多,就会卖不完,从而赔钱;如果购进过少,导致报纸不够销售,就会减少收入。
因此,存在一个最优的购进量,使得收入最大。
因此,应当根据需求来确定购进量。
然而,每天的需求是随机的,进而每天的收入也是随机的。
因此,优化问题的目标函数应是长期日平均收入,等于每天收入的期望。
准备:
调查随机量的需求规律——每天需求量为r 的概率f(r), r=0,1,2…
建模:
设每天购进n 份,日平均收入为G(n)。
已知售出一份赚a-b;退回一份赔b-c。
若r<=n,则售出r,返回n-r => 赚(a-b)r,赔(b-c)(n-r)。
若r>n,则售出n,赚(a-b)n。
目标函数
求n使G(n)最大。
求解:
视r为连续变量f(r)=>p(r)(概率密度)
结果解释:
取n,使
其中,a-b即售出一份报纸赚的钱,b-c即退回一份报纸赔的钱。
报童 数学建模

报童诀窍一、问题:报童每天清晨从报社购进报纸零售,晚上将没有卖掉的报纸退回。
设报纸每份的购进价为b ,零售价为a ,退回价为c ,假设a>b>c 。
即报童售出一份报纸赚a-b ,退回一份赔b-c 。
报童每天购进报纸太多,卖不完会赔钱;购进太少,不够卖会少挣钱。
试为报童筹划一下每天购进报纸的数量,以获得最大收入。
二、模型分析:购进量由需求量确定,需求量是随机的。
假定报童已通过自己的经验或其他渠道掌握了需求量的随机规律,即在他的销受范围内每天报纸的需求量为 r 份的概率是f(r)(r=0,1,2…)有了f(r),a 和b,c 就可以建立关于购进量的优化模型。
三、模型建立:假设每天购进量是n 份,需求量是随机的,r 可以小于,等于或大于n, ,所以报童每天的收入也是随机的。
那么,作为优化模型的目标函数,不能取每天的收入,而取长期卖报(月,年)的日平均收入。
从概率论大数定律的观点看,这相当于报童每天收入的期望值,简称平均收入。
记报童每天购进n 份报纸的平均收入为G(n),如果这天的需求量r<=n,则售出r 份,退回n-r 份;如果需求量人r>n,则r 份将全部售出。
需求量为r 的概率是f(r),则()()()()[]()()()∑∑=∞+=-+----=n r n r r nf b a r f r n c b r b a n G 01问题归结为在()c b a r f ,,,已知时,求n 是G(n)最大。
四、模型求解:购进量n 都相当大,将r 视为连续变量便于分析和计算,这时概率f(r)转化为概率密度函数p(r)()()()()[]()()()⎰⎰∞-+----=n ndr r np b a dr r p r n c b r b a n G 0计算()()()()⎰---=ndrr p c b n np b a dndG 0()()()()dr r p b a n np b a n ⎰∞-+--令0=dndG 得dndG ()()()()()()dr r p b a dr r p c b n np c a n n⎰⎰∞-+---=02得到()()cb b a drr p dr r p nn --=⎰⎰∞n 应满足上式。
报童模型3种例题详解

报童模型3种例题详解报童模型是一种常用的供应链管理模型,用于衡量库存管理的最佳策略。
在这篇文章中,我们将详解报童模型的三种例题,以帮助读者更好地理解这个模型以及它的实际应用。
1. 例题一:基本的报童模型在这个例题中,假设一个报摊要订购一种杂志,供应商提供了每本杂志的成本和销售价格。
报童需要在售罄前进行订购决策,以最大化利润。
首先,我们需要确定售罄概率分布,并计算售罄带来的成本和利润。
然后,我们可以使用期望利润最大化的公式来计算最佳订购数量。
通过解决这个例题,我们可以了解如何应用报童模型来进行库存管理并最大化利润。
2. 例题二:考虑损失销售的报童模型在这个例题中,我们要考虑到如果需求超过库存时带来的损失销售。
与例题一相比,我们需要加入一个额外的指标——失销销售成本。
失销销售成本是指由于库存不足而无法满足需求而导致的损失。
针对这个例题,我们需要计算售罄带来的损失成本,并将其加到总成本中。
然后,同样使用期望利润最大化的公式来计算最佳订购数量。
通过解决这个例题,我们可以了解如何考虑到损失销售成本来优化报童模型,以实现更准确的库存管理。
3. 例题三:考虑折扣的报童模型在这个例题中,我们假设供应商提供了折扣政策。
即在一定的订购数量上能够享受到更低的成本。
通过使用带有折扣的报童模型,我们将计算出能够最大化利润的最佳订购数量。
我们需要结合折扣成本以及其他成本来计算总成本,并使用期望利润最大化的公式来确定最佳订购数量。
通过解决这个例题,我们可以了解如何考虑折扣政策来优化报童模型,并在实践中应用这一模型。
通过上述三个例题的解析,我们可以更加深入地理解报童模型及其在供应链管理中的应用。
这个模型不仅能够帮助我们进行库存管理,还能够优化成本并最大化利润。
在实际业务中,我们可以根据具体情况灵活运用报童模型,以实现更加高效的供应链管理。
数学建模

数学建模一1、问题呈现报童每天清晨从报社购进报纸零售,晚上将没有卖完的报纸退回。
设每份报纸的购进价为,零售价为,退回价为,应该自然地假设。
这就是说,报童售出一份报纸赚,退回一份报纸赔。
报童如果每天购进的报纸太少,不够卖的,会少赚钱;如果购进太多,卖不完,将要赔钱。
请你为报童筹划一下,他应该如何确定每天购进报纸的数量,以获得最大的收入。
2、数学建模基本假设1、假设报童现在要与报社签定一个长期的订购合同,所以要确定每日的订购量n。
2、假设报纸每日的需求量是r,但报童是一个初次涉足卖报行业的菜鸟,毫无经验,无法掌握需求量r的分布函数,只知道每份报纸的进价b、售价a及退回价c。
3、假设每日的定购量是n。
4、报童的目的是尽可能的多赚钱。
3、知识准备应该根据需求量r确定需求量n,而需求量r是随机的,所以这是一个风险决策问题。
而报童却因为自身的局限,无法掌握每日需求量的分布规律,已确定优化模型的目标函数。
但是要得到n 值,我们可以从卖报纸的结果入手,结合r与n 的量化关系,从实际出发最终确定n值。
由常识可以知道卖报纸只有赚钱、不赚钱不赔钱、赔钱会有三种结果。
4、模型解析解:设报纸具有时效性每份报纸进价b元,卖出价a元,卖不完退回份报纸c元。
设每日的订购量为n,如果订购的多了,报纸剩下会造成浪费,甚至陪钱。
订的少了,报纸不够卖,又会少赚钱。
为了获得最大效益,现在要确定最优订购量n。
n的意义。
n是每天购进报纸的数量,确定n一方面可以使报童长期以内拥有一个稳定的收入,另一方面也可以让报社确定每日的印刷量,避免纸张浪费。
所以,笔者认为n的意义是双重的。
本题就是让我们根据a、b、c及r来确定每日进购数n。
建立模型现在用简单的数学式表示这三种结果。
1、赚钱。
赚钱又可分为两种情况:①r>n,则最终收益为(a-b)n (1)②r<n,则最终收益为(a-b)r-(b-c)(n-r)>0整理得:r/n>(b-c)/(a-c) (2)2、由(2)式容易得出不赚钱不赔钱。
报童问题
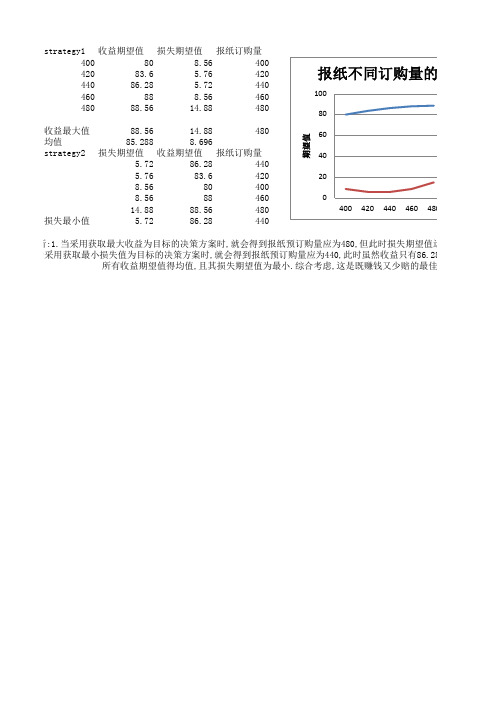
strategy1收益期望值损失期望值报纸订购量
42083.6 5.76420
44086.28 5.72440
460888.56460
48088.5614.88480
收益最大值88.5614.88480
均值85.2888.696
strategy2损失期望值收益期望值报纸订购量
5.728
6.28440
5.7683.6420
8.5680400
8.5688460
14.8888.56480
损失最小值 5.7286.28440
分析:1.当采用获取最大收益为目标的决策方案时,就会得到报纸预订购量应为480,但此时损失期望值达到.当采用获取最小损失值为目标的决策方案时,就会得到报纸预订购量应为440,此时虽然收益只有86.28,但
所有收益期望值得均值,且其损失期望值为最小.综合考虑,这是既赚钱又少赔的最佳选
值达到最大.不是最佳选择.28,但此时期望收益值高于最佳选择.。
数学建模之报童收益最大期望问题

报童收益期望最大问题教程一:复习期望求解公式 ,二:报童问题报童进报纸每份价格a 元,卖价b 元,退还c 元,市场需求m 份报纸概率m p (假定平均需求λ份), 可以只考虑500≤m , 若报童进报n 份,求收益平均Income(n) 解答:对应市场需求m 份报纸,报童收益为[][]()[][]()m I m a b m I m n c a m a b n n ∞+-+----,1,0)())(()(,对应概率为m p因此,收益平均Income(n)=[][]()[][](){}∑=∞+-+----5000,1,0)())(()(m m n np m I m a b m I m n c a m a b例题:若a=0.4, b=0.6, c=0.3, !200200m e p mm -=,求Income 对n 表达矩阵 Income(n)=[][]()[][](){}∑=∞+-+----5000,1,0)())(()(m m n np m I n a b m I m n c a m a ba=0.4;b=0.6;c=0.3; lamda=200;for n=1:500for i=1:500; %忽略i=0情况gailv(i)=exp(-lamda+i*log(lamda)-sum(log(1:i)));Income(i)=((b-a)*i-(a-c)*(n-i))*(i<=n)+(b-a)*n*(i>n);endExpectationIncome(n)=sum(gailv.*Income);endplot(ExpectationIncome)在这里,ExpectationIncome是报童收益向量问题1、报童应该准备买进多少份报纸,使得期望收益达到最大?for i=1:500if ExpectationIncome(i)==max(ExpectationIncome);thebestamount=iendend运行结果thebestamount =206问题2、现在,若报童还卖另外一份报纸,对应a=0.5;b=0.7;c=0.4;lamda=250;两份报纸,报童各应准备买进多少份,使得期望收益达到最大?解答:显然,如果报童资金足够,每份报纸进货可以分别计算如问题一,得到,第一份报纸进货206,第二份报纸进货257,但是,如果报童总资金不足206*0.4+257*0.5=210.9000元,报童该如何进货呢?比如,报童只有150元)最大应该此时,假定第一份报纸买入i=1:206,计算第二份报纸在范围(257买入量时两份报纸总收益矩阵将a=0.4;b=0.6;c=0.3; lamda=200时报童收益向量定义为AA=ExpectationIncome; 将a=0.5;b=0.7;c=0.4;lamda=250时报童收益向量定义为B. B=ExpectationIncome;for i=1:206if (150-i*0.4)/0.5>=257;totalincome(i)=A(i)+max(B);elsetotalincome(i)=A(i)+B(ceil((150-i*0.4)/0.5));endendplot(totalincome)050100150200250 4850525456586062646668for i=1:206if totalincome(i)==max(totalincome)newspaperone=i, newspapertwo=(150-0.4*newspaperone)/0.5,maxincome=max(totalincome)endend。
报童数学建模

报童数学建模 IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】报童诀窍一、问题: 报童每天清晨从报社购进报纸零售,晚上将没有卖掉的报纸退回。
设报纸每份的购进价为b ,零售价为a ,退回价为c ,假设a>b>c 。
即报童售出一份报纸赚a-b ,退回一份赔b-c 。
报童每天购进报纸太多,卖不完会赔钱;购进太少,不够卖会少挣钱。
试为报童筹划一下每天购进报纸的数量,以获得最大收入。
二、模型分析:购进量由需求量确定,需求量是随机的。
假定报童已通过自己的经验或其他渠道掌握了需求量的随机规律,即在他的销受范围内每天报纸的需求量为r 份的概率是f(r)(r=0,1,2…)有了f(r),a 和b,c 就可以建立关于购进量的优化模型。
三、模型建立:假设每天购进量是n 份,需求量是随机的,r 可以小于,等于或大于n,,所以报童每天的收入也是随机的。
那么,作为优化模型的目标函数,不能取每天的收入,而取长期卖报(月,年)的日平均收入。
从概率论大数定律的观点看,这相当于报童每天收入的期望值,简称平均收入。
记报童每天购进n 份报纸的平均收入为G(n),如果这天的需求量r<=n,则售出r份,退回n-r 份;如果需求量人r>n,则r 份将全部售出。
需求量为r 的概率是f(r),则问题归结为在()c b a r f ,,,已知时,求n 是G(n)最大。
四、模型求解:购进量n 都相当大,将r 视为连续变量便于分析和计算,这时概率f(r)转化为概率密度函数p(r)计算令0=dn dG 得dn dG ()()()()()()dr r p b a dr r p c b n np c a n n ⎰⎰∞-+---=02 得到()()c b b a dr r p dr r p n n--=⎰⎰∞0 n 应满足上式。
()10=⎰∞dr r p 使报童日平均收入达到最大的购进量为()ca b a dr r p n --=⎰0 根据需求量的概率密度p(r)的图形可以确定购进量n 在图中用p1,p2分别表示曲线p(r)下的两块面积,则cb b a P P --=21 O nr因为当购进n 份报纸时,()dr r p P n ⎰=01是需求量r 不超过n 的概率; ()dr r p P n ⎰∞=2是需求量r 超过n 的概率,既卖完的概率,所以上式表明,购进的份数n 应使卖不完与卖完的概率之比,恰好等于卖出一份赚的钱a-b 与退回一份赔的钱b-c 之比。
报童问题——精选推荐

报童问题关于报童问题的分析摘要本⽂讨论了单周期的随即贮存模型——报童问题。
通过运⽤插值拟合等基本模型,运⽤概率论与数理统计、数值积分等背景知识,得出每天报纸需求量的概率分布,建⽴报童收益模型,以达到报童最⼤收益为⽬的,使报童每天的买进量与需求量尽可能地吻合,以使损失最少,收益最⼤。
在问题⼀中,⾸先求出概率分布)(r f 。
再设定每天报纸的买进量是定值,并将其代⼊建⽴好的报童收益模型中求出平均收益最⼤值,得出nr r f =)(,7358.33)(=n MaxG ,200=n 。
在问题⼆中,即将第⼀问中的概率分布)(r f 转化为概率密度)(r p ,在matlab ⼯具箱⼦cftool 中计算得出此时概率密度为正态分布,将问题⼀模型中的求和转化为积分,通过对⽬标通过数值积分等⼿段得出报童每天不同买进量下每天平均收⼊,从⽽分析得出每天的最优报纸进货量n 。
其中2)98.54)1.190(()(--=x er p ,=)(n G 672.84,=n 207。
关键词随即贮存,概率分布,概率密度,平均收益,数值积分1、问题重述1.1问题背景在实际⽣产⽣活过程中,经常会遇到⼀些随时间、地点、背景不同⽽发⽣变化的事物,例如报纸的销售的问题。
如果报纸的销售量⼩于需求量,则会给报童带来缺货损失,失去⼀部分潜在客户,⼀部分报纸失销(为简化计算,在本模型中我们忽略缺货损失);如果报纸的销售量⼤于需求量,则会导致⼀部分报纸被退回报社,给报童造成⼀部分退货损失,减少盈利。
所以在实际考虑中,应使报纸的购⼊量尽可能地吻合需求量,减少报童的损失,获得更⼤的盈利。
1.2报童获利途径报童以每份0.3元的价格买进报纸,以0.5元的价格出售。
当天销售不出去的报纸将以每份0.2元的价格退还报社。
根据长期统计,假设已经得到了159天报纸需求量的情况。
对现有数据分析,得出报童每天最佳买进报纸量,使报童的平均总收⼊最⼤。
1.3问题提出现在需⽤数学建模解决以下问题:问题1:若将据报纸需求量看作离散型分布,试根据给出统计数据,求出报纸需求量的分布律,并建⽴数学模型,确定报童每天买进报纸的数量,使报童的平均总收⼊最⼤?问题2:若将据报纸需求量看作连续型分布,试根据给出的统计数据,进⾏分布假设检验,确定该报纸需求量的分布,并建⽴数学模型,确定报童每天买进报纸的数量,使报童的平均总收⼊最⼤?2、模型假设(1)假设报童在以后的⽇⼦⾥需求量概率分布概率密度遵循这159天的规律(2)假设不考虑缺货损失(3)假设报童进报纸量达到⼀定数量后不会产⽣贮存等其他费⽤(4)假设报童每天都能买进计算出来的应进报纸量3、符号说明r报纸需求量(rf报纸需求量概率密度(离散型))p报纸需求量概率密度(连续型)(r)n每天报纸买进量)(n G 报童每天购进n 份报纸的平均收⼊ )(n g报童⼀天的利润收⼊1p n r <时的概率 2p n r >时的概率 i s 每天卖出报纸量 i b每天退回报纸量4、问题分析单周期随机贮存在实际⽣产⽣活中经常遇到,单周期即只订⼀次(缺时也不订),期后可处理余货;随机因素是需求和拖后时间,统计规律为历史资料。
