报童__数学建模
数学建模:报童的策略

数学建模:报童的策略一、论文题目报童每天清晨从报社购进报纸零售,晚上将没有卖掉的报纸退回。
设报纸每份的购进购价为b,零售价为a,退回价为c,应该自然的假设为a>b>c,这就是说,报童售出一份报纸赚a―b,退回一份赔b―c,报童每天如果购进的报纸太少,不够卖的,会少赚钱;如果购进太多,卖不完,将要赔钱。
请你为报童筹划一下,他应如何确定每天购进报纸的数量,以获得最大的收入。
二、问题的重述。
报纸具有时效性每份报纸进价b元,卖出价a元,卖不完退回份报纸c元。
设每日的订购量为n,如果订购的多了,报纸剩下会造成浪费,甚至陪钱。
订的少了,报纸不够卖,又会少赚钱。
为了获得最大效益,现在要确定最优订购量n。
n的意义。
n是每天购进报纸的数量,确定n一方面可以使报童长期以内拥有一个稳定的收入,另一方面也可以让报社确定每日的印刷量,避免纸张浪费。
所以,笔者认为n的意义是双重的。
本题就是让我们根据a、b、c及r来确定每日进购数n。
三、基本假设1、假设报童现在要与报社签定一个长期的订购合同,所以要确定每日的订购量n。
2、假设报纸每日的需求量是r,但报童是一个初次涉足卖报行业的菜鸟,毫无经验,无法掌握需求量r的分布函数,只知道每份报纸的进价b、售价a及退回价c。
3、假设每日的定购量是n。
4、报童的目的是尽可能的多赚钱。
四、建立模型应该根据需求量r确定需求量n,而需求量r是随机的,所以这是一个风险决策问题。
而报童却因为自身的局限,无法掌握每日需求量的分布规律,已确定优化模型的目标函数。
但是要得到n值,我们可以从卖报纸的结果入手,结合r与n的量化关系,从实际出发最终确定n值。
由常识可以知道卖报纸只有赚钱、不赚钱不赔钱、赔钱会有三种结果。
现在用简单的数学式表示这三种结果。
1、赚钱。
赚钱又可分为两种情况:①r>n,则最终收益为(a-b)n (1)②r<n,则最终收益为(a-b)r-(b-c)(n-r)>0整理得:r/n>(b-c)/(a-c) (2)2、由(2)式容易得出不赚钱不赔钱。
优化,报童,变分模型

建模
因存储量不足而造成缺货时,可以认为存储量q t 为
负值(如图所示),周期仍记为 T ,Q 是每周期的存储
量,当 t T1 时,q t 0, 故有
Q rT1.
⑻
在 T1到 T这段缺货时间内需求率
不变,q t 按原斜率继续下降,
q Q
缺货损失费c3 越大, 越小(越接近1),从而
lim T T , lim Q Q, lim R Q.
c3
c3
c3
由此说明不容许缺货是容许缺货的特殊情况.
二、生猪出售的最佳时机
一饲养场每天投入4元资金用于饲料、设备、人力, 估计可使一头80公斤重的生猪每天增加2公斤. 目前生 猪出售的市场价格为每公斤8元,但是预测每天会降低 0.1元. 问该场该什么时候出售这样的生猪,如果这样 的估计和预测有出入,对结果有多大的影响.
由大数定律,报童每天的平均收入因为每天收入的期望 值来表示.
设每天卖出r份报纸的概率为 f r , 因而期望收入为
n
G n a br b cn r f r
r0
a bnf r.
⑴
r n1
从而问题转变为求出进货量 n,使期望收入Gn 达到最
大.
解模
为了用微积分的方法解决该问题,将变量连续化,从
用相对改变量来衡量结果对参数的敏感程度。t 对 r的敏
感程度记为S (t, r), 定义式为
S(t, r) t / t dt r .
⑸
r / r dr t
由⑶式,得
dt dr
40r
40r r2
60
60 r2 ,
再代入⑸式,得
数学建模题目附标准答案

各种信息。用数学语言来描述问题。 2 模型假设:根据实际对象的特征和建模的目的,对问题进行必要
的简化,并用精确的语言提出一些恰当的假设。猫虿驢绘燈鮒诛髅貺庑。 3 模型建立:在假设的基础上,利用适当的数学工具来刻划各变量
现在,我们来证明:如果上述假设条 件成立,那么答案是肯定的。以长方桌的中 心为坐标原点作直角坐标系如图所示,方桌 的四条腿分别在 A、B、C、D 处,A、B,C、D 的初始位置在与 x 轴平行,再假设有一条在 x 轴上的线 ab,则 ab 也与 A、B,C、D 平行。当方桌绕中心 0 旋转时, 对角线 ab 与 x 轴的夹角记为 。矚慫润厲钐瘗睞枥庑赖。
本题就是让我们根据本题就是让我们根据本题就是让我们根据aa来确定每日进购数来确定每日进购数来确定每日进购数nn基本假设基本假设基本假设111假设报童现在要与报社签定一个长期的订购合同所以要确假设报童现在要与报社签定一个长期的订购合同所以要确假设报童现在要与报社签定一个长期的订购合同所以要确定每日的订购量定每日的订购量定每日的订购量nn假设报纸每日的需求量是假设报纸每日的需求量是假设报纸每日的需求量是rr但报童是一个初次涉足卖报行业但报童是一个初次涉足卖报行业但报童是一个初次涉足卖报行业的菜鸟毫无经验无法掌握需求量的菜鸟毫无经验无法掌握需求量的菜鸟毫无经验无法掌握需求量rr的分布函数的分布函数的分布函数只知道每份报纸只知道每份报纸只知道每份报纸的进价的进价的进价bbb售价售价售价aa及退回价及退回价及退回价cc333假设每日的定购量是假设每日的定购量是假设每日的定购量是nn444报童的目的是尽可能的多赚钱
最后重点分析(2)式。
显然式中 r 表需求量,n 表订购量,(b-c)表示退回一份儿报纸赔
报童模型

报童模型(Newsboy model)
问题:
报童出售报纸,零售价a>购进价b>退回价c。
因此,每售出一份报纸,赚a-b,每退回一份报纸赔b-c。
那么,报童每天要购进多少份报纸才能使收入最大?
分析:
如果购进太多,就会卖不完,从而赔钱;如果购进过少,导致报纸不够销售,就会减少收入。
因此,存在一个最优的购进量,使得收入最大。
因此,应当根据需求来确定购进量。
然而,每天的需求是随机的,进而每天的收入也是随机的。
因此,优化问题的目标函数应是长期日平均收入,等于每天收入的期望。
准备:
调查随机量的需求规律——每天需求量为r 的概率f(r), r=0,1,2…
建模:
设每天购进n 份,日平均收入为G(n)。
已知售出一份赚a-b;退回一份赔b-c。
若r<=n,则售出r,返回n-r => 赚(a-b)r,赔(b-c)(n-r)。
若r>n,则售出n,赚(a-b)n。
目标函数
求n使G(n)最大。
求解:
视r为连续变量f(r)=>p(r)(概率密度)
结果解释:
取n,使
其中,a-b即售出一份报纸赚的钱,b-c即退回一份报纸赔的钱。
报童 数学建模

报童诀窍一、问题:报童每天清晨从报社购进报纸零售,晚上将没有卖掉的报纸退回。
设报纸每份的购进价为b ,零售价为a ,退回价为c ,假设a>b>c 。
即报童售出一份报纸赚a-b ,退回一份赔b-c 。
报童每天购进报纸太多,卖不完会赔钱;购进太少,不够卖会少挣钱。
试为报童筹划一下每天购进报纸的数量,以获得最大收入。
二、模型分析:购进量由需求量确定,需求量是随机的。
假定报童已通过自己的经验或其他渠道掌握了需求量的随机规律,即在他的销受范围内每天报纸的需求量为 r 份的概率是f(r)(r=0,1,2…)有了f(r),a 和b,c 就可以建立关于购进量的优化模型。
三、模型建立:假设每天购进量是n 份,需求量是随机的,r 可以小于,等于或大于n, ,所以报童每天的收入也是随机的。
那么,作为优化模型的目标函数,不能取每天的收入,而取长期卖报(月,年)的日平均收入。
从概率论大数定律的观点看,这相当于报童每天收入的期望值,简称平均收入。
记报童每天购进n 份报纸的平均收入为G(n),如果这天的需求量r<=n,则售出r 份,退回n-r 份;如果需求量人r>n,则r 份将全部售出。
需求量为r 的概率是f(r),则()()()()[]()()()∑∑=∞+=-+----=n r n r r nf b a r f r n c b r b a n G 01问题归结为在()c b a r f ,,,已知时,求n 是G(n)最大。
四、模型求解:购进量n 都相当大,将r 视为连续变量便于分析和计算,这时概率f(r)转化为概率密度函数p(r)()()()()[]()()()⎰⎰∞-+----=n ndr r np b a dr r p r n c b r b a n G 0计算()()()()⎰---=ndrr p c b n np b a dndG 0()()()()dr r p b a n np b a n ⎰∞-+--令0=dndG 得dndG ()()()()()()dr r p b a dr r p c b n np c a n n⎰⎰∞-+---=02得到()()cb b a drr p dr r p nn --=⎰⎰∞n 应满足上式。
建模实验四(报童的诀窍)
实验四报童的诀窍报童每天清晨从报社购进报纸零售,晚上将没有卖掉的报纸退回。
设报纸每份的购进价为b,零售价为a,退回价为c,应该自然的假设为a>b>c,这就是说,报童售出一份报纸赚a-b,退回一份赔b-c,报童每天如果购进的报纸太少,不够卖的,会少赚钱;如果购进太多,卖不完,将要赔钱。
请你为报童筹划一下,他应如何确定每天购进报纸的数量,以获得最大的收入。
为了掌握需求量的随机规律,可以用收集历史资料或向其他报童调查的办法做市场预测。
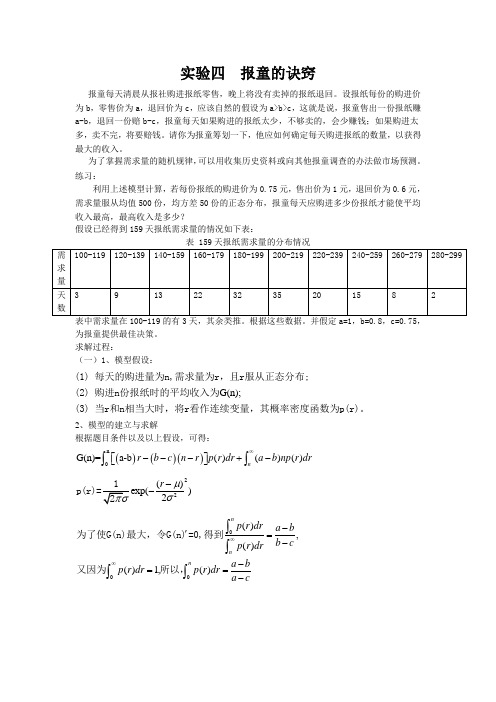
练习:利用上述模型计算,若每份报纸的购进价为0.75元,售出价为1元,退回价为0.6元,需求量服从均值500份,均方差50份的正态分布,报童每天应购进多少份报纸才能使平均收入最高,最高收入是多少?假设已经得到159天报纸需求量的情况如下表:表 159天报纸需求量的分布情况为报童提供最佳决策。
求解过程:(一)1、模型假设:G(n);(1) 每天的购进量为n,需求量为r,且r服从正态分布;(2) 购进n份报纸时的平均收入为(3) 当r和n相当大时,将r看作连续变量,其概率密度函数为p(r)。
2、模型的建立与求解根据题目条件以及以上假设,可得:()()()nG(n)=a-b()()()nr b c n r p r dr a b np r dr∞---+-⎡⎤⎣⎦⎰⎰22())2rμσ--1p(r)=00(),()()1,()nnnp r dr a bb cp r dra bp r dr p r dra c∞∞-'=--==-⎰⎰⎰⎰为了使G(n)最大,令G(n)=0,得到又因为所以,0 1.0,0.75,0.6,500,500.25()0.6250.40n a b c a b p r dr a c μσ=====-===-⎰已知:则Matlab 利用软件求解,得:n=515.9320程序代码如下:>> n = norminv(0.625,500,50)n =515.9320即此时报童每天应该购进约516份报纸。
报童模型

缺货损失厌恶的报童问题摘要:报童问题是随机存贮管理的基本问题之一。
在预期理论的框架下,我们通过引入损失厌恶参数,基于损失期望最小原则,对经典的报童问题进行了重新思考,给出了缺货损失厌恶的报童的最优定货量的计算公式及订购量与期望损失关系的数学模型.关键词:存贮管理;预期理论;期望损失1、引言不确定性决策一直都是决策理论的基本问题之一。
报童问题是随机存贮理论的基本模型之一,国内外关于报童问题的研究已有很长一段时间,人们也从不同的角度得出了一些令大家可接受且比较满意的方案和数学模型。
如Tsan rt.al[1]提出报童问题的均值方差模型,并且得出如果报童可能最大化期望利润,使得利润方差受到限制,那么其最佳订购量总是小于经典报童问题的订购量;Schweitzer, Cachon[2] 提出效用最大化的报童问题,且得出基于偏爱的不同而有不同的效用函数,(这些偏爱对报童的决策进程有着重要影响);Eeckhoudt et.al[5]研究了风险及风险厌恶对报童问题的效应;Porteus[5]通过对敏感度的定量分析,研究了带风险效用和风险厌恶的报童问题;文平[6]关于损失厌恶的报童—预期理论下的报童问题新解一文,基于Kahneman 和Tversky[6]于1979年提出的预期理论,也得出了比较理想的模型。
然而他们中的多数都是从获利期望值最大和期望效用理论的角度来考察的。
但是,报童问题也是一种经典的单阶段存贮问题。
对报童而言,他每一天的报纸都有三种结果:报纸卖不完、不够卖、刚好够卖。
这三种结局只有最后一种情况下才能达到报童的最大利润,因为报童的最大利润是订购量刚好和市场需求一致,即刚好够卖,也刚好卖完。
在过去关于报童问题的种种模型中,都很少考虑到报纸不够卖,即脱销的情况,此时大多是以刚好满足市场需求的情况来处理。
其实不然,对于这类薄利多销的报童问题而言,他们都不希望自己是做保本生意,都希望充分利用好市场,最大限度地获取利润。
报童__数学建模

报童诀窍一、问题:报童每天清晨从报社购进报纸零售,晚上将没有卖掉的报纸退回。
设报纸每份的购进价为b ,零售价为a ,退回价为c ,假设a>b>c 。
即报童售出一份报纸赚a-b ,退回一份赔b-c 。
报童每天购进报纸太多,卖不完会赔钱;购进太少,不够卖会少挣钱。
试为报童筹划一下每天购进报纸的数量,以获得最大收入。
二、模型分析:购进量由需求量确定,需求量是随机的。
假定报童已通过自己的经验或其他渠道掌握了需求量的随机规律,即在他的销受范围内每天报纸的需求量为 r 份的概率是f(r)(r=0,1,2…)有了f(r),a 和b,c 就可以建立关于购进量的优化模型。
三、模型建立:假设每天购进量是n 份,需求量是随机的,r 可以小于,等于或大于n, ,所以报童每天的收入也是随机的。
那么,作为优化模型的目标函数,不能取每天的收入,而取长期卖报(月,年)的日平均收入。
从概率论大数定律的观点看,这相当于报童每天收入的期望值,简称平均收入。
记报童每天购进n 份报纸的平均收入为G(n),如果这天的需求量r<=n, 则售出r 份,退回n-r 份;如果需求量人r>n,则r 份将全部售出。
需求量为r 的概率是f(r),则 ()()()()[]()()()∑∑=∞+=-+----=n r n r r nf b a r f r n c b r b a n G 01 问题归结为在()c b a r f ,,,已知时,求n 是G(n)最大。
四、模型求解:购进量n 都相当大,将r 视为连续变量便于分析和计算,这时概率f(r)转化为概率密度函数p(r)()()()()[]()()()⎰⎰∞-+----=n n dr r np b a dr r p r n c b r b a n G 0 计算()()()()⎰---=n dr r p c b n np b a dndG 0()()()()dr r p b a n np b a n ⎰∞-+-- 令0=dn dG 得dndG ()()()()()()dr r p b a dr r p c b n np c a n n ⎰⎰∞-+---=02得到()()c b b a dr r p dr r p n n--=⎰⎰∞0 n 应满足上式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
报童诀窍
一、问题:
报童每天清晨从报社购进报纸零售,晚上将没有卖掉的报纸退回。
设报纸每份的购进价为b,零售价为a,退回价为c,假设a>b>c。
即报童售出一份报纸赚a-b,退回一份赔b-c。
报童每天购进报纸太多,卖不完会赔钱;购进太少,不够卖会少挣钱。
试为报童筹划一下每天购进报纸的数量,以获得最大收入。
二、模型分析:
购进量由需求量确定,需求量是随机的。
假定报童已通过自己的经验或其他渠道掌握了需求量
,a和
n-r份;
p(r)
n
c
b
b
a
-
-
=
因为当购进n份报纸时,()dr
r
p
P n⎰=0
1
是需求量r不超过n的概率;
()dr
r
p
P
n⎰
∞
=
2
是需求量r超过n的概率,既卖完的概率,所以上式表明,购进的份数n应使卖不完与卖完的概率之比,恰好等于卖出一份赚的钱a-b与退回一份赔的钱b-c之比。
五、结论:
当报童与报社签订的合同使报童每份赚钱与赔钱之比约大时,报童购进的份数就应该越多。
六、问题求解:
利用上述模型计算,若每份报纸的购进价为0.75元,售出价为1元,退回价为0.6元,需求量
服从均值500份,均方差50份的正态分布,报童每天应购进多少份报纸才能使平均收入最高,最高收入是多少?
当a=1,b=0.75,c==0.6时需求量r 服从)50,500(~2N r 分布。
3
56.075.075.0121=--=--=c b b a P P 对应的正态分布表得到对应概率为0.9515 所以购进量为5.3128
5500=⨯ 当r<=n 时最高收入为()15.78951.05.31275.01=⨯⨯-
当r>n。
