用比例的知识解答应用题
比例法解答行程应用题

1.一辆汽车从甲地开往乙地,每小时行50千米,返回时每小时行60千米,已知去时用了6小时,那么返回时用了几小时?2.甲、乙两车分别从A,B两地同时出发相向而行,甲车每小时行50千米,乙车的速度是甲车的4/5.当甲车行至全程的2/5时,乙车距中点还有36千米。
A,B两地相距多少千米?3.甲、乙两车同时分别从A,B两地同时出发相向而行,当甲车行了全程的1/4时,乙车行了全程的1/3,当乙车行完全程时,甲车距终点还有20千米。
A,B两地相距多少千米?4.甲、乙两车的速度分别是50千米/时、40千米/时,乙车先从B站开往A站,当到离B站72千米的D地时,甲车从A站开往B站,在C地与乙车相遇,如下图。
如果甲、乙两车相遇地C地离A,B两站的路程比是3:4,那么A,B两站之间的路程是多少千米?5.小红骑自行车从甲地到乙地,前一段是上坡路,后一段是下坡路,已知小红上坡每小时行8千米,下坡每小时行22千米,来回一趟共用了3小时。
甲、乙两地相距多少千米?6.一辆汽车从甲地到乙地先上坡后下坡,上坡和下坡的路程比是5:4,汽车上坡和下坡所用时间比是7:3.求这辆汽车上坡和下坡的速度之比。
7.一辆汽车从甲地到乙地,去时每小时行48千米,返回时每小时行60千米,返回时比去时少用了48分钟。
甲、乙两地相距多少千米?8.一辆汽车从甲地到乙地,去时每小时行60千米,返回时速度减少了1/5,这样返回就比去时多用了1小时。
甲、乙两地相距多少千米?9.甲、乙两车分别从A,B两地同时出发,相向而行,甲车每小时行48千米,乙车每小时行42千米。
当乙车行至全程的7/20时,甲车距中点还有24千米,A,B两地相距多少千米?10.甲、乙两车分别从A,B两地同时出发相向而行,甲车每小时行50千米,乙车每小时行60千米,两车相遇时,甲车比乙车少行了50千米.A,B两地相距多少千米?11.甲/乙两车同时分别从A,B两地出发相向而行,当甲车行了全程的3/5时,乙车行了全程的3/4,当乙车行完全程时,甲车距终点还有30千米.A,B两地相距多少千米?12.A,B两地相距380千米,甲、乙两车同时分别从A、B两地出发相向而行,当甲车行了全程的2/3时,乙车行了全程的3/5.那么甲、乙两车相遇时,各行了多少千米?13.甲、乙两车分别从A,B两地同时出发相向而行,甲车每小时行48千米,乙车每小时行60千米,当甲车到达B地时,乙车已超过A地20千米。
解比例应用题

1) 水果店一天运进苹果、香蕉、梨共390 千克,苹果的重量是梨的 1 . 5 倍,香蕉的重量是梨的 3/ 4,三种水果各运进多少千克?(2)—缸水,用去 1 / 2 和 5 桶,还剩 30% ,这缸水有多少桶?(3)有一快棱长 20 厘米的正方体木料,刨成一个底面直径最大的圆柱体,刨去木料的体积是多少?⑷一根钢管长10 米,第一次截去它的7 / 10, 第二次又截去余下的 1 / 3,还剩多少米?(5) 两个小组装配收音机,甲组每天装配50 台,第一天完成了总任务的10% , 这时乙组才开始装配,每天装配 40 台,完成这批任务时,甲组做了多少天?(6)修筑一条公路,完成了全长的2/ 3 后,离中点 16.5 千米,这条公路全长多少千米?(7) 师徒两人合做一批零件,徒弟做了总数的 2 / 7, 比师傅少做21 个,这批零件有多少个?(8) 两队修一条公路,甲队每天修全长的 1 / 5,乙队独做7 . 5 天修好。
如果两队合修2天后,其余由乙队独修,还要几天完成?(9) 仓库里有一批化肥,第一次取出总数的2/ 5,第二次取出总数的 1 / 3 少 12 袋,这时仓库里还剩24 袋,两次共取出多少袋?Z.(10)前轮在720米的距离里比后轮多转40 周,如果后轮的周长是 2 米,求前轮的周长。
(11)甲数是甲乙丙三数的平均数的 1 ? 2 倍。
如果乙丙两数和是99 ,求甲数是多少?(12)有一工程计划用工人800 名,限 100 天完成。
不料从开工起,做35 天后因事故停工,停工 25 天后继续开工,如果要在限期内完工,应增加工人多少名?(13)水果店以2元钱1 ? 5 千克的价格买进苹果若干千克,又以 4 元钱 2 ? 5 千克的价格卖出去。
如果店里想得到100 元钱的利润,这个水果店必须卖出水果多少千克?(14)甲乙丙三人行走的速度分别为每分钟30 米、 40 米和 50 米。
甲乙同在 A 地,丙在B 地。
知识点精讲比例应用题

知识点精讲比例应用题一、简单比例关系应用题。
1. 已知甲、乙两数的比是5:3,甲数是25,求乙数。
- 解析:设乙数为x,因为甲、乙两数的比是5:3,即(甲)/(乙)=(5)/(3)。
已知甲数是25,则(25)/(x)=(5)/(3),交叉相乘得5x = 25×3,5x=75,解得x = 15。
2. 一种合金中铜和锌的比是2:3,现在有铜12克,需要多少克锌才能制成这种合金?- 解析:设需要锌x克,因为铜和锌的比是2:3,即(铜)/(锌)=(2)/(3)。
已知铜12克,则(12)/(x)=(2)/(3),交叉相乘得2x=12×3,2x = 36,解得x = 18克。
3. 某班男、女生人数比是4:5,男生有20人,这个班共有多少人?- 解析:设女生有x人,因为男、女生人数比是4:5,(男生人数)/(女生人数)=(4)/(5),已知男生20人,则(20)/(x)=(4)/(5),交叉相乘得4x=20×5,4x = 100,解得x = 25人。
那么这个班共有20 + 25=45人。
二、比例在工程问题中的应用。
4. 一项工程,甲、乙两队的工作效率比是3:4,甲队单独做需要12天完成,乙队单独做需要多少天完成?- 解析:工作总量 = 工作效率×工作时间。
设乙队单独做需要x天完成。
因为甲、乙两队的工作效率比是3:4,设甲队工作效率为3a,乙队工作效率为4a。
甲队单独做需要12天完成,工作总量为3a×12 = 36a。
乙队工作总量也为36a,工作效率为4a,则工作时间x=(36a)/(4a)=9天。
5. 甲、乙两个工程队合修一条路,甲、乙两队的工作效率比是5:3,两队合修6天完成,单独修甲队比乙队少用多少天?- 解析:设甲队工作效率为5a,乙队工作效率为3a,工作总量=(甲队工作效率 + 乙队工作效率)×工作时间=(5a + 3a)×6=48a。
比与比例应用题

比和比例应用题1、在比例尺是1:2500000的地图上,量得两城市间的距离是8厘米,如画在比例尺是1:8000000的地图上,图上距离是多少厘米?2、水泥、石子、黄沙各有5吨,用水泥、石子、黄沙按5:3:2拌制成混凝土,若用完石子,水泥缺几吨?黄沙多几吨?3、一个车间有两个小组,第一小组和第二小组人数的比是5:3,如果第一小组有14人到第二小组时,第一小组与第二小组人数的比是1:2,两个小组原来各有多少人?4、一块长方体砖,长与宽的比是2:1,宽与高的比是2:1,长、宽、高共35厘米,这块砖的体积是多少?5、有一块铜锌合金,其中铜与锌的比是2:3。
现在加入锌6克,共得新合金36克,求在新合金内铜与锌的比。
6、买甲、乙两种铅笔共210支,甲种铅笔每支3角,乙种铅笔每支4角,两种铅笔用去的钱相同,问甲种铅笔买了几支?7、第一小学六年级学生分三组参加植树,第一组和第二组人数的比是5:4,第二组和第三组人数的比是3:2,已知第一组人数比二、三组人数总和少15人。
六年级参加植树的共多少人?8、车过河交过渡费3元,马过河交过渡费2元,人过河交过渡费1元。
某天过河的车和马数目的比是2:9,马和人数目的比为3:7,共收得过渡费945元,求这天过渡的车、马和人的数目各是多少?9、有两个相同的瓶子装满酒精溶液,一个瓶子中酒精与水的体积之比是3:1,而另一个瓶中酒精与水的比是4:1,若把两瓶酒精溶液混合,混合液中酒精和水的体积之比是多少?10、小明买了一件上衣和两条裤子,小华也买了一件上衣,但只买了一条裤子,结果他们用去的钱数之比是3:2。
已知一件上衣的价钱是3.5元,那么一条裤子的价钱是多少元?11、甲、乙两包糖的重量比是4:1,如果从甲包取出10克放入乙包后,甲、乙两包糖的重量比为7:5,那么两包糖的重量总和是多少克?12、甲、乙两人步行速度之比是7:5,甲、乙分别由A、B两地同时出发,如果相向而行,0.5小时后相遇,如果他们同向而行,那么甲追上乙需要多少时间?13、在一幅地图上,5厘米的长度表示地面上150千米的距离,求这幅地图的比例尺。
解比例应用题专项练习

解比例应用题专项练习班级:姓名:家长签名:1、一幅地图,图上的4厘米,表示实际距离200千米,这幅图的比例尺是多少?2、甲、乙两地相距240千米,画在比例尺是1∶3000000的地图上,长度是多少厘米?3、在一幅地图上,用3厘米的线段表示实际距离600千米。
量得甲、乙两地的距离是4.5厘米,甲、乙两地的实际距离是多少千米?4、运来一批纸装订成练习本,每本36页,可订40本,若每本30页,可订多少本?5、在一幅比例尺是1:30000 的地图上,量得东、西两村的距离是12.3厘米,东、西两村的实际距离是多少米?6、甲地到乙地的实际距离是120千米,在一幅比例尺是1:6000000的地图上,应画多少厘米?7、一幅地图,图上的4厘米,表示实际距离200千米,这幅图的比例尺是多少?8、在一幅比例尺是1:4000 的平面图上,量得一块三角形的菜地的底是12厘米,高是8厘米,这块菜地的实际面积是多少公顷?9、一辆汽车2小时行驶130千米。
照这样的速度,从甲地到乙地共行驶5小时。
甲、乙两地相距多少千米?(用比例解)10、一辆汽车从甲地开往乙地,每小时行64千米,5小时到达。
如果要4小时到达,每小时需行驶多少千米?(用比例解)11、修一条公路,原计划每天修360米,30天可以修完。
如果要提前5天修完,每天要修多少米?(用比例解)12、修一条路,如果每天修120米,8天可以修完;如果每天修150米,可以提前几天可以修完?(用比例方法解)13、修一条公路,总长12千米,开工3天修了1.5千米。
照这样计算,修完这条路还要多少天?(用比例解答)14、修一条路,如果每天修120米,8天可以修完;如果每天多修30米,几天可以修完?(用比例方法解)15、小明买4本同样的练习本用了4.8元,138元可以买多少本这样的练习本?(用比例解答)16、工厂有一批煤,计划每天烧2.4吨,42天可以烧完。
实际每天节约12.5%,实际可以烧多少天?(比例解)17、解放军某部行军演习,4小时走了22.4千米,照这样的速度又行了6小时,一共行了多少千米?(用比例方法解)18、一对互相啮合的齿轮,主动轮有60个齿,每分转80转。
用比例知识解应用题

用比例知识解应用题一、比的应用题(一)解题方法:(1)比的知识解应用题例:学校书画节的展品共有800件。
其中美术展品与书法展品的比是5∶3,两种展品各有多少件?解:美术展品:书法展品=5∶3美术展品占总展品的535+ = 85 书法展品占总展品的533+=83 美术展品=800×85=100×5=500(件) 书法展品=800×83=100×3=300(件) (2)用方程解比的应用题例:学校书画节的展品共有800件。
其中美术展品与书法展品的比是5∶3,两种展品各有多少件?分析:美术展品:书法展品=5∶3设美术展品为5x ,则书法展品为3x美术展品+书法展品=8005x +3x =8008x =800x =100美术展品=5x =5×100=500(件) 书法展品=3x =3×100=300(件)(二)提高练习1、喜盈门大酒店要按男女人数的比3∶5招收一批服务员,结果招收了48人,其中女服务员有多少人?2、某实验小学男女教师人数的比是2∶5,女教师有35人,男教师有多少人?二、比例尺应用题(一)基本知识:比例尺=图上距离:实际距离实际距离=图上距离:比例尺图上距离=实际距离×比例尺(二)提高训练1、甲、乙两城市间的实际距离是120千米,在比例尺1∶4000000的地图上,这两个城市间的图上距离是多少?2、在比例尺是1∶4000000的中国地图上,量得北京到韶山的距离是35厘米。
北京到韶山的实际距离是多少千米?三、比例应用题(一)解题方法1、比值一定,用正比例解题例:一农民收割小麦,3天收割了165公顷,照这样计算,8天可以收割多少公顷小麦?分析:①题中相关联的两种量是()和()。
②“照这样计算”就是说()是一定的。
③题中相关联的两种量成()比例。
④解:设。
⑤列比例式:。
2、乘积一定,用反比例解题例:一辆汽车从甲地开往乙地,每小时行80千米,5小时到达。
精选解比例应用题50道

1、甲地到乙地的实际距离是120千米,在一幅比例尺是1:6000000的地图上,应画多少厘米?2、幅地图,图上的4厘米,表示实际距离200千米,这幅图的比例尺是多少?3、在一幅比例尺是1:4000 的平面图上,量得一块三角形的菜地的底是12厘米,高是8厘米,这块菜地的实际面积是多少公顷?4、运来一批纸装订成练习本,每本36页,可订40本,若每本30页,可订多少本?5、在一幅比例尺是1:30000 的地图上,量得东、西两村的距离是12.3厘米,东、西两村的实际距离是多少米?6、甲地到乙地的实际距离是120千米,在一幅比例尺是1:6000000的地图上,应画多少厘米?7、一幅地图,图上的4厘米,表示实际距离200千米,这幅图的比例尺是多少?8、在一幅比例尺是1:4000 的平面图上,量得一块三角形的菜地的底是12厘米,高是8厘米,这块菜地的实际面积是多少公顷?9、一辆汽车2小时行驶130千米.照这样的速度,从甲地到乙地共行驶5小时。
甲、乙两地相距多少千米?(用比例解)10、一辆汽车从甲地开往乙地,每小时行64千米,5小时到达.如果要4小时到达,每小时需行驶多少千米?(用比例解)11、修一条公路,原计划每天修360米,30天可以修完。
如果要提前5天修完,每天要修多少米?(用比例解)12、修一条路,如果每天修120米,8天可以修完;如果每天修150米,可以提前几天可以修完?(用比例方法解)13、修一条公路,总长12千米,开工3天修了1.5千米。
照这样计算,修完这条路还要多少天?(用比例解答)14、修一条路,如果每天修120米,8天可以修完;如果每天多修30米,几天可以修完?(用比例方法解)15、小明买4本同样的练习本用了4。
8元,138元可以买多少本这样的练习本?(用比例解答)16、工厂有一批煤,计划每天烧2.4吨,42天可以烧完。
实际每天节约12.5%,实际可以烧多少天?(比例解)17、解放军某部行军演习,4小时走了22.4千米,照这样的速度又行了6小时,一共行了多少千米?(用比例方法解)18、一对互相啮合的齿轮,主动轮有60个齿,每分转80转。
较复杂的用比例解应用题
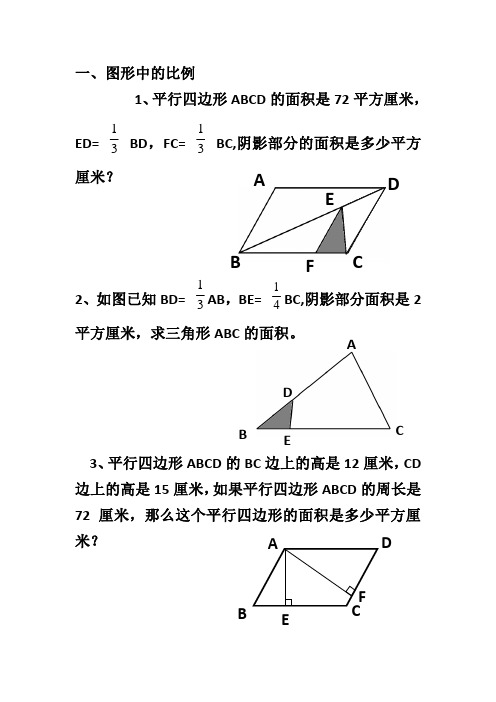
A B C D E F 1 一、图形中的比例1、平行四边形ABCD 的面积是72平方厘米, ED= 31 BD ,FC= 31 BC,阴影部分的面积是多少平方厘米?2、如图已知BD= 31AB ,BE= 41BC,阴影部分面积是2平方厘米,求三角形ABC 的面积。
3、平行四边形ABCD 的BC 边上的高是12厘米,CD 边上的高是15厘米,如果平行四边形ABCD 的周长是72厘米,那么这个平行四边形的面积是多少平方厘米?A B C D ED C A B EF4、已知四边形ABCD 中,三角形AOB 的面积是12平方厘米,三角形AOD 的面积是8平方厘米,三角形DOC 的面积是24平方厘米,求四边形ABCD 的面积。
二、行程中的比例:1、甲乙两车同时从A 、B 两地相对开出,4小时相遇,然后各自行驶4.5小时,这时乙车正好到达A 地,甲车超过B 地50千米。
A 、B 两地相距多少千米?2、甲乙两车从A 、B 两城相对开出,已知甲车的速度与乙车的速度比为5:6,甲车先从A 城开出55千米后,乙车才从B 城出发,两车相遇时,甲车比乙车多行驶了30千米,求AB 城的距离。
3、甲、乙二人同时从A 到B 地,当甲行全程的40﹪,乙距B 地还有150千米;当甲到B 地,乙距B 地的路程与甲所行的路程比是3:8,求A 、B 两地相距多少千米?4、甲乙两车从AB 两地同时出发,30分钟相遇,相遇后又行7.5分钟,这时乙到中点;当甲到B 地时,乙A B C DO距A 地20千米,求AB 之间距离?5、某人骑车计划用 2小时从甲地到乙地,由于途中有一段4千米的道路正在维修,走这段路的速度降低20%,因此比计划多用6分钟.甲乙两地相距多少千米?6、一辆汽车从甲地开往乙地,如果把车速提高25%,可以比原定时间提前24分钟到达;如果原速度行驶60千米后再提高车速的 51 ,则可提前10分钟到达乙地,甲乙两地相距多少千米?7、甲、乙两车以5:4的速度,同时从A 、B 两地相对开出,相遇后,乙车提速,每小时比原来多行18千米,结果两车恰好同时到达对方出发地,总用时6小时,A 、B 两地相距多少千米?8、甲、乙两车以5:4的速度同时从AB 两地出发相向而行,相遇后甲车降速20%,乙车提速20%,继续前进。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用比例的知识解答应用题
1.基础知识训练。
判断下面各题中的两种量成不成比例?成什么比例?(口答。
)
(1)工作总量一定,工作效率和工作时间。
(2)速度一定,路程和时间。
(3)绳子的长度不变,剪下的米数和剩下的米数。
(4)单价一定,总价和数量。
(5)煤的总量一定,每天烧煤量和能够烧的天数。
(6)圆的半径和它的面积。
学生回答后,可让他们说说正、反比例关系的相同点及不同点,正、反比例的判断方法。
[订正:(1)成反比例(2)成正比例(3)不成比例(4)成正比例(5)成反比例(6)不成比例]
2.对比练习,加深理解。
教师谈话:我们已经学习了正、反比例的意义及正、反比例的应用题,这一节课要复习。
(1)教师提问:用正、反比例知识解答应用题的步骤是什么?关键是什么?
先判断题中的数量关系成不成比例,成什么比例;再根据题中的比例关系,找到等量关系;然后把其中的未知数量用x表示,列出方程解答。
关键是正确判断题中的数量关系成不成比例,成什么比例。
(2)基本练习,区分比较。
出示复习题。
(全班同学动笔完成,指名板演。
)
①修一条公路,总长12千米。
开工3天修了1.5千米。
照这样计算,修完这条路共用几天?
②修一条公路,计划每天修0.5千米,24天完成。
实际每天修0.6千米。
实际多少天修完?
[订正:
①解:设修完这条路共用x天。
答:修完这条路共用24天。
②解:设实际x天修完。
答:实际20天完成。
]
订正时,可让学生说说解答正、反比例应用题的相同点和不同点是什么?
[相同点是解题步骤和解题关键相同;不同点是正比例应用题根据商一定列比例式,反比例应用题根据积一定列比例式,所列出的比例式的形式不同。
] (3)变式练习,加深理解。
出示复习题。
①修一条公路,总长12千米。
开工3天修了1.5千米。
照这样计算,修完这条公路还要多少天?
②修一条公路,计划每天修0.5千米,24天完成。
实际每天多修0.1千米。
实际多少天可以修完?
指导学生审题,并与前面的基本题进行比较,找出它们的相同点和不同点,然后让学生独立解答,指名板演。
学生可能有如下的解法:
①解法一:
解:设修完这条路还要x天。
解法二:
解:设修完这条路一共用x天。
答:修完这条路一共用21天。
②解:设实际x天可以修完。
(0.5+0.1)x=0.5×24
0.6x=12
x=20
答:实际20天可以完成。
订正时,重点让学生说说这两题在列式时和前面基本题有什么不同,为什么?(强调列式时要注意对应关系。
)
(4)多种解法,培养能力。
教师谈话:以上两题你们可以用其它方法解答吗?试一试。
学生独立解答,指名板演。
[订正:
①(12-1.5)÷(1.5÷3)=21(天)
或:12÷(1.5÷3)-3=21(天)
②24×0.5 ÷(0.5+0.1)=20(天)]
订正时,可先让学生说说解题思路,然后比较算术解法和用比例知识解答各自的优点。
在此基础上,教师小结:这些应用题用算术方法解,计算时比较方便,但是遇到稍复杂的题目,用比例知识列方程解答容易思考。
今后解答这类题时,可以根据具体情况,灵活选用适当的方法解答。
3.巩固练习,灵活运用。
(1)用比例知识解答。
(全班动笔完成。
)
①某车队运送一批救灾物资,原计划每小时行40千米,7.5小时到达灾区。
实际每小时行了50千米。
照这样计算,行完全程需要多少小时?
②100克蜂蜜里含有34.5克葡萄糖。
照这样计算,2千克蜂蜜含有多少克葡萄糖?多少克蜂蜜里含有207克葡萄糖?
[订正:
①解:设行完全程用x小时。
50x=40×7.5
x=6
②解:设2000克蜂蜜含有x克葡萄糖。
解:设x克蜂蜜里含有207克葡萄糖。
(2)选择合适的方法解答。
(全班动笔完成。
)
①学校买来塑料绳135米,先剪下9米做了5根跳绳。
照这样计算,剩下的塑料绳还能做几根跳绳?
②生产小组加工一批零件,原计划用14天,平均每天加工1500个零件。
任务?
[订正:①(135-9)÷(9÷5)=70(根)
或:135÷(9÷5)- 5=70(根)
订正时,可让学生说说解题思路,如用其它的方法,只要列式合理,计算正确,就算对。
(3)用多种方法解。
(全班动笔完成。
)
大齿轮与小齿轮的齿数比是4∶3,大齿轮有36个齿,小齿轮有多少个齿?
(4)思考题。
(供学有余力的学生解答)
一间长4.8米,宽3.6米的房间,用边长0.15米的正方形瓷砖铺地面,需要768块。
在长6米,宽4.8米的房间里,如果用同样的瓷砖来铺,需要多少块?如果在第一个房间改铺边长0.2米的正方形瓷砖,要用多少块?
[提示:如果瓷砖的大小不变时,房间地面的面积与瓷砖的块数成正比例,所以只要求出两个房间地面的面积,就可以求出第二个房间需要多少块瓷砖。
解法是:解:设需用x块瓷砖。
如果都是在第一个房间铺,瓷砖的大小变了,总面积一定,瓷砖的块数与每块瓷砖的面积成反比例。
(注意这里是与瓷砖的面积成反比例,而不是与瓷砖的边长成反比例。
)解法是:
解:设要用x块瓷砖。
0.152×768=0.22×x
x=432]
4.布置作业。
(略)。
