2019 九年级数学 几何综合
2019年北京市初三一模数学-几何综合专题(教师版)
2019一模几何综合专题一、旋转变换1.（等边三角形+对称＋旋转）(2019通州一模27)如图，在等边ABC △中，点D 是线段BC 上一点.作射线AD ，点B 关于射线AD 的对称点为E .连接CE 并延长，交射线AD（1）设BAF α∠=，用α表示BCF ∠的度数；（2）用等式表示线段AF 、CF、EF 之间的数量关系，并证明. 解：（1）连接AE . ∵点B 关于射线AD 的对称点为E ，∴AE =AB ，BAF EAF α∠=∠=∵ABC △是等边三角形， ∴AB AC =，60BAC ACB ∠=∠=︒. ∴602EAC α∠=︒-，AE AC =. 1分∴()1180602602ACE αα∠=︒-︒-=︒+⎡⎤⎣⎦. ∴6060BCF ACE ACB αα∠=∠-∠=︒+-︒=. ……………… 2分另解：借助圆. （2）AF EF CF -=证明：如图，作60FCG ∠=︒交AD 于点G ，连接BF . ……………… 3分 ∵BAF BCF α∠=∠=，ADB CDF ∠=∠， ∴60ABC AFC ∠=∠=︒. ∴△FCG 是等边三角形.∴GF = FC . ……………… 4分 ∵ABC △是等边三角形，∴BC AC =，60ACB ∠=︒. ∴ACG BCF α∠=∠=.在△ACG 和△BCF 中，CA CB ACG BCF CG CF =⎧⎪∠=∠⎨⎪=⎩，，， ∴△ACG ≌△BCF .∴AG BF =. ……………… 5分 ∵点B 关于射线AD 的对称点为E ， ∴BF EF =. ……………… 6分 ∴AF AG GF -=.∴AF EF CF -=. ……………… 7分另一种证法：作60FAH ∠=︒交FC 的延长线于点H ，连接BF .2.（等边三角形＋旋转）(2019平谷一模27)在△ABC中，∠ABC=120°，线段AC绕点A逆时针旋转60°得到线段AD，连接CD，BD交AC于P．（1）若∠BAC=α，直接写出∠BCD的度数（用含α的代数式表示）；（2）求AB，BC，BD之间的数量关系；（3）当α=30°时，直接写出AC，BD的关系．解：（1）∠BCD=120°－α． ······························································（2）解：方法一：延长BA使AE=BC，连接DE． (2)由（1）知△ADC是等边三角形，∴AD=CD．∵∠DAB+∠DCB=∠DAB+∠DAE=180°，∴∠DAB=∠DAE．∴△ADE≌△CDB． (3)∴BD=BE．∴BD=AB+BC． (4)方法二：延长AB使AF=BC，连接CF． (2)∠BDC=∠ADE．∵∠ABC=120°，∴∠CBF=60°．∴△BCF是等边三角形．∴BC=CF．∵∠DCA=∠BCF=60°，∴∠DCA+∠ACB=∠BCF+∠ACB．即∠DCB=∠ACF．∵CA=CD，∴△ACF≌△DCB． (3)∴BD=AF．∴BD=AB+BC． (4)（3）AC，BD的数量关系是：AC ； (5)位置关系是：AC⊥BD于点P． (6)H O DCBA3.（等边三角形＋旋转）(2019延庆一模27).已知：四边形ABCD 中，120ABC ∠=︒，60ADC ∠=︒，AD =CD ，对角线AC ，BD相交于点O ，且BD 平分∠ABC ，过点A 作AH BD ⊥，垂足为H ． （1）求证：ADB ACB ∠=∠；（2）判断线段BH ，DH ，BC 之间的数量关系；并证明．解：（1）证明：∵∠ADC =60°，DA=DC∴△ADC 是等边三角形． ……1分 ∴∠DAC =60°,AD=AC ． ∵∠ABC=120°,BD 平分∠ABC ∴∠ABD=∠DBC =60°．∴∠DAC =∠DBC =60° ∵∠AOD =∠BOC∠ADB=180°- ∠DAC -∠AOD∠ACB=180°- ∠DBC -∠BOC∴∠ADB=∠ACB ……3分（2）结论：DH=BH+BC ……4分 证明：在HD 上截取HE=HB ……5分∵AH ⊥BD∴∠AHB=∠AHE =90° ∵AH =AH∴△ABH ≌△AEH ∴AB=AE, ∠AEH=∠ABH =60° ……6分 ∴∠AED=180°-∠AEH=120° ∴∠ABC=∠AED=120° ∵AD=AC, ∠ADB=∠ACB ∴△ABC ≌△AED∴DE=BC ……7分 ∵DH=HE+ED∴DH=BH+BC ……8分4.（等边三角形+旋转）(2019密云一模27)已知ABC ∆为等边三角形，点D 是线段AB 上一点（不与A 、B 重合）.将线段CD 绕点C 逆时针旋转60︒得到线段CE.连结DE 、BE. （1）依题意补全图1并判断AD 与BE 的数量关系.（2）过点A 作AF EB ⊥交EB 延长线于点F.用等式表示线段EB 、DB 与AF 之间的数量关系并证明.27.（1）补全图形AD 与BE 的数量关系为AD=BE .................................2分（2）∵∠ACB=∠DCE= 60°, ∴∠ACD=∠BCE 又∵AC=BC,CD=CE ∴△ACD ≌△BCE∴AD=BE, ∠CBE=∠CAD=60°∴∠ABF=180°-∠ABC-∠CBE=60° 在Rt AFB ∆中，32AF AB = ∴BE+BD=32AB.................................7分图2D CBA图1A B CD DEBA5.（正方形+旋转+最值）(2019东城一模27)如图，在正方形ABCD 中，E 是边BC 上一动点（不与点B ，C 重合），连接DE ，点C 关于直线DE 的对称点为C ʹ，连接ACʹ并延长交直线DE 于点P ，F 是AC ′中点，连接DF ．（1）求∠FDP 的度数；（2）连接BP ，请用等式表示AP ，BP ，DP 三条线段之间的数量关系，并证明． （3）连接ACACC ′的面积最大值．解：（1）由对称可知 CD ＝C ′D ，∠CDE ＝∠C ′DE ． 在正方形ABCD 中，AD ＝CD ，∠ADC ＝90°， ∴AD ＝C ′D ．又∵F 为AC ′中点，∴DF ⊥AC ′，∠ADF ＝∠C ′DF ．……………………………………………………1分∴∠FDP ＝∠FDC ′＋∠EDC ′=12∠ADC ＝45°．…………………2分（2）结论：BP ＋DPAP ．……………………………………………………3分 如图，作AP ′⊥AP 交PD 延长线于P ′， ∴∠P AP ′＝90°．在正方形ABCD 中，DA ＝BA ，∠BAD ＝90°， ∴∠DAP ′＝∠BAP ．由（1）可知∠APD ＝45°， ∴∠P ′＝45°．∴AP ＝AP ′……………………………………………………4分在△BAP 和△DAP ′中，BA DA BAP DAP AP AP =⎧⎪'∠=∠⎨⎪'=⎩，∴△BAP ≌△DAP ′（SAS ）……………………………………………………5分 ∴BP ＝DP ′．P BAP BA∴DP＋BP＝PP′＝．（3－1……………………………………………………7分P'B A6.（等腰直角三角形+旋转）(2019房山一模27).已知：Rt△ABC中，∠ACB=90°，AC=BC.(1) 如图1，点D是BC边上一点(不与点B，C重合)，连接AD，过点B作BE⊥AD，交AD的延长线于点E，连接CE.若∠BAD=α，求∠DBE的大小(用含α的式子表示) ；(2) 如图2，点D在线段BC的延长线上时，连接AD，过点B作BE⊥AD，垂足E在线段AD上，连接CE.①依题意补全图2；②用等式表示线段EA，EB和EC之间的数量关系，并证明.图1 图2解：（1）解: 依题意，∠CAB=45°，∵∠BAD=α，∴∠CAD=45α︒-.∵∠ACB=90°，BE⊥AD，∠ADC=∠BDE，∴∠DBE=∠CAD=45α︒-. …………………………………2分（2）解：①补全图形如图…………………………………4分②猜想：当D在BC边的延长线上时，EB - EAEC.…………………………………5分证明：过点C作CF⊥CE，交AD的延长线于点F.∵∠ACB=90°，∴∠ACF=∠BCE.∵CA=CB，∠CAF =∠CBE，∴△ACF≌△BCE.…………………………………6分∴AF=BE，CF=CE.∵∠ECF=90°，∴EFEC.即AF-EAEC.AB A∴7分7.（等腰直角三角形+旋转）(2019门头沟一模27). 如图，∠AOB = 90°，OC 为∠AOB 的平分线，点P 为OC 上一个动点，过点P 作射线PE 交OA 于点E ．以点P 为旋转中心，将射线PE 沿逆时针方向旋转90°，交OB 于点F ．（1）根据题意补全图1，并证明PE = PF ；（2）如图1，如果点E 在OA 边上，用等式表示线段OE ，OP 和OF 之间的数量关系，并证明； （3）如图2，如果点E 在OA 边的反向延长线上，直接写出线段OE ，OP 和OF 之间的数量关系．图1 图227．（本小题满分7分）解：（1）补全图形（如图1）； ……………………………… 1分证明：略. ……………………………………… 3分（2）线段OE ，OP 和OF 之间的数量关系是OF +OE =2OP . ……………………………… 4分证明：如图2，作PQ ⊥PO 交OB 于Q .∴ ∠2+∠3 = 90°，∠1+∠2 = 90°. ∴ ∠1=∠3.又∵ OC 平分∠AOB ，∠AOB =90°， ∴∠4 =∠5 = 45°. 又∵ ∠5 +∠6 = 90°， ∴∠6 = 45°，∴∠4 = ∠6 . ∴ PO = PQ .∴ △EPO ≌ △FPQ . ……………………… 5分 ∴ PE =PF ，OE = FQ .又∵OQ = OF +FQ = OF + OE .又∵ OQ =2OP ，∴OF + OE =2OP . ……………………… 6分（3）线段OE ，OP 和OF 之间的数量关系是OF - OE =2OP . ………………………… 7分PPEECCBBOOAA图2图18.（等腰直角三角形+旋转）(2019燕山一模27)如图，在△ABC 中，AB ＝BC ，∠B ＝90°，点D 为线段BC 上一个动点(不与点B ，C 重合)，连接AD ，将线段AD 绕点D 顺时针旋转90°得到线段DE ，连接EC ．(1) ① 依题意补全图1；② 求证：∠EDC ＝∠BAD ； (2) ① 小方通过观察、实验，提出猜想：在点D 运动的过程中，线段CE 与BD 的数量关系始终不变，用等式表示为： ； ② 小方把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法： 想法1：过点E 作EF ⊥BC ，交BC 延长线于点F ，只需证△ADB ≌△DEF ． 想法2：在线段AB 上取一点F ，使得BF ＝BD ，连接DF ，只需证△ADF ≌△DEC ． 想法3：延长AB 到F ，使得BF ＝BD ，连接DF ，CF ，只需证四边形DFCE 为平行四边形． ……请你参考上面的想法，帮助小方证明①中的猜想．(一种方法即可)27．(1)①补全的图形如图的所示；………………………………1分②证明：∵∠ADE ＝∠B ＝90°，∴∠EDC ＋∠ADB ＝∠BAD ＋∠ADB ＝90°，∴∠EDC ＝∠BAD ． ………………………………3分(2) ①CE ＝2BD ． ………………………………4分②想法1：证明：如图，过点E 作EF ⊥BC ，交BC 延长线于点F ，∴∠F ＝90°．在△ADB 和△DEF 中，∠B ＝∠F ＝90°，∠EDC ＝∠BAD ，AD ＝DE ， ∴△ADB ≌△DEF ， ∴AB ＝DF ，BD ＝EF ．图1 D C B A 备用图 A B CD AB ECD EA。
2019届初三数学中考复习 中考 几何综合题 课件(33张PPT)
基本模型
D
C
G H
F
A
E
B
D
A
E
H B
回归教材
研读教材 原型外延
课本 八年级下册 69页 复习题18 第14题
A
D
B
E
C
研读教材
原型外延
D
C
G
F
A
E
B
回归教材
如图，四边形ABCD是正方形，点 E是边BC上的中点，∠AEF=90゜，且 F EF交正方形外角的平分线CF于点F， 求证AE=EF.
如图，在正方形ABCD中，E是边 AB上的一动点（不与点A，B重合）， 连接DE，点A关于直线DE的对称点为 F，连接EF并延长交BC于点G，连接 DG，过点E作EH⊥DE交DG的延长线 于点H，连接BH. H （1）求证：GF=GC （2）用等式表示线段BH与AE的数量 关系，并证明.
D
C
G H
F
A
E
B
2018中考 第27题
如图，在正方形ABCD中，E是边AB上的一动点 （不与点A，B重合），连接DE，点A关于直线DE的 对称点为F，连接EF并延长交BC于点G，连接DG， 过点E作EH⊥DE交DG的延长线于点H，连接BH. （1）求证：GF=GC （2）用等式表示线段BH与AE的数量关系，并证明.
D
C
G H
F
A
E
B
2018中考 第27题
如图，在正方形ABCD中，E是边AB上的一动点 （不与点A，B重合），连接DE，点A关于直线DE的 对称点为F，连接EF并延长交BC于点G，连接DG， 过点E作EH⊥DE交DG的延长线于点H，连接BH. （1）求证：GF=GC （2）用等式表示线段BH与AE的数量关系，并证明.
2019中考数学几何综合试卷精选汇编(含解析答案)
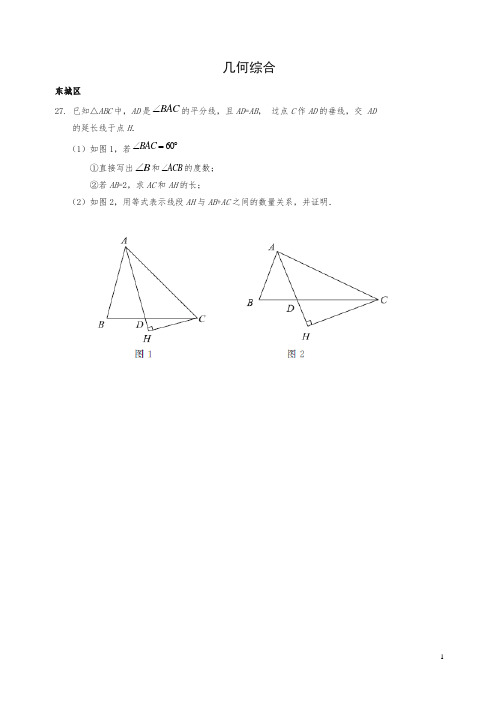
几何综合东城区27. 已知△ABC 中，AD 是BAC ∠的平分线，且AD =AB ， 过点C 作AD 的垂线，交 AD的延长线于点H ．（1）如图1，若60BAC ∠=︒①直接写出B ∠和ACB ∠的度数； ②若AB =2，求AC 和AH 的长；（2）如图2，用等式表示线段AH 与AB +AC 之间的数量关系，并证明．27. （1）①75B ∠=︒，45ACB ∠=︒；--------------------2分②作DE ⊥AC 交AC 于点E .Rt △ADE 中，由30DAC ∠=︒，AD=2可得DE =1，AE . Rt △CDE 中，由45ACD ∠=︒，DE=1，可得EC =1.∴AC 1=.Rt △ACH 中，由30DAC ∠=︒，可得AH ； --------------4分（2）线段AH 与AB +AC 之间的数量关系：2AH =AB +AC证明： 延长AB 和CH 交于点F ，取BF 中点G ，连接GH . 易证△ACH ≌△AFH . ∴AC AF =,HC HF =. ∴GH BC ∥. ∵AB AD =， ∴ ABD ADB ∠=∠. ∴ AGH AHG ∠=∠ . ∴ AG AH =.∴()2222AB AC AB AF AB BF AB BG AG AH +=+=+=+==. --------------7分 西城区27．正方形ABCD 的边长为2，将射线AB 绕点A 顺时针旋转α，所得射线与线段BD 交于点M ，作CE AM ⊥于点E ，点N 与点M 关于直线CE 对称，连接CN ．（1）如图，当045α︒<<︒时， ①依题意补全图．②用等式表示NCE ∠与BAM ∠之间的数量关系：__________．（2）当4590α︒<<︒时，探究NCE ∠与BAM ∠之间的数量关系并加以证明． （3）当090α︒<<︒时，若边AD 的中点为F ，直接写出线段EF 长的最大值．CDBA图1备用图C DBAM【解析】（1）①补全的图形如图所示：NEMABD C②2NCE BAM ∠=∠．（2）1902MCE BAM ∠+∠=︒，连接CM ，NQMABDC EDAM DCM ∠=∠，DAQ ECQ ∠=∠，∴2NCE MCE DAQ ∠=∠=∠，∴12DCM NCE ∠=∠，∵BAM BCM ∠=∠， 90BCM DCM ∠+∠=︒，∴1902NCE BAM ∠+∠=︒． （3）∵90CEA ∠=︒， ∴点E 在以AC 为直径的圆上，E∴max 1EF FO r =+=+27点（（27．.解：（1）作PF ⊥DE 交DE 于F . ∵PE ⊥BO ，60AOB ∠=， ∴30OPE ∠=.∴30DPA OPE ∠=∠=.∴120EPD ∠=. ……………1分∵DP PE =,6DP PE +=, ∴30PDE ∠=,3PD PE ==.∴cos30DF PD =⋅︒=∴2DE DF ==分 （2）当M 点在射线OA上且满足OM =DMME的值不变，始终为1.理由如下： ………………4分 当点P 与点M 不重合时，延长EP 到K 使得PK PD =. ∵,DPA OPE OPE KPA ∠=∠∠=∠, ∴KPA DPA ∠=∠. ∴KPMDPM ∠=∠.∵PK PD =,PM 是公共边, ∴KPM △≌DPM △. ∴MKMD =. ………………5分作ML ⊥OE 于L ,MN ⊥EK 于N .∵60MO MOL =∠=， ∴sin 603ML MO =⋅=. ………………6分∵PE ⊥BO ,ML ⊥OE ,MN ⊥EK ， ∴四边形MNEL 为矩形. ∴3EN ML ==.∵6EK PE PK PE PD =+=+=, ∴EN NK =. ∵MN ⊥EK , ∴MK ME =. ∴ME MK MD ==,即1DMME=. 当点P 与点M 重合时，由上过程可知结论成立. ……………7分 丰台区27．如图，Rt△ABC 中，∠ACB = 90°，CA = CB ，过点C 在△ABC 外作射线CE ，且∠BCE = α，点B 关于CE 的对称点为点D ，连接AD ，BD ，CD ，其中AD ，BD 分别交射线CE 于点M ，N . （1）依题意补全图形；（2）当α= 30°时，直接写出∠CMA 的度数；（3）当0°<α< 45°时，用等式表示线段AM ，CN 之间的数量关系，并证明．ABCE27．解：（1）如图； …………………1分（2）45°； …………………2分 （3）结论：AM CN ． …………………3分 证明：作AG ⊥EC 的延长线于点G ．∵点B 与点D 关于CE 对称， ∴CE 是BD 的垂直平分线． ∴CB =CD ． ∴∠1=∠2=α．∵CA =CB ，∴CA =CD ．∴∠3=∠CAD ． ∵∠4=90°， ∴∠3=12（180°-∠ACD ）=12（180°-90°-α-α）=45°-α．∴∠5=∠2+∠3=α+45°-α=45°．…………………5分 ∵∠4=90°，CE 是BD 的垂直平分线， ∴∠1+∠7=90°，∠1+∠6=90°． ∴∠6=∠7． ∵AG ⊥EC ，∴∠G =90°=∠8． ∴在△BCN 和△CAG 中， ∠8=∠G ，∠7=∠6，BC =CA ，∴△BCN ≌△CAG ．∴CN =AG ． ∵Rt△AMG 中，∠G =90°，∠5=45°， ∴AM AG ．∴AMCN ． …………………7分 （其他证法相应给分.）石景山区27．在正方形ABCD 中，M 是BC 边上一点，点P 在射线AM 上，将线段AP 绕点A 顺时针旋转90°得到线段AQ ，连接BP ，DQ ． （1）依题意补全图1；（2）①连接DP ，若点P ，Q ，D 恰好在同一条直线上，求证：2222DP DQ AB +=； ②若点P ，Q ，C 恰好在同一条直线上，则BP 与AB 的数量关系为： ．27．（1）补全图形如图1. ………………… 1分（2）①证明：C图1连接BD ，如图2，∵线段AP 绕点A 顺时针旋转90°得到线段AQ ， ∴AQ AP =，90QAP ∠=°． ∵四边形ABCD 是正方形， ∴AD AB =，90DAB ∠=°． ∴12∠=∠．∴△ADQ ≌△ABP ． ………………… 3分 ∴DQ BP =，3Q ∠=∠．∵在Rt QAP ∆中，90Q QPA ∠+∠=°， ∴390BPD QPA ∠=∠+∠=°． ∵在Rt BPD ∆中，222DP BP BD +=， 又∵DQ BP =，222BD AB =，∴2222DP DQ AB +=． ………………… 5分 ②BP AB =． ………………… 7分 证明：过点A 作AE⊥PQ 于E ，连接BE AC ∴AE 是△PAQ 的垂线∵三△PAQ 是等腰直角三角形（已证） ∴AE 是等腰直角三角形PAQ 的垂线，角平分线 ∴∠AEP=90°，AE=PE ∵正方形ABCD ∴∠ABC=90° ∠ACB=∠BAC=45° ∠AEP+∠ABC=180° ∴A ，B ，C ，E 四点共圆∴∠AEB=∠ACB=45°，∠CEB=∠BAC=45° ∴∠AEB=∠CEB=45° ∵BE=BE∴△ABE≌△PBE (SAS) ∴BP=AB 朝阳区27. 如图，在菱形ABCD 中，∠DAB =60°，点E 为AB 边上一动点（与点A ，B 不重合），连接CE ，将∠ACE 的两边所在射线CE ，CA 以点C 为中心，顺时针旋转120°，分别交射线AD 于点F ，G.（1）依题意补全图形；（2）若∠ACE=α，求∠AFC的大小（用含α的式子表示）；（3）用等式表示线段AE、AF与CG之间的数量关系，并证明．27.（1）补全的图形如图所示.……………………………………1分（2）解：由题意可知，∠ECF=∠ACG=120°.∴∠FCG=∠ACE=α.∵四边形ABCD是菱形，∠DAB=60°，∴∠DAC=∠BAC= 30°. ……………………………………………2分∴∠AGC=30°.∴∠AFC =α+30°. …………………………3分（3）用等式表示线段AE 、AF 与CG 之间的数量关系为CG AF AE 3=+.证明：作CH ⊥AG 于点H.由（2）可知∠BAC=∠DAC=∠AGC=30°.∴CA=CG. …………………………………………………5分 ∴HG =21AG. ∵∠ACE =∠GCF ，∠CAE =∠CGF ，∴△ACE ≌△GCF. ……………………………6分 ∴AE =FG .在Rt △HCG 中， .23cos CG CGH CG HG =∠⋅= ∴AG =3CG . …………………………………………7分 即AF+AE =3CG . 燕山区27．如图，抛物线)0(2>++=a c bx ax y 的顶点为M ，直线y=m 与抛物线交于点A ，B ，若△AMB 为等腰直角三角形，我们把抛物线上A ，B 两点之间的部分与线段AB 围成的图形称为该抛物线对应的准蝶形，线段AB 称为碟宽，顶点M 称为碟顶．(1)由定义知，取AB 中点N ，连结MN ，MN 与AB 的关系是 (2)抛物线221x y =对应的准蝶形必经过B (m ，m ),则m = ，对应的碟宽AB 是 (3)抛物线)0(3542>--=a a ax y 对应的碟宽在x 轴上，且AB=6. 准蝶形AMBABM11①求抛物线的解析式；②在此抛物线的对称轴上是否有这样的点P （p x ，p y ），使得∠APB 为锐角，若有，请求出p y 的取值范围.若没有，请说明理由. ,备用图27.解：(1)MN 与AB 的关系是 MN ⊥AB ，MN=21AB…………………………………2′（2） m= 2 对应的碟宽是4…………………………………4′(3) ①由已知，抛物线必过（3，0），代入)0(3542>--=a a ax y 得，03549=--a a31=a∴抛物线的解析式是3312-=x y …………………………………5′ ② 由①知，3312-=x y 的对称轴上P （0，3），P （0，-3）时，∠APB 为直角， ∴在此抛物线的对称轴上有这样的点P ，使得∠APB 为锐角，p y 的取值范围是33〉〈-p p y y 或…………………………………7′门头沟区27. 如图，在△ABC 中，AB =AC ，2A α∠=，点D 是BC 的中点，DE AB E ⊥于点，DF AC F ⊥于点. （1）EDB ∠=_________°；（用含α的式子表示）（2）作射线DM 与边AB 交于点M ，射线DM 绕点D 顺时针旋转1802α︒-，与AC 边交于点N ． ①根据条件补全图形；②写出DM 与DN 的数量关系并证明；③用等式表示线段BM CN 、与BC 之间的数量关系，B（用含α的锐角三角函数表示）并写出解题思路.27．（本小题满分7分）（1）EDBα∠=……………………………………………1分（2）①补全图形正确……………………………………2分②数量关系：DM DN=…………………………………3分∵,AB AC BD DC==∴DA平分BAC∠∵DE AB E⊥于点，DF AC F⊥于点∴DE DF=，MED NFD∠=∠……………………4分∵2Aα∠=∴1802EDFα∠=︒-∵1802MDNα∠=︒-∴MDE NDF∠=∠∴MDE NDF△≌△……………………5分∴DM DN=③数量关系：sinBM CN BCα+=⋅……………………6分证明思路：a.由MDE NDF△≌△可得EM FN=b. 由AB AC=可得B C∠=∠,进而通过BDE CDF△≌△,可得BE CF=进而得到2BE BM CN=+c.过BDERt△可得sinBEBDα=,最终得到sinBM CN BCα+=⋅……………7分大兴区27．如图，在等腰直角△ABC中，∠CAB=90°，F是AB边上一点，作射线CF，过点B作BG⊥C F于点G，连接AG．（1）求证：∠ABG=∠ACF；（2）用等式表示线段C G，AG，BG之间的等量关系，并证明．B121327.（1）证明∵ ∠CAB=90°. ∵ BG ⊥CF 于点G ， ∴ ∠BGF =∠CAB =90°.∵∠GFB =∠CFA . ………………………………………………1分 ∴ ∠ABG =∠ACF . ………………………………………………2分（2）CG+BG . …………………………………………………3分证明：在CG 上截取CH =BG ，连接AH ， …………………………4分 ∵ △ABC 是等腰直角三角形， ∴ ∠CAB =90°，AB =AC . ∵ ∠ABG =∠ACH .∴ △ABG ≌△ACH . …………………………………………………… 5分 ∴ AG =AH ,∠GAB =∠HAC . ∴ ∠GAH =90°.∴ 222AG AH GH +=.∴ GHAG . ………………………………………………………6分 ∴ CG =CH +GH+BG . ………………………………………7分 平谷区27．在△ABC 中，AB=AC ，CD ⊥BC 于点C ，交∠ABC 的平分线于点D ，AE 平分∠BAC 交BD 于点E ，过点E 作EF ∥BC 交AC 于点F ，连接DF ． （1）补全图1；（2）如图1，当∠BAC =90°时，①求证：BE=DE ；②写出判断DF 与AB 的位置关系的思路（不用写出证明过程）； （3）如图2，当∠BAC=α时，直接写出α，DF ，AE 的关系．图1BB图21427．解：（1）补全图1； (1)B（2）①延长AE ，交BC 于点H ． ····· 2 ∵AB=AC ， AE 平分∠BAC ，∴AH ⊥BC 于H ，BH=HC ．∵CD ⊥BC 于点C ， ∴EH ∥CD ．∴BE=DE ． (3)②延长FE ，交AB 于点G ．由AB=AC ，得∠ABC =∠ACB ． 由EF ∥BC ，得∠AGF =∠AFG ． 得AG=AF ．由等腰三角形三线合一得GE=E F ． ·· 4 由∠GEB =∠FED ，可证△BEG ≌△DEF ．可得∠ABE =∠FDE ． (5)从而可证得DF ∥AB ． ······· 6 （3）tan 2DF αAE ． (7)怀柔区27.如图，在△ABC 中，∠A=90°，AB=AC ，点D 是BC 上任意一点，将线段AD 绕点A 逆时针方向旋转90°，得到线段AE ，连结EC. (1)依题意补全图形；BB15B(2)求∠ECD 的度数；(3)若∠CAE=7.5°，AD=1，将射线DA 绕点D 顺时针旋转60°交EC 的延长线于点F ，请写出求AF 长的思路．27.(1)如图………………………………………………1分(2) ∵线段AD 绕点A 逆时针方向旋转90°，得到线段AE. ∴∠DAE=90°，AD=AE. ∴∠DAC+∠CAE =90°. ∵∠BAC=90°, ∴∠BAD+∠DAC =90°.∴∠BAD=∠CAE . …………………………………………………………………………2分 又∵AB=AC, ∴△ABD≌△ACE. ∴∠B=∠ACE.∵△ABC 中，∠A=90°，AB=AC, ∴∠B=∠ACB=∠ACE=45°.∴∠ECD=∠ACB+∠ACE=90°. ……………………………………………………………4分 (3)Ⅰ.连接DE,由于△ADE 为等腰直角三角形，所以可求DE=2；……………………5分 Ⅱ.由∠ADF=60°,∠CAE=7.5°，可求∠EDC 的度数和∠CDF 的度数，从而可知DF 的长； …………………………………………………………………………………………………6分 Ⅲ.过点A 作AH ⊥DF 于点H ，在Rt△ADH 中, 由∠ADF=60°，AD=1可求AH 、DH 的长； Ⅳ. 由DF 、DH 的长可求HF 的长；Ⅴ. 在Rt△AHF 中, 由AH 和HF,利用勾股定理可求AF 的长．…………………………7分16 延庆区27．如图1，正方形ABCD 中，点E 是BC 延长线上一点，连接DE ，过点B 作BF ⊥DE 于点F ，连接FC ． （1）求证：∠FBC =∠CDF ．（2）作点C 关于直线DE 的对称点G ，连接CG ，FG ．①依据题意补全图形；②用等式表示线段DF ，BF ，CG 之间的数量关系并加以证明．27.（1）证明：∵四边形ABCD 是正方形，∴∠DCB =90°． ∴∠CDF +∠E =90°． ∵BF ⊥DE ，∴∠FBC +∠E =90°． ∴∠FBC =∠CDF ．……2分（2）①……3分②猜想：数量关系为：BF =DF +CG ．图1FDEC BA GFDBA17证明：在BF 上取点M 使得BM =DF 连接CM ．∵四边形ABCD 是正方形， ∴BC =DC ．∵∠FBC =∠CDF ，BM =DF ， ∴△BMC ≌△DFC ． ∴CM =CF ，∠1=∠2． ∴△MCF 是等腰直角三角形．∴∠MCF =90°，∠4=45°． ……5分 ∵点C 与点G 关于直线DE 对称， ∴CF =GF ，∠5=∠6． ∵BF ⊥DE ，∠4=45°， ∴∠5=45°， ∴∠CFG =90°， ∴∠CFG =∠MCF ， ∴CM ∥GF ． ∵CM =CF ，CF =GF ， ∴CM =GF ，∴四边形CGFM 是平行四边形， ∴CG =MF ．∴BF =DF +CG ． ……7分顺义区27. 如图，在正方形ABCD 中，E 是BC 边上一点，连接AE ，延长CB 至点F ，使BF=BE ，过点F 作FH ⊥AE 于点H ，射线FH 分别交AB 、CD 于点M 、N ，交对角线AC 于点P ，连接AF ． （1）依题意补全图形； （2）求证：∠FAC =∠APF ；（3）判断线段FM 与PN 的数量关系，并加以证明．27．（1）补全图如图所示． ………………………………………………………… 1分 （2）证明∵正方形ABCD ，∴∠BAC =∠BCA =45°，∠ABC =90°，∴∠PAH=45°-∠BAE．∵FH⊥AE．∴∠APF=45°+∠BAE．∵BF=BE，∴AF=AE，∠BAF=∠BAE．∴∠FAC=45°+∠BAF．∴∠FAC=∠APF．…………………………… 4分Array（3）判断：FM=PN．…………………………………… 5分证明：过B作BQ∥MN交CD于点Q，∴MN=BQ，BQ⊥AE．∵正方形ABCD，∴AB=BC，∠ABC=∠BCD=90°．∴∠BAE=∠CBQ．∴△ABE≌△BCQ．∴AE=BQ．∴AE=MN．∵∠FAC=∠APF，∴AF=FP．∵AF=AE，∴AE=FP．∴FP=MN．∴FM=PN．…………………………………………………………… 8分18。
2019-九年级数学专题复习：中考数学填空压轴常见类型——几何综合
2019-2020 年九年级数学专题复习：中考数学填空压轴常有种类——几何综合（ 1）一、综述中考数学填空题既考察基本知识、技术、方法，也对考生的思想能力有必定要求．与选择题近似，填空题也不要求写出求解过程，只需结果；不一样的是，填空题没有选项，不可以利用选项的提示，可是同时也防止了遇到选项的误导．一般而言，第 14， 15 题难度较高1.几何综合常与平移、旋转、折叠（轴对称）等操作联合起来，在动向背景下考察；当题目无图或以存在性问题的形式出现时，常常需要分类议论.解题方法：①标明条件，合理转变合理标明长度、角度信息，借助图形性质进行转变．②组合特点，剖析结构在熟习的背景、结构下研究特点间的关系，如三角形，四边形，圆等．③由因导果，执果索因2.函数综合主要考察函数与几何综合问题以及数形联合思想在函数问题中的应用．解题方法：①研究坐标，表达式，剖析背景图形②梳理条件，整合信息从重点点坐标切入，研究点的坐标，函数图象，几何图形三者间的关系．③设计方案求解利用数形联合思想，将函数问题转变为方程、不等式问题求解．由几何特点表达点坐标，代入函数表达式求解．由函数表达式设出点坐标，借助几何特点求解．3.规律研究规律研究是一类由简单、局部、特别情况猜想、考证一般性规律的问题．主要考察学生概括推理能力．解题方法：①明确研究目标②经过列举简单、局部、特别的几种情况来猜想一般规律常常将序列号与目标对应起来，从首个开始列举，常列举 3- 5 组数据．数字规律常考虑和、差、积、商、乘方等关系，式子规律常考虑结构关系，图形规律常用方法是分类、补形、去重，或转变为数字规律、式子规律．③考证几何综合1.如图，把矩形 ABCD 沿 EF 翻折，点 B 恰巧落在 AD 边上的点 B′处．若 AE=2，DE=6，∠ EFB=60°，则矩形 ABCD 的面积是 __________．A'FA M DA E B'DEB FC B N C第1题图第2题图2.如图，将长为 4cm，宽为 2cm 的矩形纸片 ABCD 折叠，使点 B 落在 CD 边的中点 E 处，压平后获得折痕 MN，则线段 AM 的长为 __________．3.如图，在矩形 ABCD 中，E 是 CD 边的中点，将△ ADE 沿 AE 折叠后获得△ AFE，CG 1 ，则且点F 在矩形ABCD 内部，延伸AF 交BC 边于点G．若GB kAD__________．（用含k 的代数式表示）ABD E CGFCA B A O B第3题图第4题图4. 如图，AB是半圆O的直径，且 AB8，C为半圆O上的一点．将此半圆沿BC 所在的直线折叠，若折叠后的圆弧BC恰巧过圆心O，则图中暗影部分的面积是__________．（结果保存π）如图，AD是△ ABC的角均分线，DF⊥ AB，垂足为F，DE =DG．若△ ADG 和△ ADE 的面积分别为 50 和 39，则△DEF 的面积为 __________．AAEEGBNMFBDCCD第5题图第6题图5. 如图，在五边形 ABCDE 中，∠ BAE=125°，∠B=∠E=90°，AB=BC ，AE=DE ．点M ，N 分别在边 BC ，DE 上，当△ AMN 的周长最小时，∠ AMN+∠ANM 的度数为 __________．6. 如图，在 6×4的方格纸中，每个小正方形的极点称为格点，格点三角形甲经过旋转后获得格点三角形乙，则其旋转中心是图中的 __________．DPGCN QF甲AB 乙ME第 7题图第 8题图7. 如图，菱形 ABCD 和菱形 AEFG 开始时相互重合，现将菱形 AEFG 绕点 A 顺时针旋转，设旋转角∠ BAE=α（0°< α<360°），则当 α=___________时，菱形 AEFG 的极点 F 会落在菱形 ABCD 的对角线 AC 或 BD 所在的直线上．8. 如图，∠ ABC=90°，点 B 在⊙ O 上，∠ ABC 的两FCAE边分别交⊙ O 于点 D ，E ，BD=4，BE=8．将∠ ABCO绕点 B 顺时针旋转 30°，旋转后的对应边分别交⊙ DGO 于点 F ，G ，则点 D 到 FG 的距离为 __________．B9.如图， Rt △ 的边3 ，∠ °，∠ °．若 ABCBC 位于直线 l 上， AC=ACB=90 A=30Rt △ABC 由此刻的地点向右无滑动地翻转，则当点 A 第 3 次落在直线 l 上时，点 A 所经过的路线长为．（结果保存 π）__________AlCB10. 如图，在△ ABC 中，∠ BAC=90°， AB=5cm ，AC=2cm ，将△ ABC 绕极点 C按顺时针方向旋转 45°至△ A 1B 1C 的地点，则线段 AB 扫过地区（图中暗影部分）2的面积为 _________cm ．BEB 1DGAA1CABCF第 11题图第 12题图11. 如图，在 Rt △ ABC 中，∠ ACB=90°，∠ A=30°，AC= 4 3 ，BC 的中点为 D ，将△ ABC 绕点 C 顺时针旋转随意一个角度获得△ FEC ，EF 的中点为 G ，连结 DG ，则在旋转过程中， DG 长度的最大值是 __________．12. 如图，P 是等腰直角三角形 ABC 外一点，将 BP 绕点 B 顺时针旋转 90°到BP ′，若 ∠ AP ′B =135°， 且 P ′A :P ′C =1: 3 ， 则P ′A :PB=__________．A13. 劳技课上小敏取出了一个腰长为 8 厘米，P'底边长为 6 厘米的等腰三角形，她想用这个等腰三角形加工成一个邻边之比为 1: 2 P的平行四边形，且该平行四边形的一个内 BC角恰巧是这个等腰三角形的底角，其余顶点均在三角形的边上，则这个平行四边形较短边的长为 __________．14. 已知等边三角形 ABC 的高为 4，P 为这个三角形所在的平面内一点，若点 P 到AB 的距离是 1，点 P 到 AC 的距离是 2，则点 P 到 BC 的最小距离是________，最大距离是 ________．15. 如图，在矩形 ABCD 中， AB=3，BC=4， E 是 BC 边上一点，连结 AE ，把∠ B沿 AE 折叠，使点 B 落在点 B ′处，当△ CEB ′为直角三角形时， BE 的长为__________．AADB'DPCQ BEB E CF第16题图第17题图16.如图，已知 Rt△ABC≌ Rt△DEF ，∠C=∠F= 90°，AC=DF=3，BC=EF=4，△DEF 绕着斜边 AB 的中点 D 旋转，DE，DF 分别交 AC，BC 所在的直线于点P， Q．当△ BDQ 为等腰三角形时， AP 的长为 __________．17.如图，射线 QN 与等边三角形 ABC 的两边 AB，BC 分别交于点 M，N，且AC∥ QN，AM=BM=2cm，QM=4cm．动点 P 从点 Q 出发，沿射线 QN 以 1cm/s 的速度向右挪动，经过 t s，以点 P 为圆心， 3 cm 为半径的圆与△ ABC 的边相切（切点在边上），则 t 的值为 _______________．A CQM NB函数综合18. 在平面直角坐标系中，一次函数y 1与反比率函数 y50）的图象x 2（x3x交点的横坐标为 x0．若 k x0k 1 ，则整数 k 的值是___________．19. 如图，抛物线y x2bx 9与 y 轴订交于点 A，与过点 A 且平行于 x 轴的直2线订交于点 B（点 B 在第一象限），抛物线的极点 C 在直线 OB 上，对称轴与 x 轴订交于点 D．平移该抛物线，使其经过点 A，D，则平移后的抛物线的分析式为 __________________．yyx=1A BC- 1 O xOD x第20题图第21题图20.已知二次函数 y ax2 bx c（a≠0）的图象如下图，有以下5个结论：①abc0 ；② b a c ；③4a 2b c0 ；④ 2c3b ；⑤a b m(am b) （m1）．此中正确结论的序号是___________________．2019-九年级数学专题复习：中考数学填空压轴常有种类——几何综合21.如图， Rt△ABC 在第一象限，∠ BAC=90°，AB=AC=2，点 A 在直线 y=x 上，且点 A 的横坐yCABO 1x标为 1，AB∥x 轴， AC∥ y 轴．若双曲线 yk （k≠0）与△ABC有交点，则xk 的取值范围是 __________．22.如图，以扇形 OAB 的极点 O 为原点，半径 OB 所在的直线为 x 轴，成立平面直角坐标系，点 B 的坐标为 (2，0)．若抛物线 y 1 x2k 与扇形 OAB 的边2界总有两个公共点，则实数k 的取值范围是 __________．y yAM A B45°B EO xO x第23题图第24题图23.如图，在平面直角坐标系 xOy 中，点 B 的坐标为 (0，3 )，点 A 在第一象限，且 AB⊥OB，E 是线段 OA 的中点，点 M 在线段 AB 上．若点 B 与点 E 对于直线 OM 对称，则点 M 的坐标是 ___________．24.如图，在平面直角坐标系中，已知直线 y=x 上一点 P(1，1)，C 为 y 轴上一点，连结 PC，将线段 PC 绕点 P 顺时针旋转 90°至线段 PD，过点 D 作 x 轴的垂线，交直线 y=x 于点 A，交 x 轴于点 B，且 BD= 2AD．若直线 CD 与直线 y=x交于点 Q，则点 Q 的坐标为 ___________．yC A yQADEP DO B x B O Cx第25题图第26题图25. 如图，△ ABO 为等边三角形，点 B 的坐标为 (- 2，0)，过点 C(2， 0)作直线k CE 交 AO 于点 D，交 AB 于点 E，且使 S△ADE=S△OCD．若点 E 在双曲线 yx （x<0）上，则 k 的值为 ___________．26.如，在平面直角坐系中有Rt△ ABC ，∠ CAB=90°， AB=AC， A(- 1，0)，B(1，1)，将△ ABC 沿 x 的正方向平移，在第一象限内B，C 两点的点B，C恰巧落在反比率函数y k的象上，k 的 ______．11xyyy=x2 C1CCB1ABA O A1xHxO第 27第 2827.如，在第一象限内作射 OC，使其与 x 的角 30°，在射 OC 上取一点 A，点 A作 AH⊥x 于点 H．在抛物 y=x2（x>0）上取一点 P，在y 上取一点 Q，使得以 P，O，Q 点的三角形与△ AOH 全等，切合条件的点 A 的坐是．律研究28.有一等式： 12+22+22=32，22+32 +62 =72，32+42+122=132，42+52+202=212，⋯，察它的组成律，用你的律写出第 8 个等式：．29. 已知以下各形中的三个数之都有同样的律，依据此律， a 的是____________．1234561044936161442540036a30.如，点 B1是面 1 的等三角形 OBA 的两条中的交点，以 OB1一，结构等三角形 OB1A1（点 O，B1，A1按逆方向摆列），称第一次结构；点 B2是△ OB1A1的两条中的交点，再以2 一，结构等三角形OB2 2（点 O，B2，A2BOB A按逆方向摆列），称第二次结构；以此推，当第 n 次结构出的等三角形OB n n的 OA n与等A三角形 OBA 的 OB 第一次重合，结构停止．结构出的最后一个三角形的面是B1__________________．31. 在平面直角坐系 xOy 中，我把横坐都是整A B2O数的点叫做整点．如，已知点 A(0，4)，点 B 是 x B3A3A1A2正半上的整点，△ AOB 内部（不包含界）的整点个数 m，当 m=3 ，点 B 的横坐的全部可能是 _____________；当点 B 的横坐 4n（n正整数）， m=____________．（用含 n 的代数式表示）y4A321O 1 2 3 4 5 6 7 8 9 10 11 12 13x32.二次函数220 位于坐原点，点A1，A2，A3，⋯，y x的象如所示，点 A3A n在 y 的正半上，点 B1，B2，B3，⋯，B n在二次函数位于第一象限的象上，点C1，C2，C3，⋯，C n在二次函数位于第二象限的象上，且四形 A0B1A1C1，四形 A1B2A2C2，四形 A2B3A3C3，⋯，四形 A n- 1B n A n C n都是菱形．若∠ A0 11∠122∠ 2 3 3⋯∠ n- 1 n nBA= ABA= ABA== A BA=60°，菱形 A n- 1 n n n的周____________．B A CyA3C3B3yA2C2B2P1A1P2P3B1C1x O A1A2A3xO (A0)第 34第 3533.如，点 1 1，y1，22，y2)，⋯，n n，y n均在反比率函数y1 （）P (x) P (x P (x)xx>0的象上，若△ P11，△P2 1 2，△P3 23，⋯，△P n n- 1 n 都是等腰直角OA A A A A A A三角形，斜 OA1，A12，A23，⋯，A n- 1n 都在x上（n是大于或等于2A A A的正整数），点 P3的坐是 ____________，点 P n的坐是 ____________．用（含 n 的代数式表示）34.如，在平面直角坐系中，已知直l：y- x - 1 ，双曲yy 1，在 l 上取一点 A1， A1作 x 的垂交双曲于点xA2B11，B1 作y的垂交l于点A2；操作并研究：B2 作x的垂交双曲于点B2， B2作 y 的垂交 l 于O x AA1l点 A3；⋯；挨次获得l 上的点 A1，A2， A3，⋯， A n．点 A n的横坐a n，若 a1=2， a2=_____， a2 013=_____；若要将上述操作无穷次地行下去，a1不可以取的是 ____________．35.如，在平面直角坐系中，有若干个横、坐均整数的点，其序按中“→”方向摆列，如 (1，0)，(2，0)，(2，1)，(1，1)，(1，2)，(2，2)，⋯，依据个律，第2 014 个点的横坐 ____________．y⋯⋯321O 1 2 3 4x 36.如，已知△ OBC 是直角三角形， OB 在 x 正半上，∠ OBC=90°，且OB=1，BC= 3．将△ OBC 原点 O 逆旋 60°，再将其各大本来的 m 倍，使OB1=OC，获得△ OB1C1；将△ OB1C1原点 O 逆旋 60°，再将其各大本来的m 倍，使 OB2 =OC1，获得△ OB2C2；⋯；这样下去，获得△ OB2 014C2 014，点 C2 014的坐是 ________．yCO B x【参照答案】几何综合1．16 32． 13cm3．k 18 24．8π5．116．110°327．点 N 8． 60°， 180°或 300° 9． 1510． (4 3) π11．25π812．613．1:214．12cm 或24cm51115．1，716．3或317．13，11或 252612618． t ， ≤t ≤ 7 或 t =8=2 3函数综合19．1 20．y 2 -9 9．③④⑤x 2x21222．1 ≤ k ≤ 423．-21，k24． (1 3)225．9 926．3 36(，)-．4 442728． (3， 3) ， (3 1 2 3 23，2)3， ) ， (3 ， )，(23329．（ 1）(2 ，0) （ 2） 15°或 75°研究规律30． 82+92+722 =73231．90032． 110m nn( )33．3，4；=6 -334．4335．( 32， 3-2) ，(nn - 1， n - n - 1)36． a 2 - 3 ， a 2 0131 ； ， -1． 452 -37338． (- 22 014，- 22 014 3)． 31239。
2019年北京市各区九年级上册期末数学试卷分类汇编：几何综合【标准版】
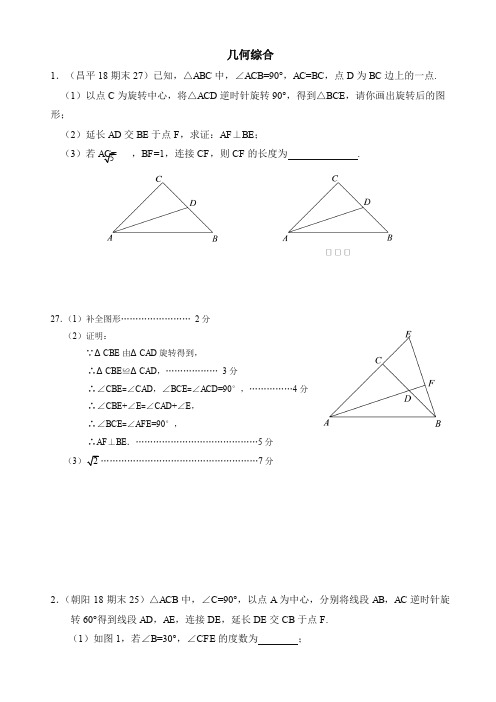
几何综合1．（昌平18期末27）已知，△ABC 中，∠ACB =90°，AC =BC ，点D 为BC 边上的一点. （1）以点C 为旋转中心，将△ACD 逆时针旋转90°，得到△BCE ，请你画出旋转后的图形；（2）延长AD 交BE 于点F ，求证：AF ⊥BE ；（3）若，BF =1，连接CF ，则CF 的长度为 .27．（1）补全图形…………………… 2分 （2）证明：∵ΔCBE 由ΔCAD 旋转得到，∴ΔCBE ≌ΔCAD ，……………… 3分∴∠CBE =∠CAD ，∠BCE =∠ACD =90°，……………4分 ∴∠CBE +∠E =∠CAD +∠E ， ∴∠BCE =∠AFE =90°，∴AF ⊥BE ．……………………………………5分（3………………………………………………7分2．（朝阳18期末25）△ACB 中，∠C =90°，以点A 为中心，分别将线段AB ，AC 逆时针旋转60°得到线段AD ，AE ，连接DE ，延长DE 交CB 于点F . （1）如图1，若∠B =30°，∠CFE 的度数为 ；（2）如图2，当30°<∠B <60°时，①依题意补全图2；②猜想CF 与AC 的数量关系，并加以证明.图1 图23．（西城18期末27）如图1，在Rt △AOB 中，∠AOB =90°，∠OAB =30°，点C 在线段OB上，OC =2BC ，AO 边上的一点D 满足∠OCD =30°．将△OCD 绕点O 逆时针旋转α度（90°<α<180°）得到△OC D ''，C ，D 两点的对应点分别为点C '，D '，连接AC '，BD '，取AC'的中点M，连接OM．（1）如图2，当C D''∥AB时，α=°，此时OM 和BD'之间的位置关系为；（2）画图探究线段OM和BD'之间的位置关系和数量关系，并加以证明．4．（丰台18期末27）如图，∠BAD=90°，AB=AD ，CB=CD ，一个以点C 为顶点的45°角绕点C 旋转，角两边与BA ，DA 交于点M ，N ，与BA ，DA 延长线交于点E ，F ，连接AC . （1）在∠FCE 旋转的过程中，当∠FCA =∠ECA 时，如图1，求证：AE =AF ； （2）在∠FCE 旋转的过程中，当∠FCA ≠∠ECA 时，如图2，如果∠B=30°，CB=2，用等式表示线段AE ，AF 之间的数量关系，并证明.27.解：（1）证明：∵AB=AD ，BC=CD ，AC=AC ，∴△ABC ≌△ADC . …1分∴∠BAC =∠DAC =45°，可证∠FAC =∠EAC =135°. ……2分 又∵∠FCA =∠ECA ，∴△ACF ≌△ACE . ∴AE =AF . ……3分 其他方法相应给分.（2）过点C 作CG ⊥AB 于点G ，求得AC =2.……4分∵∠FAC =∠EAC =135°，∴∠ACF +∠F =45°. 又∵∠ACF +∠ACE =45°，∴∠F =∠ACE . ∴△ACF ∽△AEC. ……5分 ∴ACAF AE AC =，即AF AE AC ⋅=2. ……6分 ∴2=⋅AF AE . ……7分5．（怀柔18期末27）在等腰△ABC 中，AB =AC ，将线段BA 绕点B 顺时针旋转到BD，使图1图2BD⊥AC于H，连结AD并延长交BC的延长线于点P.（1）依题意补全图形；（2）若∠BAC=2α，求∠BDA的大小（用含α的式子表示）；（3）小明作了点D关于直线BC的对称点点E，从而用等式表示线段DP与BC之间的数量关系.请你用小明的思路补全图形并证明线段DP与BC之间的数量关系.27.解：(1)如图……………………………………………1分(2) ∵∠BAC=2α，∠AHB=90°∴∠ABH=90°-2α…………………………………………………………………………… 2分∵BA=BD∴∠BDA=45°+α………………………………………………………………………………3分(3)补全图形，如图………………4分证明过程如下：∵D关于BC的对称点为E，且DE交BP于G∴DE⊥BP，DG=GE，∠DBP=∠EBP，BD=BE；…………………………………………5分∵AB=AC，∠BAC=2α∴∠ABC=90°-α由(2)知∠ABH=90°-2α∠DBP=90°-α-（90°-2α）=α∴∠DBP=∠EBP=α∴∠BDE=2α∵AB=BD∴△ABC ≌△BDE ………………………………………………………………………………6分 ∴BC =DE∴∠DPB =∠ADB -∠DBP =45°+α-α=45° ∴DP DG =21, ∴DP DE=2, ∴DPBC=2, ∴BC =2DP .………………………………………………………………………………7分6．（平谷18期末27）如图，在Rt △ABC 中，∠BAC =90°，AB=AC ．在平面内任取一点D ，连结AD （AD ＜AB ），将线段AD 绕点A 逆时针旋转90°得到线段AE ，连结DE ，CE ，BD ．（1）请根据题意补全图1；（2）猜测BD 和CE 的数量关系并证明；（3）作射线BD ，CE 交于点P ，把△ADE 绕点A 旋转，当∠EAC =90°，AB =2，AD =1时，补全图形，直接写出PB 的长．27．解：（1）如图 (1)（2）BD 和CE 的数量是：BD =CE ；·················································································2B图1B备用图∵∠DAB +∠BAE =∠CAE +∠BAE =90°，∴∠DAB=∠CAE ． ················································································································· 3 ∵AD=AE ，AB=AC ， ∴△ABD ≌△ACE ．∴BD =CE ． (4)（3）PB ． (7)7．（密云18期末27）如图，已知Rt ABC ∆中，90ACB ∠=︒，AC=BC ，D 是线段AB 上的一点（不与A 、B 重合）. 过点B 作BE ⊥CD ，垂足为E.将线段CE 绕点C 顺时针旋转90︒，得到线段CF ，连结EF.设BCE ∠度数为α.（1）①补全图形； ②试用含α的代数式表示CDA ∠.（2）若EF AB = ，求α的大小. （3）直接写出线段AB 、BE 、CF 之间的数量关系.27.（1）①补全图形.……………………………..1分②45α︒+ ……………………………..3分 （2）在FCE ∆和ACB ∆中，45CFE CAB ∠=∠=︒ ，90FCE ACB ∠=∠=︒ F C E ∆∽ ACB ∆CF EFAC AB =EF AB =2CF AC = ………………………………..5分 连结FA.90,ECB 90FCA ACE ACE ∠=︒-∠∠=︒-∠ECB FCA ∠=∠=α在Rt CFA ∆中，90CFA ∠=︒，cos FCA ∠=30FCA ∠=︒即30α=︒. ………………………………6分（3）22222AB CF BE =+ …………………………………………8分8．（石景山18期末27）在正方形ABCD中，点P在射线AC上，作点P关于直线CD的对称点Q，作射线BQ交射线DC于点E，连接BP．（1）当点P在线段AC上时，如图1．①依题意补全图1；②若EQ=BP，则∠PBE的度数为，并证明；（2）当点P在线段AC的延长线上时，如图2．若EQ=BP，正方形ABCD的边长为1，请写出求BE长的思路．（可以不写出计算结果）27．（本小题满分7分）（1）解：①正确作图………………………1分②45°………………………2分连接PD，PE易证△CPD≌△CPB∴DP=BP，∠CDP=∠CBP∵P、Q关于直线CD对称∴EQ=EP∵EQ=BP∴DP=EP∴∠C D P=∠D E P………………………………………………3分∵∠CEP+∠DEP=180°∴∠CEP+∠CBP=180°∵∠BCD=90°∴∠BPE=90°∵BP=EP∴∠PBE =45°． …………………………………………………………4分 （2）解：连接PD ，PE易证△CPD ≌△CPB ∴DP =BP ，∠1=∠2 ∵P 、Q 关于直线CD 对称， ∴EQ =EP ，∠3=∠4 ∵EQ =BP ， ∴DP =EP ∴∠3=∠1， ∴∠3=∠2 ∴∠5=∠BCE =90° ∵BP =EP ， ∴∠PEB =45° ∴∠3=∠4=22.5°，在△BCE 中，已知∠4=22.5°，BC =1，可求BE 长． ……………7分9．（东城18期末27）如图1，在△ABC 中，∠ACB =90°，AC =2，BC =B 为圆心，为半径作圆．点P 为B 上的动点，连接PC ，作PCPC '⊥，使点P '落在直线BC 的上方，且满足:P C PC '=BP ，AP '． （1）求∠BAC 的度数，并证明△AP C '∽△BPC ； （2）若点P 在AB 上时，①在图2中画出△AP’C ； ②连接BP '，求BP '的长；图1图2（3）点P 在运动过程中，BP '是否有最大值或最小值？若有，请直接写出BP '取得最大值或最小值时∠PBC 的度数；若没有，请说明理由．备用图10．（顺义18期末27）综合实践课上，某小组同学将直角三角形纸片放到横线纸上（所有横线都平行，且相邻两条平行线的距离为1），使直角三角形纸片的顶点恰巧在横线上，发现这样能求出三角形的边长．（1）如图1，已知等腰直角三角形纸片△ABC，∠ACB=90°，AC=BC，同学们通过构造直角三角形的办法求出三角形三边的长，则AB= ；（2）如图2，已知直角三角形纸片△DEF，∠DEF=90°，EF=2DE，求出DF的长；（3）在（2）的条件下，若橫格纸上过点E的横线与DF相交于点G，直接写出EG的长．27．（1）AB ；……………………….2分（2）解：过点E 作横线的垂线，交l 1，l 2于点M ，N ，……………………………..….3分∴∠DME =∠EDF = 90°，∵∠DEF =90°，∴∠2+∠3=90°，∵∠1+∠3=90°，∴∠1=∠2，∴△DME ∽△ENF ，………….…….4分 ∴DM ME DE EN NF EF==， ∵EF =2DE ， ∴12DM ME DE EN NF EF ===， ∵ME =2，EN =3，∴NF =4，DM =1.5，根据勾股定理得DE =2.5，EF =5，DF =……………………….5分 （3）EG=2.5．…………………………………………………………..…….7分11．（门头沟18期末27）如图1有两条长度相等的相交线段AB 、CD ，它们相交的锐角中有一个角为60°，为了探究AD 、CB 与CD (或AB )之间的关系，小亮进行了如下尝试：（1）在其他条件不变的情况下使得AD BC ∥，如图2，将线段AB 沿AD 方向平移AD 的长度，得到线段DE ,然后联结BE ,进而利用所学知识得到AD 、CB 与CD (或AB )之间的关系：____________________；(直接写出结果)（2）根据小亮的经验，请对图27-1的情况（AD 与CB 不平行）进行尝试，写出AD 、CB 与CD (或AB )之间的关系，并进行证明；（3）综合（1）、（2）的证明结果，请写出完整的结论 __________________________.27．（本小题满分7分）（1） AD CB AB += ……………………………………………1分（2）补全图形正确 ………………………………………2分结论：AD CB AB +＞………………………………………3分理由：如图：将线段AB 沿AD 方向平移AD 的长度，得到线段DE ,联结BE 、CE ，且可得AB DE ∥且AB DE =∴四边形A 、B 、E 、D 是平行四边形………………………4分∴AD BE =∵AB CD =∴DE CD =∵AB DE ∥,60AOD ∠=︒∴DCE △是等边三角形……………………………………5分∴CE AB =由于AD 与CB 不平行，所以C 、B 、E 构成三角形∴BE CB CE +＞……………………………………………6分∴AD CB AB +＞（3）AD CB AB +≥ …………………………………………7分12．（通州18期末24）如图1，在矩形ABCD 中，点E 为AD 边中点，点F 为BC边中点；图1 图2点G ，H 为AB 边三等分点，I ，J 为CD 边三等分点.小瑞分别用不同的方式连接矩形对边上的点，如图2，图3所示.那么，图2中四边形GKLH 的面积与图3中四边形KPOL 的面积相等吗？（1）小瑞的探究过程如下在图2中，小瑞发现， ABCD GKLH S S _______=；在图3中，小瑞对四边形KPOL 面积的探究如下. 请你将小瑞的思路填写完整： 设a S DEP =△，b S AKG =△∵AF EC ∥∴DAK DEP ∽△△，且相似比为2:1，得到a S DAK 4=△∵BI GD ∥∴ABM AGK ∽△△，且相似比为3:1，得到b S ABM 9=△ 又∵ABCD DAG S b a S 614=+=△，ABCD ABF S a b S 419=+=△ ∴a b b a S ABCD 436624+=+=∴b a ____=，b S ABCD _____=，b S KPOL _____=∴ABCD KPOL S S _____=，则GKLH KPOL S S ____（填写“”，“”或“”）（2）小瑞又按照图4的方式连接矩形ABCD 对边上的点.则ABCD ANML S S _____=.13．（海淀18期末28）在△ABC 中，∠A 90°，ABAC ．（1）如图1，△ABC 的角平分线BD ，CE 交于点Q ，请判断“QB =”是否正确：_______（填“是”或“否”）；（2）点P 是△ABC 所在平面内的一点，连接P A ，PB ，且P A ．①如图2，点P 在△ABC 内，∠ABP 30°，求∠P AB 的大小；②如图3，点P 在△ABC 外，连接PC ，设∠APCα，∠BPCβ，用等式表示α，β之间的数量关系，并证明你的结论．图1 图2图3 28．解：（1）否. ………………1分（2）① 作PD ⊥AB 于D ，则∠PDB =∠PDA =90°，∵ ∠ABP =30°，∴ 12PD BP =. ………………2分∵ PB =，∴ 2PD PA =.∴ sin PD PAB PA ∠== 由∠P AB 是锐角，得∠P AB =45°. ………………3分 另证：作点P 关于直线AB 的对称点'P ，连接',',B P P A P P ，则',',','P B A P B A P A B P A B B P B P A P A P∠=∠∠=∠==.∵∠ABP =30°，∴'60P BP ∠=︒.∴△'P BP 是等边三角形.∴'P P BP =.∵PB =，∴'P P =. ………………2分 ∴222''P P PA P A =+.∴'90PAP ∠=︒.∴45PAB ∠=︒. ………………3分② 45αβ+=︒，证明如下： ………………4分 作AD ⊥AP ，并取AD =AP ，连接DC ，DP .∴ ∠DAP =90°.∵ ∠BAC =90°，∴ ∠BAC +∠CAP =∠DAP +∠CAP ,即 ∠BAP =∠CAD .∵ AB =AC ，AD =AP ，∴ △BAP ≌△CAD .∴ ∠1=∠2，PB =CD . ………………5分 ∵ ∠DAP =90°，AD =AP ，∴ PD =，∠ADP =∠APD =45°.∵ PB =，∴ PD =PB =CD .∴ ∠DCP =∠DPC .∵ ∠APCα，∠BPCβ，∴ 45DPC α∠=+︒，12αβ∠=∠=-.∴ 31802902DPC α∠=︒-∠=︒-.∴ 139045ADP αβ∠=∠+∠=︒--=︒.∴45αβ+=︒. ………………7分。
云南省2019届九年级数学学业水平考试-几何综合检测及参考答案
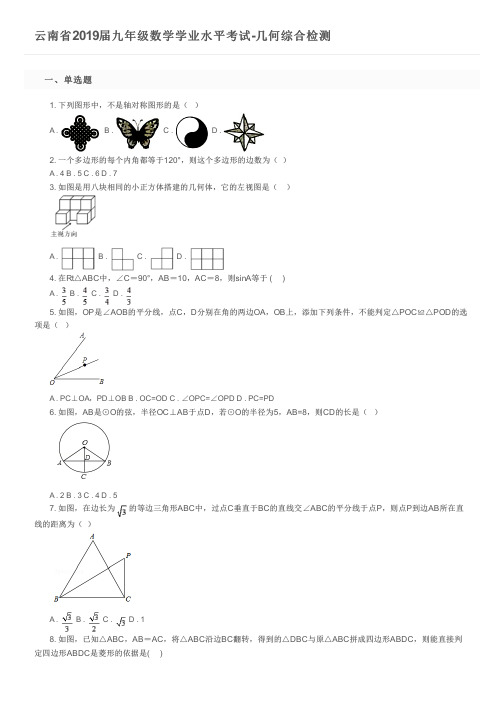
一、单选题
1. 下列图形中，不是轴对称图形的是（ ）
A.
B.
C.
D.
2. 一个多边形的每个内角都等于120°，则这个多边形的边数为（ ） A.4B.5C.6D.7 3. 如图是用八块相同的小正方体搭建的几何体，它的左视图是（ ）
A.
B.
C.
D.
4. 在Rt△ABC中，∠C＝90°，AB＝10，AC＝8，则sinA等于 ( ) A. B. C. D.
A.2B.3C.4D.5 7. 如图，在边长为 线的距离为（ ）
的等边三角形ABC中，过点C垂直于BC的直线交∠ABC的平分线于点P，则点P到边AB所在直
A. B. C. D.1
8. 如图，已知△ABC，AB＝AC，将△ABC沿边Байду номын сангаасC翻转，得到的△DBC与原△ABC拼成四边形ABDC，则能直接判 定四边形ABDC是菱形的依据是( )
17. 如图,△ABC,△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上,求证:△CDA≌△CEB．
18. 已知点E是矩形ABCD的边CD上一点，BF⊥AE于点F，求证△ABF∽△EAD.
19. 如图，在△ABC中，AB=AC=1，BC=
，在AC边上截取AD=BC，连接BD．
（1） 通过计算，判断AD2与AC•CD的大小关系； （2） 求∠ABD的度数． 20. 用如图所示矩形纸片的四个角都剪去一个边长为
请根据上图完成这个推论的证明过程．
证明：S矩形NFGD＝S△ADC－(S△ANF＋S△FGC)， S矩形EBMF＝S△ABC－(________＋________)． 易知，S△ADC＝S△ABC ， ________＝________，________＝________． 可得S矩形NFGD＝S矩形EBMF. 三、解答题 16. 如图，Rt△ABC中，∠C=90°，AB=14，AC=7，D是BC上一点，BD=8，DE⊥AB，垂足为E，求线段DE的长．
(完整word版)北京2019初三年级中考几何综合
如图，在△ABC 中，AC =BC ，∠ACB =90°，D 为AC 上一点（与点A ，C 不重合），连接BD ，过点A 作AE ⊥BD 的 延长线于E（1）①在图中作出△ABC 的外接圆⊙O ，并用文字描述 圆心O 的位置②连接OE ，求证：点E 在⊙O 上（2）①延长线段BD 至点F ，使EF =AE ，连接CF ,根据题 意补全图形②用等式表示线段CF 与AB 的数量关系，并证明 2如图，△ABC 是等边三角形，D ，E 分别是AC ，BC 边上的点，且AD = CE ，连接BD ，AE 相交于点F （1）∠BFE 的度数是（2）如果21=AC AD ，那么=BF AF （3）如果nAC AD 1=时，请用含n 的式子表示AF ，BF 的数量关系，并证明ABC DEADBF已知在△ABC 中，AB =AC ，∠BAC =α，直线l 经过点A （不经过点B 或点C ），点C 关于直线l 的对称点为点D ，连接BD ，CD（1）如图1 ①求证：点,,B C D 在以点A 为圆心，AB 为半径的圆上 ②直接写出∠BDC 的度数（用含α的式子表示）为___________（2）如图2，当α=60°时，过点D 作BD 的垂线与直线l 交于点E ，求证：AE =BD（3）如图3，当α=90°时，记直线l 与CD 的交点为F ，连接BF ．将直线l 绕点A 旋转，当线段BF 的长取得最大值时，直接写出tan FBC ∠的值4在菱形ABCD 中，∠ADC=60°，BD 是一条对角线，点P 在边CD 上（与点C ，D 不重合），连接AP ，平移ADP ∆，使点D 移动到点C ，得到BCQ ∆，在BD 上取一点H ，使HQ=HD ，连接HQ ，AH ，PH （1） 依题意补全图1 （2）判断AH 与PH 的数量关系及∠AHP 的度数，并加以证明 （3）若141AHQ ∠=︒，菱形ABCD 的边长为1，请写出求DP 长的思路（可．以不写出计算结果．．．．．．．．）BBA BCDPA BCD如图1，在正方形ABCD 中，点F 在边BC 上，过点F 作EF ⊥BC ，且FE =FC （CE <CB ），连接CE 、AE ，点G 是AE 的中 点，连接FG（1）用等式表示线段BF 与FG 的数量关系是___________________（2）将图1中的△CEF 绕点C 按逆时针旋转，使△CEF 的顶点F 恰好在正方形ABCD 的对角线AC 上，点G 仍是AE 的中点，连接FG 、DF①在图2中，依据题意补全图形②求证:DF =6正方形ABCD 中，将边AB 所在直线绕点A 逆时针旋转一个角度α得到直线AM ，过点C 作CE ⊥AM ，垂足为E ，连接BE(1) 当045α︒<<︒时，设AM 交BC 于点F① 如图1，若α＝35°，则∠BCE ＝ ° ② 如图2，用等式表示线段AE ，BE ，CE 之间的数量关系，并证明 (2) 当4590α︒<<︒时(如图3)，请直接用等式表示线段AE ，BE ，CE 之间的数量关系图2图1F 35°MBC DAEF AB EMC DαAB EMCD如图，Rt △ ABC 中，∠ACB =90°，AD 平分∠BAC ， 作AD 的垂直平分线EF 交AD 于点E ，交BC 的延长线于点F ，交AB 于点G ，交AC 于点H（1）依题意补全图形8如图，在△ABC 中，AC = BC ，∠ACB = 90°，D 是线段AC 延长线上一点，连接BD ，过点A 作AE ⊥BD 于E （1）求证：∠CAE =∠CBD（2）将射线AE 绕点A 顺时针旋转45°后，所得的射线与线段BD 的延长线交于点F ，连接CE ① 依题意补全图形② 用等式表示线段EF ，CE ，BE 之间的数量关系，并证明AABCDEM 是正方形ABCD 的边AB 上一动点（不与A ，B 重合）MC BP ⊥，垂足为P ，将CP B ∠绕点P 旋转，得到''PB C ∠，当射线'PC 经过点D 时，射线'PB 与BC 交于点N （1）依题意补全图形 （2）求证：CPD ∽∆∆BPN（3）在点M 的运动过程中，图中是否存在与BM 始终相等的线段？若存在，请写出这条线段并证明，若不存在，请说明理由10如图，在△ABC 中，AB =AC ．△ADE ∽△ABC ，连接BD ，CE （1）判断BD 与CE 的数量关系，并证明你的结论（2）若AB =2，AD =22，∠BAC =105°，∠CAD =30° ①BD 的长为②点P ，Q 分别为BC ，DE 的中点，连接PQ ，写出求PQ 长的思路如图，在ABC Rt ∆中，BC AB ABC ==∠，090，点E 为线段AB 上一动点（不与点A ，B 重合），连接CE ，将AC E ∠的两边CE ，CA 分别绕点C 顺时针旋转090，得到射线''CA CE ，，过点A 作AB 的垂线AD ，分别交射线''CA CE ，于点F ，G（1）依题意补全图形（2）若α=∠ACE ，求AFC ∠的大小（用含α的式子表示） （3）用等式表示线段AE ，AF ，与BC 之间的数量关系，并证明12如图，M 为正方形ABCD 内一点，点N 在AD 边上，且MB MN BMN 2900==∠，，点E 为MN 的中点，点P 为DE 的中点，连接MP 并延长到点F ，使得PF=PM ，连接DF （1）依题意补全图形 （2）求证：DF=BM（3）连接AM ，用等式表示线段PM 和AM 的数量关系并证明如图，正方形ABCD，将边CD绕点C顺时针旋转60°，得到线段CE，连接DE，AE，BD交于点F（1）求∠AFB的度数（2）求证：BF=EFAB，CF，EF的数量关系E。
【精品初三数学】2019北京初三数学期末分类汇编-几何综合+答案
如图，在△ABC 中，AC =BC ，∠ACB =90°，D 为AC 上一点（与点A ，C 不重合），连接BD ，过点A 作AE ⊥BD 的 延长线于E（1）①在图中作出△ABC 的外接圆⊙O ，并用文字描述 圆心O 的位置②连接OE ，求证：点E 在⊙O 上（2）①延长线段BD 至点F ，使EF =AE ，连接CF ,根据题 意补全图形②用等式表示线段CF 与AB 的数量关系，并证明 2 丰台如图，△ABC 是等边三角形，D ，E 分别是AC ，BC 边上的点，且AD = CE ，连接BD ，AE 相交于点F （1）∠BFE 的度数是（2）如果21=AC AD ，那么=BF AF （3）如果nAC AD 1=时，请用含n 的式子表示AF ，BF 的数量关系，并证明ABC DEADBF已知在△ABC 中，AB =AC ，∠BAC =α，直线l 经过点A （不经过点B 或点C ），点C 关于直线l 的对称点为点D ，连接BD ，CD（1）如图1 ①求证：点,,B C D 在以点A 为圆心，AB 为半径的圆上 ②直接写出∠BDC 的度数（用含α的式子表示）为___________（2）如图2，当α=60°时，过点D 作BD 的垂线与直线l 交于点E ，求证：AE =BD（3）如图3，当α=90°时，记直线l 与CD 的交点为F ，连接BF ．将直线l 绕点A 旋转，当线段BF 的长取得最大值时，直接写出tan FBC ∠的值4 怀柔在菱形ABCD 中，∠ADC=60°，BD 是一条对角线，点P 在边CD 上（与点C ，D 不重合），连接AP ，平移ADP ∆，使点D 移动到点C ，得到BCQ ∆，在BD 上取一点H ，使HQ=HD ，连接HQ ，AH ，PH （1） 依题意补全图1 （2）判断AH 与PH 的数量关系及∠AHP 的度数，并加以证明 （3）若141AHQ ∠=︒，菱形ABCD 的边长为1，请写出求DP 长的思路（可以不写出计算结果．．．．．．．．．）BBA BCDPA BCD如图1，在正方形ABCD 中，点F 在边BC 上，过点F 作EF ⊥BC ，且FE =FC （CE <CB ），连接CE 、AE ，点G 是AE 的中 点，连接FG（1）用等式表示线段BF 与FG 的数量关系是___________________（2）将图1中的△CEF 绕点C 按逆时针旋转，使△CEF 的顶点F 恰好在正方形ABCD 的对角线AC 上，点G 仍是AE 的中点，连接FG 、DF①在图2中，依据题意补全图形 ②求证:DF =6 燕山正方形ABCD 中，将边AB 所在直线绕点A 逆时针旋转一个角度α得到直线AM ，过点C 作CE ⊥AM ，垂足为E ，连接BE(1) 当045α︒<<︒时，设AM 交BC 于点F① 如图1，若α＝35°，则∠BCE ＝ ° ② 如图2，用等式表示线段AE ，BE ，CE 之间的数量关系，并证明 (2) 当4590α︒<<︒时(如图3)，请直接用等式表示线段AE ，BE ，CE 之间的数量关系图2图1F 35°MBC DAEF AB EMC DαAB EMCD如图，Rt △ ABC 中，∠ACB =90°，AD 平分∠BAC ， 作AD 的垂直平分线EF 交AD 于点E ，交BC 的延长线于点F ，交AB 于点G ，交AC 于点H（1）依题意补全图形8 门头沟如图，在△ABC 中，AC = BC ，∠ACB = 90°，D 是线段AC 延长线上一点，连接BD ，过点A 作AE ⊥BD 于E （1）求证：∠CAE =∠CBD（2）将射线AE 绕点A 顺时针旋转45°后，所得的射线与线段BD 的延长线交于点F ，连接CE ① 依题意补全图形② 用等式表示线段EF ，CE ，BE 之间的数量关系，并证明AABCDEM 是正方形ABCD 的边AB 上一动点（不与A ，B 重合）MC BP ⊥，垂足为P ，将CPB ∠绕点P 旋转，得到''PB C ∠，当射线'PC 经过点D 时，射线'PB 与BC 交于点N （1）依题意补全图形 （2）求证：CPD ∽∆∆BPN（3）在点M 的运动过程中，图中是否存在与BM 始终相等的线段？若存在，请写出这条线段并证明，若不存在，请说明理由10 西城如图，在△ABC 中，AB =AC ．△ADE ∽△ABC ，连接BD ，CE （1）判断BD 与CE 的数量关系，并证明你的结论 （2）若AB =2，AD =22，∠BAC =105°，∠CAD =30° ①BD 的长为②点P ，Q 分别为BC ，DE 的中点，连接PQ ，写出求PQ 长的思路如图，在ABC Rt ∆中，BC AB ABC ==∠，090，点E 为线段AB 上一动点（不与点A ，B 重合），连接CE ，将ACE ∠的两边CE ，CA 分别绕点C 顺时针旋转090，得到射线''CA CE ，，过点A 作AB 的垂线AD ，分别交射线''CA CE ，于点F ，G（1）依题意补全图形（2）若α=∠ACE ，求AFC ∠的大小（用含α的式子表示） （3）用等式表示线段AE ，AF ，与BC 之间的数量关系，并证明 12 东城如图，M 为正方形ABCD 内一点，点N 在AD 边上，且MB MN BMN 2900==∠，，点E 为MN 的中点，点P 为DE 的中点，连接MP 并延长到点F ，使得PF=PM ，连接DF （1）依题意补全图形 （2）求证：DF=BM（3）连接AM ，用等式表示线段PM 和AM 的数量关系并证明如图，正方形ABCD ，将边CD 绕点C 顺时针旋转60°，得到线段CE ，连接DE ，AE ，BD 交于点F （1）求∠AFB 的度数 （2）求证：BF=EF（3）连接CF ，直接用等式表示线段AB ，CF ，EF 的数量关系14 石景山在Rt △ABC 中，90ACB ∠=︒，2AC =，BC =，过点B 作直线l ∥AC ，将△ABC 绕点C 逆时针旋转得到△A B C ''，直线CA '，CB '分别交直线l 于点D E ，．（1）当点A '，D 首次重合时，①请在图1中，补全旋转后的图形； ②直接写出A CB '∠的度数； （2）如图2，若CD AB ⊥，求线段DE 的长；（3）求线段DE 长度的最小值．1（2019.1+++昌平+++初三上+++期末）（1）①圆心O 的位置在线段AB 的中点,正确画出图②∵AE ⊥BD ∴△AEB 为直角三角形 ∵点O 为线段AB 的中点 ∴OE =OA =OB =r ∴点E 在⊙O 上 （2）①补全图形=ABEA证明如下： ∵AC =BC ，∠ACB =90° ∴∠BAC =∠CBA = 45° ∵»»BCBC = ∴∠BEC =∠BAC = 45° ∵AE ⊥BD ∴∠BEA =90° ∴∠CEA =90°+ 45°= 135° ∵∠CEF =180°－∠CEB =135° ∴∠CEA =∠CEF ∵AE =EF ,∠CEA =∠CEF ,CE =C E ∴△CEA ≌△CEF ∴CF =CA ∵在等腰t ∆R ACB中，=AB∴=AB2（2019.1+++丰台+++初三上+++期末） （1）60° （2）1 （3）11AF BF n =- 证明：延长FE 至G ，使FG =FB 连接GB ，GC由（1）知，∠BFG=60° ∴△BFG 为等边三角形 ∴BF =BG ，∠FBG=∠FGB=60° ∵△ABC 是等边三角形 ∴AB=BC ，∠ABC=60°∴∠ABF=∠CBG ∴△ABF ≌△CBG∴∠BFA=∠BGC=120° ∴∠FGC=60° ∴∠FGC=∠BFG ∴FB ∥CG∴AF AD FG DC = ∵1AD AC n = ∴11AF FG n =- ∴11AF BF n =-3（2019.1+++海淀+++初三上+++期末） （1）①证明：连接AD ，如图1∵点C 与点D 关于直线l 对称 ∴AC AD = ∵AB AC = ∴AB AC AD ==∴点B C D ，，在以A 为圆心，AB 为半径的圆上CAE BD FlD A 图1②12α （2）证法一： 证明：连接CE ，如图2 ∵=60α°∴1302BDC α∠==° ∵DE BD ⊥ ∴90CDE ∠=°60BDC -∠=° ∵点C 与点D 关于直线l 对称 ∴EC ED = ∴CDE △是等边三角形∴CD CE =，60DCE ∠=° ∵AB AC =，60BAC ∠=° ∴ABC △是等边三角形 ∴CA CB =，60ACB ∠=° ∵ACE DCE ACD ∠=∠+∠，BCD ACB ACD ∠=∠+∠ ∴ACE BCD ∠=∠ ∴ACE BCD △≌△ ∴AE BD = 证法二：证明：连接AD ，如图2 ∵点C 与点D 关于直线l 对称∴AD AC AE CD =，⊥ ∴12DAE DAC ∠=∠∵12DBC DAC ∠=∠∴DBC DAE ∠=∠∵AE CD ⊥，BD DE ⊥∴90BDC CDE DEA CDE ∠+∠=∠+∠=°∴BDC DEA ∠=∠ ∵60AB AC BAC =∠=，° ∴ABC △是等边三角形 ∴CA CB AD == ∴BCD △≌ADE △ ∴AE BD = （3）134（2019.1+++怀柔+++初三上+++期末） （1）补全图形，如图所示（2）AH 与PH 的数量关系：AH =PH ，∠AHP =120° 证明：如图，由平移可知，PQ=DC ∵四边形ABCD 是菱形，∠ADC=60° ∴AD=DC ，∠ADB =∠BDQ =30° ∴AD=PQ∵HQ=HD ∴∠HQD =∠HDQ =30° ∴∠ADB =∠DQH ，∠D HQ=120°∴△ADH ≌△PQH ∴AH =PH ，∠A HD =∠P HQ ∴∠A HD+∠DHP =∠P HQ+∠DHP图2∴∠A HP=∠D HQ ∵∠D HQ=120° ∴∠A HP=120° （3）求解思路如下：由∠A HQ=141°，∠B HQ=60°解得∠A HB=81°a.在△ABH 中，由∠A HB=81°，∠A BD=30°，解得∠BA H=69°b.在△AHP 中，由∠A HP=120°，AH=PH ，解得∠PA H=30°c.在△ADB 中，由∠A DB=∠A BD= 30°，解得∠BAD =120° 由a 、b 、c 可得∠DAP =21°在△DAP 中，由∠A DP= 60°，∠DAP =21°，AD=1，可解△DAP ，从而求得DP 长5（2019.1+++通州+++初三上+++期末） （1）BF =（2）①依据题意补全图形 ②证明：如图，连接BF 、GB ∵四边形ABCD 是正方形∴AD =AB ，90ABC BAD ∠=∠=︒，AC 平分BAD ∠ ∴45BAC DAC ∠=∠=︒.在△ADF 和△ABF 中 AD AB DAC BAC AF AF =⎧⎪∠=∠⎨⎪=⎩，，，∴△ADF ≌△ABF ∴DF BF = ∵EF ⊥AC ，90ABC ∠=︒，点G 是AE 的中点 ∴AG EG BG FG === ∴点A 、F 、E 、B 在以点G 为圆心，AG 长为半径的圆上∵»»BFBF =，45BAC ∠=︒ ∴290BGF BAC ∠=∠=︒ ∴△BGF 是等腰直角三角形∴BF =∴DF =6（2019.1+++燕山+++初三上+++期末）(1) ① ∠BCE ＝35° ② AE ＝CEBE 证明：过点B 作BG ⊥BE ，交AM 于点G∴∠GBE ＝∠GBC ＋∠2＝90° ∵正方形ABCD ∴AB ＝BC ，∠ABC ＝∠1＋∠GBC ＝90° ∴∠1＝∠2A BCDP HQ∵∠ABC ＝∠CEA ＝90°，∠4＝∠5 ∴△ABF ∽△CEF∴∠α＝∠3 ∴在△ABG 和△CBE 中 ∠1＝∠2，AB ＝BC ，∠α＝∠3∴△ABG ≌△CBE ∴AG ＝CE ，BG ＝BE ∵在△BEG 中，∠GBE ＝90°，BG ＝BE ∴GE ＝2BE ∴AE ＝AG ＋GE ＝CE ＋2BE (2) AE ＋CE ＝2BE7（2019.1+++房山+++初三上+++期末） （1）补全图形如图分（2）证明:∵AD 平分∠BAC∴∠BAD =∠CAD ∵FE ⊥AD , ∠ACF =90°, ∠AHE =∠CHF ∴∠CFH =∠CAD ∴∠BAD =∠CFH , 即∠BAD =∠BFG（3）猜想: 222AB FD FB += 证明：连接AF∵EF 为AD 的垂直平分线 ∴AF=FD ，∠ ∴∠DAC +∠CAF =∠B +∠BAD ∵AD 是角平分线 ∴∠BAD =∠CAD ∴∠CAF =∠B ∴∠BAF =∠BAC +∠CAF =∠BAC +∠B =90° ∴222AB AF FB += ∴222+=AB FD FB8（2019.1+++门头沟+++初三上+++期末） （1）证明：如图1，∵ ∠ACB = 90°，AE ⊥BD ∴ ∠ACB =∠AEB = 90° 又∵ ∠1=∠2 ∴ ∠CAE =∠CBD （2）① 补全图形如图2HG FEDABC图1②2=+EF CE BE证明：在AE上截取AM，使AM=BE又∵AC=CB，∠CAE =∠CBD ∴△ACM≌△BCE∴CM=CE，∠ACM=∠BCE 又∵∠ACB =∠ACM+∠MCB=90°∴∠MCE=∠BCE+∠MCB=90°∴2.=ME CE又∵射线AE绕点A顺时针旋转45°，后得到AF，且∠AEF=90°∴EF=AE=AM+ME=BE+2CE9（2019.1+++朝阳+++初三上+++期末）10（2019.1+++西城+++初三上+++期末）11（2019.1+++大兴+++初三上+++期末）（1）补全的图形如图所示(2)解:由题意可知，∠ECF=∠ACG=90°∴∠FCG=∠ACE=α∵过点A作AB的垂线AD ∴∠BAD=90°∵AB=BC,∠ABC=90°∴∠ACB=∠CAD= 45° ∵∠ACG=90° ∴∠AGC=45° ∴∠AFC =α+45°（3）AE ,AF 与BC 之间的数量关系为2AE AF BC += 由（2）可知∠DAC=∠AGC=45° ∴CA=CG ∵∠ACE =∠GCF ，∠CAE =∠CGF ∴△ACE ≌△GCF ∴AE =FG 在Rt △ACG 中∴AG =∴AE AF +=∵AC = ∴2AE AF BC +=12（2019.1+++东城+++初三上+++期末）无答案27.解：（1）…………………………………………………………1分（2）∵点P 为线段DE 的中点 ∴DP ＝EP在△MPE 和△FPD 中 MP FP MPE FPD EP DP =⎧⎪∠=∠⎨⎪=⎩∴△MPE ≌△FPD （SAS ）…………………………………………………………2分 ∴DF ＝ME∵E 为MN 的中点 ∴MN ＝2ME ∵MN ＝2MB∴MB ＝ME＝D F ．…………………………………………………………3分（3）结论：AM = …………………………………………………………4分 连接AF由（2）可知：△MPE ≌△FPD ∴∠DFP ＝∠EMP. ∴DF ∥ME.∴∠FDN ＝∠MND.在正方形ABCD 中，AD ＝AB ，∠BAD ＝90° 又∵∠BMN ＝90°∴∠MBA ＋∠MNA ＝180° 又∵∠MNA ＋∠MND ＝180° ∴∠MBA ＝∠MND∴∠FDN ＝∠MBA …………………………………………………………5分 在△FAD 和△MAB 中 FD MB FDA MBA DA BA =⎧⎪∠=∠⎨⎪=⎩∴△F AD ≌△MAB （SAS ） ∴∠FAD ＝∠MAB FA ＝MA∴∠FAM＝∠DAB ＝90°∴△FAM 为等腰直角三角形…………………………………………………………6分 ∴FM =又∵FM ＝2PM∴ AM = …………………………………………………………7分13（2019.1+++平谷+++初三上+++期末）。
2019年全国中考数学真题分类汇编：几何综合探究题（压轴）
专题复习（八）几何综合探究题（压轴）类型1 类比探究的几何综合题类型2 与图形变换有关的几何综合题类型3 与动点有关的几何综合题类型4 与实际操作有关的几何综合题类型5 其他类型的几何综合题类型1 类比探究的几何综合题（2019河南）（2019吉林）（2019烟台）（2019广西北部湾）（2019武汉）在△ABC 中，∠ABC ＝90°，，M 是BC 上一点，连接AM n BCAB =(1) 如图1，若n ＝1，N 是AB 延长线上一点，CN 与AM 垂直，求证：BM ＝BN(2) 过点B 作BP ⊥AM ，P 为垂足，连接CP 并延长交AB 于点Q① 如图2，若n ＝1，求证：BQBM PQ CP =② 如图3，若M 是BC 的中点，直接写出tan ∠BPQ 的值（用含n 的式子表示）（2019襄阳）（2019常德）（2019岳阳）（2019 德州）（2019 青岛）23．（本小题满分10 分）问题提出：如图，图①是一张由三个边长为 1 的小正方形组成的“L”形纸片，图②是一张a⨯b 的方格纸（a⨯ b的方格纸指边长分别为a，b 的矩形，被分成a⨯b个边长为 1 的小正方形，其中a≥2 ，b≥2，且a，b 为正整数）．把图①放置在图②中，使它恰好盖住图②中的三个小正方形，共有多少种不同的放置方法？问题探究：为探究规律，我们采用一般问题特殊化的策略，先从最简单的情形入手，再逐次递进，最后得出一般性的结论．探究一：把图①放置在 2 ⨯2的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？如图③，对于2⨯2的方格纸，要用图①盖住其中的三个小正方形，显然有4 种不同的放置方法．探究二：把图①放置在3⨯2的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？如图④，在3⨯2的方格纸中，共可以找到 2 个位置不同的 2 2 ⨯方格，依据探究一的结论可知，把图①放置在3⨯2 的方格纸中，使它恰好盖住其中的三个小正方形，共有2 ⨯ 4＝8种不同的放置方法．探究三：把图①放置在 a ⨯ 2 的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？如图⑤，在 a ⨯ 2 的方格纸中，共可以找到_________个位置不同的2⨯2方格，依据探究一的结论可知，把图①放置在 a ⨯ 2 的方格纸中，使它恰好盖住其中的三个小正方形，共有_________种不同的放置方法．探究四：把图①放置在 a ⨯ 3 的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？如图⑥，在a⨯ 3 的方格纸中，共可以找到_________个位置不同的2⨯ 2方格，依据探究一的结论可知，把图①放置在 a ⨯ 3 的方格纸中，使它恰好盖住其中的三个小正方形，共有_________种不同的放置方法．……问题解决：把图①放置在 a ⨯ b的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？（仿照前面的探究方法，写出解答过程，不需画图．）问题拓展：如图，图⑦是一个由 4 个棱长为 1 的小立方体构成的几何体，图⑧是一个长、宽、高分别为a，b ，c （a≥2 ，b≥2 ，c≥2 ，且a，b，c 是正整数）的长方体，被分成了 a ⨯b ⨯c 个棱长为 1 的小立方体．在图⑧的不同位置共可以找到_________个图⑦这样的几何体．答案：（2019 威海）（2019 台州）（2019 绍兴）答案：（2019 绍兴）答案：（2019 嘉兴）23．小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．(1)温故：如图 1，在△中，⊥ 于点，正方形 的边在上，顶点 ， 分ABC AD BC D PQMN QM BC P N 别在，AB 上，若 ，，求正方形 的边长．AC 6BC =4AD =PQMN (2)操作：能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作：如图 2，任意画△，在上任取一点，画正方形 ，使，在边上， 在△ 内，连结 并延ABC AB P 'P Q M N ''''Q 'M 'BC N 'ABC BN '长交 于点N ，画⊥于点，⊥ 交于点，⊥ 于点，得到四边形AC NM BC M NP NM AB P PQ BC QP ．小波把线段 称为“波利亚线”．PQMN BN (3)推理：证明图2 中的四边形 是正方形．PQMN (4)拓展：在(2)的条件下，于波利业线 上截取 ，连结 ，(如图 3)．当 BN NE NM -EQ EM 3tan 4NBM ∠=时，猜想∠的度数，并尝试证明．QEM 请帮助小波解决“温故”、“推理”、“拓展”中的问题．答案：（2019 南京）答案：（2019 连云港）27．(本题满分14分)问题情境：如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），垂直于AE 的一条直线MN分别交AB、AE、CD于点M、P、N．判断线段DN、MB、EC之间的数量关系，并说明理由．问题探究：在“问题情境”的基础上，（1）如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ，并延长交边AD于点F．求∠AEF 的度数；（2）如图3，当垂足P 在正方形ABCD 的对角线BD 上时，连接AN ，将△APN 沿着AN 翻折，点P 落在点P'处．若正方形ABCD 的边长为4 ，AD 的中点为S ，求P'S 的最小值．问题拓展：如图4，在边长为4的正方形ABCD 中，点M 、N 分别为边AB 、CD 上的点，将正方形ABCD 沿着MN 翻折，使得BC 的对应边B'C'恰好经过点A ，C'N 交AD 于点F ．分别过点A 、F 作AG ⊥MN ，FH ⊥MN ，垂足分别为G 、H ．若AG ＝，请直接写出FH 的长．52答案：（2019淄博）（2019贵港）（2019齐齐哈尔）（2019绥化）（2019黑龙江龙东）1.（2019德州）（1）如图1，菱形AEGH的顶点E、H在菱形ABCD的边上，且∠BAD=60°，请直接写出HD：GC：EB的结果（不必写计算过程）（2）将图1中的菱形AEGH绕点A旋转一定角度，如图2，求HD：GC：EB；（3）把图2中的菱形都换成矩形，如图3，且AD：AB=AH：AE=1：2，此时HD：GC：EB的结果与（2）小题的结果相比有变化吗？如果有变化，直接写出变化后的结果（不必写计算过程）；若无变化，请说明理由．解：（1）连接AG，∵菱形AEGH的顶点E、H在菱形ABCD的边上，且∠BAD=60°，∴∠GAE=∠CAB=30°，AE=AH，AB=AD，∴A，G，C共线，AB-AE=AD-AH，∴HD=EB，延长HG交BC于点M，延长EG交DC于点N，连接MN，交GC于点O，则GMCN也为菱形，∴GC⊥MN，∠NGO=∠AGE=30°，∴=cos30°=，∵GC=2OG，∴=，∵HGND为平行四边形，∴HD=GN，∴HD：GC：EB=1：：1．（2）如图2，连接AG，AC，∵△ADC和△AHG都是等腰三角形，∴AD：AC=AH：AG=1：，∠DAC=∠HAG=30°，∴∠DAH=∠CAG，∴△DAH∽△CAG，∴HD：GC=AD：AC=1：，∵∠DAB=∠HAE=60°，∴∠DAH=∠BAE，在△DAH和△BAE中，∴△DAH≌△BAE（SAS）∴HD=EB，∴HD：GC：EB=1：：1．（3）有变化．如图3，连接AG，AC，∵AD：AB=AH：AE=1：2，∠ADC=∠AHG=90°，∴△ADC∽△AHG，∴AD：AC=AH：AG=1：，∵∠DAC=∠HAG，∴∠DAH=∠CAG，∴△DAH∽△CAG，∴HD：GC=AD：AC=1：，∵∠DAB=∠HAE=90°，∴∠DAH=∠BAE，∵DA：AB=HA：AE=1：2，∴△ADH∽△ABE，∴DH：BE=AD：AB=1：2，∴HD：GC：EB=1：：2类型2 与图形变换有关的几何综合题（2019十堰）（2019山西），把△ADE 沿D E翻折，点A的对应（2019郴州）如图1，矩形A BCD 中，点E为A B 边上的动点（不与A，B 重合）点为A1 ，延长EA1交直线D C 于点F，再把∠BEF 折叠，使点B的对应点B1落在E F 上，折痕EH 交直线B C 于点H．（1）求证：△A1DE∽△B1EH；（2）如图2，直线M N 是矩形A BCD 的对称轴，若点A1恰好落在直线M N 上，试判断△DEF 的形状，并说明理由；（3）如图3，在（2）的条件下，点G为△DEF 内一点，且∠DGF=150°，试探究DG，EG，FG 的数量关系．图1 图2 图3（2019淮安）（2019吉林）（2019包头）（2019自贡）25.（本题满分12分）（1）如图1，E 是正方形ABCD 边AB 上的一点，连接BD 、DE ，将∠BDE 绕点D 逆时针旋转90°，旋转后角的两边分别与射线BC 交于点F 和点G .①线段DB 和DG 之间的数量关系是 DB=DG ；②写出线段BE ，BF 和DB 之间的数量关系.BDBF BE 2=+（2）当四边形ABCD 为菱形，∠ADC =60°，点E 是菱形ABCD 边AB 所在直线上的一点，连接BD 、DE ，将∠BDE 绕点D 逆时针旋转120°，旋转后角的两边分别与射线BC 交于点F 和点G .①如图2，点E 在线段AB 上时，请探究线段BE 、BF 和BD 之间的数量关系，写出结论并给出证明；②如图3，点E 在线段AB 的延长线上时，DE 交射线BC 于点M ，若BE =1，AB =2，直接写出线段GM 的长度.图1图2 图3（2）①BDBF BE 3=+理由如下：在菱形ABCD 中，∠ABD=∠CBD=∠ABC=30°，由旋转120°可得，∠EDF=∠BDG=120°，∴∠EDF-21∠BDF=∠BDG-∠BDF ，即∠FDG=∠BDE.在△DBG 中，∠G=180°-∠BDG-∠DBG=30°，∴∠DBG=∠G=30°，∴BD=DG.在△BDE 和△GDF 中∴△BDE ≌△△GDF （ASA ），∴BE=GF⎪⎩⎪⎨⎧∠=∠=∠=∠DGF DBE DG BD BDE GDF ∴BE+BF=BF+GF=BG.过点D 作DM ⊥BG 于点M 如图所示：∵BD=DG ，∴BG=2BM.在Rt △BMD 中，∠DBM=30°，∴BD=2DM ，设DM=a ，则BD=2a ，BM=.∴BG=，∴a 3a 323232==aa BD BG ∴BF+BE=BD.3②GM 的长度为.理由：∵，FC=2DC=4，CM=BC=，∴GM=3191==BE GF 3234319（2019济宁）（2019 金华）24.如图，在等腰Rt△ABC中，∠ACB=90°，AB=14 。
2019届中考数学总复习：几何综合问题
题能力的探究性的问题、方案设计的问题等等
. 主要特点是图形较复杂，覆盖面广、涉及的知识点较多，
题设和结论之间的关系较隐蔽，常常需要添加辅助线来解答
.
几何综合题的呈现形式多样，如折叠类型、探究型、开放型、运动型、情景型等，背景鲜活，具有
实用性和创造性，考查方式偏重于考查考生分析问题、探究问题、综合应用数学知识解决实际问题的能
AP
时，△ PAQ∽△ ABC，则有：
BC AB
6 t 2t
，解得 t=3 （ s），
6 12
即当 t=3s 时，△ PAQ∽△ ABC；
所以，当 t=1.2s 或 3s 时，以点 Q、 A、 P 为顶点的三角形与△ ABC相似．
【总结升华】 本题是动态几何题，同时也是一道探究题．要求学生具有一定的发现、归纳和表达能力，
.
【答案与解析】
解：（1）对于任何时刻 t ， AP=2t ，DQ=t， QA=6-t ．
当 QA=AP时，△ QAP为等腰直角三角形，即 6-t=2t ，解得： t=2 （s），
所以，当 t=2s 时，△ QAP为等腰直角三角形．
（ 2）在△ QAC中， QA=6-t ， QA边上的高 DC=12，
1
1
∴ S△QAC= QA?DC= （6-t ）?12=36-6t ．
2
2
在△ APC中， AP=2t， BC=6，
1
1
∴ S△APC= AP?BC= ?2t ?6=6t ．
2
2
∴ S 四边形 QAPC=S△QAC+S△ APC=（ 36-6t ） +6t=36 （ cm2）．
由计算结果发现：在 P、 Q两点移动的过程中，四边形
2019届中考数学总复习：几何综合问题
2019届中考数学总复习：几何综合问题【中考展望】几何综合题是中考试卷中常见的题型，大致可分为几何计算型综合题与几何论证型综合题，它主要考查学生综合运用几何知识的能力.这类题型在近几年全国各地中考试卷中占有相当的分量，不仅有选择题、填空题、几何推理计算题以及代数与几何的综合计算题,还有更注重考查学生分析问题和解决问题能力的探究性的问题、方案设计的问题等等.主要特点是图形较复杂，覆盖面广、涉及的知识点较多，题设和结论之间的关系较隐蔽，常常需要添加辅助线来解答.几何综合题的呈现形式多样，如折叠类型、探究型、开放型、运动型、情景型等，背景鲜活，具有实用性和创造性，考查方式偏重于考查考生分析问题、探究问题、综合应用数学知识解决实际问题的能力.以几何为主的综合题常常在一定的图形背景下研究以下几个方面的问题：1、证明线段、角的数量关系（包括相等、和、差、倍、分及比例关系等）；2、证明图形的位置关系（如点与线、线与线、线与圆、圆与圆的位置关系等）；3、几何计算问题；4、动态几何问题等.【方法点拨】一、几何计算型综合问题，常常涉及到以下各部分的知识：1、与三角形有关的知识；2、等腰三角形，等腰梯形的性质；3、直角三角形的性质与三角函数；4、平行四边形的性质；5、全等三角形，相似三角形的性质；6、垂径定理，切线的性质，与正多边形有关的计算；7、弧长公式与扇形面积公式.二、几何论证型综合题的解答过程，要注意以下几个方面：1、注意图形的直观提示，注意观察、分析图形，把复杂的图形分解成几个基本图形，通过 添加辅助线补全或构造基本图形；2、注意分析挖掘题目的隐含条件、发展条件，为解题创造条件打好基础，要由已知联想经 验，由未知联想需要，不断转化条件和结论来探求思路，找到解决问题的突破点；3、要运用转化的思想解决几何证明问题，运用方程的思想解决几何计算问题，还要灵活运用 数学思想方法如数形结合、分类讨论、转化、方程等思想来解决问题.【典型例题】类型一、动态几何型问题1．如图，在矩形ABCD 中，AB=12cm ，BC=6cm ，点P 沿AB 边从点A 开始向点B 以2cm/s 的速度移动；点Q 沿DA 边从点D 开始向点A 以1cm/s 的速度移动.如果P 、Q 同时出发，用t(s)表示移动的时间（0≤t ≤6），那么：⑴当t 为何值时，△QAP 为等腰直角三角形？⑵求四边形QAPC 的面积；提出一个与计算结果有关的结论；⑶当t 为何值时，以点Q 、A 、P 为顶点的三角形与△ABC 相似？D AB C QP【思路点拨】⑴中应由△QAP 为等腰直角三角形这一结论，需补充条件AQ=AP ，由AQ=6－t ，AP=2t ，可求出t 的值；⑵中四边形QAPC 是一个不规则图形，其面积可由矩形面积减去△DQC 与△PBC 的面积求出；⑶中由于题目中未给出三角形的相似对应方式，因此需分类讨论. 【答案与解析】解：（1）对于任何时刻t ，AP=2t ，DQ=t ，QA=6-t ．当QA=AP 时，△QAP 为等腰直角三角形，即6-t=2t ，解得：t=2（s ），所以，当t=2s 时，△QAP 为等腰直角三角形．（2）在△QAC 中，QA=6-t ，QA 边上的高DC=12，∴S △QAC =12QA •DC=12（6-t ）•12=36-6t ． 在△APC 中，AP=2t ，BC=6， ∴S △APC =12AP •BC=12•2t •6=6t ． ∴S 四边形QAPC =S △QAC +S △APC =（36-6t ）+6t=36（cm 2）．由计算结果发现：在P 、Q 两点移动的过程中，四边形QAPC 的面积始终保持不变．（也可提出：P 、Q 两点到对角线AC 的距离之和保持不变）（3）根据题意，可分为两种情况，在矩形ABCD 中：①当QA AP AB BC=时，△QAP ∽△ABC ，则有： 62126t t -=，解得t=1.2（s ）， 即当t=1.2s 时，△QAP ∽△ABC ；②当QA AP BC AB=时，△PAQ ∽△ABC ，则有： 62612t t -=，解得t=3（s ）， 即当t=3s 时，△PAQ ∽△ABC ；所以，当t=1.2s 或3s 时，以点Q 、A 、P 为顶点的三角形与△ABC 相似．【总结升华】本题是动态几何题，同时也是一道探究题．要求学生具有一定的发现、归纳和表达能力，这就要求我们通过计算分析，抓住其本质，揭示出变中不变的规律．四边形QAPC 的面积也可由△QAC 与△CAP 的面积求出，；⑶中考查了分类讨论的数学思想，结论具有一定的开放性.2．（永春县校级月考）如图，在梯形ABCD 中，AD ∥BC ，AD=3，CD=5，BC=10，梯形的高为4，动点M 从点B 出发沿线段BC 以每秒2个单位长度向终点C 运动；动点N 同时从点C 出发沿线段CD 以每秒1个单位长度的速度向终点D 运动．设运动的时间为t 秒（1）直接写出梯形ABCD 的中位线长；（2）当MN ∥AB 时，求t 的值；（3）试探究：t 为何值时，使得MC=MN ．【思路点拨】（1）直接利用梯形中位线的定理求出即可；（2）平移梯形的一腰，根据平行四边形的性质和相似三角形的性质求解；（3）利用MC=MN时，结合路程=速度×时间求得其中的有关的边，运用等腰三角形的性质和解直角三角形的知识求解．【答案与解析】解：（1）∵AD=3，BC=10，∴梯形ABCD的中位线长为：（3+10）÷2=6.5；（2）如图1，过D作DG∥AB交BC于G点，则四边形ADGB是平行四边形．∵MN∥AB，∴MN∥DG，∴BG=AD=3．∴GC=10﹣3=7．由题意知，当M、N运动到t秒时，CN=t，CM=10﹣2t．∵DG∥MN，∴△MNC∽△GDC．∴=，即=．解得，t=；（3）当MC=MN时，如图2，过M作MF⊥CN于F点，FC=NC=t．∵∠C=∠C，∠MFC=∠DHC=90°，∴△MFC∽△DHC，∴=，即=，解得：t=．综上所述，t=时，MC=MN．【总结升华】解决动点问题，首先就是要找谁在动，谁没动，通过分析动态条件和静态条件之间的关系求解，但是对于大多数题目来说，都有一个由动转静的拐点.3.（2016秋•泗阳县期末）（1）已知：如图1，△ABC为等边三角形，点D为BC边上的一动点（点D 不与B 、C 重合），以AD 为边作等边△ADE ，连接CE ．求证：①BD=CE ，②AC=CE+CD ；聪明的小明做完上题后进行了进一步变式探究．（2）如图2，在△ABC 中，∠BAC=90°，AC=AB ，点D 为BC 上的一动点（点D 不与B 、C 重合），以AD 为边作等腰Rt △ADE ，∠DAE=90°（顶点A 、D 、E 按逆时针方向排列），连接CE ，类比题（1），请你猜想线段BD 、CD 、DE 之间会有怎样的关系，请直接写出，不需论证；（3）如图3，在（2）的条件下，若D 点在BC 的延长线上运动，以AD 为边作等腰Rt △ADE ，∠DAE=90°（顶点A 、D 、E 按逆时针方向排列），连接CE ．①题（2）的结论还成立吗？请说明理由；②连结BE ，若BE=10，BC=6，求AE 的长．【思路点拨】（1）①根据等边三角形的性质就可以得出∠BAC=∠DAE=60°，AB=BC=AC ，AD=DE=AE ，进而就可以得出△ABD ≌△ACE ，即可得出结论；②由△ABD ≌△ACE ，以及等边三角形的性质，就可以得出AC=DC+CE ；（2）先判定△ABD ≌△ACE （SAS ），得出∠B=∠ACE=45°，BD=CE ，在Rt △DCE 中，根据勾股定理得出CE 2+CD 2=DE 2，即可得到BD 2+CD 2=DE 2；（3）①运用（2）中的方法得出BD 2+CD 2=DE 2；②根据Rt △BCE 中，BE=10，BC=6，求得CE=22106-=8，进而得出CD=8﹣6=2，在Rt △DCE 中，求得DE=2228+=，最后根据△ADE 是等腰直角三角形，即可得出AE 的长．【答案与解析】解：（1）①如图1，∵△ABC 和△ADE 是等边三角形，∴∠BAC=∠DAE=60°，AB=BC=AC ，AD=DE=AE ，∴∠BAC ﹣∠DAC=∠DAE ﹣∠DAC ，∴∠BAD=∠EAC ．在△ABD 和△ACE 中，，∴△ABD ≌△ACE （SAS ），∴BD=CE ；②∵BD=CE ，AC=BC ，又∵BC=BD+CD ，∴AC=CE+CD ；（2）BD 2+CD 2=DE 2．证明：如图2，∵∠BAC=∠DAE=90°，∴∠BAC ﹣∠DAC=∠DAE ﹣∠DAC ，即∠BAD=∠CAE ，在△ABD 与△ACE 中，，∴△ABD ≌△ACE （SAS ），∴∠B=∠ACE=45°，BD=CE ，∴∠B+∠ACB=∠ACE+∠A CB=90°，∴∠BCE=90°，∴Rt △DCE 中，CE 2+CD 2=DE 2，∴BD 2+CD 2=DE 2；（3）①（2）中的结论还成立．理由：如图3，∵∠BAC=∠DAE=90°，∴∠BAC+∠DAC=∠DAE+∠DAC ，即∠BAD=∠CAE ，在△ABD 与△ACE 中，，∴△ABD ≌△ACE （SAS ），∴∠ABC=∠ACE=45°，BD=CE ，∴∠ABC+∠ACB=∠ACE+∠ACB=90°，∴∠BCE=90°=∠ECD ，∴Rt △DCE 中，CE 2+CD 2=DE 2，∴BD 2+CD 2=DE 2；②∵Rt △BCE 中，BE=10，BC=6，∴22106-=8，∴BD=CE=8，∴CD=8﹣6=2，∴Rt △DCE 中，2228+68∵△ADE 是等腰直角三角形，∴683422== 【总结升华】本题属于三角形综合题，主要考查了全等三角形的判定与性质，等边三角形的性质，等腰直角三角形的性质以及勾股定理的综合应用.举一反三：【变式】△ABC 是等边三角形，P 为平面内的一个动点，BP=BA ，若0︒＜∠PBC ＜180°，且∠PBC 平分线上的一点D 满足DB=DA ，（1）当BP 与BA 重合时（如图1），∠BPD= °；（2）当BP 在∠ABC 的内部时（如图2），求∠BPD 的度数；（3）当BP 在∠ABC 的外部时，请你直接写出∠BPD 的度数，并画出相应的图形．【答案】（1）∠BPD= 30°；（2）如图3，连结CD ．∵ 点D 在∠PBC 的平分线上，∴ ∠1=∠2．∵ △ABC 是等边三角形，∴ BA=BC=AC ，∠ACB= 60°．∵ BP=BA ，∴ BP=BC ．∵ BD= BD ，∴ △PBD ≌△CBD ．∴ ∠BPD=∠3．∵ DB=DA ，BC=AC ，CD=CD ，∴ △BCD ≌△ACD ．∴ 134302ACB ∠=∠=∠=︒．∴ ∠BPD =30°．（3）∠BPD= 30°或 150°.类型二、几何计算型问题【高清课堂：几何综合问题 例1 】 4.如图，直角三角形纸片ABC 中，∠ACB=90°，AC=8，BC=6．折叠该纸片使点B 与点C 重合，折痕与AB 、BC 的交点分别为D 、E.(1) DE 的长为 ；(2) 将折叠后的图形沿直线AE 剪开，原纸片被剪成三块，其中最小一块的面积等于 ．【思路点拨】（1）由题意可得：DE是线段BC的垂直平分线，易证DE∥AC，即DE是△ABC的中位线，即可求得DE的长；（2）由DE∥AC，DE=12AC，易证△AOC∽△EOD，根据相似三角形的对应边成比例，即可求得OA：OE=2，然后求得△ACE的面积，利用等高三角形的面积比等于对应底的比，即可求得答案．【答案与解析】（1）根据题意得：DE⊥BC，CE=BE，∵∠ACB=90°，即AC⊥BC，∴DE∥AC，∴AD=BD，∴DE=12AC=12×8=4；（2）∵DE∥AC，DE=12 AC，∴△AOC∽△EOD，∴OA：OE=AC：DE=2，∵CE=12BC=12×6=3，∵∠ACB=90°，AC=8，∴S△ACE=12CE•AC=12×3×8=12，∴S△OCE=13S△ACE=4，∴S△ADE+S△ODE=S△ABC-4-12=8，∴其中最小一块的面积等于4．【总结升华】考查了折叠的性质、直角三角形的性质、三角形中位线的性质以及相似三角形的判定与性质．此题难度适中，注意数形结合思想的应用，注意掌握折叠前后图形的对应关系,是一道典型的几何综合题．举一反三【变式】在边长为2的菱形ABCD中，∠B=45°，AE为BC边上的高，将△ABE沿AE所在直线翻折得△AB′E，那么△AB′E与四边形AECD重叠部分的面积是 . 【答案】在Rt△ABE中，∵∠B=45°，AB=2，∴AE=BE=2，∴S△ABE=1．由翻折的性质可知：△AB′E≌△ABE，∴EB′=EB=2∴B′C=BB′－BC=22－2，∵四边形ABCD是菱形，∴CF∥BA．∴∠ B′FC=∠B′AB=90°, ∠B′CF=∠B=45°∴CF=2'=2-22B C，∴SB FC△'=221CF=3－22∴S阴=SB E′△A －SB FC′△=22－2．5．如图，在等腰梯形ABCD中，AB∥DC，∠A=45°，AB=10 cm，CD=4 cm，等腰直角△PMN的斜边MN=10 cm， A点与N点重合， MN和AB在一条直线上，设等腰梯形ABCD不动，等腰直角△PMN沿AB所在直线以1 cm／s的速度向右移动，直到点N与点B重合为止.(1)等腰直角△PMN在整个移动过程中与等腰梯形ABCD重叠部分的形状由________形变化为________形；(2)设当等腰直角△PMN移动x (s)时，等腰直角△PMN与等腰梯形ABCD重叠部分的面积为y(cm2)，求y 与x之间的函数关系式；(3)当x=4 (s)时，求等腰直角△PMN与等腰梯形ABCD重叠部分的面积.【思路点拨】（1）根据已知求出∠PNM=∠DAB=45°，求出∠AEN，根据等腰直角三角形的判定判断即可；推出∠DAB=∠PNM=45°，根据等腰梯形的判定判断即可；（2）可分为以下两种情况：①当0＜x≤6时，重叠部分的形状为等腰直角△EAN，AN=x（cm），过点E作EH⊥AB于点H，则EH平分AN，求出EH，根据三角形的面积公式求出即可；②当6＜x≤10时，重叠部分的形状是等腰梯形ANED，求出AN=x（cm），CE=BN=10-x，DE=x-6，过点D作DF⊥AB于F，过点C作CG⊥AB于G，求出DF，代入梯形面积公式求出即可.【答案与解析】(1)等腰直角三角形；等腰梯形.(2)等腰直角△PMN在整个移动过程中与等腰梯形ABCD重合部分图形的形状可分为以下两种情况：①当0＜x≤6时，重叠部分的形状为等腰直角△EAN(如图①).此时AN=x(cm)，过点E作EH⊥AB于点H，则EH平分AN，∴EH=AN=x，∴y=S△ANE=AN·EH=x·x=.②当6＜x≤10时，重叠部分的形状是等腰梯形ANED(如图②)．此时，AN=x(cm)，∵∠PNM=∠B=45°，∴EN∥BC，∵CE∥BN，∴四边形ENBC是平行四边形，CE=BN=10-x，DE=4-(10-x)=x-6，过点D作DF⊥AB于F，过点C作CG⊥AB于G，则AF=BG，DF=AF=(10-4)=3，∴y=S梯形ANED=(DE+AN)·DF=(x-6+x)×3=3x-9.综上，.(3)当等腰直角△PMN运动到PN边经过点D时，移动时间为6(s)，∴当x=4 (s)时，y=x2=×42=4.∴当x=4 (s)时，等腰直角△PMN与等腰梯形ABCD重叠部分的面积是4cm2.【总结升华】本题主要考查对等腰梯形的性质和判定，等腰三角形的性质和判定，三角形的内角和定理，三角形的面积，平移的性质，等腰直角三角形等知识点的理解和掌握，综合运用这些性质进行推理和计算是解此题的关键．举一反三：【变式】如图，等腰梯形ABCD中，AB=15，AD=20，∠C=30°．点M、N同时以相同速度分别从点A、点D开始在AB、AD(包括端点)上运动.(1)设ND的长为x，用x表示出点N到AB的距离，并写出x的取值范围；(2)当五边形BCDNM面积最小时，请判断△AMN的形状.【答案】(1)过点N作BA的垂线NP，交BA的延长线于点P.则AM=x，AN=20-x.∵四边形ABCD是等腰梯形，AB∥CD，∠D=∠C=30°，∴∠PAN=∠D=30°.在Rt△APN中，PN=AN×sin∠PAN=(20-x)，即N到AB距离为(20-x).∵点N在AD上，0≤x≤20，点M在AB上，0≤x≤15，∴x取值范围是0≤x≤15.(2)∵S五边形BCDNM=S梯形-S△AMN且S梯形为定值，∴当S五边形BCDMN最小时，应使S△AMN最大据(1)，S△AMN=AM·NP=.∵＜0，∴当x=10时，S△AMN有最大值.∴当x=10时，S五边形BCDNM有最小值．当x=10时，即ND=AM=10，AN=AD-ND=10，即AM=AN．则当五边形BCDNM面积最小时，△AMN为等腰三角形.【巩固练习】一、选择题1.（2016•天水）如图，边长为2的等边△ABC和边长为1的等边△A′B′C′，它们的边B′C′，BC位于同一条直线l上，开始时，点C′与B重合，△ABC固定不动，然后把△A′B′C′自左向右沿直线l 平移，移出△ABC外（点B′与C重合）停止，设△A′B′C′平移的距离为x，两个三角形重合部分的面积为y，则y关于x的函数图象是（）A．B． C． D．2.如图，将直角三角形ABC沿着斜边AC的方向平移到△DEF的位置（A、D、C、F四点在同一条直线上）．直角边DE交BC于点G．如果BG=4，EF=12，△BEG的面积等于4，那么梯形ABGD的面积是（）A.16B.20C.24D.28二、填空题3.（2016•海淀区二模）据传说，古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理，在金字塔影子的顶部立一根木杆，借助太阳光线构成两个相似三角形，来测量金字塔的高度．如图所示，木杆EF 的长为2m，它的影长FD为3m，测得OA为201m，则金字塔的高度BO为 m．4.如图，线段AB=8cm，点C是AB上任意一点（不与点A、B重合），分别以AC、BC为斜边在AB的同侧作等腰直角三角形（△AMC和△CNB），则当BC=_____________cm时，两个等腰直角三角形的面积和最小．三、解答题5.有一根直尺的短边长2cm，长边长10cm，还有一块锐角为45°的直角三角形纸板，它的斜边长12cm．如图①，将直尺的短边DE与直角三角形纸板的斜边AB重合，且点D与点A重合；将直尺沿AB方向平移（如图②），设平移的长度为xcm（0≤x≤0 ），直尺和三角形纸板的重叠部分（图中阴影部分）的面积为Scm2．（1）当x=0时（如图①），S=________；（2）当0＜x≤4时（如图②），求S关于x的函数关系式；（3）当4＜x＜6时，求S关于x的函数关系式；（4）直接写出S的最大值．6. 问题情境：如图①，在△ABD与△CAE中，BD=AE，∠DBA=∠EAC，AB=AC，易证：△ABD≌△CAE．（不需要证明）特例探究：如图②，在等边△ABC中，点D、E分别在边BC、AB上，且BD=AE，AD与CE交于点F．求证：△ABD≌△CAE．归纳证明：如图③，在等边△ABC中，点D、E分别在边CB、BA的延长线上，且BD=AE．△ABD与△CAE 是否全等？如果全等，请证明；如果不全等，请说明理由．拓展应用：如图④，在等腰三角形中，AB=AC，点O是AB边的垂直平分线与AC的交点，点D、E分别在OB、BA的延长线上．若BD=AE，∠BAC=50°，∠AEC=32°，求∠BAD的度数．7.如图正三角形ABC的边长为6cm,⊙O的半径为rcm，当圆心O从点A出发，沿着线路AB－BC－CA运动，回到点A时，⊙O随着点O的运动而移动.⑴若r=3cm,求⊙O首次与BC边相切时，AO的长；⑵在⊙O移动过程中，从切点的个数来考虑，相切有几种不同的情况？写出不同情况下r的取值范围及相应的切点的个数；⑶设⊙O在整个移动过程中，在△ABC内部，⊙O未经过的部分面积为S，在S＞0时，求关于r的函数解析式，并写出自变量r的取值范围.A(O)OB C8.（2015•德州）（1）问题：如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°，求证：AD•BC=AP•BP．（2）探究：如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．（3）应用：请利用（1）（2）获得的经验解决问题：如图3，在△ABD中，AB=6，AD=BD=5，点P以每秒1个单位长度的速度，由点A出了，沿边AB向点B运动，且满足∠DPC=∠A，设点P的运动时间为t（秒），当以D为圆心，以DC为半径的圆与AB 相切时，求t的值．9.如图，直角梯形ABCD中，AD∥BC，∠B=90°，AB=12 cm，BC=9 cm，DC=13 cm，点P是线段AB上一个动点.设BP为x cm，△PCD的面积为y cm2．(1)求AD 的长；(2)求y与x之间的函数关系式，并求出当x为何值时，y有最大值？最大值是多少？(3)在线段AB上是否存在点P，使得△PCD是直角三角形？若存在，求出x的值；若不存在，请说明理由.10.如图，平行四边形ABCD中，AB=10，AD=6，∠A=60°，点P从点A出发沿边线AB—BC以每秒1个单位长的速度向点C运动，当P与C重合时停下运动，过点P作AB的垂线PQ交AD或DC于Q.设P运动时间为t秒，直线PQ扫过平行四边形ABCD的面积为S.求S关于t的函数解析式.【答案与解析】一、选择题1.【答案】B.【解析】如图1所示：当0＜x≤1时，过点D作DE⊥BC′．∵△ABC和△A′B′C′均为等边三角形，∴△DBC′为等边三角形．∴DE=32BC′=32x．∴y=12BC′•DE=34x2．当x=1时，y=34，且抛物线的开口向上．如图2所示：1＜x≤2时，过点A′作A′E⊥B′C′，垂足为E．∵y=12B′C′•A′E=12×1×32=34．∴函数图象是一条平行与x轴的线段．如图3所示：2＜x≤3时，过点D作DE⊥B′C，垂足为E．y=12B′C•DE=34（x﹣3）2，函数图象为抛物线的一部分，且抛物线开口向上．故选：B．2.【答案】B.二、填空题3.【答案】134.4.【答案】4.三、解答题5.【答案与解析】（1）由题意可知：当x=0时，∵△ABC是等腰直角三角形，∴AE=EF=2，则阴影部分的面积为：S=12×2×2=2；故答案为：2；（2）在Rt△ADG中，∠A=45°，∴DG=AD=x，同理EF=AE=x+2，∴S梯形DEFG=12（x+x+2）×2=2x+2．∴S=2x+2；（3）①当4＜x＜6时（图1），GD=AD=x，EF=EB=12-（x+2）=10-x，则S△ADG=12AD•DG=12x2，S△BEF=12（10-x）2，而S△ABC=12×12×6=36，6.【答案与解析】特例探究：证明：∵△ABC 是等边三角形，∴AB=AC ，∠DBA=∠EAC=60°，在△ABD 与△CAE 中， AB CA DBA EAC BD AE =⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△CAE （SAS ）；归纳证明：△ABD 与△CAE 全等．理由如下：∵在等边△ABC 中，AB=AC ，∠ABC=∠BAC=60°， ∴∠DBA=∠EAC=120°． 在△ABD 与△CAE 中，AB CA DBA EAC BD AE =⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△CAE （SAS ）；拓展应用：∵点O 在AB 的垂直平分线上，∴OA=OB ，∴∠OBA=∠BAC=50°，∴∠EAC=∠DBC ．在△ABD 与△CAE 中，AB CA DBA EAC BD AE=⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△CAE （SAS ），∴∠BDA=∠AEC=32°，∴∠BAD=∠OBA-∠BDA=18°．7.【答案与解析】(1).设⊙O 首次与BC 相切于点D ，则有OD ⊥BC ．在直角三角形BDO 中，∵∠OBD=60°，∴OB=03sin 60=2． ∴AO=AB-OB=6-2=4（厘米）；（2）由正三角形的边长为6厘米．可得出它的一边上的高为33厘米．①当⊙O 的半径r=33厘米时，⊙O 在移动中与△ABC 的边共相切三次，即切点个数为3； ②当0＜r ＜33时，⊙O 在移动中与△ABC 的边相切六次，即切点个数为6；③当r ＞33时，⊙O 与△ABC 不能相切，即切点个数为0．（3）如图，易知在S ＞0时，⊙O 在移动中，在△ABC 内部为经过的部分为正三角形．记作△A ′B ′C ′，这个正三角形的三边分别于原正三角形三边平行，且平行线间的距离等于r ． 连接AA ′，并延长AA ′，分别交B ′C ′，BC 于E ，F 两点．则AF ⊥BC ，A ′E ⊥B ′C ′，且EF=r ．又过点A ′作A ′G ⊥AB 于G ，则A ′G=r ．∵∠GAA ′=30°，∴AA ′=2x ．∴△A ′B ′C ′的高A ′E=AF-3r=9-3r ，B ′C ′=233A ′E=23（3-r ）．∴△A ′B ′C ′的面积S=12B ′C ′•A ′E=33 （3-r ）2．∴所求的解析式为S=33（3-r ）2（0＜r ＜3）． 8.【答案与解析】解：（1）如图1，∵∠DPC=∠A=∠B=90°，∴∠ADP+∠APD=90°，∠BPC+∠APD=90°，∴∠ADP=∠BPC，∴△ADP∽△BPC，∴=，∴AD•BC=AP•BP；（2）结论AD•BC=AP•BP仍然成立．理由：如图2，∵∠BPD=∠DPC+∠BPC，∠BPD=∠A+∠ADP，∴∠DPC+∠BPC=∠A+∠ADP．∵∠DPC=∠A=∠B=θ，∴∠BPC=∠ADP，∴△ADP∽△BPC，∴=，∴AD•BC=AP•BP；（3）如图3，过点D作DE⊥AB于点E．∵AD=BD=5，AB=6，∴AE=BE=3．由勾股定理可得DE=4．∵以点D为圆心，DC为半径的圆与AB相切，∴DC=DE=4，∴BC=5﹣4=1．又∵AD=BD，∴∠A=∠B，∴∠DPC=∠A=∠B．由（1）、（2）的经验可知AD•BC=AP•BP，∴5×1=t（6﹣t），解得：t1=1，t2=5，∴t的值为1秒或5秒．9.【答案与解析】(1)如图1，作DE⊥BC于点E．据题意知，四边形ABED是矩形，AB=DE，AD=BE.在Rt△DEC中，∠DEC=90°，DE=12，CD=13，∴ EC=5．∴AD=BE=BC-EC=4．(2)若BP为x，则AP=12-x.S△BPC=BP·BC=x. S△APD=AP·AD=24-2x.∴S△PCD=S梯形ABCD-S△BPC-S△APD=78-x-24+2x=-x+54.即 y=-x+54，0≤x≤12.当x=0时，y取得最大值为54 cm2.(3)若△PCD是直角三角形，∵∠BCP＜90°，∴∠PCD≠90°∴分两种情况讨论，如图2.①当∠DPC=90°时∵∠APD+∠BPC=90°，∠BPC+∠PCB=90°，∴∠APD=∠PCB.∴ △APD∽△BCP.∴.即.解得x=6.∠APD=∠BPC=45°的情况不存在，不考虑.②当∠P1DC=90°时，在Rt△P1BC中，P1C2=BP12+BC2=x2+92，在Rt△P1AD中，P1D2=P1A2+AD2=(12-x)2+42，∵∠P1DC=90°，CD2+P1D2=P1C2.即132+(12-x)2+42=x2+92.解得.综上，当x=6或，△PCD是直角三角形.10.【答案与解析】当Q点与D点重合时，AQ=AD=6，此时AP=AQ=3=t当P与B点重合时，t=10，当P点运动到C时，t=16，∴分三类情况讨论(1)当0≤t≤3时，如图：AP=t，PQ=t，∴S=AP·PQ=t2(2)当3＜t≤10时，示意图：过D作DH⊥AB于H，AD=t，则DH=AD sinA=6·=3，AH=ADcosA=3∴DQ=PH=AP-AH=t-3∴S=(AP+DQ)·DH=(t+t-3)·3=3t-(3)当10＜t≤16时，如图：AB+BP=tCP=AB+BC-(AB+BP)=16-t∴CQ=CP=8-QP=·CQ=8-t∴S=S□ABCD-S△CPQ=AB·h -·CQ·PQ=10·3-·(8-)·(8-)=30-(64-8t+)=综上，.第21 页共21 页。
2019年初三数学中考复习 几何综合题探究 课件(共22张PPT)
线于点H,连接BH. (1)求证:GF=GC;
好题精练
(2)用等式表示线段BH与AE的数量关系,并证明.
思路分析 第(1)问需要通过正方形的性质和轴对称的性质解决; 第(2)问需要通过构造全等三角形,利用等腰直角三角形的性质解决.
2.在正方形ABCD中,BD是一条对角线.点P在射线CD上(与点C,D不重合),连 接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于点H,连接AH,PH. (1)若点P在线段CD上,如图1. ①依题意补全图1; ②判断AH与PH的数量关系与位置关系并加以证明; (2)若点P在线段CD的延长线上,且∠AHQ=152°,正方形ABCD的边长为1,请写出求DP长的思 路.(可以不写出计算结果)
中考数学 (北京专用)
几何综合题
正方形作为一
种简单而优美的 图形,既反映了 特殊四边形的所 有特征,又能与 图形变换等重要 的几何方法有机 地融为一体.
1.如图,在正方形ABCD中,E是边AB上的一动点(不与点A,B重合),连接DE,点
A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长
5
(2)①依题意补全图形.
②证法一:在AB上截取AG=EC,连接EG.
∵AB=BC,∴GB=EB. ∵∠B=90°,∴∠BGE=45°,∴∠AGE=135°.
如图,正方形ABCD,G为BC延长线上一点,E为射线BC上一点,连接 AE. (1)若E为BC的中点,将线段EA绕着点E顺时针旋转90°,得到线段EF,连接CF. ①请补全图形; ②求证:∠DCF=∠FCG; (2)若点E在BC的延长线上,过点E作AE的垂线交∠DCG的平分线于点M,判断AE与EM的数量 关系并证明你的结论.
华师大版2019秋九年级数学上册专题 6.难点探究专题：相似与几何图形的综合问题
难点探究专题：相似与几何图形的综合问题——突破相似与三角形、四边形等综合问题及含动点的解题思路◆类型一 相似与三角形1．(娄底中考)一块直角三角板ABC 按如图放置，顶点A 的坐标为(0，1)，直角顶点C 的坐标为(－3，0)，∠B ＝30°，则点B 的坐标为 ．第1题图第2题图2．(无锡中考)如图，Rt △ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4，将边AC 沿CE 翻折，使点A 落在AB 上的点D 处．再将边BC 沿CF 翻折，使点B 落在CD 的延长线上的点B ′处，两条折痕与斜边AB 分别交于点E 、F ，则线段B ′F 的长为（ ）A.35B.45C.23D.32◆类型二 相似与四边形3．★(黄石中考)现有多个全等直角三角形，先取三个拼成如图①所示的形状，R 为DE 的中点，BR 分别交AC ，CD 于P ，Q ，易证BP ∶PQ ∶QR ＝3∶1∶2.(1)若取四个直角三角形拼成如图②所示的形状，S 为EF 的中点，BS 分别交AC ，CD ，DE 于P ，Q ，R ，则BP ∶PQ ∶QR ∶RS ＝ ；(2)若取五个直角三角形拼成如图③所示的形状，T 为FG 的中点，BT 分别交AC ，CD ，DE ，EF 于P ，Q ，R ，S ，则BP ∶PQ ∶QR ∶RS ∶ST ＝ .4．★★(安徽中考)如图①，在四边形ABCD 中，点E 、F 分别是AB 、CD 的中点，过点E 作AB 的垂线，过点F 作CD 的垂线，两垂线交于点G ，连接AG 、BG 、CG 、DG ，且∠AGD ＝∠BGC .(1)求证：AD ＝BC ；(2)求证：△AGD ∽△EGF ；(3)如图②，若AD 、BC 所在直线互相垂直，求ADEF 的值．◆类型三 运用相似解决几何图形中的动点问题5．如图，在正方形ABCD 中，M 是BC 边上的动点，N 在CD 上，CN ＝14CD ，若AB ＝1，设BM ＝x ，当x ＝时，以A 、B 、M 为顶点的三角形和以N 、C 、M 为顶点的三角形相似．6．★(钦州中考)如图，在平面直角坐标系中，以点B (0，8)为端点的射线BG ∥x 轴，点A 是射线BG 上的一个动点(点A 与点B 不重合)，在射线AG 上取AD ＝OB ，作线段AD 的垂直平分线，垂足为E ，与x 轴交于点F ，过点A 作AC ⊥OA ，交射线EF 于点C ，连接OC 、CD ，设点A 的横坐标为t .(1)用含t 的式子表示点E 的坐标为 ； (2)当t 为何值时，∠OCD ＝180°？7．★如图，在一块直角三角板ABC 中，∠C ＝90°，∠A ＝30°，BC ＝1，将另一个含30°角的△EDF 的30°角的顶点D 放在AB 边上，E 、F 分别在AC 、BC 上，当点D 在AB 边上移动时，DE 始终与AB 垂直，若△CEF 与△DEF 相似，求AD 的长度．难点探究专题：相似与几何图形的综合问题1．(－3－3，33) 解析：如图，过点B 作BE ⊥x 轴于点E .易证△EBC ∽△OCA ，∴EB OC ＝BC CA ＝ECOA .∵点A的坐标为(0，1)，点C 的坐标为(－3，0)，∴OA ＝1，OC ＝3，∴AC ＝OA 2＋OC 2＝10.在Rt △ACB 中，∠B ＝30°，∴AB ＝2AC ＝210，∴BC ＝AB 2－AC 2＝30，∴BCAC ＝ 3.∴BE ＝33，EC ＝3，∴EO ＝EC ＋CO ＝3＋3，∴点B 的坐标为(－3－3，33)．2．B 解析：在Rt △ABC 中，∵∠ACB ＝90°，AC ＝3，BC ＝4，∴AB ＝5.∵将边AC 沿CE 翻折，使点A 落在AB 上的点D 处，∴AE ＝DE ，CE ⊥AB .易得△AEC ∽△ACB ，∴AC AB ＝AE AC ，∴AE ＝95.∵S △ABC ＝12AB ·CE ＝12AC ·BC ，∴CE ＝125.∵将边BC 沿CF 翻折，使点B 落在CD 的延长线上的点B ′处，∴∠ECF ＝45°，∴EF ＝CE ＝125，∴BF＝AB －AE －EF ＝5－95－125＝45.故选B.3．(1)4∶1∶3∶2 (2)5∶1∶4∶2∶3 解析：(1)由题意可知ABBC ＝CE ＝12BE .设CQ＝a .∵S 是EF 的中点，∴EF ＝2ES .∵CD ∥EF ，∴△BCQ ∽△BES ，∴CQ ES ＝BC BE ＝12，∴ES ＝2CQ ＝2a ，∴AB ＝CD＝EF ＝2ES ＝4a ，QD ＝3a .∵AB ∥CD ，∴△ABP ∽△CQP ，∴BP QP ＝AB CQ ＝41.同理：PQ QR ＝CQ QD ＝13，QR RS ＝QDES＝32.∴BP ∶PQ ∶QR ∶RS ＝ 4∶1∶3∶2.故答案为4∶1∶3∶2； (2)设CP ＝b .由题意可知BC ＝CE ＝EG ＝13BG .∵T 是FG 的中点，∴FG＝2TG .∵AC ∥DE ，∴△BCP ∽△BER ，∴CP ER ＝BC BE ＝12，∴RE ＝2CP ＝2b .同理：△BCP ∽△BGT ，∴CP TG ＝BC BG ＝13，∴TG ＝3CP ＝3b ，∴AC ＝DE ＝FG ＝6b ，∴AP ＝5b ，DR ＝4b ，FT ＝3b .∵AB ∥CD ，∴△ABP ∽△CQP ，∴BP QP ＝APCP ＝51.同理：PQ QR ＝CP DR ＝14，QR RS ＝ DR RE ＝42，RS ST ＝ RE FT ＝23.∴BP ∶PQ ∶QR ∶RS ∶ST ＝ 5∶1∶4∶2∶3.故答案为5∶1∶4∶2∶3.方法点拨：根据已知条件，充分利用图形中平行的条件，连续用相似三角形的判定与性质，得出线段之间的比例关系，“遇平行，想相似；用相似，得比例”是相似形的常用思路之一．4．(1)证明：∵点E 是AB 的中点，GE ⊥AB ，∴GE 是线段AB 的垂直平分线，∴AG ＝BG .同理可得GD ＝GC .在△AGD 与△BGC 中，⎩⎪⎨⎪⎧AG ＝BG ，∠AGD ＝∠BGC ，GD ＝GC ，∴△AGD ≌△BGC ，∴AD ＝BC ；(2)证明：∵∠AGD ＝∠BGC ，∴∠AGB ＝∠DGC .∵AG ＝BG ，DG ＝CG ，且E 、F 分别为AB 、CD 的中点，∴∠AGE ＝12∠AGB ，∠DGF ＝12∠DGC ，∴∠AGE ＝∠DGF ，∴∠AGE －∠DGE ＝∠DGF －∠DGE ，即∠AGD ＝∠EGF .∵GE ⊥AB ，GF ⊥CD ，∴∠AEG ＝∠DFG ＝90°，∴△AGE ∽△DGF ，∴AG DG ＝GE GF ，∴AG GE ＝DG GF .又∵∠AGD＝∠EGF ，∴△AGD ∽△EGF ；(3)解：如图，延长AD 交BC 的延长线于点M .∵AD 、BC 所在的直线互相垂直，∴∠DAB ＋∠ABC ＝90°，即∠DAB ＋∠ABG ＋∠GBC ＝90°.由(1)可知△AGD ≌△BGC ，∴∠GAD ＝∠GBC .∴∠DAB ＋∠ABG ＋∠GAD ＝90°，即∠GAB ＋∠GBA ＝90°.由(1)可知AG ＝BG ，∴∠GAB ＝∠GBA ，∴∠GAB ＝45°.又∵GE ⊥AB ，∴∠AEG ＝90°，∴GA ＝AE 2＋GE 2＝2GE ，∴GA GE ＝ 2.由(2)可知△AGD ∽△EGF ，∴AD EF ＝GAGE＝2.5.12或456．解：(1)(t ＋4，8)(2)∵EF 是线段AD 的垂直平分线，点C 在射线EF 上，AD ＝BO ＝8，∴AE ＝DE ＝12AD ＝4，∠AEC ＝90°，∴∠ECA＋∠EAC ＝90°.又∵AO ⊥CA ，∴∠OAC ＝90°，∴∠BAO ＋∠EAC ＝90°，∴∠ECA ＝∠BAO .又∵BG ∥x 轴，∴BG ⊥y 轴，则∠OBA ＝90°，∴∠AEC ＝∠OBA ，∴△ABO ∽△CEA ，∴BO EA ＝AB CE ，即84＝t CE .∴CE ＝12t .当∠OCD ＝180°时，点C 在线段OD 上．∵EF ⊥BG ，BO ⊥BG ，∴CE ∥BO ，∴△CDE ∽△ODB ，∴CE OB ＝DE DB ，即12t 8＝4t ＋8，∴12t 2＋4t－32＝0，解得t 1＝45－4，t 2＝－45－4(不合题意，舍去)．∴当t ＝45－4时，∠OCD ＝180°.7．解：∵∠C ＝90°，∠A ＝30°，∴∠B ＝60°.∵∠EDF ＝30°，ED ⊥AB 于D ，∴∠FDB ＝60°，∴△BDF 是等边三角形．∵BC ＝1，∴AB ＝2.∵BD ＝BF ，∴2－AD ＝1－CF ，∴AD ＝CF ＋1.(Ⅰ)如图①，若∠FED ＝90°，则∠FED ＝∠ADE ，∴EF ∥AB ，∴∠CEF ＝∠A ＝30°，∴CF ＝12EF ，∠CEF ＝∠EDF .又∵∠C ＝∠FED ＝90°，∴△CEF ∽△EDF ，∴CF EF ＝EF DF ，即CF 2CF ＝2CF 1－CF ，解得CF ＝15，∴AD ＝15＋1＝65；(Ⅱ)如图②，若∠EFD ＝90°，则∠CFE ＝180°－90°－60°＝30°，∴CE ＝12EF ，∠CFE ＝∠FDE .又∵∠C ＝∠EFD＝90°，∴△CEF ∽△FED ，∴CF FD ＝CE FE ，即CF 1－CF ＝12，解得CF ＝13，∴AD ＝13＋1＝43.综上所述，若△CEF 与△DEF 相似，AD 的长为65或43.。
2019北京各区初三一模数学分类汇编——几何综合题
2019北京各区初三一模数学分类汇编——几何综合题 （房山）26．在平面直角坐标系xOy 中，二次函数2y x mx n =++的图象经过点 A (−1，a )，B (3，a )，且顶点的纵坐标为 -4．（1）求 m ，n 和 a 的值；（2）记二次函数图象在点 A ，B 间的部分为 G (含 点A 和点B )，若直线 2y kx =+与 图象G 有公共点，结合函数图象，求 k 的取值范围．（门头沟）26．在平面直角坐标系xOy 中，一次函数4y x =+的图象与x 轴交于点A ，与过点（0，5）平行于x 轴的直线l 交于点B ，点A 关于直线l 的对称点为点C ．（1）求点B 和点C 坐标；（2）已知某抛物线的表达式为222y x mx m m =-+-．① 如果该抛物线顶点在直线4y x =+上，求m 的值；② 如果该抛物线与线段BC 有公共点，结合函数图象，直接写出m 的取值范围．（密云）26.已知抛物线，抛物线的顶点为P.（1）求点P 的纵坐标.（2）设抛物线x 轴交于A 、B 两点，1122(,),(,)A x y B x y ，21x x >. ①判断AB 长是否为定值，并证明.②已知点M （0，-4），且MA≥5，求21-x x m +的取值范围.（平谷）26．平面直角坐标系xOy 中，抛物线3222-+-=m mx x y 与y 轴交于点A ，过A 作AB ∥x 轴与直线x =4交于B 点．（1）抛物线的对称轴为x = （用含m 的代数式表示）；（2）当抛物线经过点A ，B 时，求此时抛物线的表达式；（3）记抛物线在线段AB 下方的部分图象为G （包含A ，B 两点），点P （m ,0）是x 轴上一动点，过P 作PD ⊥x 轴于P ，交图象G 于点D ，交AB 于点C ，若CD ≤1，求m 的取值范围．（石景山）26．在平面直角坐标系xOy 中，直线1y kx =+(0)k ≠经过点(2,3)A ，与y 轴交于点B ，与抛物线2y ax bx a =++的对称轴交于点(,2)C m .（1）求m 的值；（2）求抛物线的顶点坐标；（3）11(,)N x y 是线段AB 上一动点，过点N 作垂直于y 轴的直线与抛物线交于点22(,)P x y ,33(,)Q x y （点P 在点Q 的左侧）．若213x x x <<恒成立，结合函数的图象，求a 的取值范围．（通州）26. 已知二次函数2y x ax b =-+在0x =和4x =时的函数值相等．（1）求二次函数2y x ax b =-+的对称轴；（2）过P （0，1）作x 轴的平行线与二次函数2y x ax b =-+的图象交于不同的两点M 、N .①当2MN =时，求b 的值；②当=4PM PN +时，请结合函数图象，直接写出b 的取值范围．（延庆）26．在平面直角坐标系xOy 中，抛物线2432y ax ax a =-+-（0a ≠）的对称轴与x轴交于点A ，将点A 向右平移3个单位长度，向上平移2个单位长度，得到点B ．（1）求抛物线的对称轴及点B 的坐标；（2）若抛物线与线段AB 有公共点，结合函数图象，求a 的取值范围．（燕山）26．在平面直角坐标系xOy 中，抛物线223(0)y ax ax a a =--≠的顶点为D ，与x 轴交于A ，B 两点(A 在B 的左侧)．(1) 当1a =时，求点A ，B ，D 的坐标；(2) 横，纵坐标都是整数的点叫做整点．若抛物线在点A ，B 之间的部分与线段AB 所围成的区域内(不含边界)恰有7个整点，结合函数图象，求a 的取值范围．（西城）26．在平面直角坐标系xOy 中，已知抛物线2y x mx n =-+．（1）当2m =时，①求抛物线的对称轴，并用含n 的式子表示顶点的纵坐标；②若点1(2,)A y -，22(,)B x y 都在抛物线上，且21y y >，则2x 的取值范围是_______；（2）已知点P (－1,2)，将点P 向右平移4个单位长度，得到点Q ．当n ＝3时，若抛物线与线段PQ 恰有一个公共点，结合函数图像，求m 的取值范围．（顺义）26.在平面直角坐标系xOy 中，抛物线 2(3)3y mx m x =+--（0m >）与x 轴交于A 、B 两点（点A 在点B 左侧），与y 轴交于点C , 4=AB ，点D 为抛物线的顶点.（1）求点A 和顶点D 的坐标；（2）将点D 向左平移4个单位长度，得到点E ,求直线BE 的表达式；（3）若抛物线26=-y ax 与线段DE 恰有一个公共点，结合函数图象，求a 的取值范围.（丰台）26．在平面直角坐标系xOy 中，抛物线c bx ax y ++=2过原点和点A （-2，0）.（1）求抛物线的对称轴；（2）横、纵坐标都是整数的点叫做整点．已知点B （0AB 围成的封闭区域（不含边界）为W ．①当=1a 时，求出区域W 内的整点个数；②若区域W 内恰有3个整点，结合函数图象，直接写出a 的取值范围．。
2019年北京市初三一模数学-几何综合专题(教师版)
2019 一模几何综合专题一、旋转变换1.（等边三角形+对称＋旋转）(2019 通州一模27)如图，在等边△ABC中，点D 是线段BC 上一点. 作射A 线A D ，点B 对于射线A D 的对称点为E.连结CE 并延伸，交射线A D 于点F .（1）设B AF ，用表示∠BCF 的度数；（2）用等式表示线段AF 、CF 、EF 之间的数目关系，并证明.解：（1）连结AE. ∵点B对于射线A D 的对称点为E，A BDC ∴AE= A B，BAF EAF . F E∵△ABC 是等边三角形，∴AB AC ，BAC ACB 60 .DB C∴EAC 60 2 ，AE AC . ⋯⋯⋯⋯⋯⋯ 1 分F E∴1ACE 180 60 2 60 .2∴BCF ACE ACB 60 60 . ⋯⋯⋯⋯⋯⋯ 2 分另解：借助圆.（2）AF EF CF证明：如图，作FCG 60 交AD 于点G，连结BF. ⋯⋯⋯⋯⋯⋯ 3 分∵BAF BCF ，ADB CDF ，∴ABC AFC 60 .∴△FCG 是等边三角形.∴GF = FC . ⋯⋯⋯⋯⋯⋯ 4 分∵△ABC 是等边三角形，A∴BC AC，ACB 60 .G∴ACG BCF .在△ACG 和△BCF 中，DCA CB，BCACG BCF，F ECG CF，∴△ACG≌△BCF .∴AG BF . ⋯⋯⋯⋯⋯⋯ 5 分∵点B对于射线A D 的对称点为E，∴BF EF . ⋯⋯⋯⋯⋯⋯ 6 分∴AF AG GF .∴AF EF CF . ⋯⋯⋯⋯⋯⋯7 分另一种证法：作FAH 60 交F C 的延伸线于点H，连结BF.2.（等边三角形＋旋转）(2019 平谷一模27)在△ABC 中，∠ABC =120°，线段AC绕点 A 逆时针旋转60°得到线段AD，连结CD，BD 交AC 于P．D （1）若∠BAC=α，直接写出∠BCD 的度数（用含α的代数式表示）；（2）求AB，BC，BD 之间的数目关系；（3）当α=30°时，直接写出AC，BD 的关系．CP解：（1）∠BCD =120°－α． (1)（2）解：A B 方法一：延伸BA 使AE=BC ，连结DE． (2)D由（1）知△ADC 是等边三角形，∴AD=CD ．∵∠DAB+∠DCB =∠DAB +∠DAE =180°，∴∠DAB=∠DAE．∴△ADE≌△CDB．∴BD=BE ．···················3 CP∴BD=AB+BC ． (4)方法二：延伸AB 使AF=BC ，连结CF． (2)E A B∠BDC =∠ADE．∵∠ABC=120°，∴∠CBF =60°．D∴△BCF 是等边三角形．∴BC=CF ．∵∠DCA =∠BCF =60°，∴∠DCA +∠ACB=∠BCF +∠ACB．即∠DCB =∠ACF．PC∵CA=CD ，A B∴△ACF≌△DCB．···················3 F ∴BD=AF ．∴BD=AB+BC ． (4)（3）AC，BD 的数目关系是：3AC BD ；2 (5)地点关系是：AC⊥BD 于点P． (6)3（. 等边三角形＋旋转）(2019 延庆一模27).已知：四边形ABCD 中，ABC 120 ，ADC 60 ，AD =CD，D 对角线A C，BD订交于点O，且BD 均分∠ABC，过点 A 作AH BD ，垂足为H．（1）求证：ADB ACB ；（2）判断线段BH ，DH，BC 之间的数目关系；并证明．AOH解：（1）证明：∵∠ADC = 60°，DA=DCBC ∴△ADC 是等边三角形．⋯⋯ 1 分∴∠DAC =60°A,D=AC ．∵∠ABC= 120°,BD 均分∠ABC∴∠ABD= ∠DBC =60°．∴∠DAC =∠DBC =60°∵∠AOD =∠BOC∠ADB= 180°- ∠DAC -∠AOD∠ACB= 180°- ∠DBC -∠BOC∴∠ADB= ∠ACB ⋯⋯ 3 分（2）结论：DH=BH+BC ⋯⋯ 4 分证明：在HD 上截取HE=HB ⋯⋯ 5 分∵AH⊥BD∴∠AHB= ∠AHE =90°∵AH =AH∴△ABH ≌△AEH∴AB=AE, ∠AEH= ∠ABH =60°⋯⋯ 6 分∴∠AED= 180°-∠AEH= 120°∴∠ABC= ∠AED= 120°∵AD=AC, ∠ADB= ∠ACB∴△ABC≌△AED∴DE=BC ⋯⋯ 7 分∵DH=HE+ED∴DH=BH+BC ⋯⋯ 8 分4.（等边三角形+旋转）(2019 密云一模27)已知ABC为等边三角形，点 D 是线段AB 上一点（不与 A 、B 重合）.将线段CD绕点C 逆时针旋转60 获得线段CE.连结D E、BE.（1）依题意补全图1并判断AD 与BE的数目关系.（2）过点 A 作A F EB 交E B延伸线于点 F .用等式表示线段 E B、DB与AF 之间的数目关系并证明.C CA BD A BD图1图227. （1）补全图形CEA DBAD 与BE的数目关系为A D=BE .................................2 分（2）∵∠ACB=∠DCE= 60°,∴∠ACD=∠BCE又∵AC=BC,CD=CE∴△ACD≌△BCE∴AD=BE, ∠CBE=∠CAD=60°∴∠ABF=180°- ∠ABC-∠CBE=60°在Rt AFB中，AFAB32∴BE+BD=32AB.................................7 分5.（正方形+旋转+最值）(2019东城一模27)如图，在正方形ABCD 中，E 是边B C 上一动点（不与点B，C 重合），连结DE，点C 对于直线D E 的对称点为C?，连结AC?并延伸交直线D E 于点P，F 是AC′中点，连接DF ．（1）求∠FDP 的度数；（2）连结BP，请用等式表示AP，BP，DP 三条线段之间的数目关系，并证明．（3）连结AC，若正方形的边长为2，请直接写出△ACC′的面积最大值．A DFC'B CEP解：（1）由对称可知CD＝C′D，∠CDE＝∠C′DE．在正方形ABCD 中，AD＝CD，∠ADC＝90°，∴AD＝C′D．又∵F为A C′中点，∴DF⊥AC′，∠ADF ＝∠C′DF ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分∠ADC＝45°．⋯⋯⋯⋯⋯⋯⋯ 2 分1∴∠FDP ＝∠FDC ′＋∠EDC′=2A DFC'B CEP（2）结论：BP＋DP＝ 2 AP．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分如图，作AP′⊥AP 交PD 延伸线于P′，∴∠PAP′＝90°．在正方形ABCD 中，DA ＝BA，∠BAD＝90°，∴∠DAP′＝∠BAP．由（1）可知∠APD＝45°，∴∠P′＝45°．∴AP＝AP′⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分BA DA在△BAP 和△DAP′中，BAP DAP，AP AP∴△BAP≌△DAP ′（SAS）⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分∴BP＝DP′．∴DP＋BP＝PP′＝ 2 AP．P'A DFC'B CEP（3） 2 －1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 7 分6.（等腰直角三角形+旋转）(2019 房山一模27).已知：Rt△ABC 中，∠ACB=90°，AC =BC .(1) 如图1，点 D 是BC边上一点( 不与点B，C 重合) ，连结AD，过点 B 作BE⊥AD，交AD 的延伸线于点E，连结CE. 若∠BAD =α，求∠DBE 的大小(用含α的式子表示) ；(2) 如图2，点D 在线段BC 的延伸线上时，连结AD，过点 B 作BE⊥AD，垂足 E 在线段AD 上，连结CE.全图2；①依题意补的数目关系，并证明.②用等式表示线段EA，EB 和EC 之间CCEDBAA B图1图2解：（1）解: 依题意，∠CAB=45°，∵∠BAD =α，∴∠CAD = 45 .∵∠ACB =90°，BE⊥AD，∠ADC =∠BDE，∴∠DBE =∠CAD =45 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分（2）解：形如图⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分全图①补②猜想：当D 在BC边的延伸线上时，EB - EA = 2 EC. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分证明：过点 C 作CF⊥CE，交AD 的延伸线于点 F.∵∠ACB =90°，∴∠ACF =∠BCE .∵CA=CB，∠CAF =∠CBE，∴△ACF≌△BCE .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分∴AF= B E，CF =CE.∵∠ECF =90°，∴EF= 2 EC.即AF - EA = 2 EC.∴EB - EA = 2 EC. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分FDCEBA7.（等腰直角三角形+旋转）(2019门头沟一模27). 如图，∠AOB = 90°，OC为∠AOB 的均分线，点P 为OC 上一个动点，过点P 作射线P E 交OA 于点E．以点P为旋转中心，将射线P E 沿逆时针方向旋转90°，交OB 于点F．（1）依据题意补全图1，并证明PE = PF；（2）如图1，假如点 E 在OA边上，用等式表示线段OE，OP 和OF 之间的数目关系，并证明；（3）如图2，假如点 E 在OA边的反向延伸线上，直接写出线段OE，OP 和OF 之间的数目关系．AACCEP POOB BE图1图227．（本小题满分7 分）解：（1）补全图形（如图1）；⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分证明：略. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分（2）线段OE，OP 和OF 之间的数目关系是OF +OE= 2 OP .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分证明：如图2，作PQ⊥PO 交OB 于Q .∴∠2+∠3 = 90 °，∠1+∠2 = 90 °.图1∴∠1=∠3.又∵OC 均分∠AOB，∠AOB =90°，∴∠4 =∠5 = 45 °.又∵∠5 +∠6 = 90 °，∴∠6 = 45 °，∴∠4 = ∠6 .∴PO = PQ.∴△EPO ≌△FPQ . ⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分∴PE=PF，OE = FQ .又∵OQ = OF +FQ = OF + OE.图2又∵OQ = 2 OP，∴OF + OE = 2 OP . ⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分（3）线段OE，OP 和OF 之间的数目关系是OF - OE= 2 OP . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分8.（等腰直角三角形+旋转）(2019 燕山一模27)如图，在△ABC 中，AB＝BC，∠B＝90°，点D为线段BC 上一个动点(不与点B，C 重合)，连结AD，将线段AD绕点D顺时针旋转90°获得线段DE，连结EC．A AB DC BD C图1备用图(1) ①依题意补全图1；②求证：∠EDC＝∠BAD；(2) ①小方经过察看、实验，提出猜想：在点 D 运动的过程中，线段CE 与BD 的数目关系一直不变，用等式表示为：；猜想的几种想法：②小方把这个猜想与同学们进行沟通，经过议论，形成了证明该想法1：过点 E 作EF⊥BC，交BC 延伸线于点F，只要证△ADB≌△DEF ．想法2：在线段AB 上取一点F，使得BF＝BD，连结DF ，只要证△ADF≌△DEC．想法3：延伸AB 到F，使得BF＝BD，连结DF，CF，只要证四边形DFCE为平行四边形．⋯⋯请你参照上边的想法，帮助小方证明①中的猜想．(一种方法即可)27．(1)①补全的图形如图的所示；AEB D C⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分②证明：∵∠ADE＝∠B＝90°，∴∠EDC＋∠ADB＝∠BAD＋∠ADB＝90°，∴∠EDC＝∠BAD．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分(2) ①CE＝ 2 BD．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分②想法1：证明：如图，过点 E 作EF⊥BC，交BC 延伸线于点F，∴∠F＝90°．在△ADB 和△DEF 中，∠B＝∠F＝90°，∠EDC＝∠BAD，AD＝DE，∴△ADB≌△DEF ，A∴AB＝DF，BD＝EF．E B D C F∵AB＝BC，∴DF＝BC，即DC＋CF＝BD＋DC，∴CF＝BD＝EF，∴△CEF 是等腰直角三角形，∴CE＝ 2 CF＝ 2 BD．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分想法2：证明：在线段AB 上取一点F，使得BF＝BD，连结DF ，∵∠B＝90°，AB＝BC，A∴DF＝ 2 BD，∵AB BC BF BD＝，＝，FEB D C∴AB－BF＝BC－BD，即AF ＝DC．在△ADF 和△DEC 中，AF＝DC，∠BAD ＝∠EDC，AD＝DE，∴△ADF ≌△DEC，∴CE＝DF＝ 2 BD．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分想法3：证明：延伸AB 到F，使得BF＝BD ，连结DF ，CF ，A∵∠B＝90°，∴DF＝ 2 BD．E 在Rt△ABD 和Rt△CBF 中，∠ABD＝∠CBF ＝90°，AB＝BC，BD＝BF，B D C∴△ABD≌△CBF，F∴AD＝CF，∠BAD＝∠BCF．∵AD＝DE，∴DE＝CF．∵∠EDC＝∠BAD，∴∠EDC＝∠BCF，∴DE∥CF，∴四边形DFCE为平行四边形，∴CE＝DF＝ 2 BD．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分9.（等腰直角三角形+旋转）(2019 丰台一模27)在△ABC 中，∠ACB =90°，AC=BC，D为A B 的中点，点E为A C 延伸线上一点，连结DE，过点 D 作DF ⊥DE 交CB 的延伸线于点F．（1）求证：BF= CE ；（2）若CE=AC，用等式表示线段DF 与AB 的数目关系，并证明．解：（1）连结CD.在△ABC 中，∠ACB= 90°，AC=BC ，D为A B 中点，∴CD⊥BD, CD=BD=DA. ...............1 分∵DF ⊥DE， F∴∠BDF = ∠CDE.∵∠F = ∠E，∴△DBF ≌△DCE . B∴BF=CE. ..................3 分DA C E（2） 5DF AB. ..................4 分2原因以下：由（1）知△DBF ≌△DCE ，∴DF=DE. ..................5 分连结BE.∵CE=CA ，∴BA=BE.∴∠A= ∠BEA= 45°.∴∠ABE= 90°.设A D=BD=a ，∴AB=BE= 2a.∴DF DE 5a .∴ 5DF AB . .........................7 分210.（等腰直角三角形+旋转＋解直角三角形）(2019 旭日一模27)如图，在Rt△ABC 中，∠A=90°，AB=AC，将线段BC绕点 B 逆时针旋转α°（0<α<180），获得线段BD，且AD∥BC．（1）依题意补全图形；（2）求知足条件的α的值；（3）若AB=2，求AD 的长．解：（1）知足条件的点 D 有两个，补全图形如图1所示．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分图1（2）如图2，过点 B 作BE⊥D1D2 于点E．由题意可知，BD 1=BD2 = B C，AE∥BC．∴∠AEB=90°．∵在Rt△ABC 中，∠BAC =90°，AB= A C，∴∠EAB=∠ABC=45°．∴在Rt△ABE 中，2BE AB ，2图2在Rt△ABC 中，2AB BC ．2∴1 1BE BC BD ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分12 2∴∠D1=∠D2=30°．∵D1D2∥BC，∴30或150．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分（3）∵AB=2，∴BE AE 2 ．∴D1E= D2E= 6 ．∴AD 的长为6 2 或 6 2 ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分11. （等边三角形+旋转）(2019怀柔一模27)如图，等边△ABC中，P 是AB上一点，过点P作PD⊥AC于点D，作PE⊥BC于点E，M是AB的中点，连结ME，MD．（1）依题意补全图形；（2）用等式表示线段BE ，AD 与AB的数目关系，并加以证明；A （3）求证：MD=M．EPBC （1）补全图形如图：A12 （2）线段BE ，AD 与AB的数目关系是：AD+ BE= AB．PDM∵△ABC是等边三角形，∴∠ A =∠B=60°．∵PD⊥AC ，PE⊥BC ，∴∠APD=∠BPE=30°，1 1∴AD= AP ，AD= AP．2 2 B E FC1 1∴AD+ BE= （AP+ BP）= AB．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分2 21 1（3）取BC中点F，连结MF．∴MF= AC．MF∥AC．2 2∴∠MFB=∠ACB=60°．∴∠ A =∠MFE=60°．1∵AM= AB，AB=AC，∴MF=M．A21∵EF+ BE= BC，21∴AD + BE= AB．∴EF=AD.2∴△MAD≌△MFE（SAS）．∴MD=M．E⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分二、轴对称变换12.（正方形+对称）(2019 西城一模27)如图，在△ABC 中，∠ABC =90°，BA=BC．将线段AB绕点 A 逆时针旋转90°获得线段AD，E 是边B C 上的一动点，连结DE 交AC 于点F，连结BF．（1）求证：FB=FD；（2）点H 在边B C 上，且BH =C E，连结AH 交BF 于点N．；①判断AH 与BF 的地点关系，并证论明你的结直接写出线段CN长度的最小值．结CN．若AB=2，请②连解：（1）证明：∵∠ABC =90°，BA=BC，∴∠BAC=∠ACB=45°．旋转90°获得AD，针点A 逆时∵AB绕∴∠BAD =90°，AB= A D．∴∠DAF =∠BAD－∠BAC=45°．∴∠BAF =∠DAF．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分∵AF=AF，∴△BAF≌△DAF ．∴FB=FD．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分（2）①AH 与BF 的地点关系：AH⊥BF．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分证明：连结DC，如图．∵∠ABC+∠BAD=180°，∴AD∥BC．∵AB=BC =AD，形．形ABCD 是平行四边∴四边∵∠ABC =90°，形ABCD 是矩形．∴四边∴AB=DC，∠ADC =∠DCB =90°．∴∠ABH =∠DCE．∵BH=CE，∴△ABH≌△DCE．∴∠BAH =∠CDE．∵△BAF≌△DAF，∴∠ABF =∠ADF．∴∠BAH＋∠ABF =∠CDE＋∠ADF =∠ADC =90°．∴∠ANB =180°－( ∠BAH＋∠ABF ) =90°．∴AH⊥BF．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分② 5 1 ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分13．（等腰三角形+对称）(2019顺义一模27)已知：如图，在△ABC 中，AB >AC，∠B=45°，点D 是BC边上一点，且AD=AC ，过点 C 作CF⊥AD 于点E，与AB 交于点F．A（1）若∠CAD =α，求∠BCF 的大小（用含α的式子表示）；（2）求证：AC=FC；（3）用等式直接表示线段BF 与DC 的数目关系．FEB DC 解：（1）过点 A 作AG⊥BC 于点G，⋯⋯⋯⋯⋯⋯⋯ 1 分∴∠2+∠4=90°，∵AD=AC ，∴∠1=∠2=12 ∠CAD =12α，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分 A∵CF⊥AD 于点E，2 1 ∴∠3+∠4=90°，∴∠3=∠2=12 ∠CAD = 12 α，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分 F1 即∠BCF=2 （2）证明：α．BE43D CG∵∠B=45°，∴∠BAG=45°，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分∵∠BAC=45°+∠1，∠AFC=45°+∠3，∴∠BAC=∠AFC，∴AC= FC．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分（3）DC 2BF ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分三、平移变换1 4.（等边三角形+平移）(2019 石景山一模27). 如图，在等边△ABC 中，D为边AC 的延伸线上一点(CD AC ) ，平移线段BC，使点C 挪动到点D，获得线段ED，M为E D 的中点，过点M 作ED 的垂线，交BC于点F，交AC 于点G．A （1）依题意补全图形；（2）求证：AG = CD；（3）连结DF 并延伸交AB 于点H，用等式表示线段AH 与CG 的数目关系，并证明．CBE M D 27．（1）补全的图形如图1所示．⋯⋯⋯⋯⋯ 1 分（2）证明：Q △ABC 是等边三角形，AAB BC CA ．GABC BCA CAB 60 ．由平移可知ED∥BC，ED =BC．⋯⋯⋯⋯ 2 分ADE ACB 60 ．B F CQ GMD 90 ，DG 2DM DE ．⋯⋯⋯⋯⋯ 3 分Q DE BC AC ，图1E M DDG AC ．AG CD ．⋯⋯⋯⋯⋯ 4 分（3）线段AH 与CG 的数目关系：AH = CG．⋯⋯⋯⋯⋯ 5 分证明：如图2，连结BE，EF ．Q ED BC, ED∥BC，AG 四边形BEDC是平行四边形．BE CD，CBE ADE ABC ．HQ GM 垂直均分ED ，B F CEF DF ．DEF EDF ．Q ED∥BC，图2E M DBFE DEF，BFH EDF ．BFE BFH ．Q BF BF ，△BEF≌△BHF ．⋯⋯⋯⋯⋯ 6 分BE BH CD AG ．Q AB AC ，AH CG ．⋯⋯⋯⋯⋯7 分四、其余15.（等腰直角三角形+全等）(2019 海淀一模27)如图，在等腰直角△ABC中，? ABC 90°，D 是线段AC上一点（CA > 2CD ），连结BD ，过点C 作BD 的垂线，交BD 的延伸线于点 E ，交BA 的延伸线于点F．（1）依题意补全图形；C （2）若? ACE α，求D A BD 的大小（用含α的式子表示）；（3）若点G 在线段CF 上，CG = BD ，连结DG．D①判断DG 与BC 的地点关系并证明；②用等式表示DG ，CG ，AB 之间的数目关系为．A B（1）补全图形，如图．CEDF A B（2）解：∵AB =BC，∠ABC =90°，∴∠BAC=∠BCA =45°．∵∠ACE=α，∴? ECB 45? α．∵CF⊥BD 交BD 的延伸线于点E，∴∠BEF =90°．∴∠F+∠ABD =90°．∵∠F+∠ECB=90°，∴? ABD ? ECB 45? α．（3）①DG 与BC 的地点关系：DG⊥BC．证明：连结BG 交AC 于点M，延伸GD 交BC 于点H，如图．∵AB =BC，∠ABD =∠ECB，BD =C G，∴△ABD≌△BCG．∴∠CBG =∠BAD =45°．∴∠ABG =∠CBG =∠BAC=45°．∴AM =BM，∠AMB =90°．C∵AD =BG，E∴DM =GM．∴∠MGD =∠GDM =45°．GMDH∴∠BHG =90°∴DG ⊥BC．F A B② 2 2 22CG = DG + AB ．。
四川省邻水县2019年九年级数学人教版几何综合题(含答案)
2019年几何合题一、选择题（每题3分，共30分）1、一个角的余角和它的补角互为补角，则这个角是（）A.30°B.45°C.60°D.75°2、如图，长方形纸片ABCD中，已知AD＝8，折叠纸片使AB边与对角线AC重合，点B 落在点F处，折痕为AE，且EF＝3，则AB的长为( )A．3 B．4 C．5 D．63、如图所示的几何体的主视图是（）A． B．C．D．4、下列图形中，既是轴对称又是中心对称图形的是（）A. B. C. D.5、下列说法错误的是（）A．通过平移或旋转得到的图形与原图形全等B．“对顶角相等”的逆命题是真命题C．圆内接正六边形的边长等于半径D．“经过有交通信号灯的路口，遇到红灯”是随机事件6、如图，在Rt△ABC中，∠C=90°，AB=10，AC=8，则sinA等于（）A．B．C．D．7、如图，AB是半圆的直径，O为圆心，C是半圆上的点，D是上的点，若∠BOC=40°，则∠D的度数为（）A．100°B．110°C．120° D．130°8、如图，若△ABC内接于半径为R的⊙O，且∠A=60°，连接OB、OC，则边BC的长为（）A．B．C．D．9、如图，某海监船以20海里/小时的速度在某海域执行巡航任务，当海监船由西向东航行至A处时，测得岛屿P恰好在其正北方向，继续向东航行1小时到达B处，测得岛屿P在其北偏西30°方向，保持航向不变又航行2小时到达C 处，此时海监船与岛屿P之间的距离（即PC的长）为（）A．40海里B．60海里C．20海里D．40海里10、如图，平行于BC的直线DE把△ABC分成面积相等的两部分，则的值为（）A．1 B．C． 1 D．二、填空题（每题4分，共24分）11、如图，直线a∥b，∠l=60°，∠2=40°，则∠3=．12、用半径为，圆心角为的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为________ ．13、如图，平行四边形ABCD中，AC、BD相交于点O，若AD=6，AC+BD=16，则△BOC的周长为_______.14、如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作⊙P．当⊙P与正方形ABCD的边相切时，BP的长为____。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
如图，在△ABC 中，AC =BC ，∠ACB =90°，D 为AC 上一点（与点A ，C 不重合），连接BD ，过点A 作AE ⊥BD 的 延长线于E
（1）①在图中作出△ABC 的外接圆⊙O ，并用文字描述 圆心O 的位置
②连接OE ，求证：点E 在⊙O 上
（2）①延长线段BD 至点F ，使EF =AE ，连接CF ,根据题 意补全图形
②用等式表示线段CF 与AB 的数量关系，并证明 2 丰台
如图，△ABC 是等边三角形，D ，E 分别是AC ，BC 边上的点，且AD = CE ，连接BD ，AE 相交于点F （1）∠BFE 的度数是
（2）如果2
1
=AC AD ，那么
=BF AF （3）如果n
AC AD 1
=时，请用含n 的式子表示AF ，BF 的数量关系，并证明
A
B
C D
E
A
D
B
F
已知在△ABC 中，AB =AC ，∠BAC =α，直线l 经过点A （不经过点B 或点C ），点C 关于直线l 的对称点为点D ，连接
BD ，CD
（1）如图1 ①求证：点,,B C D 在以点A 为圆心，AB 为半径的圆上 ②直接写出∠BDC 的度数（用含α的式子表示）为___________
（2）如图2，当α=60°时，过点D 作BD 的垂线与直线l 交于点E ，求证：AE =BD
（3）如图3，当α=90°时，记直线l 与CD 的交点为F ，连接BF ．将直线l 绕点A 旋转，当线段BF 的长取得最大值时，直接写出tan FBC ∠的值
4 怀柔
在菱形ABCD 中，∠ADC=60°，BD 是一条对角线，点P 在边CD 上（与点C ，D 不重合），连接AP ，平移ADP ∆，使点D 移动到点C ，得到BCQ ∆，在BD 上取一点H ，使HQ=HD ，连接HQ ，AH ，PH （1） 依题意补全图1 （2）判断AH 与PH 的数量关系及∠AHP 的度数，并加以证明 （3）若141AHQ ∠=︒，菱形ABCD 的边长为1，请写出求DP 长的思路（可以不写出计算结果．．．．．．．．．）
B
B
A B
C
D
P
A B
C
D
如图1，在正方形ABCD 中，点F 在边BC 上，过点F 作EF ⊥BC ，且FE =FC （CE <CB ），连接CE 、AE ，点G 是AE 的中 点，连接FG
（1）用等式表示线段BF 与FG 的数量关系是___________________
（2）将图1中的△CEF 绕点C 按逆时针旋转，使△CEF 的顶点F 恰好在正方形ABCD 的对角线AC 上，点G 仍是
AE 的中点，连接FG 、DF
①在图2中，依据题意补全图形 ②求证
:DF =
6 燕山
正方形ABCD 中，将边AB 所在直线绕点A 逆时针旋转一个角度α得到直线AM ，过点C 作CE ⊥AM ，垂足为E ，连接
BE
(1) 当045α︒<<︒时，设AM 交BC 于点F
① 如图1，若α＝35°，则∠BCE ＝ ° ② 如图2，用等式表示线段AE ，BE ，CE 之间的数量关系，并证明 (2) 当4590α︒<<︒时(如图3)，请直接用等式表示线段AE ，BE ，CE 之间的数量关系
图2
图1
F 35°
M
B
C D
A
E
F A
B E
M
C D
α
A
B E
M
C
D
如图，Rt △ ABC 中，∠ACB =90°，AD 平分∠BAC ， 作AD 的垂直平分线EF 交AD 于点E ，交BC 的延长线于点F ，交
AB 于点G ，交AC 于点H
（1）依题意补全图形
8 门头沟
如图，在△ABC 中，AC = BC ，∠ACB = 90°，D 是线段AC 延长线上一点，连接BD ，过点A 作AE ⊥BD 于E （1）求证：∠CAE =∠CBD
（2）将射线AE 绕点A 顺时针旋转45°后，所得的射线与线段BD 的延长线交于点F ，连接CE ① 依题意补全图形
② 用等式表示线段EF ，CE ，BE 之间的数量关系，并证明
A
A
B
C
D
E
M 是正方形ABCD 的边AB 上一动点（不与A ，B 重合）MC BP ⊥，垂足为P ，将CPB ∠绕点P 旋转，得到''PB C ∠，当射线'PC 经过点D 时，射线'PB 与BC 交于点N （1）依题意补全图形 （2）求证：CPD ∽∆∆BPN
（3）在点M 的运动过程中，图中是否存在与BM 始终相等的线段？若存在，请写出这条线段并证明，若不存在，请说明理由
10 西城
如图，在△ABC 中，AB =AC ．△ADE ∽△ABC ，连接BD ，CE （1）判断BD 与CE 的数量关系，并证明你的结论 （2）若AB =2，AD =22，∠BAC =105°，∠CAD =30° ①BD 的长为
②点P ，Q 分别为BC ，DE 的中点，连接PQ ，写出求
PQ 长的思路
如图，在ABC Rt ∆中，BC AB ABC ==∠，090，点E 为线段AB 上一动点（不与点A ，B 重合），连接CE ，将ACE ∠的两边CE ，CA 分别绕点C 顺时针旋转090，得到射线''CA CE ，，过点A 作AB 的垂线AD ，分别交射线''CA CE ，于点F ，G
（1）依题意补全图形
（2）若α=∠ACE ，求AFC ∠的大小（用含α的式子表示） （3）用等式表示线段AE ，AF ，与BC 之间的数量关系，并证明 12 东城
如图，M 为正方形ABCD 内一点，点N 在AD 边上，且MB MN BMN 2900==∠，，点E 为MN 的中点，点P 为DE 的中点，连接MP 并延长到点F ，使得PF=PM ，连接DF （1）依题意补全图形 （2）求证：DF=BM
（3）连接AM ，用等式表示线段PM 和AM 的数量关系并证明
如图，正方形ABCD ，将边CD 绕点C 顺时针旋转60°，得到线段CE ，连接DE ，AE ，BD 交于点F （1）求∠AFB 的度数 （2）求证：BF=EF
（3）连接CF ，直接用等式表示线段
AB ，CF ，EF 的数量关系
14 石景山
在Rt △ABC 中，90ACB ∠=︒，2AC =
，
BC =，过点B 作直线l ∥AC ，将△ABC 绕点C 逆时针旋转得到△A B C ''，直线CA '，CB '分别交直线l 于点D E ，．
（1）当点A '，D 首次重合时，
①请在图1中，补全旋转后的图形； ②直接写出A CB '∠的度数； （2）如图2，若CD AB ⊥，求线段DE 的长；
（3）求线段DE 长度的最小值．
E
A。