静矩和形心[业界优制]
合集下载
截面的形心静矩
03
截面形心静矩的性质
形心静矩的性质
1 2
线性性质
形心静矩是线性变换的，即当截面受到线性变换 （如平移或旋转）时，形心静矩的值不会改变。
面积无关性
形心静矩与截面的面积无关，只与截面的形状有 关。
3
方向性
形心静矩具有方向性，其值取决于截面的法线方 向。
截面形心静矩与截面几何形状的关系
01
02
03
积分法
积分法是通过将截面划分为若干个小 面积元，然后对每个面积元计算形心 和面积，再对所有面积元的形心和面 积进行积分来计算截面形心静矩的方 法。
积分法适用于各种形状的截面，计算 精度较高，但计算过程较为复杂，需 要使用数值积分方法进行计算。
代数法
01
代数法是通过建立截面形心静矩 的代数方程，然后求解该方程来 计算截面形心静矩的方法。
在材料力学中的应用
材料应力分析
通过截面形心静矩，可以计算出材料 的应力分布，了解材料在不同受力状 态下的行为和性能。
材料强度评估
材料稳定性分析
通过截面形心静矩，可以对材料在不 同温度、湿度等环境因素下的稳定性 进行分析，预测材料的长期性能和可 靠性。
利用截面形心静矩，可以对材料的强 度进行评估，预测材料在不同受力条 件下的失效模式和极限承载能力。
圆形截面的形心静矩
总结词
圆形截面的形心静矩计算稍微复杂一些，需要使用微积分的方法。
详细描述
圆形截面的形心静矩可以通过以下公式计算：$S_{c} = frac{pi d^4}{64}$，其中$d$是圆形截面的直径。 这个公式是通过微积分的方法得出的，可以用来计算圆形截面的形心静矩。
其他形状截面的形心静矩
圆形截面
惯性矩、静矩,形心坐标公式
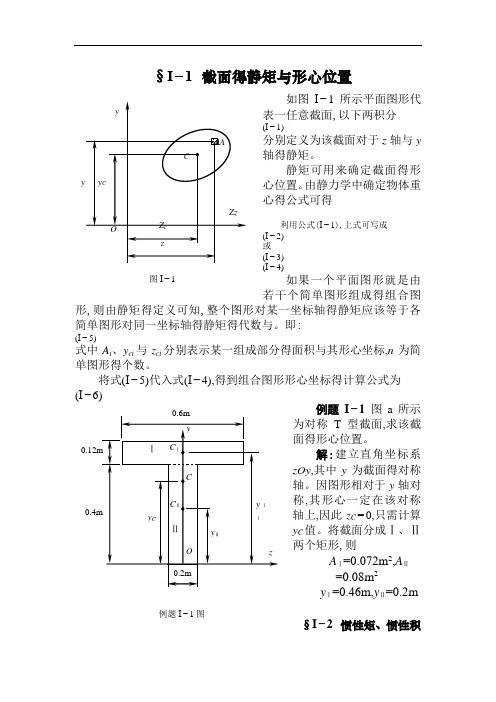
§I−1 截面得静矩与形心位置如图I −1所示平面图形代表一任意截面,以下两积分(I −1)分别定义为该截面对于z 轴与y 轴得静矩。
静矩可用来确定截面得形心位置。
由静力学中确定物体重心得公式可得利用公式(I −1),上式可写成 (I −2) 或 (I −3) (I −4)如果一个平面图形就是由若干个简单图形组成得组合图形,则由静矩得定义可知,整个图形对某一坐标轴得静矩应该等于各简单图形对同一坐标轴得静矩得代数与。
即:(I −5)式中A i 、y ci 与z ci 分别表示某一组成部分得面积与其形心坐标,n 为简单图形得个数。
将式(I −5)代入式(I −4),得到组合图形形心坐标得计算公式为 (I −6)例题I −1 图a 所示为对称T 型截面,求该截面得形心位置。
解:建立直角坐标系zOy ,其中y 为截面得对称轴。
因图形相对于y 轴对称,其形心一定在该对称轴上,因此z C =0,只需计算y C 值。
将截面分成Ⅰ、Ⅱ两个矩形,则 A Ⅰ=0.072m 2,A Ⅱ=0.08m 2y Ⅰ=0.46m,y Ⅱ=0.2m§I −2 惯性矩、惯性积例题I −1图图I −1与极惯性矩如图I −2所示平面图形代表一任意截面,在图形平面内建立直角坐标系zOy 。
现在图形内取微面积d A ,d A 得形心在坐标系zOy 中得坐标为y 与z ,到坐标原点得距离为ρ。
现定义y 2d A 与z 2d A 为微面积d A 对z 轴与y 轴得惯性矩,ρ2d A 为微面积d A 对坐标原点得极惯性矩,而以下三个积分(I −7)分别定义为该截面对于z 轴与y 轴得惯性矩以及对坐标原点得极惯性矩。
由图(I −2)可见,,所以有(I −8) 即任意截面对一点得极惯性矩,等于截面对以该点为原点得两任意正交坐标轴得惯性矩之与。
另外,微面积d A 与它到两轴距离得乘积zy d A 称为微面积d A 对y 、z 轴得惯性积,而积分(I −9)定义为该截面对于y 、z 轴得惯性积。
截面的形心静矩
形心静矩具有方向性，其方向与形心 位置有关。
形心静矩的应用
01
在结构设计中，形心静矩可用于计算截面的抗弯能 力，从而评估结构的稳定性。
02
在机械设计中，形心静矩可用于计算转动惯量，从 而评估机械设备的动态性能。
03
在船舶与海洋工程中，形心静矩可用于计算浮力与 稳性，确保船舶的安全航行。
03
截面形心静矩的计算
截面形心静矩与其他力学性能的关系研究
总结词
材料属性影响
详细描述
材料属性对截面形心静矩的影响也是未来的 研究方向之一。研究不同材料属性（如弹性 模量、泊松比等）对截面形心静矩的影响规 律，有助于更好地理解材料的力学行为，并 为新型材料的开发和优化提供理论支持。
截面形心静矩在新型材料和结构中的应用研究
05
截面形心静矩的未来研究 方向
截面形心静矩的优化计算方法
总结词
优化计算方法
详细描述
随着计算机技术的不断发展，截面形心静矩的优化计算方法成为了一个重要的研究方向。目前，研究 者们正在探索更高效、精确的数值计算方法，以解决复杂截面形状和材料属性对形心静矩计算的影响 。
截面形心静矩的优化计算方法
总结词
截面的形心静矩
contents
目录
• 截面形心静矩的定义 • 截面形心静矩的性质 • 截面形心静矩的计算 • 截面形心静矩的实例分析 • 截面形心静矩的未来研究方向
01
截面形心静矩的定义
形心
定义
形心是截面图形的几何中心，通 常用于描述截面的质量分布情况 。
计算方法
对于规则图形，形心位置可以通 过几何计算得出；对于不规则图 形，可以通过积分计算得出。
详细描述
对于圆形截面，形心静矩可以通过以 下公式计算：$I = frac{pi d^4}{64}$， 其中$d$为截面的直径。这个公式适 用于圆形截面，其中形心静矩表示截 面对其轴线的惯性矩。
静矩和形心
y
静矩和形心
S y AzC
S z AyC
1.若截面对某一轴的静矩等于零，则该轴必
过
形心； 2.若轴过形心，则截面对该轴的静矩等于零
。
静矩和形心
三、组合截面的静矩
由几个简单图形组成的截面称为组合截面 。
截面各组成部分对于某一轴的静矩之代数和 ， 等于该截面对于同一轴的静矩。
静矩和形心
n
S y
zdA
A
Ai zCi
i 1
n
S z
ydA
A
A i yCi
i 1
其中 Ai —第 i个简单截面面积；
( yCi, zCi)—第 i个简单截面的形心坐标；
静矩和形心
静矩和形心
一、静矩(面积的一次矩)
设平面图形，取 yoz 为图形所在平面的坐标 系，在坐标为（y , z）处取面积元dA。 截面对 y , z 轴的静矩为 z
y
S y
zdA
A
dA
m3
z
S z
ydA
A
O
y
静矩和形心
S y
zdA
A
Sz
ydA
A
1.静矩可正，可负，也可能等于零；
2.同一图形，对不同的坐标轴，静矩也不同。
静矩和形心
二、截面的形心(Centroid of an area)
n
Ai zCi
zC
i1 n
Ai
i1
z d
A
A
A
z
z zC
dA C
O yC
y
Sy A
y
静矩和形心
n
Ai
i1
A ydA
静矩和形心
S y AzC
S z AyC
1.若截面对某一轴的静矩等于零，则该轴必
过
形心； 2.若轴过形心，则截面对该轴的静矩等于零
。
静矩和形心
三、组合截面的静矩
由几个简单图形组成的截面称为组合截面 。
截面各组成部分对于某一轴的静矩之代数和 ， 等于该截面对于同一轴的静矩。
静矩和形心
n
S y
zdA
A
Ai zCi
i 1
n
S z
ydA
A
A i yCi
i 1
其中 Ai —第 i个简单截面面积；
( yCi, zCi)—第 i个简单截面的形心坐标；
静矩和形心
静矩和形心
一、静矩(面积的一次矩)
设平面图形，取 yoz 为图形所在平面的坐标 系，在坐标为（y , z）处取面积元dA。 截面对 y , z 轴的静矩为 z
y
S y
zdA
A
dA
m3
z
S z
ydA
A
O
y
静矩和形心
S y
zdA
A
Sz
ydA
A
1.静矩可正，可负，也可能等于零；
2.同一图形，对不同的坐标轴，静矩也不同。
静矩和形心
二、截面的形心(Centroid of an area)
n
Ai zCi
zC
i1 n
Ai
i1
z d
A
A
A
z
z zC
dA C
O yC
y
Sy A
y
静矩和形心
n
Ai
i1
A ydA
第七章 静矩及其性质
Iy Iy i i 1 n I z I z i i 1 n I yz I yz i i 1
n
I z i 、 I y i、 I yz i 分别为第个i简单图形对y轴和z轴的惯 式中， 性矩和惯性积。
22
§7-3
17
例2
求图示矩形的 I z , I y , I yz ,i y ,iz z
dz z
h
c
y
b
1 3 b 3 bh I y z dA z A 12 3 h 2 1 3 2 I z y dA hb A 12 Iy 3 iy h A 6
2
h 2
Iz 3 iz b A 6 I yz yzdA 0
z
60 96 65 (77 ) 39.7(mm ) 96 77 13
§7-2
惯性矩和惯性积
y
z y dA z
一、简单图形的惯性矩 1、定义： dA对z轴的惯性距: dA对y轴的惯性距: 图形对z轴的惯性矩:
2
dIz y dA 2 dIy z dA o
I z y 2 dA,
求圆环圆形的 I z , I y z D d y
I P I P大 I P小
1 1 D 4 d 4 32 32 1 D 4 ( 1 4 ) 32
d D
I y I z I z大 I z小
1 D 4 (1 4 ) 64
21
三、组合图形的惯性矩及惯性积 根据定义可知，组合图形对某坐标轴的惯性矩 等于各个简单图形对同一轴的惯性矩之和；组合图 形对于某一对正交坐标轴的惯性积等于各个简单图 形对同一对轴的惯性积之和。用公式可表示为
第10章平面图形的几何性质ppt课件
组合图形——由几个简单图形（如矩形、圆形等） 组成的平面图形
如：
1.静矩
n
Sx
yd A
ydA
A n
A1 An n
i 1
Ai
yd A
S xi Ai yCi A yC
i 1
i 1
n
n
S y S yi Ai xCi A xC
i 1
i 1
y
xC C yC
x O
2.形心
n
Ai xCi
Ix0
Ix
Iy 2
1 2
Ix Iy
2
4
I
2 xy
I y0
Ix
Iy 2
1 2
Ix
Iy
2
4
I
2 xy
极大值Imax 极小值Imin
例 计算所示图形的形心 主惯性矩.
120 40 z 20
25 20 10
解：该图形形心C的位置已
确定，如图所示.
过形心C选一对座标轴
C
y
y z 轴，计算其惯性矩(积).
1.5d (2d )3 3d 2(0.177d )2 [πd 4 πd 2 (0.5d 0.177d )2 ]
12
64 4
2d
0.685d 4
I zC I矩zC I圆zC
(1.5d )3 2d πd 4 0.513d 4
12
64
I yC zC 0
所以 yCzC 便是形心主轴
——反映平面图形的形状与尺寸的几何量
如：
在轴向拉（压）中：
FN A
l FNl EA
本章介绍：平面图形几何性质的定义、计算方法和性质
§10.1 静矩与形心
如：
1.静矩
n
Sx
yd A
ydA
A n
A1 An n
i 1
Ai
yd A
S xi Ai yCi A yC
i 1
i 1
n
n
S y S yi Ai xCi A xC
i 1
i 1
y
xC C yC
x O
2.形心
n
Ai xCi
Ix0
Ix
Iy 2
1 2
Ix Iy
2
4
I
2 xy
I y0
Ix
Iy 2
1 2
Ix
Iy
2
4
I
2 xy
极大值Imax 极小值Imin
例 计算所示图形的形心 主惯性矩.
120 40 z 20
25 20 10
解：该图形形心C的位置已
确定，如图所示.
过形心C选一对座标轴
C
y
y z 轴，计算其惯性矩(积).
1.5d (2d )3 3d 2(0.177d )2 [πd 4 πd 2 (0.5d 0.177d )2 ]
12
64 4
2d
0.685d 4
I zC I矩zC I圆zC
(1.5d )3 2d πd 4 0.513d 4
12
64
I yC zC 0
所以 yCzC 便是形心主轴
——反映平面图形的形状与尺寸的几何量
如：
在轴向拉（压）中：
FN A
l FNl EA
本章介绍：平面图形几何性质的定义、计算方法和性质
§10.1 静矩与形心
材料力学(附录)
40 10
20 y
1
C2
15
解：
y Ai yi A
A1
y 1
A2
y 2
A1 A2
a
10120024054400115520
x
26.25(cm)
y
Ix Ix i Ix1 Ix2
x1
I x12011203 2010(4526.25)2
单位：cm
称x0 、y0 轴为主轴，称 I x0 和I y0 为主惯性矩。
y
y0
x0
0
x
使惯性积为零的坐标轴称为主轴。平面图形对主轴的惯性 矩称为主惯性矩。
三、图形的形心主惯性轴和形心主惯性矩
主轴过形心时，称其为形心主轴。平面图形对形心主轴之
惯性矩，称为形心主惯性矩。
yC yC0
tan20
2Ixcyc Ixc Iyc
IxC I矩xC I圆xC
[1 .5 d (2 d )3 3 d 2 (d 0 .8d 2 )2 ] 3 [d 4 d 2 (1 .5 d 0 .8d 2 )2 ]3
Iy
Iy
i
I y1
Iy2
1020 3 I y1 12
0.67104(cm4)
I
y
2
40 15 12
3
1.13104(cm4)
x
Iy Iy1Iy2
y
x1
(0.671.13)104
1.8104 (cm4 )
[例] 计算图示图形对其形心轴x轴的惯性矩。
12 y
解：
x 0
20
①
y yi Ai
静矩和形心PPT课件
z2 dA
h/2
z2bdz
bh 3
A
h/2
12
dz
z
第19页/共41页
例：求图示圆平面对y、z轴的惯性矩。
d4
I p 32 Iy Iz Ip
Iy Iz
第20页/共41页
CL6TU8
三、惯性 积
z
y dA
z
O
y
I yz
yzdA
A
第21页/共41页
如果所选的正交坐标轴中，有一个坐标 轴是对称轴，则平面图形对该对坐标轴的惯
A yc2 dA 2a A yc dA a 2
dA
A
Izc a2 A
第26页/共41页
z
zc
a
yc
b
O
y
Iz IzC a2 yC b2 A
I z I zC a 2 A
I yz I yCzC abA
第28页/共41页
例：求图示平面图形对y轴的惯性矩 Iy
O
y
I p
2 dA
A
定义为图形对O点的极惯性矩
第4页/共41页
§6-1 静矩和形心
z
y dA
z
O
y
Sz
ydA
A
,
Sy
zdA
A
第5页/共41页
形心坐标： z
yC
zC
O
y
ydA
yC
A
A
,
第6页/共41页
zC
zdA
A
ACL6TU3
静矩和形心坐标之间的关系：
z yC
zC
yC
Sz A
第34页/共41页
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
或 iy
Iy A
Iz A iz2
或
iz
Iz A
i y 、iz 分别称为平面图形对y轴和z轴的惯性半径
扶风书屋
17
二、极惯性矩
z
I p
2 dA
A
y dA
z
2 y2 z2
Ip Iy Iz
O
y
扶风书屋
18
例：求图示矩形对对称轴y、z的惯性矩。
扶风书屋
CL61T9 U7
解： Iy
必等于零。 I yz 0 z
dA dA
y
扶风书屋
CL62T3 U9
几个主要定义: (1)主惯性轴 当平面图形对某一对正交坐
标轴y0、z0的惯性积 Iy0z0=0时，则坐标轴 y0、z0 称为主惯性轴。
因此，具有一个或两个对称轴的正交坐标 轴一定是平面图形的主惯性轴。
(2)主惯性矩 平面图形对任一主惯性轴的
zdA
A
ACL6T7 U3
静矩和形心坐标之间的关系：
z
yC C
zC
yC
Sz A
zC
Sy A
O
y
S y A z
C 扶风书屋
,
Sy
zC
A 8
例：计算由抛物线、y轴和z轴所围成的平面图 形对y轴和z轴的静矩，并确定图形的形心坐标。
z
y2
z
h1
b2
O
扶风书屋
y
CL6T9 U4
解：
Sy
z dA 2
扶风书屋
35
主惯性矩公式：
I
y0
Iy
Iz 2
I
z0
Iy
2
Iz
Iy
2
Iz
2
I
2 yz
Iy
2
Iz
2
I
2 yz
或简写成：
I y0 I z0
Iy
Iz 2
Iy 扶风书屋
Iz 2
2
I
2 yz
36
求形心主惯性轴的位置及形心主惯性矩 大小的步骤： 1）找出形心位置； 2）通过形心C建立参考坐标 yoz，求出
A yc2 dA 2a A yc dA a 2
dA
A
Izc a2 A
扶风书屋
27
z
zc
a
C
yc
b
O
y
Iz
I a A 2 zC扶风书屋
28
平行移轴公式：
I y I yC b2 A
I z I zC a 2 A
I yz I yCzC abA
扶风书屋
29
例：求图示平面图形对y轴的惯性矩 Iy
惯性矩称为主惯性矩。
扶风书屋
24
(3)形心主惯性轴 过形心的主惯性轴称为 形心主惯性轴。
可以证明:任意平面图形必定存在一对相 互垂直的形心主惯性轴。
(4)形心主惯性矩 平面图形对任一形心主 惯性轴的惯性矩称为形轴公式
z
zc
y
a
yc
y yc a z zc b
I y1 A z12 dA
( y sin z cos)2 dA A
Iz sin2 I y cos2 I yz sin 2
Iy
Iz 2
Iy
I z cos2
2扶风书屋
I yz sin 2 33
转轴公式：
I y1
Iy
Iz 2
Iy
Iz 2
cos 2 I yz
sin 2
I
z2 dA
h/2
z2bdz
bh 3
A
h/2
12
dz
z
扶风书屋
20
例：求图示圆平面对y、z轴的惯性矩。
d4
I p 32 Iy Iz Ip
Iy Iz
扶风书屋
CL62T1 U8
三、惯性积
z
y dA
z
O
I yz
yzdA
A扶风书屋
y
22
如果所选的正交坐标轴中，有一个坐标轴 是对称轴，则平面图形对该对坐标轴的惯性积
Iy、Iz、Iyz 3）求α0、Iy0、Iz0
第六章 平面图形的几何性质 z
y dA
z
O
扶风书屋
y CL6T1 U1
z
y dA
z
ydA
O
y
Sz
ydA
A
,
Sy
zdA
A
定义为图形对z轴扶和 风书屋y轴的静矩 2
z
y dA
z
y2 dA
O
y
Iz
y2 dA
A
,
Iy
z2 dA
A
定义为图形对z轴扶风和书屋 y轴的惯性矩 3
z
y dA
z
yzdA
z1
Iy
Iz 2
Iy
Iz 2
cos 2 I yz
sin 2
I
y1 z1
Iy
Iz 2
sin 2 I yz
扶风书屋
cos 2
34
主惯性轴方位：
设正交坐标轴y0 、z0 是主惯性轴，其方位
角为 0，则
I y0z0
Iy
2
Iz
sin 2 0
I yz
cos2 0
0
tan 2 0
2I yz Iy Iz
z
a
y
a
d
扶风书屋
CL6T30U11
解：
z
a
a
y
Iy
d (2a)3 12
d
CL6TU11
d 4
2
128
d2
8
2d
3 扶风书屋
2
d 8
2
2d
3
a 2 31
§6-4 转轴公式 主惯性轴和主惯性矩
扶风书屋
CL6T3U2 12
y1 y cos z sin z1 y sin z cos
扶风书屋
CL61T4 U6
解：
Sy
b
h 2
a a
h 4
a 2
b h2
2 4
a
2
扶风书屋
15
§6-2 惯性矩、极惯性矩和惯性积
一、惯性矩 z
y dA
z
O
y
Iz
y2dA ,
A
扶风书屋
Iy
z2 dA
A
16
工程中常把惯性矩表示为平面图形的面积与 某一长度平方的乘积，即
Iy A iy2
2h 5
3 扶风书屋
11
例：确定图示图形形心C的位置。
扶风书屋
CL61T2 U5
解： yC
Sz A
10 120 5 70 10 45 19.7mm 1200 700
zC
Sy A
10 120 60 70 10 5 39.7mm 1200 700
扶风书屋
13
例：求图示阴影部分的面积对y轴的静矩。
dA
C
zc yc bz
O
扶风书屋
yCL6T26U10
Iz
y2 dA,
A
Iy
z2 dA,
A
Iyz
yz dA
A
I zc A yc2 dA , I yc A zc2 dA , I yczc A yc zc dA
y yc a , z zc b
Iz
y 2 dA
A
A ( yc a)2 dA
O
y
I yz
yzdA
A
定义为图形对y扶风、书屋z轴的惯性积 4
z
y dA
z
2 dA
O
y
I p
2 dA
A
定义为图形对O扶风点书屋 的极惯性矩 5
§6-1 静矩和形心
z
y dA
z
O
y
Sz
A
ydA
,
扶风书屋
Sy
zdA
A
6
形心坐标： z
yC C
zC
O
y
yC
ydA
A
,
A 扶风书屋
zC
A
b 0
1
h
2
1
2
y2 b2
2
d
y
4bh 2 15
Sz
A
y dA
b 0
yh1
y2
b
2
d
y
b2h 4
z
h
z
h1
y2 b2
Oy
dy y
b扶风书屋
10
A
dA
A
b 0
h1
y2 b2
dy
2bh 3
形心坐标为:
bh 2
yC
Sz A
4 2bh
3b 8
3
4bh 2
zC
Sy A
15 2bh