组合惯性矩
(2021年整理)惯性矩及惯性积

惯性矩及惯性积编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(惯性矩及惯性积)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为惯性矩及惯性积的全部内容。
惯性矩及惯性积在讨论物体的平面动力学时,需介绍对通过质心G且与运动平面垂直的轴之惯性矩I G。
在三维动力分析时,有时需计算六个惯性量。
这些项称为惯性矩及惯性积(moments and products of inertia),其以特殊方式描述物体相对于一已确定方向及原点的坐标系统的质量分布。
惯性矩考虑下图所示的刚体,物体的微分元素dm对三坐标轴的任一轴的惯性矩(moment of inertia)可定义为:元素的质量和此元素到该轴的最短距离的平方之乘积。
例如,如图中所标示的,故dm对x轴的质量惯性矩为物体的质量惯性矩I xx为上式对整个物体的质量积分。
因此,对各轴的惯性矩可写成在此可看出惯性矩必为正的量,由于此量是质量dm与距离平方的乘积之和,而质量dm必为正。
惯性积微分元素dm相对于一组相互正交的两平面的惯性积(product of inertia)定义为:质量元素与至各平面的垂直(或最短)距离的乘积。
例如,相对于y-z及x-z 平面,上图的质量元素的惯性积dI xy为dI xy = xydm同时注意dI yx = dI xy。
对整个质量积分,物体对各平面组合的惯性积可表示为不像惯性矩必为正,惯性积可为正、负或零.其结果是视其定义的两个坐标的符号而定,因其符号的变化是彼此独立的。
特殊情况,如质量对称于两正交平面之一或两者,则相对于此二平面的惯性积将为零,在此情况下,质量元素将成对出现于对称平面的两侧,其中一例的元素,惯性积为正,两另一例对应元素的惯性积为负,故其和为零。
惯性矩

1、静矩(求形心)⎰=AZ ydA S⎰=Ay zdA SSz 、Sy 分别定义为图形对z 轴和y 轴的静矩,也称为图形对z 轴和y 轴的一次矩。
平面图形的静矩是对某一坐标而言的,同一图形对不同的坐标轴,其静矩也就不同。
静矩的数值可能为正值,可能为负值,也可能为零。
静矩的量纲是长度的三次方。
静矩用来求平面图形的形心坐标:A zdAz A ydAy AA⎰⎰==对于规则的形状,可以将其划分为若干个规则的简单图形,通过组合求的形心。
212211212211A A z A z A z A A y A y A y ++=++=注:A 为简单图形的面积(空心面积可以为负值),y 、z 为简单图形的形心坐标值2、惯性矩⎰⎰==Ay AZ dAz I dAy I 22Iz 、Iy 分别定义为图形对z 轴和y 轴的惯性矩,也称为图形对z 轴和y 轴的二次轴矩。
惯性矩始终为正值,惯性矩的量纲是长度的四次方。
计算步骤123222332202202bh bx dx x b x bdx dA z I h h Ay =⨯=⨯=⨯⨯==⎰⎰⎰左图三角形面积对z轴的惯性矩1243)()(44322hyhydyyyhydyyhI hhz=-=-=⨯-=⎰⎰右图关于z轴的惯性矩为左图的四倍34hIz=惯性距的平行移轴定理:有了它规则形状的物体就不用通过积分来求惯性矩了,省时省力(但精准度差了一些)截面图形对某轴的惯性矩,等于它对该轴平行的形心轴的惯性矩,加上两轴间距离的平方乘以截面面积。
A a I I xc x 2+=Ix ——截面图形对目标轴的惯性矩(目标轴:组合图形的形心轴) Ixc ——截面图形对形心轴的惯性矩(注意理解:此处的形心轴是指划分的规则截面的形心轴)a ——两轴之间的距离 A ——截面图形的面积3、极惯性矩图形对于任意一对互相垂直的轴的惯性矩之和,等于它对该两轴交点的极惯性矩。
I p=I z+I y4、惯性积在平面图形的坐标(x ,y )处,取微面积dA ,遍及整个图形面积的积分⎰=AyzyzdA I ,定义为图形对y ,z 轴的惯性积。
惯性矩的计算方法

第1节静矩和形心4.1静矩和形心任何受力构件的承载能力不仅与材料性能和加载方式有关.而口与构件截面的几何形状和尺寸有关.如:计算杆的拉伸与压缩变形时用到截面而积A ,计算圆轴扭转变形时用到横截面的极惯性矩I?等.A、1?等是从不同角度反映了截而的几何特性,因此称它们为截而图形的几何性质.4.1静矩和形心设有一任意截而图形如图4 一1所示,其面积为A .选収直角坐标系yoz ,在坐标为(y,z)处取一微小而积dA ,定义微而积dA乘以到y轴的距离z ,沿整个截面的积分,为图形对y轴的静矩S?,其数学表达式(4 -la )同理,图形对z轴的静矩为□4-1图41截面静矩与坐标轴的选取有关•它随坐标轴y、z的不同而不同.所以静矩的数值可能足正,也可能足负或定零.静矩的虽纲为长度的三次方.确定截面图形的形心位置(图4-1中C点):A (4-2b)第1页共30页式中T、"为截而图形形心的坐标值.若把式(4-2)改写成心"•儿,為"•乙(4 3)性质:・若截面图形的静矩等于零,则此坐标轴必定通过截面的形心.・若坐标轴通过截而形心,则截而对此轴的静矩必为零.・山于截而图形的对称轴必定通过截而形心,故图形对其对称轴的静矩恒为零。
4 )工程实际中,有些构件的截面形状比较复杂,将这些复杂的截面形状看成是山若干简单图形(如矩形、圆形等)组合g而成的.对于这样的组合截而图形,计算静矩(S»‘ r)与形心坐标(y*、z ')时,可用以下公式1-1 2-1式中A— y i , z i分别表示第,个简单图形的面积及其形心坐标值,n为组成组合图形的简单图形个数.即:组合图形对某一轴的静矩等于组成它的简单图形对同一轴的静矩的代数和.组合图形的形心坐标值等于组合图形对相应坐标轴的静矩除以组合图形的面积.组合截面图形有时还可以认为是山一种简单图形减去另一种简单图形所组成的.例4J己知T形截面尺寸如图4-2所示,试确定此截面的形心坐标值.i-1 i-1 (4-5)图4-2解:(1)选参考轴为y 轴,z 轴为对称轴,(2)将图形分成I 、口两个矩形,则= 20 x 100加朋 S 右=(10 + 140)^^34 = 2Q X 14%/,22 二注型(3)代入公式(4・5)20x100x150+20x140x70 20x100 + 20x140此=°4.2惯性矩、惯性积和惯性半径设任一截面图形(图4-3),其而积为A ・选取直角坐标系yoz ,在坐标为(y 、z)处取一微小面积dA ,定义此微2面积dA 乘以到坐标原点o 的距离的平方Q ,沿整个截面积分,为截而图形的极惯性矩I?.做而积dA 乘以到坐标轴y 的2距离的平方2 ,沿整个截而积分为截面图形对y 轴的惯性矩I 》•极惯性矩、惯性矩常简称极惯矩、惯矩.j.l ~2Z4数学表达式为打=f p^dA极惯性矩“俎(4-6)对y轴惯性矩图4-3山图4-3看到“ =y +Z 9所以有打=\A^dA= £cy2 +/)曲二必+加必即;? (4-8)式(4-8)说明截面对任一对正交轴的惯性矩之和恒等于它对该两轴交点的极惯性矩。
惯性矩
x0
x IIII 10
120
10
C
70
I y I Iy I IIy I IIIy 1.84106 mm 4
5.08106 mm 4
I xy I Ixy I IIxy I IIIxy -2.31106 mm 4
附录I 平面图形的几何性质
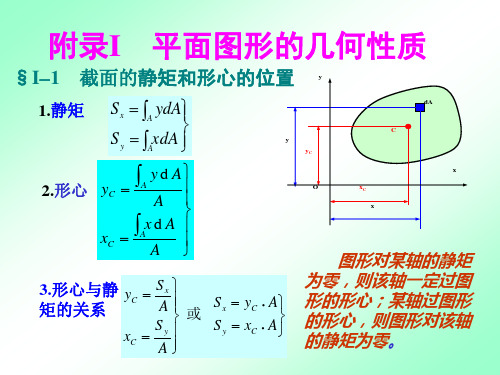
§I-1 截面的静矩和形心的位置
1.静矩
S x A ydA S y AxdA
y yC x O xC y dA C
y d A 2.形心 yC A A xd A A xC A
x
3.形心与静 yC S x S x yC A A 矩的关系 或 Sy S y xC A
yC O
dy
S x 2r 3 / 3 4r yC 2 A r / 2 3
C r
y x
例I-2 求图示图形的形心。 解:将此图形分别为I、II、III三 部分,以图形的铅垂对称轴为y轴, 过II、III的形心且与y轴垂直的轴线 取为x轴,则
yC Ay A
i Ci
10
y y1
200
10 I II O III
300
C y 150 C
x1
x
i
(20010) (5 150) 2 (10 300) 0 20010 2 (10 300) 38.8 mm
由于对称知: xC=0
§I-2 极惯性矩 惯性矩 惯性积
1.极惯性矩: I p A 2 dA 为图形对一点的极惯性矩;
[I z C 1 ( y C - y 1 ) 2 A 1 ][ I z C 2 ( y C - y 2 ) 2 A 2 ] 34530mm 4
惯性矩

§I-4 惯性矩和惯性积的转轴公式 截面的主惯性轴和主惯性矩
一、惯性矩和惯性积的转轴公式 1.公式推导: 2.转轴公式:
cos - I xy sin 2 2 2 Ix Iy Ix - Iy Iy cos I xy sin 2 2 2 Ix - Iy Ix y sin 2 I xy cos 2 2 Ix
b
x1
2
bh 2h bh bh3 I x I x a2 A 36 3 2 4
3 2
2 C
2
30 C2 2 y2 C C1 y1 zC2 zC 30 5
ห้องสมุดไป่ตู้
1
yC
zC1
z
5 yC 再求截面对形心轴的惯性矩:
求T形截面对形心轴的惯性矩 先求形心的位置: 取参考坐标系如图,则: zC 0 A i y i A1 y 1 A 2 y 2 23.75mm yC A1 A 2 Ai y C、z C即截面的形心轴。
I x I xi
i 1
n
,I y I y i ,I xy I xy i
i 1 i 1
n
n
已知: I x C 、I y C 、I x C y C ,形心在xOy坐标系下的坐标(a,b),求Ix、Iy、Ixy y b yC x
2 I x Ay 2dA A(a y C ) 2 dA A(a 2 2ay C y C )dA 2 a 2 AdA 2a A y CdA Ay CdA
101203 6010 3 ( 60 - 5 ) 2 ( 6010) 2 12 12
10
x0
x IIII 10
惯性矩的计算方法

I等. I等是从不同角度反映了截S,其数学表达式(4 -1a )(4-1b)(4 -2a )(4-2b)式中 y、 z 为截面图形形心的坐标值.若把式 (4-2) 改写成(4-3)性质:•若截面图形的静矩等于零,则此坐标轴必定通过截面的形心.•若坐标轴通过截面形心,则截面对此轴的静矩必为零.•由于截面图形的对称轴必定通过截面形心,故图形对其对称轴的静矩恒为零。
4 )工程实际中,有些构件的截面形状比较复杂,将这些复杂的截面形状看成是由若干简单图形 ( 如矩形、圆形等 ) 组合而成的.对于这样的组合截面图形,计算静矩 (S) 与形心坐标 (y、 z ) 时,可用以下公式(4-4)(4-5)式中 A, y , z 分别表示第个简单图形的面积及其形心坐标值, n 为组成组合图形的简单图形个数.即:组合图形对某一轴的静矩等于组成它的简单图形对同一轴的静矩的代数和.组合图形的形心坐标值等于组合图形对相应坐标轴的静矩除以组合图形的面积.组合截面图形有时还可以认为是由一种简单图形减去另一种简单图形所组成的.例 4-1 已知 T 形截面尺寸如图 4-2 所示,试确定此截面的形心坐标值.、两个矩形,则设任一截面图形 ( 图 4 — 3) ,其面积为 A .选取直角坐标系 yoz ,在坐标为 (y 、 z) 处取一微小面积 dA ,定义此微面积 dA 乘以到坐标原点o的距离的平方,沿整个截面积分,为截面图形的极惯性矩 I.微面积 dA 乘以到坐标轴 y 的距离的平方,沿整个截面积分为截面图形对 y 轴的惯性矩 I.极惯性矩、惯性矩常简称极惯矩、惯矩.数学表达式为极惯性矩 (4-6)对 y 轴惯性矩 (4 -7a )同理,对 z 轴惯性矩 (4-7b)由图 4-3 看到所以有即(4-8) 式 (4 — 8) 说明截面对任一对正交轴的惯性矩之和恒等于它对该两轴交点的极惯性矩。
在任一截面图形中 ( 图 4 —3) ,取微面积 dA 与它的坐标 z 、 y 值的乘积,沿整个截面积分,定义此积分为截面图形对 y 、z 轴的惯性积,简称惯积.表达式为(4-9)惯性矩、极惯性矩与惯性积的量纲均为长度的四次方. I,I,I恒为正值.而惯性积 I其值能为正,可能为负,也可能为零.若选取的坐标系中,有一轴是截面的对称轴,则截面图形对此轴的惯性积必等于零.当截面图形对某一对正交坐标轴的惯性积等于零时,称此对坐标轴为截面图形的主惯性轴.对主惯性轴的惯性矩称为主惯性矩.而通过图形形心的主惯性轴称为形心主惯性轴 ( 或称主形心惯轴 ) .截面对形心主惯性轴的惯性矩称为形心主惯性矩 ( 或称主形心惯矩 ) .例如,图 4-4 中若这对 yz 轴通过截面形心,则它们就是形心主惯性轴.对这两个轴的惯性矩即为形心主惯性矩.工程应用中 ( 如压杆稳定中 ) ,有时将惯性矩表示成截面面积与某一长度平方的乘积,即,或写成, ( 4-10 )式中 i分别称为截面图形对 y 轴、 z 轴的惯性半径.其量纲为长度的一次方.例 4-2 已知矩形截面的尺寸 b,h( 图 4-5) ,试求它的形心主惯性矩.解:取形心主惯性轴 ( 即对称轴 )y,z ,及 dA=dy,代入公式 (I— 7a ,) 得同理:例 4-3 设圆的直径为 D( 图 4-6) ,试求图形对其形心轴的惯性矩及惯性半径值.解: (1) 求惯性矩因为图形对称, y,z 为对称轴,所以 I= I这是较简单的解法.本例也可取出图 4-6 上的微面积 dA ,按积分法来求得。
组合截面惯性矩求解方法研究

中图 分 类 号 : T U 3 1 1 . 4
文献标识码 : A
在众多的力学概念中, 惯性矩极为重要, 因为构件的许 多受力指标都与之相关。作为工程技术人员, 应该熟悉惯 性矩的求解方法, 至少应该知道如何求解常见构件截面的 惯性矩。工作中, 经常需要用到截面惯性矩, 此时, 在现有
第1 5卷 第 1 1 期 2 0 1 5年 1 1月
鸡 西 大 学 学 报
J OURNA L 0F J I XI UN I VER S I T Y
Vo 1 . 1 5 No .1 1
NO Y . 2 Ol 5
文章编号 : 1 6 7 2— 6 7 5 8 ( 2 0 1 5 ) 1 1 — 0 0 5 8— 3
作 者简 介 : 吴 三元 , 硕 士, 贵 州大 学 ; 二级注册建造师 , 凯 里 碧 桂 园物 业 发 展 有 限公 司 。 基 金项 目 : 国 家 自然 科 学 基 金 ( 编号 : 5 1 4 6 8 0 0 8 ) ; 贵州大学研究生创新基金 ( 研理工 2 0 1 4 0 6 2) 。
详 细 介 绍 了如 何 运 用 A u t o C A D, P K P M, A B A Q U S等 软 件 求 解 组 合 截 面 的惯 性 矩 以及 各 自的优 缺 点 , 对 工 程 技 术 人
员而言 , 有一定的参考价值。
关键词 : 组合截面 ; 惯性 矩; P K P M; A u t o C A D
组 合 截 面 惯 性 矩 求解 方 法研 究
吴 三元 , 庄锦 亮 , 赵 玉
( 贵 州 大 学 土木 工程 学 院 , 贵州 贵阳 5 5 0 0 2 5 )
摘
要: 惯性矩是一 个重要 的截 面几何 参数 , 构件 的许 多力 学指标都 与之 相关。拟 以组合截 面 为研 究对 象 ,
截面的几何性质面积矩惯性矩惯性积平行移轴公式

1
HOHAI UNIVERSITY
2
HOHAI UNIVERSITY
例1 求如图矩形Sz和Sy
解:Sz
ydA
A
ah
ybdy
a
bh(a h) 2
A yC
同样地
Sy
bh(d
b) 2
A
zC
z b/2 b/2 a
y h/2
h/2
dy
y
d
3
HOHAI UNIVERSITY
解: A1 15050mm 2 A2 18050mm 2
150
A3 250 50mm 2
50
C1
yC1 255mm yC2 140mm
5c0
C2
yC3 25mm zC1 zC2 zC3 0
50
C3
z
yC
A1
yC1 A2 yC2 A1 A2 A3
A3
yC 3
250
y
15050 255 18050140 25050 25 mm 15050 18050 25050
i=1
同理
n
Iz =∑ Izi
i=1
n
Iyz =∑ Iyzi
i=1
12
HOHAI UNIVERSITY
例5 图示矩形中,挖去两个直径为d 的圆形,求余下 图形对z轴的惯性矩。
b/2 b/2
z
Iz
1 bh3 12
5 d 4
32y13HOHAI UNIVERSITY
14
HOHAI UNIVERSITY
作业题 求图示工字形截面对z轴的惯性矩。
b d
z
15
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、组合截面惯性矩的计算
例试计算图所示 T 形截面对形心轴 z、y的惯性矩。
图中尺寸单位为m。
解: ( 1 )确定形心位置。
’
由于y 轴为截面的对称轴,形心必在 y 轴上,故zc =0。
为确定 yc ,选参考坐标系oz1y 。
将T形分割为两个矩形,它们的面积和形心坐标分别为
)可得
由式( 4 -12
整个截面对y、z轴的惯性矩应分别等于组成它的两个矩形对y、z轴惯性矩之和,而两矩形对z轴的惯性矩应根据平行移轴公式计算,即
由于y轴通过两个矩形的形心,故可由表 7 - 1 给出的计算公式直接计算它们对y轴的惯性矩,Array
即
A1=60.25x3=180.75 y1=36+A1=216.75 A2=28x36=1008 y2=18
Yc=48.22 a1=48.22-1.5=46.72 a2=48.22-18=30.22
Is=1425578.718
L=1.1(Dδ)½=60.25mm。
