高等数学-中值定律与讲义导数的应用
合集下载
高等数学第三章中值定理与导数的应用
1 0. 当 x 0 时 0 , 因此由上式得 cos
0? 问是否可由此得出 lim cos 1 x
x0
不能 !
因为 ( x) 是依赖于 x 的一个特殊的函数.
x 0 表示 x 从右侧以任意方式趋于 0 .
备用题 1. 设 f ( x) 在 [0,1] 连续, (0 ,1) 可导,且 f (1) 0 ,
f ( x0 ) 0, 即方程有小于 1 的正根
2) 唯一性 .
f ( x) 在以 x0 , x1 为端点的区间满足罗尔定理条件 , 在 x0 , x1 之间
至少存在一点
假设另有
但
矛盾, 故假设不真!
二、拉格朗日中值定理
满足: (1) 在区间 [ a , b ] 上连续
y
y f ( x)
使
f ( x) sin ln x ,
F ( x) ln x
则 f (x) , F(x) 在 [ 1 , e ] 上满足柯西中值定理条件, f (e) f (1) f ( ) , (1, e ) 因此 F (e) F (1) F ( ) 1 cos ln 即
1
分析:
例5. 试证至少存在一点 法2 令 f ( x) sin ln x sin1 ln x
使
则 f (x) 在 [ 1 , e ] 上满足罗尔中值定理条件, 因此存在 使
1 1 f ( x) cos ln x sin1 x x
内容小结
1. 微分中值定理的条件、结论及关系
3 15 4 . _____
方程
有 3 个根 , 它们分别在区间 (1, 2) , (2 , 3) , (3 , 4) 上.
第四章中值定理与导数的应用精品文档

nxn1
lim
x
1 nxn
0
例5. 求 xl im exnx (n0,0).
型
解: (1) n 为正整数的情形.
原式
lim
x
nxn1
ex
罗xl imn(n21e)xxn2
罗罗xl imnne!x 0
例5. 求xl im exnx (n0,0).
费马引理
微
分 中
罗尔中值定理
值 定
拉格朗日中值定理
理
柯西中值定理
导数与差商
函数导数的定义为
f(x)lim f(xx)f(x)
x 0
x
即函数在点 x 处的导数等于 x 0时, 函数
在点 x 处的差商 f(xx)f(x) 的极限值.
x
我们常常需要从函数的导数所给出 的局部的或“小范围”性质, 推出其整体的 或“大范围”性质. 为此, 我们需要建立函 数的差商与函数的导数间的基本关系式, 这些关系式称为“微分学中值定理”.
证明 f(x 方 )0仅 程有三 ,并个 指实 出根 .根
证 f ( x ) C ( [ a ,b ] [ b ,, c ] [ c ,, d ] ) ,
又 f ( a ) f ( b ) f ( c ) f ( d ) 0 , f(x)是四次 ,在 (多 , ) 内 项可 ,式微 在[a, b],[b, c],[c, d]上运用罗尔 ,得 中值
x0
颠倒行不行 ?
解
倒数法
limxlnx limlnx
x0
x0 1
x
行 , 但繁些 .
存在一个选择 问题.
1
lim x lim(x) 0
lim
x
1 nxn
0
例5. 求 xl im exnx (n0,0).
型
解: (1) n 为正整数的情形.
原式
lim
x
nxn1
ex
罗xl imn(n21e)xxn2
罗罗xl imnne!x 0
例5. 求xl im exnx (n0,0).
费马引理
微
分 中
罗尔中值定理
值 定
拉格朗日中值定理
理
柯西中值定理
导数与差商
函数导数的定义为
f(x)lim f(xx)f(x)
x 0
x
即函数在点 x 处的导数等于 x 0时, 函数
在点 x 处的差商 f(xx)f(x) 的极限值.
x
我们常常需要从函数的导数所给出 的局部的或“小范围”性质, 推出其整体的 或“大范围”性质. 为此, 我们需要建立函 数的差商与函数的导数间的基本关系式, 这些关系式称为“微分学中值定理”.
证明 f(x 方 )0仅 程有三 ,并个 指实 出根 .根
证 f ( x ) C ( [ a ,b ] [ b ,, c ] [ c ,, d ] ) ,
又 f ( a ) f ( b ) f ( c ) f ( d ) 0 , f(x)是四次 ,在 (多 , ) 内 项可 ,式微 在[a, b],[b, c],[c, d]上运用罗尔 ,得 中值
x0
颠倒行不行 ?
解
倒数法
limxlnx limlnx
x0
x0 1
x
行 , 但繁些 .
存在一个选择 问题.
1
lim x lim(x) 0
第四章中值定理与导数的应用(全)

e e e( x 1) e x e
x
于是
e e x.
x
例2
证明 当x 0时,
x l n1 x x 1 x
证 设 f x ln1 x , 在[0, x]上应用拉格朗日中值定理
f x f 0 f x 0, 0 x
, 使得f () f () 0
证 则F(x)在[0,1]上 构造函数:令F(x)=xf(x), 满足罗尔中值定理的条件,于是在开区间(0,1) 内至少存在一点 ,使得
f () f () 0
二、拉格朗日中值定理 (Lagrange):
若f x 在 a, b 上连续,在a, b内可导,
f ( x 0 x ) f ( x 0 ) 0 x
C
从而当x 0时
f ( x 0 x ) f ( x 0 ) 0 x
x
0
根据函数f ( x)在x0可导的条件,再由极限 的保号性,便得到
f ( x 0 x ) f ( x 0 ) f ( x0 ) f ( x0 ) lim 0 x 0 x
即 5 使得f 0. , , 2 6 6
5
例2、不求导数,判断函数 f ( x ) ( x 1)( x 2)( x 3)的导数有几个 实根,以及其所在范围 。
解 显然,f (1) f (2) f (3) 0.
且f ( x)在[1,2]和[2,3]上满足罗尔定理条件。
则至少有一点 ,
a b,使得
f 0
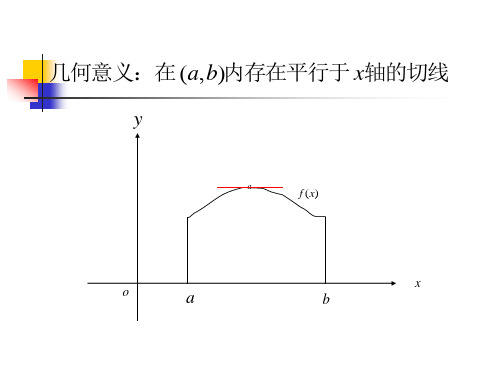
几何意义
几何上,若f x 满足罗尔定理, 则此曲线上至少存在一 点C, 过该点的切线平行于x轴如图.
第三章中值定理与导数的应用课件
那么在(a,b)内至少有一点 使等式
f (b) f (a) f ' ( ) 成立 F (b) F (a) F ' ( )
例1:验证罗尔定理对函数y ln sin x在区间
[
6
,
5
6
]的正确性
解:y ln sin x在[ , 5 ]上连续
66
y ln sin x在( , 5 )上可导
66
lim 2 cos3x 3 1 x0 3 cos2x 2
例6:求
lim
x
xn ex
(n 0, 0)
解:lim xn lim n xn1 lim n (n 1) xn2
e e x x x
x x
2 ex
lim n! 0
x n ex
例7:求 lim x sin x
且f ( ) ln 1 f (5 )
6
2
6
又
y'
c os x
ctgx
令
0
x
(
, 5 )sin x源自2 662罗尔定理正确
例2:证明arctgx arcctgx
2
证 : (arctgx arcctgx)' 1 1 0 1 x2 1 x2
arctgx arcctgx c
取x 1 c c
若f (x)是一般的函数,且它存在直到n 1 阶的导数,那么
n
f (x)
f (k) (a) (xa)k ?
k 0 k!
泰勒(Taylor)中值定理
泰勒(Taylor)中值定理 如果函数 f ( x)在含有 x0 的某个开区间(a, b)内具有直到(n 1)阶的导数,则
当 x在(a, b)内时, f ( x)可以表示为( x x0 )的一个
f (b) f (a) f ' ( ) 成立 F (b) F (a) F ' ( )
例1:验证罗尔定理对函数y ln sin x在区间
[
6
,
5
6
]的正确性
解:y ln sin x在[ , 5 ]上连续
66
y ln sin x在( , 5 )上可导
66
lim 2 cos3x 3 1 x0 3 cos2x 2
例6:求
lim
x
xn ex
(n 0, 0)
解:lim xn lim n xn1 lim n (n 1) xn2
e e x x x
x x
2 ex
lim n! 0
x n ex
例7:求 lim x sin x
且f ( ) ln 1 f (5 )
6
2
6
又
y'
c os x
ctgx
令
0
x
(
, 5 )sin x源自2 662罗尔定理正确
例2:证明arctgx arcctgx
2
证 : (arctgx arcctgx)' 1 1 0 1 x2 1 x2
arctgx arcctgx c
取x 1 c c
若f (x)是一般的函数,且它存在直到n 1 阶的导数,那么
n
f (x)
f (k) (a) (xa)k ?
k 0 k!
泰勒(Taylor)中值定理
泰勒(Taylor)中值定理 如果函数 f ( x)在含有 x0 的某个开区间(a, b)内具有直到(n 1)阶的导数,则
当 x在(a, b)内时, f ( x)可以表示为( x x0 )的一个
中值定理与导数的应用(高等数学)省名师优质课赛课获奖课件市赛课一等奖课件
函数旳极大值与极小值统称为极值,使函数取得 极值旳点称为极值点.
定义 使导数为零的点(即方程f ( x) 0的实根)叫 做函数f ( x)的驻点.
定理(必要条件) 设 f ( x) 在点x0 处具有导数,且 在 x0处取得极值,那末必定 f '( x0 ) 0.
注意:可导函数 f ( x) 的极值点必定是它的驻 点, 但函数的驻点却不一定 是极值点.
2、罗必塔法则
(1). 0 型及 型未定式 0
定义 这种在一定条件下经过分子分母分别求导再 求极限来拟定未定式旳值旳措施称为罗必塔法则.
(2). 0 , , 00,1 , 0型未定式
关键:将其他类型未定式化为罗必塔法则可处理 旳类型 ( 0 ), ( ) .
0
定理 设(1)当x 0时,函数 f ( x) 及 F ( x) 都趋于零; (2) 在 a 点的某领域内(点 a 本身可以除外 ), f ( x) 及 F ( x) 都存在且 F ( x) 0; (3) lim f ( x) 存在(或为无穷大);
(2) 在开区间 ( a , b ) 内可导
(3)在开区间 ( a , b ) 内F(x) 0
至少存在一点
(a,b) , 使
f (b) f (a) F (b) F (a)
f ( ) . F( )
注意:若令F(x)=x,则柯西中值定理变为拉氏中值 定理,即拉
0
原式
lim
x
1
1
x 1 x2
2
lim
x
1
x
2
x
2
1.
例8
求
lim
x0
tan x x2 tan
x x
.
解
定义 使导数为零的点(即方程f ( x) 0的实根)叫 做函数f ( x)的驻点.
定理(必要条件) 设 f ( x) 在点x0 处具有导数,且 在 x0处取得极值,那末必定 f '( x0 ) 0.
注意:可导函数 f ( x) 的极值点必定是它的驻 点, 但函数的驻点却不一定 是极值点.
2、罗必塔法则
(1). 0 型及 型未定式 0
定义 这种在一定条件下经过分子分母分别求导再 求极限来拟定未定式旳值旳措施称为罗必塔法则.
(2). 0 , , 00,1 , 0型未定式
关键:将其他类型未定式化为罗必塔法则可处理 旳类型 ( 0 ), ( ) .
0
定理 设(1)当x 0时,函数 f ( x) 及 F ( x) 都趋于零; (2) 在 a 点的某领域内(点 a 本身可以除外 ), f ( x) 及 F ( x) 都存在且 F ( x) 0; (3) lim f ( x) 存在(或为无穷大);
(2) 在开区间 ( a , b ) 内可导
(3)在开区间 ( a , b ) 内F(x) 0
至少存在一点
(a,b) , 使
f (b) f (a) F (b) F (a)
f ( ) . F( )
注意:若令F(x)=x,则柯西中值定理变为拉氏中值 定理,即拉
0
原式
lim
x
1
1
x 1 x2
2
lim
x
1
x
2
x
2
1.
例8
求
lim
x0
tan x x2 tan
x x
.
解
高等数学习题课(3)中值定理与导数的应用

高等数学习题课
(3)
中值定理与导数的应用
第二课 中值定理与导数应用
I. 目的要求 ⒈ 理解罗尔定理、拉格朗日定理,了解柯西定理; 会用中值定理解决诸如方程根的存在性、不等 式证明等问题; ⒉ 了解泰勒定理的条件、结论及余项,掌握函数 ex , sinx, cosx, ln(1+x), (1+x)α的麦克劳 林公式; ⒊ 熟练掌握用洛必达法则求不定型极限的方法; ⒋ 熟练掌握求函数单调区间、极值、凹凸区间、 拐点的方法,并会用其证明一些相关问题。
证:由条件易知F (x)在 [1,2]上满足罗尔定理条件, 则 (1,2),使 F(1) 0 又 F(x) 2(x 1) f (x) (x 1)2 f (x) 在 [1,1]上连续,在(1,1)内可导,且 F(1) F(1) 0 由罗尔定理, (1, 1) (1, 2) 使 F() 0 #
(a 0)有极值,试证:曲线y f (x) 在点(a, f (a))处的
切线经过坐标原点。 证:曲线 y f (x) 在 (a, f (a)) 处的切线方程为
y f (a) f (a)(x a)
即 y f (a)x [ f (a) a f (a)]
由条件 (x) 在 x a 点有极值,且易知(x)在 x a 点可导
x
2
分析:只需证明 sin x x 0 3 cos x
证:令
f
(x)
sin x 3 cos x
x
sin
1
x cos 3
x
x
,显见
f
(0)
0;
f
(x)
cos
2 3
x
1 sin
2
x
4
cos 3
x
(3)
中值定理与导数的应用
第二课 中值定理与导数应用
I. 目的要求 ⒈ 理解罗尔定理、拉格朗日定理,了解柯西定理; 会用中值定理解决诸如方程根的存在性、不等 式证明等问题; ⒉ 了解泰勒定理的条件、结论及余项,掌握函数 ex , sinx, cosx, ln(1+x), (1+x)α的麦克劳 林公式; ⒊ 熟练掌握用洛必达法则求不定型极限的方法; ⒋ 熟练掌握求函数单调区间、极值、凹凸区间、 拐点的方法,并会用其证明一些相关问题。
证:由条件易知F (x)在 [1,2]上满足罗尔定理条件, 则 (1,2),使 F(1) 0 又 F(x) 2(x 1) f (x) (x 1)2 f (x) 在 [1,1]上连续,在(1,1)内可导,且 F(1) F(1) 0 由罗尔定理, (1, 1) (1, 2) 使 F() 0 #
(a 0)有极值,试证:曲线y f (x) 在点(a, f (a))处的
切线经过坐标原点。 证:曲线 y f (x) 在 (a, f (a)) 处的切线方程为
y f (a) f (a)(x a)
即 y f (a)x [ f (a) a f (a)]
由条件 (x) 在 x a 点有极值,且易知(x)在 x a 点可导
x
2
分析:只需证明 sin x x 0 3 cos x
证:令
f
(x)
sin x 3 cos x
x
sin
1
x cos 3
x
x
,显见
f
(0)
0;
f
(x)
cos
2 3
x
1 sin
2
x
4
cos 3
x
第四章 中值定理与导数的应用

3)在(a,b)内任一点 x 处
都不等于零.
则在区间(a,b)内至少存在一点ξ,使得等式
(柯西公式) 成立. 在柯西定理中,当 F(x)=x 时,则有
,于是定理的结论变成
而这正是拉格朗日值定理的结论.因此拉格朗日中值定理是柯西中值定理的特殊情况,或者 说柯西中值定理是拉格朗日中值定理的推广.
我们先看一下柯西中值定理的几何意义,然后再证明这个定理.
7
解:1)f(x)在[0,1]上连续:
2)f(x)在(0,1)内可导(
在
(0,1)内有定义),故 f(x)满足拉格朗日中值定理的条件.
,
设
由此解得
(负根不在所给的区间内,舍去)
故取 =
,则有
成立.
即验证了拉格朗日中值定理对 f(x)=arctanx 在[0,1]上正确.
三、柯西中值定理
如果函数 f(x)和 F(x)满足条件: 1)在闭区间[a,b]上连续; 2)在开区间(a,b)内可导;
(图四) 因此它不满足条件 2),虽然满足条件 1)和 3),但定理结论不成立.从图形上看,显然没有水平 切线.
例 3. (x)=x,x∈[0,1]
函数 f(x)满足条件 1)和 2),但 f(0)≠f(1)(见图五)
(图五) 3
因此不满足条件 3),所以在(0,1)内不存在ξ,使
,也即定理的结论不成立.从图形上
看,显然也没有水平切线. (2)罗尔定理的三个条件是充分的,而不是必要的。即如果定理的三个条件不完全满足或
都不满足时,定理的结论也有可能成立.
例 4.
因为函数 f(x)在点
处不连续、不可导,
且
(见图六),
(图六) 所以 f(x)不满足罗尔定理的全部条件,但是我们可以在区间
中值定理与导数应用

嘉兴学院
10/5/2024
第四章 中值定理与导数应用
第17页
例7 证明当x [ 1 ,1]时,不等式 2
arctan x ln(1 x2 ) ln 2
4 成立.
例8 证明:若函数f (x)在(, )内 满足关系式 f (x) f (x),且f (0)=1,
则 f (x) ex.
嘉兴学院
f '() 0
嘉兴学院
10/5/2024
第四章 中值定理与导数应用
y 几何解释:
第4页
C y f (x)
o a 1
2 b x
在两端点高度相同的连续曲线弧AB上,
若除端点外处处均有不垂直于x轴的切
线存在,则此曲线弧上至少有一点C,
在该点处的切线平行于x轴.
嘉兴学院
10/5/2024
第四章 中值定理与导数应用
f (x1 x2 ) f (x2 ) f (x1)
f (x1 x2 ) f (x2 ) f (x1) f (0)
f (2 ) x1 f (1) x1 (x2 2 x1 x2 , 0 1 x1)
x1 f ( )(2 1) 0 (1 2 )
f (x1 x2 ) f (x1) f (x2 )
并求满足定理的值. 例4 证明 arcsin x arccos x
2 (1 x 1).
嘉兴学院
——证明恒等式旳一般措施
10/5/2024
第四章 中值定理与导数应用
第13页
例5 证明当x 0时, x ln(1 x) x. 1 x
例6 设 Lim f (x) K , 求 x+
Lim [ f (x a) f (x)].(a 0)
x+
嘉兴学院
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等数学-中值定律与 导数的应用
精品
一、主要内容
Cauchy 中值定理
F(x)xபைடு நூலகம்
洛必达法则
型
f g1g1 f 1g1 f
0型 0 型
00,1,0型
令y f g 取对数
0型
f g f 1g
Lagrange 中值定理
f(a)f(b)
Rolle 定理
n0
Taylor 中值定理
常用的 泰勒公式
导数的应用
6、导数的应用
(1) 函数单调性的判定法
定理 设函数y f (x)在[a,b]上连续,(在 a,b)内 可导. 10如果在(a,b)内f (x) 0,那末函y数 f (x)在 [a,b]上单调增加; 20 如果在(a,b)内f (x) 0,那末函y数 f (x)在 [a,b]上单调减.少
(2) 函数的极值及其求法
2! 4! 6!
( 2 n )!
ln( 1 x ) x x 2 x 3 ( 1 ) n x n 1 o ( x n 1 )
23
n1
1 1 x x2 xn o(xn ) 1 x
(1 x ) m 1 mx m ( m 1) x 2 2!
m (m 1) (m n 1) x n o( x n ) n!
其 R n (中 x )f (n (n 1 )1 ())( !x x 0 )n 1(在 x 0与 x之 ) 间
常用函数的麦克劳林公式
sin x x x 3 x 5 ( 1 ) n x 2 n 1 o ( x 2 n 2 )
3! 5!
( 2 n 1)!
cos x 1 x 2 x 4 x 6 ( 1 ) n x 2 n o ( x 2 n )
定义设函数f ( x)在区间(a,b)内有定义, x0是(a,b)内 的一个点,
如果存在着点 x0的一个邻域 ,对于这邻域内的 任何点x,除了点x0外, f ( x) f ( x0 )均成立,就称 f ( x0 )是函数f ( x)的一个极大值;
如果存在着点 x0的一个邻域 ,对于这邻域内的 任何点x,除了点x0外, f ( x) f ( x0 )均成立,就称 f ( x0 )是函数f ( x)的一个极小值 .
f (b) F(b)
f (a) F(a)
Ff ''(())成立.
4、洛必达法则
10. 0型及 型未定式 0
定义 这种在一定条件下通过分子分母分别求导再 求极限来确定未定式的值的方法称为洛必达法则.
20. 0 , ,00,1, 0型未定式
关键:将其它类型未定式化为洛必达法则可解决 的类型 ( 0 ), ( ) .
(3) 最大值、最小值问题
步骤:
1.求驻点和不可导点;
2.求区间端点及驻点和不可导点的函数值,比 较大小,那个大那个就是最大值,那个小那个就 是最小值; 注意:如果区间内只有一个极值,则这个极值就 是最值.(最大值或最小值)
实际问题求最值应注意:
1)建立目标函数; 2)求最值; 若目标函数只点有,唯则一该驻点 函数值即为所(求或的最最小大)值.
即f '() 0
2、拉格朗日中值定理
拉格朗日(Lagrange)中值定理 如果函数f(x) 在闭区间[a,b]上连续,在开区间(a,b)内可导,那 末在(a,b)内至少有一点(ab),使等式
f (b) f (a) f '()(ba) 成立.
有限增量公式. y f ( x 0 x ) x ( 0 1 ). 增量y的精确表达. 式
单调性,极值与最值, 凹凸性,拐点,函数 图形的描绘; 曲率;求根方法.
1、罗尔中值定理
罗尔(Rolle)定理 如果函数f (x) 在闭区间 [a,b]上连续,在开区间(a,b) 内可导,且在区间端 点的函数值相等,即f (a) f (b),那末在(a,b) 内至少有一点(a b),使得函数f (x) 在该 点的导数等于零,
驻点和不可导点统称为临界点.
定理(第一充分条件)
(1)如果x(x0 ,x0),有f'(x)0;而x(x0,x0 ),
有f'(x)0,则f(x)在x0处取得极大值.
(2)如果x(x0 ,x0),有f'(x)0;而x(x0,x0 )
有f'(x)0,则f(x)在x0处取得极小值.
(3)如果当x(x0 ,x0)及x(x0,x0 )时, f'(x)符
推论 如果函 f(x)在 数区I上 间的导数, 恒为 那末 f(x)在区I上 间是一个 . 常数
3、柯西中值定理
柯西(Cauchy)中值定理 如果函数f (x)及F(x)
在闭区间[a,b]上连续,在开区间(a,b)内可导,且F'(x)
在(a,b)内每一点处均不为零,那末在(a,b)内至少
有一点(a b),使等式
函数的极大值与极小值统称为极值,使函数取得 极值的点称为极值点.
极值是函数的局部性概念:极大值可能小于极小 值,极小值可能大于极大值.
定理(必要条件) 设 f(x )在 点 x 0 处 具 有 导 数 ,且 在 x 0 处 取 得 极 值 ,那 末 必 定 f'(x 0 ) 0 .
定义 使导数 (即 为 方 f零 (x) 程 0的点 实 )叫根 做函 f(x)的 数驻 . 点
0
注意:洛必达法则的使用条件.
5、泰勒中值定理
泰勒(Taylor)中值定理 如果函数f(x)在含有x0 的某个开区间(a,b)内具有直到(n1)阶的导数,则 当x在(a,b)内时, f(x)可以表示为(xx0)的一 个n次多项式与一个余项Rn(x)之和:
f(x)f(x0)f(x0)(xx0)f2(!x0)(xx0)2 f(nn)(!x0)(xx0)nRn(x)
号相同,则f(x)在x0处无极值.
定理(第二充分条件)设f(x)在x0 处具有二阶导数, 且f'(x0)0, f''(x0)0, 那末 (1)当f''(x0)0时, 函数f(x)在x0 处取得极大值; (2)当f''(x0)0时, 函数f(x)在x0 处取得极小值.
求极值的步骤:
(1)求导 f(数 x); (2)求驻点, f(x即 )0方 的;程 根 (3)检查 f(x)在驻点左右的f正 (x)在 负号 该点的,判 符断 号极;值点 (4) 求极值.
精品
一、主要内容
Cauchy 中值定理
F(x)xபைடு நூலகம்
洛必达法则
型
f g1g1 f 1g1 f
0型 0 型
00,1,0型
令y f g 取对数
0型
f g f 1g
Lagrange 中值定理
f(a)f(b)
Rolle 定理
n0
Taylor 中值定理
常用的 泰勒公式
导数的应用
6、导数的应用
(1) 函数单调性的判定法
定理 设函数y f (x)在[a,b]上连续,(在 a,b)内 可导. 10如果在(a,b)内f (x) 0,那末函y数 f (x)在 [a,b]上单调增加; 20 如果在(a,b)内f (x) 0,那末函y数 f (x)在 [a,b]上单调减.少
(2) 函数的极值及其求法
2! 4! 6!
( 2 n )!
ln( 1 x ) x x 2 x 3 ( 1 ) n x n 1 o ( x n 1 )
23
n1
1 1 x x2 xn o(xn ) 1 x
(1 x ) m 1 mx m ( m 1) x 2 2!
m (m 1) (m n 1) x n o( x n ) n!
其 R n (中 x )f (n (n 1 )1 ())( !x x 0 )n 1(在 x 0与 x之 ) 间
常用函数的麦克劳林公式
sin x x x 3 x 5 ( 1 ) n x 2 n 1 o ( x 2 n 2 )
3! 5!
( 2 n 1)!
cos x 1 x 2 x 4 x 6 ( 1 ) n x 2 n o ( x 2 n )
定义设函数f ( x)在区间(a,b)内有定义, x0是(a,b)内 的一个点,
如果存在着点 x0的一个邻域 ,对于这邻域内的 任何点x,除了点x0外, f ( x) f ( x0 )均成立,就称 f ( x0 )是函数f ( x)的一个极大值;
如果存在着点 x0的一个邻域 ,对于这邻域内的 任何点x,除了点x0外, f ( x) f ( x0 )均成立,就称 f ( x0 )是函数f ( x)的一个极小值 .
f (b) F(b)
f (a) F(a)
Ff ''(())成立.
4、洛必达法则
10. 0型及 型未定式 0
定义 这种在一定条件下通过分子分母分别求导再 求极限来确定未定式的值的方法称为洛必达法则.
20. 0 , ,00,1, 0型未定式
关键:将其它类型未定式化为洛必达法则可解决 的类型 ( 0 ), ( ) .
(3) 最大值、最小值问题
步骤:
1.求驻点和不可导点;
2.求区间端点及驻点和不可导点的函数值,比 较大小,那个大那个就是最大值,那个小那个就 是最小值; 注意:如果区间内只有一个极值,则这个极值就 是最值.(最大值或最小值)
实际问题求最值应注意:
1)建立目标函数; 2)求最值; 若目标函数只点有,唯则一该驻点 函数值即为所(求或的最最小大)值.
即f '() 0
2、拉格朗日中值定理
拉格朗日(Lagrange)中值定理 如果函数f(x) 在闭区间[a,b]上连续,在开区间(a,b)内可导,那 末在(a,b)内至少有一点(ab),使等式
f (b) f (a) f '()(ba) 成立.
有限增量公式. y f ( x 0 x ) x ( 0 1 ). 增量y的精确表达. 式
单调性,极值与最值, 凹凸性,拐点,函数 图形的描绘; 曲率;求根方法.
1、罗尔中值定理
罗尔(Rolle)定理 如果函数f (x) 在闭区间 [a,b]上连续,在开区间(a,b) 内可导,且在区间端 点的函数值相等,即f (a) f (b),那末在(a,b) 内至少有一点(a b),使得函数f (x) 在该 点的导数等于零,
驻点和不可导点统称为临界点.
定理(第一充分条件)
(1)如果x(x0 ,x0),有f'(x)0;而x(x0,x0 ),
有f'(x)0,则f(x)在x0处取得极大值.
(2)如果x(x0 ,x0),有f'(x)0;而x(x0,x0 )
有f'(x)0,则f(x)在x0处取得极小值.
(3)如果当x(x0 ,x0)及x(x0,x0 )时, f'(x)符
推论 如果函 f(x)在 数区I上 间的导数, 恒为 那末 f(x)在区I上 间是一个 . 常数
3、柯西中值定理
柯西(Cauchy)中值定理 如果函数f (x)及F(x)
在闭区间[a,b]上连续,在开区间(a,b)内可导,且F'(x)
在(a,b)内每一点处均不为零,那末在(a,b)内至少
有一点(a b),使等式
函数的极大值与极小值统称为极值,使函数取得 极值的点称为极值点.
极值是函数的局部性概念:极大值可能小于极小 值,极小值可能大于极大值.
定理(必要条件) 设 f(x )在 点 x 0 处 具 有 导 数 ,且 在 x 0 处 取 得 极 值 ,那 末 必 定 f'(x 0 ) 0 .
定义 使导数 (即 为 方 f零 (x) 程 0的点 实 )叫根 做函 f(x)的 数驻 . 点
0
注意:洛必达法则的使用条件.
5、泰勒中值定理
泰勒(Taylor)中值定理 如果函数f(x)在含有x0 的某个开区间(a,b)内具有直到(n1)阶的导数,则 当x在(a,b)内时, f(x)可以表示为(xx0)的一 个n次多项式与一个余项Rn(x)之和:
f(x)f(x0)f(x0)(xx0)f2(!x0)(xx0)2 f(nn)(!x0)(xx0)nRn(x)
号相同,则f(x)在x0处无极值.
定理(第二充分条件)设f(x)在x0 处具有二阶导数, 且f'(x0)0, f''(x0)0, 那末 (1)当f''(x0)0时, 函数f(x)在x0 处取得极大值; (2)当f''(x0)0时, 函数f(x)在x0 处取得极小值.
求极值的步骤:
(1)求导 f(数 x); (2)求驻点, f(x即 )0方 的;程 根 (3)检查 f(x)在驻点左右的f正 (x)在 负号 该点的,判 符断 号极;值点 (4) 求极值.
