过渡区摩擦系数λ的计算公式
布拉修斯公式适用范围

布拉修斯公式适用范围布拉修斯公式是一个在流体力学中用于计算光滑圆管内紊流摩擦系数的公式。
这一公式在特定的条件和范围内有着重要的应用。
咱先来说说布拉修斯公式到底是啥。
它长这样:λ = 0.3164 /Re^0.25 。
这里的λ是摩擦系数,Re 呢就是雷诺数。
那它能在哪些地方派上用场呢?比如说在设计一些管道系统的时候,要是管道内壁比较光滑,流体的流动状态又符合一定的条件,这时候用布拉修斯公式就能大致算出管道内的阻力情况,这对于预估能量损失、确定泵的功率啥的可太重要了。
我记得有一次,在一个工厂的改造项目中,他们要重新设计一套液体输送管道。
工程师们一开始对管道内的阻力估算不太准确,导致选的泵功率不太够,整个系统的运行效率很低。
后来经过仔细分析,发现管道内壁还算光滑,流体的流速和温度等条件也符合要求,于是就大胆地用了布拉修斯公式重新计算摩擦系数和阻力。
经过调整,选了个合适功率的泵,这下子整个系统运行得又稳又高效,工厂的生产效率也跟着上去了。
不过,布拉修斯公式也不是万能的,它有自己的适用范围。
首先,这管道内壁得足够光滑。
要是内壁粗糙得不行,那这个公式算出来的结果就偏差大了去了。
还有啊,雷诺数也得在一定范围内,通常是4000 < Re < 10^5 。
要是雷诺数太小或者太大,这个公式也就不那么灵光啦。
再比如说,在一些小型的实验室装置中,如果要精确计算流体在管道内的流动情况,光靠布拉修斯公式可能就不够了。
得结合更复杂的模型和实验数据来综合考虑。
总之,布拉修斯公式是个好工具,但咱得清楚啥时候能用,啥时候不能用,这样才能在实际应用中不出岔子,让工程设计更准确、更高效。
可别不管不顾地乱用,不然就像闭着眼睛走路,指不定就摔个大跟头呢!所以,对于布拉修斯公式的适用范围,咱们可得心里有数,这样才能在流体力学的世界里游刃有余。
粘性摩擦系数乘以速度的公式

粘性摩擦系数乘以速度的公式
粘性摩擦系数乘以速度的公式是:8τ/(ρu)^2v
摩擦系数λ=τ为剪应力
ρ为流体密度
u为流速
以一定方法求出λ,再由下式(范宁公式)即可求出流体所受阻力
hf=λ*l/d*u^2/2g
摩擦力和速度无关。
因为f=nu,n是压力,u是动摩擦因数,就是接触面的粗糙程度。
滑动摩擦力大小是与压力大小有关,与物体的材料有关,与光滑程度有关。
摩擦力与相互摩擦的物体有关,因此物理学中对摩擦力所做出的描述不一般化,也不像对其它的力那么精确。
没有摩擦力的话鞋带无法系紧,螺丝钉和钉子无法固定物体。
1。
流体流动-第七次课

常见局部阻力系数的求法: 常见局部阻力系数的求法:
1). 突扩管和突缩管 突扩管
ζ = f (
A小 A大
) = (1 −
A小 A大
)2
2). 进口和出口 进口:容器进入管道,突缩。 进口:容器进入管道,突缩。A小/A大≈0,λ=0.5 出口:管道进入容器,突扩。 出口:管道进入容器,突扩。A小/A大≈0,λ=1.0
2
简单管路流体的能量损失具有加和性。 简单管路流体的能量损失具有加和性。
2、简单管路计算 、
流量q 已知管径d、管长l、流量qV,求管路系统的能量损 失和输送功率。 失和输送功率。
已知管径d、管长l、管路系统的能量损失Σhf,求 流量q 或流速u 流量qV或流速u。 流量q 已知管长l、流量qV、管路系统的能量损失Σhf,求 管径d。
4.2 当量长度法
hf = λ ⋅
le d
⋅
u2 2
le为当量长度。 将流体流经管件时,所产生的局部阻力折 为当量长度。 将流体流经管件时,
的直管所产生的阻力。 合成相当于流经长度为le的直管所产生的阻力。
le由实验确定,可查表。 由实验确定,可查表。
五、 管道总阻力
∑h
f
= ∑ h f直 + ∑ h f局
并联和分支管路称为复杂管路。 并联和分支管路称为复杂管路。
A A B C B
并联管路
分支管路
1、 并联管路 、
V
A
1 B 2
qV=qV1+qV2
∑hfAB= ∑hf1 =∑hf2 (各支管单位质量流体阻 力损失相等) 力损失相等) 证明
zA +
zA +
pA ρg
关于牛顿内摩擦定律及流体粘度
利用量纲分析法可以得到:
( Re ,
d
)
式中: — 粗糙度
d
— 相对粗糙度
根据实验,得到莫狄(Moody)摩擦系数图。
0.1 0.09 0.08 0.07 0.06 0.05
e/l
0.05 0.04 0.03 0.02 0.015 0.01 0.008 0.006 0.0045
(1)流体阻力的表示方法
对应于机械能衡算的三种形式,流体阻力损失亦有三种表达形式:
R
h
f
kJ/kg m Pa
R g
p
f
R
阻力损失与压力差的区别: △pf —— 流体流经两截面间的机械能损失;
△p —— 任意两点间的压力差。
二者之间的关系:
u2 p We gz p f 2
1.4 流体流动阻力
1.4.1 流体的粘性和牛顿粘性定律
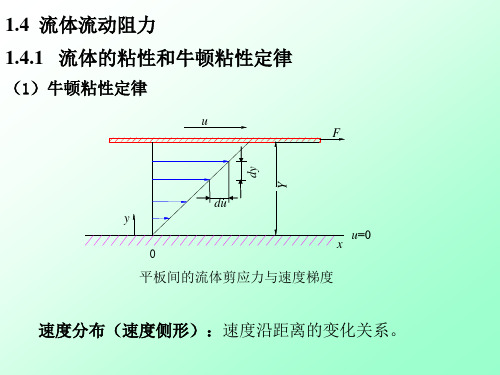
(1)牛顿粘性定律
u F dy
du
y 0 x u=0
平板间的流体剪应力与速度梯度
速度分布(速度侧形):速度沿距离的变化关系。
Y
平板间的流体剪应力与速度梯度
实测发现:
F u A Y
牛顿粘性定律:
du dy
意义:剪应力的大小与速度梯度成正比。
1.4.2 流体流动的类型---层流及湍流
(1)雷诺实验
1883年, 英国物理学家Osbone Reynolds作了如下实验。
C 墨水流线 A 玻璃管
D
B
雷诺实验
(2)雷诺实验现象
用红墨水观察管中水的流动状态 层流
(a)
过渡流
(b)
湍流
(c)
沿程阻力系数λ计算公式

沿程阻力系数λ计算公式
沿程阻力系数(Coefficient of Friction, λ)是用于描述物体在
沿一定路径或表面移动时所受到的阻力大小的一个参数。
计算沿程阻力系
数可以帮助我们理解和预测运动物体所受到的阻力大小,以及影响阻力的
因素。
1.牛顿第二定律应用:
沿程阻力力(F)可以由牛顿第二定律来计算,即F=m·a
其中m为物体的质量,a为物体的加速度。
通过实验或测量,可以测
得物体在给定路径上的加速度,然后利用该公式计算沿程阻力系数。
2.摩擦力计算:
当物体在平面上运动时,摩擦力是主要的沿程阻力。
摩擦力可以由Coulomb摩擦定律来计算。
摩擦力的大小可以用公式F=μ·N来表示
其中F为摩擦力,μ为摩擦系数,N为法向力。
摩擦系数μ一般是
通过实验测定得到的。
3.空气阻力计算:
当物体在流体(如空气)中运动时,主要存在的沿程阻力是空气阻力。
空气阻力可以用多种方法来估计。
一个常用的方法是根据物体在流体中的运动状态来近似计算空气阻力。
例如,当物体以较低速度在空气中运动时,空气阻力(F)可以用公
式F=0.5·C_d·ρ·A·V^2来计算
其中C_d为空气阻力系数,ρ为空气密度,A为物体在运动方向上的横截面积,V为物体的速度。
持续读取..。
化工传递过程过程性考核(一) - 答案

化工传递Array过程过程性考核试卷(一)一.填空题(每空1分,本大题共41分)1. 流体静力学基本方程的应用包括压力压差的测量、液位的测量和液封高度的计算。
2. 甲地大气压为100 kPa,乙地大气压为80 kPa。
某刚性设备在甲地,其内部的真空度为25 kpa,则其内部的绝对压强为75 kpa;若将其移至乙地,则其内部的表压强为-0.5 mH2O。
3. 流体流动有两种基本形态,即层流和湍流。
判断流体流动形态的无量纲数群为雷诺数,其表达形式为Re=duρ/μ,物理意义为表示流体惯性力与与黏性力比值。
4. 复杂管路分为分支管路和并联管路。
5. 常用的流量计中,孔板流量计和文丘里属于差压流量计;转子流量计属于截面流量计;测速管可测量点速度。
6. 流体在圆形直管内做层流流动,若流量不变,将管径变为原来的两倍,则平均流速变为原来的1/4 ,流动摩擦系数变为原来的2倍,直管阻力损失变为原来的1/16 。
7. 流体在一套管环隙内流动,若外管内径为50 mm,内管外径为25 mm,则其流动当量直径为25 mm.8. 流体在圆形直管内做稳态层流流动,若管截面上平均流速为0.05 m/s ,则最大流速为 1.0 m/s 。
9. 联系各单元操作的两条主线为 传递过程 和 研究工程问题的方法论 。
10. 湍流边界层可以分为 层流底层 、 过渡层 和 湍流主体 ,其中传热、传质阻力主要集中在层流底层 。
11. 随体导数的表达形式为zu y u x u θzy x ∂∂+∂∂+∂∂+∂∂=θD D 。
12. 不可压缩流体连续性方程的一般表达形式为0=•∇u。
13. 量纲分析的基础是 量纲一致性原则 和 π 定理。
14. 在研究流体的运动时,常采用两种观点,即 欧拉 观点和 拉格朗日 观点。
15. 牛顿黏性定律的表达形式为yu xd d μτ-=。
16. 流体质点的运动轨迹称为 迹线;在某一时刻,在流线上任一点的切线方向与流体在该点的速度方向相同 。
供热管网各参数计算常用公式

供热管网各参数常用计算公式1比摩阻R(P/m)——集中供热手册P 196R = 6、25×10-2×52d G ρλ 其中:λ—— 管道摩擦系数(查动力管道手册P345页)λ= 1/(1、14+2×log Kd )2 G —— 介质质量流量(t/h) 或:R=d 22λρν=6、88×10-3×25.525.02dK G ρ ρ—— 流体介质密度(kg/m 3) d —— 管道内径(m)K ——管内壁当量绝对粗糙度(m) 2、管道压力降△P(MPa)△P = 1、15R(L+∑Lg)×10-6其中:L —— 管道长度(m)∑Lg ——管道附件当量长度(m)3、管道单位长度热损q(W/m)q = 其中:T 0 —— 介质温度(℃) λ1 —— 内层保温材料导热系数(W/m 、℃)λ2 —— 外层保温材料导热系数(W/m 、℃)D 0 —— 管道外径(m)D 1 —— 内保温层外径(m)D 2 —— 外保温层外径(m)α—— 外表面散热系数[α=1、163×(10+6ϖ)]ϖ—— 环境平均风速。
预算时可取α=11、63Ln —— 自然对数底4、末端温度T ed(℃)T ed = T 0 - GC L L q g 310)(-⨯+ 其中:T 0 —— 始端温度(℃)L —— 管道长度(m)Lg —— 管道附件当量长度(m)G —— 介质质量流量(t/h)C —— 介质定容比热(kj / kg 、℃)5、保温结构外表面温度T s(℃)2122011012121)16(D D D Ln D D Ln T αλλπ++-T s = T a + απ2D q 其中:Ta ——环境温度(南方可取Ta =16℃) 6、管道冷凝水量(仅适用于饱与蒸汽)G C (t/h)G C = γ3106.3-⨯qL 其中:γ——介质汽化潜热(kj / kg)7、保温材料使用温度下的导热系数λt (W/m 、℃)λt =λo +2)(B A T T K + 其中:λo ——保温材料常态导热系数 T A —— 保温层内侧温度(℃)T B —— 保温层外侧温度(℃) K —— 保温材料热变系数超细玻璃棉K=0、00017 硅酸铝纤维K=0、00028、管道直径选择d(mm)按质量流量计算:d = 594、5ωρG按体积流量计算:d = 18、8ωνG按允许单位比摩阻计算:d = 0、0364×52R G ∆νλ其中:G —— 介质质量流量(t/h)G v —— 介质体积流量(m 3/h) ω —— 介质流速(m/s)ρ —— 介质密度(kg/m 3)ΔR —— 允许单位比摩阻(Pa/m)9、管道流速ω(m/s)ω= πρ29.0d G 其中:G —— 介质质量流量(t/h) ρ —— 介质密度(kg/m 3)d —— 管道内径(m)10、安全阀公称通径(喉部直径)选择DN(mm)A = φ133.49010P G 则 DN =πA ⨯20 其中:A —— 安全阀进气口计算面积(cm 2)G ——介质质量流量(t/h)P —— 安全阀排放压力(MPa)φ——过热蒸汽校正系数,取0、8—0、88DN ——安全阀通径计算值(mm)。
管径选择与管道压力降计算(一)1~60

管径选择与管道压力降计算第一部分管径选择1.应用范围和说明1.0.1本规定适用于化工生产装置中的工艺和公用物料管道,不包括储运系统的长距离输送管道、非牛顿型流体及固体粒子气流输送管道。
1.0.2对于给定的流量,管径的大小与管道系统的一次投资费(材料和安装)、操作费(动力消耗和维修)和折旧费等项有密切的关系,应根据这些费用作出经济比较,以选择适当的管径,此外还应考虑安全流速及其它条件的限制。
本规定介绍推荐的方法和数据是以经验值,即采用预定流速或预定管道压力降值(设定压力降控制值)来选择管径,可用于工程设计中的估算。
1.0.3当按预定介质流速来确定管径时,采用下式以初选管径:d=18.81W0.5 u-0.5ρ-0.5(1.0.3—1)或d=18.81V00.5 u-0.5(1.0.3—2)式中d——管道的内径,mm;W——管内介质的质量流量,kg/h;V0——管内介质的体积流量,m3/h;ρ——介质在工作条件下的密度,kg/m3;u——介质在管内的平均流速,m/s。
预定介质流速的推荐值见表2.0.1。
1.0.4当按每100m计算管长的压力降控制值(⊿Pf100)来选择管径时,采用下式以初定管径:d=18.16W0.38ρ-0.207 µ0.033⊿P f100–0.207(1.0.4—1)或d=18.16V00.38ρ0.173 µ0.033⊿P f100–0.207(1.0.4—2)式中µ——介质的动力粘度,Pa·s;⊿P f100——100m计算管长的压力降控制值,kPa。
推荐的⊿P f100值见表2.0.2。
1.0.5本规定除注明外,压力均为绝对压力。
2.管道内流体常用流速范围和一般工程设计中的压力降控制值2.0.1管道内各种介质常用流速范围见表2.0.1。
表中管道的材质除注明外,一律为钢。
该表中流速为推荐值。
2.0.2管道压力降控制值见表2.0.2-1和表2.0.2-2,该表中压力降值为推荐值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
过渡区摩擦系数λ的计算公式水力计算是暖通空调工程设计中最基本的计算任务之一。
当流体在圆管中的流动状态处于光滑区和过渡区时,其摩擦阻力系数λ的计算公式均需用迭代法逼近求解。
若设计中手边没有适用的水力计算表,需自己临时计算制表时,则计算起来相当麻烦。
其中,光滑管区已有其他学者提出的足够精确的计算公式,而在过渡区,虽也有学者提出计算公式,但计算误差相当大。
为此,笔者在实践中总结出一公式。
公式表达为:λ=β(K/d+58/R e)^0.29 ,式中R e为雷诺数;K为绝对粗糙度,mm;d为圆管内径,mm;β为过渡区λ的计算系数,见下表。
用该公式计算,误差很小,在常用范围内最大误差不超过1%。
过渡区λ的计算系数β值表
此表完成于2003年3月11日星期二下午6时52分,从而使用Excell进行采暖水力计算速度和准确性达到了一个新水平。
PPR,PE-X,PAP三种不同塑料管材的沿程损失计算
经过实际测试塑料管中的沿程损失理论计算公式与实际有明显的差距,具体分析如下:
由于管材原材料差别及制造工艺不同所致。
铝塑复合管的内壁材料一般是聚乙烯(PE),或交联聚乙烯(PE-X),与交联聚乙烯(PE-X)管的材质相近或相同,水力条件也相近,故水头损失也相近并均大于理论计算值,而PP-R管是以聚丙烯(PP)和1%~7%的乙烯为原料,采用气相共聚法均匀聚合而成,其水力条件比PE-X和PAP更优,因此,水头损失小于理论计算值。
各修正系数如下:对于PE-X和PAP管的沿程水头损失计算时,乘以1.12的修正系数。
对于PP-R管的沿程水头损失计算时,乘以0.947的修正系数。
另通过试验证实PE-X ,PAP和PP-R管的沿程水头损失比钢管的沿程水头损失小得多,流速越大水头损失减少的幅度也越大。
此数据取自《给水排水》-2003-8期。
另本期还有大空间的《南京国际展览中心》消防给水设计的有关高大空间用雨淋系统的介绍。
