单块矩形板计算
四边简支矩形板计算

四边简支矩形板计算项目名称_____________日期_____________设计者_____________校对者_____________一、构件编号: LB-1二、示意图三、依据规范《建筑结构荷载规范》 GB50009-2001《混凝土结构设计规范》 GB50010-2010四、计算信息1.几何参数计算跨度: Lx = 11000 mm; Ly = 7500 mm板厚: h = 400 mm2.材料信息混凝土等级: C30 fc=mm2 ft=mm2 ftk=mm2Ec=×104N/mm2钢筋种类: HRB400 fy = 360 N/mm2Es = ×105 N/mm2最小配筋率: ρ= %纵向受拉钢筋合力点至近边距离: as = 55mm保护层厚度: c = 40mm3.荷载信息(均布荷载)永久荷载分项系数: γG =可变荷载分项系数: γQ =准永久值系数: ψq =永久荷载标准值: qgk = m2可变荷载标准值: qqk = m24.计算方法:弹性板5.边界条件(上端/下端/左端/右端):简支/简支/简支/简支6.设计参数结构重要性系数: γo =泊松比:μ =五、计算参数:1.计算板的跨度: Lo = 7500 mm2.计算板的有效高度: ho = h-as=400-55=345 mm六、配筋计算(lx/ly=11000/7500=< 所以按双向板计算):向底板钢筋1) 确定X向板底弯矩Mx = 表中系数(γG*qgk+γQ*qqk)*Lo2= +***+**= kN*m2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= *×106/**1000*345*345)=3) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2* =4) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = **1000*345*360= 354mm25) 验算最小配筋率ρ = As/(b*h) = 354/(1000*400) = %ρ<ρmin = % 不满足最小配筋要求所以取面积为As = ρmin*b*h = %*1000*400 = 800 mm2采取方案⌲12@140, 实配面积807 mm2向底板钢筋1) 确定Y向板底弯矩My = 表中系数(γG*qgk+γQ*qqk)*Lo2= +***+**= kN*m2) 确定计算系数αs = γo*My/(α1*fc*b*ho*ho)= *×106/**1000*345*345)=3) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2* =4) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = **1000*345*360= 638mm25) 验算最小配筋率ρ = As/(b*h) = 638/(1000*400) = %ρ<ρmin = % 不满足最小配筋要求所以取面积为As = ρmin*b*h = %*1000*400 = 800 mm2采取方案⌲12@100, 实配面积1131 mm2七、跨中挠度计算:Mk -------- 按荷载效应的标准组合计算的弯矩值Mq -------- 按荷载效应的准永久组合计算的弯矩值1.计算荷载效应Mk = Mgk + Mqk= +**+* = kN*mMq = Mgk+ψq*Mqk= +**+** = kN*m2.计算受弯构件的短期刚度 Bs1) 计算按荷载荷载效应的两种组合作用下,构件纵向受拉钢筋应力σsk = Mk/*ho*As) 混规(7.1.4-3)= ×106/*345*1131) = N/mmσsq = Mq/*ho*As) 混规(7.1.4-3)= ×106/*345*1131) = N/mm2) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积: Ate = *b*h = *1000*400= 200000mm2ρte = As/Ate 混规(7.1.2-4)= 1131/200000 = %3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψk = 混规(7.1.2-2)= =因为ψ不能小于最小值,所以取ψk =ψq = 混规(7.1.2-2)= =因为ψ不能小于最小值,所以取ψq =4) 计算钢筋弹性模量与混凝土模量的比值αEαE = Es/Ec = ×105/×104 =5) 计算受压翼缘面积与腹板有效面积的比值γf矩形截面,γf=06) 计算纵向受拉钢筋配筋率ρρ = As/(b*ho)= 1131/(1000*345) = %7) 计算受弯构件的短期刚度 BsBsk = Es*As*ho2/[ψk++6*αE*ρ/(1+ γf')](混规(7.2.3-1)) = ×105*1131*3452/[*++6**%/(1+*]= ×104 kN*m2Bsq = Es*As*ho2/[ψq++6*αE*ρ/(1+ γf')](混规(7.2.3-1)) = ×105*1131*3452/[*++6**%/(1+*]= ×104 kN*m23.计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增大影响系数θ当ρ'=0时,θ= 混规(7.2.5)2) 计算受弯构件的长期刚度 BBk = Mk/(Mq*(θ-1)+Mk)*Bs (混规(7.2.2-1))= *+*×104= ×104 kN*m2Bq = Bsq/θ (混规(7.2.2-2))= ×104/= ×104 kN*m2B = min(Bk,Bq)= min,=4.计算受弯构件挠度f max = f*(q gk+q qk)*Lo4/B= *+*×104=5.验算挠度挠度限值fo=Lo/250=7500/250=fmax=≤fo=,满足规范要求!八、裂缝宽度验算:1.跨中X方向裂缝1) 计算荷载效应Mx = 表中系数(qgk+ψqqk)*Lo2= +**+**= kN*m2) 带肋钢筋,所以取值v i=3) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/*ho*As) 混规(7.1.4-3)=×106/*345*807)=mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=*b*h=*1000*400=200000 mm2ρte=As/Ate 混规(7.1.2-4)=807/200000 =因为ρte= < ,所以让ρte=6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ= 混规(7.1.2-2)= =7) 计算单位面积钢筋根数nn=1000/dist = 1000/140=78) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=7*12*12/(7**12)=129) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es**C+*Deq/ρte) (混规(7.1.2-1)=**×105**40+*12/= ≤ , 满足规范要求2.跨中Y方向裂缝1) 计算荷载效应My = 表中系数(qgk+ψqqk)*Lo2= +**+**= kN*m2) 带肋钢筋,所以取值v i=3) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/*ho*As) 混规(7.1.4-3)=×106/*345*1131)=mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=*b*h=*1000*400=200000 mm2ρte=As/Ate 混规(7.1.2-4)=1131/200000 =因为ρte= < ,所以让ρte=6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ= 混规(7.1.2-2)= =7) 计算单位面积钢筋根数nn=1000/dist = 1000/100=108) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=10*12*12/(10**12)=129) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es**C+*Deq/ρte) (混规(7.1.2-1)=**×105**40+*12/= ≤ , 满足规范要求。
四边简支矩形板计算

四边简支矩形板计算项目名称_____________日期_____________设计者_____________校对者_____________一、构件编号: LB-1二、示意图三、依据规范《建筑结构荷载规范》 GB50009-2001《混凝土结构设计规范》 GB50010-2010四、计算信息1.几何参数计算跨度: Lx = 11000 mm; Ly = 7500 mm板厚: h = 400 mm2.材料信息混凝土等级: C30 fc=14.3N/mm2 ft=1.43N/mm2 ftk=2.01N/mm2Ec=3.00×104N/mm2钢筋种类: HRB400 fy = 360 N/mm2Es = 2.0×105 N/mm2最小配筋率: ρ= 0.200%纵向受拉钢筋合力点至近边距离: as = 55mm保护层厚度: c = 40mm3.荷载信息(均布荷载)永久荷载分项系数: γG = 1.200可变荷载分项系数: γQ = 1.400准永久值系数: ψq = 1.000永久荷载标准值: qgk = 15.000kN/m2可变荷载标准值: qqk = 0.000kN/m24.计算方法:弹性板5.边界条件(上端/下端/左端/右端):简支/简支/简支/简支6.设计参数结构重要性系数: γo = 1.00泊松比:μ = 0.200五、计算参数:1.计算板的跨度: Lo = 7500 mm2.计算板的有效高度: ho = h-as=400-55=345 mm六、配筋计算(lx/ly=11000/7500=1.467<2.000 所以按双向板计算):1.X向底板钢筋1) 确定X向板底弯矩Mx = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0287+0.0707*0.200)*(1.200*15.000+1.400*0.000)*7.52 = 43.374 kN*m2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= 1.00*43.374×106/(1.00*14.3*1000*345*345)= 0.0253) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.025) = 0.0264) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*345*0.026/360= 354mm25) 验算最小配筋率ρ = As/(b*h) = 354/(1000*400) = 0.088%ρ<ρmin = 0.200% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.200%*1000*400 = 800 mm2采取方案⌲12@140, 实配面积807 mm22.Y向底板钢筋1) 确定Y向板底弯矩My = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0707+0.0287*0.200)*(1.200*15.000+1.400*0.000)*7.52 = 77.430 kN*m2) 确定计算系数αs = γo*My/(α1*fc*b*ho*ho)= 1.00*77.430×106/(1.00*14.3*1000*345*345)= 0.0453) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.045) = 0.0474) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*345*0.047/360= 638mm25) 验算最小配筋率ρ = As/(b*h) = 638/(1000*400) = 0.160%ρ<ρmin = 0.200% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.200%*1000*400 = 800 mm2采取方案⌲12@100, 实配面积1131 mm2七、跨中挠度计算:Mk -------- 按荷载效应的标准组合计算的弯矩值Mq -------- 按荷载效应的准永久组合计算的弯矩值1.计算荷载效应Mk = Mgk + Mqk= (0.0707+0.0287*0.200)*(15.000+0.000)*7.52 = 64.525 kN*mMq = Mgk+ψq*Mqk= (0.0707+0.0287*0.200)*(15.000+1.0*0.000)*7.52 = 64.525 kN*m2.计算受弯构件的短期刚度 Bs1) 计算按荷载荷载效应的两种组合作用下,构件纵向受拉钢筋应力σsk = Mk/(0.87*ho*As) 混规(7.1.4-3)= 64.525×106/(0.87*345*1131) = 190.077 N/mmσsq = Mq/(0.87*ho*As) 混规(7.1.4-3)= 64.525×106/(0.87*345*1131) = 190.077 N/mm2) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积: Ate = 0.5*b*h = 0.5*1000*400= 200000mm2ρte = As/Ate 混规(7.1.2-4)= 1131/200000 = 0.566%3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψk = 1.1-0.65*ftk/(ρte*σsk) 混规(7.1.2-2)= 1.1-0.65*2.01/(0.566%*190.077) = -0.115因为ψ不能小于最小值0.2,所以取ψk = 0.2ψq = 1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)= 1.1-0.65*2.01/(0.566%*190.077) = -0.115因为ψ不能小于最小值0.2,所以取ψq = 0.24) 计算钢筋弹性模量与混凝土模量的比值αEαE = Es/Ec = 2.0×105/3.00×104 = 6.6675) 计算受压翼缘面积与腹板有效面积的比值γf矩形截面,γf=06) 计算纵向受拉钢筋配筋率ρρ = As/(b*ho)= 1131/(1000*345) = 0.328%7) 计算受弯构件的短期刚度 BsBsk = Es*As*ho2/[1.15ψk+0.2+6*αE*ρ/(1+ 3.5γf')](混规(7.2.3-1)) = 2.0×105*1131*3452/[1.15*-0.115+0.2+6*6.667*0.328%/(1+3.5*0.0)]= 4.798×104 kN*m2Bsq = Es*As*ho2/[1.15ψq+0.2+6*αE*ρ/(1+ 3.5γf')](混规(7.2.3-1)) = 2.0×105*1131*3452/[1.15*-0.115+0.2+6*6.667*0.328%/(1+3.5*0.0)]= 4.798×104 kN*m23.计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增大影响系数θ当ρ'=0时,θ=2.0 混规(7.2.5)2) 计算受弯构件的长期刚度 BBk = Mk/(Mq*(θ-1)+Mk)*Bs (混规(7.2.2-1))= 64.525/(64.525*(2.0-1)+64.525)*4.798×104= 2.399×104 kN*m2Bq = Bsq/θ (混规(7.2.2-2))= 4.798×104/2.0= 2.399×104 kN*m2B = min(Bk,Bq)= min(23990.371,23990.371)= 23990.3714.计算受弯构件挠度f max = f*(q gk+q qk)*Lo4/B= 0.00752*(15.000+0.000)*7.54/2.399×104= 14.879mm5.验算挠度挠度限值fo=Lo/250=7500/250=30.000mmfmax=14.879mm≤fo=30.000mm,满足规范要求!八、裂缝宽度验算:1.跨中X方向裂缝1) 计算荷载效应Mx = 表中系数(qgk+ψqqk)*Lo2= (0.0287+0.0707*0.200)*(15.000+1.00*0.000)*7.52= 36.145 kN*m2) 带肋钢筋,所以取值v i=1.03) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=36.145×106/(0.87*345*807)=149.222N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*400=200000 mm2ρte=As/Ate 混规(7.1.2-4)=807/200000 = 0.0040因为ρte=0.0040 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*149.222)=0.2247) 计算单位面积钢筋根数nn=1000/dist = 1000/140=78) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=7*12*12/(7*1.0*12)=129) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.224*149.222/2.0×105*(1.9*40+0.08*12/0.0100)=0.0547mm ≤ 0.20, 满足规范要求2.跨中Y方向裂缝1) 计算荷载效应My = 表中系数(qgk+ψqqk)*Lo2= (0.0707+0.0287*0.200)*(15.000+1.00*0.000)*7.52= 64.525 kN*m2) 带肋钢筋,所以取值v i=1.03) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=64.525×106/(0.87*345*1131)=190.077N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*400=200000 mm2ρte=As/Ate 混规(7.1.2-4)=1131/200000 = 0.0057因为ρte=0.0057 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*190.077)=0.4137) 计算单位面积钢筋根数nn=1000/dist = 1000/100=108) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=10*12*12/(10*1.0*12)=129) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.413*190.077/2.0×105*(1.9*40+0.08*12/0.0100)=0.1282mm ≤ 0.20, 满足规范要求。
矩形裁板算法

矩形裁板算法
矩形裁板算法是一种常见的计算机图形学算法,用于将矩形裁剪成一组小矩形。
该算法可以应用于各种场景,如计算机游戏、工程绘图和图像处理等。
该算法基于两个关键概念:裁剪窗口和裁剪区域。
裁剪窗口是一个矩形,表示可见区域,而裁剪区域是待裁剪的矩形。
算法的目标是将裁剪区域中的所有小矩形都裁剪到裁剪窗口中,以便于显示。
矩形裁板算法的实现需要先确定裁剪窗口和裁剪区域的位置和
大小。
然后,将裁剪区域中的所有小矩形逐个进行裁剪,直到所有小矩形都被裁剪到裁剪窗口中。
在实际应用中,矩形裁板算法可以通过各种方式进行优化,例如采用二叉树结构来管理裁剪区域和裁剪窗口,以提高算法的效率和准确性。
此外,还可以应用一些具体的技术和算法,如线段裁剪算法和多边形裁剪算法,来处理更为复杂的几何图形。
总的来说,矩形裁板算法是一种非常有用的计算机图形学算法,可以高效地将矩形裁剪成小矩形,并将它们显示在屏幕上。
- 1 -。
矩形裁板算法

矩形裁板算法矩形裁板算法是一种用于优化材料利用率的算法,主要应用于裁剪不同尺寸的矩形板材。
该算法可以有效地帮助制造商节约材料,在生产过程中减少浪费和成本,因此深受制造业的欢迎。
实施矩形裁板算法需要考虑多个因素。
首先,需要对板材进行切割,因此需要考虑刀具大小和切割路径。
其次,需要考虑如何最大限度地利用板材,以减少浪费。
最后,需要考虑如何使裁剪过程简化,以减少需要人工干预的操作。
下面是矩形裁板算法的几个步骤:1. 将需要裁剪的矩形板材分解成若干个可裁剪的小矩形。
2. 对每个小矩形进行排列,以最大限度地利用板材。
3. 将排列好的小矩形切割出来,形成最终的板材。
4. 对于无法完全覆盖的剩余部分进行统一的处理。
在矩形裁板算法中,有许多不同的排列算法可供选择。
其中,最常用的算法是基于贪心策略的过填法(Guillotine Cutting)和回溯法(Backtracking)。
在过填法中,首先将板材切成若干个小矩形,然后对它们进行排列。
在每个阶段,算法都会选择最大的非空矩形进行切割,并将其切成更小的子矩形。
这个过程将一直持续下去,直到所有的矩形都被完全覆盖。
这个算法的优点是可以很快地得到一个较优的解,因为它总是选择最大的矩形进行切割。
在回溯法中,算法会进行深度优先搜索,找到所有可能的矩形排列方式。
在每个阶段,算法都会选择一个尚未使用的矩形进行排列,并递归地对其余矩形进行排列。
如果无法继续排列,则算法会将这个阶段标记为失败,并回溯到上一个阶段。
这个算法的优点是可以找到最优解,但计算时间相对会比较长。
在实际应用中,选择哪个算法取决于具体的需求和限制条件。
很多时候,过填法已经可以满足要求,因为它可以在短时间内得到一组较优的解。
但是,如果需要精确控制各种因素,可以使用回溯法来寻找最优解。
单块矩形板计算典型例题
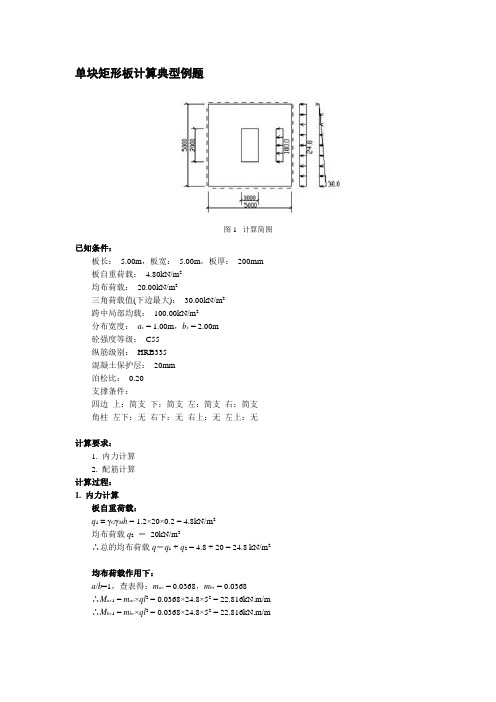
单块矩形板计算典型例题图1 计算简图已知条件:板长: 5.00m,板宽: 5.00m,板厚:200mm板自重荷载: 4.80kN/m2均布荷载:20.00kN/m2三角荷载值(下边最大):30.00kN/m2跨中局部均载:100.00kN/m2分布宽度:a x = 1.00m,b y = 2.00m砼强度等级:C55纵筋级别:HRB335混凝土保护层:20mm泊松比:0.20支撑条件:四边上:简支下:简支左:简支右:简支角柱左下:无右下:无右上:无左上:无计算要求:1. 内力计算2. 配筋计算计算过程:1. 内力计算板自重荷载:q1= γGγM h = 1.2×20×0.2 = 4.8kN/m2均布荷载q2=20kN/m2∴总的均布荷载q=q1 + q2 = 4.8 + 20 = 24.8 kN/m2均布荷载作用下:a/b=1,查表得:m ac = 0.0368,m bc = 0.0368∴M ac1 = m ac×ql2 = 0.0368×24.8×52 = 22.816kN.m/m ∴M bc1 = m bc×ql2 = 0.0368×24.8×52 = 22.816kN.m/m三角形荷载作用下:a/b=1,查表得:m amax = 0.0184,m bmax = 0.0216∴M ac2 = m amax×ql2 = 0.0184×30×52 = 13.8kN.m/m∴M bc2 = m bmax×ql2 = 0.0216×30×52 = 16.2kN.m/m跨中局部均载作用下:a x / a = 1 / 5 = 0.2,b y / b = 2 / 5 = 0.4,b / a = 1查表得:m ac = 0.143,m bc = 0.117∴M ac3 = m ac×qa x b y = 0.143×100×1×2 = 28.6kN.m/m∴M bc3 = m bc×qa x b y = 0.117×100×1×2 = 23.4kN.m/m根据叠加原理,得M ac=M ac1+M ac2+M ac3 = 22.816+13.8+28.6 = 65.216kN.m/mM bc=M bc1+M bc2+M bc3 = 22.816+16.2+23.4 = 62.416kN.m/m∵泊松比=0.2≠0,且板边无自由边,∴必须对跨中弯矩进行调整。
混凝土单筋矩形截面计算课件

挠度验算
挠度验算的目的
保证混凝土结构在使用期间不会 因挠度过大而影响结构的正常使
用和安全性能。
计算方法
根据结构力学原理,采用有限元 分析或近似计算方法,考虑结构 自重、活载、风载等作用下的挠
度。
影响因素
混凝土的弹性模量、截面尺寸、 跨度、荷载等都会影响挠度的计
算结果。
耐久性评估
耐久性评估的目的
01
钢筋的配置原则
根据结构受力要求,合理选择钢 筋的种类、规格和数量。
确保钢筋在截面中的位置和间距 满足规范要求,以保证结构的承
载力和稳定性。
考虑施工的可操作性,合理安排 钢筋的布置,以方便施工。
截面设计的基本原则
01
根据结构的功能和要求 ,确定合理的截面尺寸 和形状。
02
根据承载力要求,合理 配置钢筋,并满足构造 要求。
混凝土单筋矩形截面计 算课件
目录
Contents
• 引言 • 混凝土材料特性 • 单筋矩形截面设计原理 • 单筋矩形截面承载力计算 • 裂缝宽度和挠度验算 • 案例分析
01 引言
课程背景
混凝土结构在现代建筑中广泛应用, 单筋矩形截面作为最基本的混凝土结 构形式之一,其计算是工程设计和施 工中的重要基础。
某高层建筑,采用混凝土单筋矩形截面梁作为主 要受力构件。
结构形式
梁的截面尺寸为200mm×400mm,采用C30混 凝土,承受弯矩设计值M=150kN·m。
3
施工条件
施工现场具备标准的混凝土搅拌和浇筑设备,材 料质量符合规范要求。
案例分析方法
计算简图
根据实际工程情况,建立混凝土单筋矩形截面梁 的计算简图。
配筋率计算
根据截面尺寸和所需承载力计算 配筋率
四边固定矩形板计算书

LB-1矩形板计算项目名称_____________日期_____________设计者_____________校对者_____________一、构件编号: LB-1二、示意图三、依据规范《建筑结构荷载规范》 GB50009-2001《混凝土结构设计规范》 GB50010-2010四、计算信息1.几何参数计算跨度: Lx = 11400 mm; Ly = 8500 mm板厚: h = 400 mm2.材料信息混凝土等级: C30 fc=14.3N/mm2 ft=1.43N/mm2 ftk=2.01N/mm2Ec=3.00×104N/mm2钢筋种类: HRB400 fy = 360 N/mm2Es = 2.0×105 N/mm2最小配筋率: ρ= 0.200%纵向受拉钢筋合力点至近边距离: as = 55mm保护层厚度: c = 40mm3.荷载信息(均布荷载)永久荷载分项系数: γG = 1.200可变荷载分项系数: γQ = 1.400准永久值系数: ψq = 1.000永久荷载标准值: qgk = 39.500kN/m2可变荷载标准值: qqk = 0.000kN/m24.计算方法:弹性板5.边界条件(上端/下端/左端/右端):固定/固定/固定/固定6.设计参数结构重要性系数: γo = 1.00泊松比:μ = 0.200五、计算参数:1.计算板的跨度: Lo = 8500 mm2.计算板的有效高度: ho = h-as=400-55=345 mm六、配筋计算(lx/ly=11400/8500=1.341<2.000 所以按双向板计算):1.X向底板钢筋1) 确定X向板底弯矩Mx = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0129+0.0298*0.200)*(1.200*39.500+1.400*0.000)*8.52 = 64.434 kN*m2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= 1.00*64.434×106/(1.00*14.3*1000*345*345)= 0.0383) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.038) = 0.0394) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*345*0.039/360= 529mm25) 验算最小配筋率ρ = As/(b*h) = 529/(1000*400) = 0.132%ρ<ρmin = 0.200% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.200%*1000*400 = 800 mm2采取方案⌲14@150, 实配面积1026 mm22.Y向底板钢筋1) 确定Y向板底弯矩My = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0298+0.0129*0.200)*(1.200*39.500+1.400*0.000)*8.52 = 110.923 kN*m2) 确定计算系数αs = γo*My/(α1*fc*b*ho*ho)= 1.00*110.923×106/(1.00*14.3*1000*345*345)= 0.0653) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.065) = 0.0674) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*345*0.067/360= 924mm25) 验算最小配筋率ρ = As/(b*h) = 924/(1000*400) = 0.231%ρ≥ρmin = 0.200% 满足最小配筋要求采取方案⌲14@125, 实配面积1231 mm23.X向支座左边钢筋1) 确定左边支座弯矩M o x = 表中系数(γG*qgk+γQ*qqk)*Lo2= 0.0565*(1.200*39.500+1.400*0.000)*8.52= 193.613 kN*m2) 确定计算系数αs = γo*M o x/(α1*fc*b*ho*ho)= 1.00*193.613×106/(1.00*14.3*1000*345*345)= 0.1143) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.114) = 0.1214) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*345*0.121/360 = 1659mm25) 验算最小配筋率ρ = As/(b*h) = 1659/(1000*400) = 0.415%ρ≥ρmin = 0.200% 满足最小配筋要求采取方案⌲20@100, 实配面积3142 mm24.X向支座右边钢筋1) 确定右边支座弯矩M o x = 表中系数(γG*qgk+γQ*qqk)*Lo2= 0.0565*(1.200*39.500+1.400*0.000)*8.52= 193.613 kN*m2) 确定计算系数αs = γo*M o x/(α1*fc*b*ho*ho)= 1.00*193.613×106/(1.00*14.3*1000*345*345)= 0.1143) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.114) = 0.1214) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*345*0.121/360 = 1659mm25) 验算最小配筋率ρ = As/(b*h) = 1659/(1000*400) = 0.415%ρ≥ρmin = 0.200% 满足最小配筋要求采取方案⌲20@100, 实配面积3142 mm25.Y向上边支座钢筋1) 确定上边支座弯矩M o y = 表中系数(γG*qgk+γQ*qqk)*Lo2= 0.0704*(1.200*39.500+1.400*0.000)*8.52= 241.089 kN*m2) 确定计算系数αs = γo*M o y/(α1*fc*b*ho*ho)= 1.00*241.089×106/(1.00*14.3*1000*345*345)= 0.1423) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.142) = 0.1534) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*345*0.153/360= 2102mm25) 验算最小配筋率ρ = As/(b*h) = 2102/(1000*400) = 0.526%ρ≥ρmin = 0.200% 满足最小配筋要求采取方案⌲20@100, 实配面积3142 mm26.Y向下边支座钢筋1) 确定下边支座弯矩M o y = 表中系数(γG*qgk+γQ*qqk)*Lo2= 0.0704*(1.200*39.500+1.400*0.000)*8.52= 241.089 kN*m2) 确定计算系数αs = γo*M o y/(α1*fc*b*ho*ho)= 1.00*241.089×106/(1.00*14.3*1000*345*345)= 0.1423) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.142) = 0.1534) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*345*0.153/360= 2102mm25) 验算最小配筋率ρ = As/(b*h) = 2102/(1000*400) = 0.526%ρ≥ρmin = 0.200% 满足最小配筋要求采取方案⌲20@100, 实配面积3142 mm2七、跨中挠度计算:Mk -------- 按荷载效应的标准组合计算的弯矩值Mq -------- 按荷载效应的准永久组合计算的弯矩值1.计算荷载效应Mk = Mgk + Mqk= (0.0298+0.0129*0.200)*(39.500+0.000)*8.52 = 92.436 kN*mMq = Mgk+ψq*Mqk= (0.0298+0.0129*0.200)*(39.500+1.0*0.000)*8.52 = 92.436 kN*m 2.计算受弯构件的短期刚度 Bs1) 计算按荷载荷载效应的两种组合作用下,构件纵向受拉钢筋应力σsk = Mk/(0.87*ho*As) 混规(7.1.4-3)= 92.436×106/(0.87*345*1231) = 250.174 N/mmσsq = Mq/(0.87*ho*As) 混规(7.1.4-3)= 92.436×106/(0.87*345*1231) = 250.174 N/mm2) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积: Ate = 0.5*b*h = 0.5*1000*400= 200000mm2ρte = As/Ate 混规(7.1.2-4)= 1231/200000 = 0.615%3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψk = 1.1-0.65*ftk/(ρte*σsk) 混规(7.1.2-2)= 1.1-0.65*2.01/(0.615%*250.174) = 0.252ψq = 1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)= 1.1-0.65*2.01/(0.615%*250.174) = 0.2524) 计算钢筋弹性模量与混凝土模量的比值αEαE = Es/Ec = 2.0×105/3.00×104 = 6.6675) 计算受压翼缘面积与腹板有效面积的比值γf矩形截面,γf=06) 计算纵向受拉钢筋配筋率ρρ = As/(b*ho)= 1231/(1000*345) = 0.357%7) 计算受弯构件的短期刚度 BsBsk = Es*As*ho2/[1.15ψk+0.2+6*αE*ρ/(1+ 3.5γf')](混规(7.2.3-1)) = 2.0×105*1231*3452/[1.15*0.252+0.2+6*6.667*0.357%/(1+3.5*0.0)]= 4.637×104 kN*m2Bsq = Es*As*ho2/[1.15ψq+0.2+6*αE*ρ/(1+ 3.5γf')](混规(7.2.3-1)) = 2.0×105*1231*3452/[1.15*0.252+0.2+6*6.667*0.357%/(1+3.5*0.0)]= 4.637×104 kN*m23.计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增大影响系数θ当ρ'=0时,θ=2.0 混规(7.2.5)2) 计算受弯构件的长期刚度 BBk = Mk/(Mq*(θ-1)+Mk)*Bs (混规(7.2.2-1))= 92.436/(92.436*(2.0-1)+92.436)*4.637×104= 2.318×104 kN*m2Bq = Bsq/θ (混规(7.2.2-2))= 4.637×104/2.0= 2.318×104 kN*m2B = min(Bk,Bq)= min(23184.291,23184.291)= 23184.2914.计算受弯构件挠度f max = f*(q gk+q qk)*Lo4/B= 0.00198*(39.500+0.000)*8.54/2.318×104= 17.630mm5.验算挠度挠度限值fo=Lo/250=8500/250=34.000mmfmax=17.630mm≤fo=34.000mm,满足规范要求!八、裂缝宽度验算:1.跨中X方向裂缝1) 计算荷载效应Mx = 表中系数(qgk+ψqqk)*Lo2= (0.0129+0.0298*0.200)*(39.500+1.00*0.000)*8.52= 53.695 kN*m2) 带肋钢筋,所以取值v i=1.03) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=53.695×106/(0.87*345*1026)=174.360N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*400=200000 mm2ρte=As/Ate 混规(7.1.2-4)=1026/200000 = 0.0051因为ρte=0.0051 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*174.360)=0.3517) 计算单位面积钢筋根数nn=1000/dist = 1000/150=68) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=6*14*14/(6*1.0*14)=149) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.351*174.360/2.0×105*(1.9*40+0.08*14/0.0100)=0.1092mm ≤ 0.30, 满足规范要求2.跨中Y方向裂缝1) 计算荷载效应My = 表中系数(qgk+ψqqk)*Lo2= (0.0298+0.0129*0.200)*(39.500+1.00*0.000)*8.52= 92.436 kN*m2) 带肋钢筋,所以取值v i=1.03) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=92.436×106/(0.87*345*1231)=250.174N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*400=200000 mm2ρte=As/Ate 混规(7.1.2-4)=1231/200000 = 0.0062因为ρte=0.0062 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*250.174)=0.5787) 计算单位面积钢筋根数nn=1000/dist = 1000/125=88) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=8*14*14/(8*1.0*14)=149) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.578*250.174/2.0×105*(1.9*40+0.08*14/0.0100)=0.2582mm ≤ 0.30, 满足规范要求3.支座上方向裂缝1) 计算荷载效应M o y = 表中系数((qgk+ψqqk)*Lo2)= 0.0704*(39.500+1.00*0.000)*8.52= 200.908 kN*m2) 带肋钢筋,所以取值v i=1.03) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=200.908×106/(0.87*345*3142)=213.036N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*400=200000 mm2ρte=As/Ate 混规(7.1.2-4)=3142/200000 = 0.01576) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0157*213.036)=0.7107) 计算单位面积钢筋根数nn=1000/dist = 1000/100=108) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=10*20*20/(10*1.0*20)=209) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.710*213.036/2.0×105*(1.9*40+0.08*20/0.0157)=0.2554mm ≤ 0.30, 满足规范要求4.支座下方向裂缝1) 计算荷载效应M o y = 表中系数(qgk+ψqqk)*Lo2= 0.0704*(39.500+1.00*0.000)*8.52= 200.908 kN*m2) 带肋钢筋,所以取值v i=1.03) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=200.908×106/(0.87*345*3142)=213.036N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*400=200000 mm2ρte=As/Ate 混规(7.1.2-4)=3142/200000 = 0.01576) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0157*213.036)=0.7107) 计算单位面积钢筋根数nn=1000/dist = 1000/100=108) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=10*20*20/(10*1.0*20)=209) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.710*213.036/2.0×105*(1.9*40+0.08*20/0.0157)=0.2554mm ≤ 0.30, 满足规范要求5.支座左方向裂缝1) 计算荷载效应M o x = 表中系数(qgk+ψqqk)*Lo2= 0.0565*(39.500+1.00*0.000)*8.52= 161.344 kN*m2) 带肋钢筋,所以取值v i=1.03) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=161.344×106/(0.87*345*3142)=171.084N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*400=200000 mm2ρte=As/Ate 混规(7.1.2-4)=3142/200000 = 0.01576) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0157*171.084)=0.6147) 计算单位面积钢筋根数nn=1000/dist = 1000/100=108) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=10*20*20/(10*1.0*20)=209) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.614*171.084/2.0×105*(1.9*40+0.08*20/0.0157)=0.1774mm ≤ 0.30, 满足规范要求6.支座右方向裂缝1) 计算荷载效应M o x = 表中系数(qgk+ψqqk)*Lo2= 0.0565*(39.500+1.00*0.000)*8.52= 161.344 kN*m2) 带肋钢筋,所以取值v i=1.03) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=161.344×106/(0.87*345*3142)=171.084N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*400=200000 mm2ρte=As/Ate 混规(7.1.2-4)=3142/200000 = 0.01576) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0157*171.084)=0.6147) 计算单位面积钢筋根数nn=1000/dist = 1000/100=108) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=10*20*20/(10*1.0*20)=209) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.614*171.084/2.0×105*(1.9*40+0.08*20/0.0157)=0.1774mm ≤ 0.30, 满足规范要求。
矩形板强度、裂缝弹性计算表格

设计荷载 q 标准值 qk 有无人防 i= dx 弯矩 X向跨中 系数 Y向跨中 X向支座 Y向支座 弯矩M 钢筋fy X向跨中 钢筋d r 强度计算 计算As 间距s 实配 实配As 弯矩Mk σsk ρ'te ρte X向跨中 ψ' ψ 裂缝计算 v Wmax
四边支承板强度、裂缝计算表格
工程名称
C20 C25 C15 砼等级 fc 9.6 11.9 7.2 ftk 1.54 1.78 1.27 fc= C30 本表砼等级 计算方法:根据《建筑结构设计手册
2
业务号
C30 14.3 2.01 14.3 C35 16.7 2.20 Mpa C40 19.1 2.39 人防fcd= C45 21.1 2.51 17.2 C50 23.1 2.64 Mpa C55 25.3 2.74 ftk= C60 27.5 2.85 2.01 C65 29.7 2.93 Mpa
上
表
设计
校对
审核
审定
日期
年
月
日
静力计算》查表求得弯矩系数及弯矩。 σsk=Mk/0.87Ash0。
计算公式:Ao=M/bh ofc, r=(1+sqrt(1-2Ao))/2, As=M/fyho; wmax=acrψσsk(1.9c+0.08deq/vρte)/Es, ψ=1.1-0.65ftk/ρteσsk, 有人防组合时,材料强度按常规输入,调整系数在表格公式中自动调整。 注意:设计(标准)荷载应将自重计算在内。 板编号 1B1 8000 Lx 8000 Ly 板尺寸 1.000 Lx/Ly 8000 Lo (mm) 300 板厚h 40 c 1 左边 板支承 1 右边 1 上边 条件 1 下边 条件数 N
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
执行规范:
《混凝土结构设计规范》(GB 50010-2010), 本文简称《混凝土规范》
《建筑结构荷载规范》(GB 50009-2012), 本文简称《荷载规范》
钢筋:d - HPB300; D - HRB335; E - HRB400; F - RRB400; G - HRB500; P - HRBF335; Q - HRBF400; R - HRBF500
-----------------------------------------------------------------------
1 设计资料
1.1 计算简图
1.2 已知条件
荷载条件:
均布恒载 : 3.00kN/m2恒载分项系数 : 1.20
均布活载 : 2.00kN/m2活载分项系数 : 1.40
板容重 : 25.00kN/m3活载准永久值系数: 0.50
板厚 : 250mm 活载调整系数 : 1.00
局部集中荷载:
编号荷载属性 X(m) Y(m) 荷载数值(kN)
1 恒载 1.100 1.100 20.00
配筋条件:
材料类型 : 混凝土支座配筋调整系数: 1.00
混凝土等级 : C30 跨中配筋调整系数: 1.00
纵筋级别 : HRB400 跨中配筋方向(度): 0.00
纵筋保护层厚: 15mm
1.3 计算内容
(1) 有限元内力计算
(2) 弹性位移计算
(3) 板边及跨中最大最小弯矩位置处配筋
(4) 挠度、裂缝计算
2 计算结果
2.1 单位说明
弯矩:kN.m/m 钢筋面积:mm2/m
2.2 垂直板边弯矩
边号最大弯矩最小弯矩左中右
1 0.05
2 -0.177 0.052 -0.177 0.050
2 0.026 -0.211 0.025 -0.180 0.026
3 0.050 -0.203 0.050 -0.145 0.048
4 0.029 -0.193 0.019 -0.193 0.029
2.3 跨中弯矩
注:跨中弯矩是在用户指定方向上跨中弯矩的最大值(以下同)
x(m) y(m) 平行配筋方向垂直配筋方向
1.100 1.100 11.809 ----
1.100 1.100 ---- 11.428
2.4 垂直板边配筋
边号最大弯矩截面最小弯矩截面左中右
1 500 500 500 500 500
2 500 500 500 500 500
3 500 500 500 500 500
4 500 500 500 500 500
2.5 跨中配筋
x(m) y(m) 平行配筋方向垂直配筋方向
1.100 1.100 500 ----
1.100 1.100 ---- 500
2.6 垂直板边选筋
边号最大弯矩截面最小弯矩截面左中右
1 E12@220(514) E12@220(514) E12@220(514) E12@220(514) E12@220(514)
2 E12@220(514) E12@220(514) E12@220(514) E12@220(514) E12@220(514)
3 E12@220(514) E12@220(514) E12@220(514) E12@220(514) E12@220(514)
4 E12@220(514) E12@220(514) E12@220(514) E12@220(514) E12@220(514)
2.7 跨中选筋
x(m) y(m) 平行配筋方向垂直配筋方向
1.100 1.100 E12@220(514) ----
1.100 1.100 ---- E12@220(514)
2.8 挠度和裂缝
弹性位移/挠度 = BI/EI = 0.153
挠度最大值: 0.413mm
作用位置:
x=1.100m y = 1.100m
裂缝最大值: 0.024mm
作用位置:
x=1.100 y = 1.100(平行跨中方向配筋) 3 计算结果简图
-----------------------------------------------------------------------
【理正结构设计工具箱软件6.5PB3】计算日期: 2015-09-16 16:53:34。
