《数据结构实用教程(C语言版)》第7章 查找
实用数据结构(C++描述)(第二版)第7章

/*函数返回被查找元素x在线性表中的序号, 如果在线性表中不存在元素值x,则返回-1 */ int serch(v,n,x) int n; ET v[],x; /*ET为线性表数据类型*/ { int k; k=0; while ((k<n)&&(v[k]≠x)) k=k+1; if (k==n) k=-1; return(k); }
第7章 查找技术
7.1 7.2 7.3 7.4 7.5
顺序查找 有序表的对分查找 分块查找 二叉排序树查找 多层索引树查找
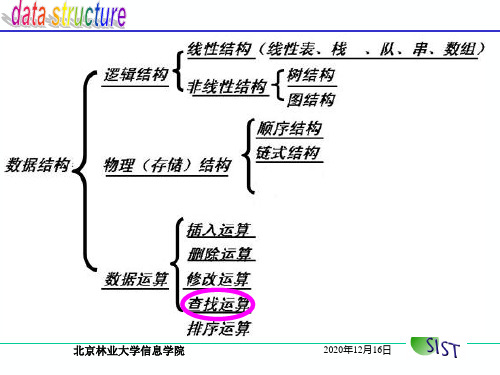
查找(Searching)又称检索,就是从一个数据 元素集合中找出某个特定的数据元素。它是数据 处理中经常使用的一种重要操作,尤其是当所涉 及的数据量较大时,查找算法的优劣对整个软件 系统的效率影响是很大的。好的查找方法可以极 大地提高程序的运行速度。
struct node { ET d; struct node *next; }; /*函数返回被查找元素x所在结点的存储地址, 如果在线性链表中不存在元素值为x的结点,则返回NULL*/ struct node *lserch(head,x) struct node *head; ET x; /*ET为线性链表中值域的数据类型*/ { struct node k; k=head; while ((k≠NULL)&&(k->d≠x)) k=k->next; return(k); }
int bserch(v,n,x) /*函数返回被查找元素x在线性表中的序号 如果在线性表中不存在元素值x,则返回-1 */ int n; ET x,v[]; { int i,j,k; i=1; j=n; while (i<=j) { k=(i+j)/2; if (v[k-1]==x) return(k-1); if (v[k-1]>x) j=k-1; else i=k+1; } return(-1); }
数据结构-第7章 查找
}
北京林业大学信息学院
2020年12月16日
顺序查找的性能分析
• 空间复杂度:一个辅助空间。 • 时间复杂度: 1) 查找成功时的平均查找长度
-1 2 3-4 5 6-7 8 9-10 11 h
1-2 2-3
4-5 5-6
7-8 8-9 10-11 11-
外结点
查找成功时比较次数:为该结点在判定树上的层次数,不超过树 的深度 d = log2 n + 1
查找不成功的过程就是走了一条从根结点到外部结点的路径d或 d-1。
北京林业大学信息学院
顺序查找
应用范围: 顺序表或线性链表表示的静态查找表 表内元素之间无序
顺序表的表示
typedef struct { ElemType *R; //表基址 int length; //表长
}SSTable;
北京林业大学信息学院
2020年12月16日
第2章在顺序表L中查找值为e的数据元素
int LocateELem(SqList L,ElemType e) { for (i=0;i< L.length;i++)
2020年12月16日
折半查找
123456 5 13 19 21 37 56
若k==R[mid].key,查找成功 若k<R[mid].key,则high=mid-1 若k>R[mid].key,则low=mid+1
找21
数据结构实用教程(C语言版)

02
03
树的定义
树是一种非线性数据结构, 由节点和边组成,具有层 次结构。
树的基本操作
包括创建树、插入节点、 删除节点、查找节点等。
树的表示方法
常用表示方法包括孩子表 示法、孩子兄弟表示法等。
二叉树的定义和基本性质
二叉树的定义
二叉树是一种特殊的树,每个节点最多有两个子节点,分 别称为左子节点和右子节点。
数据结构实用教程(c语言版)
目 录
• 引言 • 线性表 • 栈和队列 • 树和二叉树 • 图和网络 • 查找和排序 • 数据结构应用实例分析
01 引言
数据结构的重要性
01
数据结构是计算机科学的基础
数据结构是计算机科学的核心内容之一,它研究如何有效地组织、存储
和处理数据,为算法设计和程序实现提供基础支持。
Dijkstra算法和Floyd算法是常用的最短路径算法,用于求解图中两个顶点之间的最短 路径。
最小生成树算法
Prim算法和Kruskal算法是常用的最小生成树算法,用于求解连通图的最小生成树,即 连接所有顶点的边的权值和最小的子图。
网络流算法和应用
网络流算法
Ford-Fulkerson算法和Edmonds-Karp算 法是常用的网络流算法,用于求解最大流和 最小割等问题。
实例四:图的着色问题
• 问题描述:图的着色问题是一个著名的NP完全问题,它要求给图中的每个顶点 着色,使得相邻的顶点颜色不同,并且使用的颜色数量最少。
• 数据结构应用:图的着色问题可以使用邻接矩阵或邻接表来表示图的结构。邻 接矩阵是一个二维数组,用于表示顶点之间的连接关系;邻接表则使用链表来 表示每个顶点的邻居节点。在图的着色过程中,我们可以使用数组来保存每个 顶点的颜色。
《数据结构(C语言版 第2版)》(严蔚敏 著)第七章练习题答案

《数据结构(C语言版第2版)》(严蔚敏著)第七章练习题答案第7章查找1.选择题(1)对n个元素的表做顺序查找时,若查找每个元素的概率相同,则平均查找长度为()。
A.(n-1)/2B.n/2C.(n+1)/2D.n答案:C解释:总查找次数N=1+2+3+…+n=n(n+1)/2,则平均查找长度为N/n=(n+1)/2。
(2)适用于折半查找的表的存储方式及元素排列要求为()。
A.链接方式存储,元素无序B.链接方式存储,元素有序C.顺序方式存储,元素无序D.顺序方式存储,元素有序答案:D解释:折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
(3)如果要求一个线性表既能较快的查找,又能适应动态变化的要求,最好采用()查找法。
A.顺序查找B.折半查找C.分块查找D.哈希查找答案:C解释:分块查找的优点是:在表中插入和删除数据元素时,只要找到该元素对应的块,就可以在该块内进行插入和删除运算。
由于块内是无序的,故插入和删除比较容易,无需进行大量移动。
如果线性表既要快速查找又经常动态变化,则可采用分块查找。
(4)折半查找有序表(4,6,10,12,20,30,50,70,88,100)。
若查找表中元素58,则它将依次与表中()比较大小,查找结果是失败。
A.20,70,30,50B.30,88,70,50C.20,50D.30,88,50答案:A解释:表中共10个元素,第一次取⎣(1+10)/2⎦=5,与第五个元素20比较,58大于20,再取⎣(6+10)/2⎦=8,与第八个元素70比较,依次类推再与30、50比较,最终查找失败。
(5)对22个记录的有序表作折半查找,当查找失败时,至少需要比较()次关键字。
A.3B.4C.5D.6答案:B解释:22个记录的有序表,其折半查找的判定树深度为⎣log222⎦+1=5,且该判定树不是满二叉树,即查找失败时至多比较5次,至少比较4次。
(6)折半搜索与二叉排序树的时间性能()。
数据结构:第七章 查找

索引表
22 48 86 1 7 13
查38
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 22 12 13 8 9 20 33 42 44 38 24 48 60 58 74 57 86 53
查找方法比较
ASL 表结构 存储结构
顺序查找 最大
折半查找 最小
关键字输入顺序:45,24,53,12,28,90
45
24
53
12
28
90
9.4 哈希查找
基本思想:在记录的存储地址和它的关键字之间建立一 个确定的对应关系(函数关系);这样,不经过比较, 直接通过计算就能得到所查元素。
一、定义
❖哈希函数——在记录的关键字与记录的存储地址之间 建立的一种对应关系叫哈希函数。
high low
1 2 3 4 5 6 7 8 9 10 11 5 13 19 21 37 56 64 75 80 88 92
6
56
3
9
19
80
1
4
7
10
5 21 64 88
比较1次 比较2次 比较3次
2
13
5
8
37 75
11
92
比较4次
判定树(二叉排序树):描 述查找过程的二叉树
把当前查找区间的中间位 置上的结点作为根,左子表 和右子表中的结点分别作 为根的左子树和右子树
适用条件:采用顺序存储结构的有序表。 算法实现
❖设表长为n,low、high 和 mid分别指向待查元素所 在区间的上界、下界和中点,k为给定值
❖初始时,令low=1, high=n, mid=(low+high)/2 ❖让k与mid指向的记录比较
《数据结构(C语言)》第7章 查找

教学要求
❖ 建议学时:6学时 ❖ 总体要求
掌握顺序查找、折半查找的实现方法; 掌握动态查找表(二叉排序树、二叉平衡树)的构造
和查找方法; 掌握哈希表、哈希函数a structures
教学要求
❖ 相关知识点
顺序查找、折半查找的基本思想、算法实现和查找效 率分析
Data structures
静态查找表
❖ 顺序查找
❖1. 一般线性表的顺序查找
(2) 静态查找表的顺序存储结构
静态查找表采用顺序存储结构,其类型定义如下:
typedef struct
{ ElemType *elem; 建表时按实际长度分配*/
/*元素存储空间基址,
int TableLen;
/*表的长度*/
Data structures
静态查找表
❖ 分块查找
索引表的类型定义如下:
typedef struct{
Elemtype key;
/*块内最大关键字值*/
int stadr; 的位置*/
/*块中第一个记录
}indexItem;
typedef struct{
indexItem elem[n];
int length;
Data structures
静态查找表
❖ 折半查找
4.折半查找算法 算法7.2 折半查找算法
else if(L.elem[mid].key>key)high=mid-1; 前半部分继续查找*/
else low=mid+1; /*从后半部分继续查找*/
}
return -1; /*顺序表中不存在待查元素*/
(1) 基本思想 从线性表的一端开始,逐个检查关键字是否满足给定
数据结构》第七章查找

(最坏情况)
可编辑ppt
11
7.2 顺序查找
成功查找的平均查找长度为(n+1)/2。显然不成功 查找次数为n+1,其时间复杂度均为 O(n)。
顺序查找的优点是:算法简单且适用面广,它对表的 结构无任何要求。无论记录是否按关键字的大小有序,其 算法均可应用,而且上述讨论对线性链表也同样适用。
顺序查找的缺点是:查找效率低,当 n 较大时,不宜 采用顺序查找。
中
5 13 19 21 37 56 64 75 80 88 92
low>high 查找失败
123456
low high
mid 7 8 9 10 11
5 13 19 21 37 56 64 75 80 88 92
可编辑ppt
16
high low
7.3 二分法查找
从二分法查找的执行情况分析,每做一次比较,查找的 范围都缩小一半。因此二分法查找的平均查找长度为
【答案】
查找成功时,最少比较1次,最多比较5次。
2、已知如下11个数据元素的有序表(6,14,19, 21,36,57,63,76,81,89,93),请画出 查找键值为21和85的查找过程。
可编辑ppt
18
7.4 分块查找
可编辑ppt
10
01 64 5
23456 13 19 21 37 56
找64 7 8 9 10 11 64 75 80 88 92
监视哨
比较次数:
查找第n个元素: 1
查找第n-1个元素:2
……….
查找第1个元素: n
查找第i个元素: n+1-i
查找失败:
n+1
iiiii
数据结构 C语言版(严蔚敏版)第7章 图

1
2
4
1
e6 2 4
2016/11/7
29
7.3 图的遍历
从已给的连通图中某一顶点出发,沿着一 些边访遍图中所有的顶点,且使每个顶点 仅被访问一次,就叫做图的遍历 ( Graph Traversal )。 图中可能存在回路,且图的任一顶点都可 能与其它顶点相通,在访问完某个顶点之 后可能会沿着某些边又回到了曾经访问过 的顶点。 为了避免重复访问,可设置一个标志顶点 是否被访问过的辅助数组 visited [ ]。
2
1 2
V2
V4
17
结论:
无向图的邻接矩阵是对称的; 有向图的邻接矩阵可能是不对称的。 在有向图中, 统计第 i 行 1 的个数可得顶点 i 的出度,统计第 j 行 1 的个数可得顶点 j 的入度。 在无向图中, 统计第 i 行 (列) 1 的个数可得 顶点i 的度。
2016/11/7
18
2
邻接表 (出度表)
adjvex nextarc
data firstarc
0 A 1 B 2 C
2016/11/7
1 0 1
逆邻接表 (入度表)
21
网络 (带权图) 的邻接表
6 9 0 2 1 C 2 8 3 D
data firstarc Adjvex info nextarc
2016/11/7
9
路径长度 非带权图的路径长度是指此路径 上边的条数。带权图的路径长度是指路径 上各边的权之和。 简单路径 若路径上各顶点 v1,v2,...,vm 均不 互相重复, 则称这样的路径为简单路径。 回路 若路径上第一个顶点 v1 与最后一个 顶点vm 重合, 则称这样的路径为回路或环。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
返回到本节首页
返回到本节首页
2.折半查找的算法 .
所示。 (1)折半查找的算法如算法 )折半查找的算法如算法7.3所示。 所示 算法7.3 算法 int BinSearch(LineList r[], int n, KeyType k) { int low,high,mid; low=1; high=n; /*置区间初值 置区间初值 */ while(low<=high) /*查找区间 查找区间 不为空时*/ 不为空时 { mid=(low+high)/2;
【例7.1】有关键字序列 ,4,6,9,10, 】有关键字序列{2, , , , , 13,15,27,29},采用折半查找法查找 , , , , 6和17的具体过程。 的具体过程。 和 的具体过程 为低位指针, 为高位指针, 解:设low为低位指针,high为高位指针, 为低位指针 为高位指针 mid为中间位置指针。其中 为中间位置指针。 为中间位置指针 其中mid= ,若 mid所指元素大于关键字 时,这时令 所指元素大于关键字k时 所指元素大于关键字 high=mid-1,向mid前一半的表中继续 , 前一半的表中继续 查找。 所指元素小于关键字k时 查找。若mid所指元素小于关键字 时,这 所指元素小于关键字 时令low=mid+1,向mid后一半的表中 时令 , 后一半的表中 继续查找。 继续查找。当high<low时,表示不存在这 时 样的查找子表空间,查找失败。 样的查找子表空间,查找失败。
返回到本节首页
算法7.2 算法 int SeqSearch1(LineList r[],int n,KeyType k) { int i=n; r[0]=k; while(r[i].key!=k) /*若k不等于所比 若 不等于所比 较关键字时*/ 较关键字时 i--; return(i); }
返回到本节首页
顺序查找的线性表定义如下: 顺序查找的线性表定义如下: #define MaxSize 1000 大存储容量*/ 大存储容量 typedef int KeyType; 域为整型*/ 域为整型 typedef int ElemType; 类型为整型,可为其它类型*/ 类型为整型,可为其它类型 /*顺序表的最 顺序表的最 /*重定义关键字 重定义关键字 /*重定义数据域 重定义数据域
返回到本节首页
if(k==r[mid].key) return(mid); /*找到待查元素 找到待查元素 */ else if(k<r[mid].key) high=mid-1; /*未找到,继续 未找到, 未找到 在前半区间进行查找*/ 在前半区间进行查找 else low=mid+1; /*未找到,继续 未找到, 未找到 在后半区间进行查找*/ 在后半区间进行查找 } return (0); }
(a)以数组的下标作为二叉判定树结点的关键字(b)以序列中的值作为二叉判定树结点的关键字 以数组的下标作为二叉判定树结点的关键字( 图7 - 4 9个结点的二叉判定树 9个结点的二叉判定树
返回到本节首页
7.2.3 分块查找
分块查找又称为索引顺序查找,是顺序查找的一种改 分块查找又称为索引顺序查找, 进,其性能介于顺序查找和折半查找之间。 其性能介于顺序查找和折半查找之间。 分块查找把查找表分成若干块, 分块查找把查找表分成若干块,每块中的元素存储顺 序是任意的,但块与块之间必须按关键字大小有序 序是任意的, 排列。即前一块中的最大关键字小于(或大于) 排列。即前一块中的最大关键字小于(或大于)后 一块中的最小(最大)关键字值。 一块中的最小(最大)关键字值。另外还需要建立 一个索引表,索引表中的一项对应线性表的一块, 一个索引表,索引表中的一项对应线性表的一块, 索引项由关键字域和指针域组成, 索引项由关键字域和指针域组成,关键字域存放相 应块的块内最大关键字,指针域存放指向本块第一 应块的块内最大关键字, 个和最后一个元素的指针(即数组下标值)。 )。索引 个和最后一个元素的指针(即数组下标值)。索引 表按关键字值递增(或递减)顺序排列。 表按关键字值递增(或递减)顺序排列。
2.顺序查找的算法 .
(2)顺序查找的改进算法 ) 我们可以使用监视哨来改进算法。 我们可以使用监视哨来改进算法。主要思路 顺序表中数据元素存放在数组下标为1 是:顺序表中数据元素存放在数组下标为 的位置, 到n的位置,而下标为 的位置空出来作为监 的位置 而下标为0的位置空出来作为监 视哨。在查找之前, 视哨。在查找之前,先将要查找的关键字存 放到数组下标为0的位置 的位置, 放到数组下标为 的位置,从顺序表的最后 一个记录开始, 一个记录开始,从后至前依次进行给定值与 记录关键字的比较, 记录关键字的比较,若某记录的关键字与给 定值k相同 则查找成功, 相同, 定值 相同,则查找成功,返回该记录在表 中的存储位置;若查找不成功,返回0。 中的存储位置;若查找不成功,返回 。相 应的算法如算法7.2。 应的算法如算法 。
2.顺序查找的算法 .
(1)顺序查找的基本算法如下: )顺序查找的基本算法如下: 算法7.1 算法 int SeqSearch(LineList r[],int n,KeyType k) { int i=1;/*为与其改进算法匹配,方便在主函数 为与其改进算法匹配, 为与其改进算法匹配 调用,查找表存储范围为下标1..n*/ 调用,查找表存储范围为下标 while(i<=n &&r[i].key!=k) i++; if(i>n) return(0); else return(i); } 返回到本节首页
7.2.2 折半查找
折半查找又称为二分查找。这种查找方法的前 折半查找又称为二分查找。 提条件是要求待查找的查找表必须是按关键 字大小有序排列的顺序表。 字大小有序排列的顺序表。 1.折半查找的主要步骤为: .折半查找的主要步骤为: (1)置初始查找范围:low=1,high=n; )置初始查找范围: , (2)求查找范围中间项:mid= (low + high)/2 )求查找范围中间项: (3)将指定的关键字值 与中间项的关键字比 )将指定的关键字值k与中间项的关键字比 较: 若相等,查找成功, 若相等,查找成功,找到的数据元素为此时 mid 指向的位置; 指向的位置;
结束
2
3 4
5
7.1 基本概念
1.查找表 . 用于查找的数据元素集合称为查找表。 用于查找的数据元素集合称为查找表。查找表 由同一类型的数据元素构成。 由同一类型的数据元素构成。 2.静态查找表 . 在查找过程中查找表本身不发生变化, 在查找过程中查找表本身不发生变化,称为静 态查找表。对静态表的查找称为静态查找。 态查找表。对静态表的查找称为静态查找。 3.动态查找表 . 若在查找过程中可以将查找表中不存在的数据 元素插入, 元素插入,或者从查找表中删除某个数据元 则称这类查找表为动态查找表。 素,则称这类查找表为动态查找表。对动态 查找表进行的查找称为动态查找。 查找表进行的查找称为动态查找。
返回到本节首页
7.2 静态查找
静态查找主要有顺序查找、折半查找、分块 静态查找主要有顺序查找、折半查找、 查找三种。 查找三种。 7.2.1顺序查找 顺序查找 7.2.2 折半查找 7.2.3 分块查找
返回到总目录
7.2.1顺序查找 顺序查找
1.顺序查找的主要思想 . 顺序查找是一种最简单的查找方法, 顺序查找是一种最简单的查找方法,它的基本 思路是:从表的一端开始, 思路是:从表的一端开始,用所给定的关键 字依次与顺序表中各记录的关键字逐个比较, 字依次与顺序表中各记录的关键字逐个比较, 若找到相同的,查找成功;否则查找失败。 若找到相同的,查找成功;否则查找失败。
返回到本节首页
折半查找过程可用一个二叉树来描述,把当前 折半查找过程可用一个二叉树来描述, 查找区间的中间位置上的记录作为根, 查找区间的中间位置上的记录作为根,左子 表和右子表中的记录分别作根的左子树和右 子树。树中每个结点表示一个记录, 子树。树中每个结点表示一个记录,结点中 的值为该记录在表中的位置, 的值为该记录在表中的位置,则称该二叉树 为折半查找的判定树。例如例7.1关键字序 为折半查找的判定树。例如例7.1关键字序 列有9个 列有 个,关键字与数据下标的关系对应表 如图7-3所示。若用数组下标作为判定树中 所示。 如图 所示 结点的值,所对应的判定树如图7-4(a) 结点的值,所对应的判定树如图 ( ) 所示, 所示,若用查找表中的关键字作为判定树中 的结点的值,所对应的判定树如图7-4(b) 的结点的值,所对应的判定树如图 ( ) 所示。 所示。 返回到本节首页
数据结构实用教程(C语言版)
Байду номын сангаас
中国水利水电出版社
第7章 查找
本章主要介绍以下内容: 本章主要介绍以下内容: 静态查找方法,主要介绍顺序查找、折半查找和 静态查找方法,主要介绍顺序查找、 分块查找 动态查找方法, 动态查找方法,主要介绍二叉排序树查找 哈希表查找
本章目录
1
7.1 基本概念 7.2 静态查找 7.3 二叉排序树查找 7.4 哈希表查找 7.5 小结
返回到本节首页
小于中间项关键字, 若k小于中间项关键字,查找范围的低端数 小于中间项关键字 据元素指针low不变,高端数据元素指针 不变, 据元素指针 不变 high更新为 更新为mid-1; 更新为 大于中间项关键字, 若k大于中间项关键字,查找范围的高端数 大于中间项关键字 据元素指针high不变,低端数据元素指针 不变, 据元素指针 不变 low更新为 更新为mid+1; 更新为 )、(3) (4)重复步骤(2)、( )直到查找成功或 )重复步骤( )、( 查找范围为空( ),即查找失败 查找范围为空(low>high),即查找失败 ), 为止。 为止。 (5)如果查找成功,返回找到元素的存放位 )如果查找成功, 即当前的中间项位置指针mid;否则返 置,即当前的中间项位置指针 ; 返回到本节首页 回查找失败标志。 回查找失败标志。
