数列(1)rosoft Office Word 文档

合集下载

数列求和Microsoft Word 文档 (2)

第二讲数列求和(一)一、知识要点若干个数排成一列称为数列。

数列中的每一个数称为一项。

其中第一项称为首项，最后一项称为末项，数列中项的个数称为项数。

从第二项开始，后项与其相邻的前项之差都相等的数列称为等差数列，后项与前项的差称为公差。

在这一章要用到两个非常重要的公式：“通项公式”和“项数公式”。

通项公式：第n项=首项+(项数-1)×公差项数公式：项数=(末项-首项)÷公差+1二、精讲精练例题1、有一个数列：4，10，16，22.…，52.这个数列共有多少项? 【思路导航】容易看出这是一个等差数列，公差为6，首项是4，末项是52.要求项数，可直接带入项数公式进行计算。

项数=(52-4)÷6+1=9，即这个数列共有9项。

边学边练：等差数列中，首项=1.末项=39，公差=2.这个等差数列共有多少项?例题2、有一等差数列：3.7，11.15，……，这个等差数列的第100项是多少?【思路导航】这个等差数列的首项是3.公差是4，项数是100。

要求第100项，可根据“末项=首项+公差×(项数-1)”进行计算。

第100项=3+4×(100-1)=399.边学边练：一等差数列，首项=3.公差=2.项数=10，它的末项是多少?例题3、有这样一个数列：1.2.3.4，…，99，100。

请求出这个数列所有项的和。

【思路导航】如果我们把1.2.3.4，…，99，100与列100，99，…，3.2.1相加，则得到(1+100)+(2+99)+(3+98)+…+(99+2)+(100+1)，其中每个小括号内的两个数的和都是101.一共有100个101相加，所得的和就是所求数列的和的2倍，再除以2.就是所求数列的和。

1+2+3+…+99+100=(1+100)×100÷2=5050上面的数列是一个等差数列，经研究发现，所有的等差数列都可以用下面的公式求和：等差数列总和=(首项+末项)×项数÷2这个公式也叫做等差数列求和公式。

(word完整版)求数列的通项公式方法总结,推荐文档

题型四：求数列的通项公式一.公式法：当题中已知数列是等差数列或等比数列，在求其通项公式时我们就可以直接利用等差或等比数列的公式来求通项，只需求得首项及公差公比。

二.当题中告诉了数列任何前一项和后一项的递推关系即：n a 和a n-1的关系时我们可以根据具体情况采用下列方法1、叠加法：一般地，对于型如)(1n f a a n n +=+类的通项公式，且)()2()1(n f f f +++Λ的和比较好求，我们可以采用此方法来求n a 。

即：11221()()()n n n n n a a a a a a a ---=-+-++-L 1a +(2)n ≥；【例1】已知数列{}n a 满足11211,2n n a a a n n+==++，求数列{}n a 的通项公式。

解：（1）由题知：121111(1)1n n a a n n n n n n +-===-+++ 112211()())n n n n n a a a a a +(a -a a ---∴=-+-++……1111111()()()121122n n n n =-+-++-+---…… 312n=- 2、叠乘法：一般地对于形如“已知a 1，且n1n a a +=f （n ）（f （n ）为可求积的数列）”的形式可通过叠乘法求数列的通项公式。

即：121121n n n n n a a a a a a a a ---=⋅⋅⋅⋅L (2)n ≥；【例2】在数列｛n a ｝中，1a =1, (n+1)·1+n a =n ·n a ，求n a 的表达式。

解：由(n+1)·1+n a =n ·n a 得11+=+n n a a n n ， 1a a n =12a a ·23a a ·34a a …1-n n a a =n n n 11433221=-⋅⋅Λ 所以n a n 1= 3、构造法：当数列前一项和后一项即n a 和a n-1的递推关系较为复杂时，我们往往对原数列的递推关系进行变形，重新构造数列，使其变为我们学过的熟悉的数列（等比数列或等差数列）。

(完整word版)数列求和常见的7种方法(word文档良心出品)

数列求和的基本方法和技巧一、总论：数列求和7种方法：利用等差、等比数列求和公式错位相减法求和反序相加法求和分组相加法求和裂项消去法求和分段求和法（合并法求和）利用数列通项法求和二、等差数列求和的方法是逆序相加法，等比数列的求和方法是错位相减法，三、逆序相加法、错位相减法是数列求和的二个基本方法。

数列是高中代数的重要内容，又是学习高等数学的基础. 在高考和各种数学竞赛中都占有重要的地位. 数列求和是数列的重要内容之一，除了等差数列和等比数列有求和公式外，大部分数列的求和都需要一定的技巧. 下面，就几个历届高考数学和数学竞赛试题来谈谈数列求和的基本方法和技巧.一、利用常用求和公式求和利用下列常用求和公式求和是数列求和的最基本最重要的方法. 1、等差数列求和公式：d n n na a a n S n n 2)1(2)(11-+=+=2、等比数列求和公式：⎪⎩⎪⎨⎧≠--=--==)1(11)1()1(111q q q a a qq a q na S n nn3、 )1(211+==∑=n n k S nk n 4、)12)(1(6112++==∑=n n n k S nk n5、 213)]1(21[+==∑=n n k S nk n [例1] 已知3log 1log 23-=x ，求⋅⋅⋅++⋅⋅⋅+++nx x x x 32的前n 项和. 解：由212log log 3log 1log 3323=⇒-=⇒-=x x x由等比数列求和公式得 nn x x x x S +⋅⋅⋅+++=32 （利用常用公式）＝x x x n --1)1(＝211)211(21--n ＝1－n 21[例2] 设S n ＝1+2+3+…+n ，n ∈N *,求1)32()(++=n nS n S n f 的最大值.解：由等差数列求和公式得 )1(21+=n n S n ， )2)(1(21++=n n S n （利用常用公式） ∴ 1)32()(++=n n S n S n f ＝64342++n n n＝nn 64341++＝50)8(12+-nn 501≤∴ 当 88-n ，即n ＝8时，501)(max =n f二、错位相减法求和这种方法是在推导等比数列的前n 项和公式时所用的方法，这种方法主要用于求数列{a n · b n }的前n 项和，其中{ a n }、{ b n }分别是等差数列和等比数列.[例3] 求和：132)12(7531--+⋅⋅⋅++++=n n x n x x x S ………………………①解：由题可知，{1)12(--n xn }的通项是等差数列{2n －1}的通项与等比数列{1-n x}的通项之积设nn x n x x x x xS )12(7531432-+⋅⋅⋅++++=………………………. ② （设制错位） ①－②得 nn n x n x x x x x S x )12(222221)1(1432--+⋅⋅⋅+++++=-- （错位相减）再利用等比数列的求和公式得：n n n x n x x x S x )12(1121)1(1----⋅+=-- ∴ 21)1()1()12()12(x x x n x n S n n n -+++--=+[例4] 求数列⋅⋅⋅⋅⋅⋅,22,,26,24,2232n n前n 项的和. 解：由题可知，{n n 22}的通项是等差数列{2n}的通项与等比数列{n 21}的通项之积设n n nS 2226242232+⋅⋅⋅+++=…………………………………① 14322226242221++⋅⋅⋅+++=n n nS ………………………………② （设制错位） ①－②得1432222222222222)211(+-+⋅⋅⋅++++=-n n n nS （错位相减）1122212+---=n n n∴ 1224-+-=n n n S三、反序相加法求和这是推导等差数列的前n 项和公式时所用的方法，就是将一个数列倒过来排列（反序），再把它与原数列相加，就可以得到n 个)(1n a a +.[例5] 求证：n n n n n n n C n C C C 2)1()12(53210+=++⋅⋅⋅+++证明：设nn n n n n C n C C C S )12(53210++⋅⋅⋅+++=………………………….. ①把①式右边倒转过来得113)12()12(n n n n n n n C C C n C n S ++⋅⋅⋅+-++=- （反序）又由mn n m n C C -=可得nn n n n n n C C C n C n S ++⋅⋅⋅+-++=-1103)12()12(…………..…….. ②①+②得 nn n n n n n n n C C C C n S 2)1(2))(22(2110⋅+=++⋅⋅⋅+++=- （反序相加） ∴ nn n S 2)1(⋅+=[例6] 求οοοοο89sin 88sin 3sin 2sin 1sin 22222++⋅⋅⋅+++的值解：设οοοοο89sin 88sin 3sin 2sin 1sin 22222++⋅⋅⋅+++=S …………. ①将①式右边反序得οοοοο1sin 2sin 3sin 88sin 89sin 22222+++⋅⋅⋅++=S …………..② （反序）又因为 1cos sin ),90cos(sin 22=+-=x x x x ο①+②得（反序相加）)89cos 89(sin )2cos 2(sin )1cos 1(sin 2222222οοοοοο++⋅⋅⋅++++=S ＝89∴ S ＝44.5题1 已知函数（1）证明：；（2）求的值.解：（1）先利用指数的相关性质对函数化简，后证明左边=右边（2）利用第（1）小题已经证明的结论可知，两式相加得：所以.练习、求值：四、分组法求和有一类数列，既不是等差数列，也不是等比数列，若将这类数列适当拆开，可分为几个等差、等比或常见的数列，然后分别求和，再将其合并即可. [例7] 求数列的前n 项和：231,,71,41,1112-+⋅⋅⋅+++-n a a a n ，… 解：设)231()71()41()11(12-++⋅⋅⋅++++++=-n aa a S n n将其每一项拆开再重新组合得)23741()1111(12-+⋅⋅⋅+++++⋅⋅⋅+++=-n aa a S n n （分组）当a ＝1时，2)13(n n n S n -+=＝2)13(nn + （分组求和）当1≠a 时，2)13(1111n n aa S nn -+--=＝2)13(11n n a a a n -+--- [例8] 求数列{n(n+1)(2n+1)}的前n 项和.解：设k k k k k k a k ++=++=2332)12)(1(∴ ∑=++=n k n k k k S 1)12)(1(＝)32(231k k knk ++∑=将其每一项拆开再重新组合得S n ＝k k k nk n k nk ∑∑∑===++1213132（分组）＝)21()21(3)21(2222333n n n +⋅⋅⋅++++⋅⋅⋅++++⋅⋅⋅++＝2)1(2)12)(1(2)1(22++++++n n n n n n n （分组求和）＝2)2()1(2++n n n五、裂项法求和这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项（通项）分解，然后重新组合，使之能消去一些项，最终达到求和的目的. 通项分解（裂项）如：（1）)()1(n f n f a n -+= （2）οοοοοn n n n tan )1tan()1cos(cos 1sin -+=+ （3）111)1(1+-=+=n n n n a n （4）)121121(211)12)(12()2(2+--+=+-=n n n n n a n （5）])2)(1(1)1(1[21)2)(1(1++-+=+-=n n n n n n n a n(6) nnn n n n n n S n n n n n n n n n a 2)1(11,2)1(12121)1()1(221)1(21+-=+-⋅=⋅+-+=⋅++=-则（7）)11(1))((1CAn B An B C C An B An a n +-+-=++=（8）n a ==[例9] 求数列⋅⋅⋅++⋅⋅⋅++,11,,321,211n n 的前n 项和.解：设n n n n a n -+=++=111（裂项）则 11321211+++⋅⋅⋅++++=n n S n （裂项求和）＝)1()23()12(n n -++⋅⋅⋅+-+- ＝11-+n [例10] 在数列{a n }中，11211++⋅⋅⋅++++=n nn n a n ，又12+⋅=n n n a a b ，求数列{b n }的前n 项的和. 解： ∵ 211211nn n n n a n =++⋅⋅⋅++++=∴ )111(82122+-=+⋅=n n n n b n （裂项）∴ 数列{b n }的前n 项和)]111()4131()3121()211[(8+-+⋅⋅⋅+-+-+-=n n S n （裂项求和）＝)111(8+-n ＝18+n n[例11] 求证：οοοοοοοο1sin 1cos 89cos 88cos 12cos 1cos 11cos 0cos 12=+⋅⋅⋅++ 解：设οοοοοο89cos 88cos 12cos 1cos 11cos 0cos 1+⋅⋅⋅++=S ∵οοοοοn n n n tan )1tan()1cos(cos 1sin -+=+ （裂项） ∴οοοοοο89cos 88cos 12cos 1cos 11cos 0cos 1+⋅⋅⋅++=S （裂项求和）＝]}88tan 89[tan )2tan 3(tan )1tan 2(tan )0tan 1{(tan 1sin 1οοοοοοοοο-+-+-+- ＝)0tan 89(tan 1sin 1οοο-＝οο1cot 1sin 1⋅＝οο1sin 1cos 2 ∴ 原等式成立答案：六、分段求和法（合并法求和）针对一些特殊的数列，将某些项合并在一起就具有某种特殊的性质，因此，在求数列的和时，可将这些项放在一起先求和，然后再求S n .[例12] 求cos1°+ cos2°+ cos3°+···+ cos178°+ cos179°的值.解：设S n ＝ cos1°+ cos2°+ cos3°+···+ cos178°+ cos179°∵ )180cos(cos οοοn n --= （找特殊性质项）∴S n ＝（cos1°+ cos179°）+（ cos2°+ cos178°）+ （cos3°+ cos177°）+···+（cos89°+ cos91°）+ cos90° （合并求和）＝ 0[例13] 数列{a n }：n n n a a a a a a -====++12321,2,3,1，求S 2002.解：设S 2002＝2002321a a a a +⋅⋅⋅+++由n n n a a a a a a -====++12321,2,3,1可得,2,3,1654-=-=-=a a a,2,3,1,2,3,1121110987-=-=-====a a a a a a……2,3,1,2,3,1665646362616-=-=-====++++++k k k k k k a a a a a a∵ 0665646362616=+++++++++++k k k k k k a a a a a a （找特殊性质项） ∴ S 2002＝2002321a a a a +⋅⋅⋅+++ （合并求和）＝)()()(66261612876321++++⋅⋅⋅+++⋅⋅⋅+⋅⋅⋅+++⋅⋅⋅+++k k k a a a a a a a a a a2002200120001999199819941993)(a a a a a a a +++++⋅⋅⋅+++⋅⋅⋅+＝2002200120001999a a a a +++ ＝46362616+++++++k k k k a a a a ＝5[例14] 在各项均为正数的等比数列中，若103231365log log log ,9a a a a a +⋅⋅⋅++=求的值.解：设1032313log log log a a a S n +⋅⋅⋅++=由等比数列的性质 q p n m a a a a q p n m =⇒+=+ （找特殊性质项）和对数的运算性质 N M N M a a a ⋅=+log log log 得)log (log )log (log )log (log 6353932310313a a a a a a S n ++⋅⋅⋅++++= （合并求和）＝)(log )(log )(log 6539231013a a a a a a ⋅+⋅⋅⋅+⋅+⋅＝9log 9log 9log 333+⋅⋅⋅++ ＝10七、利用数列的通项求和先根据数列的结构及特征进行分析，找出数列的通项及其特征，然后再利用数列的通项揭示的规律来求数列的前n 项和，是一个重要的方法.[例15] 求32111111111111个n ⋅⋅⋅+⋅⋅⋅+++之和. 解：由于)110(91999991111111-=⋅⋅⋅⨯=⋅⋅⋅k k k 43421321个个（找通项及特征） ∴ 32111111111111个n ⋅⋅⋅+⋅⋅⋅+++ ＝)110(91)110(91)110(91)110(91321-+⋅⋅⋅+-+-+-n （分组求和）＝)1111(91)10101010(9113214434421个n n +⋅⋅⋅+++-+⋅⋅⋅+++ ＝9110)110(1091nn ---⋅＝)91010(8111n n --+ [例16] 已知数列{a n }：∑∞=+-+++=11))(1(,)3)(1(8n n n n a a n n n a 求的值. 解：∵ ])4)(2(1)3)(1(1)[1(8))(1(1++-+++=-++n n n n n a a n n n （找通项及特征）＝])4)(3(1)4)(2(1[8+++++⋅n n n n （设制分组）＝)4131(8)4121(4+-+++-+⋅n n n n （裂项）∴ ∑∑∑∞=∞=∞=++-+++-+=-+1111)4131(8)4121(4))(1(n n n n n n n n n a a n （分组、裂项求和）＝418)4131(4⋅++⋅＝313提高练习：1．已知数列{}n a 中，n S 是其前n 项和，并且1142(1,2,),1n n S a n a +=+==L ，⑴设数列),2,1(21ΛΛ=-=+n a a b n n n ，求证：数列{}n b 是等比数列； ⑵设数列),2,1(,2ΛΛ==n a c n nn ，求证：数列{}n c 是等差数列；2．设二次方程n a x 2-n a +1x +1=0(n ∈N)有两根α和β，且满足6α-2αβ+6β=3．(1)试用n a 表示a 1n +；3．数列{}n a 中，2,841==a a 且满足n n n a a a -=++122 *N n ∈⑴求数列{}n a 的通项公式；⑵设||||||21n n a a a S +++=Λ，求n S ；。

(word完整版)数列基础知识归纳,文档

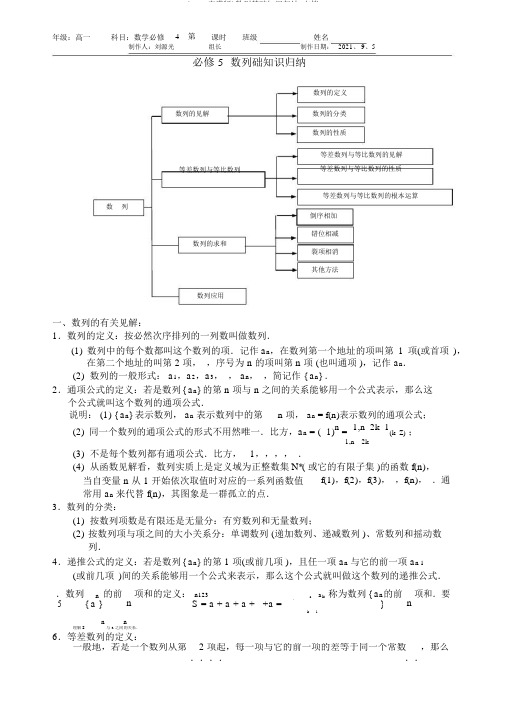
年级：高一科目：数学必修4第课时班级姓名制作人：刘源光组长制作日期：2021、 9、5必修 5数列础知识归纳数列的定义数列的见解数列的分类数列的性质等差数列与等比数列的见解等差数列与等比数列等差数列与等比数列的性质等差数列与等比数列的根本运算数列倒序相加错位相减数列的求和裂项相消其他方法数列应用一、数列的有关见解：1．数列的定义：按必然次序排列的一列数叫做数列．(1) 数列中的每个数都叫这个数列的项．记作a n，在数列第一个地址的项叫第1 项(或首项)，在第二个地址的叫第 2 项，，序号为 n 的项叫第 n 项 (也叫通项 )，记作 a n．(2)数列的一般形式： a1，a2，a3，， a n，，简记作 { a n} ．2．通项公式的定义：若是数列{ a n} 的第 n 项与 n 之间的关系能够用一个公式表示，那么这个公式就叫这个数列的通项公式．说明： (1) { a n} 表示数列， a n表示数列中的第n 项， a n = f(n)表示数列的通项公式；(2)同一个数列的通项公式的形式不用然唯一．比方，a n = ( 1)n = 1,n 2k 1(k Z)；1,n 2k(3)不是每个数列都有通项公式．比方， 1，，，，．(4)从函数见解看，数列实质上是定义域为正整数集N*( 或它的有限子集 )的函数 f(n)，当自变量 n 从 1 开始依次取值时对应的一系列函数值常用 a n来代替 f(n)，其图象是一群孤立的点．f(1)，f(2)，f(3)，，f(n)，．通3．数列的分类：(1)按数列项数是有限还是无量分：有穷数列和无量数列；(2)按数列项与项之间的大小关系分：单调数列 (递加数列、递减数列 )、常数列和摇动数列．4．递推公式的定义：若是数列{ a n} 的第 1 项(或前几项 )，且任一项 a n与它的前一项 a n 1 (或前几项)间的关系能够用一个公式来表示，那么这个公式就叫做这个数列的递推公式．．数列n的前n 项和的定义： n123n ak称为数列{ a n的前n项和．要n5{ a }S = a + a + a + +a =}k1n n理解 S与 a 之间的关系．6．等差数列的定义：一般地，若是一个数列从第 2 项起，每一项与它的前一项的差等于同一个常数，那么．．．．．．这个数列就叫等差数列，这个常数叫做等差数列的公差，公差平时用字母 d 表示．．即：{ a n为等比数列n + 1n n + 1n n + 2n n2 }a a = d 2a= a + a a = kn + b S = An + Bn 7．等比数列的定义：一般地，若是一个数列从第 2 项起，每一项与它的前一项的比等于同一个常数，那么．．．．．．这个数列就叫做等比数列，这个常数叫做等比数列的公比．公比平时用字母 q 表示 (q0)，即： { a n} 为等比数列a n + 1： a n = q (q0)2a n a n 2 ．a n 1注意条件“从第 2 项起〞、“常数〞q．由定义可知：等比数列的公比和项都不为零．二、等差、等比数列的性质：等差数列 (AP)等比数列 (GP)通项公式a n1n1n 11，= a + (n 1)d a = a q (a 0 q 0)n(a1a n )n(n 1) d na1 , q1,前 n 项和S n na1S n a1 (1 q n ), q 1.221q①a n = a m + (n m)d②m + n = s + t，那么 a m + a n =a s + a t性质③S m，2m m， 3m2m，成S S S SAP①a n = a m q n m②m + n = s + t，那么 a m n s ta = a a③S m，2m m， 3m2m，成GP S S S S(q 1 或 m 不为偶数 )④a k，k + m，k + 2m，成AP，d④ak，k + m，k + 2m，成maa= md aa GP，q = q 注： 1．等差 (等比 )数列 { a n} 的任意等距离的项组成的数列仍为等差(等比 )数列．2．三个数成等差的想法：a d，a，a + d；四个数成等差的想法： a 3d，a d，a + d， a + 3d；，，；四个数成等比的错误想法：3，a/q，aq，aq3(为3．三个数成等比的想法： a/q a aq a/q 什么？ )nc a n(c > 0)是等比数列．4．{ a } 为等差数列，那么5．{ b n} ( b n > 0)是等比数列，那么 {log c b n } ( c > 0 且 c 1) 是等差数列．6．公差为 d 的等差数列 { a n} 中，假设 d > 0，那么 { a n} 是递加数列；假设 d = 0，那么 { a n} 是常数列；假设 d < 0，那么 { a n} 是递减数列．7．等比数列 { a n} 中，假设公比为 q，那么(1) 当 a1 > 0，q > 1 或 a1 < 0，0 < q < 1 时为递加数列；(2) 当 a1 < 0，q > 1 或 a1 > 0，0 < q < 1 时为递减数列；(3) 当 q < 0 时为摇动数列；(4) 当 q = 1 时为常数列．8．等差数列前 n 项和最值的求法：(1)a1 > 0， d < 0 时， S n有最大值； a1 < 0， d > 0 时， S n有最小值．(2)S n最值的求法：①假设 S n，可用二次函数最值的求法 (n N*) ；②假设 a n，那么n取最值时n 的值(n N*)能够下确定：n 最大值a n0(或n 最小S S Sa n 10值 a n0)．a n10三、常有数列通项的求法：1．定义法 (利用 AP，GP 的定义 )．2．累加法 (a n + 1a n = c n型)：a n = a1 + (a2 a1) + (a3 a2) + + (a n a n 1) = a1 + c1 + c2 ++ c n 1(n2)．3．公式法： a nS 1 (n 1) ．S nS n 1 (n 2)4．累乘法 (an 1c n 型 )：a n = a 1a 2 a 3 L a n = a 1c 1c 2c n1(n2)．a n= qaa 1 a 2 a n 10)型，转变为 a + x = q(a + x)．可5．待定系数法： a+ b (q 0，q 1，bn + 1 nn + 1n 以将其改写变形成以下形式： a n + 1 + b = q(a n + b )，于是可依据等比数列的定义求出其通项公式．q 1q 1 6．间接法 (比方： a n + 1 a n = 4a n + 1a n1 14 )．a n 1a n四、数列的求和方法：除化归为等差数列或等比数列求和外，还有以下一些常用方法：1．拆项求和法 (a= bnc )：将一个数列拆成假设干个简单数列(如等差数列、等比数列、nn常数数列等等 )，尔后分别求和．如 n n ． a = 2n + 32．并项求和法：将数列的相邻两项 (或假设干项 )并成一项 (或一组 )先求和，尔后再求 S n ．如“S n12 22 32 42 52 62 L(2 n 1)2 (2 n)2 〞的求和．= f(n + 1)f(n)，使得正3．裂项相消法：将数列的每一项拆 (裂开 )成两项之差，即 an负项能互相抵消，剩下首尾假设干项．用裂项相消法求和，需要掌握一些常有的裂项，如： a n( An 1C ) C 1 ( 1 1 C ) 、 1 = 1 1 、 1 1 ( ab) 等． B )( An B An B An n(n 1) n n 1 a b a b4．错位相减法：将一个数列的每一项都作相同的变换，尔后将获取的新数列错动一个地址与原数列的各项相减，这是模拟推导等比数列前 n 项和公式的方法．对一个由等差数列及等比数列对应项之积组成的数列的前 n 项和，常用错位相减法．即错位相减法一般只要求解决下述数列的求和：假设 a n = b n c n ，其中 { b n } 是等差数列， { c n } 是等比数列，那么数列 { a n } 的求和运用错位相减法．记 S n1 12 23 3+n n ，那么 n1 22 3+n 1 n n n + 1= b c + b c + b c + b c qS = b c + b c + b c + b c ，如 a n = (2n 1) 2n ．5．倒序相加法：将一个数列的倒数第 k 项(k = 1，2，3，， n)变为顺数第 k 项，尔后将获取的新数列与原数列相加，这是模拟推导等差数列前 n 项和公式的方法．注意： (1) “数列求和〞是数列中的重要内容，在中学高考范围内，学习数列求和不需要学习任何理论，上面所述求和方法可是将一些常用的数式变换技巧运用于数列求和之中．(2) “错位〞与“倒序〞求和的方法是比较特其他方法．(3) 数列求通项及和的方法多种多样，要视详尽状况采纳合适的方法．(4) 重要公式：① 1 + 2 + + n = 1 ； ② 22 + 2 1 33+ 2 n(n + 1)1 +2 + n = 6 n(n + 1)(2n + 1)；③ 1 + 2 +n 3 = (1 + 2 + + n)2 = 1 n 2(n + 1)2；4* ④ 等差数列中， S m + n* ⑤ 等比数列中， S m + n= S m + S n + mnd ；= S n + q n S m = S m + q mS n ． ab(1 b)n五、分期付款(按揭贷款 )：每次还款x(1b)n 1元(贷款 a 元，n 次还清，每期利率为 b)．。

(完整word版)数列求和的各种方法

教学目标1熟练掌握等差、等比数列的前n 项和公式.2 •掌握非等差、等比数列求和的几种常见方法.3•能在具体的问题情境中识别数列的等差关系或等比关系，并能用相关知识解决相应的问题. 教学内容知识梳理1求数列的前n 项和的方法 (1) 公式法①等差数列的前n 项和公式n n 1 ,=na i + d .2②等比数列的前n 项和公式 (I )当 q = 1 时，S n = na i ;(2) 分组转化法把数列的每一项分成两项或几项，使其转化为几个等差、等比数列，再求解. (3) 裂项相消法把数列的通项拆成两项之差求和，正负相消剩下首尾若干项. (4) 倒序相加法这是推导等差数列前 n 项和时所用的方法，将一个数列倒过来排序，如果原数列相加时，若有公因式可提，并且剩余项的和易于求得，则这样的数列可用倒序相加法求和.(5) 错位相减法这是推导等比数列的前 n 项和公式时所用的方法，主要用于求｛a n • b n ｝的前n 项和，其中｛a n ｝和｛b n ｝分别是等差数列和等比数列.⑹并项求和法一个数列的前n 项和中，可两两结合求解，则称之为并项求和.形如 a n = (— 1)n f (n)类型，可采用两项合并求解.例如，S n = 1002— 992+ 982 — 972+…+ 22 — 12= (100 + 99) + (98 + 97)+…+ (2 + 1) = 5 050.数列求和的方法n a i a n Si=—2(n )当q 丰1时,a i 1 q n 1 qa 1 — a n q 1 - q③常见的数列的前 n 项和：1+n=垃 1) , 1+3+5+••…+(2r — 1)= n 22122232+n 2n(n 罟,13 23 33+n 32n(n 1)等22. 常见的裂项公式 1 (1)-n n=1 _1 ______ 1 ；⑶ 2n 1 2n 12(2n—1 2n +1⑷ =2 -nn1n2 2nn1 n1n21 1 1 1⑹设等差数列｛an ｝的公差为d ,则站=歳-齐).数列求和题型考点一公式法求和一 11. (2016新课标全国I)已知｛a n ｝是公差为3的等差数列，数列｛b n ｝满足b 1= 1 , b 2 = 3 , a n b n + 1 + b n +1 = nb n . (1) 求｛a n ｝的通项公式； (2) 求｛b n ｝的前n 项和.2. (2013新课标全国I, 17)已知等差数列｛a n ｝的公差不为零，a 1= 25,且a 1, an , a 13成等比数列 (1) 求｛a n ｝的通项公式； (2) 求 a 1+ a 4+ a 7+ …+ a 3n — 2.变式训练 1.(2015四川，16)设数列｛a n ｝(n = 1, 2, 3,…)的前n 项和S n满足S n = 2a n — a 1，且a 1, a 2+1, a 3成等差数列.(1)求数列｛ a n ｝的通项公式；1⑵设数列 a 的前n 项和为T n ，求T n .2. （2014 福建，17）在等比数列｛a n ｝中，a 2= 3, a 5= 81. （1）求 a n ；⑵设b n = log 3a n ,求数列｛b n ｝的前n 项和S n .1⑵-n n k11 1 k (n n + k )；(5) n + . n + kn).考点二错位相减法1.（山东）已知数a的前n项和S n=3n2+8n, b n是等差数列，且a n b n b n（I）求数列b n的通项公式；（I）令C n(a n1）n 1求数列c n的前n项和T n.(b n2)n2.（2015 天津，18）已知数列｛a n｝满足a n+ 2= qa n（q 为实数，且q丰1,）n I N*, a1= 1,a2 = 2,且a2+ a3, a3+ a4,a4 + a5成等差数列.（1）求q的值和｛a n｝的通项公式；⑵设b n=lpg d, n I N*,求数列｛b n｝的前n项和.a2n-1变式训练1. （2014 江西，17）已知首项都是1 的两个数列｛a n｝, ｛b n｝（b n M0 n IN*）满足a n b n+ 1-a n + 1b n+ 2b n+ 1b n= 0.（1）令C n=严，求数列｛C n｝的通项公式；b n⑵若b n= 3旷1，求数列｛a n｝的前n项和S n.2. (2014四川，19)设等差数列｛a n｝的公差为d，点(a n, b n)在函数f(x)= 2x的图象上(n I N*).(1) 若a i = - 2,点(a8, 4b7)在函数f(x )的图象上，求数列｛a n｝的前n项和S n；1 a n(2) 若a1= 1,函数f(x)的图象在点(a2, b2)处的切线在x轴上的截距为2-应，求数列恳的前n项和T n.3. (2015湖北，18)设等差数列｛a n｝的公差为d，前n项和为S n,等比数列｛b n｝的公比为q，已知b1= a1, b2 =2, q = d, S10 = 100.(1) 求数列｛a n｝, ｛b n｝的通项公式；(2) 当d>1时，记C n= b n求数列｛C n｝的前n项和T n.4. (2015 •东，18)设数列｛a n｝的前n项和为S.已知2S n= 3n+ 3.(1) 求｛a n｝的通项公式；(2) 若数列｛ b n｝满足a n b n= log3a n，求｛ b n｝的前n项和T n.* 11 15. (2015 浙江，17)已知数列｛a n｝和｛ b n｝满足a1= 2, 3= 1, a n+1 = 2a n( n I N), 3 + qb2 +§b3+…+：b n= b n+1 —1(nI N*).(1)求a n与b n ；⑵记数列｛ a n b n｝的前n项和为T n，求T n.6. (2015 湖南，19)设数列｛a n｝的前n 项和为S n,已知a i= 1, a2= 2,且a n+2= 3S n—S n+1 + 3, n I N .(1)证明：a n+ 2= 3a n ；⑵求S n.考点三分组求和法1. (2015 福建，17)在等差数列｛a n｝中，a2= 4, a4+ a7= 15.(1) 求数列｛ a n｝的通项公式；(2) 设b n= 2an 2+ n,求b1 + b2 + b3+…+ b10 的值.n2+ n *2. (2014湖南，16)已知数列｛a n｝的前n项和S n= — , n I N .(1)求数列｛ a n｝的通项公式；⑵设b n= 2an+ (—1)n a n,求数列｛b n｝的前2n项和.变式训练1. (2014北京，15)已知｛a n｝是等差数列，满足a i = 3, a4= 12,数列｛b n｝满足b i = 4, b4= 20,且｛b n —a n｝为等比数列.(1)求数列｛a n｝和｛b n｝的通项公式；⑵求数列｛ b n｝的前n项和.考点四裂项相消法1. (2015新课标全国I, 17)S n为数列｛a n｝的前n项和.已知a n>0, a¥+ 2a n= 4S n+ 3.(1) 求｛a n｝的通项公式；1(2) 设b n= ，求数列｛b n｝的前n项和.a n a n+12. (2011新课标全国，17)等比数列｛a n｝的各项均为正数，且2a i+ 3a2= 1, a3= 9a2a6.(1) 求数列｛ a n｝的通项公式；1 »(2) 设b n= log3a1+ log3a2+・・・ + log3a n，求数列匚的前n项和.3. (2015安徽，18)已知数列｛a n｝是递增的等比数列，且• + a4= 9, a2a3= 8.(1)求数列｛a n｝的通项公式；⑵设S n为数列｛a n｝的前n项和，b n = 1，求数列｛ b n｝的前n项和T n.S n Si + 1变式训练1. (2013 江西，16)正项数列｛a n｝满足：a^—(2n- 1)a n—2n= 0.(1)求数列｛ a n｝的通项公式a n；1⑵令b n= 5 +〔)an，求数列｛b n｝的前n项和T n.2. (2013 大纲全国，17)等差数列｛a n｝中，a7= 4, a i9= 2a9. (1)求｛a n｝的通项公式；1⑵设b n= ，求数列｛b n｝的前n项和S n.na n13. 在数列｛a n｝中，a1 = 1，当n>2时，其前n项和S n满足&= a n S n-勺.(1) 求3的表达式；S n(2) 设b n = 2^1求｛b n｝的前n项和T n.考点五倒序相加法1 1 12 2 014 已知函数f(x)=丙(X I R). (1)证明：f(x)+ f(1-x) =1；(2)若S= f(2015)+ f(2015)+…+ 口歳)，贝y S=变式训练4X 1 2 2 0141. ------------------------------------------------------------------------------------------------------- 设f(x)=4^2，若S=f(2015)+f(2015)+ …+ f(2"0i5)，则S= ---------------------------------------------------------考点六并项求和1. ___________________________________________________________________________ (2012新课标，16)数列｛a n｝满足a n+1+ (—1)% = 2n —1,则｛a n｝的前60项和为___________________________2. (2014山东，19)在等差数列｛a n｝中，已知公差d= 2, a2是a i与a4的等比中项(1) 求数列｛ a n｝的通项公式；(2) 设b n= a n n 1，记T n=—b l+ b2 - b3+ b4—…+ ( —1)n b n，求T n.~2变式训练1. (2014山东理，19)已知等差数列｛a n｝的公差为2,前n项和为S n,且S1, S2, S4成等比数列(1) 求数列｛ a n｝的通项公式；—4n(2) 令b n= (—1)n—1，求数列｛b n｝的前n项和T n.a n a n+1考点七数列｛|a n|｝的前n项和问题11. ______________________________________________________________ （2011 北京,11）在等比数列｛a n｝中，若a i = 2，a4=—4，则公比q = __________________________________ ；a i|+ |a2|+ ••• + |a n| = ______变式训练1. （2013浙江，19）在公差为d的等差数列｛a n｝中，已知a1= 10,且a1, 2a2+ 2, 5a3成等比数列.（1）求d, a n；12. (2013湖南，15)设S n为数列｛a n｝的前n项和，S n= (—1)n a n—尹n I N*，则:(1) a3= _________ ；(2) S1 + S2 + …+ S100 = ________ .⑵若 d v0,求a |+ |a2| + |a3|+ …+ |a n|.考点八周期数列1.已知数列2 008,2 009,1，—2 008 , —2 009 ,…，这个数列的特点是从第二项起，每一项都等于它的前后两项之和，则这个数列的前 2 014项之和S2 014等于（）A. 2 008B. 2 010C. 1 D . 0变式训练n n1.（2012福建）数列｛a n｝的通项公式a n= ncosg，其前n项和为S n,则S2 012等于（）A.1 006B.2 012C.503D.0考点九数列与不等式的应用1. （2014新课标全国I, 17）已知数列｛a n｝满足a1= 1, a n+1= 3a n+ 1.1（1）证明a n + 2是等比数列，并求｛a n｝的通项公式；1 1 1 3（2）证明一 + —+ …+—<;.a1 a2 a n 21 *2. (2015 浙江，20)已知数列｛a n｝满足a1 = 2且a n+1 = a n —a n(n I N ).a n *(1)证明：1 W W 2( I N );a n+ 1⑵设数列｛ a2｝的前n项和为S n,证明:1 S n 1--------- —----------2 (n + 2) n 2 (n + 1)(n IN*).23.(2013江西，理)正项数列｛a n｝的前项和｛a n｝满足：S n2 2(n n 1)S n (n n) 0(1)求数列｛a n｝的通项公式a n；n 1(2)令b n门，数列｛bn｝的前n项和为T n。

数列求和Word版含答案

数列求和【课前回顾】1．公式法(1)等差数列{a n }的前n 项和S n ＝n (a 1＋a n )2＝na 1＋n (n －1)d2. 推导方法：倒序相加法．(2)等比数列{a n }的前n 项和S n ＝⎩⎪⎨⎪⎧na 1，q ＝1，a 1(1－q n )1－q ，q ≠1.推导方法：乘公比，错位相减法． (3)一些常见的数列的前n 项和： ①1＋2＋3＋…＋n ＝n (n ＋1)2； ②2＋4＋6＋…＋2n ＝n (n ＋1)； ③1＋3＋5＋…＋2n －1＝n 2. 2．几种数列求和的常用方法(1)分组转化求和法：一个数列的通项公式是由若干个等差或等比或可求和的数列组成的，则求和时可用分组求和法，分别求和而后相加减．(2)裂项相消法：把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得前n 项和．(3)错位相减法：如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么求这个数列的前n 项和即可用错位相减法求解．(4)倒序相加法：如果一个数列{a n }与首末两端等“距离”的两项的和相等或等于同一个常数，那么求这个数列的前n 项和即可用倒序相加法求解．【课前快练】1．在数列{a n }中，a n ＝1n (n ＋1)，若{a n }的前n 项和为2 0172 018，则项数n 为( )A ．2 014B ．2 015C ．2 016D ．2 017解析：选D 因为a n ＝1n (n ＋1)＝1n －1n ＋1，所以S n ＝1－12＋12－13＋…＋1n －1n ＋1＝1－1n ＋1＝n n ＋1＝2 0172 018，所以n ＝2 017.2．数列{1＋2n -1}的前n 项和为( ) A ．1＋2nB ．2＋2nC ．n ＋2n －1D ．n ＋2＋2n解析：选C 由题意得a n ＝1＋2n －1，所以S n ＝n ＋1－2n1－2＝n ＋2n －1.3．数列{a n }的前n 项和为S n ，已知S n ＝1－2＋3－4＋…＋(－1)n -1·n ，则S 17＝________. 解析：S 17＝1－2＋3－4＋5－6＋…＋15－16＋17＝1＋(－2＋3)＋(－4＋5)＋(－6＋7)＋…＋(－14＋15)＋(－16＋17)＝1＋1＋1＋…＋1＝9.答案：9考点一公式法、分组转化法求和方法(一) 公式法求和几类可以使用公式法求和的数列(1)等差数列、等比数列以及由等差数列、等比数列通过加、减构成的数列，它们可以使用等差数列、等比数列的求和公式求解．(2)奇数项和偶数项分别构成等差数列或等比数列的，可以分项数为奇数和偶数时，分别使用等差数列或等比数列的求和公式．(3)等差数列各项加上绝对值，等差数列乘(－1)n 等．1．(2017·北京高考)已知等差数列{a n }和等比数列{b n }满足a 1＝b 1＝1，a 2＋a 4＝10，b 2b 4＝a 5.(1)求{a n }的通项公式；(2)求和：b 1＋b 3＋b 5＋…＋b 2n －1. 解：(1)设等差数列{a n }的公差为d .因为⎩⎪⎨⎪⎧a 1＝1，a 2＋a 4＝10，所以2a 1＋4d ＝10，解得d ＝2，所以a n ＝2n －1. (2)设等比数列{b n }的公比为q .因为b 1＝1，b 2b 4＝a 5，所以b 1q ·b 1q 3＝9. 解得q 2＝3.所以b 2n －1＝b 1q 2n －2＝3n －1. 从而b 1＋b 3＋b 5＋…＋b 2n －1＝1＋3＋32＋…＋3n －1＝3n －12.方法(二) 分组转化法求和 1．分组转化求和的通法数列求和应从通项入手，若无通项，则先求通项，然后通过对通项变形，转化为等差数列或等比数列或可求数列的前n 项和的数列求和．2．分组转化法求和的常见类型2．在数列{a n }中，a 1＝1，a 2＝2，a n ＋2－a n ＝1＋(－1)n ，那么S 100的值为( ) A ．2 500 B ．2 600 C ．2 700D ．2 800解析：选B 当n 为奇数时，a n ＋2－a n ＝0，所以a n ＝1，当n 为偶数时，a n ＋2－a n ＝2，所以a n ＝n ，故a n ＝⎩⎪⎨⎪⎧1，n 为奇数，n ，n 为偶数，于是S 100＝50＋(2＋100)×502＝2 600.3．已知数列{a n }的前n 项和S n ＝n 2＋n2，n ∈N *.(1)求数列{a n }的通项公式；(2)设b n ＝2a n ＋(－1)n a n ，求数列{b n }的前2n 项和．解：(1)当n ＝1时，a 1＝S 1＝1；当n ≥2时，a n ＝S n －S n －1＝n 2＋n 2－(n －1)2＋(n －1)2＝n .a 1＝1也满足a n ＝n ，故数列{a n }的通项公式为a n ＝n . (2)由(1)知a n ＝n ，故b n ＝2n ＋(－1)n n . 记数列{b n }的前2n 项和为T 2n ，则T 2n ＝(21＋22＋…＋22n )＋(－1＋2－3＋4－…＋2n )．记A ＝21＋22＋…＋22n ，B ＝－1＋2－3＋4－…＋2n ，则A ＝2(1－22n )1－2＝22n ＋1－2，B ＝(－1＋2)＋(－3＋4)＋…＋[－(2n －1)＋2n ]＝n . 故数列{b n }的前2n 项和T 2n ＝A ＋B ＝22n ＋1＋n －2.考点二错位相减法求和1．掌握解题“3步骤”2．注意解题“3关键”(1)要善于识别题目类型，特别是等比数列公比为负数的情形；(2)在写出“S n ”与“qS n ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“S n －qS n ”的表达式；(3)在应用错位相减法求和时，若等比数列的公比为参数，应分公比q ＝1和q ≠1两种情况求解．3．谨防解题“2失误”(1)两式相减时最后一项因为没有对应项而忘记变号．(2)对相减后的和式的结构认识模糊，错把中间的n －1项和当作n 项和．【典型例题】(2017·山东高考)已知{a n }是各项均为正数的等比数列，且a 1＋a 2＝6，a 1a 2＝a 3. (1)求数列{a n }的通项公式；(2){b n }为各项非零的等差数列，其前n 项和为S n .已知S 2n ＋1＝b n b n ＋1，求数列⎩⎨⎧⎭⎬⎫b n a n 的前n项和T n .[思维路径](1)可利用已知条件a 1＋a 2＝6，a 1a 2＝a 3列出关于首项a 1和公比q 的两个方程，解方程可得a 1，q ，从而求得通项公式．(2)由S 2n ＋1＝b n b n ＋1，利用求和公式及性质，推出数列{b n }的通项公式，结合(1)进而求出⎩⎨⎧⎭⎬⎫b n a n 的通项公式，观察其特点用错位相减法求和即可．解：(1)设{a n }的公比为q ，由题意知a 1(1＋q )＝6，a 21q ＝a 1q 2.又a n ＞0，解得a 1＝2，q ＝2，所以a n ＝2n . (2)由题意知，S 2n ＋1＝(2n ＋1)(b 1＋b 2n ＋1)2＝(2n ＋1)b n ＋1，又S 2n ＋1＝b n b n ＋1，b n ＋1≠0，所以b n ＝2n ＋1.令c n ＝b na n，则c n ＝2n ＋12n ，因此T n ＝c 1＋c 2＋…＋c n ＝32＋522＋723＋…＋2n －12n －1＋2n ＋12n ，又12T n ＝322＋523＋724＋…＋2n －12n ＋2n ＋12n ＋1，两式相减得12T n ＝32＋⎝⎛⎭⎫12＋122＋…＋12n －1－2n ＋12n ＋1 ＝32＋1－⎝⎛⎭⎫12n －1－2n ＋12n ＋1 ＝52－2n ＋52n ＋1，所以T n ＝5－2n ＋52n. 【针对训练】已知数列{a n }的前n 项和S n ＝3n 2＋8n ，{b n }是等差数列，且a n ＝b n ＋b n ＋1. (1)求数列{b n }的通项公式；(2)令c n ＝(a n ＋1)n ＋1(b n ＋2)n，求数列{c n }的前n 项和T n .解：(1)由题意知，当n ≥2时，a n ＝S n －S n －1＝6n ＋5，当n ＝1时，a 1＝S 1＝11，满足上式，所以a n ＝6n ＋5. 设数列{b n }的公差为d .由⎩⎪⎨⎪⎧ a 1＝b 1＋b 2，a 2＝b 2＋b 3，即⎩⎪⎨⎪⎧11＝2b 1＋d ，17＝2b 1＋3d ，可解得⎩⎪⎨⎪⎧b 1＝4，d ＝3.所以b n ＝3n ＋1.(2)由(1)知c n ＝(6n ＋6)n ＋1(3n ＋3)n ＝3(n ＋1)·2n ＋1，又T n ＝c 1＋c 2＋…＋c n ，得T n ＝3×[2×22＋3×23＋…＋(n ＋1)×2n ＋1]， 2T n ＝3×[2×23＋3×24＋…＋(n ＋1)×2n ＋2]，两式作差，得－T n ＝3×[2×22＋23＋24＋…＋2n ＋1－(n ＋1)×2n ＋2] ＝3×⎣⎢⎡⎦⎥⎤4＋4(1－2n )1－2－(n ＋1)×2n ＋2 ＝－3n ·2n ＋2，所以T n ＝3n ·2n ＋2.考点三裂项相消法求和1．裂项相消法求和的实质和解题关键裂项相消法求和的实质是将数列中的通项分解，然后重新组合，使之能消去一些项，最终达到求和的目的，其解题的关键就是准确裂项和消项．(1)裂项原则：一般是前边裂几项，后边就裂几项，直到发现被消去项的规律为止． (2)消项规律：消项后前边剩几项，后边就剩几项，前边剩第几项，后边就剩倒数第几项．2．常见数列的裂项方法角度(一) 形如a n ＝1n (n ＋k )型1．(2017·全国卷Ⅱ)等差数列{a n }的前n 项和为S n ，a 3＝3，S 4＝10，则∑k ＝1n1S k＝________.解析：设等差数列{a n }的首项为a 1，公差为d ，依题意有⎩⎪⎨⎪⎧ a 1＋2d ＝3，4a 1＋6d ＝10，解得⎩⎪⎨⎪⎧a 1＝1，d ＝1，所以S n ＝n (n ＋1)2，1S n ＝2n (n ＋1)＝2⎝⎛⎭⎫1n －1n ＋1，因此∑k ＝1n1S k ＝2⎝⎛⎭⎫1－12＋12－13＋…＋1n －1n ＋1＝2n n ＋1.答案：2nn ＋1角度(二) 形如a n ＝1n ＋k ＋n型2．(2018·江南十校联考)已知函数f (x )＝x α的图象过点(4,2)，令a n ＝1f (n ＋1)＋f (n )，n ∈N *.记数列{a n }的前n 项和为S n ，则S 2 018＝( )A. 2 017－1B. 2 018－1C. 2 019－1D. 2 019＋1解析：选C 由f (4)＝2可得4α＝2，解得α＝12，则f (x )＝x 12.∴a n ＝1f (n ＋1)＋f (n )＝1n ＋1＋n＝n ＋1－n ，S 2 018＝a 1＋a 2＋a 3＋…＋a 2 018＝(2－1)＋(3－2)＋(4－3)＋…＋( 2 018－2 017)＋( 2 019－ 2 018)＝ 2 019－1. 角度(三) 形如a n ＝n ＋1n 2(n ＋2)2型3．正项数列{a n }的前n 项和S n 满足：S 2n －(n 2＋n －1)S n －(n 2＋n )＝0.(1)求数列{a n }的通项公式a n ； (2)令b n ＝n ＋1(n ＋2)2a 2n，数列{b n }的前n 项和为T n .证明：对于任意的n ∈N *，都有T n<564. 解：(1)由S 2n －(n 2＋n －1)S n －(n 2＋n )＝0，得[S n －(n 2＋n )](S n ＋1)＝0.由于{a n }是正项数列，所以S n >0，S n ＝n 2＋n . 于是a 1＝S 1＝2，当n ≥2时，a n ＝S n －S n －1＝n 2＋n －(n －1)2－(n －1)＝2n . 综上，数列{a n }的通项公式为a n ＝2n . (2)证明：由于a n ＝2n ，故b n ＝n ＋1(n ＋2)2a 2n＝n ＋14n 2(n ＋2)2＝116⎣⎡⎦⎤1n 2－1(n ＋2)2. T n ＝116⎣⎡1－132＋122－142＋132－152＋…＋1(n －1)2－1(n ＋1)2＋⎦⎤1n 2－1(n ＋2)2＝116⎣⎡⎦⎤1＋122－1(n ＋1)2－1(n ＋2)2<116⎝⎛⎭⎫1＋122＝564.【针对训练】(2018·天一大联考)设等差数列{a n }的前n 项和为S n ，首项a 1＝1，且S 2 0182 018－S 2 0172 017＝1. (1)求S n ； (2)求数列⎩⎨⎧⎭⎬⎫1S n S n ＋1的前n 项和T n .解：(1)设数列{a n }的公差为d ，因为S n n ＝na 1＋n (n －1)2dn ＝a 1＋(n －1)d2，所以⎩⎨⎧⎭⎬⎫S n n 为一个等差数列，所以S 2 0182 018－S 2 0172 017＝d2＝1，所以d ＝2，故S nn ＝n ，所以S n ＝n 2. (2)因为1S n S n ＋1＝1n (n ＋1)＝1n －1n ＋1，所以T n ＝⎝⎛⎭⎫1－12＋⎝⎛⎭⎫12－13＋…＋⎝⎛⎭⎫1n －1n ＋1＝1－1n ＋1＝n n ＋1. 【课后演练】1．已知等差数列{a n }的前n 项和为S n ，若S 3＝9，S 5＝25，则S 7＝( ) A ．41 B ．48 C ．49D ．56解析：选C 设S n ＝An 2＋Bn ，由题知⎩⎪⎨⎪⎧S 3＝9A ＋3B ＝9，S 5＝25A ＋5B ＝25，解得A ＝1，B ＝0，∴S 7＝49.2．已知数列{a n }的通项公式是a n ＝2n －3⎝⎛⎭⎫15n，则其前20项和为( ) A ．380－35⎝⎛⎭⎫1－1519 B ．400－25⎝⎛⎭⎫1－1520 C ．420－34⎝⎛⎭⎫1－1520 D ．440－45⎝⎛⎭⎫1－1520 解析：选C 令数列{a n }的前n 项和为S n ，则S 20＝a 1＋a 2＋…＋a 20＝2(1＋2＋…＋20)－3⎝⎛⎭⎫15＋152＋…＋1520＝2×20×(20＋1)2－3×15⎝⎛⎭⎫1－15201－15＝420－34⎝⎛⎭⎫1－1520.3．已知数列{a n }满足a 1＝1，a n ＋1＝⎩⎪⎨⎪⎧2a n ，n 为正奇数，a n ＋1，n 为正偶数，则其前6项之和是( )A ．16B ．20C ．33D ．120解析：选C 由已知得a 2＝2a 1＝2，a 3＝a 2＋1＝3，a 4＝2a 3＝6，a 5＝a 4＋1＝7，a 6＝2a 5＝14，所以S 6＝1＋2＋3＋6＋7＋14＝33.4． 5个数依次组成等比数列，且公比为－2，则其中奇数项和与偶数项和的比值为( ) A ．－2120 B ．－2 C ．－2110D ．－215解析：选C 由题意可设这5个数分别为a ，－2a,4a ，－8a,16a ，故奇数项和与偶数项和的比值为a ＋4a ＋16a －2a －8a＝－2110，故选C.5．已知{a n }是首项为1的等比数列，S n 是{a n }的前n 项和，且9S 3＝S 6，则数列⎩⎨⎧⎭⎬⎫1a n 的前5项和为( )A.158或5B.3116或5C.3116D.158解析：选C 设{a n }的公比为q ，显然q ≠1，由题意得9(1－q 3)1－q ＝1－q 61－q，所以1＋q 3＝9，得q ＝2，所以⎩⎨⎧⎭⎬⎫1a n 是首项为1，公比为12的等比数列，前5项和为1－⎝⎛⎭⎫1251－12＝3116.6．化简S n ＝n ＋(n －1)×2＋(n －2)×22＋…＋2×2n －2＋2n －1的结果是( )A ．2n ＋1＋n －2 B ．2n ＋1－n ＋2 C ．2n －n －2D ．2n ＋1－n －2解析：选D 因为S n ＝n ＋(n －1)×2＋(n －2)×22＋…＋2×2n －2＋2n －1，① 2S n ＝n ×2＋(n －1)×22＋(n －2)×23＋…＋2×2n －1＋2n ，②所以①－②得，－S n ＝n －(2＋22＋23＋…＋2n )＝n ＋2－2n ＋1，所以S n ＝2n ＋1－n －2. 7．已知数列：112，214，318，…，⎝⎛⎭⎫n ＋12n ，…，则其前n 项和关于n 的表达式为________．解析：设所求的前n 项和为S n ，则S n ＝(1＋2＋3＋…＋n )＋⎝⎛⎭⎫12＋14＋…＋12n ＝n (n ＋1)2＋12⎝⎛⎭⎫1－12n 1－12＝n (n ＋1)2－12n ＋1. 答案：n (n ＋1)2－12n ＋1 8．在数列{a n }中，若a 1＝2，且对任意正整数m ，k ，总有a m ＋k ＝a m ＋a k ，则{a n }的前n 项和S n ＝________.解析：依题意得a n ＋1＝a n ＋a 1，即有a n ＋1－a n ＝a 1＝2，所以数列{a n }是以2为首项、2为公差的等差数列，a n ＝2＋2(n －1)＝2n ，S n ＝n (2＋2n )2＝n (n ＋1)．答案：n (n ＋1)9．已知正项数列{a n }满足a 2n ＋1－6a 2n ＝a n ＋1a n .若a 1＝2，则数列{a n }的前n 项和S n ＝________.解析：∵a 2n ＋1－6a 2n ＝a n ＋1a n ，∴(a n ＋1－3a n )(a n ＋1＋2a n )＝0， ∵a n >0，∴a n ＋1＝3a n ，又a 1＝2，∴数列{a n }是首项为2，公比为3的等比数列， ∴S n ＝2(1－3n )1－3＝3n －1.答案：3n －110．已知数列{a n }满足a 1＝1，a n ＋1·a n ＝2n (n ∈N *)，则S 2 018＝________. 解析：∵数列{a n }满足a 1＝1，a n ＋1·a n ＝2n ，① ∴n ＝1时，a 2＝2，n ≥2时，a n ·a n －1＝2n －1，② 由①÷②得a n ＋1a n －1＝2，∴数列{a n }的奇数项、偶数项分别成等比数列， ∴S 2 018＝1－21 0091－2＋2(1－21 009)1－2＝3·21 009－3.答案：3·21 009－311．已知数列{a n }中，a n ＝－4n ＋5，等比数列{b n }的公比q 满足q ＝a n －a n －1(n ≥2)且b 1＝a 2，则|b 1|＋|b 2|＋|b 3|＋…＋|b n |＝( )A ．1－4nB ．4n －1 C.1－4n3D.4n －13解析：选B 由已知得b 1＝a 2＝－3，q ＝－4， ∴b n ＝(－3)×(－4)n －1，。

数列模型及应用word

数列模型及应用word数列是由一系列有序的数按照一定规律排列而成的集合。

数列是数学中的一个重要概念，具有广泛的应用。

在实际生活中，数列模型可以帮助我们解决各种问题。

下面我将从数列的定义、分类及其应用三个方面展开详细回答。

首先，数列是一系列有序的数按照确定的规律排列而成的集合。

数列中的每个数称为该数列的项，每个数列都有一个起始项，通常用a1表示，以及一个通项公式。

数列的常用形式有等差数列、等比数列、斐波那契数列等。

等差数列是指数列中各项之间的差值都相等的数列。

其通项公式为an=a1+(n-1)d，其中a1为首项，d为公差，n为项数。

等差数列常见的应用场景有：1.日常生活中，经常会进行等差数列的计算。

比如，我们经常会遇到一些有规律的数列，比如每天存款增加一定的金额，或者每天的步数增加相同的步数等。

通过计算等差数列可以帮助我们了解某个数列的发展趋势。

2.在经济学中，等差数列被广泛应用于一些经济指标的分析。

比如，每年的国内生产总值增长率、物价指数增长率等，可以通过等差数列的概念来计算和描述。

等比数列是指数列中各项之间的比值都相等的数列。

其通项公式为an=a1*r^(n-1)，其中a1为首项，r为公比，n为项数。

等比数列常见的应用场景有：1.在金融领域，等比数列可用于计算复利。

比如，存款利率为r的情况下，每年的利息就形成一个等比数列。

2.在自然界中，等比数列也有很多应用。

比如，每天二分之一的细菌数量，每代细胞数量的增长等。

斐波那契数列是指数列中每一项等于前两项之和的数列。

其通项公式为an=an-1+an-2，其中a1和a2为首两项。

斐波那契数列的应用非常广泛，比如：1.在自然界中，斐波那契数列可以用来描述植物的生长。

比如，一个植物的高度等于前两天的高度之和。

2.在计算机科学中，斐波那契数列被广泛应用于算法和数据结构的设计。

比如，递归算法中常常使用斐波那契数列，以及在计算期权价格、股票价格等金融领域也会用到斐波那契数列。

数列(4) Microsoft Office Word 文档

24、数列（4）—数列求和一、基础知识（必记）1．公式法(1)如果一个数列是等差数列或等比数列，则求和时直接利用等差、等比数列的前n 项和公式，注意等比数列公比q 的取值情况要分或 .2．倒序相加法如果一个数列{a n }，首末两端等“距离”的两项的和相等或等于同一常数，那么求这个数列的前n 项和，即可用倒序相加法，如等差数列的前n 项和即是用此法推导的．3．错位相减法如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么这个数列的前n 项和即可用此法来求，如等比数列的前n 项和就是用此法推导的．4．裂项相消法把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得其和．5．分组转化求和法若一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成，则求和时可用分组转化法，分别求和然后相加减．6．并项求和法一个数列的前n 项和中，可两两结合求解，则称之为并项求和. 形如a n ＝(－1)n f (n )类型，可采用两项合并求解．例如S n ＝1002－992＋982－972＋…＋22－12＝(100＋99)＋(98＋97)＋…＋(2＋1)＝5 050.二、基础自测：1．数列a 1＋2，…，a k ＋2k ，…，a 10＋20共有十项，且其和为240，则a 1＋…＋a k ＋…＋a 10之值为( )A ．31B ．120C ．130D ．1852．数列12×4，14×6，16×8，…，12n (2n ＋2)，…的前n 项和为( ) A.n 2n ＋2 B.n 4n ＋4 C.2n n ＋1 D.2n 2n ＋1 3．已知数列{a n }的通项公式是a n ＝2n －12n ，其前n 项和S n ＝32164，则项数n 等于( ) A ．13 B ．10 C ．9 D ．64．已知数列{a n }的前n 项和为S n ，且a n ＝n ·2n ，则S n ＝________.5．已知数列⎩⎨⎧⎭⎬⎫a n n 的前n 项和为S n ，且满足a 1＝1，a n ＝a n －1＋n ，则S n 等于________．三、基本题型：1、S n ＝1＋⎝⎛1＋12＋⎝⎛⎭⎫1＋12＋14＋…＋⎝⎛⎭⎫1＋12＋14＋…＋12n －1.2、(2010·课标全国)设数列{a n }满足a 1＝2，a n ＋1－a n ＝3·22n －1.(1)求数列{a n }的通项公式；(2)令b n ＝na n ，求数列{b n }的前n 项和S n .3、求和S n ＝1＋3x ＋5x 2＋7x 3＋…＋(2n －1)·x n －14、(2010·山东)已知等差数列{a n }满足：a 3＝7，a 5＋a 7＝26. {a n }的前n 项和为S n .(1)求a n 及S n ；(2)令b n ＝112 n a (n ∈N *)，求数列{b n }的前n 项和T n .5、(2010·青岛模拟)在数列{a n }中，a 1＝1，a n ＋1＝a n ＋c (c 为常数，n ∈N ＋)，且a 1，a 2，a 5成公比不等于1的等比数列．(1)求c 的值；6、函数f (x )＝14x ＋2x ∈R )， (1)若x 1＋x 2＝1，求f (x 1)＋f (x 2)；(2)若n ∈N ＋，求f ⎝⎛⎭⎫12012＋f ⎝⎛⎭⎫22012＋…＋f ⎝⎛⎭⎫20112012.四、基础练习：（一）、选择题1．数列{a n }的前n 项和为S n ，若a n ＝1n (n ＋1)，则S 5等于( ) A ．1 B.56 C.16 D.1302．(2010·南宁模拟)已知F (x )＝f ⎝⎛⎭⎫x ＋12－1是R 上的奇函数，a n ＝f (0)＋f ⎝⎛⎭⎫1n ＋f ⎝⎛⎭⎫2n ＋…＋f ⎝⎛n －1n ＋f (1)(n ∈N *)，则数列{a n }的通项公式为( )A ．a n ＝n －1B ．a n ＝nC ．a n ＝n ＋1D ．a n ＝n 23．数列{(－1)n ·n }的前2 012项的和S 2 012为( )A ．－2 012B ．－1C ．2 012D ．1 006（二）、填空题4．已知数列{a n }中，a 1＝2，点(a n －1，a n )(n >1，且n ∈N ＋)满足y ＝2x －1，则a 1＋a 2＋…＋a 10＝________.5．数列1,412，714，1018，…前10项的和为________．（三）、解答题6．在等差数列{a n }中，a 5＝5，S 3＝6.(1)若T n 为数列⎩⎨⎧⎭⎬⎫1a n a n ＋1的前n 项和，求T n ； (2)若a n ＋1≥λT n 对任意的正整数n 都成立，求实数λ的最大值．五、课后练习(一)、选择题1．数列12·5，15·8，18·11，…，1(3n －1)·(3n ＋2)，…的前n 项和为( ) A.n 3n ＋2 B.n 6n ＋4 C. 3n 6n ＋4 D.n ＋1n ＋22．公差不为零的等差数列{a n }的前n 项和为S n ，若a 4是a 3与a 7的等比中项，S 8＝32，则S 10等于( )A ．18B ．24C ．60D ．903．S n ＝1－22＋32－42＋…＋(－1)n －1·n 2等于( ) A ．－n (n ＋1)2 B.n (n ＋1)2 C ．(－1)n －1·n (n ＋1)2D ．(－1)n ·n (n ＋1)2 4．数列{a n }的通项公式a n ＝1n ＋n ＋2(n ∈N *)，若前n 项和为S n ，则S n 为( ) A.n ＋2－1 B.n ＋2＋n ＋1－2－1 C.12(n ＋2－1) D.12(n ＋2＋n ＋1－2－1) 5．已知数列{a n }的前n 项和S n ＝an 2＋bn (a 、b ∈R )，且S 25＝100，则a 12＋a 14等于( )A ．16B ．8C ．4D ．不确定 6．设函数f (x )＝x m ＋ax 的导函数f ′(x )＝2x ＋1，则数列⎩⎨⎧⎭⎬⎫1f (n )(n ∈N *)的前n 项和是( ) A.n n ＋1 B.n ＋2n ＋1 C.n n －1 D.n ＋1n(二)、填空题7．数列{a n }的通项公式是a n ＝1n ＋n ＋1，若前n 项和为10，则项数为________．8．已知数列{a n }的前n 项和S n ＝n 2－4n ＋2，则|a 1|＋|a 2|＋…＋|a 10|＝________.9．对于数列{a n }，定义数列{a n ＋1－a n }为数列{a n }的“差数列”，若a 1＝2，{a n }的“差数列”的通项为2n，则数列{a n }的前n 项和S n ＝________.10．设f (x )是定义在R 上恒不为0的函数，对任意x ，y ∈R ，都有f (x )·f (y )＝f (x ＋y )，若a 1＝12，a n ＝f (n )(n 为常数)，则数列{a n }的前n 项和S n 的取值范围是________．(三)、解答题11．数列{a n }的前n 项和为S n ，a 1＝1，a n ＋1＝2S n (n ∈N *)(1)求数列{a n }的通项a n ；(2)求数列{na n }的前n 项和T n .12．已知函数y ＝f (x )的图象经过坐标原点，其导函数为f ′(x )＝6x －2. 数列{a n }的前n 项和为S n ，点(n ，S n )(n ∈N *)均在函数y ＝f (x )的图象上．(1)求数列{a n }的通项公式；(2)设b n ＝3a n a n ＋1，T n 是数列{b n }的前n 项和，求使得T n <m 20对所有n ∈N *都成立的最小正整数m .。

(word完整版)数列全部题型归纳(非常全面,经典),推荐文档

数列百通通项公式求法 (一)转化为等差与等比1、已知数列{}n a 满足11a =，211n n a a -=+（,n N *∈２≤n ≤８），则它的通项公式n a 什么2.已知{}n a 是首项为2的数列，并且112n n n n a a a a ---=，则它的通项公式n a 是什么3.首项为2的数列，并且231n n a a -=，则它的通项公式n a 是什么4、已知数列{}n a 中，10a =，112n na a +=-，*N n ∈.求证：11n a ⎧⎫⎨⎬-⎩⎭是等差数列；并求数列{}n a 的通项公式；5.已知数列{}n a 中，13a =，1222n n a a n +=-+，如果2n n b a n =-，求数列{}n a 的通项公式（二）含有n S 的递推处理方法1）知数列{a n }的前n 项和S n 满足log 2（S n +1）=n +1，求数列{a n }的通项公式.2.）若数列{}n a 的前n 项和n S 满足，2(2)8n n a S +=则，数列n a3）若数列{}n a 的前n 项和n S 满足，111,0,4n n n n a S S a a -=-≠=则，数列na4）12323...(1)(2)n a a a na n n n +++=++求数列n a（三）累加与累乘（1）如果数列{}n a 中111,2nn n a a a -=-=(2)n ≥求数列n a（2）已知数列}{n a 满足31=a ，)2()1(11≥-+=-n n n a a n n ，求此数列的通项公式(3) 12+211,2,=32n n n a a a a a +==-,求此数列的通项公式.（4）若数列{}n a 的前n 项和n S 满足，211,2n n S n a a ==则，数列n a（四）一次函数的递推形式1. 若数列{}n a 满足1111,12n n a a a -==+(2)n ≥，数列n a2 .若数列{}n a 满足1111,22n n n a a a -==+ (2)n ≥，数列n a（五）分类讨论（1）2123(3),1,7n n a a n a a -=+≥==，求数列n a（2）1222,(3)1,3nn a n a a a -=≥==，求数列n a（六）求周期16 （1） 121,41nn na a a a ++==-，求数列2004a（2）如果已知数列11n n n a a a +-=-，122,6a a ==，求2010a拓展1：有关等和与等积（1）数列{n a }满足01=a ,12n n a a ++=,求数列{a n }的通项公式（2）数列{n a }满足01=a ,12n n a a n ++=,求数列{a n }的通项公式(3).已知数列满足}{n a )(,)21(,3*11N n a a a n n n ∈=⋅=+,求此数列{a n }的通项公式.拓展2 综合实例分析1已知数列{a n }的前n 项和为n S ，且对任意自然数n ，总有()1,0,1n n S p a p p =-≠≠（1）求此数列{a n }的通项公式(2)如果数列{}n b 中，11222,,n b n q a b a b =+=<，求实数p 的取值范围2已知整数列{a n }满足31223341 (3)n n n n a a a a a a a a --+++=，求所有可能的n a3已知{}n a 是首项为１的正项数列，并且2211(1)0(1,2,3,)n n n n n a na a a n +++-+==L ，则它的通项公式n a 是什么4已知{}n a 是首项为1的数列，并且134n n n a a a +=+，则它的通项公式n a 是什么5、数列{}n a 和{}n b 中，1,,+n n n a b a 成等差数列，n b ，1+n a ，1+n b 成等比数列，且11=a ，21=b ，设nn n b a c =，求数列{}n c 的通项公式。

(完整word版)第一章数列的基本知识

第一章数列1.1 数列的基本知识习题 1。

1。

11. 下列说法正确的是（ )A 、数列－2， 0, 1, 6, 7可表示为｛－2， 0， 1， 6， 7 ｝B 、每个数列中，首项是唯一的C 、数列是由有限或无限个数随意组成的D 、在数列{}n a 中,95=a 表示这个数列第5项的序号是92、已知数列51，101,151，201……，则401是它的第（ )项 3、观察下面各数列的特点,填上适当的数：（1)2, 2， 2 2, 2 2, 2……（2)1， 8， 27, 125， 343,……（3）－3,,－1,，1，，5,7 ,11……（4）17，15， ,11，3 ,5,34、按数列分类，数列2， 4, 6， 8，…,100是数列;数列1，21,41，81，……是数列。

5、根据数列的定义，判断下列数的排列都是数列吗？(1）1， 0, 1， 0, 1, 0（2）0， 0， 0（3）21，32，43，54,…… 6、判断下面各题中的两个数列是否是相同的数列？为什么? (1）0，1 ,2, 3……和1， 2, 3……（2)1， 2， 3， 4, 5和1， 2， 3， 4, 5…（3）1,21,31，41，51和51，41,31，21，1 7、写出由正奇数的倒数按从大到小的顺序排列的数列，能否写出由正奇数的倒数按从小到大的顺序排列的数列？为什么？ 8、2011年是农历兔年,请你按顺序写出2011年以后的六个农历兔年的年份习题1.1.21、已知数列{}n a 的通项公式为32+-=n n a ，则=-23a a2、已知数列的前四项，写出它们的一个通项公式（1）3， 4， 5， 6…… (2）1,21,31，41…… (3）—1,21，31-，41… (4）211⨯，321⨯-，431⨯，541⨯-…… 3、根据下面数列{}na 的通项公式，写出它们的前5项，并写出各数列的第10项. (1)nn a n 212-= （2）()()121+-=n a nn（3）()na n n 211+-= 4、观察下面数列的特点,用适当的数填空，并对每一个数列各写出一个通项公式（1）2， 4（）,16， 32( ），128，（）（2）（ ),4 ，3 ，2, 1，( ），—1，（） 5、已知数列的通项公式是()1+=n n a n（1）182是不是这个数列中的项?如果是，是第几项?（2）100是不是这个数列中的项？6、写出下面数列{}na 的前5项（1）51=a ,31+=+n n a a（2）32=a ，62=a ,n n n a a a -=++12习题1。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

21、数列（1）—数列的概念一、基础知识（必记） 1．数列的定义
按照排列着的一列数称为数列，数列中的每一个数叫做这个数列的。

排在第一位的数称为这个数列的第1项(通常也叫做 )
3.数列的表示法
（1）数列的一般形式可以写成： .
(2)数列的表示法分别为、、、。

4．数列的通项公式
如果数列{a n }的第n 项与之间的关系可以用一个式子来表示，那么这个公式叫做这个数的通项公式．
5．数列的递推公式
若一个数列首项确定，其余各项用与的关系式表示(如a n ＝2a n －1＋1，n >1)，则这个关系式就称为数列的递推公式．
6、正确把握a n 与S n 的关系为a n ＝⎩
⎪⎨⎪⎧
S n －S n －1(n ≥2)
S 1(n ＝1)
二、基础自测
1．1，23，35，47，5
9，…的一个通项公式a n 是( )
A.n 2n ＋1
B.n 2n －1
C.n
2n －3
D.n
2n ＋3
2．下列图案中小球的个数构成一个数列，则该数列的第5项为( )
A ．20
B ．21
C ．22
D ．23
3．(2010·安徽)设数列{a n }的前n 项和S n ＝n 2，则a 8的值为( )
A ．15
B ．16
C ．49
D ．64
4．已知数列⎩⎨⎧⎭⎬⎫
n 2n 2
＋1，则0.98是它的第________项． 5．数列{a n }中，a n ＝
1n ＋n ＋1
，S n ＝9，则n ＝________.
三、基本题型
1、由数列的前几项，写出数列的一个通项公式写出下列数列的一个通项公式； (1)3,5,9,17,33，…； (2)12，2，92，8，25
2，…； (3)2，5，22，11，…； (4)1,0,1,0，…；
(5)0.9,0.99,0.999,0.9999…….
2、根据下列条件，确定数列{a n }的通项公式． (1)a 1＝1，a n ＋1＝3a n ＋2； (2)a 1＝1，11--=
n n a n
n a (n ≥2)；
(3)已知数列{a n }满足a n ＋1＝a n ＋3n ＋2，且a 1＝2，求a n .
3、已知数列{a n }的前n 项和S n ＝－n 2＋34n (n ∈N *)，求{a n }的通项公式．
4、设函数f (x )＝log 2x －log x 2(0<x <1)，数列{a n }满足f (n a
2)＝2n (n ∈N *
)． (1)求数列{a n }的通项公式；
(2)判断数列{a n }的单调性，并给出证明．
5、已知数列{a n}的前n项和S n＝－n2＋24n(n∈N*)．
(1)求{a n}的通项公式；
(2)当n为何值时，S n达到最大？最大值是多少？
四、基础练习
（一）、选择题
1．数列0,1,0，－1,0,1,0，－1，…的一个通项公式是()
A.(－1)n＋1
2
B．cos
nπ
2
C．cos
n＋1
2
π D．cos
n＋2
2
π
2．已知数列{a n}的前n项和S n＝n2－9n，第k项满足5<a k<8，则k等于() A．9B．8C．7D．6
3．已知数列{a n}的通项a n＝na
nb＋c
(a、b、c都是正实数)，则a n与a n＋1的大小关系是()
A．a n>a n＋1B．a n<a n＋1 C．a n＝a n＋1D．不能确定
（二）、填空题
4．数列{－2n2＋29n＋3}中最大项是________
5．数列{a n}中，a1＝1，a2＝5，a n＋2＝a n＋1－a n(n∈N*)，则a2 012＝________.
三、解答题
6．已知数列{a n}的通项公式为a n＝n2－n－30.
(1)求数列的前三项，60是此数列的第几项？
(2)n为何值时，a n＝0，a n>0，a n<0?
(3)该数列前n项和S n是否存在最值？说明理由．
五、课后作业：
（一）、选择题
1．已知数列{a n }的通项公式是a n ＝2n 3n ＋1
，那么这个数列是( )
A ．递增数列
B ．递减数列
C ．摆动数列
D ．常数列
2．已知数列{a n }满足a 1＝0，a n ＋1＝
a n －33a n ＋1
(n ∈N *
)，则a 2012等于( )
A ．0
B ．－ 3 C. 3 D.32
3．下列对数列的理解有四种：
①数列可以看成一个定义在N *
(或它的有限子集{1,2，…，n })上的函数； ②数列的项数是有限的；
③数列若用图象表示，从图象上看都是一群孤立的点； ④数列的通项公式是唯一的．其中说法正确的序号是( )
A ．①②③
B ．②③④
C ．①③
D ．①②③④
4．数列{a n }中，a 1＝1，对于所有的n ≥2，n ∈N *都有a 1·a 2·a 3·…·a n ＝n 2，则a 3＋a 5等于( )
A.
6116 B.259 C.2516 D.31
15
5．下列关于星星的图案构成一个数列，该数列的一个通项公式是( )
A ．a n ＝n 2－n ＋1
B ．a n ＝
n (n －1)2 C ．a n ＝n (n ＋1)
2
D ．a n ＝
n (n ＋2)
2
6．(2010·烟台模拟)数列{a n }满足a n ＋1
＝⎩⎨⎧
2a n ，0≤a n <
12
2a n
－1，1
2
≤a n
<1，若a 1＝2
5
，则a 2 012等于( )
A.15
B.25
C.35
D.4
5
（二）、填空题 7．数列53，108，17
a ＋
b ，a －b 24
，…中，有序数对(a ，b )可以是________．
8．(2010·江苏如皋)对于数列{a n }，定义数列{a n ＋1－a n }为数列{a n }的“差数列”，若a 1＝2，{a n }的“差数列”的通项公式为2n ，则数列{a n }的前n 项和S n ＝________.
10．(2010·哈尔滨模拟)将全体正整数排成一个三角形数阵：
1
23
456
78910
……………
按照以上排列的规律，第15行从左向右的第3个数为________．
（三）、解答题
11．(2010·宿州模拟)已知数列{a n}满足a1＝1，a n＝a n－1＋3n－2(n≥2)．
(1)求a2，a3；
(2)求数列{a n}的通项公式．
12．(2010·湖南六市联考)对于给定数列{c n}，如果存在实常数p，q使得c n＋1＝pc n＋q对于任意n∈N*都成立，我们称数列{c n}是“M类数列”．
(1)若a n＝2n，b n＝3·2n(n∈N*)，数列{a n}、{b n}是否为“M类数列”？若是，指出它对应的实常数p，q；若不是，请说明理由；
(2)若数列{a n}是“M类数列”，求证：数列{a n＋1＋a n}是“M类数列”．。