异面直线的判定练习题及答案
异面直线所成的角专题训练

异面直线所成的角专题训练1.在正方体ABCD-A1B1C1D1中,异面直线AC和XXX所成的角为多少度?答案:90度。
2.在正方体ABCD-A1B1C1D1中,AB的中点M,DD1的中点N,则异面直线B1M与CN所成的角是多少度?答案:60度。
3.在正方体ABCD-A1B1C1D1中,E为线段AC的中点,则异面直线DE与B1C所成角的大小为多少度?答案:无法确定,题目中缺少信息。
4.在三棱锥ABC-A1B1C1中,底面为正三角形,侧棱垂直于底面,AB=4,AA1=6.若E是棱BB1上的点,且BE=B1E,则异面直线A1E与AC1所成角的余弦值为多少?答案:1/3.5.在三棱锥P-ABC中,△ABC为等边三角形,△PAC为等腰直角三角形,PA=PC=4,平面PAC⊥平面ABC,D为AB的中点,则异面直线AC与PD所成角的余弦值为多少?答案:-1/2.6.在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,直线AM与CN所成角的余弦值是多少?答案:-3/5.7.在直三棱柱ABC-A1B1C1中,AC⊥BC,且CA=CC1=10,则直线B1C与直线AB1所成角的余弦值为多少?答案:5/13.8.在直三棱柱ABC-A1B1C1中,AA1=2,A1B1=2,AB⊥BC,点M是AC1的中点,则异面直线MB与AA1所成角的余弦值为多少?答案:-1/3.9.正三棱锥A-PBC的侧棱两两垂直,D,E分别为棱PA,BC的中点,则异面直线PC与DE所成角的余弦值为多少?答案:-3/5.10.在正方体ABCD-A1B1C1D1中,点E为BC的中点,点F为B1C1的中点,则异面直线AF与C1D所成角的大小为多少度?答案:无法确定,题目中缺少信息。
中,ABCD是正方形,E是AD的中点,F是BC的中点,异面直线EF与AC所成的角的正弦值为(。
)A.12B.13C.23D.110.在正方体ABCD A1B1C1D1中,E是AD的中点,F是BC的中点,异面直线EF与直线AC所成的角的正切值为(。
专题10:异面直线问题高考真题(原卷版)

专题10:异面直线问题高考真题(原卷版)一、单选题1.2018年全国普通高等学校招生统一考试理数(全国卷II )在长方体1111ABCD A B C D -中,1AB BC ==,13AA =,则异面直线1AD 与1DB 所成角的余弦值为A .15B .5C .5D .222.2017年全国普通高等学校招生统一考试理科数学(新课标2卷) 已知直三棱柱111C C AB -A B 中,C 120∠AB =,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为( )A .3B .15C .10D .3 3.2016年全国普通高等学校招生统一考试理科数学(新课标1卷) 平面过正方体ABCD —A 1B 1C 1D 1的顶点A ,,,,则m ,n 所成角的正弦值为 A . B . C . D .4.2014年全国普通高等学校招生统一考试理科数学(全国Ⅱ卷)直三棱柱ABC -A 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BM 与AN 所成角的余弦值为( )A .110 B .25 C 30D 25.2018年全国普通高等学校招生统一考试文数(全国卷II ) 在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为A .22 B .32 C 5 D .72二、解答题6.2015年全国普通高等学校招生统一考试理科数学(新课标Ⅰ)如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.(1)证明:平面AEC⊥平面AFC;(2)求直线AE与直线CF所成角的余弦值.。
异面直线所成的角测试题(含答案).docx
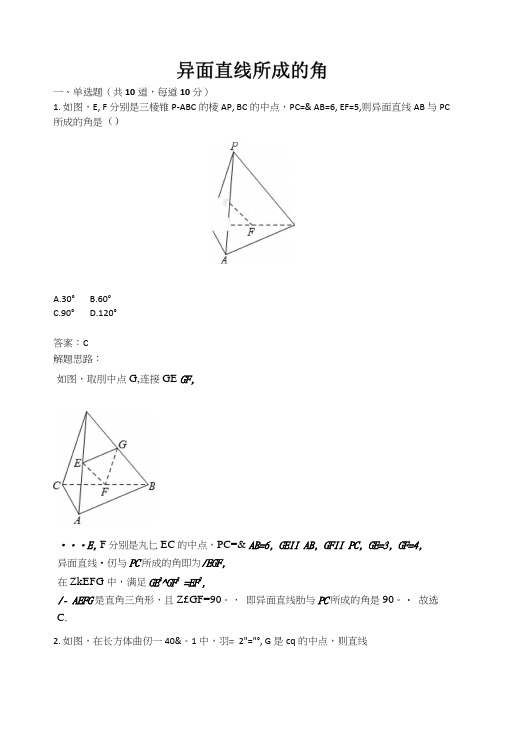
一、单选题(共10道,每道10分)1.如图,E, F分别是三棱锥P-ABC的棱AP, BC的中点,PC=& AB=6, EF=5,则异面直线AB 与PC 所成的角是()A.30°B.60°C.90°D.120°答案:C解题思路:如图,取刖中点G,连接GE GF,•・・E, F分别是丸匕EC的中点,PC=& AB=6, GEII AB, GFII PC, GE=3, GF=4,异面直线•仞与PC所成的角即为/EGF,在ZkEFG 中,满足GE2^GF2 =EF2,/- AEFG是直角三角形,且Z£GF=90。
,即异面直线肋与PC所成的角是90。
・故选C.2.如图,在长方体曲仞一40&。
1中,羽= 2"="°, G是cq的中点,则直线4G与EG所成角的大小是()A.30°B.45°C.60°D.120°答案:C解题思路:如图,取44]的中点E,连接EG, BE,易证,EG,・・・直线4G与PG所成的角可转化为EG与BG所成的角,即ZBGE,T AA X— 2AB = 2AD , G是CQ 的中点,/. /\BGE是等边三角形,••厶GE=6g即直线赵C芍BG所成的角是60。
・故选C.试题难度:三颗星知识点:界面直线及其所成的角3.如图,在正方体曲CD-40iCi£)i屮,点p在线段上运动,则异面直线CP与牌所成的角&的取值范围是()A.O。
<^<90°B 0° GW 90°C.0。
W0W 60°D 0°60°答案:D解题思路:如图,连接川C, CD1,则码II CD,,异面直线CP与码所成的角即为CP与C®所成的角, 即e=ZPCD\,•・• △zpc是等边三角形,・•・当点P和点加重合时,扫60。
异面直线专题复习附答案

2014~2015学年度第一学期综合训练(二)异面直线一、选择题——对异面直线的理解1.没有公共点的两条直线的位置关系是( )(A)平行 (B)异面 (C)平行或异面 (D)不能确定 2.分别在两相交平面内的两条直线的位置关系是( )(A)异面 (B)平行 (C)平行或异面 (D)平行或异面或相交 3.两条异面直线指的是( ) (A)(B)某一平面内的一条直线和这个平面外的一条直线(C)(D)4.a 、b 是异面直线,b 、c 也是异面直线,那么a 、c 的位置是( )(A)异面 (B)异面或平行 (C)异面或相交 (D)相交、平行或异面 5.说出正方体中各对线段的位置关系:(1) AB 和CC 1; (2)A 1C 和BD 1; (3)A 1A 和CB 1;(4)A 1C 1和CB 1; (5)A 1B 1和DC ; (6)BD 1和DC.6.在棱长为1的正方体ABCD —A 1B 1C 1D 1中,M 和N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成角的余弦值是()32((()()55A B C D二、求异面直线所成角例 S 是正三角形ABC 所在平面外的一点,如图SA =SB =SC ,且∠ASB =∠BSC =∠CSA =2π,M 、N 分别是AB 和SC 的中点.求异面直线SM 与BN 所成的角的余弦值.练习、 如图,在直三棱柱ABC -A 1B 1C 1中,∠BCA =90°,M 、N 分别是A 1B 1和A 1C 1的中点,若BC =CA =CC 1,求BM 与AN 所成的角.B M AN CS B 1(第5题)A 1ABC 1D 1C D B 1(第6题)A 1AB C 1 D 1 CD M N ANMA 1 C 1B 1课后巩固: 一、选择题1.正方体ABCD —A 1B 1C 1D 1中,直线BC 1与AC(A)相交且垂直 (B)相交但不垂直 (C)异面且垂直 (D)异面但不垂直 2.设a 、b 、c 是空间中的三条直线,下面给出四个命题:①如果a ⊥b 、b ⊥c ,则a ∥c ;②如果a 和b 相交,b 和c 相交,则a 和c 也相交;③如果a 、b 是异面直线,c 、b 是异面直线,则a 、c 也是异面直线; ④如果a 和b 共面,b 和c 共面,则a 和c 也共面 在上述四个命题中,真命题的个数是()(A)4 (B)3 (C)2 (D)1 (E)0 3.如果直线l 和n 是异面直线,那么和直线l 、n 都垂直的直线(A)不一定存在 (B)总共只有一条(C)总共可能有一条,也可能有两条 (D)有无穷多条 4.如图,四面体S-ABC 的各棱长都相等,如果E 、F 分别为SC 、AB 的中点,那么异面直线EF 与SA 所成的角等于(A)90° (B)60° (C)45° (D)30°5.如图,A 1B 1C 1—ABC 是直三棱柱(三侧面为矩形),∠BCA=90°, 点D 1、F 1 分别是A 1B 1、A 1C 1BC=CA=CC 1,则BD 1与AF 1所成角的余弦值是()105(()2A B二.如图,四面体ABCD 中,AC ⊥BD,且AC =4,BD =3,M 、N 分别是AB 、CD 的中点,求MN 和BD所成角的正切值三.如图,四面体ABCD 中,AB ⊥BC ,AB ⊥BD ,BC ⊥CD ,且AB =BC =6,BD =8,E 是AD 中点,求BE 与CD 所成角的余弦值四.如图,正三棱柱的九条棱都相等,三个侧面都是正方体,M 、N 分别是BC 和A 1C 1MN 与CC 1所成角的余弦值。
考点练习(必修二):异面直线的判定(附答案)

异面直线的判定1. 如图,正方体ABCD-A1B1C1D1中,判断下列直线的位置关系:①直线A1B与直线D1C的位置关系是________;②直线A1B与直线B1C的位置关系是________;③直线D1D与直线D1C的位置关系是________;④直线AB与直线B1C的位置关系是________.2. 若a、b是异面直线,b、c是异面直线,则()A.a∥c B.a、c是异面直线C.a、c相交D.a、c平行或相交或异面3. 若a,b,c是空间3条直线,a∥b,a与c相交,则b与c的位置关系是()A.异面B.相交C.平行D.异面或相交4. 若直线a、b、c满足a∥b,a、c异面,则b与c()A.一定是异面直线B.一定是相交直线C.不可能是平行直线D.不可能是相交直线5. 如下图所示,点P,Q,R,S分别在正方体的4条棱上,且是所在棱的中点,则直线PQ 与RS是异面直线的一个图是________.6. 在长方体ABCD-A1B1C1D1中,与棱AA1垂直且异面的棱有________.7. 如下图所示是一个正方体的平面展开图,则在正方体中,AB与CD的位置关系为()A.相交B.平行C.异面而且垂直D.异面但不垂直8. 若P是两条异面直线l,m外的任意一点,则()A.过点P有且仅有一条直线与l,m都平行B.过点P有且仅有一条直线与l,m都垂直C.过点P有且仅有一条直线与l,m都相交D.过点P有且仅有一条直线与l,m都异面9. 如右图所示,正方体ABCD-A1B1C1D1中,M,N分别是A1B1,B1C1的中点.问:(1)AM和CN是否是异面直线?说明理由.(2)D1B和CC1是否是异面直线?说明理由.参考答案1. 【自主解答】根据题目条件知道直线A1B与直线D1C在平面A1BCD1中,且没有交点,则两直线“平行”,所以①应该填“平行”;点A1、B、B1在一个平面A1BB1内,而C不在平面A1BB1内,则直线A1B与直线B1C“异面”.同理,直线AB与直线B1C“异面”.所以②④都应该填“异面”;直线D1D与直线D1C相交于D1点,所以③应该填“相交”.【答案】①平行②异面③相交④异面2. D 若a、b是异面直线,b、c是异面直线,那么a、c可以平行,可以相交,可以异面.3. 答案:D4. C 若a∥b,a、c是异面直线,那么b与c不可能平行,否则由公理4知a∥c.5. 答案:③6.【解析】如图,与棱AA1垂直且异面的棱有DC,BC,D1C1,B1C1.【答案】DC,BC,D1C1,B1C17. 答案:D8. 答案:B9. 解:(1)不是异面直线.理由:∵M,N分别是A1B1,B1C1的中点,∴MN∥A1C1.又A1A D1D,而D1D C1C,∴A1A C1C.∴四边形A1ACC1为平行四边形.∴A1C1∥AC,得到MN∥AC.∴A,M,N,C在同一个平面内,故AM和CN不是异面直线.(2)是异面直线.证明如下:假设D1B与CC1在同一个平面D1CC1内,则B∈平面CC1D1,C∈平面CC1D1,∴BC⊂平面CC1D1.而BC⊥平面CC1D1,BC⊄平面CC1D1,∴假设不成立,故D1B与CC1是异面直线.。
异面直线的判定练习题及答案

5.平行六面体 ABCD-A 1B 1C 1D 1中,求证:CD 所在的直线与 BC i 所在的直线是异面直线.异面直线的判定 1•已知空间四边形 ABCD , E 、H 分别是AB 、AD 的中点, 三等分点(如图),求证:(1) 对角线AC 、BD 是异面直线;(2) 直线EF 和HG 必交于一点,且交点在 AC 上.F 、G 分别是边BC 、DC 的 2.A 是厶BCD 平面外的一点,E 、F 分别是BC 、AD 的中点,(1)求证:直线EF 与BD 是异面直线;3.已知:平面 af 平面3 =a b? a, b A a=A c? B 且c // a ,求证: b 、c 是异面直线.4.已知不共面的三条直线 与BC 是异面直线.a 、b 、c 相交于点 P , A € a , B € a , C € b , D € c ,求证:ADD C小结:常用方法是反证法(1)利用反证法证明对角线AC、BD是共面直线,推出矛盾,从而证明是异面直(2)说明直线EF和HG必交于一点,然后证明这点在平面ADC内.又在平面ABC内,必在它们的交线AC 上.:⑴假设对角线AC、BD在同一平面a内,则A、B、C、D都在平面a内,这与ABCD是空间四边形矛盾,:.AC、BD是异面直线.(2)T E、H分别是AB、AD的中点所以EH平行且等于1/2BD,又F、G分另堤BC、DC的三等分点,EG平行等于2/3BD,. •: EH// FG,且EH v FG.:FE与GH 相交设交点为0,又0在GH 上, GH在平面ADC内,•:O在平面ADC内.同理,0在平面ABC内.从而0在平面ADC与平面ABC的交线AC 上.2. (1)假设EF与BD不是异面直线,则EF与BD共面,得到A、B、C、D在同一平面内,矛盾.(1)证明:用反证法•设EF与BD不是异面直线,_则EF与BD共面,从而DF与BE共面,即AD与BC共面,所以A、B、C、D在同一平面内,这与A是厶BCD平面外的一点相矛盾.故直线EF与BD是异面直线.3证明b、c是异面直线,比较困难,考虑使用反证法,即若b与c不是异面直线,则b// c或b与C相交,证明b// c或b与c相交都是不可能的, 从而证明b、c是异面直线证明:用反证法:若b与c不是异面直线,则b// c或b与c相交(1)若b// c. :a//c,•: a//b 这与a H b=A矛盾;(2)若b,c相交于B,则B E B,又a H b=A:.A E AB? 3 即b? B这与b np =AF盾:-b,c是异面直线.4证明:法一:(反证法)假设AD和BC共面,所确定的平面为a那么点P、A、B、C、D都在平面a内,•:直线a b、c都在平面a内,与已知条件a b、c不共面矛盾,假设不成立,:AD和BC是异面直线.法二:(直接证法):a n c=P •:它们确定一个平面,设为a由已知C?平面a, B E平面a,AD?平面a, B?AD,:・AD和BC是异面直线.5证明:用反证法,假设CD1所在的直线与BC1所在的直线不是异面直线.设直线CD1与BC1共面aV C, D1E CD1, B, C1E BC1, •: C, D1, B, C1E a •/ CC1 / BB1,:.CC1, BB1 确定平面BB1C1C, :. C, B, C1 E 平面BB1C1C.T不共线的三点C, B, C1只有一个平面,•:平面a与平面BB1C1C重合••:D1E平面BB1C1C,矛盾.因此,假设错误,即CD1所在的直线与BC1所在的直线是异面直线。
异面直线的判定(含答案)

异面直线的判定一、单选题(共9道,每道11分)1.在三棱锥的六条棱中任选两条,则这两条棱所在直线互为异面直线的概率是( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:异面直线的判定2.下列四个命题:①分别在两个平面内的两条直线是异面直线;②和两条异面直线都垂直的直线有且只有一条;③和两条异面直线都相交的两条直线必异面;④若a和b是异面直线,b和c是异面直线,则a和c也是异面直线.其中真命题有( )A.3个B.2个C.1D.0个答案:D解题思路:试题难度:三颗星知识点:异面直线的判定3.设A为空间一点,是两条直线,α,β是两个平面,有下列四个命题:①若,,则可能为异面直线;②若,,则;③已知为异面直线,,,,,则α∥β;④若α⊥β,,则.其中正确命题的序号是( )A.①③B.②④C.②③D.①④答案:A解题思路:试题难度:三颗星知识点:直线与平面垂直的判定4.如图,正方体的所有面对角线中,与面对角线成异面直线的有( )A.7条B.6条C.5条D.4条答案:C解题思路:试题难度:三颗星知识点:异面直线的判定5.如图,在四棱锥P-ABCD中,已知底面ABCD是矩形,则各棱所在直线中互为异面直线的共有( )A.4对B.6对C.8对D.12对答案:C解题思路:试题难度:三颗星知识点:异面直线的判定6.如图是正方体纸盒的平面展开图,则直线AB,CD在原正方体中的位置关系是( )A.平行B.垂直C.相交成60°D.异面且成60°角答案:D解题思路:试题难度:三颗星知识点:表面展开图7.如图,已知正方体的棱长为a,则下列结论不正确的是( )A.异面直线与所成的角为60°B.直线与垂直C.直线与平行D.三棱锥的体积为答案:C解题思路:试题难度:三颗星知识点:异面直线的判定8.如图,在正四棱柱中,E,F分别是的中点,则下列结论不成立的是( )A.EF与垂直B.EF与BD垂直C.EF与CD异面D.EF与异面答案:D解题思路:试题难度:三颗星知识点:异面直线的判定9.如图,在正方体中,O是底面正方形ABCD的中心,M是的中点,N是上的动点,则直线NO,AM的位置关系是( )A.平行B.相交C.异面垂直D.异面不垂直答案:C解题思路:试题难度:三颗星知识点:异面直线的判定。
专题10:异面直线问题高考真题(解析版)

专题10:异面直线问题高考真题(解析版)一、单选题1.2018年全国普通高等学校招生统一考试理数(全国卷II )在长方体1111ABCD A B C D -中,1AB BC ==,1AA =1AD 与1DB 所成角的余弦值为A .15BCD.2【答案】C 【解析】分析:先建立空间直角坐标系,设立各点坐标,利用向量数量积求向量夹角,再根据向量夹角与线线角相等或互补关系求结果.详解:以D 为坐标原点,DA,DC,DD 1为x,y,z轴建立空间直角坐标系,则11(0,0,0),(1,0,0),(1,1D A B D ,所以11(1,0,3),(1,1AD DB =-=,因为1111111cos ,2ADDB AD DB AD DB ⋅-===⨯,所以异面直线1AD 与1DB 所成角,选C. 点睛:利用法向量求解空间线面角的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”,求出平面的法向量;第四,破“应用公式关”. 2.2017年全国普通高等学校招生统一考试理科数学(新课标2卷)已知直三棱柱111C C AB -A B 中,C 120∠AB=,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为() A .B C D 【答案】C 【解析】如图所示,补成直四棱柱1111ABCD A B C D -,则所求角为21111,2,21221cos603,5BC D BC BD C D AB ∠==+-⨯⨯⨯︒===,易得22211C D BD BC =+,因此111210cos 55BC BC D C D ∠===,故选C .平移法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面问题化归为共面问题来解决,具体步骤如下:①平移:平移异面直线中的一条或两条,作出异面直线所成的角; ②认定:证明作出的角就是所求异面直线所成的角; ③计算:求该角的值,常利用解三角形;④取舍:由异面直线所成的角的取值范围是(0,]2π,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.求异面直线所成的角要特别注意异面直线之间所成角的范围.3.2016年全国普通高等学校招生统一考试理科数学(新课标1卷) 平面过正方体ABCD —A 1B 1C 1D 1的顶点A ,,,,则m ,n 所成角的正弦值为A .B .C .D .【答案】A 【解析】试题分析:如图,设平面平面=,平面 平面=,因为平面,所以,则所成的角等于所成的角.延长,过作,连接,则为,同理为,而,则所成的角即为所成的角,即为,故所成角的正弦值为,选A.【考点】平面的截面问题,面面平行的性质定理,异面直线所成的角.【名师点睛】求解本题的关键是作出异面直线所成的角,求异面直线所成角的步骤是:平移定角、连线成形、解形求角、得钝求补.4.2014年全国普通高等学校招生统一考试理科数学(全国Ⅱ卷)直三棱柱ABC -A 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BM 与AN 所成角的余弦值为( ) A .110B .25C 30D .22【答案】C 【解析】以C 为原点,直线CA 为x 轴,直线CB 为y 轴,直线1CC 为z 轴,则设CA=CB=1,则(0,1,0)B ,11(,,1)22M ,A (1,0,0),1(,0,1)2N ,故11(,,1)22BM =-,1(,0,1)2AN =-,所以cos ,BM AN BM AN BM AN⋅〈〉==⋅3465=⋅30C. 考点:本小题主要考查利用空间向量求线线角,考查空间向量的基本运算,考查空间想象能力等数学基本能力,考查分析问题与解决问题的能力.5.2018年全国普通高等学校招生统一考试文数(全国卷II )在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为A .22B .32C .52D .72【答案】C 【分析】利用正方体1111ABCD A B C D -中,//CD AB ,将问题转化为求共面直线AB 与AE 所成角的正切值,在ABE ∆中进行计算即可. 【详解】在正方体1111ABCD A B C D -中,//CD AB ,所以异面直线AE 与CD 所成角为EAB ∠,设正方体边长为2a ,则由E 为棱1CC 的中点,可得CE a =,所以5BE a =,则55tan 22BE a EAB AB a ∠===.故选C.【点睛】求异面直线所成角主要有以下两种方法:(1)几何法:①平移两直线中的一条或两条,到一个平面中;②利用边角关系,找到(或构造)所求角所在的三角形;③求出三边或三边比例关系,用余弦定理求角; (2)向量法:①求两直线的方向向量;②求两向量夹角的余弦;③因为直线夹角为锐角,所以②对应的余弦取绝对值即为直线所成角的余弦值.二、解答题6.2015年全国普通高等学校招生统一考试理科数学(新课标Ⅰ)如图,四边形ABCD 为菱形,∠ABC =120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE =2DF ,AE ⊥EC .(1)证明:平面AEC⊥平面AFC;(2)求直线AE与直线CF所成角的余弦值.【答案】(1)见解析;(2).【解析】试题分析:(Ⅰ)连接BD,设BD∩AC=G,连接EG,FG,EF,在菱形ABCD 中,不妨设GB=1易证EG⊥AC,通过计算可证EG⊥FG,根据线面垂直判定定理可知EG⊥平面AFC,由面面垂直判定定理知平面AFC⊥平面AEC;(Ⅱ)以G为坐标原点,分别以的方向为轴,y轴正方向,为单位长度,建立空间直角坐标系G-xyz,利用向量法可求出异面直线AE与CF所成角的余弦值.试题解析:(Ⅰ)连接BD,设BD∩AC=G,连接EG,FG,EF,在菱形ABCD中,不妨设GB=1,由∠ABC=120°,可得AG=GC=.由BE⊥平面ABCD,AB=BC可知,AE=EC,又∵AE⊥EC,∴EG=,EG⊥AC,在Rt△EBG中,可得BE=,故DF=.在Rt△FDG中,可得FG=.在直角梯形BDFE中,由BD=2,BE=,DF=可得EF=,∴,∴EG⊥FG,∵AC∩FG=G,∴EG⊥平面AFC,∵EG面AEC,∴平面AFC⊥平面AEC.(Ⅱ)如图,以G为坐标原点,分别以的方向为轴,y轴正方向,为单位长度,建立空间直角坐标系G-xyz,由(Ⅰ)可得A(0,-,0),E(1,0,),F(-1,0,),C(0,,0),∴=(1,,),=(-1,-,).…10分故.所以直线AE与CF所成的角的余弦值为.考点:空间垂直判定与性质;异面直线所成角的计算;空间想象能力,推理论证能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
异面直线的判定
1.已知空间四边形ABCD,E、H分别是AB、AD的中点,F、G分别是边BC、DC的三等分点(如图),求证:(1)对角线AC、BD是异面直线;
(2)直线EF和HG必交于一点,且交点在AC上.
¥
是△BCD平面外的一点,E、F分别是BC、AD的中点,
(1)求证:直线EF与BD是异面直线;
3.已知:平面α∩平面β=a,b⊂α,b∩a=A,c⊂β且c∥a,求证:b、c是异面直线.
,
4.已知不共面的三条直线a、b、c相交于点P,A∈a,B∈a,C∈b,D∈c,求证:AD与
BC是异面直线.
{
5.平行六面体ABCD-A1B1C1D1中,求证:CD1所在的直线与BC1所在的直线是异面直线.
%
小结:常用方法是反证法
(1)利用反证法证明对角线AC、BD是共面直线,推出矛盾,从而证明是异面直
(2)说明直线EF和HG必交于一点,然后证明这点在平面ADC内.又在平面ABC内,必在它们的交线AC上.
:(1)假设对角线AC、BD在同一平面α内,
则A、B、C、D都在平面α内,这与ABCD是空间四边形矛盾,∴AC、BD是异面直线.
(2)∵E、H分别是AB、AD的中点所以EH平行且等于1/2BD, 又F、G分别是BC、DC的三等分点,
EG平行等于2/3BD,.∴EH∥FG,且EH<FG.∴FE与GH相交
设交点为O,又O在GH上,GH在平面ADC内,∴O在平面ADC内.
同理,O在平面ABC内.从而O在平面ADC与平面ABC的交线AC上.
2.(1)假设EF与BD不是异面直线,则EF与BD共面,得到A、B、C、D在同一平面内,矛盾.
3.(1)证明:用反证法.设EF与BD不是异面直线,
4.则EF与BD共面,从而DF与BE共面,即AD与BC共面,
5.所以A、B、C、D在同一平面内,这与A是△BCD平面外的一点相矛盾.
6.故直线EF与BD是异面直线.
7.3.证明b、c是异面直线,比较困难,考虑使用反证法,即若b与c不是异面直线,则b∥c或b与c相交,证明b∥c或b与c相交都是不可能的,从而证明b、c是异面直线证明:用反证法:
8.若b与c不是异面直线,则b∥c或b与c相交
9.(1)若b∥c.∵a∥c,∴a∥b这与a∩b=A矛盾;
10.(2)若b,c相交于B,则B∈β,又a∩b=A,
11.∴A∈β∴AB⊂β,即b⊂β这与b∩β=A矛盾
12.∴b,c是异面直线.
4.证明:法一:(反证法)假设AD和BC共面,所确定的平面为α,
5.那么点P、A、B、C、D都在平面α内,∴直线a、b、c都在平面α内,与已知条件a、b、c不共面矛盾,
6.假设不成立,∴AD和BC是异面直线.
7.法二:(直接证法)∵a∩c=P,∴它们确定一个平面,
8.设为α,由已知C∉平面α,B∈平面α,AD⊂平面α,B∉AD,∴AD和BC是异面直线.
9.证明:用反证法,
10.假设CD1所在的直线与BC1所在的直线不是异面直线.
11.设直线CD1与BC1共面α.
12.∵C,D1∈CD1,B,C1∈BC1,∴C,D1,B,C1∈α∵CC1∥BB1,∴CC1,BB1确定平面BB1C1C,∴C,B,C1∈平面BB1C1C.
13.∵不共线的三点C,B,C1只有一个平面,∴平面α与平面BB1C1C重合.∴D1∈平面BB1C1C,矛盾.
14.因此,假设错误,即CD1所在的直线与BC1所在的直线是异面直线
{。
