等腰直角三角形题型
专题03 等腰(直角)三角形中动点问题(老师版)

专题3等腰(直角)三角形中动点问题【典型例题】1.(2021·黑龙江集贤·八年级期末)如图,等腰三角形ABC的底边BC长为3,面积是18,腰AC的垂直平分线分别交AC、AB边于点E、F.若点D为DC边的中点,点M为线段EF上一动点,则CDM周长的最小值为___.【答案】13.5【解析】【分析】连接MA、AD,易得MA=MC,则△CMD的周长为:MC+MD+CD=MA+MD+CD≥AD+CD,当M点在线段AD上时,△CMD的周长最小,再由面积可求得AD的长,从而可求得周长的最小值.【详解】如图,连接MA、AD∵EF垂直平分线段AC∴MA=MC∴△CMD的周长=MC+MD+CD=MA+MD+CD≥AD+CD∵点D为DC边的中点,BC=3∴1 1.52CD BC==∵AB=AC ∴AD⊥BC∴118 2BC AD⨯=即1318 2AD⨯=∴AD=12∴AD+CD=12+1.5=13.5即△MCD的周长的最小值为13.5故答案为:13.5【点睛】本题考查了等腰三角形的性质,线段垂直平分线的性质定理,三角形的面积,两点之间线段最短等知识,关键是利用线段的垂直平分线的性质定理作辅助线MA,把MC+MD的最小值问题转化为两点间线段最短来解决.【专题训练】一、填空题1.(2022·江苏昆山·八年级期末)如图,∠ABC=30°,AB=6,动点P从点B出发,以每秒1个单位长度的速度沿射线BC运动,设点P的运动时间为t秒,当△ABP是以AB为底的等腰三角形时,t的值为______秒.【答案】【解析】【分析】过点P作PD⊥AB于点D,根据等腰三角形有性质得到BD=3,再根据30度角的直角三角形的性质结合勾股定理即可求解.【详解】解:过点P作PD⊥AB于点D,∵△ABP是以AB为底的等腰三角形,即BP=PA,∴BD=DA=12AB=3,∵∠ABC=30°,∴BP=2PD,即12BP=PD,∵BP2-PD2=BD2,∴BP2-14BP2=32,解得:BP=∵点P的运动速度是每秒1个单位长度,∴t的值为故答案为:【点睛】本题考查了等腰三角形的性质,含30度角的直角三角形的性质,勾股定理等知识点,解答本题的关键是明确题意,找出所求问题需要的条件.2.(2021·浙江·诸暨市暨阳初级中学八年级期中)如图∠MAN=60°,若△ABC的顶点B在射线AM上,且AB=6,动点C从点A出发,以每秒1个单位沿射线AN运动,当运动时间t是_______秒时,△ABC是直角三角形.【答案】3或12【解析】【分析】分∠ACB=90°和∠ABC=90°两种情况,根据含30°角的直角三角形的性质求出AC,再求出答案即可.【详解】解:如图:当△ABC是以∠ACB=90°的直角三角形时,∵∠MAN=60°,∴∠ABC=30°,∴AC=13 2AB=,∴运动时间t=3311AC==秒,当△ABC是以∠ABC=90°的直角三角形时,∵∠MAN=60°,∴∠ACB=30°,∴AC=212AB=,∴运动时间t=121211AC==秒,当运动时间t是3或12秒时,△ABC是直角三角形.故答案为:3或12【点睛】本题考查了三角形的内角和定理和含30°角的直角三角形的性质,能熟记含30°角的直角三角形的性质是解此题的关键.3.(2022·新疆·乌鲁木齐市第四中学八年级期末)如图,在边长为6,面积为ABC中,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是_______【答案】【解析】【分析】由等边三角形的对称性得到MC=BM,再利用垂线段最段解题.【详解】解:过点C 作CN AB ⊥于点N ,BD Q 平分∠BAC ,△ABC 为等边三角形,BM MC∴=∴BM +MN MC MN =+,当CN AB ⊥时,=MC MN CN +最小等边△ABC 面积为6,CN ∴故答案为:【点睛】本题考查轴对称—最短路径问题、等边三角形的性质等知识,是重要考点,掌握相关知识是解题关键.4.(2021·福建省罗源第二中学八年级期中)如图,在等腰△ABC 中,AB =AC ,∠BAC =120°,BC =30cm ,一动点P 从B 向C 以每秒2cm 的速度移动,当P 点移动____________秒时,PA 与△ABC 的腰垂直.【答案】5或10【解析】【分析】根据等腰三角形性质求出∠B =∠C =30°,分PA ⊥AC 和PA ⊥AB 两种情况分类讨论,得到BP =10cm 或BP =20cm ,即可求出点P 移动的时间.【详解】解:∵AB =AC ,∠BAC =120°,∴∠B =∠C =30°.如图①,当PA ⊥AC 时,∵∠C =30°.∴PC =2AP ,∠APC =60°,∴∠B =∠BAP =30°,∴AP =BP ,∴PC =2BP ,∴BP =13BC =13×30=10cm ,∴P 点移动了10÷2=5(秒);如图②当PA⊥AB时,∵∠B=30°.∴PB=2BP,∠APB=60°,∴∠C=∠CAP=30°,∴AP=CP,∴BP=2CP,∴BP=23BC=23×30=20cm,∴P点移动了20÷2=10(秒).故答案为:5或10【点睛】本题考查了等腰三角形的性质与判定,直角三角形性质等知识,熟知相关定理,根据条件分类讨论是解题关键5.(2022·福建省泉州实验中学八年级期末)如图,在等腰△ABC中,∠BAC=30°,AB=AC,BC=4,点P、Q、R分别为边BC、AB、AC上(均不与端点重合)的动点,△PQR周长的最小值是______.【答案】423【解析】【分析】过BC的中点P作AB,AC的对称点M,N,连接MN交AB与Q,交AC于R,则此时△PQR周长最小,求出MQ,RQ,RN即可解决问题.【详解】过点P作AB,AC的对称点M,N,连接MN交AB于Q,交AC于R,设AP交MN于点D,则PQ MQ =,PR RN =,∴PQR 周长为PQ QR PR MQ QR EN MN ++=++≥,当,,,M Q R N 四点共线时,即当点P 是BC 的中点时,PQR 的周长最小,如图∵30BAC ∠=︒,∴75B C ∠=∠=︒,150MPN ∠=︒,∴15M N ∠=∠=︒,∴75MQB PQB B ∠=∠=∠=︒,∴MN BC ∥,2PQ PB ==,同理2PR PC ==,∵⊥AP BC ,∴AP MN ⊥.DP MN∴⊥PQ PR =DQ DR∴=∵180757530PQR ∠=︒-︒-︒=︒,∴Rt PDQ 中,112QD PQ ==∴==2QR DQ =⨯=,∴PQR 周长的最小值是22PQ QR PR ++=+=4+.故答案为:4+【点睛】本题是三角形综合题,考查了轴对称的性质,等边三角形的性质,等腰三角形的性质,含30度角的直角三角形的性质,勾股定理,正确的作出辅助线是解题的关键.6.(2022·辽宁铁西·八年级期末)同学们,我们在今后的学习中会学到这个定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图,在Rt △ABC 中,∠ACB =90°,若∠ABC =30°,则12AC AB =.问题:在Rt △ABC ,∠ACB =90°,∠ABC =30°,AC D 是边BC 的中点,点E 是斜边AB 上的动点,连接DE ,把△BDE 沿直线DE 折叠,点B 的对应点为点F .当直线DF ⊥AB 时,AE 的长为_____.【答案】2或2【解析】【分析】如图1所示,设DF 与AB 交点为G ,先求出AB ==3BC ,由D 是BC 的中点,可以得到1322BD BC ==,由折叠的性质可知∠F =∠B =30°,BE =EF ,即可得到1324DG BD ==,1122EG EF BE ==,BG ==,由此即可求出AE 的长;如图2所示,同理可得1324DG BD ==,4BG ==,1122EG EF BE ==,则32BE BG GE BG =+==,AE AB BE =-=【详解】解:如图1所示,设DF 与AB 交点为G ,∵∠ABC =30°,∠ACB =90°,∴2AB AC ==∴BC =,∵D 是BC 的中点,∴1322BD BC ==,由折叠的性质可知∠F =∠B =30°,BE =EF ,∵DF ⊥AB ,∴∠DGB =∠FGB =90°,∴1324DG BD ==,1122EG EF BE ==,∴4BG ==,∴2332BE BG ==,∴AE AB BE =-=如图2所示,延长FD 与AB 交于点G ,同理可求出1324DG BD ==,4BG ==,1122EG EF BE ==,∴22BE BG GE BG =+==,∴2AE AB BE =-=,故答案为:2【点睛】本题主要考查了含30度角的直角三角形的性质,勾股定理,旋转的性质,熟练掌握含30度角的直角三角形的性质是解题的关键.7.(2021·全国·八年级专题练习)如图,60BOC ∠=︒,点A 是BO 延长线上的一点,10cm OA =,动点P 从点A 出发沿AB 以3cm/s 的速度移动,动点Q 从点O 出发沿OC 以1cm/s 的速度移动,如果点P Q ,同时出发,用(s)t 表示移动的时间,当t =_________s 时,POQ △是等腰三角形;当t =_________s 时,POQ △是直角三角形.【答案】52或54或10【解析】【分析】根据POQ ∆是等腰三角形,分两种情况进行讨论:点P 在AO 上,或点P 在BO 上;根据POQ ∆是直角三角形,分两种情况进行讨论:PQ AB ⊥,或PQ OC ⊥,据此进行计算即可.【详解】解:如图,当PO QO =时,POQ ∆是等腰三角形,103PO AO AP t =-=-,OQ t =,∴当PO QO =时,103t t -=,解得52t =;如图,当PO QO =时,POQ ∆是等腰三角形,310PO AP AO t =-=-,OQ t =,∴当PO QO =时,310t t -=,解得5t =;如图,当PQ AB ⊥时,POQ ∆是直角三角形,且2QO OP =,310PO AP AO t =-=-,OQ t =,∴当2QO OP =时,2(310)t t =⨯-,解得4t =;如图,当PQ OC ⊥时,POQ ∆是直角三角形,且2QO OP =,310PO AP AO t =-=-,OQ t =,∴当2QO OP =时,2310t t =-,解得:t =10.故答案为:52或5;4或10.【点睛】本题主要考查了等腰三角形的性质以及直角三角形的性质,解决问题的关键是进行分类讨论,分类时注意不能遗漏,也不能重复.二、解答题8.(2021·浙江余杭·八年级期中)如图,已知在ABC 中,90B ∠=︒,10AC =,6BC =,若动点P 从点B 开始,按B A C B →→→的路径运动,且速度为每秒2个单位长度,设出发的时间为t 秒.(1)出发2秒后,求CP 的长.(2)出发几秒钟后,CP 恰好平分ABC 的周长.(3)当t 为何值时,BCP 为等腰三角形?【答案】(1)PC 52(2)出发3秒钟后,CP 恰好平分△ABC 的周长(3)t =3或5.4或6或6.5时,△BCP 为等腰三角形【解析】【分析】(1)勾股定理求得AB 的长,进而根据速度求得出发2秒后BP 的长,Rt BCP △中勾股定理求解即可;(2)由于CP 恰好平分ABC 的周长,则P 点不可能位于线段BC 和AC 上,即对P 点在线段AB 上进行探究,根据题意列出一元一次方程,解方程求解即可;(3)①当P 在AB 上时,若BP =BC 时,②当P 在AC 上时,若BP =BC 时,③当P 在AC 上时,若CB =CP 时,④当P 在AB 上时,若PC =PB 时,根据题意列出一元一次方程解方程求解即可(1)由∠B =90°,AC =10,BC =6,∴AB =8,∵P 从点B 开始,按B →A →C →B ,且速度为2,∴出发2秒后,则BP =4,AP =6,∵∠B =90°,∴在Rt BCP △中,由勾股定理得PC 22226452BP BC +=+=;(2)P 点不可能位于线段BC 和AC 上,即对P 点在线段AB 上进行探究,根据题意可得,6+2t =10+8-2t ;解得t =3∴出发3秒钟后,CP 恰好平分△ABC 的周长(3)①当P 在AB 上时,若BP =BC 时,得到2t =6;则t =3,②当P 在AC 上时,若BP =BC 时,过点B 作BD AC ⊥,则68 4.810AB BC BD AB ⨯⨯===在Rt BDP △中,22226 4.8 3.6PD PD BD =-=-=在Rt ADB 中,22228 4.8 6.4AD AB BD =-=-=8 6.4 3.610.8BA AP BA AD PD ∴+=+-=+-=即210.8t =解得 5.4t =③当P 在AC 上时,若CB =CP 时,810612BA PA BA AC PC +=+-=+-=即212t =解得6t =④当P 在AC 上时,若PC =PB 时,15PA AB ==8513BA AP ∴+=+=得到2t=6;则t=6.5.综上可得t=3或5.4或6或6.5时,△BCP为等腰三角形.【点睛】本题考查了勾股定理,一元一次方程的应用,等腰三角形的性质与判定,分类讨论是解题的关键.9.(2022·吉林·八年级期末)如图,△ABC是等腰直角三角形,∠ACB=90°,AB=6.动点P从点A出发,以每秒2个单位长度的速度在射线AB上运动.点P出发后,连接CP,以CP为直角边向右作等腰直角三角形CDP,使∠DCP=90°,连接PD,BD.设点P的运动时间为t秒.(1)△ABC的AB边上高为;(2)求BP的长(用含t的式子表示);(3)就图中情形求证:△ACP≌△BCD;(4)当BP:BD=1:2时,直接写出t的值.【答案】(1)3(2)当0<t≤3时,PB=6-2t;当t>3时,PB=2t-6;(3)见解析(4)t的值为2或6.【解析】【分析】(1)根据等腰直角三角形的性质解答即可;(2)根据两种情况,利用线段之间关系得出代数式即可;(3)根据SAS证明△ACP与△CBD全等即可;(4)利用全等三角形的性质解得即可.(1)解:∵△ABC是等腰直角三角形,∠ACB=90°,AB=6,∴△ABC的AB边上高=12AB=3,故答案为:3;(2)解:∵AB=6,动点P从点A出发,以每秒2个单位长度的速度在射线AB上运动,∴点P在线段AB上运动的时间为62=3(秒),当0<t≤3时,PB=6-2t,当t>3时,PB=2t-6;(3)证明:∵△ABC是等腰直角三角形,∠ACB=90°,∴AC=BC,∵∠PCD=90°,CP=CD,∴∠ACP+∠PCB=90°,∠PCB+∠BCD=90°,∴∠ACP=∠BCD,在△ACP与△CBD中,AC BC ACP BCD CP CD =⎧⎪∠=∠⎨⎪=⎩,∴△ACP ≌△CBD (SAS );(4)解:∵△ACP ≌△CBD ,∴AP =BD ,当BP :BD =1:2,即BD =2BP 时,当0<t ≤3时,2t =2(6-2t ),解得:t =2;当BP :BD =1:2,即BD =2BP 时,当t >3时,2t =2(2t -6),解得:t =6,综上所述,t 的值为2或6.【点睛】本题是三角形的综合题,关键是根据等腰直角三角形的性质和全等三角形的判定和性质解答.10.(2022·福建·厦门一中八年级期末)在锐角△ABC 中,∠B =45°,∠C =60°,AD ⊥BC 于点D.(1)如图1,过点B 作BG ⊥AC 于点G ,求证:AC =BF ;(2)动点P 从点D 出发,沿射线DB 运动,连接AP ,过点A 作AQ ⊥AP ,且满足AP AQ =.①如图2,当点P 在线线段BD 上时,连接PQ 分别交AD 、AC 于点M 、N .请问是否存在某一时刻使得△APM 和△AQN 成轴对称,若有,求此刻∠APD 的大小;若没有,请说明理由.②如图3,连接BQ ,交直线AD 与点F ,当点P 在线段BD 上时,试猜想BP 和DF 的数量关系并证明;当点P 在DB 的延长线上时,若27AD FD =,请直接写出PB BD 的值.【答案】(1)证明过程见解析.(2)①存在某一时刻使得△APM 和△AQN 成轴对称,∠APD =30°,理由见解析.②BP =2DF ,47PB BD =【解析】【分析】(1)根据已知条件,证明△BDF 和△ADC 全等,即可得出AC =BF .(2)①因为∠C =60°在Rt △ABC 中∠CAD =30°,∠PAQ =90°,由对称的性质可知∠PAD =∠QAC =30°,所以可以得出∠APD =60°;②过Q 作QE ⊥AD ,交AD 与点E ,可证△APD ≌△QAE ,得出AE =PD ,再证△APD ≌△QAE ,得出EF =DF ,再通过等量代换即可.(1)证明:∵AD ⊥BC∴∠ADB =∠ADC =90°又∵∠B =45°∴△ABD 是等腰直角三角形∴AD =BD∵BG ⊥AC∴∠BGC =90°又∵∠C =60°∴∠DAC =90°-∠C =90°-60°=30°∠FBD =90°-∠C =90°-60°=30°∴∠DAC =∠FBD在△BDF 和△ADC 中,FBD CDA BDF ADC BD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDF ≌△ADC ∴AC =BF(2)①存在某一时刻使得△APM 和△AQN 成轴对称∵AQ ⊥AP∴∠QAP =90°由(1)的证明知∠DAC =30°,根据对称的性质,得∠PAD =∠QAC =2QAP CAD ∠-∠=90︒︒-302=30°∵∠ADP =90°∴∠APD =90°-∠PAD =90°-30°=60°②BP =2DF理由如下:如图4所示,过Q 作QE ⊥AD ,交AD 与点E ,那么∠AEQ =∠FEQ =90°∴∠AQE +∠QAE =90°又∵∠PAD +∠QAE =90°∴∠AQE =∠PAD在△APD 和△QAE 中,AQE PAD AEQ PDA AQ AP ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△APD ≌△QAE ∴AE =PD ;AD =QE∴DE =BP又∵AD =BD∴BD =QE在△QEF 和△BDF 中,QEF BDF EFQ DFB EQ DB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△QEF ≌△BDF∴EF =DF∴BP =2DF当点P 在DB 的延长线上时,如下图所示,由上述证明过程可知PB =2DF ,BD =AD又已知27AD FD∴DF =27AD∴PB =2×27BD =47BD ∴PB BD =47【点睛】本题考查了三角形全等的判定与性质,解题的关键是通过适当的作辅助线找等量关系从而得出三角形全等,再由全等的性质找出线段的关系,本题是一道压轴题,比较难.11.(2022·北京顺义·八年级期末)我们定义:在等腰三角形中,腰与底的比值叫做等腰三角形的正度.如图1,在△ABC 中,AB =AC ,AB BC的值为△ABC 的正度.已知:在△ABC 中,AB =AC ,若D 是△ABC 边上的动点(D 与A ,B ,C 不重合).(1)若∠A =90°,则△ABC 的正度为;(2)在图1,当点D 在腰AB 上(D 与A 、B 不重合)时,请用尺规作出等腰△ACD ,保留作图痕迹;若△ACD的正度是2,求∠A 的度数.(3)若∠A 是钝角,如图2,△ABC 的正度为35,△ABC 的周长为22,是否存在点D ,使△ACD 具有正度?若存在,求出△ACD 的正度;若不存在,说明理由.【答案】(1)22(2)图见解析,∠A =45°(335.【解析】【分析】(1)当∠A=90°,△ABC是等腰直角三角形,故可求解;(2)根据△ACD的正度是22,可得△ACD是以AC为底的等腰直角三角形,故可作图;(3)由△ABC的正度为35,周长为22,求出△ABC的三条边的长,然后分两种情况作图讨论即可求解.【详解】(1)∵∠A=90°,则△ABC是等腰直角三角形∴AB=AC∵AB2+AC2=BC2∴BC∴△ABC2故答案为:2 2;(2)∵△ACD1)可得△ACD是以AC为底的等腰直角三角形故作CD⊥AB于D点,如图,△ACD即为所求;∵△ACD是以AC为底的等腰直角三角形∴∠A=45°;(3)存在∵△ABC的正度为3 5,∴ABBC=35,设:AB=3x,BC=5x,则AC=3x,∵△ABC的周长为22,∴AB+BC+AC=22,即:3x+5x+3x=22,∴x=2,∴AB=3x=6,BC=5x=10,AC=3x=6,分两种情况:①当AC=CD=6时,如图过点A 作AE ⊥BC 于点E ,∵AB =AC ,∴BE =CE =12BC =5,∵CD =6,∴DE =CD −CE =1,在Rt △ACE 中,由勾股定理得:AE =在Rt △AED 中,由勾股定理得:AD =∴△ACD 的正度=AC AD =②当AD =CD 时,如图由①可知:BE =5,AE ,∵AD =CD ,∴DE =CE −CD =5−AD ,在Rt △ADE 中,由勾股定理得:AD 2−DE 2=AE 2,即:AD 2−(5−AD )2=11,解得:AD =185,∴△ACD 的正度=185365AD AC ==.综上所述存在两个点D ,使△ABD 具有正度.△ABD 35.【点睛】此题考查了等腰三角形的性质,解题的关键是理解正度的含义、熟知勾股定理与等腰三角形的性质.12.(2022·北京西城·八年级期末)在ABC 中,120BAC ∠=︒,AB AC =,AD 为ABC 的中线,点E 是射线AD 上一动点,连接CE ,作60CEM ∠=︒,射线EM 与射线BA 交于点F .(1)如图1,当点E 与点D 重合时,求证:2AB AF =;(2)如图2,当点E 在线段AD 上,且与点A ,D 不重合时,①依题意,补全图形;②用等式表示线段AB ,AF ,AE 之间的数量关系,并证明.(3)当点E 在线段AD 的延长线上,且ED AD ≠时,直接写出用等式表示的线段AB ,AF ,AE 之间的数量关系.【答案】(1)见解析;(2)AB AF AE =+,证明见解析;(3)当AD ED >时,AB AF AE =+,当AD ED <时,AB AE AF=-【解析】【分析】(1)根据等腰三角形三线合一的性质得60BAD CAD ∠=∠=︒,90ADC ∠=︒,从而可得在Rt ADB 中,30B ∠=︒,进而即可求解;(2)画出图形,在线段AB 上取点G ,使EG EA =,再证明()BGE FAE ASA ≅,进而即可得到结论;(3)分两种情况:当AD ED >时,当AD ED <时,分别画出图形,证明()BHE FAE ASA ≅或()NEF AEC ASA ≅,进而即可得到结论.【详解】(1)∵AB AC =,∴ABC 是等腰三角形,∵120BAC ∠=︒,∴30B C ∠=∠=︒,18012060FAC ∠=︒-︒=︒,∵AD 为ABC 的中线,∴60BAD CAD ∠=∠=︒,90ADC ∠=︒,∴6060120DAF CAD FAC ∠=∠+∠=︒+︒=︒,∵60CEM ∠=︒,∴906030ADF ∠=︒-︒=︒,∴180(12030)30AFD ∠=︒-︒+︒=︒,∴AD AF =,在Rt ADB 中,30B ∠=︒,∴22AB AD AF ==;(2)AB AF AE =+,证明如下:如图2,在线段AB 上取点G ,使EG EA =,∵60BAC ∠=︒,∴AEG △是等边三角形,∴60AEG ∠=︒,120BGE FAE ∠=∠=︒,∵ABC 是等腰三角形,AD 为ABC 的中线,∴EB EC =,BED CED ∠=∠,∴AEB AEC ∠=∠,即AEG GEB CEF AEF ∠+∠=∠+∠,∵60CEF AEG ∠=∠=︒,∴GEB AEF ∠=∠,在BGE △与FAE 中,GEB AEF EG EA BGE FAE ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()BGE FAE ASA ≅,∴GB AF =,∴AB GB AG AF AE =+=+;(3)当AD ED >时,如图3所示:与(2)同理:在线段AB 上取点H ,使EH EA =,∵60BAD ∠=︒,∴AEH △是等边三角形,∴120BHE FAE ∠=∠=︒,60AEH ∠=︒,∵ABC 是等腰三角形,AD 为ABC 的中线,∴BED CED ∠=∠,∵60CEF AEH ∠=∠=︒,∴HEB AEF ∠=∠,∴()BHE FAE ASA ≅,∴HB AF =,∴AB HB AH AF AE =+=+,当AD ED <时,如图4所示:在线段AB 的延长线上取点N ,使EN EA =,∵60BAD ∠=︒,∴AEN △是等边三角形,∴60AEN FNE ∠=∠=︒,∵60CEF AEN ∠=∠=︒∴NEF AEC ∠=∠,在NEF 与AEC △中,60FNE CAE EN EA NEF AEC ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩,∴()NEF AEC ASA ≅,∴NF AC AB ==,=,∴BN AF=-=-,∴AB AN BN AE AF∴AB AE AF=-.【点睛】本题考查全等三角形的判定与性质、等腰三角形的性质以及等边三角形的判定与性质,根据题意做出辅助线找全等三角形是解题的关键.。
等腰三角形与直角三角形练习题

等腰三角形与直角三角形练习题一、等腰三角形练习题(一)基础巩固1、已知等腰三角形的一个内角为 80°,则它的另外两个内角分别是多少度?解:当 80°的角为顶角时,底角的度数为:(180° 80°)÷ 2 = 50°,所以另外两个内角分别是 50°,50°。
当 80°的角为底角时,顶角的度数为:180° 80°× 2 = 20°,所以另外两个内角分别是 80°,20°。
2、等腰三角形的两边长分别为 6 和 8,则其周长是多少?解:当腰长为 6 时,三边长分别为 6,6,8,因为 6 + 6>8,所以能组成三角形,此时周长为 6 + 6 + 8 = 20。
当腰长为 8 时,三边长分别为 8,8,6,因为 8 + 6>8,所以能组成三角形,此时周长为 8 + 8 + 6 = 22。
综上,其周长为 20 或 22。
3、一个等腰三角形的周长为 20,其中一边长为 8,求另外两边的长。
解:当 8 为腰长时,底边长为 20 8× 2 = 4,因为 8 + 4>8,所以能组成三角形,此时另外两边长分别为 8,4。
当 8 为底边时,腰长为(20 8)÷ 2 = 6,因为 6 + 6>8,所以能组成三角形,此时另外两边长分别为 6,6。
(二)能力提升1、等腰三角形一腰上的高与另一腰的夹角为 30°,则顶角的度数为多少?解:当等腰三角形为锐角三角形时,腰上的高与另一腰的夹角为30°,则顶角为 60°。
当等腰三角形为钝角三角形时,腰上的高与另一腰的夹角为 30°,则顶角的外角为 60°,所以顶角为 120°。
综上,顶角的度数为 60°或 120°。
2、如图,在△ABC 中,AB = AC,D 是 BC 边上的中点,∠B =30°,求∠1 和∠ADC 的度数。
等腰直角三角形存在性(通用版)(含答案)

等腰直角三角形存在性(通用版)试卷简介:考查在动态框架和函数框架下等腰直角三角形存在性的处理原则,调用存在性问题的处理手段,分析定点、动点,从直角入手,确定分类,借助等腰三角形自身的性质或构造弦图模型解决问题。
一、单选题(共5道,每道20分)1.如图,抛物线交x轴于A,C两点(点A在点C的右侧),交y轴于点B.点D的坐标为(-1,0),若在直线AB上存在点P,使得以A,D,P为顶点的三角形是等腰直角三角形,则点P的坐标为( )A. B.(-1,3)或(1,2)C.(-1,4)或(1,2)D.(-1,4),(1,2)或(5,-2)答案:C解题思路:1.解题要点①观察题目特征,确定为等腰直角三角形存在性问题.②分析定点、动点、不变特征.从直角入手,分类讨论.③画图,表达线段长,借助等腰直角三角形性质建等式.2.解题过程由题意得,A(3,0),B(0,3),AO=BO=3.在△ADP中,A,D为定点,P为直线AB上的动点.①当点A是直角顶点时,在直线AB上不存在点P,使△ADP为等腰直角三角形.②如图,当点D为直角顶点时,过点D作⊥DA,交直线AB于点.由∠1=45°可得,为等腰直角三角形,点满足题意.此时,点的坐标为(-1,4).③如图,当点P为直角顶点时,过点D作⊥AB于点.易知为等腰直角三角形,点满足题意.过点作轴于点M.易得,OM=1,∴点的坐标为(1,2).综上得,点P的坐标为(-1,4)或(1,2).试题难度:三颗星知识点:等腰直角三角形存在性2.如图,抛物线与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.P是线段AC上的一个动点(不与点A,C重合),过点P作平行于x轴的直线,交BC于点Q,若在x轴上存在点R,使得△PQR是等腰直角三角形,则点R的坐标为( )A. B.C. D.答案:C解题思路:1.解题要点①观察题目特征,确定为等腰直角三角形存在性问题.②分析定点、动点、不变特征.从直角入手,分类讨论.③画图,表达线段长,借助等腰直角三角形性质建等式.2.解题过程由题意,得A(-1,0),B(3,0),C(0,2),则,.设,则,PQ=-2m+4.①如图,当点Q为直角顶点时,PQ=RQ.,,由-2m+4=m,得,∴.②如图,当点P为直角顶点时,PQ=PR.,,由-2m+4=m,得,∴.③如图,当点R为直角顶点时,RP=RQ.过点R作RD⊥于点D,则,由,得m=1,∴.综上得,点R的坐标为.试题难度:三颗星知识点:等腰直角三角形存在性3.如图,二次函数的图象与x轴交于A,B两点(点A在点B的左侧),以AB为边在x轴上方作正方形ABCD,P是x轴上的一动点(不与点A重合),连接DP,过点P作PE⊥DP交y轴于点E.当△PED是等腰直角三角形时,点P的横坐标为( )A.-4B.-3C.-3或-4D.-4或4答案:D解题思路:∵,∴A(-3,0),B(1,0).∵四边形ABCD是正方形,∴D(-3,4).∵∠DPE=90°,要使得△PED是等腰直角三角形,只能是DP=PE.设点P的横坐标为.①如图,当时,∵∠DAP=∠DPE=90°,∴∠ADP+∠DPA=∠OPE+∠DPA,∴∠ADP =∠OPE.又∵∠DAP=∠POE=90°,DP=PE,∴△ADP≌△OPE,∴OP=AD=4,∴.②如图,当时,易证△DAP≌△POE,∴OP=AD=4,∴(不合题意,舍去).③如图,当时,易证△DAP≌△POE,∴OP=AD=4,∴.综上得,当△PED是等腰直角三角形时,点P的横坐标为-4或4.试题难度:三颗星知识点:等腰直角三角形存在性4.如图,已知直线经过A(0,1),B(1,0)两点,P是x轴正半轴上的一动点,且OP的垂直平分线交直线于点Q,交x轴于点M,直线经过点A且与x轴平行.若在直线上存在点C,使得△CPQ是以Q为直角顶点的等腰直角三角形,则点C的坐标为( )A.(1,1)B.(1,1)或(2,1)C.(2,1)D.(1,1)或(0,1)答案:A解题思路:1.解题要点①观察题目特征,确定为等腰直角三角形存在性问题.②分析定点、动点、不变特征.③从已知出发,借助等腰直角三角形的性质(直角和两腰相等)和坐标系处理斜放置直角的原则,构造弦图模型解决问题.2.解题过程由题意得,OA=OB=1,△AOB为等腰直角三角形,点C的纵坐标为1.①如图,当点Q在x轴上方时,延长MQ交直线于点E,则ME⊥.易证△CEQ≌△QMP,△QMB为等腰直角三角形,四边形AOME为矩形,∴CE=QM=MB,AE=OM,∴AC=AE+CE=OM+MB=OB=1,∴点C的坐标为(1,1).②如图,当点Q在x轴下方时,延长QM交直线于点F.同理,得CF=QM=MB,AF=OM,∴AC=AF-CF=OM-MB=OB=1,∴点C的坐标为(1,1).综上得,点C的坐标为(1,1).试题难度:三颗星知识点:等腰直角三角形存在性5.如图,在平面直角坐标系xOy中,直线y=x+4与x轴、y轴分别交于点A,B,D为线段AB 上一动点,过点D作x轴的垂线,垂足为点C,CD的延长线交抛物线于点E,连接BE.若△DBE为等腰直角三角形,则点D的坐标为( )A.(-2,2)B.(-2,6)C.(-3,4)或(-2,6)D.(-3,1)或(-2,2)答案:D解题思路:由题意得,A(-4,0),B(0,4),∴OA=OB.又∵∠AOB=90°,∴∠BAO=45°.∵CD⊥x轴,∴∠ADC=45°,∴EDB=45°.在△DBE中,B是定点,D,E均为动点,要使得△DBE为等腰直角三角形,需从直角出发进行分类讨论.①如图,当点E为直角顶点时,BE∥AO.此时点E的纵坐标为4,代入二次函数表达式可得点E的坐标为(-3,4),∴,∴.②如图,当点B为直角顶点时,BE⊥AB.由直线AB的斜率为1可知直线BE的斜率为-1,结合点B的坐标(0,4),可求得直线BE的表达式为y=-x+4.由得,,∴点E的坐标为(-2,6),∴,∴.综上得,点D的坐标为(-3,1)或(-2,2).试题难度:三颗星知识点:等腰直角三角形存在性。
等腰三角形三线合一典型题型
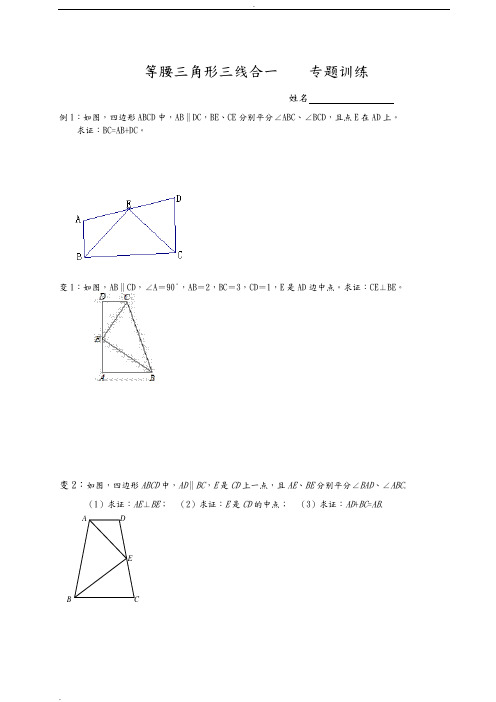
等腰三角形三线合一专题训练姓名例1:如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
求证:BC=AB+DC。
变1:如图,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD边中点。
求证:CE⊥BE。
变2:如图,四边形ABCD中,AD∥BC,E是CD上一点,且AE、BE分别平分∠BAD、∠ABC.(1)求证:AE⊥BE;(2)求证:E是CD的中点;(3)求证:AD+BC=AB.变3:△ABC 是等腰直角三角形 ,∠BAC=90°,AB=AC.⑴若D 为BC 的中点,过D 作DM ⊥DN 分别交AB 、AC 于M 、N ,求证:(1)DM =DN 。
⑵若DM ⊥DN 分别和BA 、AC 延长线交于M 、N 。
问DM 和DN 有何数量关系。
(1) 已知:如图,AB=AC ,E 为AB 上一点,F 是AC 延长线上一点,且BE=CF ,EF 交BC 于点D . 求证:DE=DF .M N D C BAM ND CB ADBCF AE(2)已知:如图,AB=AC ,E 为AB 上一点,F 是AC 延长线上一点,且,EF 交BC 于点D ,且D 为EF 的中点. 求证:BE=CF .DBCF AE利用面积法证明线段之间的和差关系1、如图,在△ABC 中,AB=AC ,P 为底边BC 上的一点,PD ⊥AB 于D ,PE ⊥AC 于E ,•CF ⊥AB 于F ,那么PD+PE 与CF 相等吗?变1:若P点在直线BC上运动,其他条件不变,则PD 、PE与CF的关系又怎样,请你作图,证明。
FF1、已知等腰三角形的两边长分别为4、9,则它的周长为( )A 17B 22C 17或22D 13根据等腰三角形的性质寻求规律 例1.在△ABC 中,AB=AC ,∠1=12∠ABC ,∠2=12∠ACB ,BD 与CE 相交于点O ,如图,∠BOC 的大小与∠A 的大小有什么关系? 若∠1=13∠ABC ,∠2=13∠ACB ,则∠BOC 与∠A 大小关系如何? 若∠1=1n ∠ABC ,∠2=1n∠ACB ,则∠BOC 与∠A 大小关系如何?会用等腰三角形的判定和性质计算与证明例2.如图,等腰三角形ABC 中,AB=AC ,一腰上的中线BD•将这个等腰三角形周长分成15和6两部分,求这个三角形的腰长及底边长.利用等腰三角形的性质证线段相等例3.如图,P 是等边三角形ABC 内的一点,连结PA 、PB 、PC ,•以BP 为边作∠PBQ=60°,且BQ=BP ,连结CQ .(1)观察并猜想AP 与CQ 之间的大小关系,并证明你的结论.(2)若PA :PB :PC=3:4:5,连结PQ ,试判断△PQC 的形状,并说明理由.例1、等腰三角形底边长为5cm ,腰上的中线把三角形周长分为差是3cm 的两部分,则腰长为( ) A 、2cm B 、8cm C 、2cm 或8cm D 、不能确定例2、已知AD 为△ABC 的高,AB=AC ,△ABC 周长为20cm ,△ADC 的周长为14cm ,求AD 的长。
等腰直角三角形构建三垂直全等的常见题型
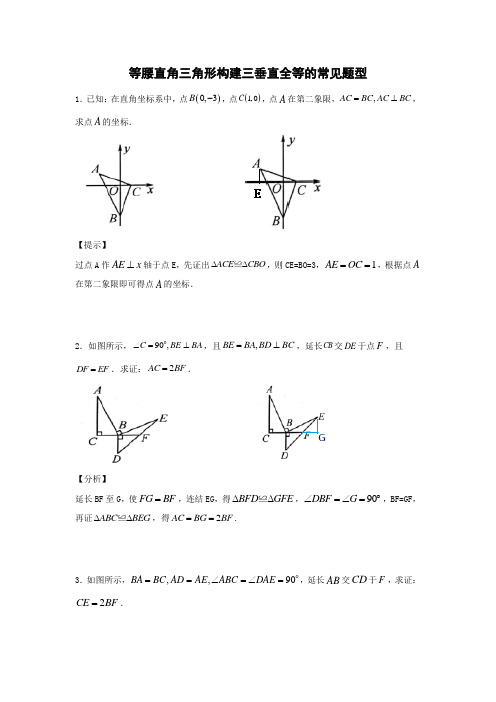
等腰直角三角形构建三垂直全等的常见题型1.已知:在直角坐标系中,点()0,3B -,点()1,0C ,点A 在第二象限,,AC BC AC BC =⊥,求点A 的坐标.【提示】过点A 作AE x ⊥轴于点E ,先证出ACE CBO ∆∆≌,则CE=BO=3,1AE OC ==,根据点A 在第二象限即可得点A 的坐标.2.如图所示,90,C BE BA ∠=⊥o ,且,BE BA BD BC =⊥,延长CB 交DE 于点F ,且DF EF =.求证:2AC BF =.【分析】延长BF 至G ,使FG BF =,连结EG ,得BFD GFE ∆∆≌,90DBF G ∠=∠=︒,BF=GF ,再证ABC BEG ∆∆≌,得2AC BG BF ==.3.如图所示,,,90BA BC AD AE ABC DAE ==∠=∠=o,延长AB 交CD 于F ,求证:2CE BF =.【分析】过点D 作DG AF ⊥,交AF 的延长线于点G.可证ADG EAB ∆∆≌,根据全等三角形的性质得DG AB BC ==,AG BE =,则CE=BG ,再证BFC GFD ∆∆≌,得BF GF =,即可得CE=BG=2BF.4.如图,A (-2,0),B (0,4)以B 点为直角顶点在第二象限作等腰直角△ABC(1)求C 点的坐标;(2)如图2点E 为y 轴正半轴上一动点,以E 为直角顶点作等腰直角△AEM ,过M 作MN ⊥x 轴于N ,求OE-MN 的值.【分析】(1)作CE ⊥y 轴于E ,易证△CBE ≌△BAO ,即可得点C 的坐标;(2)作MF ⊥y 轴于F ,易证△AOE ≌△EFM ,可得OE -MN=EF=OA 即可求得答案.5.过原点的直线l 经过A (3,1),将此直线绕原点逆时针方向旋转45︒后所对应的直线的解析式为________.【分析】在平面直角坐标系中画出旋转前后的图形,过点A 作AB OA ⊥交OE 于点B ,AD x ⊥轴于点D ,BC AD ⊥交AD 的延长线于点C ,利用AAS 可证AOD BAC ≅V V ,由全等三角形对应边相等可知BC 、AC 长,易知点B 坐标,可设直线的解析式为y kx =,将点B 坐标代入求解即可.6.如图1,已知A (a ,0),B (0,b )分别为两坐标轴上的点,且a ,b 满足a 2﹣24a+|b ﹣12|=﹣144,且3OC=OA .(1)求A 、B 、C 三点的坐标;(2)若D (2,0),过点D 的直线分别交AB 、BC 于E 、F 两点,且DF=DE ,设E 、F 两点的横坐标分别为x E 、x P ,求x E +x P 的值;(3)如图2,若M (4,8),点P 是x 轴上A 点右侧一动点,AH ⊥PM 于点H ,在HM 上取点G ,使HG=HA ,连接CG ,当点P 在点A 右侧运动时,∠CGM 的度数是否改变?若不变,请求其值;若改变,请说明理由.【分析】(1)由偶次方和算术平方根的非负性质求出a 和b 的值,得出点A 、B 的坐标,再求出OC ,即可得出点C 的坐标;(2)作EG ⊥x 轴于G ,FH ⊥x 轴于H ,由三角形的面积关系得出DF=DE ,由AAS 证明△FDH≌△EDG,得出DH=DG,即可得出结果;(3)连接MA、MC,过C作CT⊥PM于T,证明△CMT≌△MAH,可证明△CGT是等腰直角三角形,可求得∠CGM=45°。
初二等腰直角三角形类型题

初二等腰直角三角形类型题
在初二数学中,等腰直角三角形是一个重要的几何图形。
它包含了等腰三角形和直角三角形的特点,因此也被称为“两者兼备”的三角形。
在解题时,我们可以根据等腰直角三角形的特性,运用勾股定理、正弦定理、余弦定理等知识来求解各种问题,如求斜边长、角度大小、面积等。
下面就让我们来看几道典型的初二等腰直角三角形类型题吧!
1. 已知等腰直角三角形的直角边长为3cm,求斜边长。
解:由勾股定理可知,斜边长为√(3+3)=√18=3√2 (cm)。
2. 已知等腰直角三角形斜边长为4√2 cm,求底边长。
解:同样由勾股定理可知,底边长为4√2/√2=4 (cm)。
3. 已知等腰直角三角形的底边长为6 cm,求面积。
解:由勾股定理可知,斜边长为6√2 cm。
面积为1/2×6×6=18 (cm)。
4. 已知等腰直角三角形的斜边长为10 cm,底边长为x cm,求x的值。
解:由勾股定理可知,x+ x=10,化简为2x=100,故x=√50 (cm)。
以上就是几道典型的初二等腰直角三角形类型题,希望能对大家的数学学习有所帮助。
- 1 -。
等腰直角三角形难题

等腰直角三角形难题一、选择题(共8小题)1如图,在等腰直角△ ABC中AC=AB , BD丄AH于D, CH丄AH于H , HE、DF分别平分 / AHC和/ADB,则下列结论中①△ AHC BDA ;②DF丄HE ;③DF=HE ;④AE=BF其中,正确的结论有()(只需填写序号)A .① ③④B .①C .①②③D .① ②③④2. (2012?黄埔区一模)将一个斜边长为妊的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到另一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到又一个等腰直角三角形(如图3),若连续将图1的等腰直角三角形折叠n次后所得到的等腰直角三角形(如图3 .如图:△ ABC 中,/ ACB=90 ° ° / CAD=30 ° ° AC=BC=AD , CE 丄CD,且CE=CD,连接BD , DE , BE ,则下列结论:①/ ECA=165 ° °②BE=BC ;③AD丄BE;④4•如图,在2 X3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为5.如图,△ ABC 中,AC=BC , / ACB=90 ° AE 平分/ BAC 交BC 于E, BD 丄AE 于D , DM 丄AC 于M,连CD .下列结论:①AC+CE=AB ;②CD^AE;③/ CDA=45 °④丫严=定值.其中正确的有(n+1)的斜边长为()启"其中正确的是(B .①②④C •①③④D .①②③④I* (k 1\ ----------------- JB . 38 C. 46 D . 50C.A . 246.如图,在等腰Rt △ ABC的斜边AB上取两点M , N,使/ MCN=45 °记AM=m , MN=n , BN=x,则以线段x、m、n为边长的三角形的形状是()考虑接缝),如图2所示.小明所用正方形包装纸的边长至少为()二、填空题(共12小题)(除非特别说明,请填准确值)9.下列说法:①如图1, △ ABC中,AB=AC , /A=45 °则厶ABC能被一条直线分成两个小等腰三角形.②如图2, △ ABC中,AB=AC , / A=36 ° BD , CE分别为/ ABC , / ACB的角平分线,且相交于点F,则图中等腰三角形有6个.③如图3, △ ABC是等边三角形,CD丄AD,且AD // BC,贝U AD=^AB .④如图4, △ ABC中,点E是AC上一点,且AE=AB,连接BE并延长至点D,使AD=AC , / DAC= / CAB,则/ DBC=g/ DAB其中,正确的有___________________ (请写序号,错选少选均不得分)A .锐角三角形C.钝角三角形B .直角三角形D .随x、m、n的变化而改变7. (2006?防城港)如图,在五边形ABCDE 中,/ A= / B, / C= / D= / E=90 ° DE=DC=4 , AB^2,则五边形B. II.:8 (2010?鼓楼区二模)小明将一张正方形包装纸, 剪成图1所示形状,用它包在一个棱长为10的正方体的表面(不D. 10+10 :■:A/DA . 1个A . 4010.已知△ ABC中,AB=AC , / BAC=90 °直角/ EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点F、F,若FC=3厘米,BE=4厘米,则△ EFP的面积为__________________ 平方厘米.11.一个三角形三个内角之比为1: 1 : 2,则这个三角形的三边比为_______________12.一个三角形不同顶点的三个外角的度数比是3: 3: 2,则这个三角形是_________________ 三角形.13.(2003?黄浦区一模)已知第一个等腰直角三角形的面积为1,以第一个等腰直角三角形的斜边为直角边画第二个等腰直角三角形,又以第二个等腰直角三角形的斜边为直角边画第三个等腰直角三角形,以此类推,第13个等腰直角三角形的面积是 ______________ .14. (2007?天水)如图,AD是厶ABC的一条中线,/ ADC=45度.沿AD所在直线把△ ADC翻折,使点C落在15.如图,在等腰Rt△ ABC中,/ C=90 ° AC=8 , F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE .连接DE、DF、EF.在此运动变化过程中,有下列五个结论:①△ DFE是等腰直角三角形;②四边形CDFE不可能为正方形;③DE长度的最小值为4; ④四边形CDFE的面积保持不变;⑤△ CDE面积的最大值为 &其中正确结论是_ 一.16.(2011?贵阳)如图,已知等腰Rt△ ABC的直角边长为I,以Rt△ ABC的斜边AC为直角边,画第二个等腰Rt△ ACD , 再以Rt△ ACD的斜边AD为直角边,画第三个等腰Rt△ ADE ,…,依此类推到第五个等腰Rt△ AFG,则由这五个等腰直角三角形所构成的图形的面积为_________________ .D17.已知△ ABC 的三边长a、b 、c 满足J 己-]+ b - 1 +亠二。
初三数学等腰三角形的性质和判定试题

初三数学等腰三角形的性质和判定试题1.等腰三角形的底边长为6,它的周长不大于20,则腰长x的取值范围是_______。
【答案】【解析】根据等腰三角形的性质结合周长不大于20即可列不等式求解.由题意得,.【考点】等腰三角形的性质点评:不等式的应用在初中数学中极为广泛,与各个知识点的结合极为容易,因而是中考的热点,在各种题型中均有出现,一般难度不大,需特别注意.2.如图,在⊿ABC中,AB=AC,过∠ABC和∠ACB的平分线的交点O作DE∥BC,交AB于D,交AC于E,则图中的等腰三角形有___________个,它们分别是____________。
【答案】5,△ABC,△ADE,△DBO,△ECO,△BCO【解析】由AB=AC可得∠ABC=∠ACB,再根据角平分线的性质结合平行线的性质即可判断.∵AB=AC∴∠ABC=∠ACB∵OB平分∠ABC,OC平分∠ACB∴∠ABO=∠OBC,∠ACO=∠OCB∵DE∥BC∴∠DOB=∠OBC,∠EOC=∠OCB∴∠DOB=∠ABO=∠EOC=∠ACO∴BD=OD,CE=OE,OB=OC∵DE∥BC∴∠ADE=∠ABC,∠AED=∠ACB∴∠ADE=∠AED∴AD=AE∴等腰三角形有△ABC,△ADE,△DBO,△ECO,△BCO共5个.【考点】角平分线的性质,平行线的性质点评:角平分线的性质与平行线的性质在初中数学中极为广泛,与各个知识点的结合极为容易,因而是中考的热点,在各种题型中均有出现,一般难度不大,需特别注意.3.如图,在⊿ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD=6cm,DC=3cm,则D到AB的距离为______。
【答案】3cm【解析】角平分线的性质:角平分线上的点到角两边的距离相等.∵∠C=90°,AD平分∠BAC,DC=3cm∴D到AB的距离为3cm.【考点】角平分线的性质点评:角平分线的性质在初中数学中极为广泛,与各个知识点的结合极为容易,因而是中考的热点,在各种题型中均有出现,一般难度不大,需特别注意.4.将两块直角三角板的直角顶点重合为如图所示的形状,若∠AOD=127°,则∠BOC=________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有关等腰Rt三角形的题形
在初二几何中,有几组等腰直角三角形题形非常典型。
现介绍如下:
一.多垂直、锐角相等
例1: △ABC中, ∠BAC=90°, AB=AC, D为BC A 上一点,过B,C做BE⊥AD, CF⊥AD
求证: BE=EF+CF
证:∵BE⊥AD,∠BAC=90° E ∴∠EBA=∠CAF B D C 易证: △EBA≌△FAC
∴AE=FC, BE=AF F
∴BE=EF+CF
A
例2: △ABC中, ∠B=22.5°, AB的垂直平分
线交BC于D, 过D作DE⊥AC于E,
AF⊥BC于F交DE于G , G E
求证: GF=FC.
证:∵∠B=22.5°∴∠ADF=45°
∵AF⊥DC ∴AF=DF B D F C ∵DE⊥AC, AF⊥DC
∴∠FDG=∠CAF. 易证△CAF≌△GDF
∴GF=FC
A
思考题:1.△ABC中, ∠BAC=90°,AB=AC,
AD⊥BC 于D, E为AC上一点,
BE交AD于H, AF⊥BE于G. G E
求证:DH=DF H
B D F C
2.△ABC中, ∠BAC=90°, AB=AC, A
AD⊥BC于D, E为AD延长线上一点,
AG⊥BE于G..
求证: BE=AF, DE=DF
F D
B C
G E
二.通过三线合一构造全等
例1:△ABC中,∠BAC=90°,AB=AC, A
AB是BC边上中线,∠ABF=∠CAE,
求证:EF∥AC
证:Rt△ABC中,AD为中线
∴BD=AD,∠ABD=∠DAC=45° F
又∵∠ABF=∠CAE
∴∠DBF=∠DAE
∴易证:△DBF≌△DAE B D E C ∴DE=DF,∴∠FED=∠C=45°
∴EF∥AC
例2:等腰Rt△ABC中,∠A=90°,P为BC延长
线上一点,PE⊥AB,PF⊥AC,M为BC
中点连ME、MF E
求证:ME=MF,ME⊥MF A
证:由题意知矩形AFPE
∴PF==AE,∠MAC=∠FPC=45°
∴∠MAE=∠FCM=135°
∴易证△AME≌△CMF
∴ME=MF,∠AME=∠PMF C P 又∵∠AME+∠EMC=90° B M F ∴∠EMC=∠PMF=90°
∴ME⊥MKF
思考题:
1.△ABC中,∠A=90°,AB=AC, A
AD⊥BC过D作DE⊥DF
求证:DE=DF E
F
B D C
2.△ABC中,∠A=90°,AB=AC, A
AD⊥BC,H为BC上一点,
HE⊥AB,HF⊥AC连DE、DF E
求证:DE=DF,ED⊥DF
F
B D H
C 三.利用垂直与等腰构造全等
例1:△ABC中,∠BAC=90°,AB=AC,
平分∠ABC,CE⊥BD交BD
求证:BD=2CE
证:∵BD平分∠ABC,且CE⊥BE
∴延长CE、BA交于F
易证:△FBE≌△CBE
∴FE=CE,△ABD≌△ACF
∴BD=CF=2CE
例2:△ABC中,∠BAC=90°,AB=AC,
D、E在BC上,∠DAE=45°,若
BD=2,CE=3 A
求DE的长
解:∵∠DAE=45°
∴∠BAD+∠CAE=45°
∴作∠HAD=∠BAD,
取AH=AB连DH、EH
∴易证:△ABD≌△AHD B D E C ∴DB=DH=2,∠AHD=∠B=45°,
∠EAH=∠CAE
易证:△CAE≌△HAE H
∴EH=EC=3,∠AHE=∠C
∴在Rt△DHE中,易求DE
思考题:
1.△ABC中,∠BAC=90°AB=AC, A
F为AC中点,连BF作AE⊥BF交
BF于E,交BC于D
求证:∠AFB=∠CFD E F
B D C
2.△ABC中,∠A=90°,AB=AC, A
D在ABC内,且∠ABD=30°
BA=BD
求证:DA=DC
D
B C。
