2017年福州大学812自动控制原理模拟答案
2017年福州大学812自动控制原理模拟答案详解
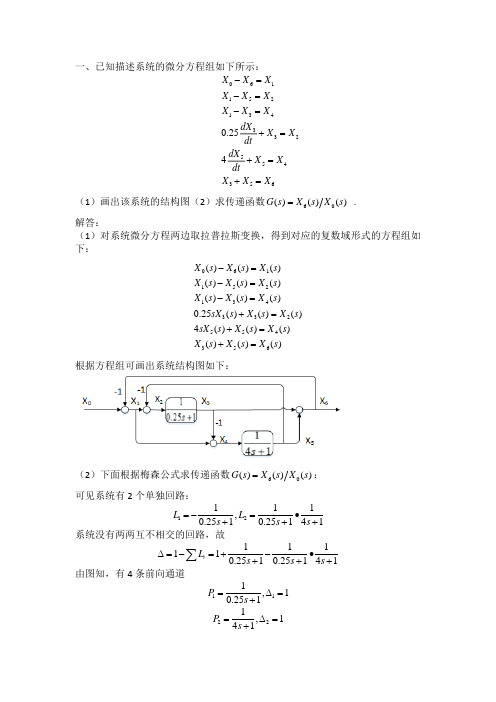
一、已知描述系统的微分方程组如下所示:0611521343325543560.254X X X X X X X X X dX X X dt dXX X dtX X X -=-=-=+=+=+=(1)画出该系统的结构图(2)求传递函数60()()()G s X s X s = .解答:(1)对系统微分方程两边取拉普拉斯变换,得到对应的复数域形式的方程组如下:061152134332554356()()()()()()()()()0.25()()()4()()()()()()X s X s X s X s X s X s X s X s X s sX s X s X s sX s X s X s X s X s X s -=-=-=+=+=+=根据方程组可画出系统结构图如下:(2)下面根据梅森公式求传递函数60()()()G s X s X s =: 可见系统有2个单独回路:12111,0.2510.25141L L s s s =-=•+++系统没有两两互不相交的回路,故111110.2510.25141i L s s s ∆=-=+-•+++∑由图知,有4条前向通道111,10.251P s =∆=+ 221,141P s =∆=+3311,1410.251P s s =-•∆=++ 4411,10.25141P s s =-•∆=++根据梅森公式得46102111111()0.25141410.2510.25141111()10.2510.251414.258.251i ii P X s s s s s s s X s s s s s s s =∆+-•-•++++++==∆+-•+++=++∑ 二、已知一控制系统的结构图如下,(1)确定该系统在输入信号()1()r t t = 下的时域性能指标:超调量%σ ,调节时间S t 和峰值时间P t ;(2)当()21(),()4sin3r t t n t t =•=时,求系统的稳态误差。
自动控制原理课后习题答案

C1 ( s ) R1 ( s ) (2)求传递函数阵 G(s),其中,C(s)=G(s)R(s), C(s)= ,R(s)= 。 C 2 ( s ) R2 ( s )
8
图 2.80 习题 2.16 图
解: (1)
G1G2 G3 (1 G5 H 2 ) C1 ( s) G11 ( s) R1 ( s) 1 G5 H 2 G3 H 1 G5 G7 G8 G1G5 G6 G7 C 2 ( s) G21 ( s) R1 ( s) 1 G5 H 2 G3 H 1 G5 G7 G8 G3G4 G5 G9 C1 ( s) G12 ( s) R2 ( s) 1 G5 H 2 G3 H 1 G5 G7 G8 G4 G5 G( C 2 ( s) 6 1 G3 H 1) G22 ( s) R2 ( s) 1 G5 H 2 G3 H 1 G5 G7 G8
解:
(a)
u u du u u 1 ur uc i2 dt , 2 c , i1 , i1 ( 1 C1 1 ) , i2 1 , u 2 R1 R2 dt R3 R4 R5 C2
R1 R3 R4 C1C 2 RRRC c 1 3 4 2 u c u c u r u R5 R2 R5
解:
(a)
G( s)
G( s)
0.5K s 3.5s 2 s 0.5K
3
(b)
G1G2 G3G4 G1G5 G6 (1 G4 H 2 ) 1 G1G2 H 1 G1G2 G3 G1G5 G4 H 2 G1G2 G4 H 1 H 2
2.14 试梅逊公式求图 2.78 所示结构图的传递函数 C(s)/R(s)。
自动控制原理课后习题答案.docx
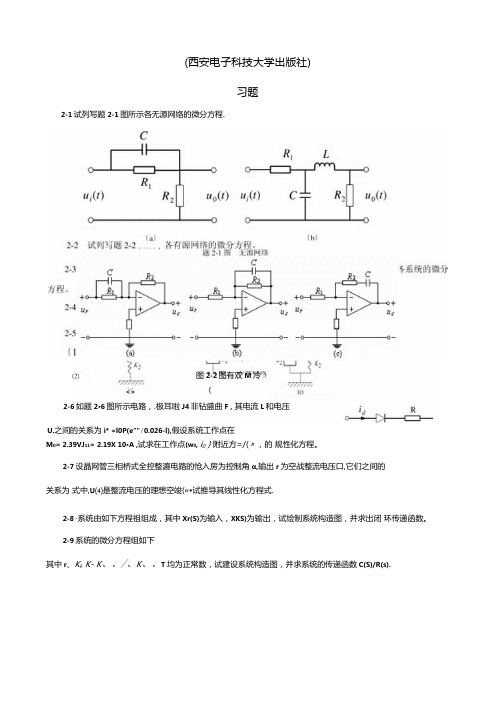
(西安电子科技大学出版社)习题2-1试列写题2-1图所示各无源网络的微分方程.M 0= 2.39VJ 11= 2.19X 10∙A ,试求在工作点(w 0, i 0}附近方=/(〃,的 规性化方程。
2-7设晶网管三相桥式全控整漉电路的怆入房为控制角α,输出r 为空战整流电压口,它们之间的 关系为 式中,U ⑷是整流电压的理想空竣(«•试推导其线性化方程式.2-8 ∙系统由如下方程祖组成,其中Xr(S)为输入,XKS)为输出,试绘制系统构造图,并求出闭 环传递函数。
2-9系统的微分方程组如下其中r 、K l . K- K 、、/、K 、、T 均为正常数,试建设系统构造图,并求系统的传递函数C(S)/R(s).图2-2图有双M 冷 ⑵(W <»U.之间的关系为i* =l0P(e""∕0.026-l),假设系统工作点在 2-6如题2∙6图所示电路,.极耳啦J4非钻盛曲F ,其电流L 和电压2-10试化简即2-10图所示的系统构造图.并求传递函数C(S)11R(S), K(S) C(S)/ C(S) R(S) 筑书规图所材 Gl C(S) G,卡G 5佛与函数 国S) C(S) G) 5 “七; Hl 弟统 £(S) M(S)2-16零初 设某 2-17 g (t) = 7-5e 6f . 咫2∙ 15图求系统 的传速函数, 始条件下的输出响试求该系统的传递 2-18系统的 W'> I 控制系统构造t f 1*1 2-16 W 系统构造图 R(S) ΛU) 2-15 E(S) C (Λ I I - L_rτ∏J ∙13图 系统G:" r ,(5) E(S)凤 F) R ⑸M ⑸松) ⅛4和脉冲响应函数, 单位脉冲响应为。
大学期末考试自动控制原理题集( 附带答案)

自动控制原理1一、 单项选择题(每小题1分,共20分)1. 系统和输入已知,求输出并对动态特性进行研究,称为( C )A.系统综合B.系统辨识C.系统分析D.系统设计2. 惯性环节和积分环节的频率特性在(A )上相等。
A.幅频特性的斜率B.最小幅值C.相位变化率D.穿越频率3. 通过测量输出量,产生一个与输出信号存在确定函数比例关系值的元件称为( C )A.比较元件B.给定元件C.反馈元件D.放大元件4. ω从0变化到+∞时,延迟环节频率特性极坐标图为(A )A.圆B.半圆C.椭圆D.双曲线5. 当忽略电动机的电枢电感后,以电动机的转速为输出变量,电枢电压为输入变量时,电动机可看作一个( B )A.比例环节B.微分环节C.积分环节D.惯性环节6. 若系统的开环传 递函数为2)(5 10+s s ,则它的开环增益为(C ) A.1 B.2 C.5 D.107. 二阶系统的传递函数52 5)(2++=s s s G ,则该系统是(B ) A.临界阻尼系统 B.欠阻尼系统 C.过阻尼系统 D.零阻尼系统8. 若保持二阶系统的ζ不变,提高ωn ,则可以(B )A.提高上升时间和峰值时间B.减少上升时间和峰值时间C.提高上升时间和调整时间D.减少上升时间和超调量9. 一阶微分环节Ts s G +=1)(,当频率T1=ω时,则相频特性)(ωj G ∠为(A ) A.45° B.-45° C.90° D.-90°10.最小相位系统的开环增益越大,其( D )A.振荡次数越多B.稳定裕量越大C.相位变化越小D.稳态误差越小11.设系统的特征方程为()0516178234=++++=s s s s s D ,则此系统 ( A )A.稳定B.临界稳定C.不稳定D.稳定性不确定。
12.某单位反馈系统的开环传递函数为:())5)(1(++=s s s k s G ,当k =( C )时,闭环系统临界稳定。
福州大学自动控制原理期末复习资料非常有用!

a
p z
i 1 i j 1
n
m
j
nm
2 ( 2) 0 1
④ 确定分离点和分离角; K * (0.5s 1) 0 可得: 由 1 G(s) 1 2 0.5s s 1
*
(s 2 2s 2) K s2 dK * (2s 2) (s 2) 1 (s 2 2s 2) 0 2 ds (s 2)
b1 b1 b2 b1 1 a1 a5 a5b1 a1b3 c2 b1 b1 b3 b1
其中: 1 a0 b1 a1 a1
a2 a1a2 a0 a3 a3 a1
劳斯列表每一列最后一个非零元素都是常数项。 每个偶数行的最后元素都是常数项。
劳斯列表最后两行都只有一个元素。 计算劳斯列表时,为了简化其后的数值计算,可用一 正整数去除或乘某一整行,这时,并不改变稳定性结论。
L G G H
1 3 4
l1 G3G4 H3 n 1 P 1 G1G2G3G4 l2 G2G3 H 2 l3 G1G2G3G4 H1
3
G2G3 H2 G1G2G3G4 H1
L
2
0
1 G3G4 H3 G2G3 H2 G1G2G3G4 H1
s2 s1 s0 1 2K * 2 K* 2 0 2K * 2
*
j
p 135 2
1
K: 0
故根轨迹与虚轴不相交。
b 3.414
5
z 45
2
1 90 p 1
4
3
⑦ 绘制根轨迹。
2
参数根轨迹
前面讨论的系统根轨迹的绘制都是以根轨迹增益 K *为 可变参量,这种根轨迹称为常规根轨迹。 从理论上讲,可变参量可以选择为系统的任何参数, 如开环零点、极点,时间常数和反馈系数等,这种根轨迹 称为参数根轨迹,或广义根轨迹。
福州大学自动控制原理历年考研真题

百度认证店铺:考研资料
2018年福州大学812自动控制原理初试真题回忆
1、已知结构图和特性方程,求传递函数参数。
就是用梅森公式解,不难。
2、已知某二阶系统经过PD修正后,给出求出
c(t)=1-1.01e^(-1.5t)sin(2.6t+83.6°),求超调量和调节时间。
3、已知已知闭环多项式(没有给出具体的式子),试用劳斯判据分析已圆心为(-a,j0)半径为a的圆内闭环极点个数,只写分析过程,无需计算。
4、已知特征方程d(s)=ks(s方+6s+10)+1,画出k的根轨迹。
5、已知含参数的开环传函数及输出c(t)及谐振频率,带宽频率,求系统参数
6、已知频率特性求输出响应,不难,就是用叠加原理。
7、串联校正,g(s)=300/s(0.02s+1),要求校正后相角大于45度
8、给出开环传函(比较复杂有计算量),要求用奈氏判据分析稳定
分享考研资料,助力考研成功!。
自动控制原理课后参考答案

第一章1-1图1-2是液位自动控制系统原理示意图。
在任意情况下,希望液面高度c维持不变, 试说明系统工作原理并画岀系统方块图。
图1-2 液位自动控制系统解:被控对象:水箱;被控量:水箱的实际水位;给定量电位器设定水位U r(表征液位的希望值C r);比较元件:电位器;执行元件:电动机;控制任务:保持水箱液位高度不变。
工作原理:当电位电刷位于中点(对应U r)时,电动机静止不动,控制阀门有一定的开度,流入水量与流出水量相等,从而使液面保持给定高度C r,一旦流入水量或流出水量发生变化时,液面高度就会偏离给定高度C r。
当液面升高时,浮子也相应升高,通过杠杆作用,使电位器电刷由中点位置下移,从而给电动机提供一定的控制电压,驱动电动机,通过减速器带动进水阀门向减小开度的方向转动,从而减少流入的水量,使液面逐渐降低,浮子位置也相应下降,直到电位器电刷回到中点位置,电动机的控制电压为零,系统重新处于平衡状态,液面恢复给定高度r。
反之,若液面降低,则通过自动控制作用,增大进水阀门开度,加大流入水量,使液面升高到给定高度C r。
系统方块图如图所示:1-10 下列各式是描述系统的微分方程,其中c(t)为输岀量,r (t)为输入量,试判断哪些是线性定常或时变系统,哪些是非线性系统?2c(t) =5 r2(t) t d2(^(1) dt ;3 2d c(t) 3d c(t) 6dc(t) --- 3 3 ---- 2 6 — dt dt dt xdc(t) dr(t)t c(t) =r(t) 3 dt dtc(t) = r(t)cos t 5 ;dr (t) tc(t) =3r(t)6 5 r(.)d. (5) dt =;(6)c(t)訂 2 ⑴;0, t ::: 6c(t)= “r(t), t 畠 6.(7) -解:(1)因为c(t)的表达式中包含变量的二次项 『(t),所以该系统为非线性系统。
(2) 因为该微分方程不含变量及其导数的高次幕或乘积项,且各项系数均为常数,所以该 系统为线性定常系统。
自动控制原理习题及答案.doc【范本模板】

第一章 习题答案1—1 根据题1—1图所示的电动机速度控制系统工作原理图(1) 将a,b 与c ,d 用线连接成负反馈状态;(2) 画出系统方框图。
解 (1)负反馈连接方式为:d a ↔,c b ↔;(2)系统方框图如图解1-1 所示.1-2 题1-2图是仓库大门自动控制系统原理示意图。
试说明系统自动控制大门开闭的工作原理,并画出系统方框图。
题1-2图 仓库大门自动开闭控制系统解 当合上开门开关时,电桥会测量出开门位置与大门实际位置间对应的偏差电压,偏差电压经放大器放大后,驱动伺服电动机带动绞盘转动,将大门向上提起。
与此同时,和大门连在一起的电刷也向上移动,直到桥式测量电路达到平衡,电动机停止转动,大门达到开启位置。
反之,当合上关门开关时,电动机带动绞盘使大门关闭,从而可以实现大门远距离开闭自动控制。
系统方框图如图解1-2所示。
1-3 题1—3图为工业炉温自动控制系统的工作原理图。
分析系统的工作原理,指出被控对象、被控量和给定量,画出系统方框图.题1-3图 炉温自动控制系统原理图解 加热炉采用电加热方式运行,加热器所产生的热量与调压器电压c u 的平方成正比,c u 增高,炉温就上升,c u 的高低由调压器滑动触点的位置所控制,该触点由可逆转的直流电动机驱动.炉子的实际温度用热电偶测量,输出电压f u 。
f u 作为系统的反馈电压与给定电压r u 进行比较,得出偏差电压e u ,经电压放大器、功率放大器放大成a u 后,作为控制电动机的电枢电压。
在正常情况下,炉温等于某个期望值T °C,热电偶的输出电压f u 正好等于给定电压r u 。
此时,0=-=f r e u u u ,故01==a u u ,可逆电动机不转动,调压器的滑动触点停留在某个合适的位置上,使c u 保持一定的数值。
这时,炉子散失的热量正好等于从加热器吸取的热量,形成稳定的热平衡状态,温度保持恒定。
当炉膛温度T °C 由于某种原因突然下降(例如炉门打开造成的热量流失),则出现以下的控制过程:控制的结果是使炉膛温度回升,直至T °C 的实际值等于期望值为止。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、已知描述系统的微分方程组如下所示:0611521343325543560.254X X X X X X X X X dX X X dtdX X X dtX X X -=-=-=+=+=+= (1)画出该系统的结构图(2)求传递函数60()()()G s X s X s =.解答:(1)对系统微分方程两边取拉普拉斯变换,得到对应的复数域形式的方程组如下:061152134332554356()()()()()()()()()0.25()()()4()()()()()()X s X s X s X s X s X s X s X s X s sX s X s X s sX s X s X s X s X s X s -=-=-=+=+=+=根据方程组可画出系统结构图如下:(2)下面根据梅森公式求传递函数60()()()G s X s X s =: 可见系统有2个单独回路:12111,0.2510.25141L L s s s =-=∙+++系统没有两两互不相交的回路,故111110.2510.25141i L s s s ∆=-=+-∙+++∑由图知,有4条前向通道111,10.251P s =∆=+ 221,141P s =∆=+3311,1410.251P s s =-∙∆=++ 4411,10.25141P s s =-∙∆=++根据梅森公式得46102111111()0.25141410.2510.25141111()10.2510.251414.258.251i ii P X s s s s s s s X s s s s s s s =∆+-∙-∙++++++==∆+-∙+++=++∑ 二、已知一控制系统的结构图如下,(1)确定该系统在输入信号()1()r t t =下的时域性能指标:超调量%σ,调节时间S t 和峰值时间P t ;(2)当()21(),()4sin3r t t n t t =∙=时,求系统的稳态误差。
解答:(1)由于只考虑输入信号()r t ,可以忽略()N t ,即()0N s = 系统开环传递函数为2188()4268G s s s s s ==++++系统闭环传递函数为2228()868()81()616168G s s s s G s s s s s ++Φ===++++++ 对比二阶系统标准闭环传递函数可知40.75n ωξ=⎧⎨=⎩(这里根据分母求,可以理解为分子上有比例因子)1.795100% 2.8%31(5%)psnt set sσξω===⨯===∆=(2)由题意知,该系统是个线性系统,满足叠加原理,故可以分别求取,()21()r t t=∙和()4sin3n t t=分别作用于系统时的稳态误差1ess和2ess,系统的稳态误差就等于12ess ess ess=+。
A)()21()r t t=∙单独作用时,由系统的开环传递函数知,系统静态误差系数1pK=,所以稳态误差1ess为11211pessK=⨯=+B)()4sin3n t t=单独作用时,系统的结构图为系统的闭环传递函数为:28(4)()616sss s+Φ=++频率特性为:28(4)()616jjjωωωω+Φ=+-当系统作用为()4sin3n t t=时,3ω=,所以28(34)3224(3) 2.0763163718j jjj j++Φ===⨯+-+2418(3)arctan arctan0.5564327j∠Φ=-=-系统的输出为:24(3)sin(3(3))8.56sin(30.5564)ess j t jt=⨯Φ+∠Φ=-所以系统的误差为:1218.56sin(30.5564)ess ess ess t =+=+-三、证明根轨迹分离点公式。
1111mnj i j i d z d p ===--∑∑ 证明:设控制系统结构图如图所示前向通道传递函数为:*11()()()fii Gqii s z G s Ks p ==-=-∏∏反馈通道传递函数为:1*1()()()kjj Hhjj s z H s K s p ==-=-∏∏则闭环传递函数为:*11*11()()()()1()()()()fhGiji j nm iji j Ks z s p G s s G s H s s p K s z ====--Φ==+-+-∏∏∏∏(3-1)其中***G HK K K =为开环系统根轨迹增益,,f l m q h n +=+= 由(3-1),闭环系统的特征方程为*11()()()0nmi ji j D s s p Ks z ===-+-=∏∏根轨迹在平面上相遇,说明闭环特征方程由重根,设重根为d。
根据代数方程中重根的条件,有()0,()0D s D s ∙== 即*11()()0nmiji j s p K s z ==-+-=∏∏*11()()0n m i j i j d s p K s z ds ==⎡⎤-+-=⎢⎥⎣⎦∏∏ 或*11()()n miji j s p K s z ==-=--∏∏(3-2)*11()()n m i j i j d d s p K s z ds ds ==-=--∏∏(3-3) 式(3-3)除(3-2),得1111()()()()mnj i j i nmiji j d d s z s p ds ds s p s z ====--=--∏∏∏∏即11ln ()ln ()mnj i j i d s z d s p ds ds==--=∏∏(3-4)因为1111ln ()ln()ln ()ln()nni i i i mmj j j j s p s p s z s z ====-=--=-∑∏∑∏式(3-4)可写为11ln()ln()nm j i i j d s z d s p ds ds ==--=∑∑ 有1111nmi j i j s p s z ===--∑∑ 证毕。
四、单位反馈系统如图所示,其中21(),0()(22)G s a s s a s s =>+++为待定参数。
(1)设()0C G s K =>,已知系统四条根轨迹只有一个分离点(或会合点)-1,确定参数a 并画出根轨迹图。
(2)确定根轨迹和虚轴的交点并由此确定使闭环系统稳定的K 值。
(3)确定系统输出无衰减振荡分量时的闭环传递函数。
解答:(1)由分离点的计算公式1111011d d a d j d j+++=++-++ 依题意,将分离点1d =-,代入上式得2a = 则开环传递函数2()(2)(22)KG s s s s s =+++a 、开环极点123,40,2,1p p p j ==-=-±数目4n =;系统有四条根轨迹;分别起始于开环极点,终止于无穷远点;b 、实轴上根轨迹段为(2,0)-;c 、渐近线与实轴的夹角为45,135,225,315αϕ= 渐近线与实轴的交点1ασ=-;d 、由已知,得分离点为-1;由以上计算得到的参数,绘制根轨迹如图所示:(2)根轨迹与虚轴的交点由1()0G s +=,得特征方程为4324640s s s s K ++++=列劳斯表如下:43210164452045s K s s KK s s K- 要与虚轴有交点,则有全零行,即20405K K -=⇒= 辅助方程:21,2550s s j +=⇒=±综上,与虚轴的交点是j ±,使闭环系统稳定的K 值范围应是05K <<。
(3)要使闭环系统的输出无衰减振荡分量,则闭环系统应无共轭复数极点,即闭环极点均为实极点。
显然只有1s =-点能满足要求,所以分离点处对应的四重实极点即为所求的闭环极点。
此时系统的闭环传递函数为:41()(1)s s Φ=+。
五、控制系统的结构图如图(a )所示,其中1()G s 的频率特性如图(b )(0,0T τ>>)(a )控制系统结构图(b )1()G s 的频率特性(1)写出1()G s 的表达式;(2)设221()G s s =,求出系统的开环传递函数; (3)画出系统的幅相频率特性曲线,并用Nyquist 稳定判据分析其稳定性。
解答:(1)由(b )图知,环节1()G s 由一个惯性环节和一个一阶微分环节组成,其为:11()1Ts G s s τ+=+ (2)系统的开环传递函数2(1)()(1)K Ts G s s s τ+=+ (3)由(b )图可以看出,T Nyquist τ>曲线(草图)如图所示:由图可以看出,Nyquist 曲线不包围(1,0)j -点,即0N =,而且0P =,所以系统稳定。
六、由实验测得某最小相位系统的幅频特性对数标图如图所示,试求: (1)系统的开环传递函数G(s)并画出系统的相频特性曲线; (2)计算系统的相角裕度γ和幅值裕度g K ;(3)闭环系统对单位阶跃输入和单位斜坡输入的稳态误差分别是多少?解答:(1)低频段渐近线的斜率为-20,故系统为Ⅰ型系统。
延长低频段渐近线,经计算得1ω=时,()20lg 40100L K K ω==⇒= 由ABC ∆知,11146640(lg5lg )5100.5/AB rad sωωω=-=-=⇒=由此可得系统的开环传递函数为100()(21)(0.21)G s s s s =++(相频特性曲线画草图就可以了)(2)由100()120.2c c c cA ωωωω≈=⨯⨯,求得系统的穿越频率 6.3/c rad s ω=18090arctan(2 6.3)arctan(0.2 6.3)47γ=--⨯-⨯=-根据()90arctan2arctan0.2180g g g ϕωωω=---=- ,得 1.58/g rad s ω= 系统在相交交界处的开环幅值为100()63.8820.2g g g gA ωωωω≈=⨯⨯幅值裕度为20lg ()36g g K A db ω=-=-(3)由于该系统不稳定,所以讨论稳态误差是无意义的。
七、某火炮指挥系统是一个单位负反馈系统,其开环传递函数为()(0.21)(0.51)KG s s s s =++,系统最大输出速度为2r/min ,输出位置的容许误差小于2度,求:(1)确定满足上述指标的最小K 值,计算该 K 值下的相位裕量和幅值裕量;(2)前向通路中串联超前校正网络0.41()0.081c s G s s +=+,试计算相位裕量。
解答:(1)系统为I 型系统,2360/6062A K ess ⨯===所以6()(0.21)(0.51)G s s s s =++可以求得3.53.5 3.5180()18090arctan arctan4.925c c G j ωγω==+∠=---=-令[]Im ()0G j ω=,得10.86()g g h G j ωω=== (2)加入串联校正后,开环传递函数为60.41()(0.21)(0.51)0.081s G s s s s s +=+++求得4.84.8 4.8 4.8 4.8180()180arctan 90arctan arctan arctan 20.22.52512.5c c G j ωγω==+∠=+----=八、设()(1)(0.251)o KG s s s s =++,设计串联校正装置,使系统满足下列性能指标:15,40,0.5c K s γω-≥≥≥ 。
