四川师范大学数学专业综合考研真题试题2013年—2019年
四川师范大学《333教育综合》[专业硕士]历年考研真题及详解
![四川师范大学《333教育综合》[专业硕士]历年考研真题及详解](https://img.taocdn.com/s3/m/a90aee0017fc700abb68a98271fe910ef12dae62.png)
本书收录了四川师范大学“333教育综合”的考研真题(附赠有2019年考研真题及2020年回忆版真题,仅提供试题,没有提供详解)。
考研真题是每个考生复习备考必不可少的资料,通过研究历年真题能洞悉考试出题难度和题型,了解常考章节与重要考点,有效指明复习方向。
特别说明:本资料中的真题为赠送资料,版权归学校及相关单位,在此对版权所有者表示感谢,如有不妥我们将无条件处理。
2012年四川师范大学《333教育综合》[专业硕士]考研真题2012年四川师范大学《333教育综合》[专业硕士]考研真题及详解2013年四川师范大学《333教育综合》[专业硕士]考研真题2013年四川师范大学《333教育综合》[专业硕士]考研真题及详解2014年四川师范大学《333教育综合》[专业硕士]考研真题2014年四川师范大学《333教育综合》[专业硕士]考研真题及详解2015年四川师范大学《333教育综合》[专业硕士]考研真题2015年四川师范大学《333教育综合》[专业硕士]考研真题及详解2016年四川师范大学《333教育综合》[专业硕士]考研真题(回忆版)2016年四川师范大学《333教育综合》[专业硕士]考研真题(回忆版)及详解2017年四川师范大学《333教育综合》[专业硕士]考研真题(回忆版)2017年四川师范大学《333教育综合》[专业硕士]考研真题(回忆版)及详解2018年四川师范大学《333教育综合》[专业硕士]考研真题2018年四川师范大学《333教育综合》[专业硕士]考研真题及详解附赠:2019年四川师范大学《333教育综合》[专业硕士]考研真题附赠:2020年四川师范大学《333教育综合》[专业硕士]考研真题(回忆版)2012年四川师范大学《333教育综合》[专业硕士]考研真题一、名词解释题(共6小题,每小题5分,共30分)1三舍法2苏格拉底法3白板说4心理发展5原型启发6自我效能感二、简答题(共4小题,每小题10分,共40分)1简述墨家的教育实践与教育思想。
四川师范大学教育学333考研-历年教育综合考研试题

四川师范大学2019年333教育综合考研试题
一、名词解释(每题5分,共30分)
1.教育制度
2.三舍法
3.国防教育法
4.苏格拉底法
5.有教无类
6.课程目标
二、简答题(每题10分,共40分)
1.简述我国教育目的的基本精神。
2.简述影响品德形成的因素。
3.简述陈鹤琴的活教育论。
4.简述科举制度的影响。
三、论述题(每题20分,共80分)
l.论述卢梭的自然主义教育理论。
2.论述建构主义学习理论的观点和对我国中小学教学的启示。
3.论述文化对教育的制约与影响。
4.论述教学过程中直接经验和间接经验的关系。
四川师范大学2020年333教育综合考研试题
一、名词解释(每题5分,共30分)
1.义务教育
2.活动课程
3.九品中正制
4.要素教育论
5.设计教学法
6.京师同文馆
二、简答题(每题10分,共40分)
1.简述教育的政治功能。
2.简述问题解决能力的培养措施。
3.简述陶行知生活教育的主要内容。
4.简述书院教育的特点。
三、论述题(每题20分,共80分)
1.试论述需要层次理论以及对中小学教师工作的启示。
2.试论述教育过程的性质特点。
3.试论述西方教育史上的教育与生产劳动相结合主张。
4.试论述教师劳动的特点和价值。
2019年四川师范大学教育学综合614真题

2019年四川师范大学教育学综合614真题
2019年四川师范大学教育学综合614真题辨析题:
1校园中的非正式群体没有积极作用,
2中国古代书院是学术研究机构,
3奥苏贝尔的有意义学习和罗杰斯的有意义学习具有相同的内涵4定性研究和定量研究的区别只是资料性质的分析,
简答题
1.简述全面发展教育的构成
2.教育的文化功.教育观察研究的记录方法
2013年考研数学一真题与解析完整版

2013硕士研究生入学考试数学一真题及解析来源:文都教育1.已知极限0arctan limkx x xc x ®-=,其中k ,c 为常数,且0c ¹,则()A. 12,2k c ==-B. 12,2k c ==C. 13,3k c ==-D. 13,3k c ==答案(D )解析:用洛必达法则222112100011arctan 1111lim limlim lim (1)kk k k x x x x xx x x x cx kx kx x k x ---®®®®--+-+====+因此112,k c k-==,即13,3k c ==2.曲面2cos()0x xy yz x +++=在点(0,1,1)-处的切平面方程为()A. 2x y z -+=-B. 0x y z ++=C. 23x y z -+=-D. 0x y z --=答案(A )解析:法向量(0,1,1)(,,)(2sin()1,sin(),),|(1(1,,1,1)x y z n F F F x y xy x xy z y n -==-+-+=-切平面的方程是:1(0)1(1)1(1)0x y z ---++=,即2x y z -+=-。
3.设1()2f x x =-,102()sin (1,2,)n b f x n xdx n p ==ò,令1()s i n nnS x b n x p ¥==S ,则()A .34B. 14C. 14-D. 34-答案(C )解析:根据题意,将函数在[1,1]-展开成傅里叶级数(只含有正弦,不含余弦),因此将函数进行奇延拓:1||,(0,1)2()1||,(1,0)2x x f x x x ì-Îïï=íï-+Î-ïî,它的傅里叶级数为()s x ,它是以2为周期的,则当(1,1)x Î-且()f x 在x处连续时,()()s x f x =。
2019年数一考研真题及答案

2019年数一考研真题及答案2019年的数学一(数学基础)考研真题是考研考生备考的重要参考资料。
本文将为大家整理并解析2019年数学一考研真题及答案,以帮助考生更好地应对考试。
一、选择题部分1. 设函数$ f(x) $在$ x=a $处连续,则满足条件$ \lim\limits_{x \to a^-} f(x) = \lim\limits_{x \to a^+} f(x) = f(a) $的是()。
A. 可导函数B. 非单调函数C. 非奇异函数D. 周期函数正确答案:A解析:根据连续函数的定义可得,函数在$ x=a $处连续的充要条件是$ \lim\limits_{x \to a^-} f(x) = \lim\limits_{x \to a^+} f(x) = f(a) $。
故选项A为正确答案。
2. 曲面$ z = x^2 - y^2 $在点$ (1,1,0) $的切平面方程为()。
A. $ x+y=0 $B. $ x-y=0 $C. $ x+y=1 $D. $ x-y=1 $正确答案:B解析:切平面的法向量等于曲面的法向量,即$ \mathrm{n} = (2x, -2y, 1) $。
带入点$ (1,1,0) $,得到法向量$ \mathrm{n} = (2,-2,1) $,切平面方程为$ 2(x-1)-2(y-1)+0 = 0 $,化简得$ x - y = 0 $。
故选项B为正确答案。
二、填空题部分1. 线性方程组$ Ax = b $若有解,则齐次线性方程组$ Ax = 0 $必有()个线性无关的解。
正确答案:$ r $解析:线性方程组的解空间维数等于非齐次线性方程组的解空间维数减去齐次线性方程组的解空间维数。
根据线性方程组的基本定理,有$ r+m = n $,其中$ r $为非齐次线性方程组的秩,$ m $为齐次线性方程组的基础解系的维数,$ n $为未知量的个数。
所以齐次线性方程组的维数为$ m = n-r $,其有$ r $个线性无关的解。
2010-2019年(近10年)考研数学一真题
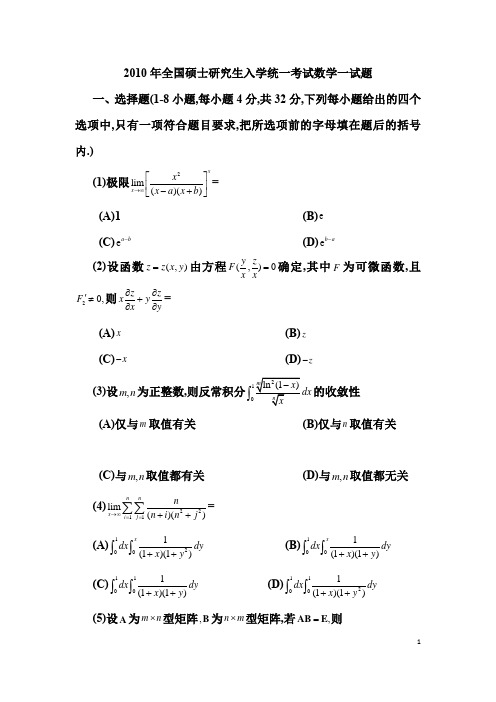
2010年全国硕士研究生入学统一考试数学一试题 一、选择题(1-8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)极限= (A)1 (B) (C)(D)(2)设函数由方程确定,其中为可微函数,且则= (A) (B) (C)(D)(3)设为正整数,则反常积分的收敛性(A)仅与取值有关 (B)仅与取值有关(C)与取值都有关 (D)与取值都无关(4)= (A)(B)(C)(D) (5)设为型矩阵为型矩阵,若则2lim ()()xx x x a x b →∞⎡⎤⎢⎥-+⎣⎦e e a b -e b a -(,)z z x y =(,)0y zF x x=F 20,F '≠z z xy x y∂∂+∂∂x z x -z -,mn 0⎰m n ,m n ,m n 2211lim ()()nnx i j nn i n j →∞==++∑∑12001(1)(1)xdx dy x y ++⎰⎰1001(1)(1)xdx dy x y ++⎰⎰11001(1)(1)dx dy x y ++⎰⎰112001(1)(1)dx dy x y ++⎰⎰A m n ⨯,B n m ⨯,=AB E(A)秩秩 (B)秩秩(C)秩秩 (D)秩秩(6)设为4阶对称矩阵,且若的秩为3,则相似于(A) (B)(C)(D) (7)设随机变量的分布函数则= (A)0(B)1(C)(D)(8)设为标准正态分布的概率密度为上均匀分布的概率密度,()f x =为概率密度,则应满足(A)(B)(C)(D)(),m =A ()m =B (),m =A ()n =B (),n =A ()m =B (),n =A ()n =B A 20,+=A A A A 1110⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭1110⎛⎫⎪⎪ ⎪- ⎪⎝⎭1110⎛⎫⎪- ⎪ ⎪- ⎪⎝⎭1110-⎛⎫⎪- ⎪ ⎪- ⎪⎝⎭X ()F x =00101,21e 2x x x x -<≤≤->{1}P X =11e 2--11e --1()f x 2,()f x [1,3]-12()()af x bf x 0x x ≤>(0,0)a b >>,a b 234a b +=324a b +=1a b +=2a b +=二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.)(9)设求= .(10)=.(11)已知曲线的方程为起点是终点是则曲线积分= .(12)设则的形心的竖坐标= .(13)设若由形成的向量空间的维数是2,则= . (14)设随机变量概率分布为则= .三、解答题(15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.) (15)(本题满分10分)求微分方程的通解.(16)(本题满分10分)20e ,ln(1),ttx y u du -==+⎰220t d ydx =2π⎰L 1{[1,1]},y x x =-∈-(1,0),-(1,0),2L xydx x dy +⎰22{(,,)|1},x y z x y z Ω=+≤≤Ωz 123(1,2,1,0),(1,1,0,2),(2,1,1,),T T T α=-==ααα123,,ααααX {}(0,1,2,),!CP X k k k ===2EX 322e x y y y x '''-+=求函数的单调区间与极值.(17)(本题满分10分)(1)比较与的大小,说明理由 (1) 记求极限(18)(本题满分10分)求幂级数的收敛域及和函数.(19)(本题满分10分)设为椭球面上的动点,若在点的切平面与面垂直,求点的轨迹并计算曲面积分其中是椭球面位于曲线上方的部分.(20)(本题满分11分)221()()e xt f x x t dt -=-⎰10ln [ln(1)]nt t dt +⎰10ln (1,2,)n t t dt n =⎰10ln [ln(1)](1,2,),n n u t t dt n =+=⎰lim .n x u →∞121(1)21n nn x n -∞=--∑P 222:1S x y z yz ++-=S P xoy P ,C ,I ∑=∑S C设已知线性方程组存在两个不同的解.(1)求(2)求方程组的通解.(21)(本题满分11分)设二次型在正交变换下的标准形为且的第三列为 (1)求(2)证明为正定矩阵,其中为3阶单位矩阵.(22)(本题满分11分) 设二维随机变量的概率密度为求常数及条件概率密度(23)(本题满分11 分)设总体的概率分布为11010,1,111a λλλ⎛⎫⎛⎫⎪ ⎪=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭A b =A x b ,.a λ=A x b 123(,,)T fx x x =A x x x y =Q 2212,y y +Q .T .A +A E E ()X Y +2222(,)e,,,x xy y f x y A x y -+-=-∞<<∞-∞<<∞A |(|).Y X f y x X其中未知,以来表示来自总体的简单随机样本(样本容量为)中等于的个数试求常数使为的无偏估计量,并求的方差.2011年全国硕士研究生入学统一考试数学一试题一、选择题:1~8小题,每小题4分,共32分,下列每题给出的四个选项中,只有一(0,1)θ∈i N X n i (1,2,3),i =123,,,a a a 31i i i T a N ==∑θT个选项符合题目要求,请将所选项前的字母填在答题纸...指定位置上. (1) 曲线234(1)(2)(3)(4)y x x x x =----的拐点是( )(A) (1,0). (B) (2,0). (C) (3,0). (D) (4,0). (2) 设数列{}n a 单调减少,lim 0n n a →∞=,1(1,2,)nn kk S an ===∑ 无界,则幂级数1(1)nn n a x ∞=-∑的收敛域为( )(A) (1,1]-. (B) [1,1)-. (C) [0,2). (D) (0,2].(3) 设函数()f x 具有二阶连续导数,且()0f x >,(0)0f '=,则函数()ln ()z f x f y =在点(0,0)处取得极小值的一个充分条件是( )(A) (0)1f >,(0)0f ''>. (B) (0)1f >,(0)0f ''<. (C) (0)1f <,(0)0f ''>. (D) (0)1f <,(0)0f ''<.(4) 设4ln sin I x dx π=⎰,40ln cot J x dx π=⎰,40ln cos K x dx π=⎰,则,,I J K 的大小关系是( )(A) I J K <<. (B) I K J <<. (C) J I K <<. (D) K J I <<.(5) 设A 为3阶矩阵,将A 的第2列加到第1列得矩阵B ,再交换B 的第2行与第3行得单位矩阵,记1100110001P ⎛⎫ ⎪= ⎪ ⎪⎝⎭,2100001010P ⎛⎫ ⎪= ⎪ ⎪⎝⎭,则A =( ) (A) 12PP . (B) 112P P -. (C) 21P P . (D) 121P P -.(6) 设1234(,,,)A αααα=是4阶矩阵,*A 为A 的伴随矩阵,若(1,0,1,0)T 是方程组0Ax =的一个基础解系,则*0A x =的基础解系可为( )(A)13,αα. (B) 12,αα. (C) 123,,ααα. (D) 234,,ααα.(7) 设1()F x ,2()F x 为两个分布函数,其相应的概率密度1()f x ,2()f x 是连续函数,则必为概率密度的是( )(A)12()()f x f x . (B)212()()f x F x .(C)12()()f x F x . (D)1221()()()()f x F x f x F x +.(8) 设随机变量X 与Y 相互独立,且()E X 与()E Y 存在,记{}max ,U X Y =,{}min ,V X Y =则()E UV =( )(A)()()E U E V ⋅. (B)()()E X E Y ⋅. (C)()()E U E Y ⋅. (D)()()E X E V ⋅.二、填空题:9~14小题,每小题4分,共24分,请将答案写在答题纸...指定位置上. (9) 曲线0tan (0)4π=≤≤⎰xy tdt x 的弧长s = .(10) 微分方程cos x y y e x -'+=满足条件(0)0y =的解为y = . (11) 设函数20sin (,)1xyt F x y dt t =+⎰,则2202x y Fx==∂=∂ .(12) 设L 是柱面方程221x y +=与平面=+z x y 的交线,从z 轴正向往z 轴负向看去为逆时针方向,则曲线积分22L y xzdx xdy dz ++=⎰ . (13) 若二次曲面的方程22232224x y z axy xz yz +++++=,经过正交变换化为221144y z +=,则a = .(14) 设二维随机变量(),X Y 服从正态分布()22,;,;0N μμσσ,则()2E XY= .三、解答题:15~23小题,共94分.请将解答写在答题纸...指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分10分)求极限110ln(1)lim()x e x x x-→+.(16)(本题满分9分)设函数(,())z f xy yg x =,其中函数f 具有二阶连续偏导数,函数()g x 可导且在1x =处取得极值(1)1g =,求211x y zx y==∂∂∂.(17)(本题满分10分)求方程arctan 0k x x -=不同实根的个数,其中k 为参数.(18)(本题满分10分)(Ⅰ)证明:对任意的正整数n ,都有111ln(1)1n n n<+<+ 成立. (Ⅱ)设111ln (1,2,)2n a n n n=+++-=,证明数列{}n a 收敛.(19)(本题满分11分)已知函数(,)f x y 具有二阶连续偏导数,且(1,)0f y =,(,1)0f x =,(,)Df x y dxdy a =⎰⎰,其中{}(,)|01,01D x y x y =≤≤≤≤,计算二重积分''(,)xyDI xy fx y dxdy =⎰⎰.(20)(本题满分11分)设向量组123(1,0,1)(0,1,1)(1,3,5)T T T ααα===,,,不能由向量组1(1,1,1)T β=,2(1,2,3)T β=,3(3,4,)T a β=线性表示.(I) 求a 的值;(II) 将123,,βββ由123,,ααα线性表示.(21)(本题满分11分)A 为三阶实对称矩阵,A 的秩为2,即()2r A =,且111100001111A -⎛⎫⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭.(I) 求A 的特征值与特征向量;(II) 求矩阵A . (22)(本题满分11分)设随机变量X 与Y且{}221P X Y ==.(I) 求二维随机变量(,)X Y 的概率分布; (II) 求Z XY =的概率分布; (III) 求X 与Y 的相关系数XY ρ.(23)(本题满分 11分) 设12,,,n X X X 为来自正态总体20(,)μσN 的简单随机样本,其中0μ已知,20σ>未知.X 和2S 分别表示样本均值和样本方差.(I) 求参数2σ的最大似然估计量2σ∧; (II) 计算2()E σ∧和2()D σ∧.2012年全国硕士研究生入学统一考试数学一试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.(1)曲线221x xy x +=-渐近线的条数为()(A )0 (B )1 (C )2 (D )3(2)设函数2()(1)(2)()x x nx f x e e e n =---,其中n 为正整数,则'(0)f = (A )1(1)(1)!n n --- (B )(1)(1)!n n -- (C )1(1)!n n -- (D )(1)!n n - (3)如果(,)f x y 在()0,0处连续,那么下列命题正确的是( ) (A )若极限00(,)limx y f x y x y→→+存在,则(,)f x y 在(0,0)处可微 (B )若极限2200(,)limx y f x y x y→→+存在,则(,)f x y 在(0,0)处可微 (C )若(,)f x y 在(0,0)处可微,则极限00(,)limx y f x y x y →→+存在 (D )若(,)f x y 在(0,0)处可微,则极限2200(,)limx y f x y x y →→+存在 (4)设2kx k eI e=⎰sin x d x (k=1,2,3),则有D(A )I 1< I 2 <I 3.(B) I 2< I 2< I 3. (C) I 1< I 3 <I 1,(D) I 1< I 2< I 3.(5)设1234123400110,1,1,1c c c c αααα-⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪===-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭其中1234,,,c c c c 为任意常数,则下列向量组线性相关的是( )(A )123,,ααα (B )124,,ααα (C )134,,ααα(D )234,,ααα(6)设A 为3阶矩阵,P 为3阶可逆矩阵,且1112P AP -⎛⎫⎪= ⎪ ⎪⎝⎭,()123,,P ααα=,()1223,,Q αααα=+则1Q AQ -=( ) (A )121⎛⎫ ⎪ ⎪ ⎪⎝⎭ (B )112⎛⎫⎪ ⎪ ⎪⎝⎭(C )212⎛⎫ ⎪ ⎪ ⎪⎝⎭ (D )221⎛⎫⎪ ⎪ ⎪⎝⎭(7)设随机变量x 与y 相互独立,且分别服从参数为1与参数为4的指数分布,则{}=<y x p ()1124()()()()5355A B C D(8)将长度为1m 的木棒随机地截成两段,则两段长度的相关系数为()1)(21)(21)(1)(--D C B A二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题..纸.指定位置上. (9)若函数)(x f 满足方程0)(2)()('''=-+x f x f x f 及x e x f x f 2)()('=+,则)(x f =________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4。 (15分 )设 c″
)0,∑
曰
`?收
敛
且
曰″,3刀
满
足
c日 仰=四
″+泸?,刀
=1,2,· `试 证 明 :∑ 智
收敛 ,
5.(15分 )设 (θ /’
=刂
£ 罟
匆 ,g(θ
ˉ =(f召 '2匆 )2,石
≥0.证 明:当
x≥
0时 ,
/、(豸 )+g(艿 )=号 ,
6口 (zO分 )设 /(冗 )在 [0,l]上连续且满足0<阴 兰/(艿 )≤ 〃 ,证 明:
专业代码:045104考试源自 目代码:四川 师 范 大 学
zO13年 攻读硕士学位研究生
入学考试试题
: 专业名称
考试科 目名称:
学科教学(数 学)
数学专业综合(含 数学分析、高等代数)
(本 试 卷共
大题
小题,满分 150
分)
说明:(1)试题和答卷分离,所有答题 内容须写在答题纸上,写 在试题或草稿纸上
的内容无效 ;
(2)答题时,可 不抄题,但 须写明所答试题序号; (3)答题时,严 禁使用红色笔或铅笔答题。
1(10分 )计算∫濠 寸抵. (
2(10分 )设 /(x,ヵ =
;2+y2≠ 0
2+y2=0 ,证 明:/(x,力 在(0,0)点 连续但不
可微 ,
3.(1θ 分 )设 “/,/)满 足 争 +争 =09证 明zr圪 D=笏 (艿 2~y2,2V)满 足
l/’(豸 )珈 刂诗沙Γ‰笋
Γ
︱
︱
ˉ︱
︱
︱
︱
︱ ︱
7.(10分)设 /fx,是 数域 P上 的 ″次多项式 ,试给 出尸⑴ |r⑺ 的充分必要条件,
l xI x氵
Xf
l
豸2
艿 :
·‘2
8口 (15分 )计 算行列式 l jr3 x:
jrf
1 犭J9 石;
9.(15分 ) 设 /是 刀级矩阵,且 /2刮 ,证 明 mnk“ -E″ J+rank⒄ )=刀 °
10.(15分 )设 /是 刀级实矩阵,证 明 /的特征值全为实数的充分必要条件是存 在正交矩阵 r,使 得 「I/Γ 为三角阵。
11.(15分 ) 已知 /是 P上 的 刀维线性空间,r是 /上 的线性变换,且
证 明 TV0kerT=V。
