结构力学第三章习题及答案
结构力学 朱慈勉 第3章课后答案全解
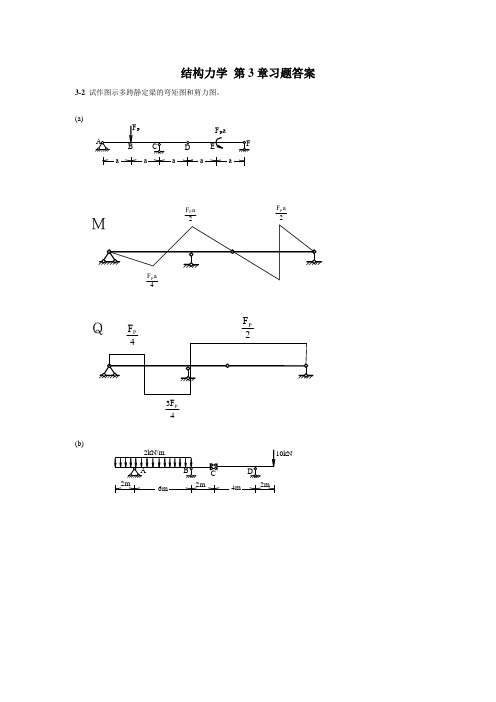
结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aa aaa2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
lx l lx28ql M2221()222116121618c B C BC C q ql M l x x qx xM M M M ql ql x ql x l=-+===∴=∴=∴=中F D()2ql x -3-6 试作图示刚架的弯矩和剪力图。
(a)9090405M2B 209(4.53)645()0.5209459405,135()453135,0.5209900.520990F F E E CF CD BA R R M R M M M ⨯⨯-=⨯∴=↑=⨯⨯-⨯==↑=⨯==⨯⨯==⨯⨯=对点求矩14.25424213.5 1.50.2525.75A 72425 2.50.5()C 420.524 4.25()3.5(),0.25()5.752.1,24 4.253.752.5E K B B B B A A EF K M M R R H H V H Q Q =⨯-⨯⨯==⨯+⨯=⨯+⨯⨯=⨯→=-↓⨯⨯+⨯=⨯→=→∴=↑=←===⨯-=左对点求矩:对点求矩:2 2.1(c)80/3Q8080380,61603330():(2023304)/2120():61201030420211320()380()3DA ED C C B B A M M H F V A V V V =⨯==⨯==←=⨯⨯+⨯=↑⨯+⨯=⨯+⨯⨯∴=-↓∴=↑对点求矩对点求矩(d)8/34/388414233:41614284()4:441426()38(),03DAB BB BA AMA V VC H HH V=⨯-⨯⨯=⨯⨯+⨯⨯=⨯→=↑⨯-⨯⨯=⨯→=←∴=←=对点求矩对点求矩(e)2FaF2Fa2FaF F F2F----+2Fa2Fa2FaM Q02(),020322222(),2()4(),0C B p E B FB P H P FH P F PD P DM V F M H VM F a a H F a V aH F V FH F V=→=↑=→==→⨯+⨯=⨯+⨯∴=←=↓∴=→=∑∑∑(f)进一步简化BHIH8:4(),4()4(),4(),42810B BI I AH KN V KNH KN V KN M N m=→=↓=-←=-↑=⨯=•可知84 (g)2aqa22221.5()21.50 1.5()0,, 1.5C CA AGF GHHqaqa H a H qaqa a H a H qaH M qa M qa+=⨯→=→⨯+⨯=→=-←===对点求矩:对F点求矩:。
结构力学 第三章 作业参考答案

B
M图(kN m)
(1) (2)
解: (1)求支座反力
∑M = 0 ∑F = 0
A y
取左边或者右边为隔离体,可得:
∑M ∑F
x
C
=0
⇒ FBx =
M h
(3) (4)
=0
最后容易做出结构的弯矩图。
3—18 试作图示刚架的 M 图。
C 0.8kN/m 0.5kN/m D E
14.625 4.225 12.8375
3—19 试作图示刚架的 M 图。
20kN
24 16
C
24
16
B FAx A FBy FAy
FBx
1m
2m
2m
2m
M图(kN m)
(1) (2) (3)
解:对整体:
∑M ∑F
y
A
=0
FBy × 4 + FBx ×1 = 20 × 2 FAy + FBy = 20 FAx − FBx = 0 FBx × 2 − FBy × 2 = 0
40kN m
10kN m M图(kN m)
32.5kN
20kN
20kN F(kN) S
解:求支座反力。取整体:
47.5kN
∑M ∑F
A
=0
FB × 8 − 20 ×10 − 10 ×10 × 3 − 40 = 0 FAy + FB − 10 ×10 − 20 = 0
然后即可做出弯矩图,利用弯矩图即可作出剪力图。
然后即可做出整个刚架的弯矩图。结点受力校核如下图。
D
qL 4 qL 2 qL 2
qL 4
qL 4
E
qL 2 qL 2
结构力学(王焕定第三版)教材习题第三章答案全解——哈工大老师提供
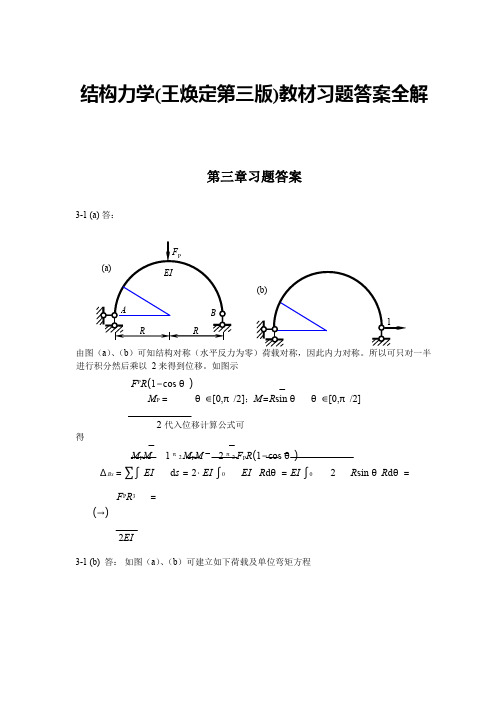
结构力学(王焕定第三版)教材习题答案全解第三章习题答案3-1 (a) 答:由图(a )、(b )可知结构对称(水平反力为零)荷载对称,因此内力对称。
所以可只对一半进行积分然后乘以 2 来得到位移。
如图示F P R (1−cos θ)M P = θ∈[0,π/2];M =R sin θ θ∈[0,π/2]2 代入位移计算公式可得M P M1 π2 M P M2 π2 F P R (1−cos θ)∆Bx = ∑∫ EId s = 2⋅ EI ∫0EI R d θ= EI ∫02 R sin θR d θ=F P R 3 =(→)2EI3-1 (b) 答: 如图(a )、(b )可建立如下荷载及单位弯矩方程EIBARRF P( a )1pR ∆Bx =∑∫ MEIM d s =∫0π2 MEI P M R d θ= q EI 4∫0π2(1−2cos θ+cos 2 θ)R d θqR 4 ⎡ θ 1⎤3π⎞ qR 4= EI ×⎢θ−2sin θ+ 2 + 4sin2θ⎥⎦0 =⎝⎜ 4 − 2⎠⎟ 2EI (→)2 ⎣3-2 答:作M P 图和单位力弯矩图如下图: 由此可得内力方程根据题意EI (x ) = EI (l + x )代入位移公式积分可得 2 2 P 0s i n ( ) d (1 c o s ) (1 c o s ) q M R q R M R θθ α α θθ − = = − = − ∫AqRBα θ1( a ) θ( b )ABlq 03 0 p 6 x q M M xl = = xP M 图2 0 6q l1lM 图 x5 83 82l 代入位移公式并积分(查积分表)可得M P M l 2 q0x4∆Bx =∑∫ EI d x =∫0 6EI(l + x) d x7q0l40.07 ql4= (ln 2−)× = (→)123EI EI3-3 答:分别作出荷载引起的轴力和单位力引起的轴力如下图所示:由此可得C 点的竖向为移为:F NP F N1F NP F N1 ∆Cy =∑∫EA d s=∑ EA l =65112.5 kN× ×6 m+2×(62.5 kN× ×5 m+125 kN× ×5 m+75 kN× ×6 m)= 88EA=8.485×10−4 m当求CD 和CE 杆之间的夹角改变使:施加如图所示单位广义力并求作出F N2 图,则F∆=∑∫ F NP EA F N2 ds =∑ NP EAF N2 l2×62.5 kN ×(−0.15)×5 m +(−112.5 kN)×0.25×6 m =EA=−1.4×10−4 rad( 夹角减小)3-4 (a)答:先作出M p和M 如右图所示。
结构力学下册第三章(部分)

D MB B
Me y1
FBx
AC 段:
FBy
M (x)
=
FA x
−
MA
=
⎜⎛ ⎝
F0
+
Me
+
MA 2a
+
MB
⎟⎞x ⎠
−
MA
∂M (x) = x ∂F0
∂M (x) = x −1 ∂M A 2a
∂M (x) = x ∂M B 2a
BD 段: M ( y1 ) = FBx y1 + M B = F0 y1 + M B
∫ ∫ (b)非线性杆的应变能密度
vε
=
σdε
ε
=
Bε 1 2dε
ε
= 2 Bε 3 2 3
ΔAy
D
G ΔAx
相应的应变能表达式
∫ Vε
=
V vε dV
=
2 Bε 3 2 Al = 3
2BAl ⎜⎛ ε l ⎟⎞3 2 3 ⎝l⎠
=
2BAl ⎜⎛ Δl ⎟⎞3 2 3 ⎝l⎠
杆的变形和节点位移间的关系与(a)情况相同,故结构的应变能
Δ Ay
− Δ Axctg30°
sin 30° =
Δ Ay 2
−
3Δ Ax 2
∑ Vε =
应变能:
EA 2li
(Δli
)2
=
EA 2(2a)
⎜⎜⎝⎛
Δ Ay 2
−
3 2
Δ Ax
⎟⎟⎠⎞ 2
+
EA 2( 3a)
Δ2Ax
[( ) ] = EA 48a
9+6
3 Δ2Ax − 6
结构力学第三章习题参考解答

FAy 6 FAx 2 0
1 ql 2A
1 ql 4
取整体:M A 0
Fy 0
取AC: MC 0
取整体: Fx 0
l
l
0.45ql
FBy
1 2l
ql 3l 2
3 ql 4
FAy
ql
3 4
ql
1 4
ql
FAx
2 ql 2 l4
1 ql 2
FBx
1 ql 2
l 2
1 ql B2 3 ql 4
取左段
FNK
ql cos
3l 4
1 q 3 l 2 2 4
9 ql 2 32
D
C
q
3 ql
4
A
1 ql
l
4
1 ql
4
1 ql 4
3 ql
4
FQ KN
1 ql 2
E
4
1 ql 2 4
9 ql2 32
1 ql
B
4
ql 2 8
M KNm
l
1 ql
4
1 ql
4
1 ql
4
FN KN
1 ql2 4
1 ql 4
3-12解:
q C
q
3 ql
4
A
l
1 ql
B
4
Fy 0
FAy
1 ql 4
1 ql 4
l
l
1 ql
4
取BC:
MC 0
FBx
1 4
ql
取整体:
Fx 0
FAx
ql
1 ql 4
3 ql 4
AD段的最大弯矩 M x 3 qlx 1 qx2 dM 3 ql qx 0
结构力学第三章习题及答案
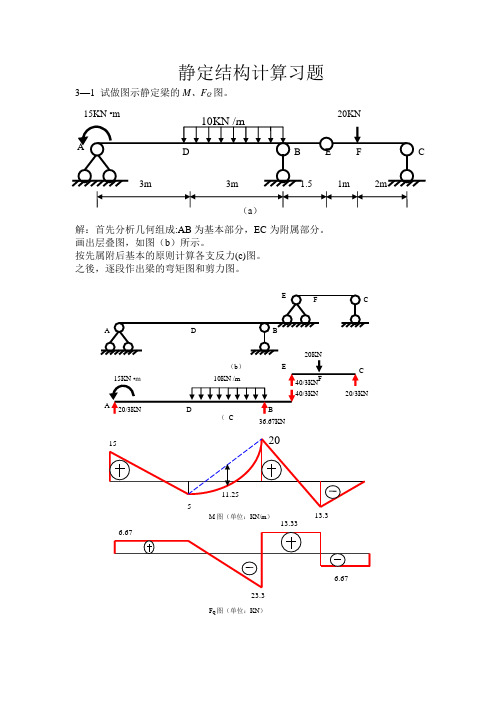
静定结构计算习题3—1 试做图示静定梁的M 、F Q 图。
解:首先分析几何组成:AB 为基本部分,EC 为附属部分。
画出层叠图,如图(b )所示。
按先属附后基本的原则计算各支反力(c)图。
之後,逐段作出梁的弯矩图和剪力图。
36.67KN15KN •m 20KNM 图(单位:KN/m )13.323.313.33F Q 图(单位:KN )3—3 试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力F AX =48kN (→) M A =60 KN •m (右侧受拉) (2)逐杆绘M 图 (3)绘F Q 图 (4)绘N 图(5)校核: 内力图作出后应进行校核。
(略)3—7 试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力F AX =20kN (←) F AY =38kN(↑) F BY =62kN(↑) (2)逐杆绘M 图BCM 图(单位:KN/m ) F Q 图(单位:KN )3030F AX F N图(单位:60)20)(3)绘F Q 图 (4)绘N 图(5)校核: 内力图作出后应进行校核。
(略)3—9 试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力F AX =0.75qL (←) F AY =-0.25qL( ) F BY =0.25qL(↑) (2)逐杆绘M 图 (3)绘F Q 图 (4)绘N 图(5)校核: 内力图作出后应进行校核。
(略)3—11试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力F BX =40KN (←) F AY =30KN (↑) F BY =50kN(↑) (2)逐杆绘M 图 (3)绘F Q 图 (4)绘N 图(5)校核: 内力图作出后应进行校核。
(略)C(a )qBY 23—17 试求图示抛物线三铰拱的支座反力,并求截面D 和E 的内力。
(完整版)西北工业大学航空学院结构力学课后题答案第三章静定结构的内力与变形
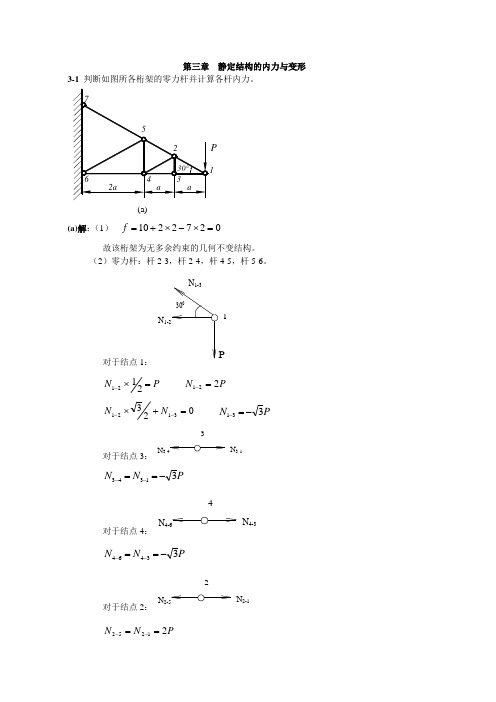
第三章 静定结构的内力与变形3-1 判断如图所各桁架的零力杆并计算各杆内力。
1P(a) (a)解:(1)0272210=⨯-⨯+=f故该桁架为无多余约束的几何不变结构。
(2)零力杆:杆2-3,杆2-4,杆4-5,杆5-6。
对于结点1:N 1-2PN 1-33001P N =⨯-2121 P N 221=-0233121=+⨯--N N P N 331-=-对于结点3:N 3-43N 3-1P N N 31343-==--对于结点4:N 4-64N 4-3P N N 33464-==--对于结点2:N 2-52N 2-1PN N 21252==--对于结点5:N 5-75N 5-2P N N 22575==--(b)(b)解:(1)082313=⨯-+=f故该桁架为无多余约束的几何不变结构。
(2)零力杆:杆1-2,杆2-3,杆2-4,杆5-4,杆6-4,杆6-7,杆6-8,杆1-5。
对于结点5:P5N 5-8P N -=-85对于结点8:N 7-88N 5-8Fθ05528785=+⨯--N N P N 55287=-对于结点7:N 7-47N 7-8P N 55247=-对于结点4:N 3-44N 7-4P N N 5524743==--对于结点3:N 1-33N 3-4P N N 5524331==--2(c)(c)解:(1)026228=⨯-⨯+=f故该桁架为无多余约束的几何不变结构。
(2)零力杆:杆1-2,杆2-3,杆2-4,杆4-3,杆4-6。
对于结点1:N 1-61N 1-3Pθ05561=+⨯-P N P N 561-=-05526131=⨯+--N N P N 231=-对于结点3:3N 3-1N 3-5P N N 21353==--(e)(d)解:(1)02112316=⨯-⨯+=f故该结构为无多余约束的几何不变结构。
(2)零力杆:杆4-5,杆5-6,杆4-6,杆7-6,杆2-3,杆2-8,杆2-9,杆1-2,杆9-11,杆8-9,杆9-11.对于结点4:4N 4-7N 3-4450PP N 2243=- P N 2274=-对于结点7:7N 4-7N 3-7N 8-7P N N 22227374=⨯-=-- P N -=-73P N 2278=-对于结点3:3N 3-4N 3-7N 8-7022734332=⨯+=---N N N P N 2283=-对于结点8:022228982=⨯⎪⎭⎫ ⎝⎛+=--N P N运用截面法:N 1-2N 9-10N 9-11PP23456789由对9点的力矩平衡:0222221=⨯⨯-⨯+⨯-P a P a a N 021=-N对于结点9:9N 2-9N 9-11N 9-10N 9-88911910922---=⨯+N N N P N 22109-=-8N 3-8(e)(e)解:(1)024125=⨯-++=f故该结构为无多余约束的几何不变结构。
结构力学章节习题及参考答案

习题2.1(6)图
习题2.2填空
(1)习题2.2(1)图所示体系为_________体系。
习题2.2(1)图
(2)习题2.2(2)图所示体系为__________体系。
习题2-2(2)图
习题2.2(5)图
(6)习题2.2(6)图所示体系为_________体系,有_________个多余约束。
习题2.2(6)图
(7)习题2.2(7)图所示体系为_________体系,有_________个多余约束。
习题2.2(7)图
习题2.3对习题2.3图所示各体系进行几何组成分析。
习题2.3图
第3章静定梁与静定刚架习题解答
习题7.2(4)图
习题9.3用力矩分配法计算习题7.3图所示连续梁,作弯矩图和剪力图,并求支座B的反力。
(1)(2)
习题7.3图
习题9.4用力矩分配法计算习题7.4图所示连续梁,作弯矩图。
(1)(2)
习题7.4图
习题9.5用力矩分配法计算习题7.5图所示刚架,作弯矩图。
(1)(2)
习题7.5图
第11章影响线及其应用习题解答
习题11.1是非判断题
(1)习题8.1(1)图示结构BC杆轴力的影响线应画在BC杆上。( )
习题8.1(1)图习题8.1(2)图
(2)习题8.1(2)图示梁的MC影响线、FQC影响线的形状如图(a)、(b)所示。
(3)习题8.1(3)图示结构,利用MC影响线求固定荷载FP1、FP2、FP3作用下MC的值,可用它们的合力FR来代替,即MC=FP1y1+FP2y2+FP3y3=FR 。( )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
静定结构计算习题
3—1 试做图示静定梁的M 、F Q 图。
解:首先分析几何组成:AB 为基本部分,EC 为附属部分。
画出层叠图,如图(b )所示。
按先属附后基本的原则计算各支反力(c)图。
之後,逐段作出梁的弯矩图和剪力图。
36.67KN
15KN •m 20KN
M 图(单位:KN/m )
13.3
23.3
13.33
F Q 图(单位:KN )
3—3 试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力
F AX =48kN (→) M A =60 KN •m (右侧受拉) (2)逐杆绘M 图 (3)绘F Q 图 (4)绘N 图
(5)校核: 内力图作出后应进行校核。
(略)
3—7 试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力
F AX =20kN (←) F AY =38kN(↑) F BY =62kN(↑) (2)逐杆绘M 图
B
C
M 图(单位:KN/m ) F Q 图(单位:KN )
30
30
F AX F N
图(单位:
60
)
20
)
(3)绘F Q 图 (4)绘N 图
(5)校核: 内力图作出后应进行校核。
(略)
3—9 试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力
F AX =0.75qL (←) F AY =-0.25qL( ) F BY =0.25qL(↑) (2)逐杆绘M 图 (3)绘F Q 图 (4)绘N 图
(5)校核: 内力图作出后应进行校核。
(略)
3—11试做图示静定刚架的内力(M 、F Q 、F N )图,并校核所得结果。
解:(1)计算支反力
F BX =40KN (←) F AY =30KN (↑) F BY =50kN(↑) (2)逐杆绘M 图 (3)绘F Q 图 (4)绘N 图
(5)校核: 内力图作出后应进行校核。
(略)
C
(a )
q
BY 2
3—17 试求图示抛物线三铰拱的支座反力,并求截面D 和E 的内力。
解:1、由已知设抛物线方程为y=ax 2
+bx+c
坐标系如图(a )所示,有图可以看出, x=0 y=0;x=10 y=4;x=20 y=0 可以求得
B
C
D
E
100K
5m
5m
5m
5m
20KN/m
4m
Y
X
(a)
40KN
m
y y m x x y x x y D D D 34.0'554252'542512===+
-=+-=20KN/m
A B
C
D
E
F
4m
2m
2m
2m 80
80
120
120
80
M 图(单位:KN/m )
30
50
40
40
F Q 图(单位:KN )
40
50
F N 图(单位:KN )
2、计算支反力
首先,考虑三铰拱的整体平衡。
由 ∑MB=0 及∑MA=0 得F AY =F BY =100KN 由 ∑X=0 可得 H AX =H BX =F H
取左半拱为隔离体,由∑MC=0 H AX =H BX =F H =125KN 3、
4、求D 、E 点的内力
3—18 试用节点法计算图示桁架中各杆的内力。
解:(1)首先由桁架的整体平衡条件求出支反力。
(2)截取各结点解算杆件内力。
m
y y m
x E E E 34.0'15=-==928
.0cos 371.0sin ==D D ϕϕ928
.0cos 371.0sin =-=E E ϕϕKN 1000=左QD F KN 00=右QD F KN
500E -=Q F KN
5005100M 0D =⨯=KN
3755.25101010015100M 0
E
=⨯⨯-⨯-⨯=KN y F M D H D 1253125-500*M 0D =⨯=-=KN F F F D H D QD QD 4.46sin cos 0=-=ϕϕ左左KN y F M E H E 03125-375*M 0
E =⨯=-=KN
F F F D H D QD QD
4.46sin cos 0-=-=ϕϕ右右KN F F F D H D QD D 1.153cos sin 0N =+=ϕϕ左左116cos sin 0N =+=D H D QD D F F F ϕϕ右右KN F F F E H Q Q 0sin cos E 0E E =-=ϕϕKN
F F F H E Q 6.134cos sin E 0E NE =+=ϕϕ
F N78=
F N81=-5
F N12N81
F X17
分析桁架的几何组成:此桁架为简单桁架,由基本三角形345按二元体规则依次装入新结点构成。
由最后装入的结点8开始计算。
(或由8结点开始)
然后依次取结点7、2、6、3计算。
到结点5时,只有一个未知力F N54,最后到结点4时,轴力均已求出,故以此二结点的平衡条件进行校核。
3—19 试用截面法求3—18中杆23、62、67的内力。
解:支反力已求出。
作截面Ⅰ-Ⅰ,取左部分为隔离体。
由06=∑M 得
031545.22432=⨯+⨯-⨯-N F 得 F N32=-11.25KN
同理由02=∑M 得 得 F N67=3.75KN
把F N62 沿力的作用线平移到2点,并分解为水平力F X62和竖向力F Y62 由0=∑X F 0=∑Y F 得F X62=7.5KN F Y62=10KN
F 4X F 5X 5kN 5kN 5kN
F 4X F 5X
Y62。
