北京大学2012年保送生考试数学试题解析

合集下载

2012年全国普通高等学校招生统一考试理科数学(北京卷带解析

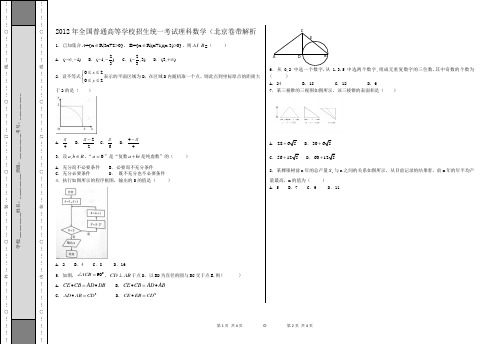
第1页共4页 ◎ 第2页共4页2012年全国普通高等学校招生统一考试理科数学（北京卷带解析1．已知集合={x R|3x+2>0}A ∈，B={x R|(x+1)(x-3)>0}∈，则A B =（） A ．(,1)-∞- B ．2(1,)3-- C ．2(,3)3-D ．(3,)+∞ 2．设不等式0202x y ≤≤⎧⎨≤≤⎩表示的平面区域为D ，在区域D 内随机取一个点，则此点到坐标原点的距离大于2的是（）A ．4π B．22π- C ．6π D ．44π- 3．设,a b R∈，“0a =”是“复数a bi +是纯虚数”的（） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 4．执行如图所示的程序框图，输出的S 的值是（）A ．2B ．4C ．8D ．165．如图，090ACB ∠=，CD AB ⊥于点D ，以BD 为直径的圆与BC 交于点E.则( )A. CE CB AD DB ∙=∙B. CE CB AD AB ∙=∙C. 2AD AB CD ∙= D. 2CE EB CD ∙=6．从0,2中选一个数字.从 1.3.5中选两个数字,组成无重复数字的三位数.其中奇数的个数为( )A. 24B. 18C. 12D. 67．某三棱锥的三视图如图所示，该三棱锥的表面积是（）A ．28+．30+ C ．56+．60+8．某棵果树前n 年的总产量n S 与n 之间的关系如图所示，从目前记录的结果看，前m 年的年平均产量最高，m 的值为（）A ．5B ．7C ．9D ．11A DBCE第3页共4页◎第4页共4页第II卷（非选择题）请点击修改第II卷的文字说明二、填空题（题型注释）9．直线21x ty t=+⎧⎨=--⎩(t为参数)与曲线3cos3sinxyαα=⎧⎨=⎩(“为多α数)的交点个数为10．已知{}na为等差数列，nS为其前n项和，若112a=，23S a=，则2a=nS=11．在△ABC中，若2,7a b c=+=,1cos4B=-，则b=12．在直角坐标系xOy中.直线l过抛物线=4x的焦点F.且与该抛物线相交于A、B两点.其中点A在x轴上方。

2012年北京大学保送生数学试题及解答

1．已知数列{}n a 为正项等比数列，且34125a a a a +--=，求56a a +的最小值．2．已知()f x 为二次函数，且()()()()()(),,,a f a ff a f f f a 成正项等比数列，求证：()f a a =．3．称四个顶点都落在三角形三边上的正方形叫三角形的内接正方形．若锐角三角形ABC 的三边满足a b c >>，证明：这个三角形的内接正方形边长的最小值为sin sin ac Ba c B+．4．从O 点发出两条射线12,l l ，已知直线l 交12,l l 于,A B 两点，且OAB S c ∆=（c 为定值），记AB 中点为X ，求证：X 的轨迹为双曲线．5．已知()1,2,,10i a i =满足1210121030,21a a a a a a +++=<，求证：()1,2,,10i a i ∃=，使1i a <．X参考解答2．已知数列{}n a 为正项等比数列，且34125a a a a +--=，求56a a +的最小值．解：设数列{}n a 的公比为()0q q >，则231115a q a q a a q +--=，12351a q q q ∴=+--()251(1)q q =+-．由10a >知1q >．()454556111a a a q a q a q q ∴+=+=+()()44225511(1)1q q q q q q =⋅+=+-- 222211515122011q q q q ⎛⎫⎛⎫=++=-++≥ ⎪ ⎪--⎝⎭⎝⎭，当且仅当22111q q -=-即q =56a a +有最小值20． 2．已知()f x 为二次函数，且()()()()()(),,,a f a ff a f f f a 成正项等比数列，求证：()f a a =．证法一：设()()20f x mx nx t m =++≠，数列()()()()()(),,,a f a ff a f f f a 的公比为()0q q >，则()()()()()()()()223,,f a aq ff a f aq aq f f f a f aq aq=====，2ma na t aq∴++=①22()m aq naq t aq ++=②2223()m aq naq t aq ++=③①-②得()()()22111ma q na q aq q ∴-+-=-， ②-③得()()()2222111ma q qnaq q aq q ∴-+-=-．若1q =，则()f a a =；若1q ≠，则()21ma q na aq++=与()21ma q q na aq ++=矛盾．()f a a ∴=．证法二：由()()()()()(),,,a f a f f a f f f a 成等比数列得()()()()()()()()()f f f a f f a f a a f a f f a ==， ()()()()()()()()()()()()f f f a f f a f f a f a f a af f a f a --∴=--．∴三点()()()()()()()()()()()(),,,,,A a f a B f a f a Cf a f a 满足ABBC kk =，,,A B C ∴三点共线，与,,A B C 三点在抛物线上矛盾，()f a a ∴=．3．称四个顶点都落在三角形三边上的正方形叫三角形的内接正方形．若锐角三角形ABC 的三边满足a b c >>，证明：这个三角形的内接正方形边长的最小值为sin sin ac Ba c B+．解：如图所示，设正方形MNPQ 的边长为x ，AE MNAD BC=， sin sin c B x x c B a -∴=，sin sin 2ac B abcx a c B Ra bc∴==++．同理可得其它两用人才种情况下内接正方形边长为,22abc abcRb ac Rc ab++． ()()()2220Rb ac Ra bc b a R c +-+=--<，()()()2220Rc ab Ra bc c a R b +-+=--<，∴这个三角形的内接正方形边长的最小值为sin sin ac Ba c B+．4．从O 点发出两条射线12,l l ，已知直线l 交12,l l 于,A B 两点，且OAB S c ∆=（c 为定值），记AB 中点为X ，求证：X 的轨迹为双曲线．解：以12,l l 的角平分线所在直线为x 设AOx BOx α∠=∠=，,OA a OB b ==，(),X x y 则1sin 22OAB S ab c α∆==，2sin 2c ab α=．()()cos ,sin ,cos ,sin A a a B b b αααα-，cos cos ,2sin sin ,2a b x a b y αααα+⎧=⎪⎪∴⎨-⎪=⎪⎩cos 2(2)sin 2xa b y a b αα+⎧=⎪⎪∴⎨-⎪=⎪⎩22(1)(2)-得D Q EPNMCBAX22222cos sin sin 2x y cab ααα-==，∴X 的轨迹为双曲线． 5．已知()1,2,,10i a i =满足1210121030,21a a a a a a +++=<，求证：()1,2,,10i a i ∃=，使1i a <．证明：用反证法，假设()1,2,,10i a i ∀=， 1i a ≥．令()11,2,,10i i a b i =+=，则0i b ≥，且121020b b b +++=．()()()12101210111a a a b b b ∴=+++121012231b b b b b b b =+++++++12232121b b b b =+++≥与121021a a a <矛盾，()1,2,,10i a i ∴∃=，使1i a <．。

2012年保送生招录考试数学试题参考答案

2 0 1 2 年保送生招录考试数学试题参考答案及评分说明说明：1．如果考生的解答正确，思路与本参考答案不同，可参照本评分说明制定相应的评分细则评分． 2．每题都要评阅完毕，不要因为考生的解答中出现错误而中断对该题的评阅．当考生的解答在某一步出现错误，影响了后继部分时，如果该步以后的解答未改变这道题的内容和难度，则可视影响的程度决定后面部分的给分，但不得超过后面部分应给分数的一半；如果这一步以后的解答有较严重的错误，就不给分．3．为阅卷方便，解答题的解题步骤写得较为详细，但允许考生在解答过程中，合理地省略非关键性的步骤．4．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 5．每题评分时只给整数分数．一．精心选一选（每小题3分，本大题满分24分）题号1 2 3 4 5 6 7 8 答案A D CBCD B C二．细心填一填（每小题3分，本大题满分24分）9．14 10．－21 11．48% 12．1413．15° 14． 3 15． x ＞－671216．2三．专心解一解（本大题满分72分） 17．解：加减消去x 得，(2a －b )y =2a －3∵2a －b ≠0， ∴y = 2a －3 2a －b ，代入求得x = 6－2b2a －b.∴方程组的解为 ·········································································· 4分由已知得即或 ·························· 8分由a 、b 均为不超过4的正整数可得或 ··················· 10分18．解：（1）图中相等线段有BE =EA =EC ，DE =DA ．证明：Rt △CED 中，∵∠CDE =60° ∴∠ECD =30°，∴DE = 12 CD =DA ．∴∠DAE =∠DEA=∠ECD =30°，∴EC =EA ．又∵∠BAC =45°，∠BDC =60°，∠DAE =30°，∴∠DBA =∠EAB =15°． ∴BE =EA =EC ． ············································································································· 4分（2）△ADE ∽△AEC ，△ABC ∽△BDC .证明：在△ADE 与△AEC 中，∠DAE =∠CAE ，∠AED =∠ACE ． ∴△ADE ∽△AEC . ······································································································ 6分 Rt △CEB 中，∵BE = EC ，∴∠EBC =∠ECB =45°，又∵∠DBA =15°，∴∠ABC =∠BDC =60°.在△ABC 与△BDC 中，∠ABC =∠BDC ，∠ACB =∠BCD ∴△ABC ∽△BDC . ······································································································ 8分（3）过点A 作AF ⊥BD 交BD 的延长线于点F ，∵S △CEB =12 BE ·CE ，S △BEA =12BE ·AF ，∴S △BEC ∶S △BEA = CE ∶AF ．∵CE ∶AF =CD ∶DA =2：1 ， ∴S △BEC ∶S △BEA =2：1 ·········································· 12分19．解：（1）证明：在△ABC 中，∠CAB =∠CBA ，在△EDC 中，∠CDE =∠E ，∵∠CAB =∠CDB ，∠CDE =∠CBA ，∴∠CDB =∠E . 又∵∠CAE =∠CBD ，AC =BC ∴△CAE ≌△CBD ，∴AE =BD . ··································································· 6分（说明：用其他方法证明△CAE ≌△CBD 可比照给分）（2）若AC ⊥BC ，∵△CAE ≌△CBD ，∴∠ACB =∠ECD =90°，∴∠CDE =∠CED =45°，∴DE = 2 CD 又∵AD ＋BD = AD ＋EA =DE ，∴AD ＋BD = 2 CD ···················································· 12分20．解：（1）△ABC 是直角三角形.∵a 、b 、是关于x 的方程x 2－(4＋c )x ＋4c ＋8 =0的两个实数根， ∴a ＋b = 4＋c ，ab =4c ＋8.∵a 2＋b 2 =(a ＋b )2－2ab =(4＋c )2－2(4c ＋8)= c 2. 即a 2＋b 2 = c 2，∵a 、b 、c 是△ABC 的三边， ∴△ABC 是直角三角形. ····························································································· 6分（2）∵25a ·sin A =9c ，Rt △ABC 中，sin A = ac∴25a ·a c =9c ，∴a c = 35y = 2a －3 2a －b . x = 6－2b2a －b， 2a －3 2a －b ＞0.6－2b2a －b ＞0， 2a －b ＞0， a ＞32 ， b ＜3. 2a －b ＜0， a ＜32 ， b ＞3.a = 2，3，4，b = 1，2， a = 1， b = 4. C ABE D C AD B OE （第19题）设a =3k ，c =5k ，则b =c 2－a 2 =25k 2－9k 2 =4k .将a =3k ，b =4k ，c =5k 代入a ＋b =4＋c 得3k ＋4k =4＋5k 可得k =2∴a =6，b =8，c =10. ···································································································· 12分 21．解：（1）∵OC =3OB ，点B 的坐标为(1，0)，∴点C 的坐标为(0，－3).把B 、C 两点的坐标代入y =ax 2＋3ax ＋c 可求得a = 34，c =－3，∴抛物线的解析式为y =34 x 2＋94x －3 ·········································································· 3分（2）由34 x 2＋94x －3=0解得x 1=－4，x 1=1，∵点A 在点B 的左侧，∴点A 的坐标为(－4，0)连接DB （如图1），则S 四边形ABCD =S △AOD ＋S △COD ＋S △COB∵点D 是线段AC 下方抛物线上的动点，设点D 的坐标为（x ，34 x 2＋94x －3）则x ＜0，且34 x 2＋94 x －3＜0，∴S △AOD = 12 OA ·|34 x 2＋94 x －3|=－32 x 2－92x ＋6， S △COD = 12 OC ·|x |=－32 x ，S △COB = 12 OC ·OB =32， ∴S 四边形ABCD =－32 x 2－92 x ＋6－32 x ＋32 =－32 ( x ＋2) 2＋272，∴当x =－2时，四边形ABCD 的面积有最大值272····················································· 7分（3）①如图2，当CP 是平行四边形的一边即CP ∥AE 时，点P 与点C 关于抛物线的对称轴x =－2对称，点P 的横坐标为x = －3，把x = －3 代入y =34 x 2＋94x －3 可求得y =－3∴此时点P 坐标为(－3，－3). ··················································································· 9分 ②如图3、图4当CP 是平行四边形的对角线即PE ∥AC 时，点P 、C 到x 轴距离相等.即点P 的纵坐标为y = 3，把y = 3代入y =34 x 2＋94x －3 可求得x 1 = －3－41 2 ，x 2= －3＋41 2.此时点P 坐标为(－3－412， 3)（如图3）或(－3＋41 2 ， 3)（如图4） ··············································································· 12分22．解：设这些数中，﹣1的个数x 个，0的个数y 个，1的个数z 个，2的个数w 个. 则已知的两个等式可化为即 ①＋②得z ＋3w =1056 ③，则w = 1056－z 3，∴0≤w ≤352，且w 是整数. ······················································· 4分设a 15＋a 25＋…＋a 20125=A ，则A =(﹣1)5·x ＋05·y ＋15·z ＋25·w =﹣x ＋z ＋32w =100﹣2 w ＋32w =100＋30w . ∵0≤w ≤352，∴100≤A ≤10560.∴A 的最小值为100，最大值为10560. ······································································ 8分当A 取得最小值100时，w =0，由①，②可求得x =956，z =1056，进而可求得y =0. ∴当A 取得最小值时，﹣1的个数956，0的个数是0，1的个数是1056，2的个数是0. ······················· 11分当A 取得最大值10560时，w =352，由①，②可求得x =604，z =0，进而可求得y =1056. ∴当A 取得最小值时，﹣1的个数是604，0的个数是1056，1的个数是0，2的个数是352. ·················· 14分D x （图1） B C y A Ox x （图2） B C y A O P E （图3） B C y A O E x （图4） B C yA O P E P﹣1·x ＋0·y ＋1·z ＋2·w =100， (﹣1)2·x ＋02·y ＋12·z ＋22·w =2012.﹣x ＋z ＋2w =100，① x ＋z ＋4w =2012. ②。

北大真题集

北约”的数学题型为5道解答题，各20分，总分为100分，内容上每年都会考一到两题的平面几何，这个知识点是上海学生在初中就学过的，但在全国高考中是作为考核内容的。

此外，三角形和解析几何等也都是“北约”每年的考核重点，难度略高于本市实验性示范性高中平时做的题目。

“2012年“北约”自主招生选拔联合考试数学真题及答案北大联合自招，基本题型包括在阅读文本中选择正确或最好的表达形式、文言综合阅读、现代文学作品阅读、写作等几个部分。

文学作品阅读的选材广泛，因为作品时代差异和作家风格不同，对考生有很强的挑战性，王振宇老师建议：一要把握常见基础题型。

比如理解句子含义，分析段落内涵这类常见题目的答题技巧;二是以读促写，以写悟读，将阅读与写作有效结合起来，提高自我独立阅读能力、培养多角度、个性化思维素养。

三有良好阅读习惯，北约类试题文本阅读都是千字文，卷面试题量大、解题时间有限，考生应积极进行快速阅读训练，迅速理清作者的思想、意图、感受，体验作品的思想境界和作者对人、事、物的感情倾向等能力尤其重要。

关于写作，考生可看一下过去三年北约的作文题目：(北京大学2011)鲁迅曾说：“无尽的远方，无数的人们，都与我有关。

”你认为这是怎样的一种关联?你自己与“无尽的远方，无数的人们”是以什么方式相关联?试结合上述问题，以《无尽的远方，与无数的人们》为题写一篇作文。

(北京大学2010)今年是北京大学中文系林庚教授诞辰100周年，有人评价林庚“建安风骨，盛唐气象，少年精神，布衣情怀”。

请从中选择一个四字短语为题，写一篇要求在诗情画意中富含哲理的散文。

(北京大学2009)有腐败分子认为：腐败，是一种人人难免的“普遍本性”，它有助于刺激消费……请你写一篇800字文章、观点,要求至少有5处正确引用古诗文。

从过去三年北约的作文题目我们不难看出，命题者将学生表达能力和感悟能力结合起来，文章要写得有诗情画意，且要富有哲理，这就有一定的难度的。

2012北大自主招生数学试题

2012北⼤⾃主招⽣数学试题2012北⼤⾃主招⽣数学试题(理科)1.求x 的取值范围,使得()21f x x x x =+++-是增函数.2.1的实数根的个数.3.已知22(2)(2)0x x m x x n -+-+=的4个根组成⾸项为14的等差数列,求m n -.4.已知锐⾓ABC ?的外接圆的圆⼼为O ,求O 到三⾓形三边的距离之⽐.5.已知点(2,0),(0,2)A B -,若点C 是圆2220x x y -+=上的动点,求ABC ?⾯积的最⼩值.6.在1,2,,2012中取⼀组数,使得任意两数之和不能被其差整除,最多能取多少个数？7.设点A 、B 、C 分别在边长为1的正三⾓形的三边上,求222AB BC CA ++的最⼩值.8.若关于x 的⽅程sin 4sin 2sin sin 3x x x x a -=在[0,)π有唯⼀解的a ,求实数a 的范围.9.求证:若圆内接五边形的每个⾓都相等,则它为正五边形.10.求证:对于任意的正整数n ,(1n 的形式,其中s N +∈.2012年清华等五校⾃主招⽣试题??通⽤基础测试数学⼀、选择题1.若P 为ABC ?内部任⼀点(不包括边界),且()(2)0PB PA PB PA PC -+-=,则ABC ?必为( )A.直⾓三⾓形B.等边三⾓形C.等腰直⾓三⾓形D.等腰三⾓形2.圆锥的轴截⾯SAB 是边长为2的等边三⾓形,O 为底⾯中⼼,M 为SO 的中点,动点P 在圆锥底⾯内(包括圆周).若MA MP ⊥,则P 点形成的轨迹的长度为( )C.3D.32 3.某种型号的计算器上有⼀个特殊的按键,在计算器上显⽰正整数n 时按下这个按键,会等可能的将其替换为0,1,2,,1n -中的任意⼀个数.如果初始时显⽰2011,反复按这个按键使得最终显⽰0,那么这个过程中,9,99,999都出现的概率是( ) A.4110 B.5110 C.6110 D.7110 4.已知,R αβ∈,直线1sin sin sin cos x y αβαβA.0B.1C.1-D.25.若正整数集合A k 的最⼩元素为1,最元素为2007,并且各元素可以从⼩到⼤排成⼀个公差为k 的等差数列,则并集1759A A 中的元素个数为A.119B.120C.151D.1546.三⾓式111cos 0cos1cos1cos 2cos88cos89+++化简为 A.cot1csc1 B.tan1csc1 C.cot1sec1 D.tan1sec17．设k<3,k≠0，则⼆次曲线2213x y k k -=-与22152x y +=必有 (A)不同的顶点；(B)不同的准线；(C)相同的焦点；(D)相同的离⼼率．8.若P 为椭圆221169x y +=l 在第⼀象限上的动点，过点P 引圆x 2＋y 2=9的两条切线PA 、PB ，切点分别为A 、B ，直线AB 与x 轴、y 轴分别交于点M 、N ，则S MON ?的最⼩值为( )(A)92;(B)(C)274;(D) 9. 设x 1、x 2是实系数⼀元⼆次⽅程ax 2＋bx ＋c=0的根，若x 1是虚数，212x x 是实数,则 248200711111222221x x x x x S x x x x x =++++++ ? ? ? ?的值为A.0B.?1003C.1004D.?100410.函数f:R →R ，对任意的实数x 、y ，只要x+y≠0，就有f(xy)=()()f x f y x y++成⽴,则函数f(x)(x ∈R)的奇偶性为(A)⼀定是奇函数； (B)⼀定是偶函数; (C)既是奇函数，⼜是偶函数； (D)既不是奇函数，⼜不是偶函数．⼆、解答题11. 系统内有2k?1(k ∈N+)个元件，每个元件正常⼯作的概率为p(012.已知2n n x x f x x n =++++(*n N ∈),求证:当n 为偶数时,⽅程()0n f x =⽆解;当n 为奇数时,⽅程()0n f x =有唯⼀解n x ,且2n n x x +<. 13．已知锐⾓三⾓形ABC中，BE⊥AC于点E,CD⊥AB于点D，且BC=25，CE＝7,BD=15，若BE、CD交于点H，联结DE，以DE为直径作圆，该圆与AC交于另⼀点F，求AF的长度．14.已知有n(n≥2)位乒乓球选⼿，他们互相进⾏了若⼲场乒乓球双打⽐赛，并且发现任两名选⼿作为队友恰好只参加过⼀次⽐赛，试求n的所有可能值·15．已知动点P在y轴上投影为H,A(?2,0),B(2,O)，满⾜2AP BP PH.2||(1)求点P的轨迹⽅程C;(2)已知⼀条直线过点B，且与曲线C交于x轴下⽅两点C、D，M为CD中点，求M与点Q(0，?2)连线的斜率取值范围．2012年名牌⼤学⾃主招⽣考试试题(3)适⽤⾼校：北京理⼯⼤学、同济⼤学等⼗三校⼀、选择题1．正四⾯体的4个⽽上分别写若l,2,3,4,将4个这样的均匀正四⾯体投掷于桌⽽上，与桌⾯接触的4个⾯上的4个数的乘积被4整除的概率是( )(A)18 (B)964(C)116 (D)1316 2．设a>0,b ＞0，c ＞0，且a+b+c=1，则22a b c 的最⼤值为( )(A)613 (B)43123 (C)34123 (D)6123．已知F 1、F 2分别为双曲线22221x y a b-=的左、右焦点,P 为双曲线左⽀上的任意⼀点, 若221||||PF PF 的最⼩值为8a, 则双曲线的离⼼率的取值范围为( ) (A)(l ，+∞); (B)(0,3]； (C)(1,2]； (D)(1,3]4．如果关于x 的⽅程2x 2+3ax+a 2?a ＝0⾄少有⼀个根等于l 的根，那么实数a 的值( )(A)不存在；(B)有⼀个；(C)有三个；(D)有四个．5.5个顶点不共⾯的五边形叫空间五边形,空间五边形的5条边所在直线中,互相垂直的直线对⾄多有( )(A)5对; (B)6对; (C)7对; (D)8对.6．已知定义在实数集R 上的函数f(x),其值域也是R,井且时任意x 、y ∈R ．都有f[xf(y)]=xy,则|f(2007)等于( )(A)0; (B)1; (C)20072; (D)20077．若k 是正位数,且0242401020054010401040104010333C C C C +?+?++?能被2k 整除,则k 的最⼤值为( )(A)2004; (B)2005; (C)2006; (D)2008.8.已知⾮零向量AB 与AC 满⾜0||||AB AC BC AB AC ??+= ,且12||||AB AC AB AC =则ABC ?为( ) (A)三边均为不相等的三⾓形; (B)直⾓三⾓形; (C)等腰⾮等边三⾓形; (D)等边三⾓形.x 、y 、z 的⽅程组333(6),(6),(6),y x z y x z -=-=-=的实数解的组数有( )(A)有⼀组解； (B)有两组解; (C)有⽆穷多组解； (D)⽆法确定10．在欧⾮杯排球赛中，欧洲的参赛队伍⽐⾮洲的参赛队伍多9⽀,每两⽀球队赛⼀场，胜者得1分，败者得0分,若欧洲球队所得总分为⾮洲球队所得总分的9倍，则⾮洲球队的各⽀球队中得分的最⼤可能值是( )(A)8; (B)9; (C)10; (D)11.⼆、解答题11.在m(m≥2)个不同数的排列P 1 P 2 ?P m 中, 若1≤i(1)求a 4、a 5，并写出a n 的表达式；(2)令b n =11n n n n a a a a +++,求证：2n<12n b b b +++ <2n+3,n=1,2，…12.在ABC ?中，⾓A 、B 、C 所对的边分别为a 、b 、c, 已知sinA ＋sinC=msinB(m ∈R)，且4(A?C)+4cosB+cos2B=1.(1)求证：b 2=4ac;(2)当m=54， b=1时,求a 、c 的值； (3)若⾓B 为最⼤内⾓(即B≥A 且B≥C)．求实数m 的取值范围.13．已知a、b为实数，i为虚数单位．且关于z的⼆次⽅程4z2+(2a+i)z?8b(9a+4)?2(a+2b)i=0⾄少有⼀个实根．求这个实根的最⼤值．14.双曲线C的渐近线⽅程为x±2y=0,点A(5,0)到双曲线C上动点P(1)求双曲线⽅程；(2)若过点B(1,0)的直线l交双曲线C上⽀⼀点M，下⽀⼀点N，且4MB=5BN,求直线l的⽅程．15．由抛物线x=y2＋2与点(3,1)处的法线及x轴、y轴所围成⼀个平⾯图形．(1)求此平⾯图形的⾯积；(2)求该平⾯图形绕x轴旋转所成旋转体的体积．2013年“北约”⾃主招⽣试题⼀、以⼆、在6×6的表中停放3辆完全相同的红⾊车和3辆完全相同的⿊⾊车，每⼀⾏、每⼀列都只有⼀辆车，每辆车占⼀格，共有多少种停放⽅法？三、已知x2=2y+5,y2=2x+5，求x3?2x2y2+y2的值。

2012年北京大学保送生面试考

2012年北京大学保送生面试考“物价2012年清华大学保送生笔试考“狼爸据北京青年报讯昨天，北京大学(微博)举行了保送生面试，笔试今日进行。

与以往面试类似，北大考题涉及的话题领域宽泛，“物价上涨”、“神八与天宫交会对接”等时下热点事件成为考题。

面试延续了以往的小组面试形式，5名考生面对三位考官，每名考生抽一道题，并且有一次换题机会。

今年每场面试的时间为40分钟，比以往缩短了10分钟，这意味着考生之间现场讨论的时间减少。

据一位考官称，面试时间减少不会影响对学生的评判。

昨天上午的面试题目五花八门，既有生活类话题，也有宗教之类的抽象话题。

据考生们介绍，有一道题是“我国经济增长的同时也带来了物价上涨，你怎样看待这个问题？”一名来自辽宁的考生说，他从中学食堂价格上涨谈到通胀对生活的影响，建议政府应该给低收入群体发放补贴。

据考官透露，思维灵活、视野开阔的考生易得高分。

比如，谈到“神八与天宫交会对接”时，有考生不仅从科技角度思考，而且联系到美国、俄罗斯、中国之间的太空竞争，还从全人类的角度分析了各国重复建设空间站对资源的消耗。

记者了解到，保送生考试总共600分，其中笔试占500分，面试成绩只占100分。

笔试今天开考，上午进行语文、数学、英语(论坛)的考试，下午将根据文理科的不同，分别进行历史、政治以及物理、化学的考试转播到腾讯微博本报讯昨天，清华大学(招生办)同时举行保送生的笔试和自主招生“领军计划”的面试。

那些进考场之前还在恶补时事热点的考生发现，事先准备的都没用上。

据清华招办负责人透露，面试时有的考生令考官刮目相看，有的则被问懵了。

“领军计划”是清华2012年自主招生中特殊的一部分，旨在选拔“志向远大、追求卓越、品学兼优、素质全面”的应届高中毕业生，由清华指定的全国211所中学推荐，然后由清华用面试的方式选拔。

昨天上午参加面试的有240多名考生。

记者看到，很多备考的考生在考场外还捧着资料在恶补时事热点。

但面试结束后走出考场的考生大多告诉记者，事先准备的几乎都没用上。

2012年普通高等学校招生全国统一考试理数北京卷pdf版含答案

( )
∴= A1B 0 ，3，− 2 3 , A1E =(−2 ，−1，0)
设平面 A1BE 法向量为 n = ( x ，y ，z)
则
A1B
⋅
n
=0
A1E ⋅ n =0
∴
3
y
−
2
3z
= 0 ∴
z
=
3y 2
−2x − y =0
x
=
−y 2
( )
∴ n = −1，2 ， 3
( ) 又∵ M −1，0 ， 3
( ) ( ) ( ) （求： s2=
1 n
2
x1 − x +
2
x2 − x + +
xn
−
x
2
，其中
x
为数据
x1
，
x2
，…，
xn
的平均数）
18．（本小题共 13 分）
已知函数 f ( x) = ax2 + 1(a > 0) ， g ( x=) x3 + bx ．（1）若曲线 y = f ( x) 与曲线 y = g ( x) 在它们的交点 (1，c) 处具有公共切线，求 a ，b 的值；
4
5
6
7
8
答案
D
D
B
C
A
B
B
C
二、填空题
题号答案
9
10
11
n2 + n
2
1；
4
4
12
13
14
3
1；1
(−4 ，− 2)
三、解答题 15．
解：
= f (x) (sin x − cos x)s= in 2x (sin x − cos x)2sin x= cos x 2(sin x − cos x) cos x

2012年北约自主招生文科试题及答案

北京大学自主招生数学（文科）解答24. 解法一：（4分）（6分）（6分）（2分）说明1. 直接猜出取中点时取得最小值43，得2分.解答二：建立坐标系，设)0,(a A ，)3,(b b B ，))1(3,(c c C -222CA BC AB ++6126422882222+--+--++=c c bc ca ab c b a （4分）61263215215)2(2222+--++++-=c b bc c b c b a （6分） 4343)43(536)1563(215)2(2222≥+-+-+++-=c c b c b a （6分）当43 =c ，41 =b ，21 =a 时，222CA BC AB ++取到最小值43 (2分)说明1. 原点取在别处（比如某边中点），可相应给分解答三：建立坐标系，设)0,(x A ，))21(3,(y y B -，))21(3,(z z C +222CA BC AB ++2333422882222++-+--++=z y yz xz xy z y x （4分） 4343)41(536)51(215)2(2222≥+++-+++-=z z y z y x （6分）4343)43(536)1563(215)2(2222≥+-+-+++-=c c b c b a （6分）当且仅当41- =z ，41 =y ，0 =x 时，222CA BC AB ++取到最小值43 (2分)25. 证明：内角相等的圆内接五边形必为正五边形。

解法一：证明: 假设圆内接五边形每条边所对应的弧长分别是x ， y ， z ，u ，v . 利用等角对等弧这一结论我们有x + y + z = y + z + u （5分）同理 x + y + z = y + z + u =z + u + v = u + v + x = v + x + y (10 分)由此可知 x = y = z = u = v (15 分)再利用等弧对等弦，所以圆内接五边形的五条边都相等. (20分)解法二：证明: 假设圆内接五边形每条边所对应的弧长分别是x ， y ， z ，u ，v . 利用等角对等弧这一结论我们有 x + y + z = y + z + u （5分）x = u (10 分)同理 x = y = z = u = v (15 分)再利用等弧对等弦，所以圆内接五边形的五条边都相等. (20分) 解法三：证明: 连接CE∵ ABCE 是圆内接四边形∴ ∠A+∠1=180° ∠B+∠2=180°∵ ∠A=∠B∴ ∠1=∠2 （5分） ∵ ∠1+∠3=∠2+∠4∴ ∠3=∠4 （10分） ∴ DE = CD （15分）同理 AB=BC= CD =DE = AE 所以圆内接五边形的五条边都相等. (20分)解法四：连接CE∵ ABCE 是圆内接四边形 ∴ ∠A+∠1=180° ∵ ∠A=108°∴ ∠1= 72° (5分)∴ ∠BOE=2∠1= 144° (10分) 同理 ∠BOD=144°∴ ∠EOD=360°-144°-144°=72° (15分) 同理 ∠AOB=∠BOC=∠COD=∠DOE=∠EOA=72°∴ AB=BC=CD=DE=EA∴圆内接五边形的五条边都相等. (20分)解法五：证明: ∵∠BAE=∠ABC ∠1=∠2∴∠3=∠10 (5分)∵∠3=∠4 ∠9=∠10∴∠4=∠9∵∠BCD=∠AED∴∠5=∠8∵∠5=∠6 ∠7=∠8∴∠6=∠7 (或∠6=∠7= 54°) (10分) ∴∠5+∠6=∠7+∠8∴∠COD=∠DOE∴ CD=DE (15分)同理 AB=BC= CD =DE = AE所以圆内接五边形的五条边都相等. (20分)解法六：∵半径相等∴∠1=∠2 ∠3=∠4 ∠5=∠6 ∠7=∠8 ∠9=∠10∵∠1+∠2+∠3+… +∠9+∠10 =540°∴（∠1+∠10）+（∠4+∠5）+∠8=270°∵∠1+∠10=108°∠4+∠5=108°∴∠8= 54°（5分）∴∠9+∠8 = 108°∴∠9= 54°∴∠8=∠9 （10分）∵∠9+∠10=∠7+∠8∴∠AOE=∠DOE∴ AE=DE (15分)同理AB=BC= CD =DE = AE所以圆内接五边形的五条边都相等. (20分)解法七：∵同弧AB所对的角相等∴∠1=∠2 (5分)∵∠BAE=∠ABC AB=AB∴△ABC ≌△ABE (10分)∴ BC=AE (15分)同理AB=BC= CD =DE = AE所以圆内接五边形的五条边都相等. (20分)解法八：∵∠B=∠E∴ AC=AD （5分）∴∠1=∠2∵ ∠1+∠3=∠2+∠4∴ ∠3=∠4 (10分) ∴ A B=AE (15分)同理 AB=BC= CD =DE = AE 所以圆内接五边形的五条边都相等. (20分)解法九：∵ ∠B=∠E ∴ AC=AD （5分） ∴ ∠1=∠2 ∵ ∠1+∠3=∠2+∠4∴ ∠3=∠4 (10分) ∵ ∠B=∠E AC=AD∴ △ABC ≌ △ADE （15分） ∴ BC=AE同理 AB=BC= CD =DE = AE 所以圆内接五边形的五条边都相等. (20分)解法十：设AB=a, AE= b2 ，BC= b 1,∵ ∠BAE=∠ABC= 108° ∴ AC=BE （5分）设 AC=BE=c 由余弦定理，得在△ABC 中 c 2= a 2+ b 12 －2 a b cos 108° ①在△ABE 中 c 2= a 2 +b 22 －2 a b cos 108° ② （10分） ①-②,得（b 1－b 2）(b 1+b 2－2 a b cos 108°）= 0 ∵ cos 108°＜0∴ b 1+b 2－ 2 a b cos 108°＞0 （若同学没有这一步，则这道题只得10分） ∴ b 1= b 2 即BC=AE (15分) 同理 AB=BC= CD =DE = AE 所以圆内接五边形的五条边都相等. (20分)解法十一：∵ 圆内接五边形的各内角相等 ∴ AC=BD∴∠A0C=∠BOD (5分) ∴∠A0B+∠B0C=∠COD+∠BOC∴∠A0B =∠COD (10分) ∴ AB=CD (15分)同理 AB=BC= CD =DE = AE 所以圆内接五边形的五条边都相等. (20分)阅卷说明：1、只画图，没有证明，记0分。

2012年保送生考试专项练习参考答案

2012年保送生考试专项练习参考答案专练一21.B 22.A 23.A 24.C 25.D26.C 27.D 28.C 29.B 30.C31.A 32.B 33.C 34.B 35.B专练二36.C 37.A 38.D 39.B 40.D 41.A 42.B 43.C 44.C 45.A76. How about/What about youWhat are you going to doWhat do you want to doWhat’s your plan…77. Because there is/there will be ...Because I want to go to .. …78. Would you like to go with me…79. Can/May/Could I take a camera with me…80. where shall we meet…76 To my hometown／Australia／Shanghai／I'm going to my hometown／Australia／Shanghai/…77 Where are you going(for your summer holidays)What are you going to do this summerWhat’s your plan (for summer holidays)／What are your plans (for Summer holidays)／What plans do you have (for summer holidays)／…What about you／How about you／…78 1 help my grandparents do farm workI feed chickens，water plants and ride horsesl go swimming and boating/I play basketball or tennis／…79 I'm going with my cousin／my brother/…With my cousin／my brother／…My cousin／brother／…is going with meMy parents／…are going with me…76. Yes, please/ thanks/ sir Thank you …77. Can/Could you tell me where the nearest hotel is/how I can get to the nearest hotel/where I can find the nearest hotel/which is the way to the nearest hotelCan/Could you tell me where to find the nearest hotel/how to get to the nearest hotelCan/Could you tell me the way to the nearest hotelWhere is the nearest hotelWhich is the way to the nearest hotelHow can I get to the nearest hotel …78. There’s a post office nearby/over there/down the street/…You can get/buy one in a/the post office (nearby/over there/down the street/…)You can find a post office (nearby/over ther/down the street/…)…79. Is it open nowIs it closed in the eveningDoes it close in the evening…80. (The)Euro (Hotel)It’s called (the) Euro(Hotel)The name of the hotel is (the)Euro(Hotel)Its name is (the) Euro (Hotel)36~40 CADCB 41~45 BCDAC76.Where did you go(just now)/Where were you(just now)/…77.When is it/When shall we go there/When are we going to help them/…78.What’s wrong(with you)/What’s the matter (with you) /What happened(to you) /What’s yourtrouble/…79.Much better/I am feeling much better/I am getting better and better/Not so good/Not very well …80.Many thanks/Thank you(very much)/Thanks a lot/Thanks for you r help/It’s very kind of you…专练三46.B 47.B 48.C 49.D 50.D 56.D 57.A 58.B 59.C 60.A专练四66.helpful 67.from 68.wasting 69.earlier 70.if 71.received 72.my 73.but 74.years 5.third66 speaking 67 their 68 first 69 wants 70 dropped 71 dirty 72 lesson 73 times 74 has 75 always66. meeting 67. earlier 68. wonderful 69. through 70. stopped 71. our 72. but 73. rooms 74. was 75. soon66．Have 67.building 68.look 69.more 70.enough 71.but 72.first 73.finished 74.in 75.them61 62 63 64 65 DBEAG。

北京大学保送生数学真题及答案

北京大学保送生数学真题及答案2012年北京大学保送生考试数学试题及参考答案1．已知数列{}na 为正项等比数列，且34125a a a a +--=，求56aa +的最小值．解：设数列{}na 的公比为()0q q >，则231115a qa q a a q +--=，12351a q q q ∴=+--()251(1)q q =+-．由1a>知1q >．()454556111a a a q a q a q q ∴+=+=+()()44225511(1)1q q q q q q =⋅+=+--222211515122011qq q q ⎛⎫⎛⎫=++=-++≥ ⎪ ⎪--⎝⎭⎝⎭，当且仅当22111qq -=-即q =56aa +有最小值20．2．已知()f x 为二次函数，且()()()()()(),,,a f a f f a f f f a 成正项等比数列，求证：()f a a =．证法一：设()()20f x mx nx t m =++≠，数列()()()()()(),,,a f a f f a f f f a 的公比为()0q q >，则()()()()()()()()223,,f a aq f f a f aq aq f f f a f aq aq =====，2ma na t aq∴++=①22()m aq naq t aq ++=②2223()m aq naq t aq ++=③①-②得()()()22111ma q na q aq q ∴-+-=-， ②-③得()()()2222111ma q q naq q aq q ∴-+-=-．若1q =，则()f a a =；若1q ≠，则()21ma q na aq++=与()21ma q q na aq++=矛盾．()f a a ∴=．证法二：由()()()()()(),,,a f a f f a f f f a 成等比数列得()()()()()()()()()f f f a f f a f a af a f f a ==，()()()()()()()()()()()()f f f a f f a f f a f a f a af f a f a --∴=--．∴三点()()()()()()()()()()()(),,,,,A a f a B f a f a C f a f a 满足ABBCkk =，,,A B C ∴三点共线，与,,A B C 三点在抛物线上矛盾，()f a a ∴=．3．称四个顶点都落在三角形三边上的正方形叫三角形的内接正方形．若锐角三角形ABC 的三边满足a b c >>，证明：这个三角形的内接正方形边长的最小值为sin sin ac B a c B+．解：如图所示，设正方形MNPQ 的边长为x ，AE MNAD BC=，sin sin c B x x c B a -∴=，sin sin 2ac B abcx a c B Ra bc∴==++．同理可得其它两用人才种情况下内接正方形边长为D Q EPNMCB A,22abc abcRb ac Rc ab++． ()()()2220Rb ac Ra bc b a R c +-+=--<，()()()2220Rc ab Ra bc c a R b +-+=--<，∴这个三角形的内接正方形边长的最小值为sin sin ac Ba c B+． 4．从O 点发出两条射线12,l l ，已知直线l 交12,l l 于,A B两点，且OABSc∆=（c 为定值），记AB 中点为X ，求证：X 的轨迹为双曲线．解：以12,l l 的角平分线所在直线为x 示的直角坐标系．设AOx BOx α∠=∠=，,OA a OB b ==，(),X x y ，则1sin 22OABS ab c α∆==，2sin 2c ab α=．()()cos ,sin ,cos ,sin A a a B b b αααα-，cos cos ,2sin sin ,2a b x a b y αααα+⎧=⎪⎪∴⎨-⎪=⎪⎩(1)cos 2(2)sin 2xa b y a b αα+⎧=⎪⎪∴⎨-⎪=⎪⎩22(1)(2)-得22222cos sin sin 2x y cab ααα-==，∴X 的轨迹为双曲线． 5．已知()1,2,,10ia i =满足1210121030,21a aa a a a +++=<，求证：()1,2,,10i a i ∃=，使1ia <．X证明：用反证法，假设()1,2,,10ia i ∀=， 1ia ≥．令()11,2,,10i i a b i =+=，则i b ≥，且121020b b b +++=．()()()12101210111a aa b b b ∴=+++121012231b b b b b b b =+++++++12232121b bb b =+++≥与121021a a a <矛盾，()1,2,,10ia i ∴∃=，使1ia <．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

所以最大的内接正方形边长为
生
．
注：题较易，要考查平面几何、角函数与不等式有关本主三
的知识和方法．
２方法一：设ｘ＝％ｎ＋（）ｍｘｘｌｍ＃０，比数列的公比为ｑ，）等则厂ａ＝２ｎ＋＝ａ（）ｍａ＋ａｌｑ … ① ＿ｎ）ｍ（），ａ＋＝ｆａ … …（，）＝ｆｏ＋）ｌｑ（）
§
ｂ＋ｓｎＣａｉ
二（－ｉＡ）ｏ１ｓｎ＞．
２Ｒ
现了在知识交汇点处命题的特点，有利于考查学生的基础知识和较强的综合思维水平．时也进一步说明，考的重点也是自同高主招生的热点，广大的考生指明了备考的方向．向
不存在共线三点，而，从假设不成立．
注：次函数历来是各级考试命题的热点，题给出的两种二本
方法体现了理解二次函数的两个视角，代数法和图像法．法即方
一
求证： △ＡＢｃ的最大的内接正方形边长为
北大保送生考试同样考过这样的考题：２ｌ北大保送））（Ｏ１
ｐ＋ｘｑ，）＝只有一个实数根，证：ｑ≥ 今年能够不避）ｏ求ｐ，熟题，出全新的试题，人耳目一新，能可贵．不管怎样，命让难但万
３．设内接正方形为ＤＥＧ，易知正方形必有两顶点分别在Ｆ △ＡＢＣ的两边上，两顶点在同一边上，另不妨设Ｄ在ＡＣ上，Ｇ在ＢＣ上，Ｅ、Ｂ上，正方形边长为，角Ｃ所对边４Ｂ及相应边上的
１ｏｌ）【
注重灵活运用二次函数的解析式，借助与方程的内在联系，并
巧妙地进行代数变形，最终导出结论成立；法二强调二次函并方
数图像上无三点共线的特征，体现了对图像的深刻理解．０１２１年
２已知厂为一个二次函数ａ．（）且ｏ）
ａ））
ｎ）成））
ｑａ－ａ
正等比数列，证ｎ＝求）３在锐角 △ＡＢＣ中，．角４，Ｃ所对的边分别为ａ，ｃ。６Ｂ，ｂ，且＞＞
。，
；＝即点线抛线＝一三共，物上；，庐篆则但
变不离其宗，住二次函数理解的两个视角可谓是宗法．抓
５知＞，１， …，，．０：，３１且∑啦３，Ｉ＜１证：已ｉ２，０＝Ｉ２，啦０＿求中
至少有一个小于１．二、析解１设正等比数列｛｝公比为ｑ，ａ（３ｑ）５，ｌ．％的则・ｑｇ－－１＝ａ＝
：里
；
ｑ＋ｇ＿ｑ一１ｑ＿１２２
令＝２，ｘＯ且一ｘｑ１则＞，ｑ一１：－
２此时，ｌ＝ｘ０。＝１ｌｌ／２．￣ｑ
：、５
＋１５２２：２３（）＋
同理，他情形的正方形边长分别为其＝
４以射线Ｚ，成角的平分线为ｘ，点０且垂直于的．Ｚ所轴过轴
直线为Ｙ建立直角坐标系．动点（％）射线ｚｚ方程分轴设，。：，的
／ｎ）＝ｎ，）］，（）＋＝）），Ｌ（）＋Ｌ）ｚｎ）ｎ）……③ 由②一 ①得，［ｎ一２＋Ｌ）。＝ｏ一］，厂（）ｎ］ｎａ一］ｑ）ａ．ｎ
２１年２０２月
试题赏析
试究
１等比数列｛｝足ａｏ啦ａ５求ｏ０的最小值．．正满４￣一１，，，＋３一＝５６＋
另一方面，斜率 “ ＝
－，ａ，一ｎ
一ｑａｑｑ＝－ａ
，
ｋ＝
、ｃｂ＿ｎＩＡｓｉ
．
ｃｓｎ＋ａｉＢ
＞
ｂ－ｉＡｂｎｅｓ
甘
ｃ（一ｉ）０）１。＞及！
２Ｒ
＞
ｃｓｎＢ＋ａｉ
注：本题将函数与数列这两个重要的数学概念与方法整合在一起，重考查等比数列基本量、数最值的理解和应用，着函体
丽５
・・，由。。得
：
高的长分别为ｃｈ，角形面积为ｓ由Ｄ／Ｂ，ｃ、ｃ三，Ｇ／Ａ得一－ｈＸ：
ｈｃ
，
又
从而，ｓａａ（ｑ）！：ａ６ｌ＋＝ｑ＝
ａｓｎ２＝，＾＝ｓｎ，ｃｉＢ＝Ｓｃ则ａｉＢ＝
Ｃ＋ａｓ１嘣
．
４点０发引两条射线ｚｚ动直线ｚｚｚ交于点Ａ、．从出：，，与，相Ｂ，
线段ＡＢ的中点为点，动点的轨迹为，，线ｆ，直线Ｚ且射。ｚ及围成的三角形ＯＡＢ的面积为定值ｃ．（）Ｉ求证：，关于Ｚ，的角平分线成反射对称；。Ｚ（Ｉ求证：Ｔ双曲线．Ｉ），为