2023学年北师大版九年级数学上学期专项讲练1-27 《特殊平行四边形》全章复习与巩固(基础篇)
2022-2023学年北师大版九年级数学上册第一章特殊平行四边形单元测试题含答案

第一章 特殊平行四边形一 选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)1.如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,下列说法不正确的是 ( )A.AB ∥DCB.AC=BDC.AC ⊥BDD.OA=OB(第1题) (第2题)2.如图,菱形ABCD 的对角线AC ,BD 相交于点O ,E 为AD 的中点,连接OE ,若OE=3,则菱形ABCD 的周长为 ( )A.10B.12C.16D.243.如图,正方形ABCD 的对角线AC ,BD 相交于点O ,P 为边BC 上一点,且BP=OB ,则∠COP= ( ) A.15° B.22.5° C.25°D.17.5°(第3题) (第4题)4.如图,在矩形ACBE 中,∠ABC=30°,AB 交CE 于点D ,若AC=2,则CD 的长为 ( )A.2B.3C.4D.55.如图,EF 过矩形ABCD 的对角线的交点O ,且分别交AB ,CD 于点E ,F ,那么阴影部分的面积是矩形ABCD 面积的 ( )A.15B.14C.13D.310(第5题) (第6题)6.如图,已知▱ABCD 的对角线AC ,BD 相交于点O ,下列说法正确的是( ) A.当OA=OB 时,▱ABCD 为菱形 B.当AB=AD 时,▱ABCD 为正方形 C.当∠ABC=∠BCD 时,▱ABCD 为矩形 D.当AC ⊥BD 时,▱ABCD 为正方形7.如图,在矩形ABCD 中,BC=8,AB=4,点E ,F 分别为AD 和BC 的中点,连接CE ,DF ,交于点O ,连接AO ,则AO 的长为( )A.2√10B.5√2C.32√10 D.4√2(第7题)(第8题)8.如图,在四边形ABCD中,点E,F,G,H分别是AB,BD,CD,AC的中点,要使四边形EFGH是菱形,四边形ABCD应满足的一个条件是()A.AD=BCB.AC⊥BDC.AC=BDD.AB=CD9.如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB'C'D',边B'C'与DC 相交于点O,则OC的长是() A.2√2-2 B.2+√2 C.2-√2 D.√2(第9题)(第10题)10.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B'处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是() A.12 B.24 C.12√3 D.16√3二填空题(共5小题,每小题3分,共15分)11.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若∠A=26°,则∠DCA=.(第11题)(第12题)12.如图,在平面直角坐标系中,矩形木框OABC的顶点B的坐标为(1,2),若固定OA,向左推矩形木框OABC,使点B落在y轴上的点B'处,则点C的对应点C'的坐标为.13.对下列现象中蕴含的数学原理阐述正确的是(填序号).图(1)图(2)图(3)①如图(1),工人师傅在做矩形门窗时,不仅要测量出两组对边的长度相等,还要测量出两条对角线的长度相等,以确保门窗是矩形.其依据是“对角线相等的四边形是矩形”.②如图(2),将两张等宽的矩形纸条交叉叠放在一起,重合部分构成的四边形ABCD一定是菱形.其依据是“有一组邻边相等的平行四边形是菱形”.③把一张矩形纸片按图(3)的方式折一下,然后沿EF裁剪,打开就可以得到正方形.其依据是“有一组邻边相等的矩形是正方形”.14.如图,P是正方形ABCD的对角线BD上一点,PE⊥DC于点E,PF⊥BC于点F,若CF=3,CE=4,则AP的长是.(第14题)(第15题)15.如图,在边长为6的菱形ABCD中,∠DAB=60°,E为AB的中点,F为AC上一动点,连接EF,BF,则EF+BF的最小值是.三解答题(共6小题,共55分)16.(7分)如图,正方形ABCD中,点E,F分别在边CD,AD上,DE=AF,BE与CF相交于点G.(1)求证:BE=CF.(2)若BC=4,DE=1,求CF的长.17.(8分)如图,矩形ABCD的对角线AC,BD相交于点O,过点B作AC的平行线交DC的延长线于点E.(1)求证:BD=BE.(2)若BE=10,CE=6,连接OE,求△ODE的面积.18.(8分)如图,在矩形ABCD中,AB=3 cm,BC=6 cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止.点P,Q的速度都是1 cm/s.连接PQ,AQ,CP.设点P,Q运动的时间为t s.(1)当t为何值时,四边形ABQP是矩形?(2)当t为何值时,四边形AQCP是菱形?19.(9分)如图(1),在菱形纸片ABCD中,∠A=45°.对其进行如下操作:如图(2),现将纸片进行折叠,使点A与点D重合,点C与点D重合,折痕分别为EG,FH,且两条折痕的延长线交于点O.(1)求∠EOF的度数;(2)四边形DGOH是菱形吗?请说明理由.图(1)图(2)20.(10分)我们给出如下定义:把对角线互相垂直的四边形叫做“对角线垂直四边形”.如图(1),在四边形ABCD中,AC⊥BD于点O,四边形ABCD就是“对角线垂直四边形”.(1)下列四边形,一定是“对角线垂直四边形”的是.①平行四边形,②矩形,③菱形,④正方形.(2)如图(2),在“对角线垂直四边形ABCD”中,点E,F,G,H分别是边AB,BC,CD,DA的中点.求证:四边形EFGH是矩形.图(1)图(2)(3)小明说:计算“对角线垂直四边形”的面积可以仿照求菱形的面积的方法,其面积是对角线长的乘积的一半.小明的说法正确吗?如果正确,请结合图(1)说明理由;如果不正确,请给出反例.21.(13分)如图(1),矩形ABCD的对角线AC,BD相交于点O,过点D作DP∥OC,且DP=OC,连接CP.(1)猜想:请你判断四边形CODP的形状,并说明理由.(2)证明:如果将矩形变为菱形,如图(2),请你判断四边形CODP的形状,并说明理由.(3)应用:如果将矩形变为正方形,如图(3),请你判断四边形CODP的形状,并说明理由.图(1)图(2)图(3)答案解析1.C根据矩形的性质可知,矩形的对角线不一定互相垂直.故选C.【归纳总结】矩形的有关性质①边,矩形的对边平行且相等;②角,矩形的四个角都是直角;③对角线,矩形的对角线互相平分且相等.2.D根据菱形的性质可知,O是AC的中点.∵E为AD的中点,∴OE为△ACD的中位线,∴CD=2OE=6.又菱形的四边相等,∴菱形ABCD的周长为6×4=24.故选D.【一题多解】由题意得∠AOD=90°.在Rt△AOD中,∵E为AD的中点,∴AD=2OE=2×3=6,∴菱形ABCD的周长为6×4=24.故选D.3.B∵四边形ABCD是正方形,∴∠BOC=90°,∠OBC=45°.∵BP=OB,∴∠BOP=∠BPO=12(180°-45°)=67.5°,∴∠COP=90°-67.5°=22.5°.故选B.4.A∵四边形ACBE是矩形,∴∠ACB=90°,D为AB的中点.∵AC=2,∠ABC=30°,∴AB=2AC=4,∴CD=12AB=2,故选A.5.B∵四边形ABCD为矩形,∴OB=OD,AB∥CD,∴∠EBO=∠FDO.在△EBO与△FDO中,∵∠EOB=∠FOD,OB=OD,∠EBO=∠FDO,∴△EBO≌△FDO,∴S阴影部分=S△AEO+S△EBO=S△AOB.∵S△AOB=12S△ABC=14S矩形ABCD,∴S阴影部分=14S矩形ABCD.故选B.【数学思想】本题利用全等三角形把不规则图形的面积转化为较简单的规则图形的面积,进而利用整体思想求解.6.C∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.又OA=OB,∴AC=BD,由“对角线相等的平行四边形是矩形”,可判定▱ABCD为矩形,故选项A中说法错误.当AB=AD时,由菱形的定义可知,▱ABCD为菱形,故选项B中说法错误.∵在▱ABCD中,AB∥CD,∴∠ABC+∠BCD=180°.又∠ABC=∠BCD,∴∠ABC=90°.由矩形的定义,可判定▱ABCD为矩形,故选项C中说法正确.当AC⊥BD时,根据“对角线互相垂直的平行四边形是菱形”,可判定▱ABCD为菱形,但无法判定其为正方形,故选项D中说法错误.故选C.7.A连接EF,过点O作OM⊥AD于点M,易证四边形EFCD为正方形,∴OM=MD=12AB=2,∴AM=6.在Rt△AOM中,由勾股定理,得AO=√AM2+OM2=2√10.8.A∵点E,F,G,H分别是AB,BD,CD,AC的中点,∴GH∥AD,EF∥AD,FG∥BC,HE∥BC,且GH=12AD,EH=12BC,∴EF∥GH,HE∥FG,∴四边形EFGH是平行四边形.当AD=BC时,GH=EH,此时平行四边形EFGH是菱形.故选A.9.C如图,连接B'C,AC.∵旋转角∠BAB'=45°,∠BAC=45°,∴点B'在对角线AC上.∵AB=AB'=BC=1,∴AC=√2,∴B'C=√2-1.在等腰直角三角形OB'C中,OB'=B'C=√2-1,∴OC=√2(√2-1)=2-√2.故选C.10.D在矩形ABCD中,∵AD∥BC,∴∠DEF=∠EFB=60°.由翻折可知,∠EFB'=60°,∠A'B'F=∠B=90°,∠A'=∠A=90°,A'E=AE=2,A'B'=AB.在△EFB'中,∵∠B'EF=∠EFB'=60°,∴△EFB'是等边三角形.在Rt△A'EB'中,∵∠A'B'E=90°-60°=30°,∴B'E=2A'E=4,∴A'B'=2√3,即AB=2√3.∵AE=2,DE=6,∴AD=AE+DE=2+6=8,∴矩形ABCD的面积=AB·AD=2√3×8=16√3.故选D.AB=AD,∴∠DCA=∠A=26°.11.26°【解析】∵∠ACB=90°,D是AB的中点,∴DC=1212.(-1,√3)【解析】∵四边形OABC是矩形,点B的坐标为(1,2),∴OA=1,AB=2.由题意得AB'=AB=2,四边形OAB'C'是平行四边形,∴OB'=√AB'2-OA2=√3,B'C'=OA=1,∴点C的对应点C'的坐标为(-1,√3).13.②③【解析】①∵两组对边的长度相等,∴四边形是平行四边形.又对角线相等,∴该平行四边形是矩形(对角线相等的平行四边形是矩形),故①错误.②如图,由矩形的对边平行,可得AB∥CD,AD∥BC,∴四边形ABCD是平行四边形.过点D分别作AB,BC边上的高DE,DF,则DE=DF.∵平行四边形ABCD的面积=AB×DE=BC×DF,∴AB=BC,∴平行四边形ABCD为菱形(有一组邻边相等的平行四边形是菱形),故②正确.③根据折叠可知,所得到的四边形有三个直角,∴该四边形为矩形.又有一组邻边相等,∴该矩形为正方形(有一组邻边相等的矩形是正方形),故③正确.故正确的阐述为②③.14.5【解析】如图,连接PC.∵四边形ABCD是正方形,∴AD=DC,∠ADP=∠CDP.∵PD=PD,∴△APD≌△CPD,∴AP=CP.∵四边形ABCD是正方形,∴∠DCB=90°.∵PE⊥DC,PF⊥BC,∴四边形PFCE是矩形,∴PC=EF.在Rt△CEF中,EF=√CE2+CF2=√42+32=5,∴AP=CP=EF=5.15.3√3【解析】∵四边形ABCD是菱形,∴点B,D关于AC对称,AB=AD.如图,连接BD,ED,则ED 的长即为EF+BF的最小值.∵∠DAB=60°,∴△ABD是等边三角形.∵E为AB的中点,∴DE⊥AB,AE=12AB=3.在Rt△ADE中,根据勾股定理,得ED=√AD2-AE2=√62-32=3√3,∴EF+BF 的最小值为3√3.16.【参考答案】(1)证明:∵四边形ABCD是正方形,∴BC=CD=DA,∠BCE=∠CDF=90°.(2分)∵DE=AF,∴CE=DF.(3分)在△BCE和△CDF中,{BC=CD,∠BCE=∠CDF, CE=DF,∴△BCE≌△CDF,∴BE=CF.(5分) (2)∵CD=AD=BC=4,AF=DE=1,∴DF=3.在Rt△CDF中,CF=√CD2+DF2=5.(7分) 17.【参考答案】(1)证明:∵四边形ABCD是矩形,∴AC=BD,AB∥CD.又BE∥AC,∴四边形ABEC是平行四边形,∴AC=BE,∴BD=BE.(3分)(2)如图,过点O作OF⊥CD于点F.∵四边形ABCD是矩形,∴∠BCD=90°,∴∠BCE=90°.在Rt△BCE中,根据勾股定理可得BC=8.∵BE=BD,∴CD=CE=6,∴DE=12.∵OD=OC,∴CF=DF.又OB=OD,∴OF为△BCD的中位线,∴OF=12BC=4,∴S△ODE=12DE·OF=12×12×4=24.(8分)18.【参考答案】(1)由题意得,BQ=DP=t,AP=CQ=6-t.在矩形ABCD中,∠B=90°,AD∥BC.要使四边形ABQP是矩形,则BQ=AP,即t=6-t,解得t=3.故当t=3时,四边形ABQP是矩形.(4分) (2)由题意得,四边形AQCP是平行四边形.要使平行四边形AQCP是菱形,则AQ=CQ,即√32+t2=6-t,解得t=94.故当t=94时,四边形AQCP是菱形.(8分)19.【参考答案】(1)由折叠可知∠DEG=∠DFH=90°.∵四边形ABCD是菱形,∴AB∥CD,∠C=∠A=45°,∴∠A+∠ADC=180°,∴∠ADC=135°.∵∠EOF+∠DEG+∠DFH+∠ADC=360°,∴∠EOF=360°-90°-90°-135°=45°.(4分) (2)是菱形.(5分)理由:由折叠可知∠ADG=∠A=45°,∠CDH=∠C=45°.∵∠ADC=135°,∴∠GDC=∠ADH=90°.∵∠AEG=∠CFH=90°,∴GE∥DH,GD∥HF,∴四边形DGOH是平行四边形.(7分)∵∠A=∠C,AD=CD,∠ADG=∠CDH,∴△ADG≌△CDH,∴DG=DH,∴四边形DGOH是菱形.(9分)20.【参考答案】(1)③④(2分) (2)∵点E,F,G,H分别是边AB,BC,CD,DA的中点,∴HG∥AC,EF∥AC,∴HG∥EF.同理可得HE∥GF.∴四边形EFGH是平行四边形.(4分)∵DB⊥AC,∴HE⊥HG,∴∠EHG=90°,∴四边形EFGH是矩形.(6分) (3)正确.(7分)理由:S四边形ABCD=S△ADC+S△BAC=12AC·OD+12AC·BO=12AC(OD+OB)=12AC·BD,即“对角线垂直四边形”的面积是对角线长的乘积的一半.(10分)【提分技法】解决中点四边形的有关方法(1)解决中点四边形问题,往往借助三角形的中位线的性质证明四边形的对边相等或平行.(2)中点四边形的形状由原来四边形对角线的特征决定.连接矩形各边中点得到的四边形是菱形;连接菱形各边中点得到的四边形是矩形;连接正方形各边中点得到的四边形是正方形.21.【解题思路】(1)由DP∥OC且DP=OC,得四边形CODP是平行四边形,根据矩形的性质得OC=OD,从而可证得四边形CODP是菱形;(2)由DP∥OC且DP=OC,得四边形CODP是平行四边形,又根据菱形的性质得∠DOC=90°,从而证得四边形CODP是矩形;(3)由DP∥OC且DP=OC,得四边形CODP 是平行四边形,又由正方形的性质得∠DOC=90°,OD=OC,从而证得四边形CODP是正方形.【参考答案】(1)四边形CODP是菱形.(1分)理由:∵DP∥OC,DP=OC,∴四边形CODP是平行四边形.(2分)∵四边形ABCD是矩形,∴AC=BD,OC=12AC,OD=12BD,∴OC=OD,∴四边形CODP是菱形.(4分) (2)四边形CODP是矩形.(5分)理由:∵DP∥OC,DP=OC,∴四边形CODP是平行四边形.∵四边形ABCD是菱形,∴AC⊥BD,∴∠DOC=90°,∴四边形CODP是矩形.(8分) (3)四边形CODP是正方形.(9分)理由:∵DP∥OC,DP=OC,∴四边形CODP是平行四边形.∵四边形ABCD是正方形,∴AC⊥BD,AC=BD,OC=12AC,OD=12BD,∴∠DOC=90°,OC=OD,(12分)∴四边形CODP是正方形.(13分)。
2023学年北师大版九年级数学上学期专项讲练1-21 特殊平行四边形“将军饮马”(基础篇)
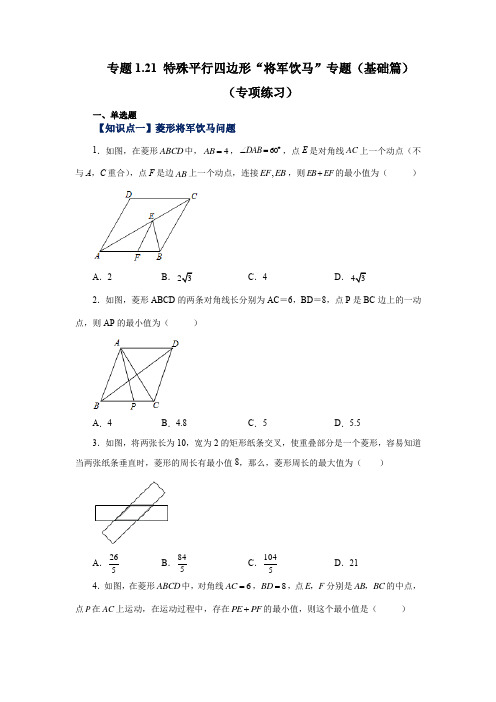
专题1.21 特殊平行四边形“将军饮马”专题(基础篇)(专项练习)一、单选题【知识点一】菱形将军饮马问题1.如图,在菱形ABCD 中,4AB =,60DAB ∠=︒,点E 是对角线AC 上一个动点(不与A ,C 重合),点F 是边AB 上一个动点,连接,EF EB ,则EB EF +的最小值为( )A .2B .C .4D .2.如图,菱形ABCD 的两条对角线长分别为AC =6,BD =8,点P 是BC 边上的一动点,则AP 的最小值为( )A .4B .4.8C .5D .5.53.如图,将两张长为10,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值8,那么,菱形周长的最大值为( )A .265B .845C .1045D .214.如图,在菱形ABCD 中,对角线6AC =,8BD =,点E F ,分别是AB BC ,的中点,点P 在AC 上运动,在运动过程中,存在PE PF +的最小值,则这个最小值是( )A .3B .4C .5D .6【知识点二】矩形将军饮马问题5.如图,在Rt ABC ∆中,090,5,12BAC AB AC ∠===,点D 是BC 上的一个动点,过点D 分别作DM AB ⊥于点M ,DN AC ⊥于点N ,连接MN ,则线段MN 的最小值为( )A .132B .13C .6013D .30136.如图,△ABC 中,BC =4,D 、E 分别是线段AB 和线段BC 上的动点,且BD=DE ,F 是线段AC 上一点,且EF=FC ,则DF 的最小值为( )A .3B .2C .2.5D .47.如图,ABC 中,∠C =90°,AC =10,BC =8,线段DE 的两个端点D 、E 分别在边AC ,BC 上滑动,且DE =6,若点M 、N 分别是DE 、AB 的中点,则MN 的最小值为( )A.10B 3 C .6 D .38.如图,在Rt ABC 中,90CAB ∠=︒,16AB =,6AC =,两顶点A ,B 分别在平面直角坐标系的y 轴,x 轴的正半轴上滑动,点C 在第一象限内,连接OC ,则OC 的长的最大值为( )A .16B .18C .8+D .8+【知识点三】正方形将军饮马问题9.如图,正方形ABCD 的面积为12,∠ABE 为正三角形,点E 在正方形ABCD 内,在对角线AC 上取一点P ,使PD PE +最小,则这个最小值为( )AB .C .D .10.如图,正方形ABCD 的边长为2,E 是BC 的中点,点P 是AC 边上的一个动点,连结BP ,EP ,则BP +EP 的最小值为( )B C D+1A11.如图,已知正方形ABCD中,点E,F分别在边CD,BC上,连接AE,DF.若AB= +的最小值为()DE BF=,则AE DFA.B.C.D.12.如图,正方形ABCD的边长为4,点E、F分别为BC、CD的中点,点P是对角线BD上的动点,则四边形PECF周长的最小值为()A.4B.4+C.8D.4+二、填空题【知识点一】菱形将军饮马问题13.如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD的方向平移得到△A'B'D',分别连接A'C,A'D,B'C,则A'C+B'C的最小值为_____.14.如图,四边形ABCD 是菱形,对角线AC ,BD 相交于点O ,AC =BD =4,点P 是AC 上一动点,点E 是AB 的中点,则PD +PE 的最小值为______________.15.如图,在菱形ABCD 中,45B ∠=︒,BC =E ,F 分别是边CD ,BC 上的动点,连接AE ,EF ,G ,H 分别为AE ,EF 的中点,连接GH ,则GH 的最小值为________.16.如图,直角三角形ABC 中,1AC =,2BC =,P 为斜边AB 上一动点.PE BC ⊥,PF CA ⊥,则线段EF 长的最小值为________.【知识点二】矩形将军饮马问题17.如图,在矩形ABCD 中,AB =3a ,BC =4a ,若点E 是边AD 上一点,点F 是矩形内一点,∠BCF =30°,则EF +12CF 的最小值是_____.18.如图,点E 是矩形纸片ABCD 的边BC 上的一动点,沿直线AE 折叠纸片,点B 落在点B '位置,连接C B '.若AB =3,BC =6,则线段C B '长度的最小值为 ________________.19.如图,已知直线344y x =+与x 轴交于点A ,与y 轴交于点B ,P 为线段AB 上的个动点,过点P 分别作PF x ⊥轴于点F ,PE y ⊥轴于点E ,连接EF ,则EF 长的最小值为______.20.如图,在矩形ABCD 中,3AB =,4BC =,E 为BC 中点,F 为CD 上一动点,则AF EF +的最小值为______.【知识点三】正方形将军饮马问题21.如图,正方形ABCD 的边长为6,点E ,F 分别为边BC ,CD 上两点,CF BE =,AE 平分∠BAC ,连接BF ,分别交AE ,AC 于点G ,M ,点P 是线段AG 上的一个动点,过点P+的最小值为______.作PN∠AC,垂足为N,连接PM,则PM PN22.定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最长距离,在平面内有一个正方形,边长为4,中心为O,在正方形外有一点P,OP=4,当正方形绕着点O旋转时,则点P到正方形的最长距离的最小值为____________.23.如图,在正方形ABCD中,AB=2,F是BD边上的一个动点,连接AF,过点B作BE∠AF于E,在点F变化的过程中,线段DE的最小值是______.24.如图,正方形ABCD边长为4,对角线AC上有一动点P,过P作PE⊥PC于E,PF⊥AB于F,连接EF,则EF的最小值为_____.三、解答题25.如图,在边长为2的菱形ABCD中,60∠=︒,M是AD边的中点,N是ABA边上的一动点,将AMN 沿MN 所在直线翻折得到A MN '△,求点A '到BC 距离的最小值.26.如图,将矩形纸片ABCD 沿对角线AC 折叠,使点B 落在点E 处,AE 交CD 于点F ,且已知AB =8,BC =4(1)判断∠ACF 的形状,并说明理由; (2)求∠ACF 的面积;(3)点P 为AC 上一动点,则PE +PF 最小值为_________________.27.如图,点P(3m-1,-2m+4)在第一象限的角平分线OC上,AP∠BP,点A在x轴正半轴上,点B在y轴正半轴上.(1)求点P的坐标.(2)当∠APB绕点P旋转时,∠OA+OB的值是否发生变化?若变化,求出其变化范围;若不变,求出这个定值.∠请求出OA2+OB2的最小值.参考答案1.B 【分析】在菱形ABCD 中,点B 关于AB 对称点为点D ,过点D 作AB 的垂线交于点F ,交AC 于点E ,这时EB EF +最小为DF ,根据三角函数得,sin60DF AD =⋅︒即可算出答案.解:如图所示,连接DE ,DF ABCD 是菱形,CD CB ∴=,DCA BCE ∠=∠,CE CE =,()CDE CBE SAS ∴≅,BE DE ∴=,EB EF DE EF DF ∴+=+≤,当DF AB ⊥时,DF 最小, 这时30,ADF ∠=︒::2,AF DF AD ∴=∴4DF AD ===EB EF ∴+≤即EB EF +的最小值为 故选:B .【点拨】本题考查菱形的性质和轴对称最短路线问题,解题关键是得到EB EF +的最小值为菱形ABCD 中AB 边上的高.2.B 【分析】由垂线段最短,可得AP∠BC 时,AP 有最小值,由菱形的性质和勾股定理可求BC的长,由菱形的面积公式可求解.解:如图,设AC与BD的交点为O,∠点P是BC边上的一动点,∠AP∠BC时,AP有最小值,∠四边形ABCD是菱形,∠AC∠BD,AO=CO=12AC=3,BO=DO=12BD=4,∠BC5=,∠S菱形ABCD=12×AC×BD=BC×AP,∠AP=245=4.8,故选:B.【点拨】本题考查了菱形的性质,勾股定理,确定当AP∠BC时,AP有最小值是本题关键.3.C【分析】画出图形,设菱形的边长为x,根据勾股定理求出周长即可.解:当两张纸条如图所示放置时,菱形周长最大,设这时菱形的边长为xcm,在Rt∠ABC中,由勾股定理:x2=(10﹣x)2+22,解得:x=265,∠4x=1045,即菱形的最大周长为1045cm.故选:C.【点拨】此题考查矩形的性质,本题的解答关键是怎样放置纸条使得到的菱形的周长最大,然后根据图形列方程.4.C【分析】先根据菱形的性质求出其边长,再作E关于AC的对称点E′,连接E′F,则E′F即为PE +PF的最小值,再根据菱形的性质求出E′F的长度即可.解:∠四边形ABCD是菱形,对角线AC=6,BD=8,∠AB5,作E关于AC的对称点E′,连接E′F,则E′F即为PE+PF的最小值,∠AC是∠DAB的平分线,E是AB的中点,∠E′在AD上,且E′是AD的中点,∠AD=AB,∠AE=AE′,∠F是BC的中点,∠E′F=AB=5.故选C.【点拨】本题考查的是轴对称−最短路线问题及菱形的性质,熟知菱形的性质是解答此题的关键.5.C【分析】先证四边形AMDN 是矩形,连接AD ,则MN =AD ,当AD 最短时,MN 取最小值. 解:如图,连接AD ,在Rt ABC ∆中,090,5,12BAC AB AC ∠===,13BC ∴=,DM AB ⊥于点M ,DN AC ⊥于点N ,90DMN DNA ∴∠=∠=︒,∴ 四边形MDNA 是矩形,MN AD ∴=,当AD BC ⊥时,AD 最短, 1122S ABC AB AB BC AD ∆==, 512601313AB AC AD BC ⨯∴===, ∠线段MN 的最小值为6013, 故选:C .【点拨】本题考查了勾股定理,矩形的判定和性质,垂线段最短,做辅助线AD 是解本题的关键.6.B【分析】过点D 作DG ∠BC 于点G ,过点F 作FH ∠BC 于点H ,当DF ∠FH 时,DF 取得最小值,据此求解即可.解:过点D 作DG ∠BC 于点G ,过点F 作FH ∠BC 于点H ,如图:∠BD =DE ,EF =FC ,∠BG =GE ,EH =HC ,当DF ∠FH 时,DF 取得最小值,此时,四边形DGHF 为矩形,∠DF =GH =12BE +12EC =12BC =2. 故选:B .【点拨】本题考查了等腰三角形的性质,矩形的判定和性质,解题的关键是灵活运用所学知识解决问题.7.B【分析】根据三角形斜边中线的性质求得12CN AB =132CM DE ==,由当C 、M 、N 在同一直线上时,MN 取最小值,即可求得MN 的最小值.解:ABC ∆中,90C ∠=︒,10AC =,8BC =,AB ∴== 6DE =,点M 、N 分别是DE 、AB 的中点,12CN AB ∴=132CM DE ==, 当C 、M 、N 在同一直线上时,MN 取最小值,MN ∴3,故选:B .【点拨】本题考查了直角三角形斜边中线的性质,勾股定理的应用等,明确C 、M 、N 在同一直线上时,MN 取最小值是解题的关键.8.B【分析】取AB 的中点P ,连接OP 、CP ,利用直角三角形斜边中线等于斜边的一半,可得182OP AP AB ===,再由勾股定理,可得CP =10,再由三角形的三边关系,即可求解. 解:如图,取AB 的中点P ,连接OP 、CP ,∠16AB =, ∠182OP AP AB === , 在Rt ACP 中,6AC =,由勾股定理得:10CP == ,∠18OC OP CP ≤+= ,∠当O 、P 、C 三点共线时,OC 最大,最大值为18.故选:B .【点拨】本题主要考查了直角三角形的性质,勾股定理,三角形的三边关系,熟练掌握相关知识是解题的关键.9.B【分析】由于点B 与D 关于AC 对称,所以连接BE ,BE 与AC 的交点即为点P 的特殊位置,此时PD +PE =BE 最小,而BE 是等边∠ABE 的边,BE =AB ,由正方形ABCD 的面积为12,可求出AB 的长,从而得出结果.解:连接BD ,与AC 交于点F .∠点B 与D 关于AC 对称,∠PD =PB ,∠PD +PE =PB +PE =BE 最小.∠正方形ABCD 的面积为12,∠AB ===又∠∠ABE 是等边三角形,∠BE =AB =∠PD PE +的最小值为故选:B .【点拨】此题主要考查了轴对称——最短路线问题,难点是确定点P 的位置.注意充分运用正方形的性质:正方形的对角线互相垂直平分.再根据对称性确定点P 的位置即可,灵活运用对称性解决此类问题的关键.10.A【分析】根据正方形是轴对称图形,AC 所在的直线是正方形的一条对称轴,进而根据对称性可知,BP +EP =PD +PE ,当,,D P E 在同一直线上时,BP EP +的值最小为DE 的长,进而根据勾股定理求得DE 的值.解:连接BD ,∠正方形是轴对称图形,AC 所在的直线是正方形的一条对称轴,∠无论P 在什么位置,都有PD =PB ;故均有BP +EP =PD +PE 成立;连接DE 与AC ,所得的交点,即为BP +EP 的最小值时的位置, 如图所示:此时BP +EP =DE ,∠正方形ABCD 的边长为2,∠DC =BC =2,∠E 是BC 的中点,∠EC =1,在Rt∠DEC 中,DE故选:A .【点拨】本题考查了轴对称的性质,勾股定理,理解对角线所在的直线是正方形的对称轴是解题的关键.11.B【分析】连接AF 作A 关于BC 的对称点A ',连接A F ',则AF A F '=,证明ADE ABE ≌,可得AF AE =,根据AE DF AF DF A F DF A D ''+=+=+≥,勾股定理即可求得A D ',即AE DF +的最小值.解:如图,连接AF 作A 关于BC 的对称点A ',则AF A F '=,四边形ABCD 是正方形,90,ADE ABF BAD AB AD ∴∠=∠=∠=︒=,DE BF =,∴ADE ABE ≌AF AE ∴=,AF A F '=,AE A F '∴=,AE DF AF DF A F DF A D ''+=+=+≥,∴AE DF +的最小值为A D '的长, 15AB =AD AB ∴==Rt AA D '△中AA '= ∴A D '==∴AE DF +的最小值为故选B【点拨】本题考查了正方形的性质,线段和最值问题,添加辅助线将AE 转化为A F '是解题的关键.12.C【分析】作E 关于BD 的对称点E ',连接E F '交BD 于点O ,根据轴对称性质及两点之间,线段最短,得到四边形PECF 的周长最小,即OE OF +最小,再利用三角形三边关系解题即可.解:如图,作E 关于BD 的对称点E ',连接E F '交BD 于点O ,故点P 与点O 重合时,四边形PECF 的周长最小,即OE OF +最小, E 和E '关于BD 对称,则,4OE OE EO OF E O OF ''=+=+=连接E P ',同样E P PE '=,EP PF E P PF E F ''+=+>而4E F E O OF ''=+=,即EP PF E F '+>所以当P 与O 重合时,四边形PECF 周长最小,即为4228++=,故选:C .【点拨】本题考查正方形的性质、轴对称与最值问题等知识,是重要考点,难度较易,掌握相关知识是解题关键.13【分析】根据菱形的性质得到AB =1,∠ABD =30°,根据平移的性质得到A ′B ′=AB =1,A ′B ′∠AB ,推出四边形A ′B ′CD 是平行四边形,得到A ′D =B ′C ,于是得到A 'C +B 'C 的最小值=A ′C +A ′D 的最小值,根据平移的性质得到点A ′在过点A 且平行于BD 的定直线上,作点D 关于定直线的对称点E ,连接CE 交定直线于A ′,则CE 的长度即为A 'C +B 'C 的最小值,求得DE =CD ,得到∠E =∠DCE =30°,于是得到结论.解:∠在边长为1的菱形ABCD 中,∠ABC =60°,∠AB =CD =1,∠ABD =30°,∠将∠ABD 沿射线BD 的方向平移得到∠A 'B 'D ',∠A ′B ′=AB =1,A ′B ′∠AB ,∠四边形ABCD 是菱形,∠AB =CD ,AB ∠CD ,∠∠BAD =120°,∠A ′B ′=CD ,A ′B ′∠CD ,∠四边形A ′B ′CD 是平行四边形,∠A ′D =B ′C ,∠A 'C +B 'C 的最小值=A ′C +A ′D 的最小值,∠点A ′在过点A 且平行于BD 的定直线上,∠作点D 关于定直线的对称点E ,连接CE 交定直线于A ′,则CE 的长度即为A 'C +B 'C 的最小值,∠∠A ′AD =∠ADB =30°,AD =1,∠∠ADE =60°,DH =EH =12AD =12, ∠DE =1,∠DE =CD ,∠∠CDE =∠EDB ′+∠CDB =90°+30°=120°,∠∠E =∠DCE =30°,如图,过点D 作DH ∠EC 于H , ∠EH CH =,1122DH CD ==,∠CH ==∠CE =2CH【点拨】本题考查了轴对称-最短路线问题,菱形的性质,平行四边形的判定和性质,含30度角的直角三角形的性质,平移的性质,正确地理解题意是解题的关键.14.【分析】连接DE ,依据菱形的性质即可计算得到DE 的长,再根据线段的性质,即可得到PD +PE 的最小值为DE 的长.解:如图,连接DE ,∠四边形ABCD 是菱形,对角线AC ,BD 相交于点O ,ACBD =4,∠AO =12AC BO =12BD =2,AC ∠BD ,∠AB 4,∠AB =AD =BD ,即△ABD 是等边三角形,点E 是AB 的中点, DE AB ⊥∴,∠DE∠DP +PE ≥DE ,∠PD +PE 的最小值为DE 的长,即PD +PE 的最小值为故答案为:【点拨】此题考查了轴对称,最短路线问题,勾股定理,等边三角形的性质,关键是掌握菱形的性质以及线段的性质:两点之间,线段最短.15【分析】连结AF ,利用中位线的性质GH=12AF ,要使GH 最小,只要AF 最小,由点F 在BC ,当AF∠BC 时,AF 最小,利用菱形性质求出AB =45B ∠=︒确定△ABF 为等腰直角三角形,得出AF=BF ,由勾股定理得:22222AB BF AF AF =+=求出AF 即可.解:连结AF ,∠G ,H 分别为AE ,EF 的中点,∠GH∠AF ,且GH=12AF ,要使GH 最小,只要AF 最小,由点F 在BC ,当AF∠BC 时,AF 最小,在菱形ABCD 中,BC = ∠AB =在Rt △ABF 中,45B ∠=︒,∠∠ABF 为等腰直角三角形,∠AF=BF ,由勾股定理得:22222AB BF AF AF =+=,∠(22=2AF ,∠AFGH 最小=12【点拨】本题考查动点图形中的中位线,菱形的性质,等腰直角三角形的性质,勾股定理应用问题,掌握中位线的性质,菱形性质,等腰直角三角形的性质, 点F 在BC 上,AF 最短,点A 到BC 直线的距离最短时由点A 向直线BC 作垂线,垂线段AF 为最短是解题关键.16【分析】先连接PC, 判定四边形ECFP 是矩形, 得到EF=PC, 再根据当PC 最小时, EF 也最小, 根据垂线段最短, 可得当CP∠AB 时, PC 最小, 最后根据面积法, 求得CP 的长即可得到线段EF 长的最小值.解:连接PC,PE∠BC, PF∠CA,∴∠PEC=∠PFC=∠C=o 90,∴四边形ECFP 是矩形,∴EF=PC,∴当PC 最小时, EF 也最小,垂线段最短,∴当CP∠AB 时,PC 最小,AC=1, BC=2,∴又当CP∠AB 时1122AC BC AB CP ⨯⨯=⨯⨯,PC=AC BCAB ⨯∴线段EF【点拨】本题主要考查矩形的判定与性质及垂线段最短.17.3a【分析】作辅助线,先根据直角三角形30度角的性质可知12CF =FH ,得GH 的长是EF +12CF 的最小值,从而得结论.解:过F 作GH ∠CD ,交AD 于G ,BC 于H ,如图:∠四边形ABCD是矩形,∠∠D=∠BCD=90°,AD∠BC,∠GH∠AD,∠CHF=90°,∠∠BCF=30°,∠FH=12 CF,∠点E是边AD上一点,∠EF+12CF=EF+FH,即EF+12CF的最小值是GH,∠∠GHC=∠BCD=∠D=90°,∠四边形DGHC是矩形,∠GH=CD=AB=3a,即EF+12CF的最小值是3a;故答案为:3a.【点拨】本题考查了矩形的判定和性质,平行线的性质,直角三角形30度角的性质等知识,解题关键是确定EF+12CF的最小值是GH.18.3【分析】连接AC,当A、B'、C共线时,C B'的值最小,进而解答即可.解:如图,连接AC.∠折叠,∠AB=A B'=3,∠四边形ABCD是矩形,∠∠B=90°,∠AC=∠C B'≥AC﹣A B',∠当A、B'、C共线时,C B'的值最小为:3,故答案为:3.【点拨】本题考查翻折变换、矩形的性质、勾股定理等知识,解题的关键是熟练掌握基本知识,作出正确的辅助线,属于中考常考题型.19.16 5【分析】由矩形的性质可知EF=OP,可知当OP最小时,则EF有最小值,由垂线段最短可知当OP⊥AB时,满足条件,求得A、B两点的坐标,即可求得EF的最小值.解:在一次函数344y x=+中,令x=0,则y=4,令y=0,则x=163-,∴A(0,4),B(163-,0).∵PE⊥y轴于点E,PF⊥x轴于点F,∠∠PEO=∠PFO=90°,∠∠EOF=90°,∴四边形PEOF是矩形,∴EF=OP,∴当OP⊥AB时,OP取得最小值,此时EF最小,∵A(0,4),点B坐标为(163-,0),∴OA=4,O B=163,由勾股定理得:AB203 =,∵12AB•OP=12OA•OB,∴OP=165.故答案为:16 5【点拨】本题考查的是一次函数图象上点的坐标特点,矩形的性质,熟知矩形的性质和一次函数与坐标轴交点特征,熟练进行计算是解答此题的关键.20.【分析】作点E 关于点C 的对称点M ,连接AM 交CD 于点F ,连接EF ,则此时AF EF +的值最小,根据矩形的性质和勾股定理得出AM 的值即可解:作点E 关于点C 的对称点M ,连接AM 交CD 于点F ,连接EF ,则此时AF EF +的值最小,EF =MF ;EC =MC ,∠EF +AF =AM∠4BC =,E 为BC 中点,∠BE =CE =2,∠BM =6;在矩形ABCD 中,3AB =,∠∠B =90°,∠===A M故答案为:【点拨】本题考查了矩形的性质、勾股定理、两点之间线段最短等知识;正确的作出辅助线是解题的关键.21.【分析】根据题意PM PN PM PH +=+MH ≥MQ ≥,进而证明ABG ≌AMG ,可得6AM AB ==,勾股定理求解即可.解:如图,作PH AB ⊥,MQ AB ⊥,连接MH.PN ∠AC ,AE 平分∠BAC ,PN PH ∴=,PM PN PM PH ∴+=+MH ≥MQ ≥,∴MQ 即为所求,四边形ABC D 是正方形正方形,,AB BC ABE BCF ∴=∠=∠,又CF BE =,ABE BCF ∴△≌△,BAE CBF ∴∠=∠,90BAE BEA ∠+∠=︒,90CBF BEA ∴∠+∠=︒,AE BF ∴⊥,90AGB AGM ∴∠=∠=︒,AE 平分∠BAC ,BAG MAG ∴∠=∠,在ABG 与AMG 中,ABG AMG AG AGBAG MAG ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴ABG ≌AMG ,6AM AB ∴==, AC 是正方形的对角线,45MAQ CAB ∴∠=∠=︒,∴==,MQ AM+的最小值为即PM PN故答案为:【点拨】本题考查了角平分线的性质,正方形的性质,垂线段最短,根据题意求得+的最小值是MQ的长是解题的关键.PM PN22.44【分析】由题意以及正方形的性质得OP过正方形ABCD的顶点时,点P到正方形的最长距离取得最小值,最小值为P A.解:如图,OP过顶点A时,点O与这个图上所有点的连线中,OA最大,此时点P到正方形的最长距离取得最小值,最小值为P A,∠正方形ABCD边长为2,O为正方形中心,∠∠OAB=∠OBA=45°,OA∠CB,∠OA=OB,∠OP=4,∠最小值为P A=4故答案为:4【点拨】本题考查了旋转的性质,正方形的性质,理解点到图形的距离是解题的关键.231##1-【分析】取AB的中点G,以G为圆心,AB为直径作圆G,当D、E、G共线时,此时DE取得最小值.解:∠BE ∠AF 于E ,即∠AEB =90°,取AB 的中点G ,∠点E 的运动轨迹为以AB 为直径,G 为圆心的圆弧.当D 、E 、G 三点共线时,DE 取得最小值,如图,∠AB =AD =2,∠AG =EG =1,∠DG=∠DE 1.即线段DE 1.1.【点拨】本题主要考查了正方形的性质,圆的性质,勾股定理,本题关键是确定DE 取最小值的位置.24.【分析】由垂线段最短可得当点P 是正方形对角线AC 和BD 的交点时,此时BP 最小,可证四边形BEPF 是矩形,可得FE =BP ,即EF 的最小值为BP 的最小值为解:当点P 是正方形对角线AC 和BD 的交点时,此时BP 最小,∵四边形ABCD 是正方形,∴BD ⊥AC 于点P ,∵正方形ABCD 边长为4,∴BP =12BD =12×∵PE ⊥BC ,PF ⊥AB ,AB ⊥BC ,∴四边形BEPF 是矩形,∴FE =BP ,∴EF 的最小值为BP 的最小值为故答案为:【点拨】本题考查了正方形的性质,垂线段最短,矩形的判定与性质,灵活运用这些性质解决问题是解题的关键.251【分析】解:由折叠知A M AM '=,又∠M 是AD 的中点,∠MA MA MD '==,故点A '在以点M 为圆心MA 长为半径的AmD 上,如解图,过点M 作ME BC ⊥于点E ,在菱形ABCD 中,2AB =,60A ∠=︒,∠ABD △是等边三角形∠M 是AD 的中点,∠点E 与点B 重合,∠EM =故点A 'A'到BC 距离的最小值为1EM A M '-=.26.(1)∠ACF 是等腰三角形,理由见分析;(2)10;(3【分析】(1)根据折叠的性质可得:∠1=∠2,再由矩形的性质,可得∠2=∠3,从而得到∠1=∠3,即可求解;(2)设FD =x ,则AF =CF =8-x ,再由勾股定理,可得DF =3,从而得到CF =5,即可求解;(3)连接PB ,根据折叠的性质可得∠ECP ∠∠BCP ,从而得到PE =PB ,进而得到当点F 、P 、B 三点共线时,PE +PF 最小,最小值为BF 的长,再由勾股定理,即可求解.解:(1)∠ACF 是等腰三角形,理由如下:如图,由折叠可知,∠1=∠2,∠四边形ABCD是矩形,∠AB∠CD,∠∠2=∠3,∠∠1=∠3,∠AF=CF,∠∠ACF是等腰三角形;(2)∠四边形ABCD是矩形且AB=8,BC=4,∠AD=BC=4,CD=AB=8,∠D=90°,设FD=x,则AF=CF=8-x,在Rt∠AFD中,根据勾股定理得AD2+DF2=AF2,∠42+x2=(8-x)2,解得x=3,即DF=3,∠CF=8-3=5,∠11541022ACFS CF AD=⋅⋅=⨯⨯=;(3)如图,连接PB,根据折叠得:CE=CB,∠ECP=∠BCP,∠CP=CP,∠∠ECP∠∠BCP,∠PE=PB,∠PE+PF=PE+PB,∠当点F、P、B三点共线时,PE+PF最小,最小值为BF的长,由(2)知:CF=5,∠BC=4,∠BCF=90°,∠BF,即PE+PF.【点拨】本题主要考查了矩形与折叠问题,等腰三角形的判定,熟练掌握矩形和折叠的性质是解题的关键.27.(1)P(2,2);(2)∠不变,定值为4;∠OA2+OB2的最小值为8.【分析】(1)根据在第一象限的角平分线OC上的点的横坐标与纵坐标相等,构建方程求出m 即可.(2)∠过点P作PM∠y轴于M,PN∠OA于N.证明四边形OMPN是正方形,再证明∠PMB∠∠PNA(ASA),推出BM=AN,可得结论;∠根据垂线段最短原理以及勾股定理即可求解.(1)解:∠点P(3m-1,-2m+4)在第一象限的角平分线OC上,∠3m-1=-2m+4,∠m=1,∠P(2,2);(2)∠过点P作PM∠y轴于M,PN∠OA于N.∠∠PMO=∠PNO=∠MON=90°,∠四边形OMPN 是矩形,∠OP 平分∠MON ,PM ∠OM ,PN ∠ON ,∠PM =PN ,∠四边形OMPN 是正方形,∠P (2,2),∠PM =PN =OM =ON =2,∠AP ∠BP ,∠∠APB =∠MPN =90°,∠∠MPB +∠BPN =∠BPN +∠NP A =90°,∠∠MPB =∠NP A ,在△PMB 和△PNA 中,MPB NPA PM PN PMB PNA ∠=∠⎧⎪=⎨⎪∠=∠⎩,∠∠PMB ∠∠PNA (ASA ),∠BM =AN ,∠OB +OA =OM -BM +ON +AN =2OM =4.∠连接AB ,∠∠AOB =90°,∠OA 2+OB 2=AB 2.∠∠BP A =90°,∠AB 2=P A 2+PB 2=2P A 2,∠OA 2+OB 2=2P A 2,当P A 最小时,OA 2+OB 2也最小.根据垂线段最短原理,P A最小值为2.∠OA2+OB2的最小值为8.【点拨】本题考查坐标与图形变化-旋转,全等三角形的判定和性质,勾股定理等知识,解题的关键是正确寻找全等三角形解决问题.。
北师大版九年级数学上册第一章特殊的平行四边形综合练习题(含答案,教师版)

北师大版九年级数学上册第一章特殊的平行四边形综合练习题(含答案,教师版)北师大版九年级数学上册第一章特殊的平行四边形综合练习题1.如图,以正方形ABCD的顶点A为坐标原点,直线AB为x轴建立平面直角坐标系,对角线AC与BD相交于点E,P为BC上一点,点P坐标为(a,b),则点P绕点E顺时针旋转90°得到的对应点P′的坐标是(D)A.(a-b,a) B.(b,a) C.(a-b,0) D.(b,0)2.如图,菱形ABCD边长为6,∠BAD=120°,点E,F分别在AB,AD上且BE=AF,则EF的最小值为(A).A.B..D3.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C4.如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD的方向平移得到△A′B′D′,分别连接A′C,A′D,B′C,则A′C+B′C5.菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,-1),当EP+BP最短时,点P6.如图,在平面直角坐标系中,矩形OABC 的两边OA ,OC 分别在x 轴和y 轴上,并且OA =5,OC =3.若把矩形OABC 绕着点O 逆时针旋转,使点A 恰好落在BC 边上的A 1处,则点C 的对应点C 1的坐标为(-95,125).7.如图,∠MON =90°,矩形ABCD 的顶点A ,B 分别在边OM ,ON 上,当B 在边ON 上运动时,A 随之在边OM 上运动,矩形ABCD 的形状保持不变,其中AB =4,BC =1,在运动过程中,点D 到点O8.如图,在矩形纸片ABCD 中,AB =8,BC =6,点E 是AD 的中点,点F 是AB 上一动点.将△AEF 沿直线EF 折叠,点A 落在点A ′处.在EF 上任取一点G ,连接GC ,GA ′,CA ′,则△CGA ′周长的最小值为9.如图,在△ABC 中,∠ABC =90°,BD 为AC 的中线,过点C 作CE ⊥BD 于点E ,过点A 作BD 的平行线,交CE 的延长线于点F ,在AF 的延长线上截取FG =BD ,连接BG ,DF.(1)求证:四边形BDFG 为菱形;(2)若AG =13,CF =6,则四边形BDFG 的周长为20.证明:∵∠ABC =90°,BD 为AC 的中线,∴BD =12AC.∵AG ∥BD ,BD =FG ,∴四边形BDFG 是平行四边形.∵CF ⊥BD ,∴CF ⊥AG.又∵点D 是AC 中点,∴DF =12AC.∴BD =DF.∴四边形BDFG 是菱形.10.如图,E ,F 分别是矩形ABCD 的边AD ,AB 上的点,EF =EC ,且EF ⊥EC. (1)求证:AE =DC ; (2)若DC =2,则BE =2.证明:在矩形ABCD 中,∠A =∠D =90°,∴∠EFA +∠AEF =90°. ∵EF ⊥EC ,∴∠FEC =90°. ∴∠AEF +∠CED =90°. ∴∠EFA =∠CED. 在△AEF 和△DCE 中,∠A =∠D ,∠EFA =∠CED ,EF =CE ,∴△AEF ≌△DCE(AAS).∴AE =DC.11.已知:在矩形ABCD 中,BD 是对角线,AE ⊥BD 于点E ,CF ⊥BD 于点F. (1)如图1,求证:AE =CF ;(2)如图2,当∠ADB =30°时,连接AF ,CE ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD 面积的18.解:(1)证明:∵四边形ABCD 是矩形,∴AB =CD ,AB ∥CD ,AD ∥BC. ∴∠ABE =∠CDF. ∵AE ⊥BD ,CF ⊥BD ,∴∠AEB =∠CFD =90°.在△ABE 和△CDF 中,∠ABE =∠CDF ,∠AEB =∠CFD ,AB =CD ,∴△ABE ≌△CDF(AAS).∴AE =CF. (2)S △ABE =S △CDF =S △BCE =S △ADF =18S 矩形ABCD .12.如图,在四边形ABCD 中,BC ∥AD ,BC =12AD ,点E 为AD 的中点,点F 为AE 的中点,AC⊥CD ,连接BE ,CE ,CF.(1)判断四边形ABCE 的形状,并说明理由;(2)如果AB =4,∠D =30°,点P 为BE 上的动点,求△PAF 周长的最小值.解:(1)四边形ABCE 是菱形,理由如下:∵点E 是AD 的中点,∴AE =12AD.∵BC =12AD ,∴AE =BC.∵BC ∥AD ,∴四边形ABCE 是平行四边形.∵AC ⊥CD ,点E 是AD 的中点,∴CE =AE =DE. ∴四边形ABCE 是菱形.(2)∵四边形ABCE 是菱形.∴AE =EC =AB =4,点A ,C 关于BE 对称.2AE=2.∴当PA+PF最小时,△PAF的周长最小,即点P为CF与BE的交点时,△PAF的周长最小.此时△PAF的周长为PA+PF+AF=CF+AF.∵CE=DE,∴∠ECD=∠D=30°,∠ACE=90°-30°=60°.∴△ACE是等边三角形.∴AC=AE=CE=4.∵AF=EF,∴CF⊥AE.∴CF=AC2-AF2=2 3.△PAF周长的最小值为CF+AF=23+2.13.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D 作DE⊥BC,垂足为F,交直线MN于点E,连接CD,BE.(1)求证:CE=AD;(2)当D为AB的中点时,四边形CDBE是什么特殊四边形?说明你的理由;(3)若D为AB的中点,则当∠A的大小满足什么条件时,四边形CDBE是正方形?请说明你的理由.解:(1)证明:∵DE⊥BC,∴∠DFB=90°.∵∠ACB=90°,∴∠ACB=∠DFB.∴AC∥DE.∵MN∥AB,即CE∥AD,∴四边形ADEC是平行四边形.∴CE=AD.(2)四边形CDBE是菱形.理由:∵CE=AD,∴BD=CE.∵BD∥CE,∴四边形CDBE是平行四边形.∵∠ACB=90°,D为AB的中点,∴CD=BD.∴四边形CDBE是菱形.(3)当∠A=45°时,四边形CDBE是正方形.理由:∵∠ACB=90°,∠A=45°,∴∠ABC=∠A=45°.∴AC=BC.∵D为AB的中点,∴CD⊥AB.∴∠CDB=90°.又∵四边形CDBE是菱形,∴四边形CDBE是正方形.14.如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连接EC,连接AP并延长交CD于点F,连接BP,交CE于点H.(1)若∠PBA∶∠PBC=1∶2,判断△PBC的形状,并说明理由;(2)求证:四边形AECF为平行四边形.解:(1)△PBC是等边三角形,理由如下:在矩形ABCD中,∠ABC=90°,∵∠PBA∶∠PBC=1∶2,∴∠PBC=60°.由折叠的性质,得PC=BC.∴△PBC是等边三角形.(2)证明:由折叠的性质,得△EBC≌△EPC.∴BE=PE.∴∠EBP=∠EPB.∵E为AB的中点,∴BE=AE.∴AE=PE.∴∠EPA=∠EAP.∵∠EBP +∠EPB +∠EPA +∠EAP =180°,∴∠EPB +∠EPA =90°. ∴∠BPA =90°,即BP ⊥AF.由折叠的性质,得BP ⊥CE ,∴AF ∥CE. ∵四边形ABCD 是矩形,∴AE ∥CF. ∴四边形AECF 为平行四边形.15.如图,将一张矩形纸片ABCD 沿直线MN 折叠,使点C 落在点A 处,点D 落在点E 处,直线MN 交BC 于点M ,交AD 于点N.(1)求证:CM =CN ;(2)若△CMN 的面积与△CDN 的面积比为3∶1,求MNDN的值.解:(1)证明:由折叠的性质,得∠ENM =∠DNM ,又∵∠ANE =∠CND ,∴∠ANM =∠CNM. ∵四边形ABCD 是矩形,∴AD ∥BC. ∴∠ANM =∠CMN. ∴∠CMN =∠CNM. ∴CM =CN.(2)过点N 作NH ⊥BC 于点H ,则四边形NHCD 是矩形,∴HC =DN ,NH =DC. ∵S △CMN S △CDN =12MC ·NH12ND ·NH =MC ND=3,∴MC =3ND =3HC.∴MH =2HC.设DN =x ,则HC =x ,MH =2x. ∴CM =CN =3x.在Rt △CDN 中,DC =CN 2-DN 2=22x. 在Rt △MNH 中,MN =MH 2+HN 2=23x. ∴MN DN =23x x=2 3. 16.在正方形ABCD 中,点E ,F 分别在边BC ,AD 上,DE =EF ,过点D 作DG ⊥EF 于点H ,交AB 边于点G.(1)如图1,求证:DE =DG ;(2)如图2,将EF 绕点E 逆时针旋转90°得到EK ,点F 对应点K ,连接KG ,EG.若H 为DG 的中点,在不添加任何辅助线及字母的情况下,请直接写出图中所有与EG 长度相等的线段(不包括EG).解:(1)证明:∵四边形ABCD 是正方形,∴AD =DC ,AD ∥BC ,∠DAG =∠DCE =90°. ∴∠DEC =∠EDF.∵DE =EF ,∴∠EFD =∠EDF. ∴∠EFD =∠DEC.∵DG ⊥EF ,∴∠GHF =90°. ∴∠DGA +∠AFH =180°. ∵∠AFH +∠EFD =180°,∴∠DGA =∠EFD =∠DEC. 在△DAG 和△DCE 中,∠DGA =∠DEC ,∠DAG =∠DCE ,DA =DC ,∴△DAG ≌△DCE(AAS).∴DG =DE.(2)与线段EG 相等的线段有:DE ,DG ,GK ,KE ,EF.17.如图,BD 是正方形ABCD 的对角线,线段BC 在其所在的直线上平移,将平移得到的线段记为PQ ,连接PA ,过点Q 作QO ⊥BD ,垂足为O ,连接OA ,OP.(1)如图1所示,求证:AP =2OA ;(2)如图2所示,PQ 在BC 的延长线上,如图3所示,PQ 在BC 的反向延长线上,猜想线段AP ,OA 之间有怎样的数量关系?请直接写出你的猜想,不需证明.解:(1)证明:∵四边形ABCD 是正方形,∴AB =BC ,∠ABD =∠CBD =45°. ∵QO ⊥BD ,∴∠BOQ =90°. ∴∠BQO =∠CBD =45°.∴OB =OQ. ∵PQ =BC ,∴AB =PQ.在△ABO 和△PQO 中,OB =OQ ,∠ABO =∠PQO ,AB =PQ ,∴△ABO ≌△PQO(SAS).∴OA =OP ,∠AOB =∠POQ. ∵∠BOP +∠POQ =90°,∴∠BOP +∠AOB =90,即∠AOP =90°. ∴△AOP 是等腰直角三角形.∴AP =2OA.(2)当PQ 在BC 的延长线上时,线段AP ,OA 之间的数量关系为AP =2OA ;当PQ 在BC 的反向延长线上时,线段AP ,OA 之间的数量关系为AP =2OA.。
2022-2023学年北师大版九年级数学上册《第1章特殊的平行四边形》单元综合测试题(附答案)

2022-2023学年北师大版九年级数学上册《第1章特殊的平行四边形》单元综合测试题(附答案)一.选择题(共10小题,满分30分)1.下列说法不正确的是()A.两组对边分别相等的四边形是平行四边形B.对角线相等的平行四边形是矩形C.对角线互相平分且垂直的四边形是菱形D.一个角是直角的四边形是矩形2.下列说法正确的是()A.对角线互相垂直的四边形是菱形B.矩形对角线互相垂直C.一组对边平行的四边形是平行四边形D.对角线相等的菱形是正方形3.边长是4且有一个内角为60°的菱形的面积为()A.2B.4C.8D.164.如图,在▱ABCD中,AC与BD交于点O,下列判断中不正确的是()A.若AB=BC,则▱ABCD是菱形B.若AC⊥BD,则▱ABCD是菱形C.若AC平分∠BAD,则▱ABCD是菱形D.若AC=BD,则▱ABCD是菱形5.如图,在菱形ABCD中,AE是菱形的高,若对角线AC、BD的长分别是6、8,则AE 的长是()A.B.C.D.56.如图,矩形ABCD中,对角线AC、BD交于点O.若∠ACB=30°,AC=10,则AB的长为()A.6B.5C.4D.37.如图,菱形ABCD周长为20,对角线AC、BD相交于点O,E是CD的中点,则OE的长是()A.2.5B.3C.4D.58.如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是()A.1B.2C.3D.49.如图,正方形ABCD中,点P在AC上,PE⊥AB,PF⊥BC,垂足分别为E、F,EF=3,则PD的长为()A.1.5B.2C.2.5D.310.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,若∠DHO=20°,则∠ADC的度数是()A.120°B.130°C.140°D.150°二.填空题(共5小题,满分15分)11.已知菱形的两条对角线长分别是6和8,则这个菱形的面积为.12.如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件.13.如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=120°,CE∥BD,DE∥AC,若AD=4,则四边形CODE的周长.14.如图,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F.且AD交EF于O,则∠AOF=度.15.如图,矩形ABCD中,E在AD上,且EF⊥EC,EF=EC,DE=2,矩形的周长为16,则AE的长是.三.解答题(共8小题,满分75分)16.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,AE∥CD,CE∥AB,判断四边形ADCE的形状,并证明你的结论.17.如图,在Rt△ABC中,∠ACB=90°,DE、DF是△ABC的中位线,连接EF、CD.求证:EF=CD.18.如图,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF =90°.求证:BE=CF.19.如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.(1)求证:BE=CE.(2)求∠BEC的度数.20.如图,已知AB=DC,AC=DB,AC与DB交于点M.过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N.(1)求证:△ABC≌△DCB;(2)求证:四边形BNCM是菱形.21.如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.(1)求证:四边形BEDF为菱形;(2)如果∠A=90°,∠C=30°,BD=6,求菱形BEDF的面积.22.如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,联结DB,BE,EF,FD.(1)求证:四边形DBEF是矩形;(2)如果∠A=60°,菱形ABCD的面积为,求DF的长.23.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM 的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.(1)求证:四边形ADCE为矩形;(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.(3)在(2)的条件下,若AB=AC=2,求正方形ADCE周长.参考答案一.选择题(共10小题,满分30分)1.解:A、两组对边分别相等的四边形是平行四边形是正确的,故该选项不符合题意;B、对角线相等的平行四边形是矩形是正确的,故该选项不符合题意;C、对角线互相平分且垂直的四边形是菱形是正确的,故该选项不符合题意;D、一个角是直角的四边形是矩形是错误的,故该选项符合题意;故选:D.2.解:∵两个同底的等腰三角形组成的四边形,对角线互相垂直,但不一定是菱形,∴A错误;根据矩形的性质可知B错误;根据平行四边形的判定定理可知C错误;根据正方形的判定定理可知D正确;故选:D.3.解:∵菱形一内角为60°,边长为4,∴过菱形一顶点作对边上的高为.∴面积为4×2=8.故选:C.4.解:A、由一组邻边相等的平行四边形是菱形可判断▱ABCD是菱形;B、对角线互相垂直的平行四边形是菱形可判断▱ABCD是菱形;C、由AC平分∠BAD,可得四边相等,即可判断▱ABCD是菱形;D、由对角线相等的平行四边形是矩形,可判断▱ABCD是矩形.故选:D.5.解:∵四边形ABCD是菱形∴AC⊥BD,BO=DO=4,CO=AO=3∴BC==5∵S菱形ABCD=×AC×BD=BC×AE∴24=5AE∴AE=故选:B.6.解:∵四边形ABCD是矩形,∴OA=OC=OB=OD=AC=5,∠ABC=90°,∴∠OBC=∠ACB=30°∵∠AOB=∠OBC+∠ACB∴∠AOB=60°∵OA=OB∴△AOB是等边三角形∴AB=OA=5故选:B.7.解:∵四边形ABCD为菱形,∴CD=BC==5,且O为BD的中点,∵E为CD的中点,∴OE为△BCD的中位线,∴OE=CB=2.5,故选:A.8.证明:∵四边形ABCD是正方形,∴AB∥CD,AD∥BC,AB=BC,∠ABE=∠BCF=90°,在△ABE和△BCF中,,∴△ABE≌△BCF(SAS),∴∠BFC=∠AEB,∵AD∥BC,AB∥CD,∴∠DAE=∠AEB,∠BFC=∠ABF,故图中与∠AEB相等的角的个数是3.故选:C.9.解:如图,连接PB,在正方形ABCD中,AB=AD,∠BAC=∠DAC=45°,∵AP=AP,AB=AD,∠BAC=∠DAC=45°∴△ABP≌△ADP(SAS),∴BP=DP;∵PE⊥AB,PF⊥BC,∠ABC=90°,∴四边形BFPE是矩形,∴EF=PB,∴EF=DP=3,故选:D.10.解:∵四边形ABCD是菱形,∴OB=OD,AC⊥BD,∠ADC=∠ABC,∵DH⊥AB,∴OH=OB=BD,∵∠DHO=20°,∴∠OHB=90°﹣∠DHO=70°,∴∠ABD=∠OHB=70°,∴∠ADC=∠ABC=2∠ABD=140°,故选:C.二.填空题(共5小题,满分15分)11.解:∵菱形的两条对角线长分别是6和8,∴这个菱形的面积为6×8÷2=24故答案为2412.解:添加的条件应为:AC=BD.证明:∵E,F,G,H分别是边AB、BC、CD、DA的中点,∴在△ADC中,HG为△ADC的中位线,所以HG∥AC且HG=AC;同理EF∥AC且EF=AC,同理可得EH=BD,则HG∥EF且HG=EF,∴四边形EFGH为平行四边形,又AC=BD,所以EF=EH,∴四边形EFGH为菱形.故答案为:AC=BD13.解:∵四边形ABCD是矩形,∴BD=AC,DO=BO,AO=CO,∴OD=OA,∵∠AOB=120°,∴∠DOA=60°,∴△AOD是等边三角形,∴DO=AO=AD=OC=4,∵CE∥BD,DE∥AC,∴四边形CODE是平行四边形,∴四边形CODE是菱形,∴四边形CODE的周长为:4OC=4×4=16,故答案为:16.14.解:∵DE∥AC,DF∥AB,∴四边形AEDF为平行四边形,∴OA=OD,OE=OF,∠2=∠3,∵AD是△ABC的角平分线,∵∠1=∠2,∴∠1=∠3,∴AE=DE.∴▱AEDF为菱形.∴AD⊥EF,即∠AOF=90°.故答案为:90.15.解:设CD=x,∵四边形ABCD是矩形,∴AB=CD,AD=BC,∠A=∠D=90°,∵EF⊥EC,∴∠FEC=90°,∴∠AFE+∠AEF=90°,∠AEF+∠DEC=90°,∴∠AFE=∠DEC,在△AFE和△DCE中,,∴△AFE≌△DCE(AAS),∴AE=DC=x,∵DE=2,∴AD=BC=x+2,∵矩形ABCD的周长为16,∴2(x+x+2)=16,x=3,即AE=3,故答案为:3.三.解答题(共8小题,满分75分)16.解:四边形ADCE是菱形.理由如下:∵AE∥CD,CE∥AB,∴四边形ADCE是平行四边形.又∵在Rt△ABC中,∠ACB=90°,D是AB的中点,∴CD=AD,∴四边形ADCE是菱形.17.证明:∵DE、DF是△ABC的中位线,∴DE∥BC,DF∥AC,∴四边形DECF是平行四边形,又∵∠ACB=90°,∴四边形DECF是矩形,∴EF=CD.18.证明:∵四边形ABCD是正方形,∴AB=BC,∠ABE=∠BCF=90°,∵∠AOF=90°,∠AOB=90°,∴∠BAE+∠OBA=90°,又∵∠FBC+∠OBA=90°,∴∠BAE=∠CBF(同角的余角相等),在△ABE和△BCF中∴,∴△ABE≌△BCF(ASA).∴BE=CF.19.(1)证明:∵四边形ABCD为正方形∴AB=AD=CD,∠BAD=∠ADC=90°∵三角形ADE为正三角形∴AE=AD=DE,∠EAD=∠EDA=60°∴∠BAE=∠CDE=150°在△BAE和△CDE中,∴△BAE≌△CDE∴BE=CE;(2)∵AB=AD,AD=AE,∴AB=AE,∴∠ABE=∠AEB,又∵∠BAE=150°,∴∠ABE=∠AEB=15°,同理:∠CED=15°∴∠BEC=60°﹣15°×2=30°.20.解:(1)∵在△ABC和△DCB中,∴△ABC≌△DCB(SSS);(2)∵CN∥BD、BN∥AC,∴四边形BNCM是平行四边形,∵△ABC≌△DCB,∴∠1=∠2,∴BM=CM,∴四边形BNCM是菱形.21.解:(1)∵DE∥BC,DF∥AB∴四边形DEBF是平行四边形∵DE∥BC∴∠EDB=∠DBF∵BD平分∠ABC∴∠ABD=∠DBF=∠ABC∴∠ABD=∠EDB∴DE=BE且四边形BEDF为平行四边形∴四边形BEDF为菱形;(2)如图:过点D作DH⊥BC于点H∵∠A=90°,∠C=30°,∴∠ABC=60°∴∠DBC=30°=∠C∴DB=DC=6∵DH⊥BC,∠C=30°∴DC=2DH=6∴DH=3∵DF∥AB,∴∠A=∠FDC=90°,且∠C=30°,DC=6∴DC=DF∴DF=2∵四边形BEDF为菱形∴BF=DF=2∴S四边形BEDF=BF×DH=2×3=622.(1)证明:∵CE=CD,CF=CB,∴四边形DBEF是平行四边形.∵四边形ABCD是菱形,∴CD=CB.∴CE=CF,∴BF=DE,∴四边形DBEF是矩形.(2)设DB为2a,∵∠A=60°,菱形ABCD的面积为,∴可得,解得:a=2,∴DB=4,∵∠DBC=60°,∴DF=.23.(1)证明:∵AB=AC,AD⊥BC,垂足为点D,∴∠CAD=∠BAC.∵AN是△ABC外角∠CAM的平分线,∴∠CAE=∠CAM.∵∠BAC与∠CAM是邻补角,∴∠BAC+∠CAM=180°,∴∠CAD+∠CAE=(∠BAC+∠CAM)=90°.∵AD⊥BC,CE⊥AN,∴∠ADC=∠CEA=90°,∴四边形ADCE为矩形;(2)∠BAC=90°且AB=AC时,四边形ADCE是一个正方形,证明:∵∠BAC=90°且AB=AC,AD⊥BC,∴∠CAD=∠BAC=45°,∠ADC=90°,∴∠ACD=∠CAD=45°,∴AD=CD.∵四边形ADCE为矩形,∴四边形ADCE为正方形;(3)解:由勾股定理,得=AB,AD=CD,即AD=2,AD=2,正方形ADCE周长4AD=4×2=8.。
2023学年九年级上学期数学同步精讲精练(北师大版)1-4 特殊平行四边形重难题型(讲义)(含详解)

1.4《特殊平行四边形》重难题型同步教材划重点【知识网络】知识点01平行四边形1.定义:两组对边分别平行的四边形叫做平行四边形.2.性质:(1)对边平行且相等;(2)对角相等;邻角互补;(3)对角线互相平分;(4)中心对称图形.3.面积:高底平行四边形⨯=S4.判定:边:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形.角:(4)两组对角分别相等的四边形是平行四边形;(5)任意两组邻角分别互补的四边形是平行四边形.边与角:(6)一组对边平行,一组对角相等的四边形是平行四边形;对角线:(7)对角线互相平分的四边形是平行四边形.【点石成金】平行线的性质:(1)平行线间的距离都相等;(2)等底等高的平行四边形面积相等.知识点02菱形1. 定义:有一组邻边相等的平行四边形叫做菱形.2.性质:(1)具有平行四边形的一切性质;(2)四条边相等;(3)两条对角线互相平分且垂直,并且每一条对角线平分一组对角;(4)中心对称图形,轴对称图形.3.面积:2对角线对角线高==底菱形⨯⨯S4.判定:(1)一组邻边相等的平行四边形是菱形;(2)对角线互相垂直的平行四边形是菱形;(3)四边相等的四边形是菱形.知识点03矩形1.定义:有一个角是直角的平行四边形叫做矩形. 2.性质:(1)具有平行四边形的所有性质;(2)四个角都是直角;(3)对角线互相平分且相等;(4)中心对称图形,轴对称图形.3.面积:宽=长矩形 S4.判定:(1) 有一个角是直角的平行四边形是矩形.(2)对角线相等的平行四边形是矩形.(3)有三个角是直角的四边形是矩形.【点石成金】由矩形得直角三角形的性质:(1)直角三角形斜边上的中线等于斜边的一半;(2)直角三角形中,30度角所对应的直角边等于斜边的一半.知识点04正方形1. 定义:四条边都相等,四个角都是直角的四边形叫做正方形.2.性质:(1)对边平行;(2)四个角都是直角;(3)四条边都相等;(4)对角线互相垂直平分且相等,对角线平分对角;(5) 两条对角线把正方形分成四个全等的等腰直角三角形;(6)中心对称图形,轴对称图形.3.面积:=S 正方形边长×边长=12×对角线×对角线 4.判定:(1)有一个角是直角的菱形是正方形;(2)一组邻边相等的矩形是正方形;(3)对角线相等的菱形是正方形;(4)对角线互相垂直的矩形是正方形;(5)对角线互相垂直平分且相等的四边形是正方形;(6)四条边都相等,四个角都是直角的四边形是正方形. 【典例分析】【典例1】已知,△ABC 中,∠BAC=45°,以AB 为腰以点B 为直角顶点在△ABC 外部作等腰直角三角形ABD,以AC为斜边在△ABC外部作等腰直角三角形ACE,连结BE、DC,两条线段相交于点F,试猜想∠EFC的度数并说明理由.【变式1】如图,在△ABC中,∠ACB=90°,∠B>∠A,点D为边AB的中点,DE∥BC交AC于点E,CF∥AB交DE的延长线于点F.(1)求证:DE=EF;(2)连结CD,过点D作DC的垂线交CF的延长线于点G,求证:∠B=∠A+∠DGC.【典例2】如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=5.对角线AC,BD 相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;(2)试说明在旋转过程中,线段AF与EC总保持相等;(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数.【变式2】如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F,求证:DF=BE.【典例3】在口ABCD中,对角线AC、BD相交于点O,BD=2AB,点E、F分别是OA、BC的中点.连接BE、EF.(1)求证:EF=BF;(2)在上述条件下,若AC=BD,G是BD上一点,且BG:GD=3:1,连接EG、FG,试判断四边形EBFG的形状,并证明你的结论.【典例4】如图1,已知AB∥CD,AB=CD,∠A=∠D.(1)求证:四边形ABCD为矩形;(2)E是AB边的中点,F为AD边上一点,∠DFC=2∠BCE.①如图2,若F为AD中点,DF=1.6,求CF的长度:②如图2,若CE=4,CF=5,则AF+BC= ,AF= .【变式3】已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.①求证:CD=AN;②若∠AMD=2∠MCD,求证:四边形ADCN是矩形.【典例4】如图,D是线段AB的中点,C是线段AB的垂直平分线上的一点,DE⊥AC于点E,DF⊥BC于点F.(1)求证:DE=DF;(2)当CD与AB满足怎样的数量关系时,四边形CEDF为正方形?请说明理由.【变式4】如图,一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合,过E 点作EF⊥AE交∠DCE的角平分线于F点,试探究线段AE与EF的数量关系,并说明理由.【跟踪训练】1.如图,在▱ABCD中,E,F两点在对角线BD上运动(E,F不重合),且保持BE=DF,连接AE,CF.请你猜想AE与CF有怎样的数量关系和位置关系,并说明理由.2.如图,在菱形ABCD中,∠B=60°,动点E在边BC上,动点F在边CD上.(1)如图①,若E是BC的中点,∠AEF=60°,求证:BE=DF;(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.3.在矩形ABCD中,AB=4 cm,BC=8 cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为O.(1)如图①,连接AF,CE.试说明四边形AFCE为菱形,并求AF的长.(2)如图②,动点P,Q分别从A,C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,已知点P的速度为5 cm/s,点Q的速度为4 cm/s,运动时间为t s,当以A,C,P,Q四点为顶点的四边形是平行四边形时,求t的值.4.如图,正方形ABCD的边长为8 cm,E,F,G,H 分别是AB,BC,CD,DA上的动点,且AE=BF=CG=DH.(1)求证:四边形EFGH是正方形;(2)判断直线EG是否经过一个定点,并说明理由.1.4《特殊平行四边形》重难题型同步教材划重点【知识网络】知识点01平行四边形1.定义:两组对边分别平行的四边形叫做平行四边形.2.性质:(1)对边平行且相等;(2)对角相等;邻角互补;(3)对角线互相平分;(4)中心对称图形.3.面积:高底平行四边形⨯=S4.判定:边:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形.角:(4)两组对角分别相等的四边形是平行四边形;(5)任意两组邻角分别互补的四边形是平行四边形.边与角:(6)一组对边平行,一组对角相等的四边形是平行四边形;对角线:(7)对角线互相平分的四边形是平行四边形.【点石成金】平行线的性质:(1)平行线间的距离都相等;(2)等底等高的平行四边形面积相等.知识点02菱形1. 定义:有一组邻边相等的平行四边形叫做菱形.2.性质:(1)具有平行四边形的一切性质;(2)四条边相等;(3)两条对角线互相平分且垂直,并且每一条对角线平分一组对角;(4)中心对称图形,轴对称图形.3.面积:2对角线对角线高==底菱形⨯⨯S4.判定:(1)一组邻边相等的平行四边形是菱形;(2)对角线互相垂直的平行四边形是菱形;(3)四边相等的四边形是菱形.知识点03矩形1.定义:有一个角是直角的平行四边形叫做矩形. 2.性质:(1)具有平行四边形的所有性质;(2)四个角都是直角;(3)对角线互相平分且相等;(4)中心对称图形,轴对称图形.3.面积:宽=长矩形 S 4.判定:(1) 有一个角是直角的平行四边形是矩形.(2)对角线相等的平行四边形是矩形.(3)有三个角是直角的四边形是矩形.【点石成金】由矩形得直角三角形的性质:(1)直角三角形斜边上的中线等于斜边的一半;(2)直角三角形中,30度角所对应的直角边等于斜边的一半. 知识点04正方形1. 定义:四条边都相等,四个角都是直角的四边形叫做正方形.2.性质:(1)对边平行;(2)四个角都是直角;(3)四条边都相等;(4)对角线互相垂直平分且相等,对角线平分对角;(5) 两条对角线把正方形分成四个全等的等腰直角三角形;(6)中心对称图形,轴对称图形.3.面积:=S 正方形边长×边长=12×对角线×对角线 4.判定:(1)有一个角是直角的菱形是正方形;(2)一组邻边相等的矩形是正方形;(3)对角线相等的菱形是正方形;(4)对角线互相垂直的矩形是正方形;(5)对角线互相垂直平分且相等的四边形是正方形;(6)四条边都相等,四个角都是直角的四边形是正方形. 【典例分析】【典例1】已知,△ABC 中,∠BAC=45°,以AB 为腰以点B 为直角顶点在△ABC 外部作等腰直角三角形ABD ,以AC 为斜边在△ABC 外部作等腰直角三角形ACE ,连结BE 、DC ,两条线段相交于点F ,试猜想∠EFC 的度数并说明理由.【解析】解法一:作DH//BE 交EA 延长线于H ,连接CH易证四边形BEHD 为平行四边形CEH EAB CE=AE CEH=EAB=90HE=BD=AB CEH EAB SAS CH=BE=DH CHE=ABECHD=90EFC=CDH=45⎧⎪∠∠⎨⎪⎩∴≅∴∠∠∴∠∴∠∠在△与△中△△(),解法二:作CG//BE 交AB 的延长线于G ,连接DG ,∵△ABC 与△ACE 都是等腰直角三角形,∴∠EAB=∠CAE+∠CAB=90°.又∠AEC=90°,∴AB ∥CE.∴四边形BECG 为平行四边形,∴CE=GB ,又AE=EC ,∴GB=AE.在△BGD 与△AEB 中,DB=AB ,∠DBG=∠BAE=90°,GB=AE ,∴△BGD ≌△AEB(SAS),∴∠GDB=∠ABE ,BE=DG.∵平行四边形BGCE,∴∠ABE=∠AGC ,BE=GC,∴∠GDB =∠AGC, GC= DG.∴∠DGC=∠DGA+∠AGC=∠DGA+∠GDB=90°.于是CDG △是等腰直角三角形,所以45EFC DCG ∠=∠=.【总结】通过做平行线,构造平行四边形,再证明全等,使问题得解. 【变式1】如图,在△ABC 中,∠ACB=90°,∠B >∠A ,点D 为边AB 的中点,DE ∥BC 交AC 于点E ,CF ∥AB 交DE 的延长线于点F .(1)求证:DE=EF ;(2)连结CD ,过点D 作DC 的垂线交CF 的延长线于点G ,求证:∠B=∠A+∠DGC .【点拨】(1)首先证明四边形DBCF 为平行四边形,可得DF=BC ,再证明DE=12BC ,进而得到EF=12CB ,即可证出DE=EF ; (2)首先画出图形,首先根据平行线的性质可得∠ADG=∠G ,再证明∠B=∠DCB ,∠A=∠DCA ,然后再推出∠1=∠DCB=∠B ,再由∠A+∠ADG=∠1可得∠A+∠G=∠B .【解析】证明:(1)∵DE ∥BC ,CF ∥AB ,∴四边形DBCF 为平行四边形,∴DF=BC ,∵D 为边AB 的中点,DE ∥BC ,∴DE=12BC ,∴EF=DF-DE=BC-12CB=12CB ,(2)∵DB∥CF,∴∠ADG=∠G,∵∠ACB=90°,D为边AB的中点,∴CD=DB=AD,∴∠B=∠DCB,∠A=∠DCA,∵DG⊥DC,∴∠DCA+∠1=90°,∵∠DCB+∠DCA=90°,∴∠1=∠DCB=∠B,∵∠A+∠ADG=∠1,∴∠A+∠G=∠B.【总结】此题主要考查了平行四边形的判定与性质,以及直角三角形的性质,关键是找出∠ADG=∠G,∠1=∠B.掌握在直角三角形中,斜边上的中线等于斜边的一半.【典例2】如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=5.对角线AC,BD 相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;(2)试说明在旋转过程中,线段AF与EC总保持相等;(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数.【点拨】(1)当旋转角为90°时,∠AOF=90°,由AB⊥AC,可得AB∥EF,即可证明四边形ABEF为平行四边形;(2)证明△AOF≌△COE即可;(3)当EF⊥BD时,四边形BEDF为菱形,又由AB⊥AC,AB=1,5OA=AB,即可得∠AOB=45°,求得∠AOF=45°,则可得此时AC绕点O顺时针旋转的最小度数为45°.【解析】(1)证明:当∠AOF=90°时,AB∥EF,∴四边形ABEF为平行四边形.(2)证明:四边形ABCD为平行四边形,∴AO=CO,∠FAO=∠ECO,∠AOF=∠COE.∴△AOF≌△COE∴AF=CE(3)四边形BEDF可以是菱形.理由:如图,连接BF,DE,由(2)知△AOF≌△COE,得OE=OF,∴EF与BD互相平分.∴当EF⊥BD时,四边形BEDF为菱形.AC=-=,在Rt△ABC中,512∴OA=1=AB,又AB⊥AC,∴∠AOB=45°,∴∠AOF=45°,∴AC绕点O顺时针旋转45°时,四边形BEDF为菱形.【总结】要证明四边形是菱形,先证明这个四边形是平行四边形,再利用对角线互相垂直的特征证明该平行四边形是菱形.【变式2】如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F,求证:DF=BE.【点拨】连接AC,根据菱形的性质可得AC平分∠DAE,CD=BC,再根据角平分线的性质可得CE=FC,然后利用HL证明Rt△CDF≌Rt△CBE,即可得出DF=BE.【解析】证明:连接AC,∵四边形ABCD是菱形,∴AC平分∠DAE,CD=BC,∵CE⊥AB,CF⊥AD,∴CE=FC,∠CFD=∠CEB=90°.在Rt△CDF与Rt△CBE中,,∴Rt△CDF≌Rt△CBE(HL),∴DF=BE.【总结】此题考查了菱形的性质,角平分线的性质,关键是掌握菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;角平分线的性质:角的平分线上的点到角的两边的距离相等.同时考查了全等三角形的判定与性质【典例3】在口ABCD 中,对角线AC、BD相交于点O,BD=2AB,点E、F分别是OA、BC的中点.连接BE、EF.(1)求证:EF=BF;(2)在上述条件下,若AC=BD,G是BD上一点,且BG:GD=3:1,连接EG、FG,试判断四边形EBFG的形状,并证明你的结论.【点拨】(1)根据平行四边形性质推出BD=2BO,推出AB=BO,根据三线合一定理得出BE⊥AC,在△BEC中,根据直角三角形斜边上中线性质求出EF=BF=CF即可;(2)根据矩形性质和已知求出G为OD中点,根据三角形中位线求出EG∥AD,EG=12BC,求出EG∥BC,EG=12BC,求出BF=EG,BF∥EG,EG=GF,得出平行四边形,根据菱形的判定推出即可.【解析】(1)证明:∵四边形ABCD是平行四边形,∴BD=2BO,∵BD=2AB,∴AB=BO,∵E为OA中点,∴BE⊥AC,∴∠BEC=90°,∵F为BC中点,∴EF=BF=CF,即EF=BF;(2)四边形EBFG是菱形,证明:连接CG,∵四边形ABCD是平行四边形,AC=BD,∴四边形ABCD是矩形,∴AD=BC,AB=CD,AD∥BC,BD=2BO=2OD,∴BD=2AB=2CD,∴OC=CD,∵BG:GD=3:1,OB=OD,∴G为OD中点,∴CG⊥OD(三线合一定理),即∠CGB=90°,∵F为BC中点,∴GF=12BC=12AD,∵E为OA中点,G为OD中点,∴EG∥AD,EG=12 AD,∴EG∥BC,EG=12 BC,∵F为BC中点,∴BF=12BC,EG=GF,即EG∥BF,EG=BF,∴四边形EBFG是平行四边形,∵EG=GF,∴平行四边形EBFG是菱形(有一组邻边相等的平行四边形是菱形).【总结】本题考查了平行四边形的性质和判定,矩形性质,菱形性质,三角形的中位线,直角三角形斜边上中线性质,等腰三角形的性质等知识点,主要考查学生综合运用定理进行推理的能力,注意:直角三角形斜边上中线等于斜边的一半.【典例4】如图1,已知AB∥CD,AB=CD,∠A=∠D.(1)求证:四边形ABCD为矩形;(2)E是AB边的中点,F为AD边上一点,∠DFC=2∠BCE.①如图2,若F为AD中点,DF=1.6,求CF的长度:②如图2,若CE=4,CF=5,则AF+BC= ,AF= .【解析】(1)证明:∵AB∥CD,AB=CD,∴四边形ABCD为平行四边形,∵∠A=∠D,∠A+∠D=180°,∴∠A=90°,∴四边形ABCD为矩形,(2)解:①延长DA,CE交于点G,∵四边形ABCD是矩形,∴∠DAB=∠B=90°,AD∥BC,∴∠GAE=90°,∠G=∠ECB,∵E是AB边的中点,∴AE=BE,在△AGE 和△BCE 中,,∴△AGE ≌△BCE (AAS ),∴AG=BC ,∵DF=1.6,F 为AD 中点,∴BC=3.2,∴AG=BC=3.2,∴FG=3.2+1.6=4.8,∵AD ∥BC ,∴∠DFC=∠BCF ,∵∠DFC=2∠BCE ,∴∠BCE=∠FCE ,∵AD ∥BC ,∴∠BCE=∠G ,∴CF=FG=4.8; ②若CE=4,CF=5,由①得:AG=BC ,CF=FG ,GE=CE=4,AG=AD ,∴CG=8,AF+BC=AF+AG=FG=CF=5;故答案为:5;设DF=x ,根据勾股定理得:CD 2=CF 2﹣DF 2=CG 2﹣DG 2,即52﹣x 2=82﹣(5+x )2, 解得:x=57, ∴DG=5+57=532, ∴AD=21DG=516, ∴AF=AD ﹣DF=59; 故答案为:59..【总结】本题考查了矩形的判定与性质、全等三角形的判定与性质、等腰三角形的判定、勾股定理的运用;本题有一定难度.【变式3】已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.①求证:CD=AN;②若∠AMD=2∠MCD,求证:四边形ADCN是矩形.【点拨】①根据两直线平行,内错角相等求出∠DAC=∠NCA,然后利用“角边角”证明△AMD和△CMN全等,根据全等三角形对应边相等可得AD=CN,然后判定四边形ADCN是平行四边形,再根据平行四边形的对边相等即可得证;②根据三角形的一个外角等于与它不相邻的两个内角的和推出∠MCD=∠MDC,再根据等角对等边可得MD =MC,然后证明AC=DN,再根据对角线相等的平行四边形是矩形即可得证.【解析】证明:①∵CN∥AB,∴∠DAC=∠NCA,在△AMD和△CMN中,∵DAC NCA MA MCAMD CMN ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AMD≌△CMN(ASA),∴AD=CN,又∵AD∥CN,∴四边形ADCN是平行四边形,∴CD=AN;②∵∠AMD=2∠MCD ,∠AMD=∠MCD+∠MDC,∴∠MCD=∠MDC,∴MD=MC,由①知四边形ADCN是平行四边形,∴MD=MN=MA=MC,∴AC=DN,∴四边形ADCN是矩形.【总结】要判定一个四边形是矩形,通常先判定它是平行四边形,再根据平行四边形构成矩形的条件,判定有一个角是直角或对角线相等.【典例4】如图,D是线段AB的中点,C是线段AB的垂直平分线上的一点,DE⊥AC于点E,DF⊥BC于点F.(1)求证:DE=DF;(2)当CD与AB满足怎样的数量关系时,四边形CEDF为正方形?请说明理由.【点拨】(1)由CD垂直平分线AB,可得AC=CB,得出∠ACD=∠BCD,再由∠EDC=∠FDC=90°,可证得△ACD≌△BCD,得出CE=CF即可;(2)先证明四边形CEDF是矩形,再证出因此AB=2CD时,四边形CEDF为正方形.【解析】(1)证明:∵CD垂直平分线AB,∴AC=CB.∴△ABC是等腰三角形,∵CD⊥AB,∴∠ACD=∠BCD.∵DE⊥AC,DF⊥BC,∴∠DEC=∠DFC=90°∴∠EDC=∠FDC,在△DEC与△DFC中,,∴△DEC≌△DFC(ASA),∴DE=DF;(2)解:当AB=2CD时,四边形CEDF为正方形.理由如下:∵AD=BD,AB=2CD,∴AD=BD=CD.∴∠ACD=45°,∠DCB=45°,∴∠ACB=∠ACD+∠BCD=90°,∴四边形DECF是矩形.又∵DE=DF,∴四边形CEDF是正方形.【总结】此题主要考查线段的垂直平分线的性质、全等三角形的判定及性质、正方形的判定、矩形的判定等知识点;熟练掌握正方形的判定,证明三角形全等是解决问题(1)的关键.【变式4】如图,一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合,过E 点作EF⊥AE交∠DCE的角平分线于F点,试探究线段AE与EF的数量关系,并说明理由.【点拨】AE=EF.根据正方形的性质推出AB=BC,∠BAD =∠HAD=∠DCE=90°,推出∠HAE=∠CEF,根据△HEB是以∠B为直角的等腰直角三角形,得到BH=BE,∠H=45°,HA=CE,根据CF平分∠DCE推出∠H=∠FCE,根据ASA证△HAE ≌△CEF即可得到答案.【解析】探究:AE=EF证明:∵△BHE为等腰直角三角形,∴∠H=∠HEB=45°,BH=BE.又∵CF平分∠DCE,四边形ABCD为正方形,∴∠FCE=12∠DCE=45°,∴∠H=∠FCE.由正方形ABCD知∠B=90°,∠HAE=90°+∠DAE=90°+∠AEB,而AE⊥EF,∴∠FEC=90°+∠AEB,∴∠HAE=∠FEC.由正方形ABCD知AB=BC,∴BH-AB=BE-BC,∴HA=CE,∴△AHE≌△ECF (ASA),∴AE=EF.【总结】充分利用正方形的性质和题目中的已知条件,通过证明全等三角形来证明线段相等.【跟踪训练】1.如图,在▱ABCD中,E,F两点在对角线BD上运动(E,F不重合),且保持BE=DF,连接AE,CF.请你猜想AE与CF有怎样的数量关系和位置关系,并说明理由.【解析】解:AE=CF,AE∥CF.理由如下:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD.∴∠ABE=∠CDF.又∵BE=DF,∴△ABE≌△CDF.∴AE=CF,∠AEB=∠CFD.∵∠AEB+∠AED=∠CFD+∠CFB=180°,∴∠AED=∠CFB.∴AE∥CF.2.如图,在菱形ABCD中,∠B=60°,动点E在边BC上,动点F在边CD上.(1)如图①,若E是BC的中点,∠AEF=60°,求证:BE=DF;(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.【解析】证明:(1)连接AC.∵在菱形ABCD中,∠B=60°,AB=BC=CD,∴∠BCD=180°-∠B=120°,△ABC是等边三角形.又∵E是BC的中点,∴AE⊥BC.∵∠AEF=60°,∴∠FEC=90°-∠AEF=30°.∴∠CFE=180°-∠FEC-∠BCD=180°-30°-120°=30°.∴∠FEC=∠CFE.∴EC=CF.∴BE=DF.(2)连接AC.由(1)知△ABC是等边三角形,∴AB=AC,∠ACB=∠BAC=∠EAF=60°.∴∠BAE =∠CAF.∵∠BCD=120°,∠ACB=60°,∴∠ACF=60°=∠B.∴△ABE≌△ACF.∴AE=AF.∴△AEF是等边三角形.3.在矩形ABCD中,AB=4 cm,BC=8 cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为O.(1)如图①,连接AF,CE.试说明四边形AFCE为菱形,并求AF的长.(2)如图②,动点P,Q分别从A,C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,已知点P的速度为5 cm/s,点Q的速度为4 cm/s,运动时间为t s,当以A,C,P,Q四点为顶点的四边形是平行四边形时,求t的值.【解析】解:(1)∵四边形ABCD是矩形,∴AD∥BC.∴∠OAE=∠OCF,∠AEO=∠CFO.∵EF垂直平分AC,垂足为O,∴OA=OC.∴△AOE≌△COF.∴OE=OF.∴四边形AFCE为平行四边形.又∵EF⊥AC,∴四边形AFCE为菱形.设AF =CF =x cm ,则BF =(8-x)cm ,在Rt △ABF 中,AB =4 cm ,由勾股定理得42+(8-x)2=x 2,解得x =5,∴AF =5 cm. (2)显然当P 点在AF 上,Q 点在CD 上时,A ,C ,P ,Q 四点不可能构成平行四边形;同理P 点在AB 上时,Q 点在DE 或CE 上,也不可能构成平行四边形.因此只有当P 点在BF 上,Q 点在ED 上时,才能构成平行四边形,如图,连接AP ,CQ ,若以A ,C ,P ,Q 四点为顶点的四边形是平行四边形,则PC =QA.∵点P 的速度为5 cm/s ,点Q 的速度为4 cm/s ,运动时间为t s ,∴PC =5t cm ,QA =(12-4t)cm.∴5t =12-4t ,解得t =43. ∴以A ,C ,P ,Q 四点为顶点的四边形是平行四边形时,t =43. 4.如图,正方形ABCD 的边长为8 cm ,E ,F ,G ,H 分别是AB ,BC ,CD ,DA上的动点,且AE =BF =CG =DH.(1)求证:四边形EFGH 是正方形;(2)判断直线EG 是否经过一个定点,并说明理由.【解析】(1)证明:∵四边形ABCD 为正方形,∴∠A =∠ABC =∠C =∠ADC =90°,AB =BC =CD =AD.∵AE =BF =CG =DH ,∴BE =CF =DG =AH.∴△AEH ≌△BFE ≌△CGF ≌△DHG.∴EH =EF =FG =GH ,∠1=∠2.∴四边形EFGH 为菱形.∵∠1+∠3=90°,∠1=∠2,∴∠2+∠3=90°.∴∠HEF =90°.∵四边形EFGH为菱形,∴四边形EFGH是正方形.(2)解:直线EG经过一个定点.理由如下:如图,连接BD,DE,BG.设EG与BD交于O点.∵BEDG,∴四边形BGDE为平行四边形.∴BD,EG互相平分.∴BO=OD.∴点O为正方形的中心.∴直线EG必过正方形的中心.。
2023学年北师大版九年级数学上学期专项讲练1-24 特殊平行四边形折叠(基础篇)

专题1.24 特殊平行四边形折叠专题(基础篇)(专项练习)一、单选题【知识点一】菱形折叠问题1.如图,将长方形纸片折叠,使A点落BC上的F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是()A.邻边相等的矩形是正方形B.对角线相等的菱形是正方形C.两个全等的直角三角形构成正方形D.轴对称图形是正方形AB=,则2.如图,将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF,若6BC的长为()A.2B.C.4D.3.如图,把菱形ABCD沿AH折叠,使B点落在BC上的E点处,若70∠=︒,则EDCB∠的大小为().A.15︒B.20︒C.30D.25︒4.如图,在菱形纸片ABCD中,60A∠=︒,点E是边BC上的一点,将纸片沿DE折叠,点C落在C'处,DC'恰好经过AB的中点P,则DEC∠的度数是()A.75︒B.60︒C.45︒D.78︒【知识点二】矩形将折叠问题5.如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为()A.28°B.31°C.62°D.56°6.如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将∠DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为()A.103B.203C.3D.47.如图,把矩形OABC放入平面直角坐标系中,点B的坐标为(10,8),点D是OC 上一点,将∠BCD沿BD折叠,点C恰好落在OA上的点E处,则点D的坐标是()A.(0,4)B.(0,5)C.(0,3)D.(0,2)8.如图,将矩形ABCD沿EF折叠,使点B落在边AD上的点M处,点C落在点N处,已知∠DMN=30°,连接BM,则∠AMB的度数为()A.60°B.75°C.80°D.85°【知识点三】正方形折叠问题9.如图,将正方形纸片ABCD折叠,使顶点B落在边AD上的点E处,折痕交AB于点F,交CD于点G.若1AE=,30∠=︒,则AB的长为()AFEA.2B.1C.D.2+10.如图,AC是正方形ABCD的对角线,E是BC上的点,1BE=,将ABE△沿AE折叠,使点B落在AC上点F处,则AB的长为()A.2B.3C.1D.111.把一个面积为4的正方形,通过沿虚线折叠得到一个新正方形,它的边长是()A.2 B C .1 D .1.41412.将一张正方形纸片ABCD 按如图所示的方式折叠,CE 、CF 为折痕,点B 、D 折叠后的对应点分别为B '、D ',若∠ECF =21°,则∠B 'CD '的度数为( )A .35°B .42°C .45°D .48°二、填空题【知识点一】菱形折叠问题13.如图,在菱形纸片ABCD 中,60A ︒∠=,折叠菱形纸片ABCD ,使点C 落在DP (P 为AB 的中点)所在的直线上,得到经过点D 的折痕DE ,则DEC ∠的度数为________.14.如图,在菱形ABCD 中,E 是AD 上一点,沿BE 折叠ABE △,点A 恰好落在BD 上的点F 处,连接CF ,若110DFC ∠=︒,则A ∠=__________.15.将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为_____.16.如图,将平行四边形ABCD进行折叠,折叠后AD恰好经过点C得到AD',若∠=︒==,则线段AC的长度为_________.90,5,4BAC DE CE【知识点二】矩形将折叠问题17.如图所示,把一张矩形纸片按如图所示方法进行两次折叠,得到等腰Rt∠ABC,若S△ABC=2,则S△ACD=__.18.如图,将矩形纸片ABCD折叠(AD>AB),使AB落在AD上,AE为折痕,然后将矩形纸片展开铺在一个平面上,E点不动,将BE边折起,使点B落在AE上的点G处,连接DE,若DE=EF,CE=1,则AD=________.19.如图,在矩形ABCD中,AB=4,BC=6,点E是BC的中点,点F在AD上运动,沿直线EF折叠四边形CDFE,得到四边形GHFE,其中点C落在点G处,连接AG,AH,则AG的最小值是__.20.矩形ABCD中,AB=5,AD=3,P为CD上一点,将∠ADP沿AP所在的直线折叠,得到∠AEP,当B、E、P三点共线时,tan∠DAP=_______【知识点三】正方形折叠问题21.如图,小明将一张正方形纸片对折,使得AB与CD重合,折痕为EF,展开后再沿BH折叠,使得点C刚好落在折痕EF上的C′处,若CH=1cm,则BC= _____cm.22.如图.将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为_____.23.如图,在一次综合实践活动中,小明将一张边长为10cm的正方形纸片ABCD,沿着BC 边上一点E 与点A 的连线折叠,点B '是点B 的对应点,延长EB '交DC 于点G ,经测量2cm BE =,20cm 3B G '=,则ECG 的面积为______2cm .24.如图,先将正方形纸片对折,折痕为MN ,再把B 点折叠在折痕MN 上,折痕为AE ,点B 在MN 上的对应点为H ,则HBC ∠的度数为______.三、解答题25.如果我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,该怎么办呢?小西进行了以下操作研究(如图1):第1步:对折矩形纸片ABCD ,使AD 与BC 重合,得到折痕EF ,把纸片展平. 第2步:再次折叠纸片,使点A 落在EF 上,并使折痕经过点B ,得到折痕BM ,同时得到了线段BN .小雅在小西研究的基础上,再次动手操作(如图2):将MN 延长交BC 于点G ,将△BMG 沿MG 折叠,点B 刚好落在AD 边上点H 处,连接GH ,把纸片再次展平.请根据小西和小雅的探究,完成下列问题:∠直接写出BE和BN的数量关系:;∠根据定理:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角是30°,请求出∠ABM的度数;∠求证:四边形BGHM是菱形.26.如图所示,在矩形ABCD中,AB=5,AD=8,点E,F分别是边AD,BC上的动点,且AE=CF,连接EF,将矩形ABCD沿EF折叠,使点C落在点G处,点D落在点H处,若EH与CB的延长线交于点P.(1)求证:PH=PB;(2)若∠PEA=45°,求AE的长度.27.【教材呈现】人教八年级下册数学教材第59页的部分内容.如图1,把一张矩形纸片按如图那样折一下,就可以裁出正方形纸片,为什么?(1)【问题解决】如图1,已知矩形纸片ABCD(AD>AB),将矩形纸片沿过点A的直线折叠,使点B落在边AD上,点B的对应点为F,折痕为AE,点E在BC上.求证:四边形ABEF是正方形.(请完成以下填空)证明:∠四边形ABCD是矩形,∠∠BAD=∠B=90°,∠折叠,∠AFE=∠B=90°,∠四边形ABEF是矩形()∠折叠,∠AB=(),∠四边形ABEF是正方形()(2)【问题拓展】如图2,已知平行四边形纸片ABCD(AD>AB),将平行四边形纸片沿过点A的直线折叠,使点B落在边AD上,点B的对应点为F,折痕为AE,点E在边BC上.∠求证:四边形ABEF是菱形.∠连结BF,若AE=5,BF=10,求菱形ABEF的面积.28.如图,E、F分别是正方形ABCD边AB、AD的中点,将△ABF沿BF折叠,点A 落在点Q处,连接FQ并延长,交DC于G点.(1)求证:CE=BF;(2)若AB=4,求GF的值.参考答案1.A【分析】将长方形纸片折叠,使A点落BC上的F处,可得到BA=BF,折痕为BE,沿EF剪下,故四边形ABFE为矩形,且有一组邻边相等,故四边形ABFE为正方形.解:∠将长方形纸片折叠,A落在BC上的F处,∠BA=BF,∠折痕为BE,沿EF剪下,∠四边形ABFE为矩形,∠四边形ABEF为正方形.故用的判定定理是;邻边相等的矩形是正方形.故选:A.【点拨】本题考查了正方形的判定定理,关键是根据邻边相等的矩形是正方形和翻折变换解答.2.D【分析】根据菱形及矩形的性质可得到∠BAC的度数,从而根据直角三角形的性质求得BC的长.解:∠四边形AECF为菱形,∠∠FCO=∠ECO,EC=AE,由折叠的性质可知,∠ECO=∠BCE,又∠FCO+∠ECO+∠BCE=90°,∠∠FCO=∠ECO=∠BCE=30°,在Rt∠EBC中,EC=2EB,又∠EC=AE,AB=AE+EB=6,∠EB=2,EC=4,∠Rt∠BCE中,BC故选:D.【点拨】本题主要考查了菱形的性质以及矩形的性质,解决问题的关键是根据折叠以及菱形的性质发现特殊角,根据30°的直角三角形中各边之间的关系求得BC 的长.3.A【分析】根据菱形的性质,已知菱形的对角相等,故推出70ADC B ∠=∠=︒,从而得出AED ADE ∠=∠.又因为//AD BC ,故DAE AEB ∠=∠,ADE AED ∠=∠,易得解.解:根据菱形的对角相等得70ADC B ∠=∠=︒.AD AB AE ==,AED ADE ∴∠=∠.根据折叠得70AEB B ∠=∠=︒.//AD BC ,70DAE AEB ∴∠=∠=︒,(180)255ADE AED DAE ∴∠=∠=︒-∠÷=︒.705515EDC ∴∠=︒-︒=︒.故选:A .【点拨】此题要熟练运用菱形的性质得到有关角和边之间的关系.在计算的过程中,综合运用了等边对等角、三角形的内角和定理以及平行线的性质.注意:折叠的过程中,重合的边和重合的角相等.4.A【分析】连接BD ,由菱形的性质及∠A =60°,得到三角形ABD 为等边三角形,P 为AB 的中点,利用三线合一得到DP 为角平分线,得到∠ADP =30°,∠ADC =120°,∠C =60°,进而求出∠PDC =90°,由折叠的性质得到∠CDE =∠PDE =45°,利用三角形的内角和定理即可求出所求角的度数.解:连接BD ,∠四边形ABCD为菱形,∠A=60°,∠∠ABD为等边三角形,∠ADC=120°,∠C=60°,∠P为AB的中点,∠DP为∠ADB的平分线,即∠ADP=∠BDP=30°,∠∠PDC=90°,∠由折叠的性质得到∠CDE=∠PDE=45°,在∠DEC中,∠DEC=180°−(∠CDE+∠C)=180°−(45°+60°)=75°.故选:A.【点拨】本题考查了折叠问题,菱形的性质,等边三角形的性质,以及内角和定理,熟练掌握折叠的性质是解本题的关键.5.D【分析】先利用互余计算出∠FDB=28°,再根据平行线的性质得∠CBD=∠FDB=28°,接着根据折叠的性质得∠FBD=∠CBD=28°,然后利用三角形外角性质计算∠DFE的度数.解:∠四边形ABCD为矩形,∥,∠ADC=90°,∠AD BCBDC62,∠FDB=90°-∠BDC=90°-62°=28°,∥,∠AD BC∠∠CBD=∠FDB=28°,∠矩形ABCD沿对角线BD折叠,∠∠FBD=∠CBD=28°,∠∠DFE=∠FBD+∠FDB=28°+28°=56°.故选:D.【点拨】本题考查了平行线的性质,轴对称的性质,矩形的性质,三角形的外角的性质,熟练的利用轴对称的性质得到相等的角是解本题的关键.6.A【分析】首先利用勾股定理计算出BD 的长,再根据折叠可得AD =A ′D =5,进而得到A ′B 的长,再设AE =x ,则A ′E =x ,BE =12-x ,再在Rt ∠A ′EB 中利用勾股定理可得方程:(12-x )2=x 2+82,解出x 的值,可得答案.解:∠AB =12,BC =5,∠AD =5,∠BD =13,根据折叠可得:AD =A ′D =5,∠A ′B =13-5=8,设AE =x ,则A ′E =x ,BE =12-x ,在Rt △A ′EB 中:(12-x )2=x 2+82,解得:x =103. 故选:A .【点拨】此题主要考查了图形的翻折变换,关键是掌握折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.7.C【分析】由题意可得AO =BC =10,AB =OC =8,DE =CD ,BE =BC =10,在Rt ABE △中,由勾股定理可求得6AE =,OE =4,设OD =x ,则DE =CD =8-x ,然后在Rt ODE △中,由勾股定理即可求得OD =3,继而求得点D 的坐标.解:∠点B 的坐标为(10,8),∠AO =BC =10,AB =OC =8,由折叠的性质,可得:DE =CD ,BE =BC =10,在Rt ABE △中,由勾股定理得:6AE =,∠OE =AO -AE =10-6=4,设OD =x ,则DE =CD =8-x ,在Rt ODE △中,由勾股定理得:222OD OE DE +=,即:()22248x x +=-,解得:3x =,∠OD =3,∠点D 的坐标是(0,3).故选:C.【点拨】本题主要考查了矩形的性质、折叠的性质、勾股定理,熟练掌握折叠的性质是解题的关键.8.B【分析】由四边形ABCD 是矩形,得∠A =∠ABC =90°,根据矩形ABCD 沿EF 折叠,使点B 落在边AD 上的点M 处,点C 落在点N 处,得∠NME =∠ABC =90°,ME =BE ,而∠DMN =30°,即知∠AME =60°,∠AEM =30°,即∠EMB +∠EBM =30°,可得∠EMB =∠EBM =15°,故∠AMB =∠AME +∠EMB =75°.解:∠四边形ABCD 是矩形,∠∠A =∠ABC =90°,∠矩形ABCD 沿EF 折叠,使点B 落在边AD 上的点M 处,点C 落在点N 处,∠∠NME =∠ABC =90°,ME =BE ,∠∠DMN =30°,∠∠AME =180°-∠NME -∠DMN =60°,∠∠AEM =90°-∠AME =30°,∠∠EMB +∠EBM =30°,∠ME =BE ,∠∠EMB =∠EBM =15°,∠∠AMB =∠AME +∠EMB =75°,故选:B .【点拨】本题考查了矩形中的折叠问题,解题的关键是掌握折叠的性质:折叠前后能够重合的线段相等、能够重合的角相等.9.D【分析】先求出AF和EF的长,再根据翻折变换的知识得到EF=BF,进而求出AB的长.解:∠四边形ABCD是正方形,∠∠A= 90°,AE= 1,∠AFE= 30°∠EF= 2,AF∠正方形纸片ABCD折叠,使顶点B落在边AD上的点E处,EF= BF,BF= 2,∠AB= AF+ BF故选:D.【点拨】本题主要考查了翻折变换以及正方形的性质,解题的关键是根据翻折变换得到EF=BF,此题难度不大.10.C【分析】∠BCD=45°,由折叠的性由正方形的性质得AB=BC,∠BCD=∠B=90°,∠ECF=12质得∠AFE=∠B=90°,FE=BE=1,证出△CEF是等腰直角三角形,则CE FE进而得出答案.解:∠四边形ABCD是正方形,∠BCD=45°,∠AB=BC,∠BCD=∠B=90°,∠ECF=12由折叠的性质得:∠AFE=∠B=90°,FE=BE=1,∠∠CFE=90°,∠∠CEF是等腰直角三角形,FE,∠CE=BE+CE=1∠AB=BC=1故选:C.【点拨】本题考查了翻折变换的性质、正方形的性质、等腰直角三角形的判定与性质等知识;熟练掌握翻折变换和正方形的性质是解题的关键.11.B由原正方形的面积是4,可求得原正方形的边长为2,由勾股定理可出新正方形边长.解:∠原正方形的面积是4,∠原正方形的边长,∠由折叠可得四角是等腰直角三角形,其腰长为1,由勾股定理得:新正方形边长,故选:B.【点拨】本题考查折叠问题,正方形的性质,勾股定理,掌握运用勾股定理是解题的关键.12.D【分析】可以设∠ECB'=α,∠FCD'=β,根据折叠可得∠DCE=∠D'CE,∠BCF=∠B'CF,进而可求解.解:设∠ECB'=α,∠FCD'=β,根据折叠可知:∠DCE=∠D'CE,∠BCF=∠B'CF,∠∠ECF=21°,∠∠D'CE=21°+β,∠B'CF=21°+α,∠四边形ABCD是正方形,∠∠BCD=90°,∠∠D'CE+∠ECF+∠B'CF=90°∠21°+β+21°+21°+α=90°,∠α+β=27°,∠∠B'CD'=∠ECB'+∠ECF+∠FCD'=α+21°+β=21°+27°=48°则∠B'CD'的度数为48°.故选:D.【点拨】本题考查了正方形与折叠问题,解决本题的关键是熟练运用折叠的性质.13.75°连接BD ,先证明ABD △为等边三角形,然后根据三线合一定理得到30ADP BDP ∠=∠=即可得到90PDC ∠=,则45CDE PDE ∠=∠=,再根据三角形内角和定理求解即可.解:连接BD ,∠四边形ABCD 为菱形,∠AD =AB ,60C A ∠==∠,AB∠CD ,∠180A ADC ∠+∠=,∠120ADC ∠=∠60A ∠=,∠ABD △为等边三角形,∠P 为AB 的中点,∠DP 为ADB ∠的平分线,即30ADP BDP ∠=∠=,∠90PDC ∠=,由折叠的性质得到45CDE PDE ∠=∠=,在DEC 中,()18075DEC CDE C ∠=-∠+∠=.故答案为:75°.【点拨】本题主要考查了菱形的性质,等边三角形的性质与判定,折叠的性质,三角形内角和定理,解题的关键在于能够熟练掌握相关知识进行求解.14.100︒【分析】根据菱形的性质得到AB =BC =CD =DA ,AD//BC ,∠ADB =∠CBF =∠ABD ,再根据折叠的性质得到∠BFC =∠BCF ,由三角形内角和与外角的性质得到结果.解:∠四边形ABCD 是菱形,∠AB =BC =CD =DA ,AD//BC ,∠∠ADB =∠CBF =∠ABD ,∠E 是AD 上一点,沿BE 折叠ABE △,点A 恰好落在BD 上的点F 处,∠BA =BF ,∠A =∠BFE ,∠BF =BC ,∠∠BFC =∠BCF ,∠110DFC ∠=︒,∠∠BFC =∠BCF =70°,∠∠ADB =∠CBF =40°,∠∠A =180°-2∠ADB =180°-80°=100°,故答案为:100︒.【点拨】本题主要考查了菱形的基本性质与折叠的基本性质,根据菱形的基本性质与折叠的基本性质得到边相等是解题的关键.15.23√【分析】根据菱形AECF ,得∠FCO =∠ECO ,再利用∠ECO =∠ECB ,可通过折叠的性质,结合直角三角形勾股定理求得BC 的长,则利用菱形的面积公式即可求解.解:∵四边形AECF 是菱形,AB =3,∴设BE =x ,则AE =3﹣x ,CE =3﹣x ,∵四边形AECF 是菱形,∴∠FCO =∠ECO ,∵∠ECO =∠ECB ,∴∠ECO =∠ECB =∠FCO =30°,∴2BE =CE ,∴CE =2x ,∴2x =3﹣x ,解得:x =1,∴CE =2,利用勾股定理得出:BC 2+BE 2=EC 2,BC 3=√又∵AE =AB ﹣BE =3﹣1=2,则菱形的面积=AE •BC =23√.故答案为23√.【点拨】此题主要考查了折叠问题以及勾股定理等知识,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.16.12【分析】由平行四边形的性质可得AD =BC ,AB =CD =DE +CE =9,AB //CD ,可得∠ECD '=90°,由折叠的性质可得D 'E =DE =5,AD =AD ',由勾股定理可求CD '的长,AC 的长.解:∠四边形ABCD 是平行四边形∠AD =BC ,AB =CD =DE +CE =9,AB //CD∠∠BAC =∠ACD =90°∠∠ECD '=90°∠将平行四边形ABCD 进行折叠,折叠后AD 恰好经过点C 得到AD ',∠D 'E =DE =5,AD =AD '∠CD '3∠AD '=AC +3=AD =BC∠BC 2=AB 2+AC 2,∠(AC +3)2=81+AC 2,∠AC =12故答案为:12.【点拨】本题考查了翻折变换,平行四边形的性质,求出CD '的长是本题的关键. 17.【分析】根据折叠的性质可得ACD DEC S S =,分别求出DE ,EC ,求出DEC S ,即可得出ACD S .解:如图:过点A 作AF DE ⊥于点F ,ABC 是等腰直角三角形,2ABC S =, 1·22ABC S AB BC ∴==,即2AB BC ==,AC ∴==折叠,AC CE ∴==DAC DEC SS =,纸片为矩形, ∴折叠后45FDA ∠=︒,90DFA ∠=︒,DFA ∴是等腰直角三角形,2DF FA EC CB ∴==+=,2AB EF ==,224DE DF FE ∴=+=+=+(114422ACD DEC S S DE EC ∴==⨯=⨯+⨯,故答案为:4.【点拨】本题考查了折叠问题,矩形的性质,等腰直角三角形,三角形的面积,勾股定理,通过折叠得出ACD DEC S S =是解题的关键.18.22+【分析】证明Rt △EBF ∠Rt △EB ′D (HL ),推出BF =DB ′,再证明DB ′=EC =BF =1,想办法求出AB ′,可得结论.解:由翻折的性质可知,EB =EB ′,∠B =∠AB ′E =∠EB ′D =90°,在Rt△EBF和Rt△EB′D中,EB EB EF ED'=⎧⎨=⎩,∠Rt△EBF∠Rt△EB′D(HL),∠BF=DB′,∠四边形ABCD是矩形,∠∠C=∠CDB′=∠EB′D=90°,∠四边形ECDB′是矩形,∠DB′=EC=1,∠BF=EC=1,由翻折的性质可知,BF=FG=1,∠F AG=45°,∠EGF=∠B=∠AGF=90°,∠AG=FG=1,∠AF∠AB=AB∠AD=AB′+DB故答案为:.【点拨】本题考查翻折变换,矩形的性质,全等三角形的判定和性质,等腰直角三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.19.2【分析】如图,当A、G、E共线时,AG最小,先求出AE,根据AG=AE﹣EG即可解决问题.解:如图,依题意:点G在以点E为圆心,12BC长为半径的圆上运动,当A、G、E共线时,AG最小,∠四边形ABCD 是矩形,∠∠B =90°,BE =EC =3,AB =4,∠AE5.此时AG =AE ﹣EG =5﹣3=2.故答案为2.【点拨】本题考查了矩形的性质,勾股定理,点到圆的距离,明确点和圆的位置关系是解决本题的关键.20.13【分析】由翻折可得AD =AE ,在Rt ∠ABE 中可求出BE ,设DP =EP =x ,表示出BP 和CP ,在Rt ∠BCP 中,通过勾股定理即可列出等式,解出方程,从而求出答案.解:矩形ABCD 中,AB =5,AD =3,则CD =5,BC =3,∠ADP 沿AP 所在的直线折叠,得到∠AEP ,且B 、E 、P 三点共线,∠易证∠ADP ∠∠AEP ,∠AE =AD ,DP =EP ,∠ADP =∠AEP =90°,在Rt ∠ABE 中,AB =5,AE =3,∠BE =4;设DP =EP =x ,则BP =4x +,CP=5x -,在Rt ∠BCP 中,222+BC CP BP =,即()()2223+54x x -=+,解得1x =,∠DP =1,在Rt ∠ADP 中,tan∠DAP =13DP AD =.故答案为:13.【点拨】本题主要考查翻折问题,直角三角函数和勾股定理,找准线段之间的关系,并准确计算是解题的关键.21【分析】连接CC′,证明∠BCC′是等边三角形,再由折叠的性质得到∠HBC=∠HBC′=30°,利用含30度角的直角三角形的性质求解即可解决问题.解:如图,连接CC′,由折叠的性质知,折痕为EF是BC的垂直平分线,∠BC′=CC′,又由折叠的性质知,BC= BC′,∠HBC=∠HBC′,∠BC′=CC′=BC,∠∠BCC′是等边三角形,∠∠C′BC=60°,∠∠HBC=∠HBC′=30°,在Rt△HBC中,∠HBC=30°,CH=1cm,∠HB=2cm,∠BCcm),【点拨】本题考查了翻折变换的性质,等边三角形的判定和性质,勾股定理,解决本题的关键是掌握翻折的性质.22.45°##45度【分析】首先根据正方形的性质可得∠1+∠2+∠3+∠4=∠ABC=90°,再根据折叠可得∠1=∠2=1 2∠ABD ,∠3=∠4=12∠DBC ,进而可得∠2+∠3=45°,即∠EBF =45°.解:∠四边形ABCD 是正方形,∠∠ABC =90°,根据折叠可得∠1=∠2=12∠ABD ,∠3=∠4=12∠DBC ,∠∠1+∠2+∠3+∠4=∠ABC =90°,∠∠2+∠3=45°,即∠EBF =45°,故答案为:45°.【点拨】此题主要考查了图形的翻折变换和正方形的性质,关键是找准图形翻折后,哪些角是相等的.23.403##1133 【分析】根据题意,BE B E '=,进而求得EC ,勾股定理求得CG ,即可求得ECG 的面积. 解:折叠,∴BE B E '=2cm BE =,20cm3B G '=, 2023EG ∴=+263=cm ,8EC BC BE =-=cm ∠四边形ABCD 是正方形∠90C ∠=︒Rt EGC △中103CG ==cm . 11104082233ECG S EC CG ∴=⨯⨯=⨯⨯=△2cm .故答案为:40 3【点拨】本题考查了折叠的性质,勾股定理,掌握勾股定理是解题的关键.24.15°【分析】由翻折的性质AH=AB,MN垂直平分AD,于是得到DH=AH=AB=AD,故此∠ADH 为等边三角形,由∠ADH为等边三角形可知∠HAB=30°,在∠ABH中可求得∠ABH=75°,故此可求得∠HBC=15°.解:∠MN垂直平分AD,∠DH=AH.由翻折的性质可知:AH=AB.∠正方形ABCD中,∠AH=AD=DH.∠∠ADH是一个等边三角形.∠∠DAH=60°.∠∠HAB=30°.∠AB=AH,∠∠ABH=12×(180°−30°)=75°.∠∠HBC=∠ABC−∠ABH=90°−75°=15°.故答案是:15°.【点拨】本题主要考查的是翻折的性质、线段垂直平分线的性质、等边三角形的性质和判定、等腰三角形的性质,正方形的性质,证得∠ADH是一个等边三角形是解题的关键.25.∠BE=12BN;∠∠ABM=30°;∠见分析.【分析】(1)根据折叠的性质可得BE=12AB,从而得到BE=12BN,即可求解;(2)根据在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角是30°,可得∠BNE=30°,即可求解;(3)由∠得∠ABM=30°,从而得到∠BMG是等边三角形,进而得到BM=BG,再有折叠的性质,即可求证.解:∠解:∠对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,AB,∠BE=12∠再次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到了线段BN.∠AB=BN,BN;∠BE=12∠解:∠由折叠的性质得:∠BEN=∠AEN=90°,BN,∠BE=12∠∠BNE=30°,∠∠ABN=60°,∠ABN=30°;由折叠的性质得:∠ABM=12∠证明:由∠得∠ABM=30°,∠四边形ABCD是矩形,∠∠A=∠ABC=90°,∠∠AMB=∠BMN=60°,∠MBG=60°,∠∠BMG是等边三角形,∠BM=BG,由折叠得BM=MH,BG=GH,∠BM=MH=BG=GH,∠四边形BGHM是菱形.【点拨】本题主要考查了图形的变换——折叠,矩形的性质,菱形的判定等,熟练掌握图形折叠前后对应边相等,对应角相等是解题的关键.26.(1)见分析(2)AE【分析】(1)根据∠PEF=∠PFE,证明PE=PF,再根据折叠的性质ED=EH,DE=BF,进一步计算即可证明PH=PB;(2)先证明△AEQ和△BPQ都是等腰直角三角形,设AE=CF=x,则EQ x,PQ(5-x) ,利用PE=PF代出方程求解即可.解:(1)证明:∠四边形ABCD是矩形,∠AD∠BC,∠∠DEF=∠PFE,由翻折变换可知,∠DEF=∠PEF,∠∠PEF=∠PFE,∠PE=PF;∠AD=BC,AE=FC,∠ED=BF.由折叠性质得ED=EH,∠BF=EH,∠PE-EH=PF-BF,∠PH=PB;(2)解:设PE交AB于点Q,设AE=CF=x,则DE=BF=8-x,∠∠PEA=45°,∠A=∠ABC=∠ABP=90°,∠∠AEQ=∠AQE=∠PBQ=∠QPB=45°,∠△AEQ和△BPQ都是等腰直角三角形,∠BQ=PB=5-x,由勾股定理得:EQ,PQ-x) ,∠PE=PF,∠PQ+EQ=PB+BF-x=5-x+8-x,解得:x∠AE【点拨】本题考查了翻折变换,等腰直角三角形的判定和性质,勾股定理等知识,解答本题的关键是明确题意,找出所求问题需要的条件.27.(1)有三个角是直角的四边形是矩形;AF;一组邻边相等的矩形是正方形.(2)∠证明见详解;∠菱形ABEF的面积为25【分析】(1)由矩形的性质得∠BAD=∠B=90°,再由折叠的性质得:∠AFE=∠B=90°,AB=AF,则四边形ABEF是矩形,然后由AB=AF,即可得出结论;(2)∠由平行四边形的性质得AD∠BC,则∠F AE=∠BEA,再证AB=BE,则AF=BE,得四边形ABEF是平行四边形,然后由AF=AB即可得出结论;∠由菱形面积公式得S菱形ABEF=12AE•BF,即可得出答案.(1)解:∠四边形ABCD是矩形,∠∠BAD=∠B=90°,由折叠的性质得:∠AFE=∠B=90°,∠四边形ABEF是矩形(有三个角是直角的四边形为矩形),由折叠的性质得:AB=AF,∠四边形ABEF是正方形(有一组邻边相等的矩形是正方形),故答案为:有三个角是直角的四边形为矩形;AF;有一组邻边相等的矩形是正方形;(2)∠证明:∠四边形ABCD是平行四边形,∠AD∠BC,∠∠F AE=∠BEA,由折叠的性质得:AF=AB,∠BAE=∠F AE,∠∠BEA=∠BAE,∠AB=BE,∠AF=BE,∠四边形ABEF是平行四边形,又∠AF=AB,∠平行四边形ABEF是菱形;∠解:如图,∠四边形ABEF是菱形,AE=5,BF=10,∠S菱形ABEF=12AE•BF=12×5×10=25,故菱形ABEF的面积为25.【点拨】本题是四边形综合题目,考查了矩形的判定与性质、正方形的判定、菱形的判定与性质、平行四边形的判定与性质、等腰三角形的判定、折叠的性质、平行线的性质等知识,本题综合性强,熟练掌握折叠的性质、矩形的判定与性质是解题的关键.28.(1)见分析(2)GF的值为103.【分析】(1)先判断出AF=BE,进而得出△F AB∠∠EBC(SAS),即可得出结论;(2)连接BG,根据HL证明Rt△BQG∠Rt△BCG,得QG=GC,设QG=b,在Rt△DFG 中,根据勾股定理列方程可得b,从而可得结论.解:(1)证明:∠四边形ABCD是正方形,∠AB=AD,∠A=∠ABC=90°,∠E、F分别是正方形ABCD边AB、AD的中点,∠AF=BE,∠∠F AB∠∠EBC(SAS),∠CE=BF;(2)解:如图,连接BG,由折叠得:AB=BQ,∠BQF=∠A=90°,∠AB=BC,∠BC=BQ,∠BG=BG,∠Rt△BQG∠Rt△BCG(HL),∠QG=GC,∠AB=4,F是正方形ABCD边AD的中点,设QG=b,则DF=AF=FQ=2,FG=2+b,DG=4-b,在Rt△DFG中,∠DF2+DG2=FG2,∠2222(4)(2)b b+-=+,∠b=43,即QG=43,∠GF=FQ+QG=2+43=103.∠GF的值为103.【点拨】此题主要考查了正方形的性质,全等三角形的判定和性质,勾股定理等知识,正确作辅助线是本题的关键.。
2023学年北师大版九年级数学上学期专项讲练1-14 添加一个条件构成特殊平行四边形(基础篇)

专题1.14 添加一个条件构成特殊平行四边形专题(基础篇)(专项练习)说明:此专题对于学生掌握平行四边形、特殊平行四边形的判定方法一种有效方法,对提升学生综合学习四边形十分必要,值得巩固学习。
一、单选题【知识点一】添加一个条件构成平行四边形1.如图,在四边形ABCD 中,E 是BC 边的中点,连接DE 并延长,交AB 的延长线于点F ,AB BF =.添加一个条件使四边形ABCD 是平行四边形,你认为下面四个条件中可选择的是( )A .AD BC =B .CD BF =C .A C ∠=∠D .F CDF ∠=∠2.如图,在四边形ABCD 中,AB ∥CD ,添加下列一个条件后,定能判定四边形ABCD 是平行四边形的是( )A .AB =BC B .AC =BD C .∥A =∥C D .∥A =∥B3.如图所示,在四边形ABCD 中,AD //BC ,要使四边形ABCD 成为平行四边形还需要条件( )A .AB DC = B .D B ∠=∠ C .AB AD = D .12∠=∠4.已知一个凸四边形的一条对角线被另一条对角线平分,请你从下列四个条件中再选取一个作为已知条件,使得这个四边形一定是平行四边形.你的选择是( ) A .一组对边平行; B .一组对角相等; C .一组邻边相等;D .一组对边相等.【知识点二】添加一个条件构成菱形5.ABCD 的对角线AC 与BD 相交于点O ,添加以下条件,不能判定平行四边形ABCD 为菱形的是( )A .AC BD =B .AC BD ⊥ C .ACD ACB ∠=∠D .BC CD =6.在ABCD 中,AC 与BD 相交于点O ,要使四边形ABCD 是菱形,还需添加一个条件,这个条件可以是( )A .AO =COB .AO =BOC .AO ∥BOD .AB ∥BC7.如图,下列条件能使平行四边形ABCD 是菱形的为( ) ∥AC ∥BD ;∥∥BAD =90°;∥AB =BC ;∥AC =BD .A .∥∥B .∥∥C .∥∥D .∥8.如图,在四边形ABCD 中,E ,F ,G ,H 分别是边AB ,BC ,CD ,DA 的中点.要使四边形EFGH 为菱形,可以添加的一个条件是( )A .四边形ABCD 是菱形B .AC 、BD 互相平分 C .AC =BDD .AC ∥BD【知识点三】添加一个条件构成矩形9.如图,在四边形ABCD 中,对角线AC 与BD 相交于点O ,,AO CO BO DO ==.添加下列条件,可以判定四边形ABCD 是矩形的是( )A .AB AD = B .AC BD = C .AC BD ⊥ D .ABO CBO ∠=∠10.如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,添加下列条件仍不能判断四边形ABCD 是矩形的是( )A .AB 2+BC 2=AC 2 B .AB = ADC .OA = ODD .∥ABC +∥ADC =180°11.如图,在平行四边形 ABCD 中,对角线AC 与BD 相交于点O ,添加下列条件不能判定四边形ABCD 是矩形的是( )A .AC ∥BDB .AB ∥BC C .AC =BD D .∥1=∥212.四边形ABCD 的对角线互相平分,要使它变为矩形,需要添加的条件是( ) A .AB =CDB .∥ABD =∥CBDC .AB =BCD .AC =BD【知识点四】添加一个条件构成正方形13.已知四边形ABCD 是平行四边形,下列结论不正确的是( ) A .当AB BC =时,它是菱形 B .当AC BD ⊥时,它是菱形 C .当90ABC ∠=︒时,它是矩形D .当AC BD =时,它是正方形14.在四边形ABCD 中,∥A =∥B =∥C =90°.如果再添加一个条件可推出四边形是正方形,那么这个条件可以是( ) A .AB =CDB .BC =CDC .∥D =90°D .AC =BD15.下列关于ABCD 的叙述,正确的是( ) A .若AC BD =,则ABCD 是矩形 B .若AB AD =,则ABCD 是正方形 C .若AB BC ⊥,则ABCD 是菱形D .若AC BD ⊥,则ABCD 是正方形16.如图,如果要证明四边形ABCD 为正方形,那么我们需要在四边形ABCD 是平行四边形的基础上,进一步证明( )A .AB BD =且AC BD ⊥ B .90BAD ∠=︒且AB AD = C .90BAD ∠=︒且AC BD = D .AC 和BD 互相垂直平分二、填空题【知识点一】添加一个条件构成平行四边形17.如图,点E 、F 在ABCD 的对角线AC 上,连接BE 、DE 、DF 、BF ,请添加一个条件使四边形BEDF 是平行四边形,那么需要添加的条件是______.(只填一个即可)18.如图,在平行四边形ABCD 中,E 、F 分别是AB 、DC 上的点,请添加一个条件,使得四边形EBFD 为平行四边形,则添加的条件是______.(答案不唯一,添加一个即可).19.如图,在ABCD 中,对角线AC 、BD 相交于点O ,已知点E 、F 分别是BD 上的点,请你添加一个条件_______________ ,使得四边形AFCE 是一个平行四边形.20.如图,在四边形ABCD 中,,AB CD =对角线,AC BD 相交于点,O OA OC =,请你添加一个条件____________,使四边形ABCD 是平行四边形(填一个即可).【知识点二】添加一个条件构成菱形21.如图,平行四边形ABCD 的对角线AC 与BD 交于点O ,请你添加一个条件使它是菱形,你添加的条件是______.22.如图,在∥ABC 中,D ,E ,F 分别是AB ,BC ,AC 的中点,请补充一个条件:______,使四边形DBEF 是菱形.23.如图,在四边形ABCD 中,AB 与CD 不平行,E 、F 分别是AD 、BC 的中点,G 、H 分别是BD 、AC 的中点,当AB 、CD 满足条件 _______时,有EF ∥GH .24.如图,AD BC ∥,AB DC ∥,4AB =,150ADE ∠=︒,那么A ∠=____时,四边形ABCD 是菱形.【知识点三】添加一个条件构成矩形25.如图所示,顺次连接四边形ABCD 各边中点得到四边形EFGH ,要使四边形EFGH 为矩形,应添加的条件是___;要使四边形EFGH 为菱形,应添加的条件是___(只填序号).备选答案:∥AB ∥CD ;∥AC =BD ;∥AC ∥BD ;∥AB =DC .26.ABC 中,延长BA 至D 使得AB AD =,延长CA 至E 使得AC AE =,当ABC 满足条件____________时,四边形BCDE 是矩形.27.如图,ABCD 的对角线交于点O ,请你添加一个条件,使ABCD 是矩形,这个条件可以是:___(图中不再添加其他的点或线,只需写出一个条件即可).28.如图,在ABCD 中,对角线AC 、BD 相交于点O ,若再补充一个条件能使它成为矩形,则这个条件可以是______(只填一个条件即可).【知识点四】添加一个条件构成正方形=,AC平29.如图,四边形ABCD中,对角线AC,BD相交于点O,AD//BC,OA OC分BAD∠.欲使四边形ABCD是正方形,则还需添加添加________(写出一个合适的条件即可)30.能使平行四边形ABCD为正方形的条件是___________(填上一个符合题目要求的条件即可).31.如图,四边形ABCD是平行四边形,AC与BD相交于点O,AB=AD,添加一个条件:__,可使它成为正方形.32.如图,四边形ABCD是矩形,则只须补充条件_____(用字母表示,只添加一个条件)就可以判定四边形ABCD是正方形.三、解答题∥,∥∥BAD=∥BCD这三个条件中选择其中一个你认为合33.在∥AD=BC,∥AD BC适的,补充在下面的问题中,并完成问题的解答.问题:如图,在四边形ABCD中,对角线AC,BD交于点O,OA=OC,_______(请填序号),求证:四边形ABCD为平行四边形.34.如图,四边形ABCD 的对角线AC 与BD 交于点O ,若//AB CD ,OA OC , (1)求证:四边形ABCD 是平行四边形(2)请你在不添加辅助线的情况下,添一个条件 ,使四边形ABCD 是菱形35.如图,在平行四边形ABCD 中,对角线AC 、BD 交于点O , E 、F 是AC 上两点,且AE = CF ,连接BE 、ED 、DF 、FB 得四边形BEDF .(1)求证:四边形BEDF 是平行四边形.(2)当EF 、BD 满足_____________ 条件时,四边形BEDF 是矩形.(不必证明....).36.如图,在∥ABCD 中,E 、M 分别为AD 、AB 的中点,DB ∥AD ,延长ME 交CD的延长线于点N,连接AN.(1)证明:四边形AMDN是菱形;(2)若∥DAB=45°,判断四边形AMDN的形状,并说明理由.参考答案1.D【分析】把A 、B 、C 、D 四个选项分别作为添加条件进行验证,D 为正确选项.添加D 选项,即可证明∥DEC∥∥FEB ,从而进一步证明DC =BF =AB ,且DC //AB .解:添加A 、AD BC =,无法得到AD //BC 或CD=BA ,故错误;添加B 、CD BF =,无法得到CD //BA 或AD BC =,故错误;添加C 、A C ∠=∠,无法得到ABC CDA ∠=∠,故错误;添加D 、F CDF ∠=∠∥F CDF ∠=∠,CED BEF ∠=∠,EC BE =,∥CDE BFE ∆∆≌, //CD AF ,∥CD BF =,∥BF AB =,∥CD AB =,∥四边形ABCD 是平行四边形.故选D .【点拨】本题是一道探索性的试题,考查了平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键.2.C【分析】利用平行线的判定与性质结合平行四边形的判定得出即可.解:∥AB //CD ,∥∥B +∥C =180°,当∥A =∥C 时,则∥A +∥B =180°,故AD //BC ,则四边形ABCD 是平行四边形.故选C.【点拨】本题考查了平行四边形的判定,掌握平行四边形的判定是解题的关键. 3.B【分析】根据等腰梯形的定义可判断A ;根据平行线的性质和三角形的内角和定理求出∥BAC=∥DCA,推出AB∥CD可以判断B;根据平行四边形的判定可判断C;根据平行线的性质可以判断D.解:A、符合条件AD∥BC,AB=DC,可能是等腰梯形,故A选项错误;B、∥AD∥BC,∥∥1=∥2,∥∥B=∥D,∥∥BAC=∥DCA,∥AB∥CD,∥四边形ABCD是平行四边形,故B选项正确.C、根据AB=AD和AD∥BC不能推出平行四边形,故C选项错误;D、根据∥1=∥2,推出AD∥BC,不能推出平行四边形,故D选项错误;故选B【点拨】本题主要考查对平行四边形的判定,等腰梯形的性质,三角形的内角和定理,平行线的性质和判定等知识点的理解和掌握,能综合运用性质进行推理是解此题的关键.4.A【分析】选项A,利用AAS证明∥OBC∥∥ODA(AAS),由此根据对角线互相平分的四边形是平行四边形证明.解:如图,OA=OC,∥BC∥AD,∥∥OBC=∥ODA,∥OCB=∥OAD,∥OA=OC,∥∥OBC∥∥ODA(AAS),∥OB=OD,∥四边形ABCD是平行四边形,故A选项可以使得这个四边形一定是平行四边形.选项B、C、D均不能证明这个四边形一定是平行四边形.故选:A.【点拨】此题考查了平行四边形的判定定理,熟记平行四边形的判定定理是解题的关键.5.A【分析】判定一个平行四边形是否是菱形,在平行四边形这个条件上加上对角线互相垂直,或者一组邻边相等,或者对角线平分一组对角,而对角线相等这个条件只能判定这个平行四边形是矩形,并不是菱形.解:A选项中AC=BD加上已知条件中的平行四边形可以判定平行四边形ABCD是矩形,符合题意;B选项中AC∥BD加上已知条件中的平行四边形可以判定平行四边形ABCD是菱形,不符合题意;C选项中∥ACD=∥ACB加上已知条件中的平行四边形可以判定平行四边形ABCD是菱形,不符合题意;D选项中BC=CD加上已知条件中的平行四边形可以判定平行四边形ABCD是菱形,不符合题意.故答案为:A .【点拨】本题考查菱形的应用,熟练掌握菱形的判定方法是解题关键.6.C【分析】根据菱形的判定分析即可;解:∥四边形ABCD时平行四边形,AO∥BO,∥ABCD是菱形;故选C.【点拨】本题主要考查了菱形的判定,准确分析判断是解题的关键.7.A【分析】根据菱形的判定定理以及所给条件证明平行四边形ABCD是菱形,菱形的判定方法有三种:∥定义:一组邻边相等的平行四边形是菱形;∥四边相等的四边形是菱形;∥对角线互相垂直的平行四边形是菱形.据此判断即可.解:∥▱ABCD 中,AC ∥BD ,根据对角线互相垂直的平行四边形是菱形,即可判定▱ABCD 是菱形;故∥正确;∥▱ABCD 中,∥BAD =90°,根据有一个角是直角的平行四边形是矩形,即可判定▱ABCD 是矩形,而不能判定▱ABCD 是菱形;故∥错误;∥▱ABCD 中,AB =BC ,根据一组邻边相等的平行四边形是菱形,即可判定▱ABCD 是菱形;故∥正确;∥∥ABCD 中,AC =BD ,根据对角线相等的平行四边形是矩形,即可判定∥ABCD 是矩形,而不能判定∥ABCD 是菱形;故∥错误.故正确的为∥∥故选:A .【点拨】此题考查了菱形的判定与矩形的判定定理.此题难度不大,注意掌握菱形的判定定理是解此题的关键.8.C【分析】根据E 、F 、G 、H 分别为AB 、BC 、CD 、DA 的中点,利用三角形中位线定理及AC =BD ,等量代换得到四条边相等,确定出四边形EFGH 为菱形,得证.解:应添加的条件是AC =BD ,理由为:证明:∥E 、F 、G 、H 分别为AB 、BC 、CD 、DA 的中点,且AC =BD ,∥EH =12BD ,FG =12BD ,HG =12AC ,EF =12AC , ∥EH =HG =GF =EF ,则四边形EFGH 为菱形,故选:C .【点拨】本题考查三角形中位线定理、菱形的判定,解题的关键是熟知三角形的中位线定理.9.B【分析】根据矩形的判定定理,对角线相等的平行四边形或有一个角是直角的平行四边形,逐项分析判断即可.解:由AO CO =,BO DO =,可证四边形ABCD 是平行四边形,A. AB AD =,根据邻边相等的平行四边形,可证四边形ABCD 是菱形,不符合题意;B. AC BD =,对角线相等的平行四边形是矩形,可证四边形ABCD 是矩形,符合题意;C. AC BD ⊥,根据对角线互相垂直的平行四边形是菱形,可证四边形ABCD 是菱形,不符合题意;D. ABO CBO ∠=∠,证ABO ADO ∠=∠,根据等角对等边可证AB AD =,即可证得四边形ABCD 是菱形,不符合题意.故选B【点拨】本题考查了特殊四边形菱形的证明,平行四边形的证明,矩形的证明,注意对这些证明的理解,容易混淆,小心区别对比.10.B【分析】由勾股定理的逆定理证得∥ABC =90°,根据有一个角是直角的平行四边形是矩形可判断A ;根据有一组邻边相等的平行四边形是菱形可判断B ;根据对角线相等的平行四边形是矩形可判断C ;根据有一个角是直角的平行四边形是矩形可判断D .解:A .∥AB 2+BC 2=AC 2,∥∥ABC =90°,∥▱ABCD 为矩形,故本选项不符合题意;B .∥AB =AD ,∥▱ABCD 为菱形,故本选项符合题意;C .∥四边形ABCD 是平行四边形,∥OA =OC ,OB =OD ,∥OA =OD ,∥AC =BD ,∥▱ABCD 是矩形,故本选项不符合题意;D .∥四边形ABCD 是平行四边形,∥∥ABC =∥ADC ,∥∥ABC +∥ADC =180°,∥∥ABC =∥ADC =90°,∥▱ABCD为矩形,故本选项不符合题意;故选:B.【点拨】本题考查了矩形的判定定理,勾股定理的逆定理,平行四边形的性质,熟练掌握矩形的判定方法是解决问题的关键.11.A【分析】根据菱形和矩形的判定、等腰三角形的性质、平行四边形的性质逐项判断即可得.解:A、由对角线互相垂直的平行四边形是菱形可知,添加AC BD⊥能判定ABCD是菱形,不一定是矩形,则此项符合题意;⊥能判定ABCD是B、由有一个角是直角的平行四边形是矩形可知,添加AB BC矩形,则此项不符题意;=能判定ABCD是矩形,C、由对角线相等的平行四边形是矩形可知,添加AC BD则此项不符题意;D、12∠=∠,∴=,OA OD四边形ABCD是平行四边形,AC OA BD OD∴==,2,2∴=,AC BD∴是矩形,ABCD即添加12∠=∠能判定ABCD是矩形,则此项不符题意;故选:A.【点拨】本题考查了菱形和矩形的判定、等腰三角形的性质、平行四边形的性质,熟练掌握矩形的判定方法是解题关键.12.D【分析】由四边形ABCD的对角线互相平分,得四边形是平行四边形,再由矩形的判定定理知,只需添加条件是对角线相等.解:添加AC=BD,理由如下:∥四边形ABCD的对角线互相平分,∥四边形ABCD是平行四边形,∥AC=BD,∥平行四边形ABCD是矩形,故选:D.【点拨】本题主要考查了矩形的判定,熟练掌握矩形的判定定理是解题的关键.13.D【分析】根据菱形、矩形、正方形的判定定理判断即可.解:A. 当AB=BC时,它是菱形,正确,不符合题意;B. 当AC∥BD时,它是菱形,正确,不符合题意;C. 当∥ABC=90°时,它是矩形,正确,不符合题意;D. 当AC=BD时,它是矩形,原选项不正确,符合题意.故选:D.【点拨】本题考查了菱形、矩形、正方形的判定,解题关键是熟记相关判定定理,准确进行判断.14.B【分析】先证四边形ABCD是矩形,当BC=CD时,四边形ABCD是正方形由此判断.解:∥∥A=∥B=∥C=90°,∥四边形ABCD是矩形,当BC=CD时,四边形ABCD是正方形,故选:B.【点拨】此题考查了正方形的判定定理,熟记正方形的判定定理并应用是解题的关键.15.A【分析】由菱形的判定方法、矩形的判定方法、正方形的判定方法得出选项A、B、D错误,C 正确;即可得出结论.=,解:ABCD中,AC BD∴四边形ABCD是矩形,选项A符合题意;=,ABCD中,AB AD∴四边形ABCD 是菱形,不一定是正方形,选项B 不符合题意; ABCD 中,AB BC ⊥,∴四边形ABCD 是矩形,不一定是菱形,选项C 不符合题意; ABCD 中,AC BD ⊥,∴四边形ABCD 是菱形,选项D 不符合题意;故选:A .【点拨】本题考查了平行四边形的性质、菱形的判定方法、矩形的判定方法、正方形的判定方法;熟练掌握矩形、菱形、正方形的判定方法是解决问题的关键.16.B【分析】根据正方形的性质与判定逐项分析即可.解:A .四边形ABCD 是平行四边,AC BD ⊥,AB BD =∴四边形ABCD 是菱形, B.四边形ABCD 是平行四边,AB AD =∴四边形ABCD 是菱形90BAD ∠=︒∴四边形ABCD 是正方形C. 90BAD ∠=︒且AC BD =只能判定四边形ABCD 是矩形;D .根据对角线互相垂直的平行四边形是菱形,对角线互相平分的四边形是平行四边形,所以不能判断四边形ABCD 是正方形.故选B【点拨】本题考查了菱形,矩形,正方形的性质与判定,掌握特殊四边形的性质与判定是解题的关键.17.AF CE =(答案不唯一)【分析】根据对角线互相平分的四边形是平行四边形,即可求解.解:添加:AF CE =,理由如下:连接BD 交AC 于点O ,如图,∥四边形ABCD是平行四边形,∥AO=CO,BO=DO,∥AF CE=,∥OE=OF,∥四边形BEDF是平行四边形.=(答案不唯一)故答案为:AF CE【点拨】本题主要考查了平行四边形的判定和性质,熟练掌握平行四边形的判定和性质定理是解题的关键.18.FC=AE【分析】根据四边形ABCD是平行四边形,CD∥AB,CD=AB,因此只需要证明DF=EB即可判断四边形EBFD是平行四边形,由此求解即可.解:添加条件FC=AE,∥四边形ABCD是平行四边形,∥CD∥AB,CD=AB∥CF=AE,∥DF=BE,∥四边形EBFD是平行四边形,故答案为:FC=AE.【点拨】本题主要考查了平行四边形的性质与判定,解题的关键在于能够熟练掌握平行四边形的性质与判定条件.19.DE=BF【分析】根据平行四边形的判定,可加一条件,答案不唯一.解:使四边形AECF也是平行四边形,则要证四边形的两组对边相等,或两组对边分别平行,可添加条件DE=BF,∥AD∥BC,∥∥EDA=∥FBC,∥AD=BC,DE=BF,∥∥ADE∥∥CBF,∥AE=FC,同理,∥ABF∥∥CED,∥CE=AF,∥四边形AECF是平行四边形.故答案为:DE=BF.【点拨】本题考查了平行四边形的判定与性质,通过证∥ADE∥∥CBF和∥ABF∥∥CED,得到AE=FC和CE=AF,再利用两组对边分别相等来判定平行四边形.20.OB OD=(答案不唯一)【分析】根据平行四边形的判定定理进行解答.解:添加BO=DO,∥OA=OC,OB=OD,∥四边形ABCD是平行四边形,故答案为:OB=OD(答案不唯一).【点拨】此题主要考查了平行四边形的判定,关键是掌握一组对边平行且相等的四边形是平行四边形.21.AB AD=(答案不唯一)【分析】根据菱形的判定定理“有一组邻边相等的平行四边形是菱形”,可以添加邻边相等的条件.解:条件:AB=AD,∥四边形ABCD是平行四边形,AB=AD,∥四边形ABCD是菱形.故答案为:AB=AD(答案不唯一).【点拨】本题考查了菱形的判定定理,熟练掌握菱形的判定方法是解题的关键.22.AB=BC(答案不唯一)【分析】可证DF,EF都是∥ABC的中位线,即1122EF AB EF AB DF BC DF BC==∥∥,,,,因此只需要AB=BC即可.解:添加条件AB=BC,∥D,E,F分别是AB,BC,AC的中点,∥DF,EF都是∥ABC的中位线,∥1122EF AB EF AB DF BC DF BC==∥∥,,,,∥四边形DBEF是平行四边形,∥AB=BC,∥EF=DF,∥平行四边形DBEF是菱形,故答案为:AB=BC(答案不唯一).【点拨】本题主要考查了三角形中位线定理,菱形的判定,熟知菱形的判定是解题的关键.23.AB=CD【分析】当AB=CD时,有EF∥GH,连接GE、GF、HF、EH,根据三角形的中位线定理可得EG=GF=FH=EH,则四边形EFGH是菱形,最后利用菱形的性质即可.解:当AB=CD时,有EF∥GH,理由如下:如图所示,连接GE、GF、HF、EH.∥E、G分别是AD、BD的中点,∥EG是∥ABD是中位线∥EG=12AB,同理HF =12AB ,FG =12CD ,BH =12CD .又∥AB =CD∥EG =GF =FH =EH .∥四边形EFGH 是菱形∥EF ∥GH .故答案为:AB =CD .【点拨】本题考查了三角形的中位线定理、菱形的判定与性质,找到证明EFGH 是菱形的条件是解答本题的关键.24.120︒【分析】利用一组邻边相等的平行四边形是菱形证明.解:当A ∠=120︒时,四边形ABCD 是菱形,证明:∥AD ∥BC ,AB ∥CD ,∥四边形ABCD 是平行四边形,∥150ADE ∠=︒,∥∥ADB =30°,∥A ∠=120︒,∥∥ABD =30°=∥ADB ,∥AB=AD ,∥四边形ABCD 是菱形,故答案为:120︒.【点拨】此题考查菱形的判定定理,熟记菱形的判定定理并熟练解决问题是解题的关键.25. ∥ ∥ 【分析】先证四边形EFGH是平行四边形,要使四边形EFGH为矩形,需要∥EFG=90°,即AC∥BD;当AC=BD,可判断四边形EFGH为菱形.解:依题意得,四边形EFGH是由四边形ABCD各边中点连接而成,连接AC、BD,∥E、F、G、H分别是CD、DA、AB、BC的中点,∥EF∥AC∥HG,EH∥BD∥FG,∥四边形EFGH是平行四边形,要使四边形EFGH为矩形,根据矩形的判定:有一个角为直角的平行四边形是矩形,故当AC∥BD时,∥EFG=∥EHG=90°时,四边形EFGH为矩形;要使四边形EFGH为菱形,根据矩形的判定:有一组邻边相等的平行四边形是菱形,即EF=EH,而EH=12 BD,∥AC=BD.故当AC=BD时,平行四边形EFGH为菱形故答案为:∥;∥.【点拨】本题考查了矩形和菱形的判定定理:有一个角为直角的平行四边形是矩形,邻边相等的平行四边形是菱形.也考查了平行四边形的判定以及三角形中位线的性质.26.AB AC=【分析】根据题意作出图形,结合矩形的判定定理即可求得.解:如图,ABC中,延长BA至D使得AB AD=,延长CA至E使得AC AE=,当BD EC =时,四边形BCDE 是矩形AB AD =,AC AE =AB AC ∴=故答案为:AB AC =【点拨】本题考查了矩形的性质与判定定理,掌握矩形的性质与判定定理是解题的关键.27.AC BD =【分析】根据矩形的判定定理在平行四边形的条件下,加上对角线相等,或者有一个角是直角即可 解:四边形ABCD 是平行四边形若AC BD =则四边形ABCD 是矩形故答案为:AC BD =(答案不唯一)【点拨】本题考查了矩形的判定定理,掌握矩形的判定定理是解题的关键.28.AC =BD (答案不唯一)【分析】矩形是特殊的平行四边形,矩形有而平行四边形不具有的性质是:矩形的对角线相等,矩形的四个内角是直角;可针对这些特点来添加条件.解:若使▱ABCD 变为矩形,可添加的条件是:AC =BD ;(对角线相等的平行四边形是矩形)故答案为:AC =BD (答案不唯一).【点拨】此题主要考查的是平行四边形的性质及矩形的判定方法,熟练掌握矩形和平行四边形的联系和区别是解答此题的关键.29.AC BD =(答案不唯一)【分析】由平行线的性质可知,DAC BCA ∠=∠,即易证()AOD COB ASA ≅,得出AD CB =,由此可证明四边形ABCD 为平行四边形.由角平分线的性质可知DAC BAC ∠=∠,即得出BAC BCA ∠=∠,从而证明BA BC =,即平行四边形ABCD 为菱形.故在四边形ABCD 为菱形的基础上,添加条件使其为正方形即可.解:∥//AD BC ,∥DAC BCA ∠=∠,∥在AOD △和COB △中,AOD COB AO CO DAO BCO ∠=∠⎧⎪=⎨⎪∠=∠⎩,∥()AOD COB ASA ≅,∥AD CB =,∥四边形ABCD 为平行四边形.∥AC 平分∥BAD ,∥DAC BAC ∠=∠,∥BAC BCA ∠=∠,∥BA BC =,∥平行四边形ABCD 为菱形.∥再添加AC BD =或90ABC ∠=︒等,即可证明菱形ABCD 为正方形.故答案为:AC BD =(答案不唯一).【点拨】本题考查平行线的性质,角平分线的定义,三角形全等的判定和性质,平行四边形、菱形、正方形的判定.掌握特殊四边形的判定方法是解题的关键.30.AC =BD 且AC ∥BD (答案不唯一)【分析】根据正方形的判定定理,即可求解.解:当AC =BD 时,平行四边形ABCD 为菱形,又由AC ∥BD ,可得菱形ABCD 为正方形,所以当AC =BD 且AC ∥BD 时,平行四边形ABCD 为正方形.故答案为:AC =BD 且AC ∥BD (答案不唯一)【点拨】本题主要考查了正方形的判定,熟练掌握正方形的判定定理是解题的关键. 31.∥BAD =90°【分析】根据正方形的判定即可得结论.解:因为四边形ABCD 是平行四边形,AB AD =,所以平行四边形ABCD 是菱形,如果90BAD ∠=︒,那么菱形ABCD 是正方形.故答案为:90BAD ∠=︒.【点拨】此题考查了正方形的判定和平行四边形的性质,熟练掌握正方形的判定方法是解题的关键.32.AB =AD (答案不唯一)【分析】本题中给出在矩形的基础上,可以加上有一组邻边相等即可判定四边形ABCD 是正方形.解:因为有一组邻边相等的矩形是正方形,故答案为:AB =AD (答案不唯一).【点拨】本题考查了正方形的判定,属于条件开放题目,答案不唯一,掌握知识点是解题关键.33.∥,证明见分析解:补充条件∥,∥AD BC ∥,∥∥OAD =∥OCB ,∥ODA =∥OBC ,又∥OA =OC ,∥∥AOD ∥∥COB (AAS ),∥OB =OD ,∥四边形ABCD 是平行四边形,条件∥∥无法证明四边形ABCD 是平行四边形故答案为:∥.【点拨】本题主要考查了平行四边形的判定,熟知平行四边形的判定条件是解题的关键. 34.(1)证明见分析(2)AB BC =(答案不唯一)【分析】(1)根据平行线的性质得出BAO DCO ∠=∠,ABO CDO ∠=∠,进而利用AAS 证明ABO 与CDO 全等,再利用平行四边形的判定解答即可;(2)根据菱形的判定解答即可.解:(1)证明:∥//AB CD∥BAO DCO ∠=∠,ABO CDO ∠=∠,在ABO 与CDO 中,BAO DCO ABO CDO OA OC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∥ABO CDO △≌△(AAS )∥AB CD =∥四边形ABCD 是平行四边形.(2)解:添加:AB BC =(答案不唯一).证明:∥AB BC =,又∥四边形ABCD 是平行四边形,∥四边形ABCD 是菱形.【点拨】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、菱形的判定等知识.熟练掌握平行四边形的性质与判定是解题的关键.35.(1)见分析(2)EF =BD【分析】(1)根据平行四边形的性质可得OA OC OB OD ==,,根据已知条件即可求得OE =OF ,根据对角线互相平分的四边形是平行四边形即可得证;(2)根据矩形的判定定理可知,对角线相等的平行四边形是矩形即可求解.解:(1)证明:四边形ABCD 是平行四边形,OA OC OB OD ∴==,,AE =CF ,∴OE=OF,∴四边形BFDE是平行四边形.(2)EF=BD.证明:EF=BD,四边形BFDE是平行四边形,∴四边形BEDF是矩形.【点拨】本题考查了平行四边形的性质与判定,矩形的判定定理,掌握平行四边形的性质与判定以及矩形的判定定理是解题的关键.36.(1)见分析(2)正方形,理由见分析【分析】(1)由平行四边形的性质可得DC∥AB,可得∥DAM=∥NDA,可证∥NED∥∥MEA,可得AM=ND,可证四边形AMDN是平行四边形,由直角三角形的性质可得AM=MD,可得四边形AMDN是菱形;(2)由菱形的性质可得∥DAB=∥ADM=45°,可得AM∥DM,则四边形AMDN是正方形.解:(1)证明:∥四边形ABCD是平行四边形,∥DC∥AB∥∥DAM=∥NDA,且DE=AE,∥NED=∥AEM∥∥NED∥∥MEA(ASA)∥AM=ND,且CD∥AB∥四边形AMDN是平行四边形又BD∥AD,M为AB的中点,∥在Rt∥ABD中,AM=DM=MB∥四边形AMDN是菱形(2)正方形,理由如下:∥四边形AMDN是菱形∥AM=DM∥∥DAB=∥ADM=45°,∥∥AMD=90°∥菱形AMDN是正方形.【点拨】。
2023学年九年级上学期数学同步精讲精练(北师大版)1-4 特殊平行四边形重难题型(习题)(含详解)

1.4《特殊平行四边形》重难题型习题分层训练提分要义【基础题】1.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是()A.矩形B.菱形C.对角线相等的四边形D.对角线互相垂直的四边形2.已知四边形ABCD是平行四边形,下列结论中错误的有()①当AB=BC时,它是菱形;②当AC⊥BD时,它是菱形;③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形.A.1个B.2个C.3个D.4个3.如图,在矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是()A.AF=AE B.△ABE≌△AGF C.EF=2 5 D.AF=EF4.如图,在正方形ABCD中,点P是AB上一动点(点P不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=BD;③PE2+PF2=PO2.其中正确的有()A.0个B.1个C.2个D.3个5.如图是一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α的度数为________时,两条对角线长度相等.6.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影部分和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为________.7.已知E是正方形ABCD的对角线AC上一点,AE=AD,过点E作AC的垂线,交边CD于点F,那么∠FAD=________.8.如图,在四边形ABCD中,AD∥BC,AC的垂直平分线交AD,BC于点E,F.求证:四边形AECF是菱形.9.如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.(1)求证:四边形OCED是菱形;(2)若AB=3,BC=4,求四边形OCED的面积.10.如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF.(1)求证:△BCE≌△DCF;(2)若∠FDC=30°,求∠BEF的度数.【中档题】11.如图,在矩形ABCD中,M,N分别是AD,BC的中点,E,F分别是线段BM,CM的中点.若AB=8,AD=12,则四边形ENFM的周长为________.12.如图,在△ABC中,D,E分别是AB,AC的中点,过点E作EF∥AB,交BC于点F.(1)求证:四边形DBFE是平行四边形.(2)当△ABC满足什么条件时,四边形DBFE是菱形?并说明理由.13.如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于F,连接AE.求证:(1)BF=DF;(2)AE∥BD.14.图①为长方形纸片ABCD,AD=26,AB=22,直线L,M皆为长方形的对称轴.今将长方形纸片沿着L对折后,再沿着M对折,并将对折后的纸片左上角剪下直角三角形,形成一个五边形EFGHI,如图②,最后将图②的五边形展开后形成一个八边形,如图③,且八边形的每一边长恰好均相等.(1)若图②中的HI长度为x,请用x分别表示剪下的直角三角形的勾长和股长.(2)请求出图③中八边形的一边长的数值,并写出完整的解题过程.15.如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC 于点E.(1)求证:△DCE≌△BFE;(2)若CD=2,∠ADB=30°,求BE的长.16.如图,在菱形ABCD中,AB=4,∠BAD=120°,以点A为顶点的一个60°的角∠EAF绕点A旋转,∠EAF的两边分别交BC,CD于点E,F,且E,F不与B,C,D重合,连接EF.(1)求证:BE=CF.(2)在∠EAF绕点A旋转的过程中,四边形AECF的面积是否发生变化?如果不变,求出其定值;如果变化,请说明理由.【综合题】17.如图,在△ABC 中,点O 是边AC 上一个动点,过O 作直线MN ∥BC ,设MN 交∠ACB 的平分线于点E ,交△ABC 的外角∠ACD 的平分线于点F.(1)探究线段OE 与OF 的数量关系并说明理由.(2)当点O 运动到何处,且△ABC 满足什么条件时,四边形AECF 是正方形?请说明理由.(3)当点O 在边AC 上运动时,四边形BCFE________是菱形(填“可能”或“不可能”).请说明理由.18.图,将一张矩形纸片ABCD 沿直线MN 折叠,使点C 落在点A 处,点D 落在点E 处,直线MN 交BC 于点M ,交AD 于点N.(1)求证:CM =CN ;(2)若△CMN 的面积与△CDN 的面积比为31,求MN DN的值. 19.如图,在边长为10的菱形ABCD 中,对角线BD =16,对角线AC ,BD相交于点G ,点O 是直线BD 上的动点,OE ⊥AB 于E ,OF ⊥AD 于F.(1)求对角线AC 的长及菱形ABCD 的面积.(2)如图①,当点O 在对角线BD 上运动时,OE +OF 的值是否发生变化?请说明理由.(3)如图②,当点O 在对角线BD 的延长线上时,OE +OF 的值是否发生变化?若不变,请说明理由;若变化,请探究OE ,OF 之间的数量关系.20.[阅读]在平面直角坐标系中,以任意两点P(x 1,y 1),Q(x 2,y 2)为端点的线段的中点坐标为⎝⎛⎭⎫x 1+x 22,y 1+y 22.[运用](1)如图,矩形ONEF的对角线相交于点M,ON,OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为________.(2)在平面直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D与点A,B,C 构成平行四边形的顶点,求点D的坐标.1.4《特殊平行四边形》重难题型习题分层训练提分要义【基础题】1.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是()A.矩形B.菱形C.对角线相等的四边形D.对角线互相垂直的四边形【解析】D【解析】首先根据三角形中位线定理知:所得四边形的对边都平行且相等,那么其必为平行四边形,若所得四边形是矩形,那么邻边互相垂直,故原四边形的对角线必互相垂直,由此得解.2.已知四边形ABCD是平行四边形,下列结论中错误的有()①当AB=BC时,它是菱形;②当AC⊥BD时,它是菱形;③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形.A.1个B.2个C.3个D.4个【解析】A【解析】①当AB=BC时,它是菱形,正确;②当AC⊥BD时,它是菱形,正确;③当∠ABC =90°时,它是矩形,正确;④当AC=BD时,它是矩形,因此④是错误的.3.如图,在矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是()A.AF=AE B.△ABE≌△AGF C.EF=2 5 D.AF=EF【解析】D【解析】如图,由折叠得∠1=∠2.∵AD∥BC,∴∠3=∠1.∴∠2=∠3.∴AE=AF.故选项A正确.由折叠得CD=AG,∠D=∠G=90°.∵AB=CD,∴AB=AG.∵AE=AF,∠B=90°,∴Rt△ABE≌Rt△AGF(HL).故选项B正确.设DF=x,则GF=x,AF=8-x.又AG=AB=4,∴在Rt△AGF中,根据勾股定理得(8-x)2=42+x2.解得x=3.∴AF=8-x=5.则AE=AF=5,∴BE=AE2-AB2=52-42=3.过点F作FM⊥BC于点M,则EM=5-3=2.在Rt△EFM中,根据勾股定理得EF=EM2+FM2=22+42=20=25,则选项C正确.∵AF=5,EF=25,∴AF≠EF.故选项D错误.4.如图,在正方形ABCD中,点P是AB上一动点(点P不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=BD;③PE2+PF2=PO2.其中正确的有()A.0个B.1个C.2个D.3个【解析】D【解析】∵四边形ABCD是正方形,∴∠PAE=∠MAE=45°.∵PM⊥AC,∴∠PEA=∠MEA.又∵AE=AE,∴根据“ASA”可得△APE≌△AME.故①正确.由①得PE=ME,∴PM=2PE.同理PN=2PF.又易知PF=BF,四边形PEOF是矩形,∴PN=2BF,PM=2FO.∴PM+PN =2FO+2BF=2BO=BD.故②正确.在Rt△PFO中,∵FO2+PF2=PO2,而PE=FO,∴PE2+PF2=PO2.故③正确.5.如图是一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α的度数为________时,两条对角线长度相等.【答案】90°【解析】对角线相等的平行四边形是矩形.6.如图,四边形ABCD 是菱形,O 是两条对角线的交点,过O 点的三条直线将菱形分成阴影部分和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为________.【答案】12【解析】∵菱形的两条对角线的长分别为6和8,∴菱形的面积=12×6×8=24.∵O 是菱形两条对角线的交点,∴阴影部分的面积=12×24=12. 7.已知E 是正方形ABCD 的对角线AC 上一点,AE =AD ,过点E 作AC 的垂线,交边CD 于点F ,那么∠FAD =________.【答案】22.5°【解析】如图,由四边形ABCD 是正方形,可知∠CAD =12∠BAD =45°. 由FE ⊥AC ,可知∠AEF =90°.在Rt △AEF 与Rt △ADF 中, AE =AD ,AF =AF ,∴Rt △AEF ≌Rt △ADF(HL).∴∠FAD =∠FAE =12∠CAD =12×45°=22.5°.8.如图,在四边形ABCD 中,AD ∥BC ,AC 的垂直平分线交AD ,BC 于点E ,F.求证:四边形AECF 是菱形.【解析】证明:∵EF 垂直平分AC ,∴∠AOE =∠COF =90°,OA =OC.∵AD ∥BC ,∴∠OAE =∠OCF.∴△AOE ≌△COF(ASA).∴AE =CF.又∵AE ∥CF ,∴四边形AECF 是平行四边形.∵EF ⊥AC ,∴四边形AECF 是菱形.9.如图,O 为矩形ABCD 对角线的交点,DE ∥AC ,CE ∥BD.(1)求证:四边形OCED 是菱形;(2)若AB =3,BC =4,求四边形OCED 的面积.【解析】(1)证明:∵DE ∥AC ,CE ∥BD ,∴四边形OCED 为平行四边形.∵四边形ABCD 为矩形,∴OD =OC.∴四边形OCED 为菱形.(2)解:∵四边形ABCD 为矩形,∴BO =DO =12BD. ∴S △OCD =S △OCB =12S △ABC =12×12×3×4=3. ∴S 菱形OCED =2S △OCD =6.10.如图,在正方形ABCD 中,E 为CD 边上一点,F 为BC 延长线上一点,且CE =CF.(1)求证:△BCE ≌△DCF ;(2)若∠FDC =30°,求∠BEF 的度数.(1)证明:在△BCE 与△DCF 中,⎩⎪⎨⎪⎧BC =DC ,∠BCE =∠DCF ,CE =CF ,∴△BCE ≌△DCF.(2)解:∵△BCE ≌△DCF ,∴∠EBC =∠FDC =30°.∵∠BCD =90°,∴∠BEC =60°.∵EC =FC ,∠ECF =90°,∴∠CEF =45°.∴∠BEF =105°.【中档题】11.如图,在矩形ABCD 中,M ,N 分别是AD ,BC 的中点,E ,F 分别是线段BM ,CM 的中点.若AB =8,AD =12,则四边形ENFM 的周长为________.【答案】20【解析】点N 是BC 的中点,点E ,F 分别是BM ,CM 的中点,由三角形的中位线定理可证EN ∥MC ,NF ∥ME ,EN =12MC ,FN =12MB.又易知MB =MC ,所以四边形ENFM 是菱形.由点M 是AD 的中点,AD =12得AM =6.在Rt △ABM 中,由勾股定理得BM =10.因为点E 是BM 的中点,所以EM =5.所以四边形ENFM 的周长为20.12.如图,在△ABC 中,D ,E 分别是AB ,AC 的中点,过点E 作EF ∥AB ,交BC 于点F. (1)求证:四边形DBFE 是平行四边形.(2)当△ABC 满足什么条件时,四边形DBFE 是菱形?并说明理由.【解析】(1)证明:∵D ,E 分别是AB ,AC 的中点,∴DE 是△ABC 的中位线.∴DE ∥BC.又∵EF ∥AB ,∴四边形DBFE 是平行四边形.(2)解:答案不唯一,下列解法供参考.当AB =BC 时,四边形DBFE 是菱形.理由:∵D 是AB 的中点,∴BD =12AB. ∵DE 是△ABC 的中位线,∴DE =12BC.又∵AB =BC ,∴BD =DE.又∵四边形DBFE 是平行四边形,∴四边形DBFE 是菱形.13.如图,将矩形纸片ABCD 沿对角线BD 折叠,点C 落在点E 处,BE 交AD 于F ,连接AE.求证:(1)BF =DF ;(2)AE ∥BD.【解析】证明:(1)由折叠的性质可知,∠FBD =∠CBD.因为在矩形ABCD中,AD ∥BC ,所以∠FDB =∠CBD.所以∠FBD =∠FDB.所以BF =DF.(2)因为四边形ABCD 是矩形,所以AB =DC ,AD =BC.由折叠的性质可知,DC =ED =AB ,BC =BE =AD.又因为AE =AE ,所以△AEB ≌△EAD.所以∠AEB =∠EAD.所以∠AEB =12(180°-∠AFE). 由(1)知∠DBE =∠BDF ,所以∠DBE =12(180°-∠BFD). 而∠AFE =∠BFD ,所以∠AEB =∠DBE.所以AE ∥BD.14.图①为长方形纸片ABCD ,AD =26,AB =22,直线L ,M 皆为长方形的对称轴.今将长方形纸片沿着L 对折后,再沿着M 对折,并将对折后的纸片左上角剪下直角三角形,形成一个五边形EFGHI ,如图②,最后将图②的五边形展开后形成一个八边形,如图③,且八边形的每一边长恰好均相等.(1)若图②中的HI 长度为x ,请用x 分别表示剪下的直角三角形的勾长和股长.(2)请求出图③中八边形的一边长的数值,并写出完整的解题过程.【解析】解:(1)分别延长HI 与FE ,相交于点N ,如图.∵HN =12AD =13,NF =12AB =11,HI =EF =x , ∴NI =HN -HI =13-x ,NE =NF -EF =11-x.∴剪下的直角三角形的勾长为11-x ,股长为13-x.(2)在Rt △ENI 中,NI =13-x ,NE =11-x ,∴EI =NI 2+NE 2=2x 2-48x +290.∵八边形的每一边长恰好均相等,∴EI =2HI =2x =2x 2-48x +290,整理得:x 2+24x -145=0,(x -5)(x +29)=0,解得:x =5,或x =-29(舍去).∴EI =2×5=10.故八边形的边长为10.15.如图,将矩形纸片ABCD 沿对角线BD 折叠,使点A 落在平面上的F 点处,DF 交BC 于点E.(1)求证:△DCE ≌△BFE ;(2)若CD =2,∠ADB =30°,求BE 的长.【解析】(1)证明:∵在矩形ABCD 中,AD ∥BC ,∠A =∠C =90°,∴∠ADB =∠DBC.根据折叠的性质得∠ADB =∠BDF ,∠F =∠A =90°,∴∠DBC =∠BDF ,∠C =∠F.∴BE =DE.在△DCE 和△BFE 中,⎩⎪⎨⎪⎧∠DEC =∠BEF ,∠C =∠F ,DE =BE ,∴△DCE ≌△BFE.(2)解:在Rt △BCD 中,∵CD =2,∠ADB =∠DBC =30°,∴BD =4.∴BC =2 3.在Rt △ECD 中,易得∠EDC =30°.∴DE =2EC.∴(2EC)2-EC 2=CD 2.∵CD =2,∴CE =233. ∴BE =BC -EC =433.16.如图,在菱形ABCD 中,AB =4,∠BAD =120°,以点A 为顶点的一个60°的角∠EAF 绕点A 旋转,∠EAF 的两边分别交BC ,CD 于点E ,F ,且E ,F 不与B ,C ,D 重合,连接EF.(1)求证:BE =CF.(2)在∠EAF 绕点A 旋转的过程中,四边形 AECF 的面积是否发生变化?如果不变,求出其定值;如果变化,请说明理由.【解析】(1)证明:如图,连接AC.∵四边形ABCD 为菱形,∠BAD =120°,∴∠ABE =∠ACF =60°,∠1+∠2=60°.∵∠3+∠2=∠EAF =60°,∴∠1=∠3.∵∠ABC =60°,AB =BC ,∴△ABC 为等边三角形.∴AC =AB.∴△ABE ≌△ACF.∴BE=CF.(2)解:四边形AECF的面积不变.由(1)知△ABE≌△ACF,则S△ABE=S△ACF,故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC. 如图,过A作AM⊥BC于点M,则BM=MC=2,∴AM=AB2-BM2=42-22=2 3.∴S△ABC=12BC·AM=12×4×23=4 3.故S四边形AECF=4 3.【综合题】17.如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB 的平分线于点E,交△ABC的外角∠ACD的平分线于点F.(1)探究线段OE与OF的数量关系并说明理由.(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?请说明理由.(3)当点O在边AC上运动时,四边形BCFE________是菱形(填“可能”或“不可能”).请说明理由.【解析】解:(1)OE=OF.理由如下:∵CE是∠ACB的平分线,∴∠ACE=∠BCE.又∵MN∥BC,∴∠NEC=∠BCE.∴∠NEC=∠ACE.∴OE=OC.∵CF是∠ACD的平分线,∴∠OCF=∠FCD.又∵MN∥BC,∴∠OFC=∠FCD.∴∠OFC=∠OCF.∴OF=OC.∴OE=OF.(2)当点O运动到AC的中点,且△ABC满足∠ACB为直角时,四边形AECF是正方形.理由如下:∵当点O运动到AC的中点时,AO=CO,又∵EO=FO,∴四边形AECF 是平行四边形.∵FO =CO ,∴AO =CO =EO =FO.∴AO +CO =EO +FO ,即AC =EF.∴四边形AECF 是矩形.已知MN ∥BC ,当∠ACB =90°时,∠AOE =90°,∴AC ⊥EF.∴四边形AECF 是正方形.(3)不可能理由如下:连接BF ,∵CE 平分∠ACB ,CF 平分∠ACD ,∴∠ECF =12∠ACB +12∠ACD =12(∠ACB +∠ACD)=90°.若四边形BCFE 是菱形,则BF ⊥EC.但在一个三角形中,不可能存在两个角为90°,故四边形BCFE 不可能为菱形.如18.图,将一张矩形纸片ABCD 沿直线MN 折叠,使点C 落在点A 处,点D 落在点E 处,直线MN 交BC 于点M ,交AD 于点N.(1)求证:CM =CN ;(2)若△CMN 的面积与△CDN 的面积比为31,求MN DN的值. 【解析】(1)证明:由折叠的性质可得点A ,C 关于直线MN 对称,∴∠ANM=∠CNM.∵四边形ABCD 是矩形,∴AD ∥BC.∴∠ANM =∠CMN.∴∠CMN =∠CNM.∴CM =CN.(2)解:过点N 作NH ⊥BC 于点H ,则四边形NHCD 是矩形,∴HC =DN ,NH =DC.∵△CMN 的面积与△CDN 的面积比为3∶1,∴S △CMN S △CDN =12·MC·NH 12·DN·NH =MC DN =3. ∴MC =3DN =3HC.∴MH =2HC.设DN =x ,则HC =x ,MH =2x.∴CM =3x =CN.在Rt △CDN 中,DC =CN 2-DN 2=22x ,∴NH =22x.在Rt △MNH 中,MN =MH 2+NH 2=23x.∴MN DN =23x x=2 3. 19.如图,在边长为10的菱形ABCD 中,对角线BD =16,对角线AC ,BD 相交于点G ,点O 是直线BD 上的动点,OE ⊥AB 于E ,OF ⊥AD 于F.(1)求对角线AC 的长及菱形ABCD 的面积.(2)如图①,当点O 在对角线BD 上运动时,OE +OF 的值是否发生变化?请说明理由.(3)如图②,当点O 在对角线BD 的延长线上时,OE +OF 的值是否发生变化?若不变,请说明理由;若变化,请探究OE ,OF 之间的数量关系.【解析】解:(1)在菱形ABCD 中,AG =CG ,AC ⊥BD ,BG =12BD =12×16=8, 由勾股定理得AG =AB 2-BG 2=102-82=6, 所以AC =2AG =2×6=12.所以菱形ABCD 的面积=12AC·BD =12×12×16=96. (2)不发生变化.理由如下:如图①,连接AO ,则S △ABD =S △ABO +S △AOD ,所以12BD·AG =12AB·OE +12AD·OF. 即12×16×6=12×10·OE +12×10·OF. 解得OE +OF =9.6,是定值,不变.(3)发生变化.如图②,连接AO ,则S △ABD =S △ABO -S △AOD ,所以12BD·AG =12AB·OE -12AD·OF. 即12×16×6=12×10·OE -12×10·OF. 解得OE -OF =9.6,是定值,不变.所以OE +OF 的值发生变化,OE ,OF 之间的数量关系为OE -OF =9.6.20.[阅读]在平面直角坐标系中,以任意两点P(x 1,y 1),Q(x 2,y 2)为端点的线段的中点坐标为⎝⎛⎭⎫x 1+x 22,y 1+y 22. [运用](1)如图,矩形ONEF 的对角线相交于点M ,ON ,OF 分别在x 轴和y 轴上,O 为坐标原点,点E 的坐标为(4,3),则点M 的坐标为________.(2)在平面直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D 与点A ,B ,C 构成平行四边形的顶点,求点D 的坐标.【解析】解:(1)(2,1.5)(2)设点D 的坐标为(x ,y).若以点A ,B ,C ,D 为顶点构成的四边形是平行四边形,①当AB 为对角线时,∵A(-1,2),B(3,1),C(1,4), ∴-1+32=1+x 2,2+12=4+y 2. ∴x =1,y =-1.∴点D 的坐标为(1,-1).②当BC 为对角线时,∵A(-1,2),B(3,1),C(1,4),∴3+12=-1+x 2,1+42=2+y 2. ∴x =5,y =3.∴点D 的坐标为(5,3). ③当AC 为对角线时,∵A(-1,2),B(3,1),C(1,4), ∴-1+12=3+x 2,2+42=1+y 2. ∴x =-3,y =5.∴点D 的坐标为(-3,5).综上所述,点D 的坐标为(1,-1)或(5,3)或(-3,5).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题1.27 《特殊平行四边形》全章复习与巩固(基础篇)(专项练习)一、单选题1.如图,在四边形ABCD 中,AB CD BC AD ,,且AD =DC ,则下列说法:①四边形ABCD 是平行四边形;①AB =BC ;①AC ①BD ;①AC 平分①BAD ;①若AC =6,BD =8,则四边形ABCD 的面积为24,其中正确的有( )A .2个B .3个C .4个D .5个2.如图,在菱形ABCD 中,直线MN 分别交AB 、CD 、AC 于点M 、N 和O .且AM CN =,连接BO .若65OBC ∠=︒,则DAC ∠为( )A .65︒B .30C .25︒D .20︒3.两个边长为2的等边三角形如图所示拼凑出一个平行四边形ABCD ,则对角线BD 的长为( )A .2B .4 CD .4.如图,在菱形ABCD 中,40ABC ∠=︒,点E 为对角线BD 上一点,F 为AD 边上一点,连接AE 、CE 、FE ,若AE FE =,56BEC ∠=︒,则DEF ∠的度数为( )A .16︒B .15︒C .14︒D .13︒5.如图,在△ABC 中,AC =BC ,D 、E 分别是边AB 、AC 的中点,△ADE ①△CFE ,则四边形ADCF 一定是( )A .菱形B .矩形C .正方形D .无法确定6.如图,在Rt ABC △中,D 、E 分别是直角边BC 、AC 的中点,若10DE =,则AB 边上的中线CP 的长为( )A .5B .6C .D .107.如图,在矩形ABCD 中,EF 是对角线AC 的垂直平分线,分别交AB ,CD 于点E ,F ,若8,4AB AD ==,则EF 的长为( )A .4B .8CD .8.如图,矩形ABCD 的顶点1,0A ,()0,2D ,()5,2B ,将矩形以原点为旋转中心,顺时针旋转75°之后点C 的坐标为( )A .()4,2-B .(-C .()2-D .(-9.如图所示的是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中5AE =,13BE =,则2EF 的值是( )A .128B .64C .32D .14410.正方形ABCD 的边长为4,点M ,N 在对角线AC 上(可与点A ,C 重合),MN =2,点P ,Q 在正方形的边上.下面四个结论中错误的是( )A .存在无数个四边形PMQN 是平行四边形B .存在无数个四边形PMQN 是矩形C .存在无数个四边形PMQN 是菱形D .至少存在一个四边形PMQN 是正方形11.如图,在正方形ABCD 中,等边AEF 的顶点E ,F 分别在边BC 和CD 上,则AEB ∠等于( )A .60︒B .70︒C .75︒D .80︒12.如图,在Rt①ABC 中,①BAC =90°,D 是BC 中点,分别以AB ,AC为边向外作正方形ABEF和正方形ACGH,连接FD、HD,若BC=10,则阴影部分的面积是()A.B.C.25D.50二、填空题13.如图,矩形ABCD的对角线相交于点O,DE①AC,CE①BD,已知AB=6cm,BC=8cm,则四边形ODEC的周长为______cm.14.如图,平行四边形ABCD的对角线AC与BD交于点O,请你添加一个条件使它是菱形,你添加的条件是______.15.如图,已知菱形ABCD的对角线AC,BD的长分别为6,4,则AB长为__.16.如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,则CD的长是___________.17.如图,在矩形ABCD 中,AB =6,BC =8,O 是矩形的对称中心,点E 、F 分别在边AD 、BC 上,连接OE 、OF ,若AE =BF =2,则OE +OF 的值为__________.18.如图,菱形ABCD 的对角线,AC BD 相交于点O ,过点D 作DH BC ⊥于点H ,连接OH ,若4OA =,24ABCD S =菱形,则OH 的长为___________.19.如图,四边形纸片ABCD 中,90C D ∠=∠=︒,3AD =,9BC =,8CD =,点E 在BC 上,且AE BC ⊥.将四边形纸片ABCD 沿AE 折叠,点C 、D 分别落在点C '、D 处,C D ''与AB 交于点F ,则BF 长为______.20)的矩形称为黄金矩形,如图,在黄金矩形ABCD 中,AB BC <,BC =4,ABC ∠的平分线交AD 边于点E ,则AE 的长为______.21.图,正六边形ABCDEF 的顶点B 、C 分别在正方形AGHI 的边AG GH 、上,若2AB =,则AG 的长度为_________.22.如图,已知小正方形ABCD 的面积为1,把它的各边延长一倍得到新正方形1111D C B A ;把正方形1111D C B A 的各边长按原法延长一倍得到正方形2222A B C D ;以此进行下去…则正方形2022202220222022A B C D 的面积为 ________.23.如图,正方形ABCD 的边长为6,点E ,F 分别为边BC ,CD 上两点,CF BE =,AE 平分①BAC ,连接BF ,分别交AE ,AC 于点G ,M ,点P 是线段AG 上的一个动点,过点P 作PN ①AC ,垂足为N ,连接PM ,则PM PN +的最小值为______.24.如图,在平面直角坐标系中,有一个由四个边长为1的正方形组成的图案,其中点3,7,则点B坐标为______.A坐标为()三、解答题⊥于点F.25.如图,在菱形ABCD中,BE CD⊥于点E,DF BC(1)求证:BF DE=;(2)分别延长BE和AD相交于点G,若45∠=︒,1AAB=,求DG的值.26.如图,△ABC中,①ABC=90°,O为AC的中点,连接BO并延长至D使OD=OB,连AD、CD.(1)求证:四边形ABCD为矩形;(2)若①AOB=60°,E为BC的中点,连OE,OE=2.求对角线的长及矩形的面积.27.(1)方法感悟:如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足①EAF=45°,连接EF,求证:DE+BF=EF.感悟解题方法,并完成下列填空:将①ADE绕点A顺时针旋转90°得到①ABG,此时AB与AD重合,由旋转可得:AB=AD,BG=DE,①1=①2,①ABG=①D=90°,①①ABG+①ABF=90°+90°=180°.因此,点G,B,H在同一条直线上.①①EAF=45°,①①2+①3=①BAD-①EAF=90°-45°=45°,①①1+①3=45°.即①GAF=①______.又①AG=AE,AF=AF,①GAF△≌______.①______=EF.故DE+BF=EF.(2)方法迁移:如图2,将Rt①ABC沿斜边翻折得到①ADC,点E,F分别为DC,BC边上的点,且12EAF DAB∠=∠.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.(3)问题拓展:如图3,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足12EAF DAB∠=∠,试猜想当①B,①D满足什么关系时,可使得DE+BF=EF?请说明理由.参考答案1.D【分析】由AB CD BC AD ∥,∥,可知四边形ABCD 是平行四边形,可判断①的正误;由AD =DC ,可知平行四边形ABCD 是菱形,根据菱形的性质可判断②③④⑤的正误.解:①AB CD BC AD ∥,∥,①四边形ABCD 是平行四边形,故①正确; ①AD =DC ,①平行四边形ABCD 是菱形,①AB =BC ,AC ①BD ,AC 平分①BAD ,故①①①正确; ①AC =6,BD =8, ①菱形ABCD 的面积=11682422AC BD ⨯=⨯⨯=,故①正确; ∴正确的个数有5个, 故选D .【点拨】本题考查了平行四边形的判定,菱形的判定与性质.解题的关键在于证明四边形ABCD 是菱形.2.C 【分析】根据菱形的性质,平行线的性质,全等三角形的判定定理和性质确定BA BC =,OA =OC ,根据等腰三角形三线合一的性质确定①BOC =90°,根据三角形内角和定理和平行线的性质即可求出①DAC .解:①四边形ABCD 是菱形,①AB CD ,BC AD ∥,BA BC =.①①OMA =①ONC ,①OAM =①OCN ,①DAC =①OCB . ①AM =CN ,①()ASA OAM OCN △≌△. ①OA =OC . ①BO ①AC . ①①BOC =90°. ①①OBC =65°,①①OCB =180°-①BOC -①OBC =25°. ①①DAC =①OCB =25°.故选:C.【点拨】本题考查菱形的性质,平行线的性质,全等三角形的判定定理和性质确,等腰三角形三线合一的性质,三角形内角和定理,综合引用这些知识点是解题关键.3.D【分析】连接BD交AC于点O,由平行四边形和等边三角形的性质,易证四边形ABCD是菱形,可求得AB=2,AO=1,由勾股定理可求得BO=BD的长.解:如图,连接BD交AC于点O,由题意可得ACB△和ACD△是等边三角形,且边长都为2,①AB=BC=CD=DA=AC=2,①四边形ABCD是菱形,①112AO AC==,BD=2BO,AC①BD,在Rt ABO中,由勾股定理得:BO=①2BD BO==故选:D.【点拨】本题主要考查了菱形的判定与性质、勾股定理,灵活运用菱形的性质和勾股定理求解是解题的关键.4.A【分析】先求出①BAD=140°,①ADB=①ABD=20°,然后证明①ABE①①CBE得到①BEA=①BEC=56°,则①BAE=104°,①DAE=36°,证明①EF A=①EAF=36°,则由三角形外角的性质可得①DEF=①EF A-①EDF=16°.解:①四边形ABCD是菱形,①ABC=40°,①AB=CB=AD,①ABE=①CBE=20°,AD BC∥,①①BAD=140°,①ADB=①ABD=20°,又①BE=BE,①①ABE①①CBE(SAS),①①BEA=①BEC=56°,①①BAE=104°,①①DAE=36°,①AE=FE,①①EF A=①EAF=36°,①①DEF=①EF A-①EDF=16°,故选A.【点拨】本题主要考查了菱形的性质,全等三角形的性质与判定,三角形内角和定理,等腰三角形的性质,三角形外角的性质,证明①ABE①①CBE是解题的关键.5.B【分析】根据全等三角形的性质可得AE=CE,DE=EF,再根据对角线互相平分的四边形是平行四边形判断出四边形ADCF是平行四边形,然后利用等腰三角形三线合一的性质求出①ADC=90°,再利用有一个角是直角的平行四边形是矩形解答.解:△ADE①①CFE,①AE=CE,DE=EF,①四边形ADCF是平行四边形,①AC=BC,点D是边AB的中点,①①ADC=90°,①四边形ADCF是矩形.故选:B.【点拨】本题考查了矩形、菱形、正方形的判定,全等三角形的性质,等腰三角形的性质,熟练掌握矩形的判定定理是解题的关键.6.D【分析】根据三角形中位线定理求出AB的长度,再根据直角三角形斜边上的中线是斜边的一半求解即可.解:①D 、E 分别是边BC 、AC 的中点,①DE 是①ABC 的中位线. ①12DE AB =. ①DE =10,①AB =2DE =20.①CP 是Rt ABC △中斜边AB 上的中线,, ①1102CP AB == 故选:D .【点拨】本题考查三角形中位线定理,直角三角形斜边上的中线是斜边的一半,熟练掌握这些知识点是解题关键.7.D【分析】连接CE ,设EF 交AC 于点O ,根据矩形的性质和EF 是AC 的垂直平分线,可得12OA OC AC ===EC =AE ,OA =OC ,再由勾股定理可得AE =CE =5,从而得到OE =再由①AOE ①①COF ,可得OF =OE ,即可求解.解:如图,连接CE ,设EF 交AC 于点O ,在矩形ABCD 中,BC =AD =4,AB =CD =8,①B =①ADC =90°,AB ①CD ,①AC =①12OA OC AC === ①EF 是AC 的垂直平分线,①EC =AE ,OA =OC ,设EC =AE =x ,则BE =AB -AE =8-x ,在Rt ①EBC 中,BE 2+BC 2=CE 2,①x 2=42+(8-x )2,解得:x =5,①AE =CE =5,①EF ①AC ,①OE =①AB ①CD ,①①OCF =①OAE ,①AEO =①CFO ,①OA =OC ,①①AOE ①①COF ,①OF =OE ,①2EF OE ==故选:D.【点拨】本题主要考查了矩形的性质、线段垂直平分线的性质、勾股定理、全等三角形的判定和性质,熟练掌握以上相关知识是解题的关键.8.D【分析】过点B 作BG ①x 轴于G ,过点C 作CH ①y 轴于H ,根据矩形的性质得到点C 的坐标,求出①COE =45°,OC C 作CE ①x 轴于E ,过点C 1作C 1F ①x 轴于F ,由旋转得①COC 1=75°,求出①C 1OF =30°,利用勾股定理求出OF ,即可得到答案.解:过点B 作BG ①x 轴于G ,过点C 作CH ①y 轴于H ,①四边形ABCD 是矩形,①AD =BC ,AB =CD ,AD ∥BC ,①CDA =①DAB =90°,①①HCD =①ADO =①BAG ,①①CHD =①BGA =90°,①①CHD ①①AGB (AAS ),①1,0A ,()0,2D ,()5,2B ,①CH =AG =5-1=4,DH =BG =2,①OH =2+2=4,①C (4,4),①OE =CE =4,①①COE =45°,OC如图,过点C 作CE ①x 轴于E ,过点C 1作C 1F ①x 轴于F ,由旋转得①COC 1=75°,①①C 1OF =30°,①C 1F =12OC 1=12OC①OF =①点C 1的坐标为(-,故选:D .【点拨】此题考查了矩形的性质,旋转的性质,勾股定理,直角三角形30度角的性质,熟记各知识点并综合应用是解题的关键.9.A【分析】13和5为两条直角边长时,求出小正方形的边长8,即可利用勾股定理得出EF 2的长. 解:根据题题得:小正方形的边长等于BE -AE ,①5AE =,13BE =,①小正方形的边长=13-5=8,①22288128EF=+=.故选:A【点拨】本题考查了勾股定理、正方形的性质;熟练掌握勾股定理是解决问题的关键.10.B【分析】根据正方形的判定与性质、矩形的判定与性质、菱形的判定与性质和平行四边形的判定与性质来判断即可求解.解:如图,正方形ABCD中,作线段MN的垂直平分线交AD于点P,交AB于Q点,①PQ垂直平分MN,①PM=PN,QM=QN,在正方形ABCD中,①P AN=①QAN=45°,①①APQ=①AQP=45°,①AP=AQ,①AC垂直平分PQ,①MP=MQ,①四边形PNQM是菱形,在MN运动的过程中,这样的菱形有无数个,即存在无数个这样的平行四边形,当点M与A或者C重合时,四边形PNQM是正方形,则至少存在一个四边形PNQM是正方形,即A、C、D项说法正确,①MN=2,且当点M与A或者C重合时,四边形PNQM是正方形,也是矩形,①不存在无数多个矩形,故B说法错误.故选:B.【点拨】本题考查了正方形的判定定理、矩形的判定定理、菱形和平行四边形的判定定理,熟练掌握相关定理是解答本题的关键.11.C【分析】根据题意直接证明Rt ADF Rt ABE △≌△,进而得CE CF =,可知45FEC ∠=︒,结合等边三角形的条件,即可求得AEB ∠. 解:四边形ABCD 是正方形,AD AB BC CD ∴===,90B C D ∠=∠=∠=︒, AEF 是等边三角形,AF AE ∴=,60AEF ∠=︒,在Rt ADF 和Rt ABE △中AD AB AF AE =⎧⎨=⎩, ∴Rt ADF Rt ABE △≌△(HL ),,DF BE ∴=∴CE CF =,90C ∠=︒,∴45FEC ∠=︒,又60AEF ∠=︒,180AEB AEF FEC ∴∠=︒-∠-∠,180604575=︒-︒-︒=︒,故选:C .【点拨】本题考查了HL 证明直角三角形全等,等腰直角三角形的性质,等边三角形的性质,正方形的性质,熟练以上性质是解题的关键.12.C【分析】设AB 中点为M ,AC 中点为N ,连接DM ,DN ,AD .根据三角形中位线定理,平行线的性质,正方形的性质用AB 表示出①ADF 的面积,用AC 表示出①ADH 的面积,再结合勾股定理将①ADF 与①ADH 的面积相加即可求出阴影部分的面积.解:设AB 中点为M ,AC 中点为N ,连接DM ,DN ,AD .①D 是BC 中点,M 是AB 中点,N 是AC 中点,①DM 是①ABC 的中位线,DN 是①ABC 的中位线.①DM AC ∥,12DM AC =,DN AB ∥,12DN AB =. ①①BMD =①BAC ,①DNC =①BAC .①①BAC =90°,①①BMD =90°,①DNC =90°,222AB AC BC +=.①四边形ABEF 和四边形ACGH 是正方形,①AB =AF ,AC =AH . ①211112224ADF S AF DN AB AB AB =⋅=⨯=△,211112224ADH S AH DM AC AC AC =⋅=⨯=△. ①S 阴222111444ADF ADH S S AB AC BC =+=+=△△. ①BC =10,①S 阴2110254=⨯=. 故选:C .【点拨】本题考查正方形的性质,三角形中位线定理,平行线的性质,勾股定理,综合应用这些知识点是解题关键.13.20【分析】根据矩形的性质得出①ABC =90°,AD =BC =8cm ,CD =AB =6cm ,OA =OC =12AC ,OB =OD =12BD ,AC =BD ,求出OC =OD ,根据菱形的判定得出四边形OCED 是菱形,根据菱形的性质得出OD =OC =DE =CE ,根据勾股定理求出AC ,再求出OC 即可.解:①四边形ABCD 是矩形,AB =6cm ,BC =8cm ,①①ABC=90°,AD=BC=8cm,CD=AB=6cm,OA=OC=12AC,OB=OD=12BD,AC=BD,①OC=OD,①DE①AC,CE①BD,①四边形OCED是平行四边形,又①OC=OD,①四边形OCED是菱形,①OD=OC=DE=CE,由勾股定理得:AC=(cm),①AO=OC=5cm,①OC=CE=DE=OD=5cm,即四边形ODEC的周长=5+5+5+5+5=20(cm),故答案为:20.【点拨】本题考查了矩形的性质,菱形的判定和性质,勾股定理等知识点,能熟记矩形的性质和菱形的判定定理是解此题的关键.14.AB AD=(答案不唯一)【分析】根据菱形的判定定理“有一组邻边相等的平行四边形是菱形”,可以添加邻边相等的条件.解:条件:AB=AD,①四边形ABCD是平行四边形,AB=AD,①四边形ABCD是菱形.故答案为:AB=AD(答案不唯一).【点拨】本题考查了菱形的判定定理,熟练掌握菱形的判定方法是解题的关键.15【分析】根据菱形的性质求得OA,OB的长,然后在Rt AOB∆中利用勾股定理即可求解.解:①菱形ABCD的对角线AC,BD的长分别为6,4,∴AC BD⊥,132OA AC==,122OB BD==,∴Rt AOB∆中,AB===【点拨】本题考查了菱形的性质,勾股定理,熟练掌握菱形的性质是解题的关键.16.6【分析】根据三角形中位线定理,求得BC,进而根据菱形的性质求得CD.解:四边形ABCD是菱形,AB BC CD AD∴===,E、F分别是AB、AC的中点,EF=3,26BC EF∴==,∴CD BC6==故答案为:6.【点拨】本题考查了中位线定理,菱形的性质,掌握中位线定理是解题的关键.17.【分析】如图,连接,AC,BD.过点O作OM①AD于点M交BC于点N.利用勾股定理,求出OE,可得结论.解:如图,连接,AC,BD.①O是矩形的对称中心,①O也是对角线的交点,过点O作OM①AD于点M交BC于点N.①四边形ABCD是矩形,①OA=OD=OB,①OM①AD,①AM=DM=12AD=12BC=4,①OM=12AB=3,①AE=2,①EM=AM-AE=2,①OE同法可得OF①OE+OF故答案为:【点拨】本题考查中心对称,矩形的性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.18.3【分析】由菱形面积计算公式可求得BD的长,再由直角三角形斜边上中线的性质即可求得OH 的长.解:①四边形ABCD是菱形,①AC=2OA=8,①1=242ABCDS AC BD⨯=菱形,①18=24 2BD ⨯,①BD=6,①DH①BC,O为BD的中点,①OH为直角①DHB斜边上的中线,①132OH BD==.故答案为:3.【点拨】本题考查了菱形的性质,直角三角形斜边上中线的性质,菱形面积等于两对角线乘积的一半等知识,掌握这些知识是解题的关键.19.5【分析】根据折叠的性质可得3C E CE AD '===,则6BE BC C E '=-=,勾股定理求得10AB =,证明BFC AFD ''≌,即可求得5BF AF ==.解:①90C D ∠=∠=︒,AE BC ⊥,3AD =,8CD =,①四边形ADCE 是矩形,AD BC ∥3CE AD ∴==,8AE CD ==将四边形纸片ABCD 沿AE 折叠,点C 、D 分别落在点C '、D 处,∴3C E CE AD '===,9BC =,∴6BE BC C E '=-=,Rt AEB 中,10AB ,3BC BC C E CE AD '''=--==,90FC B D ''∠=∠=︒又AD BC ∥B D AF '∴∠=∠∴BFC AFD ''≌ ∴152BF AF AB === 故答案为:5【点拨】本题考查了折叠的性质,矩形的判定,勾股定理,全等三角形的性质与判定,掌握折叠的性质与勾股定理是解题的关键.20.2【分析】根据黄金矩形的定义求出AB ,根据矩形的性质,角平分线的定义,平行线的性质求出①ABE 和①AEB ,再根据等角对等边即可求解.解:①四边形ABCD 是黄金矩形,BC =4,①AB BC =,①ABC =90°,AD BC ∥.①2AB BC ==. ①AE 平分①ABC ,①①ABE =①EBC =45°.①①AEB =①EBC =45°.①①ABE =①AEB .①2AE AB ==.故答案为:2.【点拨】本题考查矩形的性质,平行线的性质,角平分线的定义,等角对等边,综合应用这些知识点是解题关键.21.3【分析】由正六边形的性质及正方形的性质可得①BCG =30°,则由直角三角形的性质可求得BG 的长,从而可得AG 的长.解:①六边形ABCDEF 为正六边形,①①CBG =360°÷6=60°,BC =AB =2;①四边形AGHI 是正方形,①①G =90°,①9030BCG CBG ∠=︒-∠=︒, ①112122BG BC ==⨯=, ①AG =AB +BG =2+1=3.故答案为:3.【点拨】本题考查了正多边形的性质,含30度直角三角形的性质,掌握这两方面知识是解题的关键.22.20225【分析】根据三角形的面积公式,可知每一次延长一倍后,得到的一个直角三角形的面积和延长前的正方形的面积相等,即每一次延长一倍后,得到的图形是延长前的正方形的面积的5倍,从而解答.解:最初边长为1,面积为1,5,,面积52=25,53=125,以此类推,当N=2022时,正方形2022202220222022A B C D 的面积为:52022.故答案为:20225.【点拨】本题主要考查了正方形的性质,在解题时要根据已知条件找出规律,从而得出正方形的面积,这是一道常考题.23.【分析】根据题意PM PN PM PH +=+MH ≥MQ ≥,进而证明ABG ≌AMG ,可得6AM AB ==,勾股定理求解即可.解:如图,作PH AB ⊥,MQ AB ⊥,连接MH.PN ①AC ,AE 平分①BAC ,PN PH ∴=,PM PN PM PH ∴+=+MH ≥MQ ≥,∴MQ 即为所求,四边形ABC D 是正方形正方形,,AB BC ABE BCF ∴=∠=∠, 又CF BE =,ABE BCF ∴△≌△,BAE CBF ∴∠=∠,90BAE BEA ∠+∠=︒,90CBF BEA ∴∠+∠=︒,AE BF ∴⊥,90AGB AGM ∴∠=∠=︒,AE 平分①BAC ,BAG MAG ∴∠=∠,在ABG 与AMG 中,ABG AMG AG AGBAG MAG ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴ABG ≌AMG ,6AM AB ∴==, AC 是正方形的对角线,45MAQ CAB ∴∠=∠=︒,MQ AM ∴==, 即PM PN +的最小值为故答案为:【点拨】本题考查了角平分线的性质,正方形的性质,垂线段最短,根据题意求得PM PN +的最小值是MQ 的长是解题的关键.24.()5,4【分析】根据正方形的性质可得:A 向右平移2个单位,再向下平移3个单位可得点B ,再利用平移的性质可得答案.解:如图,四个边长为1的正方形组成的图案,点A 坐标为()3,7,∴ A 向右平移2个单位,再向下平移3个单位可得点B ,所以32,73,B 即5,4.B故答案为:()5,4【点拨】本题考查的是正方形的性质,坐标与图形,点的平移的坐标规律,熟练的运用点的平移坐标规律是解本题的关键.25.(1)见分析1【分析】(1)根据菱形的性质可知DC=BC ,再根据90BEC DFC ∠=∠=︒,C C ∠=∠,可证得BEC DFC ≌△△,则有EC FC =,问题得解;(2)根据菱形的性质以及①A =45°可证得①ABG 是等腰直角三角形,即可求解.(1)解:①四边形ABCD 是菱形,①CB CD =,①BE CD ⊥于点E ,DF BC ⊥于点F ,①90BEC DFC ∠=∠=︒,①BEC DFC ∠=∠,C C ∠=∠,BC CD =,①BEC DFC ≌△△,①EC FC =,①BF BC CF CD EC DE =-=-=;即BF DE =;(2)解:①四边形ABCD 是菱形,①AB CD ,AD =AB =1,①90ABG BEC ∠=∠=︒,①45A ∠=︒,①45G A ∠=∠=︒,①1AB BG ==,①①ABG 是等腰直角三角形, ①AG = ①1DG AG AD =-.【点拨】本题考查了菱形的性质和全等三角形的判定与性质,证明BEC DFC ≌△△是解答本题的关键.26.(1)见分析(2)对角线的长为8,矩形的面积为【分析】(1)由O 为AC 的中点,可得OA=OC ,然后根据对角线互相平分可证四边形ABCD 为平行四边形,又①ABC =90°,即可证明四边形ABCD 为矩形;(2)易证OE 为△ABC 的中位线,可得AB=2OE=4,根据矩形的性质和①AOB =60°,可证①AOB 为等边三角形,可得OA=BO=AB ,继而可得对角线AC =8,在Rt △ABC 中,由勾股定理可得BC .解:(1)①O 为AC 的中点,①OA=OC ,又①OD=OB ,①四边形ABCD 为平行四边形,又①①ABC =90°,①四边形ABCD 为矩形;(2)解:①OA=OC ,①E 为BC 的中点,①BE=CE ,①OE 为△ABC 的中位线,①AB=2OE=2×2=4,①ABCD 为矩形,①OA=12AC ,OB=12BD , ①AC= BD ,①OA= OB ,又①①AOB =60°,①①AOB 为等边三角形,①OA=BO=AB=4,①对角线AC=BD=2OA=8,①①ABC =90°,在Rt △ABC 中,AB=4,AC=8,①BC =① 矩形的面积4AB BC ⋅=⨯【点拨】本题主要考查了平行四边形的判定、矩形的判定、三角形中位线的判定与性质、等边三角形的判定与性质、勾股定理等,熟记相关定理是解题的关键.27.(1)EAF ;①EAF ;GF ;(2)EF =DE +BF ,见分析;(3)①B +①D =180°,见分析【分析】(1)根据图形和推理过程填空即可;(2)根据题意,分别证明AGB AED ≌△△,AGF AEF ≌△△即可得出结论. (3)根据角之间关系,只要满足∠B +∠D =180°时,就可以得出三角形全等,利用全等三角形的性质即可得出答案.解:(1)将△ADE 绕点A 顺时针旋转90°得到△ABG ,此时AB 与AD 重合,由旋转可得:AB =AD ,BG =DE ,∠1=∠2,∠ABG =∠D =90°,∴∠ABG +∠ABF =90°+90°=180°,因此,点G ,B ,F 在同一条直线上,∵∠EAF =45°,∴∠2+∠3=∠BAD ﹣∠EAF =90°﹣45°=45°,∴∠1+∠3=45°,即∠GAF =∠EAF ,又AG =AE ,AF =AF ,∴△GAF ≌△EAF (SAS ),∴GF =EF ,故DE +BF =EF ;故答案为:EAF ,△EAF ,GF .(2)EF =DE +BF ,理由如下:如图,延长CF ,作①4=①1.①将Rt①ABC 沿斜边翻折得到Rt①ADC ,点E ,F 分别为DC ,BC 边上的点,且12EAF DAB ∠=∠, ①①1+①2=①3+①5,①2+①3=①1+①5.①①4=①1,①2+①3=①4+①5,①①GAF =①F AE .①在①AGB 和①AED 中,41,,,AB AD ABG ADE ∠=∠⎧⎪=⎨⎪∠=∠⎩①AGB AED ≌△△.①AG =AE ,BG =DE .①在①AGF 和①AEF 中,,,,AG AE GAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩①AGF AEF ≌△△.①GF =EF .①DE +BF =EF .(3)当①B 与①D 满足①B +①D =180°时,可使得DE +BF =EF .如图,延长CF ,作①2=①1.①①ABC +①D =180°,①ABC +①ABG =180°,①①D =①ABG .在①AGB 和①AED 中,21,,,AB AD D ABG ∠=∠⎧⎪=⎨⎪∠=∠⎩①AGB AED ≌△△.①BG =DE ,AG =AE . ①12EAF DAB ∠=∠, ①①EAF =①GAF .在①AGF 和①AEF 中,,,,AG AE GAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩①AGF AEF ≌△△.①GF =EF ,DE +BF =EF .故当①B 与①D 满足①B +①D =180°时,可使得DE +BF =EF .【点拨】本题主要考查了正方形的性质,全等三角形的判定和性质以及旋转变换性质等知识,根据题意作出与已知相等的角,利用三角形全等是解决问题的关键.。
