实数指数幂及其运算法则PPT课件
合集下载
人教B版数学必修1第三章3.1.1 实数指数幂及其运算 课件优秀课件资料
(am)nam n(m ,nQ)
(ab)nanbn(nQ)
32
2
例1.(1)8585 __8__ (2)(83 )2 1_6___
21
3
(3)333363__ 9__(4)(a3b4 )3 _a _2 _b _4 _
11 11
(5)(a2b2)(a2b2)_ a__ _ b__
11
11
(6)(a2b2)2a__ +_ b_ +_2_a__ 2_ b_ 2_
2、根式与分数指数幂之间 的相互转化
3、有理指数幂的含义及其 运算性质
三、无理数指数幂
一般地，无理数指数幂 a ( >0,是
无理数)是一个确定的实数. 有理数指数幂的
运算性质同样适用于无理数指数幂.
巩固练习
1、计算下列各式
1
1
1
1
a2 (1) 1
b2
1
a2
1
b2
1
a2 b2 a2 b2
(2)(a 2 2 a 2 ) (a 2 a 2 )
3.1.1实数指数幂及其运算
复习：整数指数幂的运算性质:
aras ars (ar)s ars
(ab)r arbr
am an
amnmn,a0
注 ： a0,r,sZ
a n 中 ， 当 n 0 ,n Z 时 ， a 0 有 意 义
一、根式
定义1:如果xn=a(n>1,且nN*),则称x是a的n次方根.
5、2-(2k+1)-2-(2k-1)+2-2k等于( C ) A.2-2k B. 2-(2k-1) C. -2-(2k+1) D.2
1
6、(| x | 1)
中职数学-实数指数幂及其运算ppt课件
别的说明，底数都表示完整正版课数件 .
17
例3：用分数指数幂的形式表示下列各式：
a 2 a,a 33a 2, aa(式 中 a0 )
分析：此题应结合分数指数幂意义与有理指数幂运算性质。
解：
a2 aa2a1 2a21 2a5 2;
a33a2a3a2 3a32 3a131;
11
31 3
aa(aa2)2(a2)2a4.
我说明们：规若定a了>0分，数p指是数一幂个的无意理义数以，后则，ap表指示 数一个的确概定念的就实从数整. 数上指述数有推理广指到数有幂理的运数算指性 数质，. 上对述于关无于理整数数指指数数幂幂都的适运用算. 即性当质指，数对的 于范围有扩理大指到数实幂数也集同R样后适，用幂，的即运对算任性质意仍有然 理是下数述r，的s，3条均. 有下面的性质：
（ 1） － 3 ＝ （ 2 － 2） － 3 ＝ 2 （ － 2 ） （ － 3 ） ＝ 26＝ 64 ； 4
（ 16） － 3 4＝ （ 2） 4 （ － 3 4） ＝ （ 2） － 3＝ 27。
81
3完整版课件
3
8
14
练习:求值：
912，6432
,(
1
1
)5
32
完整版课件
15
⒋有理指数幂的运算性质
⑴ ar·as=ar+s (a>0,r,s∈Q)；
⑵ (ar)s=ars (a>0,r,s∈Q)；
⑶ (ab)r=ar br (a>0,b>0,r∈Q).
完整版课件
16
1.正数的正分数指数幂的意义：
m
a n na m (a 0 ,m ,n N *且 ,n 1 )
《实数指数幂及其运算法则》课件
《实运算法则的定义和性质，以及指数函数和对数 函数的相关概念和图像。掌握这些知识有助于理解实际问题中的应用。
实数指数幂的定义
• 真数指数幂的概念及特点 • 如何计算实数指数幂
同底数幂的乘法运算法则
• 解释同底数幂的乘法运算法则 • 举例演示同底数幂的乘法运算
同底数幂的除法运算法则
• 介绍同底数幂的除法运算法则的原理 • 通过实例演示同底数幂的除法运算
幂的乘法运算法则
• 解释幂的乘法运算法则的规则 • 提供实际的例子演示幂的乘法运算
幂的除法运算法则
• 说明幂的除法运算法则的概念 • 使用具体案例演示幂的除法运算
幂的幂的运算法则
• 讲解幂的幂的运算法则的原理 • 通过实际问题演示幂的幂的运算
指数函数的定义
• 描述指数函数的概念和定义 • 提供指数函数的数学表达式
指数函数的图像
• 展示指数函数的特点和图像形态 • 比较不同指数函数的图像
实数指数幂的定义
• 真数指数幂的概念及特点 • 如何计算实数指数幂
同底数幂的乘法运算法则
• 解释同底数幂的乘法运算法则 • 举例演示同底数幂的乘法运算
同底数幂的除法运算法则
• 介绍同底数幂的除法运算法则的原理 • 通过实例演示同底数幂的除法运算
幂的乘法运算法则
• 解释幂的乘法运算法则的规则 • 提供实际的例子演示幂的乘法运算
幂的除法运算法则
• 说明幂的除法运算法则的概念 • 使用具体案例演示幂的除法运算
幂的幂的运算法则
• 讲解幂的幂的运算法则的原理 • 通过实际问题演示幂的幂的运算
指数函数的定义
• 描述指数函数的概念和定义 • 提供指数函数的数学表达式
指数函数的图像
• 展示指数函数的特点和图像形态 • 比较不同指数函数的图像
中职数学 实数指数幂及其运算ppt课件
;.
4
二、零指数幂
a 0 ＝ 1（a ≠ 0 ）
练习2
（1）8 0 ＝
；
（2）(－0.8 ) 0 ＝
；
（3）式子 ( a－b ) 0 ＝1 是否恒成立？为什么？
;.
5
如果取消 ＝aaammn－n(m＞n，a≠0)中m＞n的 限制，如何通过指数的运算来表示？
计算： 23
1
（1） 2＝4
；2
＝23－4
;.
17
例3：用分数指数幂的形式表示下列各式：
a 2 a,a 33a 2, aa(式 中 a0 )
分析：此题应结合分数指数幂意义与有理指数幂运算性质。
解：
a2 aa2a1 2a21 2a5 2;
a33a2a3a2 3a32 3a131;
11
31 3
aa(aa2)2(a2)2a4.
a ;. ?
18
例4:计算下列各式（式中字母都是正数）
＝2－1
1
2－1 ＝223来自1（2） 2＝6
；8
＝23－6
＝2－3
1
2－3 ＝
23
a－1＝ （a1≠0） a
规定 a－n＝ （aa1n≠0，nN＋）
;.
6
三、负整数指数幂
a－1 ＝ a－n ＝
（1 a ≠ 0） a （1 a ≠ 0，n N＋ ) an
练习3
（1）8－2 ＝
；
（2）0.2－3 ＝ ；
⑴ ar·as=ar+s (a>0,r,s∈Q)； ⑵ (ar)s=ars (a>0,r,s∈Q)； ⑶ (ab)r=ar br (a>0,b>0,r∈Q).
;.
实数指数幂及其运算PPT课件
复习回顾
实数分类:
整数
有理数 实 数 无理数
分数
三维目标
1.知识与技能： 了解根式方根的概念及关系 理解分数指数幂的概念 掌握有理数指数幂的运算性质 2.过程与方法： 能运用性质进行化简计算 3.情感.态度与价值观： 注重类比思想的应用
整数指数幂
正整数指数幂:
指数
幂
底数
运算法则:
将正整数指数幂推广到整数指数幂
运算法则:
练算
偶次方根 奇次方根
根式性质
a （a>0,n∈N+）
练习
=a
=a2
分数指数幂
分数指数幂
有理数指数幂
运算法则:
练习
小结
1：运算性质：
2.偶次方根的性质: 正数的偶次方根是两个绝对值相等符号相反的数， 负数的偶次方根无意义，零的任何次方根为零
实数分类:
整数
有理数 实 数 无理数
分数
三维目标
1.知识与技能： 了解根式方根的概念及关系 理解分数指数幂的概念 掌握有理数指数幂的运算性质 2.过程与方法： 能运用性质进行化简计算 3.情感.态度与价值观： 注重类比思想的应用
整数指数幂
正整数指数幂:
指数
幂
底数
运算法则:
将正整数指数幂推广到整数指数幂
运算法则:
练算
偶次方根 奇次方根
根式性质
a （a>0,n∈N+）
练习
=a
=a2
分数指数幂
分数指数幂
有理数指数幂
运算法则:
练习
小结
1：运算性质：
2.偶次方根的性质: 正数的偶次方根是两个绝对值相等符号相反的数， 负数的偶次方根无意义，零的任何次方根为零
《实数指数幂》课件
定义，以及实数指数幂的运算性质。
幂的运算法则
02
包括同底数幂的乘法、除法，幂的乘方以及积的乘方等运算法
则。
无穷大与无穷小的概念
03
理解无穷大和无穷小的概念，掌握其在实数指数幂中的应用。
常见错误解析
混淆不同底数指数幂的运算
01
例如，将a^m * a^n误算为a^(m+n)，而不是正确
的a^(mn)。
实数指数幂的引入
实数指数幂的定义
实数指数幂表示一个数与一个实数的乘方。例如，$a^{m/n}$ 表示 $a$ 的 $m$ 次方再 开 $n$ 次方根。
实数指数幂的引入背景
实数指数幂的引入是为了解决一些数学问题，特别是在处理连续函数和积分时，实数指数 幂提供了更灵活和实用的工具。
实数指数幂的性质
实数指数幂具有一些重要性质，如 $a^{mn} = (a^m)^n$，$a^{m/n} = sqrt[n]{a^m}$ ，以及 $(ab)^n = a^n times b^n$。这些性质在数学和物理中有广泛的应用。
《实数指数幂》ppt课件
目录
• 引言 • 实数指数幂的性质 • 实数指数幂的运算 • 实数指数幂的性质与运算的应用 • 总结与回顾
01
引言
幂的定义与性质
幂的定义
幂是乘方运算的结果，表示一个 数连续与一个相同的数相乘的次 数。例如，$a^m$ 表示 $a$ 连 续乘以自身 $m$ 次。
幂的性质
幂具有一些基本性质，如 $a^{m+n} = a^m times a^n$ ，$(a^m)^n = a^{mn}$，以及 $a^{-m} = frac{1}{a^m}$。
，从而更好地理解和求解问题。
实数指数幂及其运算 PPT课件
2n = a xn =a
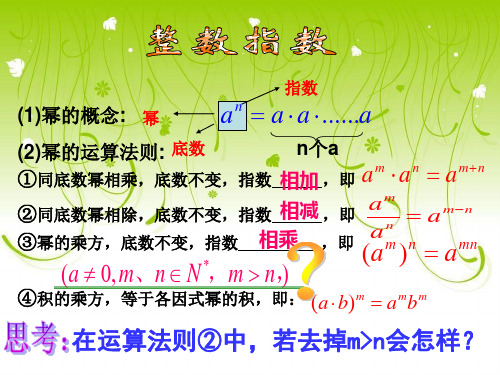
2叫a的n次方根; x叫a的n次方根.
1.方根的定义 如果xn=a,那么x叫做 a 的n次方根,其中n>1,且
n∈N*.
即 如果一个数的n次方等于a (n>1，且 n∈N*)，那么这个数叫做 a 的n次方根.
24=16 (-2)4=16
(-2)5=-32 27=128
16的4次方根是±2.
示a在实数范围内唯一的一个n次方根.
当n是偶数时, n a 只有当a≥0有意义,当a<0时 无意义. n a (a ≥ 0)表示a在实数范围内的一个 n次方根,另一个是 n a (a ≥ 0)
( n a ) n a
(1) 5 25 2, 3（ 2）3 2. 结论:an开奇次方根,则有 n an a. (2) 32 3, (3)2 3, (3)2 3.
(6)0的七次方根是_____0_.
点评:求一个数a的n次方根就是求出哪个数的n 次方等于a.
23=8
8的3次方根是2. 记作：3 8 2.
ቤተ መጻሕፍቲ ባይዱ
(-2)3=-8
-8的3次方根是-2. 记作：3 8 2.
(-2)5=-32 27=128
-32的5次方根是-2.记作：5 32 2. 128的7次方根是2. 记作：7 128 2.
-32的5次方根是-2. 2是128的7次方根.
【1】试根据n次方根的定义分别求出下
列各(数1)的25n的次平方方根根. 是___±___5_;
(2)27的三次方根是____3_; (3)-32的五次方根是_-_2__; (4)16的四次方根是_±___2_; (5)a6的三次方根是___a_2_;
的平方根.
22=4 (-2)2=4
语文版中职数学基础模块上册4.2《实数指数幂及其运算法则》ppt课件4
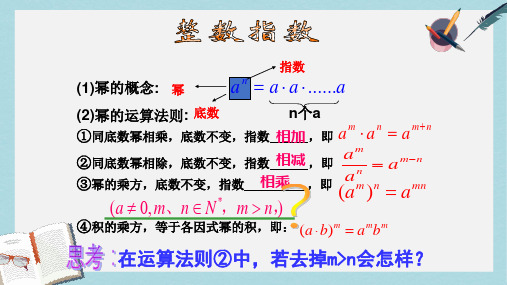
【1】下列各式中, 不正确的序号是( ① ④ ).
① 4 16 2 ② ( 5 3)5 3 ③ 5 (3)5 3 ④ 5 (3)10 3 ⑤ 4 (3)4 3
【2】求下列各式的值.
⑴ 5 32;
⑵ （ 3）4 ;
⑶ （ 2 3）2 ; ⑷ 5 2 6 .
分数指数幂在底数小于0时无意义.
⒉负分数指数幂的意义
注回意忆：负整负数分指数数指幂数的幂意在义：有意义的情况下，
总在指表数示上正.数a－，n=而a1不n (是a≠负0,n数∈,N负*)号. 只是出现
正数的负分数指数幂的意义和正数的负整
数指数幂的意义相仿，就是：
m
an
1
m
an
1 (a>0,m,n∈N*,且n>1). n am
64的6次方根是2，-2.
记作： 6 64 2.
1.正数的偶次方根有两个且互为相反数
偶次方根 2.负数的偶次方根没有意义
正数a的n次方根用符号 n a 表示(n为偶数）
(1) 奇次方根有以下性质： 正数的奇次方根是正数. 负数的奇次方根是负数. 零的奇次方根是零.
(2)偶次方根有以下性质：
r4
0.0001 104
a2 b2c
a 2b 2c 1
回顾初中知识,根式是如何定义的？有
那些规定？
①如果一个数的平方等于a,则这个数叫做 a
的平方根.
22=4 (-2)2=4
2,-2叫4的平方根.
②如果一个数的立方等于a,则这个数叫做a
的立方根.
23=8
2叫8的立方根.
(-2)3=-8
-2叫-8的立方根.
例2．如果 2x2 5x 2 0, 化简代
《实数指数幂及其运算法则》ppt课件
2.负数的偶次方根没有意义；
3.正数a的奇次次方根是一个正数，负数的奇次方根是一个负数 都表示为
n
a， （n为奇数）
4.0的任何次方根都是0，记作n 0 0.
①( 5)
2
2 3 3
5 ②( 5) 5③( 5) 5 ④ 6 6 ⑤ （ 6 ） 6 ⑥（ 6 ） 6 ⑦ （ 6 ） 6
一、（1）化负指数为正指数，
（2)化根式为分数指数幂， （3）化小数为分数 (4)遇乘积化同底或同指数幂
二、对于计算的结果，不强求统一用什么形式来表示，
但结果不能同时含有根号和分数指数，也不能既含有分 母又含有负指数。
方法规律： n （1）先把被开方数化为 a 的形式 ( a ) a （2）再利用运算法则 计算（底数不变 ，指数相乘）
回顾旧知识
整数指数幂的概念:
指数 幂 底数
正整数指数幂的概念:
a a a ......a
n
n个a
(n N
规定：
a 1
1 n a an
0
(a 0)
1 an
( a 0, n N )
导入新课题
问题：我国农业科学家在研究某农作物的生长状况时 ，得到该作物的生长时间x周（从第1周到12周）与植 x 株高度ycm之间的关系 y= . 4
r s rs
r r r
(ab) a b (a 0, b 0, r Q
课后作业
课本P71练习1、2、3题
求值
27 ， 100
2 3
-
1 2
1 -3 ，（ 4 ） ，
2 3 3 2
16 - 4 （ ） 81
3
实数指数幂及其运算 PPT课件 1 人教课标版
1 4 6 r x 6 1 x r4
0 .0001 10 4
a 2 2 1 a b c 2 b c
2
2 分数指数
2
若 x a ，则 x叫 a 的平方根（或二次方根 ）
a 0 时，两个平方根： a， a a 0时，有一个平方根： 0 a 0时，无实根
3
若 x a ，则 x叫 a 的立方根（或三次方根 ）
a 根式
n 根指数
n
正 数 a 的 正 n 次 方 根 叫 做 a 的 n 次 算 术 方 根
根式性质
( 1 )( a ) a ( n 1 , n N )
n n
a
(2) a
n n
当n为奇数时
|a |
当n为偶数时
练习1
①( 5)
4 4
5
3
②（ 5 ）
a 只有一个立方根
方根
n 若 存 在 实 数 x ， 使（ x = a aR ? ，， n1 n ? N ） ， +
则 xan 叫 的 次 方 根 。
求a 的 n 次方根，叫做把 a 开 n 次方 ,称作开方运算
偶次方根 奇次方根
n
实 a 0 n a 数 a a 0 不存在
n
a 0 a 0
（ 3 ）（ ab ） a b
转
练习2
① 8 8 ② 8
2 3
3 5
2 5
1 3 2
8
3 2 5 5
8
（ 8） 2 4
2
③ 3 3
2 3
3
3
6
3
2 33
3 3 3 3 3
高中数学 3.1.1实数指数幂及其运算 课件 新人教A版必修1
xn a
那么x叫做a的n次方根,其中 n1,且 nN*.
求a的n次方根，叫做把a开n 次方，称作开方运算．
（ 1） 22 4,(2 )2 4, 4的平方根 ? 是
（2） 23 8，23 8， 8的立方根是 8的 ？立方根是？
总结
思考
正 数 的 偶 次 方几 2 根个有？
它 们 之 间 互的 关为系相是反什数么？
解:
83 2(23)3 2233 2224
1
1002
1
1
1
1
1002 (102)2
1 10
(1)3(22)32(2)(3)2664 4
(16 )4 3(2)4(4 3) (2)327
81 3
38
例 4 用分数指数幂的形式 式(式中a>0):
表示下列各
1 .a 2 •
a1
a2•a2
21
5
a 2a2
正数的奇次方根几 有 1个？ 负数的奇次方根几 有1个？
3.根式的运算性质
(1)
n
(
a)na(n1,且 nN *)
n
(2) an
a 当n为奇数时 |a| 当n为偶数时.
１.正数的分Байду номын сангаас指数幂的意义
m
annam (a0,m ,n N *,且 n1)
２.规定
(１)
am n1m(a0,m ,nN*,且 n1) an
(２)０的正分数指数幂等于０.
(３)０的负分数指数幂无意义.
３.有理指数幂的运算性质
(１) a r•a s a r s(a 0 ,r,s Q ), (２) (ar)sar(sa0,r,s Q ),
(３) a r b a r b r ( a 0 ,b 0 ,r Q ).
那么x叫做a的n次方根,其中 n1,且 nN*.
求a的n次方根，叫做把a开n 次方，称作开方运算．
（ 1） 22 4,(2 )2 4, 4的平方根 ? 是
（2） 23 8，23 8， 8的立方根是 8的 ？立方根是？
总结
思考
正 数 的 偶 次 方几 2 根个有？
它 们 之 间 互的 关为系相是反什数么？
解:
83 2(23)3 2233 2224
1
1002
1
1
1
1
1002 (102)2
1 10
(1)3(22)32(2)(3)2664 4
(16 )4 3(2)4(4 3) (2)327
81 3
38
例 4 用分数指数幂的形式 式(式中a>0):
表示下列各
1 .a 2 •
a1
a2•a2
21
5
a 2a2
正数的奇次方根几 有 1个？ 负数的奇次方根几 有1个？
3.根式的运算性质
(1)
n
(
a)na(n1,且 nN *)
n
(2) an
a 当n为奇数时 |a| 当n为偶数时.
１.正数的分Байду номын сангаас指数幂的意义
m
annam (a0,m ,n N *,且 n1)
２.规定
(１)
am n1m(a0,m ,nN*,且 n1) an
(２)０的正分数指数幂等于０.
(３)０的负分数指数幂无意义.
３.有理指数幂的运算性质
(１) a r•a s a r s(a 0 ,r,s Q ), (２) (ar)sar(sa0,r,s Q ),
(３) a r b a r b r ( a 0 ,b 0 ,r Q ).
《实数指数幂及其运算法则》ppt课件
$(ab)^n = a^n times b^n$
$(uv)^n = u^n times v^n$
积的运算性质
$(u^n)v = u times u times ldots times u times v$（共n个u相乘）
积的运算性质2
$(u^n)v = u times (u^n)v$
积的运算性质3
$(ab)^{-n} = frac{1}{(ab)^n} = frac{1}{a^n times b^n}$
积的运算性质
$frac{a^m}{b^m} = (a/b)^m$
商的指数运算性质
$frac{a^m}{b^{-m}} = (a/b)^{m-n} = frac{a^{m-n}}{b^{m-n}}$
总结与回顾
卑鄙！只要 your question mark keeps track of keeping your work. OMRC
Cited from: "https://www.bokephases"
总结与回顾
* "
" 输入: 6th Party View : 尾声 (疏影)
# 2nd Party View
幂运算在数学、物理、工程等领域有广泛应用。
幂的应用
积运算可以用于计算多个数的乘积，简化计算过程。
在统计学中，积运算可以用于计算样本方差、标准差等统计量。
在物理学中，积运算可以用于计算多个物理量的乘积，如力矩、功等。
积的应用
商的应用
商运算可以用于计算两个数的比值，用于比较大小、排序等。
在经济学中，商运算可以用于计算成本效益比、投资回报率等。
尾声 (疏影): 6th Party View : 尾声 (疏影)
$(uv)^n = u^n times v^n$
积的运算性质
$(u^n)v = u times u times ldots times u times v$（共n个u相乘）
积的运算性质2
$(u^n)v = u times (u^n)v$
积的运算性质3
$(ab)^{-n} = frac{1}{(ab)^n} = frac{1}{a^n times b^n}$
积的运算性质
$frac{a^m}{b^m} = (a/b)^m$
商的指数运算性质
$frac{a^m}{b^{-m}} = (a/b)^{m-n} = frac{a^{m-n}}{b^{m-n}}$
总结与回顾
卑鄙！只要 your question mark keeps track of keeping your work. OMRC
Cited from: "https://www.bokephases"
总结与回顾
* "
" 输入: 6th Party View : 尾声 (疏影)
# 2nd Party View
幂运算在数学、物理、工程等领域有广泛应用。
幂的应用
积运算可以用于计算多个数的乘积，简化计算过程。
在统计学中，积运算可以用于计算样本方差、标准差等统计量。
在物理学中，积运算可以用于计算多个物理量的乘积，如力矩、功等。
积的应用
商的应用
商运算可以用于计算两个数的比值，用于比较大小、排序等。
在经济学中，商运算可以用于计算成本效益比、投资回报率等。
尾声 (疏影): 6th Party View : 尾声 (疏影)
高中数学人教B版必修一课件3.1.1实数指数幂及其运算(42张PPT)
(1)(n a)n＝___a___(n＞1，且 n∈N*)；
n (2)
an＝
a n为奇数， |a| n为偶数.
5．分数指数幂的运算法则
1
(1)an
n ＝____a____(a＞0)；
m
(2)a n
＝__(_n_a_)_m__＝____n_a_m__(a＞0，m、n∈N*，且mn 为既
约分数)；
m
(3)a－ n
＝____(a＞0，m、n∈N*，且mn 为既约分数)．
预习效果展示
1.如果 a＞0，b＞0，m、n 都是有理数，则下列各式错误的
是( )
A．(am)－n＝a－mn
B．ama－n＝am－n
C．(ab)n＝an·b－n [答案] D
D．am＋an＝am＋n
[解析] 根据有理指数幂的运算法则可知选项D错误．
3.1 指数与指数函数 第三章
3.1.1 实数指数幂及其运算 第三章
课前自主预习
情境引入导学
2010年11月1日，全国人口普查全面展开，而2000年我国 约有13亿人口．我国政府现在实行计划生育政策，人口年增 长率较低．若按年增长率1%计算，到2010年底，我国人口将 增加多少？到2020年底，我国人口总数将达到多少？如果我 们放开计划生育政策，年增长率是2%，甚至是5%，那么结果 将会是怎样的呢？会带来灾难性后果吗？
×－760＋80.25×4 2＋(3 2×
3)6－
－3223；
(2) a3b2·3 ab2 (a＞b，b＞0)．
4 a
3 b4·
b a
[解析]
(1)原式＝3213
3
＋24
1
×24
＋22×33－3213
语文版中职数学基础模块上册4.2《实数指数幂及其运算法则》ppt课件2
解：1
6 a3b4
a3b4
1
31 41
12
6 a 6b 6 a2b3 ;
2
3 a2
2
a 3 a1
2 1
a3
1
a3
.
a
课堂练习：P96、练习
例3 计算： 2 2 4 32 4 2
1
1
1
原式 2 22 25 4 24
4.2 实数指数幂及其运算法则
有理数指数幂的运算法则：
（1）am·an=am+n(a>0,m,n是有理数) （2）(am)n=amn(a>0,m,n是正有理数) （3）(ab)n=anbn(a，b>0,m,n是有理数)
例1、求下列各式的值：
2
(1) 83
; (2)
81 16
3 4
1
5
1
222 24 24
1 1 5 1
2 2 4 4
23
8
课本98页 练习、习题二
编后语
• 常常可见到这样的同学，他们在下课前几分钟就开始看表、收拾课本文具，下课铃一响，就迫不及待地“逃离”教室。实际上，每节课刚下课时的几分 钟是我们对上课内容查漏补缺的好时机。善于学习的同学往往懂得抓好课后的“黄金两分钟”。那么，课后的“黄金时间”可以用来做什么呢？
2019/8/28
最新中小学教学课件
thank
you!
2019/8/28
最新中小学教学课件
遍自己写的笔记，既可以起到复习的作用，又可以检查笔记中的遗漏和错误。遗漏之处要补全，错别字要纠正，过于潦草的字要写清楚。同时，将自己 对讲课内容的理解、自己的收获和感想，用自己的话写在笔记本的空白处。这样，可以使笔记变的更加完整、充实。 • 三、课后“静思2分钟”大有学问 • 我们还要注意课后的及时思考。利用课间休息时间，在心中快速把刚才上课时刚讲过的一些关键思路理一遍，把老师讲解的题目从题意到解答整个过 程详细审视一遍，这样，不仅可以加深知识的理解和记忆，还可以轻而易举地掌握一些关键的解题技巧。所以，2分钟的课后静思等于同一学科知识的 课后复习30分钟。
实数指数幂及其运算ppt1 人教课标版
3 3
5
③（ 2） 2 8
5 3 5
④
2
⑤ （ 3 ） | 3| 3
4 4
(a ) a a
1 3 3
1 3 3
(a ) a a
2 3
2 3 3
2 3 3
2
a 3 a
1 3
a a
3
分数指数幂
2
分数指数幂
a a(a0 )
n
1 n
a
n
1 n a
a ( a) a
读一本好书，就是和许多高尚的人谈话。 ---歌德 书籍是人类知识的总结。书籍是全世界的营养品。 ---莎士比亚 书籍是巨大的力量。 ---列宁 好的书籍是最贵重的珍宝。 ---别林斯基 任何时候我也不会满足，越是多读书，就越是深刻地感到不满足，越感到自己知识贫乏。 ---马克思 书籍便是这种改造灵魂的工具。人类所需要的，是富有启发性的养料。而阅读，则正是这种养料。 ---雨果 喜欢读书，就等于把生活中寂寞的辰光换成巨大享受的时刻。 ---孟德斯鸠 如果我阅读得和别人一样多，我就知道得和别人一样少。 ---霍伯斯[英国作家] 读书有三种方法：一种是读而不懂，另一种是既读也懂，还有一种是读而懂得书上所没有的东西。 ---克尼雅日宁[俄国剧作家・诗人] 要学会读书，必须首先读的非常慢，直到最后值得你精读的一本书，还是应该很慢地读。 ---法奇(法国科学家) 了解一页书，胜于匆促地阅读一卷书。 ---麦考利[英国作家] 读书而不回想，犹如食物而不消化。 ---伯克[美国想思家] 读书而不能运用，则所读书等于废纸。 ---华盛顿(美国政治家) 书籍使一些人博学多识，但也使一些食而不化的人疯疯颠颠。 ---彼特拉克[意大利诗人] 生活在我们这个世界里，不读书就完全不可能了解人。 ---高尔基 读书越多，越感到腹中空虚。 ---雪莱(英国诗人) 读书是我唯一的娱乐。我不把时间浪费于酒店、赌博或任何一种恶劣的游戏；而我对于事业的勤劳，仍是按照必要，不倦不厌。 ---富兰克林 书读的越多而不加思索，你就会觉得你知道得很多；但当你读书而思考越多的时候，你就会清楚地看到你知道得很少。 ---伏尔泰(法国哲学家、文学家) 读书破万卷，下笔如有神。---杜甫 读万卷书，行万里路。 ---顾炎武 读书之法无他，惟是笃志虚心，反复详玩，为有功耳。 ---朱熹 读书无嗜好，就能尽其多。不先泛览群书，则会无所适从或失之偏好，广然后深，博然后专。 ---鲁迅 读书之法，在循序渐进，熟读而精思。 ---朱煮 读书务在循序渐进；一书已熟，方读一书，勿得卤莽躐等，虽多无益。 ---胡居仁[明] 读书是学习，摘抄是整理，写作是创造。 ---吴晗 看书不能信仰而无思考，要大胆地提出问题，勤于摘录资料，分析资料，找出其中的相互关系，是做学问的一种方法。---顾颉刚 书犹药也，善读之可以医愚。 ---刘向 读书破万卷，胸中无适主，便如暴富儿，颇为用钱苦。 ---郑板桥 知古不知今，谓之落沉。知今不知古，谓之盲瞽。 ---王充 举一纲而万目张，解一卷而众篇明。 ---郑玄
5
③（ 2） 2 8
5 3 5
④
2
⑤ （ 3 ） | 3| 3
4 4
(a ) a a
1 3 3
1 3 3
(a ) a a
2 3
2 3 3
2 3 3
2
a 3 a
1 3
a a
3
分数指数幂
2
分数指数幂
a a(a0 )
n
1 n
a
n
1 n a
a ( a) a
读一本好书，就是和许多高尚的人谈话。 ---歌德 书籍是人类知识的总结。书籍是全世界的营养品。 ---莎士比亚 书籍是巨大的力量。 ---列宁 好的书籍是最贵重的珍宝。 ---别林斯基 任何时候我也不会满足，越是多读书，就越是深刻地感到不满足，越感到自己知识贫乏。 ---马克思 书籍便是这种改造灵魂的工具。人类所需要的，是富有启发性的养料。而阅读，则正是这种养料。 ---雨果 喜欢读书，就等于把生活中寂寞的辰光换成巨大享受的时刻。 ---孟德斯鸠 如果我阅读得和别人一样多，我就知道得和别人一样少。 ---霍伯斯[英国作家] 读书有三种方法：一种是读而不懂，另一种是既读也懂，还有一种是读而懂得书上所没有的东西。 ---克尼雅日宁[俄国剧作家・诗人] 要学会读书，必须首先读的非常慢，直到最后值得你精读的一本书，还是应该很慢地读。 ---法奇(法国科学家) 了解一页书，胜于匆促地阅读一卷书。 ---麦考利[英国作家] 读书而不回想，犹如食物而不消化。 ---伯克[美国想思家] 读书而不能运用，则所读书等于废纸。 ---华盛顿(美国政治家) 书籍使一些人博学多识，但也使一些食而不化的人疯疯颠颠。 ---彼特拉克[意大利诗人] 生活在我们这个世界里，不读书就完全不可能了解人。 ---高尔基 读书越多，越感到腹中空虚。 ---雪莱(英国诗人) 读书是我唯一的娱乐。我不把时间浪费于酒店、赌博或任何一种恶劣的游戏；而我对于事业的勤劳，仍是按照必要，不倦不厌。 ---富兰克林 书读的越多而不加思索，你就会觉得你知道得很多；但当你读书而思考越多的时候，你就会清楚地看到你知道得很少。 ---伏尔泰(法国哲学家、文学家) 读书破万卷，下笔如有神。---杜甫 读万卷书，行万里路。 ---顾炎武 读书之法无他，惟是笃志虚心，反复详玩，为有功耳。 ---朱熹 读书无嗜好，就能尽其多。不先泛览群书，则会无所适从或失之偏好，广然后深，博然后专。 ---鲁迅 读书之法，在循序渐进，熟读而精思。 ---朱煮 读书务在循序渐进；一书已熟，方读一书，勿得卤莽躐等，虽多无益。 ---胡居仁[明] 读书是学习，摘抄是整理，写作是创造。 ---吴晗 看书不能信仰而无思考，要大胆地提出问题，勤于摘录资料，分析资料，找出其中的相互关系，是做学问的一种方法。---顾颉刚 书犹药也，善读之可以医愚。 ---刘向 读书破万卷，胸中无适主，便如暴富儿，颇为用钱苦。 ---郑板桥 知古不知今，谓之落沉。知今不知古，谓之盲瞽。 ---王充 举一纲而万目张，解一卷而众篇明。 ---郑玄
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x 6 r 4
1 1
64
64
1
x6 1
r4 x6
r4
（2x）3
23 x3
1 8x3
0.000110 4
a2
b c2.
a2b2c1
6
有理数指数幂
a0,bo,a、b为有理数
运算法则:
（ 1 ） apaqap q
（ 2）a（ p） qapq
（ 3） (ab )p apbp
.
7
练习2
3
2
① 8585
（2）（ am） na mn
（
3）a a
m n
amn （ mn， a0）
（ 4）（ a） bm a bm. m
3
由 a m = amn （ mn， a0）
an
a0
1 a a 3
a3
a 33
0
a3 a5
a 35
a2
1 a2
将正整数指数幂推广到整数指数幂
.
4
规定：
a 0 1 （a 0）
a n
.
12
• 作业： • 课本P77 习题4.1A 组 1、 2
.
13
.
14
32
85 5 8
2
②
83
1
（83）2 22 4
③ 3 33 36 3
111
332 33 36
1 1 1 1
3 2 3 6
32
9
21
2
1
3
④（ a 3 b 4 ）3 （a3） （ 3 b4） 3a2b4
.
8
1
⑤（a 2
1
1
b2）（a 2
1
b2）
1
（ a 2）2
1
（ b 2）2
ab
1
31.5 ， 31.42 ， 31.415 ， ....
来近似地计算无理指数幂 3 2 的不足或过剩近似值。如果 ２ 的任何一个有理数
n 不足近似值记为 a
就逼近于a 一n 个, b实n 数
n
，其相应的有理数过剩近似值为 b ， 那么当
n
，因而
2 也就逼近3a于n 一, 个3bn实数
无限增大时， ，这就是说，
两个3 有2 理指数幂的序列
无限逼近3一an个 实, 数3bn
。
32
无限逼近的思想
a a > 0 一般地，当
a
，为任意实数值时，实数指数幂
都是有意义的.
可以证明，对任意的实数 a ，b ，上述. 有理指数幂的运算法则仍然成10立。即
练 习 ３ ： 化 简 下 列 各 式 (课后练习)
（ 1） （-
1 an
（a0，nN）
• 运算法则(m,n∈z)
(1) am·an=am+n
(2) (am)n=amn
(3)
am an
amn(mna, 0)
(4) (ab)m=ambm
.
5
练习:
80 1
（8）0 1
（ab）0 1
103
1 103
0.001
（ 1 ）6 2
1 ( 1 )6
2
（
x 3 ） 2 r2
-2 1
5x 3y 2
1
1
x - 1y 2）
（
-
4
5
x
1
3y
-
1
6）
6
（ 2）m + m - 1 + 2
-1
1
m 2+ m2
.
11
总结：
•1 a 0 = 1
（a 0）
•2 a - n =
1 an
（ a0， nN）
• 3 a,b R （ 1） a p a q a p q ( 2 )( a p ) q a pq (3 )( ab ) p a p b p
山阳职教中心 陈新芳
.
1
实数分类: 有理数
实 数
整数 分数
正整数 0 负整数
无理数
在初中学过整数指数幂概念及运算，这节我们将其推广 到实数正整数指数幂:
a 2 a a
a 3 a a a
指数
幂
anaa...a... 规定：a１＝ a
底数
n个
运算法则:（1）aman amn
1
11
⑥（a 2 b2）2 ab2a2b2
.
9
无理数指数幂
例： 32是一个什么样的数？
用 1 .4 ， 1 .4 1 ， 1 .4 1 4 ， ...（ .. 2 的 不 足 近 似 值 ） ；
31.4 ， 31.41 ， 31.414 ， ...
和 1 .5 ， 1 .4 2 ， 1 .4 1 5 ， ...（ .. 2 的 过 剩 近 似 值 ） ；