实数指数幂及其运算法则课件
合集下载
实数指数幂及其运算法则

另外,我们规定:
a 1(a 0); 1 n a n. a
0
二、根式
一般地,如果xn=a,那么x叫做a的n次方根(n th root),其中n>1, 且n∈N*.
x n a ; (当n是奇数)
x a
n
x n a . (当n是偶数,且a>0)
让我们认识一下这个式子:
根指数
根式
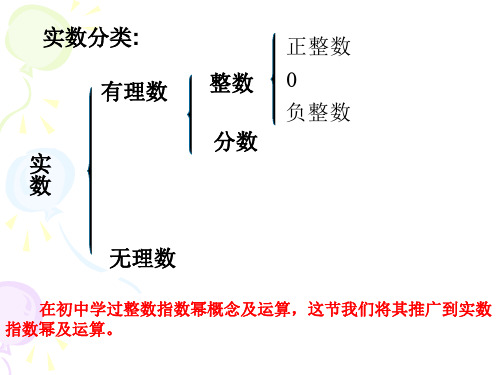
一、知识回顾
在初中,我们研究了正整数指数幂:一个数a的n次幂等于n个 a的连乘积,即 an=a· a· · · ·· a n个 正整数指数幂的运算法则有五条:
1.am· an=am+n;
2.am÷an=am-n; 3.(am)n=amn; 4.(ab)n=an· bn; 5.
a n an ( ) n (b 0)..
a 3 a , a 2 3 a 2 , a3 a .
解:
a3 a a3 a a
2 3
1 2
3
1 2
a ;
2 3
7 2
a2 3 a2 a2 a a
1 1 3 2
2
a3 a (a a ) (a ) a .
4 1 3 2
a ;
2 3
8 3
三、分数指数幂 探究:
5 10 5
a
10
(a ) a a (a 0),
5 2 5 2 12 4
4
a12 4 (a 4 ) 3 a 3 a (a 0).
2 3
0的正分数指数 幂等于0,0 的负 分数指数幂没有 意义.
3
a 2 a ( a 0), b b (b 0),
4
例1 求下列各式的值 1. 3 3
《实数指数幂及其运算法则》课件

《实运算法则的定义和性质,以及指数函数和对数 函数的相关概念和图像。掌握这些知识有助于理解实际问题中的应用。
实数指数幂的定义
• 真数指数幂的概念及特点 • 如何计算实数指数幂
同底数幂的乘法运算法则
• 解释同底数幂的乘法运算法则 • 举例演示同底数幂的乘法运算
同底数幂的除法运算法则
• 介绍同底数幂的除法运算法则的原理 • 通过实例演示同底数幂的除法运算
幂的乘法运算法则
• 解释幂的乘法运算法则的规则 • 提供实际的例子演示幂的乘法运算
幂的除法运算法则
• 说明幂的除法运算法则的概念 • 使用具体案例演示幂的除法运算
幂的幂的运算法则
• 讲解幂的幂的运算法则的原理 • 通过实际问题演示幂的幂的运算
指数函数的定义
• 描述指数函数的概念和定义 • 提供指数函数的数学表达式
指数函数的图像
• 展示指数函数的特点和图像形态 • 比较不同指数函数的图像
实数指数幂的定义
• 真数指数幂的概念及特点 • 如何计算实数指数幂
同底数幂的乘法运算法则
• 解释同底数幂的乘法运算法则 • 举例演示同底数幂的乘法运算
同底数幂的除法运算法则
• 介绍同底数幂的除法运算法则的原理 • 通过实例演示同底数幂的除法运算
幂的乘法运算法则
• 解释幂的乘法运算法则的规则 • 提供实际的例子演示幂的乘法运算
幂的除法运算法则
• 说明幂的除法运算法则的概念 • 使用具体案例演示幂的除法运算
幂的幂的运算法则
• 讲解幂的幂的运算法则的原理 • 通过实际问题演示幂的幂的运算
指数函数的定义
• 描述指数函数的概念和定义 • 提供指数函数的数学表达式
指数函数的图像
• 展示指数函数的特点和图像形态 • 比较不同指数函数的图像
实数指数幂及其运算法则PPT课件

x 6 r 4
1 1
64
64
1
x6 1
r4 x6
r4
(2x)3
23 x3
1 8x3
0.000110 4
a2
b c2.
a2b2c1
6
有理数指数幂
a0,bo,a、b为有理数
运算法则:
( 1 ) apaqap q
( 2)a( p) qapq
( 3) (ab )p apbp
.
7
练习2
3
2
① 8585
(2)( am) na mn
(
3)a a
m n
amn ( mn, a0)
( 4)( a) bm a bm. m
3
由 a m = amn ( mn, a0)
an
a0
1 a a 3
a3
a 33
0
a3 a5
a 35
a2
1 a2
将正整数指数幂推广到整数指数幂
.
4
规定:
a 0 1 (a 0)
a n
.
12
• 作业: • 课本P77 习题4.1A 组 1、 2
.
13
.
14
32
85 5 8
2
②
83
1
(83)2 22 4
③ 3 33 36 3
111
332 33 36
1 1 1 1
3 2 3 6
32
9
21
2
1
3
④( a 3 b 4 )3 (a3) ( 3 b4) 3a2b4
.
8
1
⑤(a 2
1
1
b2)(a 2
高中数学实数指数幂及其运算1理解n次方根的概念及性质课件人教版必修一
a
m n
(2)(a ) a am mn (3) n a (m n,a 0) a
m n
nm
(4)(ab)
m
a b
m m
由
am an
=
a
mn
(m n,a 0)
a0
a a 3 3 a3
3
3
a
0
1
a 35 1 2 a a a2 5 a
将正整数指数幂推广到整数指数幂
an
和
1.5 , , ,( 2的过剩近似值); 1.42 1.415 .....
来近似地计算无理指数幂 3 2的不足或过剩近似值。如果 2 的任何一个有理数 不足近似值记为 a ,其相应的有理数过剩近似值为 b , 那么当 n 无限增大
3 , , 3 3
1.5 1.42
n
1.415
时,
数
an , bn 就逼近于一个实数
a a 2b 2c 1 2 bc
2
2 分数指数
若x a,则x叫a的平方根(或二次方根)
2
a 0时,两个平方根: , a a a 0时,有一个平方根: 0 a 0时,无实根
若x a,则x叫a的立方根(或三次方根)
3
a只有一个立方根
方根
若存在实数x,使x n = a a ? R ,n ( 则x叫a的n 次方根。 1,n N + ),
求a 的 n 次方根,叫做把 a 开 n 次方 ,称作开方运算
偶次方根 奇次方根
n
实 a0 n a 数 a a 0 不存在
n
a 0 a 0
a 根式
n 根指数
n
实数指数幂运算法则课件

B
考勤点名
上节课重点学习的2个换算公式(分数指数幂与根式):
a
m n
n
a
m
a
m n
1
3
1
n
am
练习:1、 将下列各根式写成分数指数幂的形式:
2
一个非零数的负指数 幂等于它的正指数幂 的倒数
73 7
3 2
a2
a
2 3
2
2、将下列各分数指数幂写成根式的形式: 2 5 1 3 5 3 25
3 6 3 (3 2) 解: 1 1 3 3 9 2 (32 ) 3 2 3
3 1 2
1 3
3 3 2 3 2
2 3 1 3
1 2
1 3
1 3
1、化根式为分数指数幂 2、遇乘积化同底或同指 数幂
1 6
3
1 1 2 2 3 3
2
1 1 3 3
3 20 3
例1 计算下列各式的值
(1)0.125
1 3
1 3
2、底化成a n形式
1、小数化分数
1
q 3、运用(a p) a pq计算
解: 0.125
1 1 3 1 3 ( ) ( 2 3 ) 3 2 3 8
2 1
1 4、化负指数为正指数 2
33 6 ( 2) 3 9 3 2
(2)(a b )(a b )
1 2 1 2 1 2 1 2
提示: (a b)(a b) a 2 b 2
1 2 2 1 2 2
解: (a b )(a b ) (a ) (b ) a
《实数指数幂》课件

定义,以及实数指数幂的运算性质。
幂的运算法则
02
包括同底数幂的乘法、除法,幂的乘方以及积的乘方等运算法
则。
无穷大与无穷小的概念
03
理解无穷大和无穷小的概念,掌握其在实数指数幂中的应用。
常见错误解析
混淆不同底数指数幂的运算
01
例如,将a^m * a^n误算为a^(m+n),而不是正确
的a^(mn)。
实数指数幂的引入
实数指数幂的定义
实数指数幂表示一个数与一个实数的乘方。例如,$a^{m/n}$ 表示 $a$ 的 $m$ 次方再 开 $n$ 次方根。
实数指数幂的引入背景
实数指数幂的引入是为了解决一些数学问题,特别是在处理连续函数和积分时,实数指数 幂提供了更灵活和实用的工具。
实数指数幂的性质
实数指数幂具有一些重要性质,如 $a^{mn} = (a^m)^n$,$a^{m/n} = sqrt[n]{a^m}$ ,以及 $(ab)^n = a^n times b^n$。这些性质在数学和物理中有广泛的应用。
《实数指数幂》ppt课件
目录
• 引言 • 实数指数幂的性质 • 实数指数幂的运算 • 实数指数幂的性质与运算的应用 • 总结与回顾
01
引言
幂的定义与性质
幂的定义
幂是乘方运算的结果,表示一个 数连续与一个相同的数相乘的次 数。例如,$a^m$ 表示 $a$ 连 续乘以自身 $m$ 次。
幂的性质
幂具有一些基本性质,如 $a^{m+n} = a^m times a^n$ ,$(a^m)^n = a^{mn}$,以及 $a^{-m} = frac{1}{a^m}$。
,从而更好地理解和求解问题。
课件 5: 3.1.1 实数指数幂及其运算
=a96-36+76-163=a0=1.
【名师点评】 (1)当化简的式子中既有根式又有分数指数幂时,一般先 统一为分数指数幂或根式再化简.
(2)当所求根式含有多重根号时,要搞清被开方数,由里向外用分数指数 幂写出,然后再用运算法则进行化简.
(3)注意运算过程中不能随意扩大或缩小底数的范围.
变式训练
1
1
(2)原式=
a3(a-8b)
1
11
1
× 1 a3
11
1×a3b3
(2b3)2+2a3b3+(a3)2 a3-2b3
1
=a3(aa--88bb)×a13×a13b13=ab13.
题型三 条件求值问题 例4 (本题满分 12 分)已知 a12+a-12=3,求下列各式的值.
(1)a+a-1;(2)a2+a-2;(3)aa2213--aa--1232.
3.1.1 实数指数幂及其运算
学习目标
新知初探
1.整数指数幂 (1)正整数指数幂的运算法则
①am·an=__a_m+__n___;②(am)n__a_m_n____;
③aamn =__a_m-__n__(m>n,a≠0);④(ab)m=__a_m_b_m__. (2)零指数幂和负整数指数幂
1
①a0=__1___(a≠0);②a-n=__a_n__(a≠0,n∈N+).
【解】 (1)将 a12+a-12=3 两边平方,得 a+a-1+2=9, 即 a+a-1=7.(4 分) (2)将 a+a-1=7 两边平方,有 a2+a-2+2=49. ∴a2+a-2=47.(8 分)
(3)由于 a32-a-32=(2213--aa--1232=(a21-a-12)( a12-a+a-a-121+a21·a-12)=a+a-1+1=8.(12 分)
【名师点评】 (1)当化简的式子中既有根式又有分数指数幂时,一般先 统一为分数指数幂或根式再化简.
(2)当所求根式含有多重根号时,要搞清被开方数,由里向外用分数指数 幂写出,然后再用运算法则进行化简.
(3)注意运算过程中不能随意扩大或缩小底数的范围.
变式训练
1
1
(2)原式=
a3(a-8b)
1
11
1
× 1 a3
11
1×a3b3
(2b3)2+2a3b3+(a3)2 a3-2b3
1
=a3(aa--88bb)×a13×a13b13=ab13.
题型三 条件求值问题 例4 (本题满分 12 分)已知 a12+a-12=3,求下列各式的值.
(1)a+a-1;(2)a2+a-2;(3)aa2213--aa--1232.
3.1.1 实数指数幂及其运算
学习目标
新知初探
1.整数指数幂 (1)正整数指数幂的运算法则
①am·an=__a_m+__n___;②(am)n__a_m_n____;
③aamn =__a_m-__n__(m>n,a≠0);④(ab)m=__a_m_b_m__. (2)零指数幂和负整数指数幂
1
①a0=__1___(a≠0);②a-n=__a_n__(a≠0,n∈N+).
【解】 (1)将 a12+a-12=3 两边平方,得 a+a-1+2=9, 即 a+a-1=7.(4 分) (2)将 a+a-1=7 两边平方,有 a2+a-2+2=49. ∴a2+a-2=47.(8 分)
(3)由于 a32-a-32=(2213--aa--1232=(a21-a-12)( a12-a+a-a-121+a21·a-12)=a+a-1+1=8.(12 分)
第章实数指数幂及其运算【新教材】人教B版高中数学必修第二册课件
[跟进训练]
1.(1)4 -34的值是( )
A.3
B.-3
C.±3
D.81
(2)若 x6=2 021,则 x=________.
(3)已知4 a+14=-(3 a+1)3,则实数 a 的取值范围是 ________.
(1)A (2)±6 2 021 (3)(-∞,-1] [(1)4 -34=|-3|=3. (2)因为 x6=2 021,所以 x=±6 2 021. (3)因为4 a+14=|a+1|,(3 a+1)3=a+1, 所以|a+1|=-(a+1),所以 a+1≤0,即 a≤-1.]
[解] (1)
(2) 614- 3 338-( 2-1)0+(-1)2 021+2-1 = 245- 3 287-1-1+21 =52-32-32=-12.
1.化简结果的一个要求和两个不能
2.幂的运算的常规方法 (1)化负指数幂为正指数幂. (2)化根式为分数指数幂. (3)化小数为分数进行运算.
所以 1-6x+9x2= 1-3x2=|1-3x|=1-3x. (2)因为(±9)2=81,所以 81 的平方根为±9,即 a=±9,又(-2)3 =-8, 所以-8 的立方根为-2,所以 b=-2, 所以 a+b=-9-2=-11 或 a+b=9-2=7.
(3)要使 4 a-1 3有意义,则a-1 3>0,且 a-3≠0,即 a>3.]
角度二 指数式的条件求值问题
[探究问题]
1.把
a+ 1a2,a+1a2 分别展开是什么?
[提示]
a+ 1a2=a+1a+2,a+1a2=a2+a12+2.
2.a+1a2 和a-1a2 有什么关系? [提示] a+1a2=a-1a2+4.
【例 4】 已知 a+a-1=5,求下列各式的值: (1)a2+a-2;(2)a -a . [解] (1)因为 a+a-1=5, 所以 a2+a-2=(a+a-1)2-2 =52-2=23. (2)因为a -a 2=a+a-1-2=5-2=3, 所以 a -a =± 3.
实数指数幂及其运算 PPT课件
2n = a xn =a
2叫a的n次方根; x叫a的n次方根.
1.方根的定义 如果xn=a,那么x叫做 a 的n次方根,其中n>1,且
n∈N*.
即 如果一个数的n次方等于a (n>1,且 n∈N*),那么这个数叫做 a 的n次方根.
24=16 (-2)4=16
(-2)5=-32 27=128
16的4次方根是±2.
示a在实数范围内唯一的一个n次方根.
当n是偶数时, n a 只有当a≥0有意义,当a<0时 无意义. n a (a ≥ 0)表示a在实数范围内的一个 n次方根,另一个是 n a (a ≥ 0)
( n a ) n a
(1) 5 25 2, 3( 2)3 2. 结论:an开奇次方根,则有 n an a. (2) 32 3, (3)2 3, (3)2 3.
(6)0的七次方根是_____0_.
点评:求一个数a的n次方根就是求出哪个数的n 次方等于a.
23=8
8的3次方根是2. 记作:3 8 2.
ቤተ መጻሕፍቲ ባይዱ
(-2)3=-8
-8的3次方根是-2. 记作:3 8 2.
(-2)5=-32 27=128
-32的5次方根是-2.记作:5 32 2. 128的7次方根是2. 记作:7 128 2.
-32的5次方根是-2. 2是128的7次方根.
【1】试根据n次方根的定义分别求出下
列各(数1)的25n的次平方方根根. 是___±___5_;
(2)27的三次方根是____3_; (3)-32的五次方根是_-_2__; (4)16的四次方根是_±___2_; (5)a6的三次方根是___a_2_;
的平方根.
22=4 (-2)2=4
《实数指数幂及其运算法则》ppt课件
2.负数的偶次方根没有意义;
3.正数a的奇次次方根是一个正数,负数的奇次方根是一个负数 都表示为
n
a, (n为奇数)
4.0的任何次方根都是0,记作n 0 0.
①( 5)
2
2 3 3
5 ②( 5) 5③( 5) 5 ④ 6 6 ⑤ ( 6 ) 6 ⑥( 6 ) 6 ⑦ ( 6 ) 6
一、(1)化负指数为正指数,
(2)化根式为分数指数幂, (3)化小数为分数 (4)遇乘积化同底或同指数幂
二、对于计算的结果,不强求统一用什么形式来表示,
但结果不能同时含有根号和分数指数,也不能既含有分 母又含有负指数。
方法规律: n (1)先把被开方数化为 a 的形式 ( a ) a (2)再利用运算法则 计算(底数不变 ,指数相乘)
回顾旧知识
整数指数幂的概念:
指数 幂 底数
正整数指数幂的概念:
a a a ......a
n
n个a
(n N
规定:
a 1
1 n a an
0
(a 0)
1 an
( a 0, n N )
导入新课题
问题:我国农业科学家在研究某农作物的生长状况时 ,得到该作物的生长时间x周(从第1周到12周)与植 x 株高度ycm之间的关系 y= . 4
r s rs
r r r
(ab) a b (a 0, b 0, r Q
课后作业
课本P71练习1、2、3题
求值
27 , 100
2 3
-
1 2
1 -3 ,( 4 ) ,
2 3 3 2
16 - 4 ( ) 81
3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
34
当该农作物生长4周、8周、12周时植株的高度(单
3 3 3 位❖c当m指)数,为分分数别时,表应示该如为何—定—义、?又—该—如2、何—计—算?3
当该农作物生长1周、3周、5周时植株的高度(单位
13
5
cm),分别表示为—3 —4 、—3 —4 、—3 —4
分数指数幂
实数指数幂及其运算法则
探究知识
(ab) n= anbn (n Z )
(a b )r a rb r(a 0 ,b 0 ,r Q )
实数指数幂及其运算法则
应用知识:
例 (1)
2
83
(2)
(
8
2
)3
27
3
2
(3) 8
2
5
8
5
2
(4) 3 33 36 3
解 (1)8 3 (2 3 ) 3
32
23
22=4
(2)(
8
2
)3
27
(
计算(底数不变,指数相乘)
2、化根式为分数指数幂,再用法则
(a) a
注:计算的结果,不强求统一用什么形式来表示,但结果 不能同时含有根号和分数指数,也不能既含有分母又含有 负指数。
实数指数幂及其运算法则
课堂小结:
m
1.分数指数幂的定义: a n n am
m
a
n
1
(a0,m,nN且 n 1)
m
﹜ 2、整数指数幂
1.正分数指数幂的定义:
m
规定的: an na m (a 0 ,m ,n N ,且 n 1 )
2.负分数指数幂的定义:
注意:
问a题m n: 如1 何m(定a义0负,m 分,n数指N数,且 幂n?1)
an
a为什么大于零?
例如 : 4 (2) 3
无意义
an
1 an
0的正分数指数幂为0,0的负分数指数幂无意义
方法规律:
( (指12) )数先 再相把利乘被用)开运方算数法化则(为aa)n的 形a 式计算(底数不变,
实数指数幂及其运算法则
拓展2:
(1) 0 .06 1 3 4 7 0 23 3 4 1 0 6 .7 5 0 .01 21 8
实数指数幂及其运算法则
2、把下列根式也能写成a分数指数形式。
根式 n a 有意义的条件是什么?
1.正 数 a的 偶 次 方 根 有 两 个 , 它 们 互 为 相 反 数 , 正 、 负 偶 次 方 根 分 别 表 示 为
81
3
38
实数指数幂及其运算法则
有理数指数幂运算:方法规律总结
一、(1)化负指数为正指数,
(2)化根式为分数指数幂, (3)化小数为分数
(4)遇乘积化同底或同指数幂
二、对于计算的结果,不强求统一用什么形式来表示,
但结果不能同时含有根号和分数指数,也不能既含有分 母又含有负指数。
实数指数幂及其运算法则
实数指数幂及其运算法则
回顾旧知识
整数指数幂的概念:
指数
正整数指数幂的概念:
幂
anaa...a..(.nN)
底数
n个a
规定:
a0 1
(a 0)
an
1 an
1 (a 0,nN) an
实数指数幂及其运算法则
导入新课题
问题:我国农业科学家在研究某农作物的生长状况时 , 株得 高到 度该ycm作之物间的的生关长系时间y=x周(x从. 第1周到12周)与植
根指数
na
3 23
根式
被开方数
2
a的n次方根,(n﹥1且n∈N+).
5 210 5(25)2 25
10
a 5 a 10 5 ( a 5 ) 2 a 2= 5 12
( a>0)
3 a 12
a
4=
观察a
3
a a, a a 5 10 2 3结开1论方2:数根的式指4的数被能
被根指数整除时
结果的指数与被实开数指数方幂及数其运的算法则指数,根指,数数根指有式数可幂什写的么成形关分式系?
2
3 x2 x 3 1
1 3a
a3
4 (ab)3
a
3
b4
3
x y2
1 2
x2y 3
实数指数幂及其运算法则
有理数指数幂的运算则: 整数指数幂的运算则
arasars(a0,r,s Q ) aman= amn(m,nz)
(ar)sars(a0,r,s ;Q ) (a m )n=a mn (m,nz)
实数指数幂及其运算法则
试一试
1、你能把下列分数指数幂用根式表示出来吗?
1
1、 7 2
4
2、 5 6
4
3、
35
最简分数
72
5 3 3 52
4
56
1
4
35
1 5 34
分数指数幂化成根式的方法:分数指数幂的指数的分子做 根式的被开方数的指数,分母做根式的根指数
实数指数幂及其运算法则
练一练
用分数指数幂表示下列各式:
实数指数幂及其运算法则
若x2 a,则x叫a的平方根(或二次 )方根
若 ....x..3. a,则 x叫a的立方根(或三)次方根
若xn a,则 x叫a的n次方根。
方根定义: 若存在实数x,使xn a
(a R,n 1,n N), 则x叫a的n次方根。
求a的n次方根的运算,叫做开方运算
实数指数幂及其运算法则
3 a2 5 a4
a
2
a3
4
=
a5
=1
a2
实数指数幂及其运算法则
整数指数幂的运算则
aman amn (m,nz)
(am )n a mn (m,nz)
(ab)n anbn (n Z )
实数指数幂及其运算法则
正整数指数幂的运算法则
(am)n amn amanamn amamn(mn,a0) an (ab)mambm
2 3
)3
2 3
(
2
3(
)
2 3
)
3
( 2)2 9 34
32
(3)8 5 8 5
3 2
85 5
81 8
(4)3
33
36
1
3332
1
33
1
36
1111
3236
32
9
实数指数幂及其运算法则
巩固知识:
练一练:
2
1、
27 3
2、
2 26 2
3、
1
(x2 • y3 )6
方法:
1、被开方数化为a n 的形式,再用运算法则
有 理
分数指数幂
指 数
幂
an
arasars(a0,r,s Q )
3、有理指数幂的运算法则:
(ar)sars(a0,r,s Q )
实( 数a 指数b 幂) 及其r运 算法则a rb r(a 0 ,b 0 ,r Q )
课后作业
课本P71练习1、2、3题
实数指数幂及其运算法则
求值
27
2 3
1
,100
2
,(
1 4
)- 3
,
( 16
)-
3 4
81
2
27 3
2
2
( 33}3
3
3 3
32
9
100- 1 2= ( 102) - 1 2= 102 ( - 1 2) = 10- 1= 1; 10
( 1) - 3 = ( 2- 2) - 3 = 2 ( - 2 ) ( - 3 ) = 26= 64 ; 4
( 16) - 3 4= ( 2) 4 ( - 3 4) = ( 2) - 3= 27。
当该农作物生长4周、8周、12周时植株的高度(单
3 3 3 位❖c当m指)数,为分分数别时,表应示该如为何—定—义、?又—该—如2、何—计—算?3
当该农作物生长1周、3周、5周时植株的高度(单位
13
5
cm),分别表示为—3 —4 、—3 —4 、—3 —4
分数指数幂
实数指数幂及其运算法则
探究知识
(ab) n= anbn (n Z )
(a b )r a rb r(a 0 ,b 0 ,r Q )
实数指数幂及其运算法则
应用知识:
例 (1)
2
83
(2)
(
8
2
)3
27
3
2
(3) 8
2
5
8
5
2
(4) 3 33 36 3
解 (1)8 3 (2 3 ) 3
32
23
22=4
(2)(
8
2
)3
27
(
计算(底数不变,指数相乘)
2、化根式为分数指数幂,再用法则
(a) a
注:计算的结果,不强求统一用什么形式来表示,但结果 不能同时含有根号和分数指数,也不能既含有分母又含有 负指数。
实数指数幂及其运算法则
课堂小结:
m
1.分数指数幂的定义: a n n am
m
a
n
1
(a0,m,nN且 n 1)
m
﹜ 2、整数指数幂
1.正分数指数幂的定义:
m
规定的: an na m (a 0 ,m ,n N ,且 n 1 )
2.负分数指数幂的定义:
注意:
问a题m n: 如1 何m(定a义0负,m 分,n数指N数,且 幂n?1)
an
a为什么大于零?
例如 : 4 (2) 3
无意义
an
1 an
0的正分数指数幂为0,0的负分数指数幂无意义
方法规律:
( (指12) )数先 再相把利乘被用)开运方算数法化则(为aa)n的 形a 式计算(底数不变,
实数指数幂及其运算法则
拓展2:
(1) 0 .06 1 3 4 7 0 23 3 4 1 0 6 .7 5 0 .01 21 8
实数指数幂及其运算法则
2、把下列根式也能写成a分数指数形式。
根式 n a 有意义的条件是什么?
1.正 数 a的 偶 次 方 根 有 两 个 , 它 们 互 为 相 反 数 , 正 、 负 偶 次 方 根 分 别 表 示 为
81
3
38
实数指数幂及其运算法则
有理数指数幂运算:方法规律总结
一、(1)化负指数为正指数,
(2)化根式为分数指数幂, (3)化小数为分数
(4)遇乘积化同底或同指数幂
二、对于计算的结果,不强求统一用什么形式来表示,
但结果不能同时含有根号和分数指数,也不能既含有分 母又含有负指数。
实数指数幂及其运算法则
实数指数幂及其运算法则
回顾旧知识
整数指数幂的概念:
指数
正整数指数幂的概念:
幂
anaa...a..(.nN)
底数
n个a
规定:
a0 1
(a 0)
an
1 an
1 (a 0,nN) an
实数指数幂及其运算法则
导入新课题
问题:我国农业科学家在研究某农作物的生长状况时 , 株得 高到 度该ycm作之物间的的生关长系时间y=x周(x从. 第1周到12周)与植
根指数
na
3 23
根式
被开方数
2
a的n次方根,(n﹥1且n∈N+).
5 210 5(25)2 25
10
a 5 a 10 5 ( a 5 ) 2 a 2= 5 12
( a>0)
3 a 12
a
4=
观察a
3
a a, a a 5 10 2 3结开1论方2:数根的式指4的数被能
被根指数整除时
结果的指数与被实开数指数方幂及数其运的算法则指数,根指,数数根指有式数可幂什写的么成形关分式系?
2
3 x2 x 3 1
1 3a
a3
4 (ab)3
a
3
b4
3
x y2
1 2
x2y 3
实数指数幂及其运算法则
有理数指数幂的运算则: 整数指数幂的运算则
arasars(a0,r,s Q ) aman= amn(m,nz)
(ar)sars(a0,r,s ;Q ) (a m )n=a mn (m,nz)
实数指数幂及其运算法则
试一试
1、你能把下列分数指数幂用根式表示出来吗?
1
1、 7 2
4
2、 5 6
4
3、
35
最简分数
72
5 3 3 52
4
56
1
4
35
1 5 34
分数指数幂化成根式的方法:分数指数幂的指数的分子做 根式的被开方数的指数,分母做根式的根指数
实数指数幂及其运算法则
练一练
用分数指数幂表示下列各式:
实数指数幂及其运算法则
若x2 a,则x叫a的平方根(或二次 )方根
若 ....x..3. a,则 x叫a的立方根(或三)次方根
若xn a,则 x叫a的n次方根。
方根定义: 若存在实数x,使xn a
(a R,n 1,n N), 则x叫a的n次方根。
求a的n次方根的运算,叫做开方运算
实数指数幂及其运算法则
3 a2 5 a4
a
2
a3
4
=
a5
=1
a2
实数指数幂及其运算法则
整数指数幂的运算则
aman amn (m,nz)
(am )n a mn (m,nz)
(ab)n anbn (n Z )
实数指数幂及其运算法则
正整数指数幂的运算法则
(am)n amn amanamn amamn(mn,a0) an (ab)mambm
2 3
)3
2 3
(
2
3(
)
2 3
)
3
( 2)2 9 34
32
(3)8 5 8 5
3 2
85 5
81 8
(4)3
33
36
1
3332
1
33
1
36
1111
3236
32
9
实数指数幂及其运算法则
巩固知识:
练一练:
2
1、
27 3
2、
2 26 2
3、
1
(x2 • y3 )6
方法:
1、被开方数化为a n 的形式,再用运算法则
有 理
分数指数幂
指 数
幂
an
arasars(a0,r,s Q )
3、有理指数幂的运算法则:
(ar)sars(a0,r,s Q )
实( 数a 指数b 幂) 及其r运 算法则a rb r(a 0 ,b 0 ,r Q )
课后作业
课本P71练习1、2、3题
实数指数幂及其运算法则
求值
27
2 3
1
,100
2
,(
1 4
)- 3
,
( 16
)-
3 4
81
2
27 3
2
2
( 33}3
3
3 3
32
9
100- 1 2= ( 102) - 1 2= 102 ( - 1 2) = 10- 1= 1; 10
( 1) - 3 = ( 2- 2) - 3 = 2 ( - 2 ) ( - 3 ) = 26= 64 ; 4
( 16) - 3 4= ( 2) 4 ( - 3 4) = ( 2) - 3= 27。
