实数指数幂及其运算
高一数学实数指数幂及其运算

(2)10
1 (6) (3a - 1) (a ). 3
4 4
2 (a b)(a b) (7) 2 (a b)(a > b)
答案 (6)1-3a (7)b-a;a-b
推广:整数指数幂→正分数指数幂
根式与分数指数幂的互化
(a ) a
3 1 3 1 3 3
a
a a
a
7 3
a
13
1
1 2 n7 ( ) 2
1 2 n1 (2 ) ( ) 2 n 2 4 8
n 1 2
提高练习1
已知 a>0, (1) a
3 a2 1 a2
1 a2
a
1 2
=3,求下列各式的值: ;
1 2
a
1 2
1
7
(2)a a
(3)
3 a 2 1 a 2
2 3
1 3
3
a (a ) ( a )
2 3 1 3 2
a
1 2 3
又a
1 2 3
(a )
2 3 2
1 3
3
a
2
还可以看出, ( a)
3
a
2
规定:一般地, a
m n
n
am
( a 0 , m, n 均为正整数) 。 这就是正数的分数指数幂的意义。 规定: a
m n
25=32 ````
-2 叫4的平方根 2, 2叫8的立方根 -2叫-8的立方根 2叫32的5次方根 ````
2n=a
2叫a的n次方根
(1)n次方根的定义
若x a(n 1, 且n N ),
3.1.1实数指数幂及其运算

(2) (10)2 | 10 | 10
(3)4 (3 )4 | 3 | 3
(4) (a b)2 | a b | a b(a b)
例2:求下列各式的值: (1)3 (8)3 4 (3 )4
(2)(5 a b )5 (6 b a )6 (b a)
一、根式:
1.n次方根: (1)定义:
一般地,如果 xn a,那么x叫做a 的n 次方根,其中n 1 且nN 。
(2)个数:
◇当n是奇数时,正数的 n次方根是一个正数,负数的n次
方根是一个负数。
注:a的n 次方根用符号n a 表示
◇当n是偶数时:
●正数的n次方根有两个,这两个数互为相反数;
|
1
0.01 |2
8
9
(2)化简:3 a 2 a3 3 a7 3 a13 (a 0)
解:(1)原式=(0.43)13
1
(2)4
(24)0.75
1
(0.12)2
0.41 1 1 1 0.1 16 8
143
80
19
1( 3 )
1( 7 )
113
(2)原式= [a3 2 a3 2 ] [a 2 3 a 2 3 ]
9 3 7 13
a6 6 6 6 a0 1
1
例11:已知a 2
1
a 2
3,求 a
a1, a2
a2 的值
1
解:a 2
1
a 2
3
1
(a 2
1
a2
)2
9
a 2 a1 9 a a1 7 又(a a1)2 49 a2 2 a2 49 a2 a2 47
3.1.1 实数指数幂及其运算

张喜林制3.1.1 实数指数幂及其运算教材知识检索考点知识清单1.整数指数幂(1)正整数指数幂:一个数a 的n 次幂等于 ,即 (2)正整数指数幂的运算法则:=n m a a .① ;=÷n m a a ② );0,(=/>a n m =nm a )(③ ;=n ab )(④ ;=n ba)(⑤ ).0(=/b(3)整数指数幂:规定:=0a ==/- na a ),0( ⋅∈=/*),0(N n a 2.根式(l)n 次方根:一般地,如果 ,那么x 叫做a 的n 次方根,其中 . (2)方根的性质:①零的任何次方根都等于0,即:=n n a )(② ⋅∈>*),1(N n n③当n 为奇数时,=n n a ;当n 为偶数时,=n n a3.分数指数幂(1)规定:正数的正分数指数幂的意义是:=nm anmN n m a 且*,,,0(∈>为既约分数). 正数的负分数指数幂的意义是:=-nm anmN n m a 且*,,,0(∈>为既约分数) (2)运算性质:,)(,)(,.r r r r rs s r s r s b a ab a a a a a ⋅===+其中要点核心解读1.关于分数指数幂的概念n n n n a a 与))(1(这两个式子非常相似,但差别很大,一定要注意区别.(2)关于分数指数幂需要注意:①在条件*,,,0N n m a ∈>1>n 下,根式都可以写成分数指数幂的形式.②引入分数指数幂的概念后,指数概念由整数指数幂扩充为有理数指数幂,③分数指数幂不可理解为nm个a 相乘,它是根式的一种新的写法.2.关于指数运算问题(1)在进行根式和分数指数幂的某种综合运算时,要合理运用它们的性质和法则,数式的运算、化简、变形与求值在数学问题中占有重要的地位.(2)-般地,根式运算可以转化为分数指数幂的运算,运算的结果既可用根式表示又可用分数指数幂表示,但必须统一.(3)分数指数幂的运算常采用的思路有:①对于常量字母,先化成同底的再运算;对于变量字母,有时需要对字母进行讨论, ②除式的运算,用分母的“-1”次幂化为乘法运算.(4)根式的运算应该注意的几点: ①注意根式的符号:a .n 为奇数时,n n a R a ,∈与a 的符号一致;b .n 为偶数时,.0,0,0≤-≥≥n n n n a a a ②对根式进行运算时,一般先将根式化成分数指数幂,这样可以方便使用同底数幂的运算律. 3.正整数指数幂的运算性质与有理数指数幂的运算性质的联系(1)正整数指数幂与有理数指数幂的运算性质(2)为了保证正整数指数幂的性质可以从定义直接推出,限定了m 、n 都是正整数,且性质②中限定m>n ,为了取消m>n 的限制,定义了零指数幂和负整数指数幂,在引进负整数指数幂后性质②可以归人性质①,性质⑤可以归人性质④,这样上述5条可归纳为3条,即①③④,同时指数的范围扩大到了有理数,为了使②⑤对任意整数都成立,不得不规定a>0及6>0.典例分类剖析考点1 整数指数幂的运算[例1] 化简下列各式:;)()())(1(23425232b a b a b a ÷⋅-- ⋅--4301.01.0)2([解析] (1)由题目可获取以下主要信息: 两个式子都是幂的乘方以及乘除混合运算。
《实数指数幂及其运算》 学习任务单

《实数指数幂及其运算》学习任务单一、学习目标1、理解实数指数幂的概念,包括正整数指数幂、零指数幂、负整数指数幂、分数指数幂和无理数指数幂。
2、掌握实数指数幂的运算性质,能够熟练进行实数指数幂的运算。
3、运用实数指数幂的运算解决实际问题,提高数学应用能力。
二、学习重难点1、重点(1)实数指数幂的概念及其推广。
(2)实数指数幂的运算性质及应用。
2、难点(1)分数指数幂和无理数指数幂的理解。
(2)实数指数幂运算性质的灵活运用。
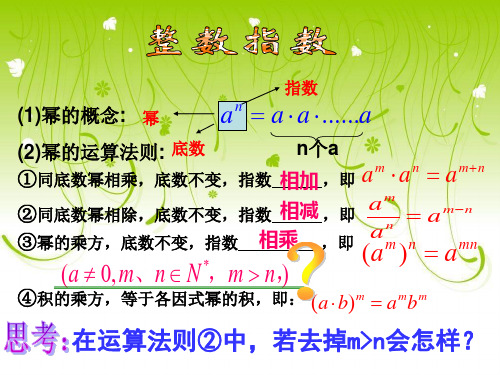
三、知识回顾1、正整数指数幂\(a^n = a×a××a\)(\(n\)个\(a\)相乘),其中\(a\)叫做底数,\(n\)叫做指数。
例如:\(2^3 = 2×2×2 = 8\)2、整数指数幂的运算性质(1)\(a^m × a^n = a^{m + n}\)(2)\((a^m)^n = a^{mn}\)(3)\((ab)^n = a^n b^n\)四、新课讲解1、零指数幂规定\(a^0 = 1\)(\(a ≠ 0\))例如:\(5^0 = 1\)思考:为什么\(0\)的\(0\)次幂没有意义?2、负整数指数幂当\(n\)是正整数时,\(a^{n} =\frac{1}{a^n}\)(\(a ≠ 0\))例如:\(2^{-3} =\frac{1}{2^3} =\frac{1}{8}\)3、分数指数幂(1)正分数指数幂\(a^{\frac{m}{n}}=\sqrtn{a^m}\)(\(a > 0\),\(m\)、\(n\)都是正整数,且\(n > 1\))例如:\(8^{\frac{2}{3}}=\sqrt3{8^2} =\sqrt3{64} =4\)(2)负分数指数幂\(a^{\frac{m}{n}}=\frac{1}{a^{\frac{m}{n}}}=\frac{1}{\sqrtn{a^m}}\)(\(a > 0\),\(m\)、\(n\)都是正整数,且\(n > 1\))例如:\(27^{\frac{2}{3}}=\frac{1}{27^{\frac{2}{3}}}=\frac{1}{\sqrt3{27^2}}=\frac{1}{9}\)4、无理数指数幂无理数指数幂\(a^α\)(\(a > 0\),\(α\)是无理数)是一个确定的实数。
实数指数幂及其运算教案

3.1.1 实数指数幂及其运算1.整数指数(1)一个数a 的n 次幂等于n 个a 的连乘积,即n n n a a a a a =⋅⋅⋅⋅个叫做a 的n 次幂,a 叫做幂的底数,n 叫做幂的指数.并规定a 1=a .(2)正整指数幂在a n 中,n 是正整数时,a n 叫做正整指数幂. 正整指数幂具有以下运算法则:①a m ·a n =a m +n ;②(a m )n =a mn ;③am a n =a m -n (a ≠0,m >n );④(ab )m=a m b m .其中m ,n ∈N +.(3)整数指数幂在上述法则③中,限制了m >n ,如果取消这种限制,那么正整指数幂就推广到了整数指数幂.规定:①a 0=1(a ≠0);②a -n =1a n (a ≠0,n ∈N +).这样,上面的四条法则可以归纳为三条:①a m ·a n =a m +n ;②(ab )n =a n b n ;③(a m )n =a mn .其中m ,n ∈Z .同时,将指数的范围由正整数扩大为整数.0的零次幂没有意义,0的负整数次幂也没有意义,因此对于整数指数幂,要求“底数不等于0”.【例1】化简:(a 2b 3)-2·(a 5b -2)0÷(a 4b 3)2.解:原式=223246423286()()1=()()a b a b a b a b----⋅⋅⋅ =(a -4·a -8)·(b -6·b -6) =a -12b -12.2.根式如果存在实数x ,使得x n =a (a ∈R ,n >1,n ∈N +),则x 叫做a 的n 次方根.求a 的n 次方根,叫做把a 开n 次方,称作开方运算. 当na 有意义时,式子na 叫做根式,n 叫做根指数,a 叫做被开方数.正数a 的正n 次方根叫做a 的n 次算术根.n 次方根具有以下性质:(1)在实数范围内,正数的奇次方根是一个正数;(2)在实数范围内,正数的偶次方根是两个绝对值相等、符号相反的数,负数的偶次方根不存在;(3)零的任何次方根都是零.根式有两个重要性质:(1)(na )n =a (n >1,n ∈N +),当n 为奇数时,a ∈R ,当n 为偶数时,a ≥0(a <0时无意义);(2)n a n =⎩⎪⎨⎪⎧a ,n 为奇数,|a |,n 为偶数. 析规律 关于根式的知识总结正数开方要分清,根指奇偶大不同, 根指为奇根一个,根指为偶双胞生. 负数只有奇次根,算术方根零或正, 正数若求偶次根,符号相反值相同. 负数开方要慎重,根指为奇才可行, 根指为负无意义,零取方根仍为零.【例2-1】已知=-a -1,则实数a 的取值范围是__________.解析:|a +1|,∴|a +1|=-a -1=-(a +1).∴a +1≤0,即a ≤-1. 答案:(-∞,-1]【例2-2】化简下列各式:;.解:(1)原式=(-2)+2|+2)=-2+(2+2)=-2.(2)=(1+1)=辨误区 根式运算应注意的问题利用na n 的性质求值运算时,要注意n 的奇偶性.特别地,当n 为偶数时,要注意a 的正负.3.分数指数幂(1)分数指数幂的意义 正分数指数幂可定义为:①1na=na (a >0);②m na =(na )m=na m⎝ ⎛⎭⎪⎫a >0,n ,m ∈N +,且m n 为既约分数.负分数指数幂的意义与负整数指数幂的意义相同,可定义为:1=m nm na a-⎝ ⎛⎭⎪⎫a >0,n ,m ∈N +,且m n 为既约分数. 提示:所谓既约分数,就是约分后化成最简形式的分数. 感悟:1.规定了分数指数幂的意义后,指数的概念就从整数指数推广到了有理指数;2.m na 与na m 表示相同的意义,所以分数指数幂与根式可以相互转化;3.通常规定分数指数幂的底数a >0,但要注意在像14()a -=4-a中的a ,则需要a ≤0.(2)有理指数幂的运算法则:①a αa β=a α+β;②(a α)β=a αβ;(3)(ab )α=a αb α(其中a >0,b >0,α,β∈Q ).析规律 有理指数幂的运算1.有理指数幂的运算性质是由整数指数幂的运算性质推广而来,可以用文字语言叙述为:(1)同底数幂相乘,底数不变,指数相加;(2)幂的幂,底数不变,指数相乘;(3)积的幂等于幂的积.2.乘法公式仍适用于有理指数幂的运算,例如:11112222()()a b a b +⋅-=a -b (a >0,b >0);111122222()2a b a b a b ±=+±(a >0,b >0).【例3-1】求值:(1)438-;(2)3481;(3)323-⎛⎫ ⎪⎝⎭;(4)2327125-⎛⎫⎪⎝⎭. 解:(1)44433433318=(2)=2=2=16⎛⎫⨯---⎪-⎝⎭. (2)333443444=(3)=3=3=27⨯.(3)332327==328-⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭. (4)2223323332733325====1255559⎛⎫--⨯-- ⎪⎝⎭⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦.点技巧 有理指数幂运算时把根式转化为幂进行有理指数幂的运算要首先考虑利用幂的运算性质,而不要将幂转化为根式的运算,像238【例3-2】求下列各式的值:(1)1123331222x x x --⎛⎫- ⎪⎝⎭;(2)2. 解:(1)原式=11121333314222=14=12x x x x x x ----⋅-⋅--.(2)原式=125222362132==a aa a a --⋅4.无理指数幂 (1)一般地,无理指数幂a α(a >0,α是无理数)是一个确定的实数; (2)有理指数幂的运算性质同样适用于无理指数幂,即: ①a α·a β=a α+β(a >0,α,β是无理数); ②(a α)β=a αβ(a >0,α,β是无理数);③(ab )α=a αb α(a >0,b >0,α是无理数). 【例4】求值:(1)213328--⋅⋅;(2)12+⋅解:(1)原式=221333(22(2)--⋅⋅=2322323222=2=2=8--+-⋅. (2)原式=12+52+21=27.5.指数幂(根式)的化简与计算化简、计算指数幂(根式)时,应注意以下几点:(1)运算顺序:先进行幂的运算,再进行乘除运算,最后进行加减运算,有括号的先算括号内的.(2)如果指数是小数,那么通常化为分数指数,这样可以随时检验运算的正确性,是常用的化简技巧.比如,(-3)2.1=2110(3)-=10(-3)21,由于(-3)21是一个负数,所以(-3)2.1无意义.(3)将其中的根式化为分数指数幂,利用指数幂的运算性质进行计算.比如,化简a a ,如果不将根式a 化为指数幂,就很难完成化简:1131222==a a a a +⋅.(4)计算或化简的结果尽量最简,如果没有特殊要求,用正分数指数幂或根式来表示均可.析规律 多重根号化为有理指数幂此类问题应熟练应用na m=m na ⎝ ⎛⎭⎪⎫a >0,m ,n ∈N +,且m n 为既约分数.当各式中含有多重根号时,要搞清被开方数,由里向外用分数指数幂写出,然后再利用指数运算法则化简.【例5-1】求下列各式的值:(1)121203170.027279--⎛⎫⎛⎫--+- ⎪ ⎪⎝⎭⎝⎭; (2)1012234122254--⎛⎫⎛⎫+⨯- ⎪⎪⎝⎭⎝⎭;(3)分析:结合指数幂的运算性质,应首先将小数化为分数,根式转化为指数幂的形式,负指数幂转化为正指数幂,再根据指数幂的运算性质求解.解:(1)原式=11232227125105(1)1=491=4510007933---⎛⎫⎛⎫⎛⎫--+--+--⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. (2)原式=112314111161=1=49100061015⎛⎫⎛⎫+⨯-+- ⎪ ⎪⎝⎭⎝⎭. (3)原式=11111111111113312636333236223123(32)=23332=2322-+++⎛⎫⎛⎫⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭=2×3=6.【例5-2】化简下列各式:(1)1373412a a a ;(2)131234()x y -;解:(1)1137537334123412==a a a a a ++.(2)1133121212493344()==x y xyx y ⨯--⨯-.1125152331123336363442125364()===xyx y x y x y x yx y------⋅⋅⋅⋅⋅.辨误区化简时注意运算顺序化简时要弄清开方、乘方等的运算顺序,同时注意运算性质及乘法公式的应用.6.知值求值问题已知代数式的值求其他代数式的值,通常又简称为“知值求值”,解决此类题目要从整体上把握已知的代数式和所求的代数式的特点,然后采取“整体代换....”或“求值后代换”两种方法求值.要注意正确地变形,像平方、立方等以及一些公式的应用问题,还要注意开方时的取值符号问题.例如,已知1122=3a a-+,求下列各式的值:(1)a+a-1;(2)a2+a-2;(3)33221122a aa a----.显然,从已知条件中解出a的值,然后再代入求值,这种方法是不可取的,而应设法从整体寻求结果与条件1122=3a a-+的联系,进而整体代入求值.将1122=3a a-+两边平方,得a+a-1+2=9,即a+a-1=7.再将上式平方,有a2+a-2+2=49,即a2+a-2=47.由于3311332222=()()a a a a----,所以有331111122222211112222()()=a a a a a a a aa a a a--------++⋅--=a+a-1+1=8.【例6-1】已知2x+2-x=5,求下列各式的值:(1)4x+4-x;(2)8x+8-x.解:(1)4x+4-x=(22)x+(22)-x=(2x)2+(2-x)2=(2x)2+2·2x·2-x+(2-x)2-2=(2x+2-x)2-2=52-2=23.(2)8x+8-x=(23)x+(23)-x=(2x)3+(2-x)3=(2x+2-x)·[(2x)2-2x·2-x+(2-x)2]=(2x+2-x)(4x+4-x-1)=5×(23-1)=110.析规律 平方在知值求值中的应用遇到式子中含有指数互为相反数的数,通常用平方进行解决,平方后观察条件和结论的关系,变形求解即可.本题中用到了两个公式(a +b )2=a 2+2ab +b 2,a 3+b 3=(a +b )(a 2-ab +b 2).【例6-2】已知a ,b 是方程x 2-6x +4=0的两根,且a >b >0,的值. 分析:观察所求式子,将所求式子平方后出现了ab 和a +b 的形式.又a ,b 为方程的两根,所以可利用根与系数的关系求解.解:由根与系数的关系可得=6,=4.a b ab +⎧⎨⎩∵a >b >0,>又∵221=105⎛.。
实数指数幂及其运算法则

实数指数幂及其运算法则实数指数幂是数学中的一个重要概念,它在数学、物理、工程等领域都有着广泛的应用。
本文将介绍实数指数幂的定义、性质以及运算法则。
一、实数指数幂的定义。
实数指数幂指的是形如a^b的数,其中a为实数,b为实数。
其中a称为底数,b称为指数。
当指数为正整数时,实数指数幂可以用连乘的形式表示,即a^b=aa...a,其中a出现了b次。
当指数为零时,实数指数幂定义为1。
当指数为负整数时,实数指数幂可以用连除的形式表示,即a^(-b)=1/(a^b)。
当底数为正数且指数为实数时,实数指数幂可以用连续开方的形式表示,即a^b=sqrt(sqrt(...(sqrt(a))...),其中开方的次数为b。
二、实数指数幂的性质。
1.相同底数的实数指数幂相乘,指数相加。
即a^m a^n =a^(m+n)。
2.相同底数的实数指数幂相除,指数相减。
即a^m / a^n =a^(m-n)。
3.不同底数的实数指数幂相乘,底数不变,指数相加。
即a^m b^m = (ab)^m。
4.不同底数的实数指数幂相除,底数不变,指数相减。
即a^m / b^m = (a/b)^m。
5.实数指数幂的乘方,指数相乘。
即(a^m)^n = a^(mn)。
6.实数指数幂的除法,指数相除。
即(a^m)^n = a^(m/n)。
7.任何数的零次幂都等于1。
即a^0 = 1。
8.任何数的一次幂都等于它本身。
即a^1 = a。
以上性质是实数指数幂运算的基本法则,可以帮助我们简化实数指数幂的运算,并且也可以推广到复数指数幂的运算中。
三、实数指数幂的运算法则。
实数指数幂的运算法则包括加减、乘除、乘方和开方等运算。
1.加减法。
对于相同底数的实数指数幂,可以直接对指数进行加减运算。
例如,2^3 + 2^4 = 2^7,2^5 2^3 = 2^2。
2.乘法。
对于相同底数的实数指数幂,可以直接对指数进行加法运算。
例如,2^3 2^4 = 2^(3+4) = 2^7。
实数指数幂及其运算
24=16 (-2)4=16 25=32
2,-2叫16的4次方根; 2叫32的5次方根;
………………………………………… 通过类比方法,可得n次方根的定义.
2n = a
xn =a
2叫a的n次方根; x叫a的n次方根.
1.方根的定义 如果xn=a,那么x叫做 a 的n次方根,其中n>1,且 n∈N*. 即 如果一个数的n次方等于a (n>1,且 n∈N*),那么这个数叫做 a 的n次方根.
【1】下列各式中, 不正确的序号是( ①
④ ).
①
③
5 5
4 5
16 2
5
5
② ( 3) 3
( 3) 3
10
④ ( 3) 3
⑤
4
( 3) 3
4
【2】求下列各式的值.
⑴ 32;
5
⑵ ( 3);
4
⑶ ( 2 3);
2
⑷ 5 2 6.
5
解: ⑴ 5 32
1.正数的偶次方根有两个且互为相反数 2.负数的偶次方根没有意义
正数a的n次方根用符号 n a 表示(n为偶数)
(1) 奇次方根有以下性质: 正数的奇次方根是正数. 负数的奇次方根是负数. 零的奇次方根是零. (2)偶次方根有以下性质: 正数的偶次方根有两个且是相反数, 负数没有偶次方根, 零的偶次方根是零.
a a
n
m n
m
(a>0,m,n∈N*,且n>1)
等于这个正数的m次幂的n次算术根. 注意:底数a>0这个条件不可少. 若无此条件会 引起混乱,例如, (-1)1/3 和 (-1)2/6 应当具有同样 的意义,但由分数指数幂的意义可得出不同的 结果:
中职数学基础模块上册《实数指数幂及其运算法则》word教案

教案名称:中职数学基础模块上册《实数指数幂及其运算法则》word教案教案编写:教学目标:1. 理解实数指数幂的概念及其运算法则。
2. 能够运用实数指数幂及其运算法则进行相关计算。
3. 培养学生的逻辑思维能力和解决问题的能力。
教学内容:一、实数指数幂的概念1. 引入实数指数幂的概念,讲解正整数指数幂、零指数幂和负整数指数幂的定义。
二、实数指数幂的运算法则1. 讲解实数指数幂的乘法法则:同底数幂相乘,底数不变,指数相加。
2. 讲解实数指数幂的除法法则:同底数幂相除,底数不变,指数相减。
3. 讲解实数指数幂的乘方法则:底数不变,指数相乘。
4. 讲解实数指数幂的幂的法则:底数不变,指数相除。
三、实数指数幂的应用1. 举例讲解实数指数幂在实际问题中的应用,如计算幂的值、求解指数方程等。
四、练习与巩固1. 安排相关练习题,让学生巩固实数指数幂的概念和运算法则。
2. 引导学生运用所学知识解决实际问题。
2. 评价学生的学习效果,对学生在学习中遇到的问题进行解答和指导。
教学方法:1. 采用讲授法,讲解实数指数幂的概念和运算法则。
2. 运用案例教学法,引导学生运用所学知识解决实际问题。
3. 设计练习题,让学生通过自主练习巩固所学知识。
4. 采用小组讨论法,促进学生之间的交流与合作。
教学资源:1. PPT课件:展示实数指数幂的概念和运算法则。
2. 练习题:用于巩固所学知识。
3. 案例材料:用于讲解实数指数幂在实际问题中的应用。
教学评价:1. 课堂问答:检查学生对实数指数幂概念和运算法则的理解程度。
2. 练习题:评估学生对实数指数幂运算法则的掌握情况。
3. 实际问题解决:评价学生运用实数指数幂知识解决实际问题的能力。
六、教学活动设计1. 导入新课:通过复习幂的概念,引导学生自然过渡到实数指数幂的学习。
2. 讲解实数指数幂的概念:详细讲解正整数指数幂、零指数幂和负整数指数幂的定义。
3. 讲解实数指数幂的运算法则:逐一讲解乘法、除法、乘方和幂的法则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、概念 【问题思考】 1.为何规定a0=1(a≠0)?
������������ m-n 提示: 根据运算法则 a ÷a = ������ =a . ������ ������ ������ 令上式中 m=n,得 am-n=a0= ������ =1. ������
m n
2.请写出满足方程x2=5与x3=7的实根x,并说明平方根与立方根的 规律性.
怎样表示?
������ 提示: ������ ������ 能用根式表示,要先明确初中所学整数指数幂的运算 ������ α β αβ 法则可推广到实数范围内.根据(a ) =a 可知(������ ������ )n=am,再根据根式 ������ ������ ������ m 的定义,可知������ ������ 是 a 的正的 n 次方程,因此������ ������ = am .
课前篇 自主预习 一 二 三
3.做一做:计算下列各式: (1)( -32)5; (3) (-8) ;
5
4 5
(2) (-6)2 ; (4) (������-������) ;
2
4
(5) (3-π)3 .
3
答案: (1)( -32)5=-32. (2) (-6)2 =|-6|=6. (3) (-8)4 =|-8|=8. (4) (������-������)2 =|x-y|= (5) (3-π)3 =3-π.
课前篇 自主预习 一 二 三
4.填写下表:
整数指数 a =a· a· …· a
n个
n
n 次方根 如果存在实数 x,使得 xn = a(a∈R,n>1,n∈N+), 则 x 叫做 a 的 n 次方 根.求 a 的 n 次方根, 叫做把 a 开 n 次方, 称作开方运算
分数指数 ������ = a =( ������ )m= ������������
1
a>0,n,m∈N+,
且 为既约分数
一般地,当a>0,α为任意实数值时,实数指数幂aα均有意义.
课前篇 自主预习 一 二 三
二、根式的性质
【问题思考】 ������ ������ 1.( a)n 与 ������������ 有何区别?请举例说明.
提示: ( ������)n 是实数 a 的 n 次方根的 n 次幂,其中实数 a 的取值由 n 的奇偶性来决定: ①当 n 为大于 1 的奇数时,a∈R.例 如,( 27) =27,( -32)5=-32,( 0)7=0; ②当 n 为大于 1 的偶数时,a≥0.例 6 4 ������ 如,( 27)4=27,( 3)2=3,( 0)6=0;若 a<0,式子( ������)n 无意义.例 如,( -2) ,( -54)4 均无意义. 因此,只要( ������)n 有意义,其值恒等于 a,即( ������)n=a.
2.填写下表: 正整指数幂 (a≠0,m,n 为整数) (1)am· an=am+n (2)(am)n=amn (3) n =am-n(m>n) a (4)(ab)m=ambm
am
有理指数幂 (a>0,b>0,α,β 为有理数) (1)aαaβ=aα+β β (2)(aα)β=aα· (3)(ab)α=aαbα
5 3
������
②当 n 为大于 1 的偶数时,其值为|a|,即 an =|a|.例 如, (-2)2 =2, 32 =3, 02 =0.
������
课前篇 自主预习 一 二 三
2.填空. ������ (1)( a)n=a(n>1,且 n∈N+); ������,������为奇数,且������ > 1,������∈N+, ������ ������ (2) ������ = |������|,������为偶数,且������ > 1,������∈N+ .
3.1.1
实数指数幂及其运算
-1-
课 标 阐 释 思 1.理解有理指数幂的 含义,会用幂的运算 法则进行有关计算. 2.通过具体实例了解 实数指数幂的意义. 3.通过本节的学习, 进一步体会“用有理 数逼近无理数”的思 想,可以利用计算器 或计算机实际操作, 感受“逼近”的过程.
维
脉
络
课前篇 自主预习 一 二 三
������ ������ 3 ������
3
5
7
2
4
课前篇 自主预习 一 二 三
������������ 是实数 an 的 n 次方根,an 是一个恒有意义的式子,不受 n 的 ������ 奇偶性限制,a∈R.但是 ������������ 的值受 n 的奇偶性限制: ������ ①当 n 为大于 1 的奇数时,其值为 a,即 an =a.例 如, (-3)3 =-3, 6.15 =6.1;
课前篇 自主预习 一 二 三
3.做一做:下列等式一定成立的是(
1 A.������2 3 ·������2 =a 9
1 ������3
)
C.(a ) =a
提示: 满足 x2=5 的实根 x=± 5;满足 x3=7 的实根 x= 7,通过归 纳可知正数有两个平方根,任意实数都只有唯一一个立方根.
3
课前篇 自主预习 一 二 三
������ 3.������ ������
������ > 0,且
������ 为既约分数,������ ������
≥ 2 能否用根式表示ຫໍສະໝຸດ 如果能,������ ������
������ ������ 1 ������ m n ������ n
a(a>0)
������
a>0,n,m
规 定:a0=1(a≠0) 1 a-n= n (a≠0,n∈N+)
a
∈N+,且 为既约分数 ������ =
������ ������
������ ������ ������
3 4
������-������,������ ≥ ������, ������-������,������ < ������.
课前篇 自主预习 一 二 三
三、指数幂的运算法则
【问题思考】
������������ m-n 1.如何推导 ������ =a (m>n,a≠0)? ������ ������������ 1 提示: ������ =am·������=am· a-n=am-n. ������ ������
