通信电路原理习题课1-4章共29页文档
(完整版)电路原理课后习题答案
因此, 时,电路的初始条件为
t〉0后,电路的方程为
设 的解为
式中 为方程的特解,满足
根据特征方程的根
可知,电路处于衰减震荡过程,,因此,对应齐次方程的通解为
式中 。由初始条件可得
解得
故电容电压
电流
7-29RC电路中电容C原未充电,所加 的波形如题7—29图所示,其中 , 。求电容电压 ,并把 :(1)用分段形式写出;(2)用一个表达式写出。
或为
第六章“储能元件”练习题
6—8求题6-8图所示电路中a、b端的等效电容与等效电感.
(a) (b)
题6—8图
6—9题6—9图中 , ; 。现已知 ,求:(1)等效电容C及 表达式;(2)分别求 与 ,并核对KVL。
题6-9图
解(1)等效电容
uC(0)=uC1(0)+uC2(0)=-10V
(2)
6—10题6-10图中 , ; , , ,求:(1)等效电感L及 的表达式;(2)分别求 与 ,并核对KCL。
应用规则2,有 ,代入以上方程中,整理得
故
又因为
当 时,
即电流 与负载电阻 无关,而知与电压 有关.
5—7求题5-7图所示电路的 和输入电压 、 之间的关系。
题5-7图
解:采用结点电压法分析。独立结点 和 的选取如图所示,列出结点电压方程,并注意到规则1,得(为分析方便,用电导表示电阻元件参数)
应用规则2 ,有 ,代入上式,解得 为
(f)理想电流源与外部电路无关,故i=—10×10—3A=—10—2A
1-5试求题1—5图中各电路中电压源、电流源及电阻的功率(须说明是吸收还是发出)。
(a) (b) (c)
题1-5图
解(a)由欧姆定律和基尔霍夫电压定律可知各元件的电压、电流如解1—5图(a)故电阻功率 (吸收20W)
北邮版通信原理课后习题的答案第四章-精品
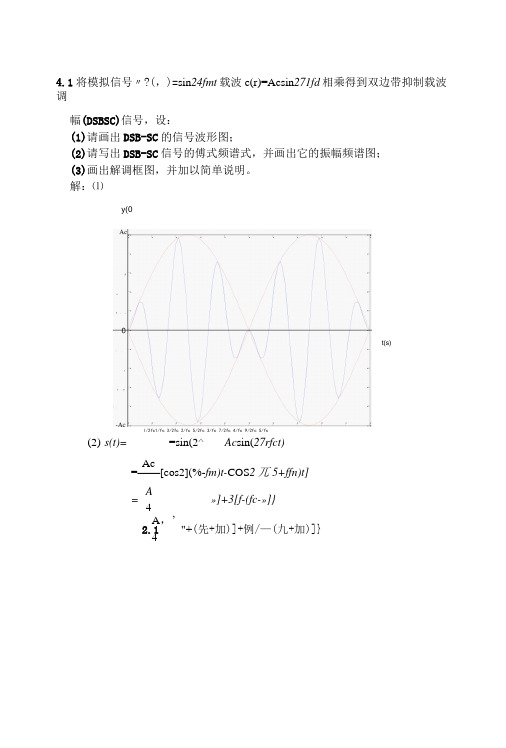
4.1将模拟信号〃?(,)=sin 24fmt 载波c(r)=Acsin 271fd 相乘得到双边带抑制载波调幅(DSBSC)信号,设:(1)请画出DSB-SC 的信号波形图;(2)请写出DSB-SC 信号的傅式频谱式,并画出它的振幅频谱图; (3)画出解调框图,并加以简单说明。
解:⑴(2) s(t)= =sin(2^ Ac sin(27rfct)Ac=——[cos2](%-fm)t-COS 2兀5+ffn)t] A = »]+3[f-(fc-»]} 4A ,’ 2.1 "+(先+加)]+例/—(九+加)]} 4y(0l/2fc1/fc 3/2fc 2/fc 5/2fc 3/fc 7/2fc 4/fc 9/2fc 5/fct(s)S ⑴八3Ac/4- Ac/2.Ac/4(3)相干解调Cos(Wct)与发端相干偏调相干解调:将接收信号与载波信号sin(2乙加)相乘,得至U A cr(t)sin(2^fct)=Acm(t)sin(2^fct)sin(2^fit)=--cos(44fct)]通过低通滤波器抑制载频的二倍频分量,得到解调信号为刈⑺=与机⑺ 2.2 已知某调幅波的展开式为:s(t)=cos(2/rxl()4r)+4COS (2TT xl.lxl040+cos(2万xl.2xl04r) (1)求调幅系数和调制信号频率;(2)写出该信号的傅式频谱式,画出它的振幅频谱图; (3)画出该信号的解调框图。
解:⑴sQ)=cos(24xl04r)+4cos(2乃xl.lxl04r)+cos(2万xl.2xl04r)=4cos(2%xl.lxl04r)[l+0.5cos(2万x0.1xl04r)] 调制系数是a=0.5;信号频率是f=1000Hz(2)S(/)=;U(/+104)+演f —i04)]+2[Mf+l.lxl()4)+5(/—1.1X104)]+-W+1.2X 104)+^(/-1.2X 104)]-fm-fc ・fc -fc+fm。
通信原理第4章课后习题答案

第四章 模拟调制学习指导4.1.1 要点模拟调制的要点主要包括幅度调制、频率调制和相位调制的工作原理。
1. 幅度调制幅度调制是用调制信号去控制载波信号的幅度,使之随调制信号作线性变化的过程。
在时域上,已调信号的振幅随基带信号的规律成正比变化;在频谱结构上,它的频谱是基带信号频谱在频域内的简单平移。
由于这种平移是线性的,因此,振幅调制通常又被称为线性调制。
但是,这里的“线性”并不是已调信号与调制信号之间符合线性变换关系。
事实上,任何调制过程都是一种非线性的变换过程。
幅度调制包括标准调幅(简称调幅)、双边带调幅、单边带调幅和残留边带调幅。
如果调制信号m (t )的直流分量为0,则将其与一个直流量A 0相叠加后,再与载波信号相乘,就得到了调幅信号,其时域表达式为[]()()()AM 0c 0c c ()()cos cos ()cos (4 - 1)s t A m t t A t m t t ωωω=+=+ 如果调制信号m (t )的频谱为M (ω),则调幅信号的频谱为[][]AM 0c c c c 1()π()()()() (4 - 2)2S A M M ωδωωδωωωωωω=++-+++- 调幅信号的频谱包括载波份量和上下两个边带。
上边带的频谱结构与原调制信号的频谱结构相同,下边带是上边带的镜像。
由波形可以看出,当满足条件|m (t )| A 0 (4-3)时,其包络与调制信号波形相同,因此可以用包络检波法很容易恢复出原始调制信号。
否则,出现“过调幅”现象。
这时用包络检波将发生失真,可以采用其他的解调方法,如同步检波。
调幅信号的一个重要参数是调幅度m ,其定义为[][][][]00max min 00max min()() (4 - 4)()()A m t A m t m A m t A m t +-+=+++ AM 信号带宽B AM 是基带信号最高频率分量f H 的两倍。
AM 信号可以采用相干解调方法实现解调。
天津大学现代通信原理课后习题答案(1-4章)

天津大学现代通信原理课后习题答案(1-4章)《现代通信原理》课后习题解答第一章绪论1-1设英文字母C出现的概率为0.023,E出现的概率为0.105,试求C与E的信息量。
11IClog2log25.44bit解:p(某)0.023IElog213.25bit0.1051-2设某地方的天气预报晴占4/8,阴占2/8,小雨占1/8,大雨占1/8,试求各每个消息的信息量。
解:8log21bit晴:阴:2bit小雨:3bit大雨:3bit。
41-3设有四个信息A、B、C、D分别以概率1/4,1/8,1/8和1/2传递,每一消息的出现的是相互独立的。
试计算其平均信息量。
解:1111H(某)P(A)log2P(B)log2P(C)log2P(D)log2P(A)P(B)P(C)P(D)11111111log2log2log2log211114882()()()()48821.75bit/符号1-4一个离散信号源每毫秒发出4种符号中的一个,各相互独立符号出现的概率分别为0.4,0.3,0.2,0.1。
求该信号源的平均信息量与信息传输速率。
解:111H(某)0.4log20.3log20.2log20.40.30.210.2log21.84bit/符号0.21.841840bit/1061-5设一信息源的输出由128个不同的符号组成,其中16个出现的概率为1/32,R其余112个出现概率为1/224,信息源每秒钟发1000个符号,且每个符号彼此独立,试计算该信息源的平均信息速率。
11解:H(某)16(1/32)log2112(1/224)log2(1/32)(1/224)6.405bit/符号Rb6.40510006405bit/第1页共26页1-6设一数字传输系统传递二进制码元的速率为1200B,试求该系统的信息传输速率,若该系统改为8进制码元传递,传码率仍为1200B,此时信息传输速率又为多少?解:Rb=RB=1200b/RbRBlog2N1200log28120033600b/1-7已知二进制数字信号的传输速率为2400b/。
通信原理各章小结及习题课共96页文档

1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
1、不要轻言放弃,否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人,常是愿意 去做,并愿意去冒险的人。“稳妥”之船,从未能从岸边走远。-戴尔.卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡,喝起来是苦涩的,回味起来却有久久不会退去的余香。
通信原理各章小结及习题课 4、守业的最好办法就是不断的发展。 5、当爱不能完美,我宁愿选择无悔,不管来生多么美丽,我不愿失 去今生对你的记忆,我不求天长地久的美景,我只要生生世世的轮 回里有你。
通信原理各章小结及习题课
ξc(t) 、ξs(t)
(1)E[ξc(t)]=0 (2)E[ξs(t)]=0 (3)Rξ(0)
= Rc(0) =Rs(0) = Rs(τ)
σξ2 =σc2 =σs2
(4)Rc(τ)
Rcs(τ) = -Rsc(τ)
(5)
同一时刻相互独立
(5) fcs(ξc, ξs)=fc(ξc)·s(ξs) f
r (t) r(kTs) 抽样判决器 t=kTs 抽样
n(t) AWGN
判决电平b
A, e(t ) A,
发送“1” 发送“ 0”
1, 判决输出 0,
r (kTs ) b r (kTs ) b
已知白噪声的双边功率谱密度为n0/2, LPF为理想 低通滤波器,截止频率为fm, 求P(0/1)及P(1/0)
(2.18) (2.19) (2.20) (2.21)
(5) R(0)-R(∞)=σ2 [方差,交流功率]
(2.22)
平稳随机过程的PSD
P ( ) R( )e j d
1 R( ) 2
P ( )e j d
P ( f ) R( )e j 2f d
1 8 { cos 10 d 0} 1 2 5 5
4 sin 5 / 5 4Sa(5 )
所以X(t)是平稳的
X (t ) lim
T /2 1 T T / 2 T
A cos(t )dt 0 A2 cos(t ) cos(t )dt
2
PY ( ) PX ( ) H ( j )
X(t)
Impulse Response h(t)
通信电路原理习题课1 4章

由巴特沃思滤波器计算曲线可得:阶次 n=3
当通带内衰减为1dB时,其对应归一化频率是0.8
由此可以得出截止频率为 4/0.8=5kHz
重新计算带宽比 Ω=20/5=4
查表得:阶次为3的衰减As结果为32dB,不满足要求
由此得带宽比需要增加,即截止频率要减小,据此取阶次为 4
通带内衰减为1dB时,其对应归一化频率是0.85
0.0104? F
L4 ? RL
?C
L4' ?
600
2? ? 4 .7 ? 10 3 ? 0 .7654
? 15 .56 mH
第1-4章
【习题】
1. 有一双电感复杂并联回路如图所示,已知 L1+L2=500uH,C=500pF,为了使 电源中的二次谐波能被回路消除,应如何分配 L1和L2 ?
解: 假设在该图上并联一个负载 (如图示),
RL P2
?
RL' ? 40K?
R总=RL' // RP // Rg R ? R总 P2 Qp ? R总? 0C ? 不接时,R总上升 ? Qp增加
BW
?
f0 Qp
,f0 不变,BW减小
第1-4章
3、低通滤波器的设计步骤:
1) 利用滤波器计算曲线,确定滤波器的阶次 n :
a.
求出带宽比
Ω=
? ?
s 0
3) 绘出实际的并联回路图。
解:
1)根据已知条件, 535kHz, 1605kHz均为
谐振频率,且比值为3,即:
1
?H ?
LC min ? 3
?L
1 LC max
C max ? 9 C min
第1-4章
【习题】
通信原理课后练习答案经典.ppt

统计独立。
⑴ 试证明 z(t)是广义平稳的;
⑵ 试画出自相关函数 Rz ( ) 的波形; ⑶ 试求功率谱密度Pz ( f ) 及功率S。
10
.精品课件.
第3章课后作业解答
⑴ 试证明 z(t)是广义平稳的; 只要证明z(t) 的均值为常数,自相关函数仅与时间
间隔 有关即可。
E[z(t )] E[m(t )cos(ct )] E[m(t )] E[cos(ct )]
E{cos[c (t1
t2 )
2 ]
cos[c (t2
t1 )]}
1 2
E{cos[c (t1
t2 )
2 ]}
1 2
cos c
0 12
.精品课件.
第3章课后作业解答
⑵ 试画出自相关函数 Rz ( ) 的波形;
Rz (
)
1 2
Rm (
) cosc
1 / 2 Rz ( )
1
1
⑶ 试求功率谱密度Pz ( f ) 及功率S。 1 / 2
E[m(t1 )cos(ct1 ) m(t2 )cos(ct2 )]
E[m(t1 ) m(t2 )] E[cos(ct1 ) cos(ct2 )]
Rm ( ) E[cos(ct1 ) cos(ct2 )]
E[cos(ct1 ) cos(ct2 )]
1 2
作业 习题:3-5、3-6、3-7、3-8
9
.精品课件.
第3章课后作业解答
3-5 已知随机过程z(t ) m(t )cos(ct ),其中,m(t)
是广义平稳过程,且自相关函数为
1 Rm ( )
1 1 0
Rm ( ) 1 0 1
0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1) 应采用哪一个可变电容器,为什么?
2) 回路电感应该等于多少?
3) 绘出实际的并联回路图。
解:
1)根据已知条件, 535kHz, 1605kHz均为
谐振频率,且比值为3,即:
1
H LCmin 3LFra bibliotek1 LCmax
C max 9 C min
第1-4章
【习题】
在两个可变电容当中, 100/12<9,不满足要求, 450/15=30>9,满足要求,
L2与C则构成并联谐振,在负载上能构产 生压降,因此:
R1
C R2
1 2 L2C
L1
1 C
L2
计算结果:
L1 =375μH, L2 =125μH
第1-4章
【习题】
2.有一并联回路在某频段内工作,频段最低频率为535kHz,最高 频率为1605kHz。现有两个可变电容器,一个电容器的最小电容 量是12pF,最大电容量是100pF;另一个电容器的最小电容量是 15pF,最大电容量是450pF。试问:
第1-4章
【习题】
1. 有一双电感复杂并联回路如图所示,已知L1+L2=500uH,C=500pF,为了使 电源中的二次谐波能被回路消除,应如何分配L1和L2 ?
解: 假设在该图上并联一个负载(如图示),
则要使二次谐波消除,则应该不让二次谐
波在负载上产生压降,因此对于二次谐波 L1
L2
要求 L2与C构成串联谐振,而对于基频L1 、
b. 作图
P1
n
P2
P3
n-1 P4
y1
Ω
如果点P4落在n与n -1的衰减线之间,则选择n
第1-4章
2) 选择电路: 满足同一要求的低通滤波器电路有两种结构, 它们互为对偶,一般选择电感少的电路;
3) 3) 根据给定的技术指标和求的阶次n,从归一化元件值 表中查的归一化元件值; 注意:要根据自己选择的电路形式选择相应的表头
当通带内衰减为1dB时,其对应归一化频率是0.8
由此可以得出截止频率为4/0.8=5kHz
重新计算带宽比 Ω=20/5=4
查表得:阶次为3的衰减As结果为32dB,不满足要求
由此得带宽比需要增加,即截止频率要减小,据此取阶次为4
通带内衰减为1dB时,其对应归一化频率是0.85
截止频率为4/0.85=4.7kHz
试求:线圈的电感 L,回路品质因数 Q 以及未知阻抗 Z 。
第1-4章
0 2f 6.28 Mrad / s
1 -1短接: 0
1 L 0.25 mH LC
Q u c 10v 100 u 0.1v
Q 1 R 1 15 .9
R0C
Q0C
第1-4章
z 接入:因为频率不变所
以只能是电阻和电容
j796
第1-4章
2:并联回路如下图所示。
已知: L 1 = L 2 =5UH,Q=100。
C 1 = C 2 =8PF,R g =40K。
P1 L1
R
L2
C1 P2
RL=10K。 试求:无阻尼谐振频率;
Rg
C2
RL
等效谐振电阻 R ; 不接RL ,BW如何变?
第1-4章
p p1 p2 1 / 2
因此,选用最小电容为15pF和最大电容为450pF的可变电容;
2) 根据以上分析, 450/15=30,因此 3) 如果取C1=15pF为获得最高频率1605kHz时回路的电容,求得电感L 4) 则最低频率535时所需的回路电容值应该为C2=9*15=135<450,反
5) 之,分析方法相同;
6) 因此要使的回路在可变电容的两个端值取得最高和最低频率需
R
' L
RL P2
R
' L
40 K
R 总=
R
' L
//
RP
//
Rg
R R总 P 2
Q p R总 0C 不接时, R总上升 Q p增加
BW
f0 Qp
, f 0 不变,
BW 减小
第1-4章
3、低通滤波器的设计步骤:
1) 利用滤波器计算曲线,确定滤波器的阶次n :
a.
求出带宽比
Ω=
s 0
=y1
重新计算带宽比 Ω=20/4.7=4.3
阶次为4的衰减As结果为44dB满足要求
第1-4章 【第二章课堂作业】
查表得归一化元件值为 C1=0.7654 L2=1.8478 C3= 1.8478 L4= 0.7654 Rs=1.0000
L2
L4
Is Rs C1 C3 RL
实际元件值
电路图
C 1 C 1 R L C 1 ' 2 4 .7 1 1 3 0 6 0 0 .7 06 0 .0 54 4 F3
L 2 R C LL 2 ' 2 6 4 .7 0 13 0 0 1 .84 3 7 .5 7 8 m 6 H
C 3 C 1 R LC 3 ' 2 4 .7 1 13 0 6 0 1 .8 04 0 .7 08 1F 04
L 4 R C LL 4 ' 2 6 4 .7 0 13 0 0 0 .76 1 5 .5 5 4 m 6 H
7) 给回路再并上一个电容,则
L 1 L(450 C) H 1 L(15 C)
C, L
第1-4章
【习题】
3) 电路结构如图示
L
C0
C
第1-4章
【习题】
3. 给定并联谐振回路的f0=5MHz,C=50pF,通频带2 f0.7=150kHz。试求电感 L和品质因数Q;若把2 f0.7加宽至300kHz,应在回路两端再并联上一个阻 值多大的电阻。
4) 根据公式求得各元件的实际值并画出电路图
第1-4章
【第二章课堂作业】
2-10 请用巴特沃思逼近法涉及一个低通滤波器,要求在频率0~4kHz范围内
衰减小于1dB,频率高于20kHz的范围衰减大于35dB,信源与负载阻抗为 600Ω。
解:Ap=1dB As=35dB 估计一个带宽比:20/4=5
由巴特沃思滤波器计算曲线可得:阶次n=3
总电容 C 总 不变,为 100pF, C 调为 200pF
C总
CC x C Cx
Cx
200pF
总电容 C 总 上的电压为 2 .5 V
Q ' u c = 2.5 = 25 u 0.1
Q'
1 (R + R x ) 0 C
Rx
47 .7
0
1 L 0 .25 mH LC
z
Rx
1 j 0C x
47.7 -
第1-4章
1:
L R1
1
V
1MHz
0.1V
C
信号源频率 F =1MHz。
电压振幅 V=0.1V。
将1-1端短接,电容C 调到
Z
100PF时谐振。此时,电容 C 两端的电压为10V。
如1-1端开路再串接一阻抗 Z (电阻和电容串联),则回路
失谐,电容 C 调到200PF时重新谐振。此时,总电容 两端 的电压为2.5V。
