特殊角的三角函数ppt课件
合集下载
沪科版九年级上册数学23.特殊角的三角函数值课件

(2)
cos sin
45 45
tan
45
(3)tan450.sin450-4sin300.cos450+cos2300
练习
1. 求下列各式的值: 2.(1)1-2 sin30°cos30° 3. (2)3tan30°-tan45°+2sin60°
4.
(3)
1
cos 60 sin 60
1 tan 30
例3 (1)如图,在Rt△ABC中,∠C
=90°,
B
AB 6, BC 3 , 6 3
求∠A的度数.
A
C
2. 如图,在RT△ABC中 ,∠ACB=900,CD⊥AB于D,已知∠B=300,计 算tan∠ACD+sin∠BCD的值.
A
D
B
C
本节课学习了什么内容?
三角函数 30°
45°
60°
sina
1、已知tanA=
5 12
,
5
sinA= 13 ,
12
cosA= 13 .
A
13x 12x
C 5x
B
1、视察下列基本图形,说出三边之比。
A
A
3 0
2
4 5
1
C1 B
C
1
B
(1)上述图形中,有几种锐角?
(2)你能根据左图,分别求出sin30° cos30°tan30°吗?
2、画出上述图形,继续探索45°60° 的情况,并填写下列表格。
• 正弦 0< sinα<1
• 余弦 0< cosα<1
• 正切
tanα>0
例1 计算: (1)2sin60°+3tan30 °+tan45°; (2)cos 245°+tan60°cos30°.
特殊角的三角函数值表高中用ppt课件
3
1
3
0
精选编辑ppt
3
3
特殊角的三角函数值表 第四象限
角
3000 3150
3300 3600
三角函数
弧度
5π/3 7π/4 11π/6 2π
sin
3 2
2 2
1 2
0
cos
1
2
2
3
1
2
2
tan
3
1
3
3
0
cot
3
1
3 不存在
3
精选编辑ppt
4
特殊角的三角函数值总表
精选编辑ppt
5
特殊角的三角函数值表 正值
精选编辑ppt
6
特殊角的三角函数值表 30°与60°正余弦值正负及互换
精选编辑ppt
7
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
精选编辑ppt
8
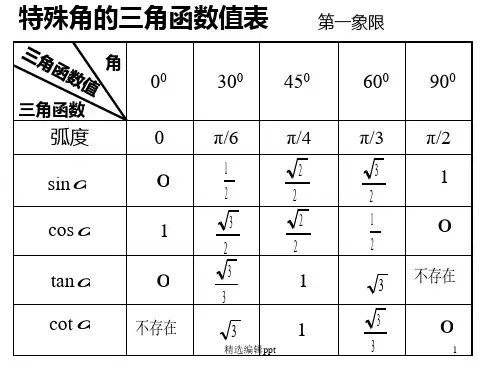
特殊角的三角函数值表 第一象限
角
00
三角函数
弧度
0
sin
0
cos
1
tan cot
0
不存在
300 450
π/6 π/4
1
2
2
2
3
2
2
2
3
1
3
3
1
精选编辑ppt
600 900
π/3 π/2
3
1
2
1
0
2
3 不存在
3
0
3
1
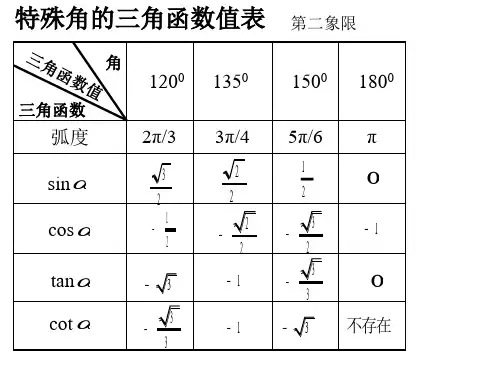
特殊角的三角函数值表 第二象限
角
1200 1350
1500 1800
三角函数
特殊角的三角函数ppt

请你谈谈对本节学习内容的 体会和感受。
3 2
∠ A=30° ∠ A=30° ∠ B=45° ∠ B=30° ∠ A=45°
1 2
2
2
3
3
(5)tanA= 1
学以致用
做一做 1、sin30°+cos60°=
1 2 +
2
1 2
- 1
=1 = 1 2
3 2 2、2sin 60°-tan45°=
3、tan60°-cos30°=
3 -
3 3 = 2 2
人教版九年级下册
特殊角的三角函数值
襄阳市第二十一中学 邵春山
学习目标
1、能根据正弦、余弦、正切、余切的定义, 求出30°、45°、60°角的三角函 数值。
2、熟记30°、45°、60°角的三角函 数值。
3、能运用三角函数解决可以转化为直角三角 的简单的实际问题。
知 识回 顾
在直角三角形中,30度 所对的直角边与斜边有 什么关系?
C
B
AB=4
1 =2 BC=4 X 2
2.解:
sinB=
AC AB
A
2
4 ?
AC=2,AB=4
∠B=30
2 1 = sinB= 4 2
O
C
B
当堂检测
(1) (2)
sin30°+cos60° sin260°+cos260°-tan45°
看谁做的快!
要动动脑筋吆! (3)等腰三角形腰长为10厘米,顶 10 3 cm 角是120°,则三角形底 边长 , 面积是 25 3 cm2 。
填一填 记一记
三角函数
角α
30°
九年级数学PPT特殊角的三角函数值课件

2 1
2
tan 300 3 3
cot 300 3
tan 600 3
cot 600 3 3
300
2
3
1
如图,求
角的四个
sin 450 4三520 角函数值,
2
cos 450 2450 2
450
tan 450 1
2
1
cot 450 1
1
请记住:
30的0 三450角6函00 数值
22
2 6 2
6
6 cot2 600 tan 600
4.
3 tan 300
6 ( 3 )2 3
解:原式
3
(2 3) 3 3 3
3
3 3
2 33 3
2 3 3
练习:计算
1.sin 30 cos2 45 0
3
2.2cos45 2 3
2.在ABC中,A 300, tan B 3, BC 2 3
则AB ________ .
如图,在△ABC中,∠C=90°,
AC=8cm,AB的垂直平分线MN交AC
于D,连结BD,若cos∠BDC=3 ,
求BC的长
5
B
N
5x 4x
C
3x
M
D
5x
A
如图,△ABC中,AB=AC,∠A =30度,AC的垂直平分线分别交
3 3 22
0
例:计算下列各值:
2.sin2 60 cos2 60
解:原式 ( 3 )2 ( 1 )2 22
3 1 sin 2 600 (sin 600)2
44
1
特殊角的三角函数值表ppt课件
0
1
0 不存在
特殊角的三角函数值表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
第三象限
角
三角函数
弧度
2100 7π/6
sin
1 2
cos
3
2
tan
3
3
cot
3
2250
5π/4
2 2
2 2 1
1
2400 2700
4π/3 3π/2
3
1
2
1 2
0
3 不存在
3
0
3
特殊角的三角函数值表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
第四象限
角
三角函数
弧度
3000 5π/3
sin
3
2
cos
1
2
tan
3
cot
3
3
3150
7π/4
2 2 2 2
1
1
3300 3600
11π/6 2π
1
0
2
3
1
2
3
0
3
3 不存在
特殊角的三角函数值总表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
特殊角的三角函数值表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
1
0 不存在
特殊角的三角函数值表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
第三象限
角
三角函数
弧度
2100 7π/6
sin
1 2
cos
3
2
tan
3
3
cot
3
2250
5π/4
2 2
2 2 1
1
2400 2700
4π/3 3π/2
3
1
2
1 2
0
3 不存在
3
0
3
特殊角的三角函数值表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
第四象限
角
三角函数
弧度
3000 5π/3
sin
3
2
cos
1
2
tan
3
cot
3
3
3150
7π/4
2 2 2 2
1
1
3300 3600
11π/6 2π
1
0
2
3
1
2
3
0
3
3 不存在
特殊角的三角函数值总表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
特殊角的三角函数值表 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
中职教育数学《特殊角的三角函数值》课件

23)²
=1;
(2)cos45 tan 45
sin 45
2
=2
2
2 -1
=0
求下列各式的值:
(1)1 2sin 30 cos30
(2)3 tan 30 tan 45 2sin 60co 601(3) 1
sin
60
tan 30
例2、 (1)如图,在Rt△ABC中,
∠C=90°,AB 6, BC 3 ,求∠A
AC= 21 ,求∠A,∠B的度数。
B
7
A
C
21
1. 计算:
12 4sin 600 (3 π)0 ( 1)1 3
解:原式 2 3 4 3 1 (3) 2
2 3 2 3 13
4
2.计算:
20110
3tan 30
1
2
|
32|
3
解:原式 1 3 3 9 (2 3) 3
1 3 9 3 2
8
3.计算:
3 3 2cos300 22 (3 )0
4. 计算:
1 π 20100 3 tan 60°+ 21
同角三角函数的基本关系
(1)sin290°+cos290° (2)sin230°+cos230°
sin 60 (3) cos 60
sin 45 (4) cos 45
同角三角函数的基本关系
cosα= tanα
±的选择时 要根据角的 象限来决定
2
sinα
=1-cos2α
等,
例题
例1:已知,sinα= - 3 且α是第三象限的角, 5
求cosα,tanα的值.
思考: 本题与例题1的主要区别在哪儿? 如何解决这个问题?
《特殊角的三角函数值》PPT课件
)
D.1
3
2
【详解】sin60°= ,tan45°=1,所以sin60°+tan45°=
2.如果α是锐角, =
1
A.2
B.
2
2
3
,那么cosα的值是(
2
C.
3
2
D.
3
2
【详解】∵α是锐角,sinα= ,
∴α=60°,
1
∴cosα=cos60°=2.
故选:A.
3
3
)
3+2
.故选B.
2
3.已知∠A是锐角,且满足3tanA﹣ 3=0,则∠A的大小为(
4、会由一个特殊角的三角函数值说出这个角的度数。
C O N T E N T S
计算含有特殊角的三角函数值的式子。
推导30°、45°、60°角的三角函数值。
LEARNING OBJECTIVES
1、推导30°、45°、60°角的三角函数值。
2、熟记30°、45°、60°角的各个三角函数值。
3、计算含有特殊角的三角函数值的式子。
第二十八章
锐角三角函数
TOPIC 28.1 ACUTE TRIANGLE (SINE, COSINE, TANGENT VALUE OF SPECIAL ANGLE)
- .
目录
1、推导30°、45°、60°角的三角函数值。
2、熟记30°、45°、60°角的各个三角函数值。
3、计算含有特殊角的三角函数值的式子。
1.对于sinα与tanα,角度越大,函数值越越大;
对于cosα,角度越大,函数值越越小.
2. 互余的两角之间的三角函数关系:
若∠A+∠B=90°,则sinA = cosB,cosA = sinB,tanA · tanB =1 .
特殊角的三角函数值表高中用ppt课件
.
此课件下载可自行编辑修改,此课件供参考! 部分内容来源于网络,如有侵权请与我联系删除!感谢你的观看!
3
3
1350
3π/4
2 2 2
2
1
1
.
1500 1800
5π/6
1 2 3 2 3 3
3
π
0
1
0
不存在
特殊角的三角函数值表 第三象限
角
三角函数
弧度
2100 7π/6
sin
1 2
cos
3
2
tan
3
3
cot
3
2250
5π/4
2 2
2 2
1
1
.
2400 2700
4π/3 3π/2
3
1
2
1 2
0
3 不存在
3
0
3
特殊角的三角函数值表 第四象限
角
三角函数
弧度
3000 5π/3
sin
3
2
cos
1
2
tan
3
cot
3
3
3150
7π/4
2 2 2 2
1
1
.
3300 3600
11π/6 2π
1
0
2
3
1
2
3
0
3
3 不存在
特殊角的三角函数值总表
.
特殊角的三角函数值表 正值
.
特殊角的三角函数值表 30°与60°正余弦值正负及互换
特殊角的三角函数值表 第一象限
角
00
三角函数
弧度
0
sin
0
此课件下载可自行编辑修改,此课件供参考! 部分内容来源于网络,如有侵权请与我联系删除!感谢你的观看!
3
3
1350
3π/4
2 2 2
2
1
1
.
1500 1800
5π/6
1 2 3 2 3 3
3
π
0
1
0
不存在
特殊角的三角函数值表 第三象限
角
三角函数
弧度
2100 7π/6
sin
1 2
cos
3
2
tan
3
3
cot
3
2250
5π/4
2 2
2 2
1
1
.
2400 2700
4π/3 3π/2
3
1
2
1 2
0
3 不存在
3
0
3
特殊角的三角函数值表 第四象限
角
三角函数
弧度
3000 5π/3
sin
3
2
cos
1
2
tan
3
cot
3
3
3150
7π/4
2 2 2 2
1
1
.
3300 3600
11π/6 2π
1
0
2
3
1
2
3
0
3
3 不存在
特殊角的三角函数值总表
.
特殊角的三角函数值表 正值
.
特殊角的三角函数值表 30°与60°正余弦值正负及互换
特殊角的三角函数值表 第一象限
角
00
三角函数
弧度
0
sin
0
特殊角的三角函数值 经典课件(最新版)
2
求AB.
C
解:过点C作CD⊥AB于点D
∠A=30°, AC 2 3,
Q sin A CD 1 , AC 2
CD 1 2 3 3. 2
A
D
B
Q cos A AD AC
3, 2
AD
3 2 2
3 3.
Q tan B CD 3 , BD 3 2 2,
求∠A的度数; B
解: 在图中,
Q sin A BC 3 2 , AB 6 2
6
3
A 45;
A
C
初中数学课件
(2)如图,AO是圆锥的高,OB是底面半径,AO= 3 OB,
求 的度数.
解: 在图中,
A
Q tan AO 3OB 3 ,
OB OB
60.
初中数学课件
特殊角的三角函数值 课件
初中数学课件
学习目标
1.运用三角函数的概念,自主探索,求出30°、45°、60° 角的三角函数值.(重点)
2.熟记三个特殊锐角的三角函数值,并能准确地加以运用. (难点)
导入新课
初中数学课件
复习引入
1.在Rt△ABC中,∠C=90°,cosA= 3 , BC=8,则 5
(2)
cos45o sin45o
tan45o.
解:(1)
cos2
60o+sin2 60o
1 2
2
3 2
2
1;
(2)
cos45o sin45o
tan45o
2 2
2 1 0. 2
初中数学课件
求AB.
C
解:过点C作CD⊥AB于点D
∠A=30°, AC 2 3,
Q sin A CD 1 , AC 2
CD 1 2 3 3. 2
A
D
B
Q cos A AD AC
3, 2
AD
3 2 2
3 3.
Q tan B CD 3 , BD 3 2 2,
求∠A的度数; B
解: 在图中,
Q sin A BC 3 2 , AB 6 2
6
3
A 45;
A
C
初中数学课件
(2)如图,AO是圆锥的高,OB是底面半径,AO= 3 OB,
求 的度数.
解: 在图中,
A
Q tan AO 3OB 3 ,
OB OB
60.
初中数学课件
特殊角的三角函数值 课件
初中数学课件
学习目标
1.运用三角函数的概念,自主探索,求出30°、45°、60° 角的三角函数值.(重点)
2.熟记三个特殊锐角的三角函数值,并能准确地加以运用. (难点)
导入新课
初中数学课件
复习引入
1.在Rt△ABC中,∠C=90°,cosA= 3 , BC=8,则 5
(2)
cos45o sin45o
tan45o.
解:(1)
cos2
60o+sin2 60o
1 2
2
3 2
2
1;
(2)
cos45o sin45o
tan45o
2 2
2 1 0. 2
初中数学课件
特殊的锐角三角函数课件
定理
正弦函数是周期函数,具有周期性。
余弦函数的公式和定理
定义
余弦函数是直角三角形中一个锐角的邻边的长度与斜边的 长度的比值。
公式
cos(α) = adjacent / hypotenuse
定理
余弦函数是周期函数,具有周期性。
THANKS
感谢观看
问题。
余切函数的图像
01
定义
余切函数是以角度为自变量,以直角三角形邻边与对边的比值为函数值
的函数。
02 03
图像特点
在直角坐标系中,余切函数的图像也是一条在区间(-∞,+∞)内的连续曲 线,并且在π/2+2kπ(k∈Z)处取得极大值,在-π/2+2kπ(k∈Z)处取得 极小值。
应用
在数学和工程领域,余切函数经常用于解决与三角形和多边形有关的几 何问题。
tan(x) = 对边长度 / 邻边长度
定义域
值域
在直角坐标系中,正切函数的定义域是{x | x ≠ kπ + π/2, k ∈ Z},即除了kπ + π/2 以外的所有实数。
正切函数的值域是全体实数,即R。
余切函数定义
余切函数定义
余切函数(cotangent) 是指直角三角形中,一个 锐角的邻边与对边的比值 。记作cot(x),其中x是一 个锐角。
正弦函数的图像
01
02
03
定义
正弦函数是以角度为自变 量,以单位圆上点的纵坐 标为函数值的函数。
图像特点
在直角坐标系中,正弦函 数的图像是一条在区间[1,1]内的连续曲线,周期 性重复且具有对称性。
应用
在物理和工程领域,正弦 函数经常用于处理振动、 波动等问题。
正弦函数是周期函数,具有周期性。
余弦函数的公式和定理
定义
余弦函数是直角三角形中一个锐角的邻边的长度与斜边的 长度的比值。
公式
cos(α) = adjacent / hypotenuse
定理
余弦函数是周期函数,具有周期性。
THANKS
感谢观看
问题。
余切函数的图像
01
定义
余切函数是以角度为自变量,以直角三角形邻边与对边的比值为函数值
的函数。
02 03
图像特点
在直角坐标系中,余切函数的图像也是一条在区间(-∞,+∞)内的连续曲 线,并且在π/2+2kπ(k∈Z)处取得极大值,在-π/2+2kπ(k∈Z)处取得 极小值。
应用
在数学和工程领域,余切函数经常用于解决与三角形和多边形有关的几 何问题。
tan(x) = 对边长度 / 邻边长度
定义域
值域
在直角坐标系中,正切函数的定义域是{x | x ≠ kπ + π/2, k ∈ Z},即除了kπ + π/2 以外的所有实数。
正切函数的值域是全体实数,即R。
余切函数定义
余切函数定义
余切函数(cotangent) 是指直角三角形中,一个 锐角的邻边与对边的比值 。记作cot(x),其中x是一 个锐角。
正弦函数的图像
01
02
03
定义
正弦函数是以角度为自变 量,以单位圆上点的纵坐 标为函数值的函数。
图像特点
在直角坐标系中,正弦函 数的图像是一条在区间[1,1]内的连续曲线,周期 性重复且具有对称性。
应用
在物理和工程领域,正弦 函数经常用于处理振动、 波动等问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∠ABC,BC=12,BD= 8 3 ,求∠A的度数及
AD的长.
A
D
B
C.
11
应用生活
操场里有一个旗杆,老师让小明去测量旗杆高度, 小明站在离旗杆底部10米远处,目测旗杆的顶部,视 线与水平线的夹角为30度,并已知目高为1.65米.然
后他很快就算出旗杆的高度了。
你想知道小明怎样 算出的吗?
?
1.65米
3
A
B
6
3
A
C
(1)
O B
.
(2)
8
练习
1、在Rt△ABC中,∠C=90°,
BC 7,AC 21
求∠A、∠B的度数.
A
B
7
C
21
.
9
练习
2. 如图,在Rt△ABC中,∠C=900,若 tanA+tanB=4,S△ABC=8.求斜边AB的长.
A
b
C
B
a
.
10
练习
3、如图,△ABC中,∠C=900,BD平分
.
6
练习
2. 如图,在Rt△ABC中,∠ACB=900, CD⊥AB于D,已知∠B=300, 计算tan∠ACD+sin∠BCD的值.
A
D
B
C
.
7
例2、(1)如图,在Rt△ABC中, ∠C=90°,AB= 6 ,BC= 3。求∠A的度数。
(2)如图,已知圆锥的高AO等于圆锥的底面半
径OB的 倍,求α.
7.3特殊角的三角函数
.
1
sinA
B
斜边
A ∠A的邻边
cosA
∠A的对边
tanA
C
.
∠A的对边 斜边
∠A的邻边 斜边
∠A的对边 ∠A的邻边
2
特殊角三角函数值
.
3
仔细观察,说说你发现
特殊角这三张角表函有数哪值osα
tanα
30°
1 2
3 2
3 3
45°
2 2 2 2
30°
10米
.
12
1?scio n232s40+ 5+ta2 t4an5n + c3o s0 26 isn3 0 0
2、在Rt△ABC中,∠C=90°,化简
1-2sinAcosA
.
13
1
60°
3 2
1 2
3
.
4
例1、求下列各式的值. (1) cos260°+sin260°
(2)csoi ns4455 -tan45
.
5
练习
1. 求下列各式的值: (1)1-2 sin30°cos30° (2)3tan30°-tan45°+2sin60°
(3) 1csoi6sn600 ta1n30
AD的长.
A
D
B
C.
11
应用生活
操场里有一个旗杆,老师让小明去测量旗杆高度, 小明站在离旗杆底部10米远处,目测旗杆的顶部,视 线与水平线的夹角为30度,并已知目高为1.65米.然
后他很快就算出旗杆的高度了。
你想知道小明怎样 算出的吗?
?
1.65米
3
A
B
6
3
A
C
(1)
O B
.
(2)
8
练习
1、在Rt△ABC中,∠C=90°,
BC 7,AC 21
求∠A、∠B的度数.
A
B
7
C
21
.
9
练习
2. 如图,在Rt△ABC中,∠C=900,若 tanA+tanB=4,S△ABC=8.求斜边AB的长.
A
b
C
B
a
.
10
练习
3、如图,△ABC中,∠C=900,BD平分
.
6
练习
2. 如图,在Rt△ABC中,∠ACB=900, CD⊥AB于D,已知∠B=300, 计算tan∠ACD+sin∠BCD的值.
A
D
B
C
.
7
例2、(1)如图,在Rt△ABC中, ∠C=90°,AB= 6 ,BC= 3。求∠A的度数。
(2)如图,已知圆锥的高AO等于圆锥的底面半
径OB的 倍,求α.
7.3特殊角的三角函数
.
1
sinA
B
斜边
A ∠A的邻边
cosA
∠A的对边
tanA
C
.
∠A的对边 斜边
∠A的邻边 斜边
∠A的对边 ∠A的邻边
2
特殊角三角函数值
.
3
仔细观察,说说你发现
特殊角这三张角表函有数哪值osα
tanα
30°
1 2
3 2
3 3
45°
2 2 2 2
30°
10米
.
12
1?scio n232s40+ 5+ta2 t4an5n + c3o s0 26 isn3 0 0
2、在Rt△ABC中,∠C=90°,化简
1-2sinAcosA
.
13
1
60°
3 2
1 2
3
.
4
例1、求下列各式的值. (1) cos260°+sin260°
(2)csoi ns4455 -tan45
.
5
练习
1. 求下列各式的值: (1)1-2 sin30°cos30° (2)3tan30°-tan45°+2sin60°
(3) 1csoi6sn600 ta1n30
