第3章+孪晶电子衍射图的分析
合集下载
电子显微镜 第三章 衍射花样分析

18
四、二次衍射花样
在较厚单晶体或两相合金中常产生二次衍射:
电子通过晶体时,产生的较强衍射线可以作 为新的入射线,在晶体中再次产生衍射。
d1晶体Ⅰ D1: 一次衍射斑点 D3: 二次衍射斑点
19
d2晶体Ⅱ
O D3 D2 D1
两相合金中的二次衍射
20
d2晶体Ⅱ
d1晶体Ⅰ
O D3 D2 D1
O
(a)
E (-200)
R1
O
B (200)
A (020)
C (220) D
OERS零阶劳厄带 测得R1=10mm,R2= 35.7mm,R3=38.1mm, R12:R22:R32=4:51:59; S属于{711},R属于 {731}; 测得R1,R2间夹角为820; 由夹角关系可得S点为 (-1 -7 1);由矢量关 系可得R点为(-3 7 1), T点(1 -7 1);晶带轴 [uvw]为[017]。
D1
O
D2
(b)
O (c)
D2 D1 (d) 两相合金二次衍射示意图
21
五、菊池花样
花样特点: 除规则斑点之外,还出现一些亮暗成对的 平行线条。
22
菊池线花样的产生及其几何特征
菊池线是由经过非弹性相干散射失 去较少能量的电子随后又受到弹性散射 所产生的。
23
入射束
入射束
试样
A B F C I
A
当晶体点阵常数较 大(即倒易面间距 较小),导致球可 同时与几层相互平 行的倒易面上的阵 点相交,产生几套 衍射斑。
5
当晶体试样较薄 时(即倒易点成杆 状) ,Ewald球可 能与几层相平行 的倒易面上的倒 易杆相交,产生 几套衍射斑。
四、二次衍射花样
在较厚单晶体或两相合金中常产生二次衍射:
电子通过晶体时,产生的较强衍射线可以作 为新的入射线,在晶体中再次产生衍射。
d1晶体Ⅰ D1: 一次衍射斑点 D3: 二次衍射斑点
19
d2晶体Ⅱ
O D3 D2 D1
两相合金中的二次衍射
20
d2晶体Ⅱ
d1晶体Ⅰ
O D3 D2 D1
O
(a)
E (-200)
R1
O
B (200)
A (020)
C (220) D
OERS零阶劳厄带 测得R1=10mm,R2= 35.7mm,R3=38.1mm, R12:R22:R32=4:51:59; S属于{711},R属于 {731}; 测得R1,R2间夹角为820; 由夹角关系可得S点为 (-1 -7 1);由矢量关 系可得R点为(-3 7 1), T点(1 -7 1);晶带轴 [uvw]为[017]。
D1
O
D2
(b)
O (c)
D2 D1 (d) 两相合金二次衍射示意图
21
五、菊池花样
花样特点: 除规则斑点之外,还出现一些亮暗成对的 平行线条。
22
菊池线花样的产生及其几何特征
菊池线是由经过非弹性相干散射失 去较少能量的电子随后又受到弹性散射 所产生的。
23
入射束
入射束
试样
A B F C I
A
当晶体点阵常数较 大(即倒易面间距 较小),导致球可 同时与几层相互平 行的倒易面上的阵 点相交,产生几套 衍射斑。
5
当晶体试样较薄 时(即倒易点成杆 状) ,Ewald球可 能与几层相平行 的倒易面上的倒 易杆相交,产生 几套衍射斑。
马氏体

点列是(111)*晶带,正六方点列为(100)*晶带,按标准图可以分别对以上花样标定。
钢中马氏体与奥氏的电子衍射分析
22
钢中两相电子衍射谱
1.以马氏体为已知相标后,确定精确相机常数: 正方形为特征基本平行四边形:
Rimm
o
di = K / Ri A
11.0 11.0 15.0 1.955 1.955 1.433
h4= h1+ h2 k4= k1+ k2 l4= l1+ l2 h3= h2-h1 k3= k2-k1 l3= l2-l1 根据以上数据可以确定带轴的指数 u,v,w 即按行列式确定:
h1 h1 h1 h1 h1
h2 h2 h2 h2 h2
uvw
即 u= k1l1-k2l1 v= l1h2-l2h1
h3= h2-h1 k3= k2-k1 l3= l2-l1
h4= h1+ h2 G1×G=[uvw] 2.180°不唯一性问题
k4= k1+ k2
l4= l1+ l2
180°不唯一性是由于倒易点阵平面和电子衍射谱显示 2 次旋转对称而产生的,因为我们无法区别 hkl
及 h kl 倒易点或衍射班点,但就晶体本身而言无需区分,但在确定晶体取向工作中是必须加以考虑 180°
二 电子衍射未知相分析基本程序:
①根据所研究的合金的主要元素的含量、熔炼、热处理、气相沉淀等工艺,查阅一切相关文献资料, 确定合金可能形成的合金相、亚稳相、间隙相。
②收集研制合金中相关资料,特别是其中合金相的晶体结构、晶体学的数据、制作(hkl)与 dhkl 表, 即晶体指数与晶面间距数据表。
③用 X 射线衍射法,分析 X 射线衍射峰的相关规律,初步确定该合金可能出现的物相及晶体结构。 ④了解电子衍射强度相关知识,因为有关晶体的点对称、微观对称及原子坐标的情况,都反映在晶体 单胞对电子散射的结构因数中,而与记录的衍射强度有关。
第3章 孪晶电子衍射图的分析
•
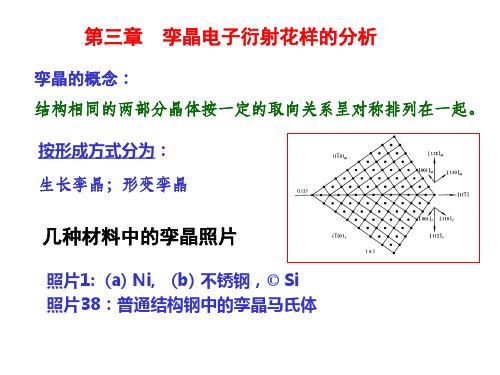
上述四种关系可简化为孪晶轴和孪生方向的两种旋转对
称关系。这样,只要将基体的倒易阵点绕孪晶轴或孪生
方向旋转1800即可得到同名孪晶的倒易阵点,此为衍射 分析的基础。
3.2 二次旋转孪晶的指数变换公式
二次旋转孪晶基体与孪晶倒易矢量的对称关系如图所示。
符号规定: gM—指数为(hkl)M的基体倒易矢量
t t t * 1 * 2 * 3 * 1 * 2 * 3
hU kV lW h tU k tV l tW
如何求解 htktlt ?
(3-1)
•
由gM、gT和gA三个倒易矢量共面,有:
g M g T mg A * * * t * t * t * (h h )a1 (k k )a2 (l l )a3 mHa1 mKa2 mLa3
b.c.c.晶体中,孪晶系统为:{112}<111> Hcp晶体中,孪晶系统为:{1012}<1011>
2. 孪晶按对称操作分类 (1)反映孪晶 以孪晶面为镜面的反映对称 以垂直于孪生方向的晶面为镜面的反映对称
(2)旋转孪晶
以孪晶轴为轴的旋转对称
以孪生方向为轴的旋转对称
旋转角度有600、900、1200、1800,其中以1800最常见。
同理,可得到任意晶系二次旋转孪晶的晶向指数变换公式
2U (uH vK wL ) u UH VK WL 2V vt (uH vK wL ) v (3-5) UH VK WL 2W wt (uH vK wL ) w UH VK WL
3.1 孪晶的晶体几何特征及倒易点阵 3.1.1 孪晶的晶体几何特征 1. 孪晶的基本要素: 孪晶面和孪生方向是用以描述孪晶特性的特征晶面和特征 方向,合称孪晶系统,亦称为孪晶的基本要素。 f.c.c.、b.c.c.、hcp结构金属晶体中,孪晶比较常见
电子衍射6(复杂电子衍射花样)—雨课堂课件

第三章 电子衍射
六、复杂电子衍射花样
菊池线的产生机理 入射电子在晶体中遭受非弹性散射→散射强度随散射方向而变 →遭受非弹性散射的电子再次受到晶面的弹性散射(Bragg衍射) →Kikuchi 线
第三章 电子衍射
六、复杂电子衍射花样
菊池线的几何特征 (1) hkl菊池线对与中心斑点到hkl衍射斑点的连线正交,而且菊
第三章 电子衍射
六、复杂电子衍射花样
所谓孪晶,通常指按一定取向关系并排生长在一起的同一物 质的两个晶粒。
上图中图a和b是CaMgSi相中的(102)孪晶在不同位向下的孪晶花样,图c 是CaMgSi相中另外一种孪晶的电子衍射花样,其孪晶面是(011)面;图d是 镁中常见的(10-12)孪晶花样。
第三章 电子衍射
池线对的间距与上述两个斑点的距离相等。
(2) 一般情况下,菊池 线对的增强线在衍射 斑点附近,减弱线在 透射斑点附近。
第三章 电子衍射
六、复杂电子衍射花样
(3) hkl菊池线对的中线对应于(hkl)面与荧光屏的截线。两条中 线的交点称为菊池极,为两晶面所属晶带轴与荧光屏的交点。
(4) 倾动晶体时,菊池 线好象与晶体固定在 一起一样发生明显的 移动。精度达0.1°
FHKL 2 [ f Au fCu fCu fCu ]2 [ f Au fCu ]2
都不消光
第三章 电子衍射
六、复杂电子衍射花样
有序 无序
第三章 电子衍射
六、复杂电子衍射花样
2、高阶劳厄带 ✓ 所有与零层倒易面平行的倒易平面统称为高层倒易面
✓ 高层倒易面中的倒易阵点由于某些原因也有可能与倒易球 相交而形成附加的电子衍射斑点,这就是高阶劳埃斑。
得上下两层倒易面与零层倒易面同时与反射球相交的机会增加; 3)当电子衍射花样不正,使得零层倒易面倾斜时,增加了高层倒易阵
孪晶的电子衍射分析方法和实例

h t h t 2 k = k + pu qv rw l t l
pu pv pw h qu qv qw k ru rv rw l
(1)
hkl 为基体某衍射斑点指数
据上述公式可知:当 ph qk rl =3n 时指数为 hkl 的孪晶斑点在基体倒易 点阵中的位置是从基体斑点 h k l 位移 2n 1 1 1 距离(指面心立方)或 n 1 1 2 距 离(指体心立方)于另一基体斑点重合。
二
面心立方孪晶分析实例: (图 1)
面心立方晶系孪晶面 pqr = 111 hkl T= h k l +
2 3
ph qk rl
11 1
Cu 是面心立方晶系 孪晶电子衍射谱分析步骤: 1. 用特征基本平行四边形法则标定基体电子衍射花样:
试标:
ri mm di A dhkl A hkl
10.6 2.028
Hale Waihona Puke 10.617.52.028 1.229
2.087 2.087 1.278 111
2 2 / 3a 2 0 p 2 pq pr 4 / 3a 2 2 2 0 qp q qr 2 / 3a 4 / a rp qr r 2 0 0 1/ c 2
h k l
a c 为点阵常数
pqr 为孪晶面。
Ti 孪晶面 102 孪晶电子衍射花样及分析示意图如下:
取特征基本平行四边形标定基体电子衍射谱
ri mm di A dhkl hkl
7.80 3.46
8.30
pu pv pw h qu qv qw k ru rv rw l
(1)
hkl 为基体某衍射斑点指数
据上述公式可知:当 ph qk rl =3n 时指数为 hkl 的孪晶斑点在基体倒易 点阵中的位置是从基体斑点 h k l 位移 2n 1 1 1 距离(指面心立方)或 n 1 1 2 距 离(指体心立方)于另一基体斑点重合。
二
面心立方孪晶分析实例: (图 1)
面心立方晶系孪晶面 pqr = 111 hkl T= h k l +
2 3
ph qk rl
11 1
Cu 是面心立方晶系 孪晶电子衍射谱分析步骤: 1. 用特征基本平行四边形法则标定基体电子衍射花样:
试标:
ri mm di A dhkl A hkl
10.6 2.028
Hale Waihona Puke 10.617.52.028 1.229
2.087 2.087 1.278 111
2 2 / 3a 2 0 p 2 pq pr 4 / 3a 2 2 2 0 qp q qr 2 / 3a 4 / a rp qr r 2 0 0 1/ c 2
h k l
a c 为点阵常数
pqr 为孪晶面。
Ti 孪晶面 102 孪晶电子衍射花样及分析示意图如下:
取特征基本平行四边形标定基体电子衍射谱
ri mm di A dhkl hkl
7.80 3.46
8.30
电子衍射图谱解析

根据(010)*面上的h0l(h+l=2n+1)斑点的分布 特征,001,102,201等斑点未有消光,表明晶体 不存在n滑移面,可确定此绿辉石晶体为有序结 构P2。
由8张电子衍射图构造的 (010)*倒易面上的取向分布
23
多次电子衍射谱
晶体对电子的散射能力强,衍射束往往可视为晶体内新的入射束而产 生二次或多次Bragg反射。这种现象称为二次衍射或多次衍射效应。
8
电子衍射谱的标定
电子衍射谱的标定是确定材料显微结构的重要步骤。一般地,这 一过程应遵循如下原则:
二维倒易平面中的任意倒易矢量 g 均垂直于晶带轴[uvw]方向(电子束反方向)
[uvw]• g hkl = uh + vk + wl = 0
若已知两倒易矢量 g1,g2,则晶带轴方向为
[uvw] = g1 × g 2 = [k1h2 − h1k2 , h1l2 − l1k2 , l1 k2 − k1l2 ]
3
TEM电子衍射的特点:
电子能量高,波长短,衍射角小,因而单晶的电子衍射 斑点坐落在一个二维网格的格点上,相当于一个二维倒易点 阵平面的投影,非常直观地显示出晶体的几何特征,使晶体 几何关系的研究变得简单方便。
原子对电子散射能力强(比X射线散射强度高104倍)。 一方面,高的散射强度可以实现微小区域(几个纳
5
TEM成像原理和电子衍射的获得
物 物镜
(物镜光 阑)
一次像 中间镜
(焦平面)
衍射谱
(视场光 阑)
二次像
投影镜
三次像
电子显微图象
电子衍射花样
TEM成像过程符合Abbe成像原理
平行电子束入射到周期结构物样 时,便产生衍射现象。
第三章 电子衍射

导出布拉格公式的构图。两个平行波(它们的波长为λ )以θ入射角照射
到晶面间距为dhkl的衍射晶体上,分别被上平面散射和下平面散射后产生
光程差,图3.2显示出两波的光程差为2 dhkl sin θ当光程差等于nλ时,波的
相长干涉将会发生,即:
2dhkl sin n
(3.1)
式中,θ是入射角或衍射角,它被定义为入射波与(hkl)晶面之间的夹角;
第三章 电子衍射
本章要点
1.电子衍射条件和X射线衍射相同,但电子衍射角极小和衍射 强度极高时,导致电子衍射在结构分析方面的特长。
2.多晶衍射环对应于晶面族{hkl}的衍射,而单晶衍射斑点对 应的是晶面组(hkl)的衍射,故单晶电子衍射花样在结构分析 中更具重要性。
3.单晶电子衍射花样就是某个零层倒易平面的放大像,因此单 晶电子衍射花样能直接反映晶体结构的对称性和周期性(平 移性)。
(a) 正点阵
(b) 倒易点阵
图3.4 体心立方正点阵的倒易点阵
3.2.2 物理条件
上述讨论指出,只有当入射束与点阵平面的夹角θ正好满足布拉格公 式时才有可能产生衍射,否则衍射强度为零 。实际并非如此,一则真实 晶体的大小是有限的,二则晶体内部还含有各式各样的晶体缺陷,因此 衍射束的强度分布有一定的角范围,相应的倒易阵点也是有一定的大小 和几何形状的。这意味着在尺寸很小的晶体中,倒易阵点要扩展,扩展 量与晶体的厚度(考虑一维的情况)成反比,当厚度为t,扩展量等于2/t, 倒易阵点扩展为倒易杆。考虑三维空间的情况,不同形状的实际晶体扩 展后的倒易阵点也就有不同的形状。对于透射电子显微镜中经常遇到的 试样,薄片晶体的倒易阵点拉长为倒易“杆”,棒状晶体为倒易“盘”, 细小颗粒晶体则为倒易“球”,如图3.5所示。
电子衍射图谱解析

测角74o基本相符。取(211)为B点指
பைடு நூலகம்
数,按矢量叠加原理,标定如图。
4 晶带轴指数
[uvw] → [110] × [2 1 1] = [1 13]
13
等价晶面的指数变换
采用d值比较法标定电子衍射谱,要使用JCPDS或JCPDF数据,但对等 价晶面只列出一个面指数,而如何确定其他等价晶面,标定电子衍射谱时 尤显重要。
20世界30年代,德国E.Ruska教授与其 导师研制出世界上第一台电子显微镜,为 开展多种电子衍射实验提供了保证。
70余年来,依托TEM的电子衍射实验, 为材料结构的研究发挥了难以估量的作用。 电子衍射与电子显微图象,以及成分分析结 合,对固体微观形貌、晶体结构以及化学组 成进行的研究,极大地丰富了固体物理、物 体化学、材料科学、地质矿物等学科的相关 知识,有力地促进了这些学科深入发展。
二次衍射的基本条件是:
g1 + g2 = g3
即:
h1k1l1 + h2k2l2 = h3k3l3
111
000
002
111
金刚石结构中,002 是禁止衍射,因二 次衍射使 002 衍射斑点通常出现。
24
六角密堆晶系中由二次衍射产生的附加斑点
012 002
012
011
001
011
010
000 010
− β1 )
2
其中
∆α = α2 − α1
∆β = β2 − β1
近似处理为: cosθ ≈ cos ∆α cos ∆β
α、β分别为双倾台记录的试样倾转角
20
一个新的Bi基超导相的结构确定
在Bi系氧化物超导体的研究中,发现一个新的物相。经EDS成分 分析,该物相为Bi4(SrLa)8Cu5O7)。下面是在电镜中绕C*轴倾转晶体获 得的一套电子衍射图谱,其倾转角分别标在每张衍射谱左下端。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2H (hU kV lW ) h HU KV LW 2 K kt (hU kV lW ) k HU KV LW 2L lt (hU kV lW ) l HU KV LW ht
(3-4)
该式适用于任意晶系二次旋转孪晶的晶面指数变换公式。 可以求出与基体倒易阵点(hkl)M同名的孪晶倒易阵点 (hkl)T在基体倒易点阵中的坐标。 因为基体与孪晶互为孪晶,也适用于把基体倒易阵点指 数变换为孪晶点阵中的指数
体心立方晶体孪晶的点阵对称关系 a) 以孪晶面为镜面的反映对称和以 孪生方向为轴的二次旋转对称
b) 以孪晶轴为轴的二次旋转对称和 以孪生方向垂直的晶面为镜面的 反映对称
3.1.2 孪晶倒易点阵的对称关系
晶体的正、倒点阵互为倒易,正点阵中存在的孪晶关 系,在相应的倒易点阵也一定存在孪晶关系。因此,有 正点阵中基体和孪晶同名指数的晶面具有对称关系,
© Si
孪晶斑点T1、T2;P处在孪晶马氏体周围高密度位错
本章内容
3.1 孪晶的晶体几何特征及倒易点阵
3.1.1 孪晶的晶体几何特征
3.1.2 孪晶倒易点阵的对称关系
3.2 二次旋转孪晶的指数变换公式 3.3 立方晶系孪晶电子衍射图的分析
3.3.1 立方晶系孪晶指数变换公式
3.3.2 面心立方晶体孪晶倒易阵点的分布特征 3.3.3 体心立方晶体孪晶倒易阵点的分布特征 3.3.4 立方晶体孪晶电子衍射图的标定
同理,可得到任意晶系二次旋转孪晶的晶向指数变换公式
2U u (uH vK wL ) u UH VK WL 2V t v (uH vK wL ) v UH VK WL 2W t w (uH vK wL ) w UH VK WL
相应的倒易矢量之间也一定有对称关系
正点阵中基体和孪晶同名的晶向有对称关系,相应的 倒易平面之间也一定有对称关系
孪晶晶体点阵所存在的四种对称关系可以用孪晶的倒 易矢量之间的关系来表达。见下图,
•
因为电子衍射图反映的是倒易点阵的某二维倒易截面, 所以,孪晶电子衍射图中衍射斑点的排列也反映孪晶的 上述四种关系。
rA Ua1 Va2 Wa3
下面的问题是: 建立hkt与htktlt之间的关系,并求 解 h tk tl t ?
•
由几何关系,有:
g M rA g T rA
(ha k a l a ) (U a1 V a 2 W a3 ) (h a k a l a ) (U a1 V a 2 W a3 )
第 3 章
孪晶的概念:ຫໍສະໝຸດ 孪晶电子衍射花样的分析结构相同的两部分晶体按一定的取向关系呈对称排列在一起。
按形成方式分为: 生长孪晶;形变孪晶
几种材料中的孪晶照片
照片1: (a) Ni, (b) 不锈钢,© Si 照片38:普通结构钢中的孪晶马氏体
(a) Ni
(b) 不锈钢
P孪晶中高密度位错
A、B、C为等倾条纹;S、Y等孪晶共格界面处,等倾条纹因s符号改变而改变 方向; T、P为非共格孪晶界,在P处显示近似垂直膜面的End-on位错列
h t m H h kt mK k l t m L l
(3-2)
•
将式(3-2)代入(3-1),有:
2(hU kV lW ) m( HU KV LW )
m 2(hU kV lW ) HU KV LW
(3-3)
•
将上式代入(3-2),有:
t t t * 1 * 2 * 3 * 1 * 2 * 3
hU kV lW h tU k tV l tW
如何求解 htktlt ?
(3-1)
•
由gM、gT和gA三个倒易矢量共面,有:
g M g T mg A * * * t * t * t * (h h )a1 (k k )a2 (l l )a3 mHa1 mKa2 mLa3
b.c.c.晶体中,孪晶系统为:{112}<111> Hcp晶体中,孪晶系统为:{1012}<1011>
2. 孪晶按对称操作分类 (1)反映孪晶 以孪晶面为镜面的反映对称 以垂直于孪生方向的晶面为镜面的反映对称
(2)旋转孪晶
以孪晶轴为轴的旋转对称
以孪生方向为轴的旋转对称
旋转角度有600、900、1200、1800,其中以1800最常见。
•
上述四种关系可简化为孪晶轴和孪生方向的两种旋转对
称关系。这样,只要将基体的倒易阵点绕孪晶轴或孪生
方向旋转1800即可得到同名的孪晶倒易阵点,这是衍射分 析的基础。
3.2 二次旋转孪晶的指数变换公式
二次旋转孪晶基体与孪晶倒易矢量的对称关系如图所示。
符号规定: gM—指数为(hkl)M的基体倒易矢量
* * * g M ha1 ka2 la3
gT—指数为(hkl)T的孪晶倒易矢量, htktlt是其在基体倒易点阵中的指数
t * t * t * gT h a1 k a2 l a3
gA—孪晶面所对应的倒易矢量,其指数为[HKL]* * * * g A Ha1 Ka2 La3 rA—孪晶轴,其指数为[UVW]
孪晶倒易矢量的对称操作
3. Bcc晶体孪晶的几何对称特征
体心立方晶体孪晶的点阵对称关系
(a) 以孪晶面为镜面的反映对称和以孪生方向为轴的二次旋转对称
(b) 以孪晶轴为轴的二次旋转对称和以孪生方向垂直的晶面为镜面的反映对称
[001]
[112]
[110]
[010]
(112)
[100] [111] (110)
3.1 孪晶的晶体几何特征及倒易点阵 3.1.1 孪晶的晶体几何特征 1. 孪晶的基本要素: 孪晶面和孪生方向是用以描述孪晶特性的特征晶面和特征 方向,合称孪晶系统,亦称为孪晶的基本要素。 f.c.c.、b.c.c.、hcp结构金属晶体中,孪晶比较常见
f.c.c.晶体中,孪晶系统为:{111}<112>
(3-4)
该式适用于任意晶系二次旋转孪晶的晶面指数变换公式。 可以求出与基体倒易阵点(hkl)M同名的孪晶倒易阵点 (hkl)T在基体倒易点阵中的坐标。 因为基体与孪晶互为孪晶,也适用于把基体倒易阵点指 数变换为孪晶点阵中的指数
体心立方晶体孪晶的点阵对称关系 a) 以孪晶面为镜面的反映对称和以 孪生方向为轴的二次旋转对称
b) 以孪晶轴为轴的二次旋转对称和 以孪生方向垂直的晶面为镜面的 反映对称
3.1.2 孪晶倒易点阵的对称关系
晶体的正、倒点阵互为倒易,正点阵中存在的孪晶关 系,在相应的倒易点阵也一定存在孪晶关系。因此,有 正点阵中基体和孪晶同名指数的晶面具有对称关系,
© Si
孪晶斑点T1、T2;P处在孪晶马氏体周围高密度位错
本章内容
3.1 孪晶的晶体几何特征及倒易点阵
3.1.1 孪晶的晶体几何特征
3.1.2 孪晶倒易点阵的对称关系
3.2 二次旋转孪晶的指数变换公式 3.3 立方晶系孪晶电子衍射图的分析
3.3.1 立方晶系孪晶指数变换公式
3.3.2 面心立方晶体孪晶倒易阵点的分布特征 3.3.3 体心立方晶体孪晶倒易阵点的分布特征 3.3.4 立方晶体孪晶电子衍射图的标定
同理,可得到任意晶系二次旋转孪晶的晶向指数变换公式
2U u (uH vK wL ) u UH VK WL 2V t v (uH vK wL ) v UH VK WL 2W t w (uH vK wL ) w UH VK WL
相应的倒易矢量之间也一定有对称关系
正点阵中基体和孪晶同名的晶向有对称关系,相应的 倒易平面之间也一定有对称关系
孪晶晶体点阵所存在的四种对称关系可以用孪晶的倒 易矢量之间的关系来表达。见下图,
•
因为电子衍射图反映的是倒易点阵的某二维倒易截面, 所以,孪晶电子衍射图中衍射斑点的排列也反映孪晶的 上述四种关系。
rA Ua1 Va2 Wa3
下面的问题是: 建立hkt与htktlt之间的关系,并求 解 h tk tl t ?
•
由几何关系,有:
g M rA g T rA
(ha k a l a ) (U a1 V a 2 W a3 ) (h a k a l a ) (U a1 V a 2 W a3 )
第 3 章
孪晶的概念:ຫໍສະໝຸດ 孪晶电子衍射花样的分析结构相同的两部分晶体按一定的取向关系呈对称排列在一起。
按形成方式分为: 生长孪晶;形变孪晶
几种材料中的孪晶照片
照片1: (a) Ni, (b) 不锈钢,© Si 照片38:普通结构钢中的孪晶马氏体
(a) Ni
(b) 不锈钢
P孪晶中高密度位错
A、B、C为等倾条纹;S、Y等孪晶共格界面处,等倾条纹因s符号改变而改变 方向; T、P为非共格孪晶界,在P处显示近似垂直膜面的End-on位错列
h t m H h kt mK k l t m L l
(3-2)
•
将式(3-2)代入(3-1),有:
2(hU kV lW ) m( HU KV LW )
m 2(hU kV lW ) HU KV LW
(3-3)
•
将上式代入(3-2),有:
t t t * 1 * 2 * 3 * 1 * 2 * 3
hU kV lW h tU k tV l tW
如何求解 htktlt ?
(3-1)
•
由gM、gT和gA三个倒易矢量共面,有:
g M g T mg A * * * t * t * t * (h h )a1 (k k )a2 (l l )a3 mHa1 mKa2 mLa3
b.c.c.晶体中,孪晶系统为:{112}<111> Hcp晶体中,孪晶系统为:{1012}<1011>
2. 孪晶按对称操作分类 (1)反映孪晶 以孪晶面为镜面的反映对称 以垂直于孪生方向的晶面为镜面的反映对称
(2)旋转孪晶
以孪晶轴为轴的旋转对称
以孪生方向为轴的旋转对称
旋转角度有600、900、1200、1800,其中以1800最常见。
•
上述四种关系可简化为孪晶轴和孪生方向的两种旋转对
称关系。这样,只要将基体的倒易阵点绕孪晶轴或孪生
方向旋转1800即可得到同名的孪晶倒易阵点,这是衍射分 析的基础。
3.2 二次旋转孪晶的指数变换公式
二次旋转孪晶基体与孪晶倒易矢量的对称关系如图所示。
符号规定: gM—指数为(hkl)M的基体倒易矢量
* * * g M ha1 ka2 la3
gT—指数为(hkl)T的孪晶倒易矢量, htktlt是其在基体倒易点阵中的指数
t * t * t * gT h a1 k a2 l a3
gA—孪晶面所对应的倒易矢量,其指数为[HKL]* * * * g A Ha1 Ka2 La3 rA—孪晶轴,其指数为[UVW]
孪晶倒易矢量的对称操作
3. Bcc晶体孪晶的几何对称特征
体心立方晶体孪晶的点阵对称关系
(a) 以孪晶面为镜面的反映对称和以孪生方向为轴的二次旋转对称
(b) 以孪晶轴为轴的二次旋转对称和以孪生方向垂直的晶面为镜面的反映对称
[001]
[112]
[110]
[010]
(112)
[100] [111] (110)
3.1 孪晶的晶体几何特征及倒易点阵 3.1.1 孪晶的晶体几何特征 1. 孪晶的基本要素: 孪晶面和孪生方向是用以描述孪晶特性的特征晶面和特征 方向,合称孪晶系统,亦称为孪晶的基本要素。 f.c.c.、b.c.c.、hcp结构金属晶体中,孪晶比较常见
f.c.c.晶体中,孪晶系统为:{111}<112>
