电机数学模型matlab仿真作业
基于MATLAB的电机仿真分析
基于MATLAB的电机仿真分析
摘要：电机是工业生产中常用的动力设备，对电机进行仿真分析可以帮助工程师们更好地了解电机的工作原理和性能特点。
本文将介绍基于MATLAB的电机仿真分析方法，并以直流电机为例进行仿真分析，通过仿真分析得出了电机的性能曲线和工作特性，为电机的设计和优化提供了参考。
关键词：电机；仿真分析；MATLAB；直流电机；性能曲线
一、引言
二、电机仿真分析的基本原理
电机的仿真分析是通过对电机的工作原理和性能参数进行数学建模，然后利用计算机软件对模型进行求解和分析。
在MATLAB中，可以通过建立电机的数学模型，然后利用工具箱中的仿真模块对电机进行仿真分析。
电机的数学建模包括电机的电气特性和机械特性两方面，其中电气特性包括电机的电路方程和电磁方程，机械特性包括电机的转子惯量、机械摩擦等参数。
通过建立完整的电机数学模型，可以对电机的性能进行准确地仿真分析。
1. 建立电机数学模型
2. 利用MATLAB进行仿真分析
在MATLAB中，可以利用Simulink工具箱对电机的数学模型进行仿真计算。
首先将电机的数学模型用Simulink建模工具进行建模，然后设置仿真参数，运行仿真模拟，得到电机的仿真结果。
通过仿真结果，可以得到电机的性能曲线、工作特性等重要参数。
3. 优化分析
根据电机的仿真结果进行分析和评估，对电机的性能进行优化。
可以通过修改电机的某些参数，重新进行仿真分析，得出最优的电机设计参数。
基于matlab永磁同步电机控制系统建模仿真方法
基于matlab永磁同步电机控制系统建模仿真方法摘要:永磁同步电机具有高效、高功率密度、低噪音等特点，在各种工业和民用应用中得到越来越广泛的应用。
本文基于matlab软件，建立了永磁同步电机控制系统的数学模型，并通过仿真验证了该模型的正确性。
在此基础上，分析了永磁同步电机控制系统的控制策略和参数调节方法，为实际应用提供了一定的参考。
关键词: matlab，永磁同步电机，控制系统，数学模型，仿真引言:永磁同步电机具有高效、高功率密度、低噪音等特点，在电动汽车、机器人、风力发电等领域得到越来越广泛的应用。
在永磁同步电机的控制中，控制系统的设计和参数调节是关键问题，直接影响永磁同步电机的性能和效率。
因此，建立永磁同步电机控制系统的数学模型，并进行仿真分析，对于实现永磁同步电机的精准控制和优化设计具有重要意义。
正文:1. 永磁同步电机的数学模型永磁同步电机的数学模型可以分为电磁模型和电路模型两部分。
其中，电磁模型描述永磁同步电机的电磁特性，电路模型描述永磁同步电机的电路特性。
永磁同步电机的电磁模型可以用矢量控制方法进行描述，电路模型可以用dq坐标系下的方程进行描述。
2. 永磁同步电机控制系统的设计永磁同步电机控制系统的设计包括控制策略和参数调节两个方面。
控制策略决定了永磁同步电机的运行方式和性能，参数调节则决定了控制系统的稳定性和精度。
控制策略一般分为开环控制和闭环控制两种。
开环控制适用于永磁同步电机的简单控制场合，例如启动、制动等。
闭环控制适用于永磁同步电机的高精度控制场合，例如速度、位置、力矩等。
参数调节方法主要有PID调节、自适应控制、模糊控制等。
PID调节是最常用的参数调节方法，适用于永磁同步电机的大多数控制场合。
自适应控制和模糊控制适用于永磁同步电机的非线性控制场合。
3. 基于matlab的永磁同步电机控制系统仿真基于matlab软件，可以快速建立永磁同步电机控制系统的数学模型，并进行仿真分析。
matlab中关于永磁同步电机的仿真例子
matlab中关于永磁同步电机的仿真例子MATLAB中关于永磁同步电机的仿真例子1. 基本电机参数配置在进行永磁同步电机的仿真前，需要先配置基本的电机参数，包括电机的额定功率、额定电压、额定转速等。
2. 电机模型的建立使用MATLAB中的Simulink模块，可以方便地建立永磁同步电机的模型。
可以利用Simulink库中的电机模块，如Permanent Magnet Synchronous Machine来构建电机模型。
3. 电机控制策略的设计在建立电机模型后，需要设计适合的控制策略来控制电机的运行。
常见的控制策略包括：•PI控制：使用Proportional-Integral (PI) 控制器来调节电机的转速和电流。
•磁场定向控制（FOC）：通过测量电机转子位置和速度，将三相交流信号转换为等效直流信号，实现对电机的控制。
4. 电机仿真完成电机模型和控制策略的设计后，可以进行电机的仿真。
使用Simulink中的仿真工具，可以模拟电机的运行情况，并观察电机的转速、电流、转矩等参数的变化过程。
5. 仿真结果分析根据仿真结果，可以分析电机的性能指标，包括：•转速响应：电机在各种工况下的转速响应特性。
•转矩输出：电机在不同负载情况下的转矩输出。
•电流波形：电机的相电流波形及电流变化情况。
•功率因数：电机在运行过程中的功率因数变化。
6. 优化和改进根据仿真结果分析的情况，可以针对电机的性能进行优化和改进，例如：•调整控制策略的参数，提高转速响应和控制精度。
•优化电机的电气设计，提高效率和功率密度。
•添加降噪措施，减少电机的噪声和振动。
7. 结论根据电机仿真的结果和优化改进的情况，得出结论，总结永磁同步电机的特性和性能，并对未来的研究方向进行展望。
以上是关于MATLAB中关于永磁同步电机的仿真例子的一些列举和详细讲解，通过Simulink工具的电机模型建立、控制策略设计、仿真结果分析和优化改进等步骤，可以深入了解和研究永磁同步电机的性能和特性，并为电机控制系统的设计和优化提供有力支持。
matlab2010b电机仿真
matlab2010b电机仿真在MATLAB 2010b中进行电机仿真可以使用Simulink和Simscape Power Systems工具箱。
下面是一个简单的示例，演示了如何使用Simulink建立并运行一个电机仿真模型。
1. 打开MATLAB 2010b软件。
2. 在Simulink库浏览器中找到电机建模组件。
可以在“Simulink”标签下的“Electrical”部分找到一些相关组件，如“Induction Motor”和“DC Motor”等。
3. 双击相应的组件，将其拖动到模型编辑器中。
可以使用这些组件来构建一个电机模型。
4. 连接电机建模组件的输入和输出端口。
例如，可以将一个输入信号传递到电机的控制端口，将输出信号连接到电机的运动端口。
5. 配置电机的参数。
双击电机组件，可以打开参数对话框，并设置电机的参数，如转矩、速度、电压等。
6. 添加其他必要的组件和连接，以完成电机模型的搭建。
7. 单击模型编辑器中的“运行”按钮，开始仿真电机模型。
可以通过观察仿真结果和信号波形来分析电机的行为和性能。
注意：MATLAB 2010b版本可能需要安装额外的工具箱才能进行电机仿真。
可以在软件安装目录下的“toolbox”文件夹中查找相关的工具箱，并确保其已经安装和激活。
此外，Simscape Power Systems工具箱也提供了一系列电机模型和仿真组件，可以用于建立更精细和复杂的电机系统模型。
可以按照类似的步骤，使用Simscape Power Systems工具箱中的电机组件进行仿真。
希望以上信息对您有帮助！。
matlab电机仿真
学院：机电学院班级：机自09-2班姓名：谢伟学号：03090943报告关于电机互锁的仿真报告我们要先明确什么叫互锁互锁，说的是几个回路之间，利用某一回路的辅助触点，去控制对方的线圈回路，进行状态保持或功能限制。
一般对象是对其他回路的控制.例如：上图是一个很典型的互锁电路图，实现的功能是电机的正反转，当实现正传的时候，关闭断路器Qs，按下正向按钮SB3，SB3的常闭触点断开，是KM2不工作，SB3的常开触点闭合，是电磁铁KM1得电，线圈KM1吸合实现自锁，电机实现正向转动，同时线圈的常闭触点断开，保证KM2不工作，防止电路短路导致的电路故障，当实现反向转动时，按下反向按钮SB2，SB2的常闭触点断开，KM1不得电，电机无法正向转动，SB2的常开触点闭合，KM2得电，线圈KM2吸合实现自锁，电机实现反向转动，同时线圈KM2 的常闭触点断开，保证KM1不工作。
以上当电机正转时保证电机反转电路断开，反转保证正转电路断开的方法叫作互锁。
利用的是两个常闭辅助触点来实现其功能的。
在实际工作中，由于坏境是变化的，负载也随着环境的变化而变化，为了测试电动机在不同负载环境下的运转情况，我们必须测试一系列不同的或者双向的负载加在电机轴上的电机反应。
此外，一个理想的负载应该回归到发电机从电网上吸收的能量。
这样的负载应该有一个有四象限的DC2或者DC4的直流电产生，这测试的时候应该通过刚性轴这两个电动机进行机械耦合连接。
因此，这个仿真实验需要两个电动机模型，AC4电动机和DC2电动机。
其中，AC4电动机是一个直流三相感应异步电动机，DC2是一个直流单向整流电动机。
在这样的系统里，一个电动机负责速度参数的设定，一个电动机负责力矩参数的设定.同时每个电动机可以充当马达或者发电机。
DC2的额定参数一般是3马力，240伏特，1800转每分钟。
AC4电动机的额定参数是3马力，380伏特，60赫兹，4级。
上图为直流电动机的工作原理图上图为桥式整流电路图注意：对于两个电动机的信号控制可以使用用户界面的最下方的机械输入菜单，下图显示了再马达—发电机结构中如何去模拟刚性轴的互相连接。
matlab机电系统仿真大作业
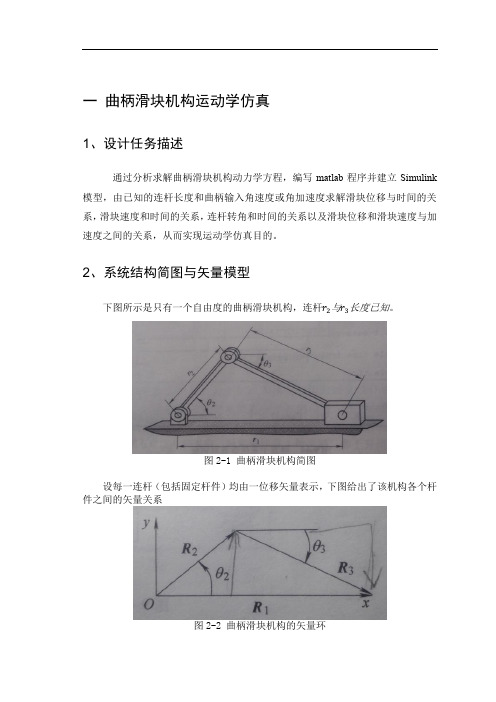
一曲柄滑块机构运动学仿真1、设计任务描述通过分析求解曲柄滑块机构动力学方程，编写matlab程序并建立Simulink 模型，由已知的连杆长度和曲柄输入角速度或角加速度求解滑块位移与时间的关系，滑块速度和时间的关系，连杆转角和时间的关系以及滑块位移和滑块速度与加速度之间的关系，从而实现运动学仿真目的。
2、系统结构简图与矢量模型下图所示是只有一个自由度的曲柄滑块机构，连杆r2与r3长度已知。
图2-1 曲柄滑块机构简图设每一连杆（包括固定杆件）均由一位移矢量表示，下图给出了该机构各个杆件之间的矢量关系图2-2 曲柄滑块机构的矢量环3．匀角速度输入时系统仿真3.1 系统动力学方程系统为匀角速度输入的时候，其输入为ω2=θ2,输出为ω3=θ3,θ3；v 1=r 1,r 1。
(1) 曲柄滑块机构闭环位移矢量方程为:R 2+R 3=R 1(2) 曲柄滑块机构的位置方程{r 2cos θ2+r 3cos θ3=r 1r 2sin θ2+r 3sin θ3=0(3) 曲柄滑块机构的运动学方程通过对位置方程进行求导，可得{−r 2ω2sin θ2−r 3ω3sin θ3=r 1r 2ω2cos θ2+r 3ω3cos θ3=0由于系统的输出是ω3与v 1，为了便于建立A*x=B 形式的矩阵，使x=[ω3v 1],将运动学方程两边进行整理，得到{v 1+r 3ω3sin θ3=−r 2ω2sin θ2−r 3ω3cos θ3=r 2ω2cos θ2将上述方程的v1与w3提取出来，即可建立运动学方程的矩阵形式(r 3sin θ31−r 3cos θ30)(ω3v 1)=(−r 2ω2sin θ2r 2ω2cos θ2) 3.2 M 函数编写与Simulink 仿真模型建立3.2.1 滑块速度与时间的变化情况以及滑块位移与时间的变化情况仿真的基本思路：已知输入w2与θ2，由运动学方程求出w3和v1，再通过积分，即可求出θ3与r1。
matlab-电机控制综合仿真任务书
任务一：利用Simpowersystem里面自带的DC电机模块，完成他励直流电机单闭环调速仿真，速度调节用PI控制方法，要求封装PI模块，给定速度100rad/s，负载由空载到1s时跳变到20N。
调节不同的PI参数，观察仿真结果总结速度波形、转矩波形的变化规律。
另外要求将scope图中的4条曲线参数导出到工作空间，并用subplot和plot函数画在同一个窗口中，每个子图加上对应的标题。
写报告时必须仿真模型图和绘制的曲线图电机相关参数如下：任务二：利用Simulink 基本模块搭建他励直流电机闭环调速系统直流电机子模块，根据以下电机数学模型搭建e M a T C I =Φe L m d T T B J dtωω--= 电机模块要求封装，参数20.05kg m J =⋅，0.02N m s m B =⋅⋅，165m C =，0.01Wb f Φ=点击封装模块时输入。
PI 控制模块要求封装，调节不同的PI 参数，得到不同的速度波形。
写报告时，要给出仿真模型和不同PI 参数的速度波形。
任务三：修改任务二的模型，使其PI 控制参数来自外部变量设定，将速度偏差的仿真结果导出到工作空间（workspace ），用m 文件编写一段循环程序调用任务二的仿真模型（调用函数为sim ），在m 文件中实现对PI 参数的调整，处理数据，得到满意的控制参数，绘制仿真结果曲线图。
M 文件中包含：设定PI 参数――调用仿真模型――速度偏差的最后100个数据点平均值是否小于某个设定值eps ――不满足，则修改PI 参数（用循环的方式修改）……最后用plot 画出速度和转矩波形，用subplot 将两个图画在一个窗口。
求数组长度函数length()，求平均值函数mean()，Subplot ，plot任务四：异步电机调速方法仿真从Help－Demos－SimPowerSystems－General Demos中调出AC Motor Drive - Vector Control (discrete) （power_acdrive.mdl）和Asynchronous Machine （power_pwm.mdl），运行看看结果，并找到相应的模块在哪，并试着自己建立同样的模型。
matlab中关于永磁同步电机的仿真例子
matlab中关于永磁同步电机的仿真例子摘要：一、Matlab中永磁同步电机仿真概述二、永磁同步电机仿真模型建立1.参数设置2.控制器设计3.仿真结果分析三、SVPWM算法在永磁同步电机仿真中的应用四、案例演示：基于DSP28035的永磁同步电机伺服系统MATLAB仿真五、总结与展望正文：一、Matlab中永磁同步电机仿真概述Matlab是一款强大的数学软件，其在电机领域仿真中的应用广泛。
永磁同步电机（PMSM）作为一种高效、高性能的电机，其控制策略和性能分析在Matlab中得到了充分的体现。
利用Matlab进行永磁同步电机仿真，可以有效验证控制策略的正确性，优化电机参数，提高系统性能。
二、永磁同步电机仿真模型建立1.参数设置：在建立永磁同步电机仿真模型时，首先需要设定电机的各项参数，如电阻、电感、永磁体磁链等。
这些参数可以根据实际电机的设计值进行设置，以保证模型与实际电机的特性一致。
2.控制器设计：控制器的设计是电机仿真模型的核心部分。
常见的控制器设计包括矢量控制（也称为场导向控制，Field-Oriented Control, FOC）、直接转矩控制（Direct Torque Control, DTC）等。
在Matlab中，可以利用现有的工具箱（如PMSM T oolbox）方便地进行控制器的设计和仿真。
3.仿真结果分析：在完成控制器设计后，进行仿真实验。
通过观察电机的转速、电流、转矩等参数的变化，可以评估控制器的性能。
同时，可以利用Matlab的图像绘制功能，将仿真结果以图表的形式展示，便于进一步分析。
三、SVPWM算法在永磁同步电机仿真中的应用SVPWM（Space Vector Pulse Width Modulation）是一种用于控制永磁同步电机的有效方法。
通过在Matlab中实现SVPWM算法，可以方便地对比不同控制策略的性能。
在仿真过程中，可以观察到SVPWM算法能够有效提高电机的转矩波动抑制能力，减小电流谐波含量，从而提高电机的运行效率。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
MATLAB在异步电机仿真中的应用摘要：在同步旋转坐标系上(M、 T 坐标系) 推导出异步电机数学模型, 并应用 MATLAB/ SIMULINK 对其进行实际仿真，并且运用电机的参数验证了所建模型的正确性，并得出电机转速、电机稳定运行三相电流、电机转矩图。
关键词：仿真异步电机数学模型 MATLAB一、引言Matlab 语言是一种面向科学工程计算的高级语言，它集科学计算自动控制信号处理神经网络图像处理等功能于一体，是一种高级的数学分析与运算软件，可用作动态系统的建模和仿真。
目前，电机控制系统越来越复杂，不断有新的控制算法被采用仿真是对其进行研究的一个重要的不可缺少的手段 Matlab 的仿真研究功能成功方便地应用到各种科研过程中。
本文将结合Matlab/Simulink 的特点，介绍异步电动机在同步旋转坐标系（M 、T 坐标系）的数学建模与仿真方法在建模与仿真之后，可利用Simulink 将模型封装起来，使用时只需调用该模型并输入电机参数即可，为变频调速系统及控制方法的仿真研究提供了一种性能可靠使用方便的电机通用仿真模型。
异步电机的动态模型是高阶、非线性、强耦合的多变量系统 ,通过坐标变换的方法对其进行简化后 , 模型简单得多, 但其非线性、多变量的本质并未改变。
描述电机的仍是一组高阶、变系数的微分方程,用传统的方法对其进行仿真分析并非易事。
为了解决这一难题,本文利用异步电动机在同步旋转坐标系上(M、T 坐标系)的电压方程、磁链方程、转矩方程、运动方程实现了异步电动机的模型。
建立好数学模型之后。
利用MATLAB/SIMULINK仿真软件成功搭建在同步旋转坐标系下的电机的数学模型。
使得模型的建立更加简洁、明了,充分利用MATLAB/ SIMULINK提供的模块,建立了普通异步电动机的仿真模型,并对实际电机进行了仿真。
二、异步电机的仿真数学模型利用MATLAB 进行电机运行状态仿真,最为关键的是建立起一个方便于仿真的电机模型。
在本文的实例中,将在同步旋转两相坐标系下对一个直接接入三相电网的异步鼠笼电机建立一个可方便用于SIMULINK仿真的电机模型。
为了区分于一般的同步旋转 d、q 坐标系统,这里采用M、T坐标轴代替d、q轴,且令M 轴与电机中转子总磁链ψ2方向一致(转子总磁链ψ2等于气隙磁链ψg 与转了漏磁链ψ21之和)，即把M轴定向到ψ2的方向。
由于ψ2固定在M轴方向上,所以转子磁链在T轴方向上就没有分量, 即ψM2=ψ2。
而转换到两相同步旋转坐标系统的一个突出优点是:当A 、B 、C 三相系统中的变量是正弦波时, M 、T 坐标变量是直流量。
111111um r im p m t ψψω=+- （1）111111ut r it p t m ψψω=+-（2） 2222um r im p ψ=+ （3） 2222(12)ut r it ψωω=+- （4） 1112m L im Lmim ψ=+ （5） 1112t L it Lmit ψ=+ （6） 2221L im Lmim ψ=+ （7）0221L it Lmit =+ （8）式中：1r 、2r 为定、转子电阻；1L 、2L 为定、转子自感；m L 为定、转子间互感；1ω为定子旋转磁场的速度；2ω为转子角速度；1m u 、1t u 、2m u 、2t u 为M 、T 轴定、转子电压；1m i 、1t i 、2m i 、2t i 为M 、T 轴定、转子电流；1m ψ、1t ψ为M 、T 轴定子磁链；ψ2为M 轴转子磁链；p 为微分算子。
将式（5）（6）（7）代入式（1）（2）（3）（4）得电压方程为：1111111111111111200220220(12)0(12)222um um r pL L pLm Lm im ut ut L r pL Lm pLm it um pLm r pL im ut Lm L r it ωωωωωωωω+--⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦（9） 由式（7）可得：22122Lmim im L L ψ=- （10）由式（8）可得：212Lmit it L =- （11）将式（10）代入式（9）中的第三个表达式可得： 22()2122r r p Lmim L L ψ+= （12）将式（10）（11）代入式（9）中的第四个表达式可得：21(12)22L it r Lm ωωψ=- （13）将式（10）（11）（12）代入式（9）中的第一个表达式可得： ()11112R pL im um Lit A ωψ+=++ （14）其中：1222LmLm R r r L L =+，12LmLm L L L =-，122LmA r L L = 将式（10）（11）代入式（9）中的第二个表达式可得：(1)111112r pL it ut Lim B ωωψ+=-+ （15） 其中：2LmB L =转矩方程为：212LmTe Npit L ψ= （16）运动方程为；2J d Te Tl Np dtω-= （17）Te 为电磁转矩；Tl 为负载转矩；Np 为电机级对数；J 为电机组转动惯量。
由（12）-（17）是以、、、为输入和为输出的异步电动机的数学模型。
建立的异步电动机的数学模型。
由（12）-（17）可以方便地画出电机在M 、T 坐标下的系统结构图，如图1所示。
图1 系统结构图由（12）-（17），我们可得图2所示异步电机在二相同步旋转坐标系 ( M 、T 坐标系)的动态结构图为。
图2 异步电动机在二相同步旋转坐标系（ M 、T 坐标系）下的动态结构图动态结构图2中参数值计算如下：12LmLmL L L =-=0.0344038， 1222LmLmR r r L L =+=7.2997338，122Lm A r L L ==6.14504，2LmB L ==0.9702， Gain5中的增益为2LmNp L =1.940387，Gain6中的增益为602*pi=9.5541， Gain7中的增益为22L r Lm=0.31812，。
三、 Simulink 下仿真异步电动机的数学模型的建立为了将电机仿真模型封装成与实际电机相同的形式，即输入为三相交流电压 定子旋转磁场速度和负载转矩，输出为电机转速三相定子电流 电磁转矩，在仿真模型的输入端增加了三相静止电压转换到两相旋转电压的转换模块，在输出端增加了两相旋转电流转换到三相静止电流的转换模块，如图3、4所示建立电压变换子模块和电流变换子模块。
电压变换子模块实现三相静止电压转换到两相旋转电压。
电流变换子模块实现两相旋转电流转换到三相静止电流。
（1） 电压变换子模块三相静止电压a111U Ub Uc 、、转换到两相同步旋转电压m 1t1U U 、的变换为：1111cos sin 12221sin cos 13330122Ua Um Ub Ut Uc θθθθ⎡⎤--⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦⎣⎦⎢⎥-⎣⎦⎢⎥⎣⎦ 参数θ为旋转坐标系M 轴与静止坐标系α轴之间的夹角。
在SIMULINK 中建立的此模块如下图2所示。
图3电压转换子模块由变换关系式在此模块中求得三相静止电压a111U Ub Uc 、、与两相同步旋转电压m 1t1U U 、的关系为：所以在此模块中Sine Wave3- Sine Wave8的函数为（2） 电流变换子模块两相同步旋转电流1im 、1it 转换到三相静止电流111ia ib ic 、、的变换为： 参数θ为旋转坐标系M 轴与静止坐标系α轴之间的夹角。
在SIMULINK 中建立的此模块如下图3所示。
101cos sin 1213-1sin cos 1322113--22ia im ib it ic θθθθ⎡⎤⎢⎥⎢⎥⎡⎤-⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦图4电流转换子模块由变换关系式在此模块中求得两相同步旋转电流1im 、1it 与三相静止电流111ia ib ic、、的关系为：所以在此模块中Sine Wave1- Sine Wave6中的函数为然后将整个图2封装成一个模块，即图5中所示的电机仿真模型环节。
至此，异步电机的仿真模型就已完成。
从图5可看出整个仿真模型被封装成一个有五个输入量、五个输出量的环节。
在使用该仿真模型时只需输入相应的电机参数 r1、r 2、L1、L2、LM、NP、J即可以进行仿真。
图5 封装后的电机模型四、仿真实例一台异步电动机的实际参数如下：，，，，，，，，，，，，。
按图4给异步电机的、、直接加入380V、50HZ,加入1440*2π相差2π/3的三相正弦电压信号，由于是同步旋转，因此给1/60=150.8的阶跃信号，电机空载起动。
起动过程的转速、电磁转矩的波形如图6所示。
图6加380V、50Hz的额定电压起动时的转矩、转速图给异步电动机模型施加380V、50HZ,相差2π/3的三相正弦电压信号，让其空载起动，到1S时再加入10的负载转矩，仿真该电机的启动过程的电机的转速、电机稳定运行三相电流、电机转速图如图7-9所示。
图7 电机转速图图8 电机稳定运行三相电流图9 电机转矩图五、结束语本文对异步电动机在同步旋转坐标系（M、T坐标系）及直流电动机的模型进行了仿真，并验证了电机模型的正确性，仿真的各种变量结果稳定可靠。
由于把电机模型封装成一个模块，因此不必关心电机的内部结构，只需把电机模型从库元件中调出并输入相应的电机参数就可方便地应用到电机变频调速系统及控制方法的仿真研究中，具有广泛的应用价值。
六、参考文献［1］陈坚.交流电机数学模型及调速系统［M］.北京：国防工业出版社，1991. ［2］陈伯时.电力拖动自动控制系统［M］.北京:机械工业出版社,1990［3］薛定宇.基于matlab/simulinK 的系统仿真技术与应用［M］.北京:清华大学出版社,2001.。