非最小相位系统
合集下载
非最小相位
非最小相位1. 什么是非最小相位？非最小相位（non-minimum phase）是信号处理和控制系统中常用的一个概念。
在信号处理中，每个系统都有一个冲激响应，冲激响应可以表示系统的频率特性。
非最小相位系统的冲激响应具有比最小相位系统更多的波动和峰值。
在信号处理领域，最小相位系统是指具有幅度响应没有零点的系统。
而非最小相位系统则具有幅度响应存在零点的特点。
零点可以导致相位响应的不稳定性，并且在频域上引入额外的波动。
2. 非最小相位的特性非最小相位系统具有以下特性：a. 频响波动非最小相位系统的幅度响应会在某些频率范围内出现大幅波动。
这是由于零点的存在使得系统在这些频率处不稳定。
频响波动可能会引入不可预测的结果，从而影响系统的性能。
b. 峰值传输延迟非最小相位系统的冲激响应中会出现峰值，这导致信号延迟。
峰值传输延迟会使得信号的处理时间增加，从而影响系统的实时性和响应速度。
c. 零相位频率非最小相位系统具有零相位频率，即在这个频率下系统的相位为0度。
这可能会导致相位失真，在特定频率下信号的相位与原始信号的相位不同。
3. 非最小相位系统的应用非最小相位系统被广泛应用于信号处理、控制系统等方面。
a. 音频处理在音频处理中，非最小相位系统可以用于实现音频效果，如均衡器、滤波器等。
这些效果常常需要调整幅度响应和频率特性，通过引入非最小相位特性可以实现更多的音频效果。
b. 通信系统在通信系统中，非最小相位系统可以用于均衡器的设计。
均衡器可以补偿信号在传输过程中受到的失真。
非最小相位均衡器可以更好地处理传输信号中的频率失真和相位失真，提高数据传输的可靠性。
c. 控制系统在控制系统中，非最小相位系统可以用于控制器的设计。
非最小相位控制器可以引入额外的相位延迟，从而改变控制系统的相位特性。
这对一些特殊的控制系统设计有重要的应用，如自适应控制、鲁棒控制等。
4. 如何处理非最小相位系统？处理非最小相位系统时，我们通常采用以下方法：a. 预失真通过在输入信号上应用适当的预失真，可以消除非最小相位系统的频响波动和相位失真。
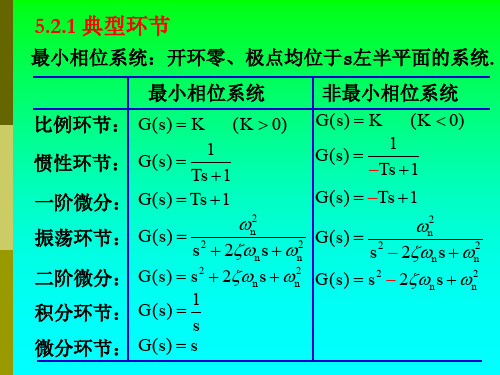
第四节最小相位系统与非最小相位系统
j5 (w)
由图可知最小相位系统是指在 具有相同幅频特性的一类系统 中，当w从0变化至∞时，系统
10
T2 的相角变化范围最小，且变化 的规律与幅频特性的斜率有关 系(如 j1(w) )。而非最小相位系 统的相角变化范围通常比前者
w 大(如j2(w)、j3(w)、j5(w))；
或者相角变化范围虽不大，但 相角的变化趋势与幅频特性的
-4.6
-2.3
0
2.3
数幅频特性的斜率。 4.6 u=ln(ww0)
上述公式称为伯德公式。该式说明对于最小相位系统，其幅频特
性与相频特性紧密联系的，当给定了幅频特性，其相频特性也随
之而定，反之亦然。因此，可只根据幅频特性（或只根据相频特
性）对其进行分析或综合；而非最小相位系统则不然，在进行分
析或综合时，必须同时考虑其幅频特性与相频特性。
最小相位系统与非最小相位系统
Sunday, July 12, 2020
1
最小相位系统和非最小相位系统
最小相位系统和非最小相位系统 定义：在右半S平面上既无极点也无零点，同时无纯滞后环节 的系统是最小相位系统，相应的传递函数称为最小相位传递函 数；反之，在右半S平面上具有极点或零点，或有纯滞后环节 的系统是非最小相位系统，相应的传递函数称为非最小相位传 递函数。 在幅频特性相同的一类系统中，最小相位系统的相位移最小， 并且最小相位系统的幅频特性的斜率和相频特性的角度之间具 有内在的关系。
u
e e u
-u
2
2
ln ctgh = ln
2
e - e u
-u
2
2
为加权函数，曲线如图
Sunday, July 12, 2020
6
由图可知最小相位系统是指在 具有相同幅频特性的一类系统 中，当w从0变化至∞时，系统
10
T2 的相角变化范围最小，且变化 的规律与幅频特性的斜率有关 系(如 j1(w) )。而非最小相位系 统的相角变化范围通常比前者
w 大(如j2(w)、j3(w)、j5(w))；
或者相角变化范围虽不大，但 相角的变化趋势与幅频特性的
-4.6
-2.3
0
2.3
数幅频特性的斜率。 4.6 u=ln(ww0)
上述公式称为伯德公式。该式说明对于最小相位系统，其幅频特
性与相频特性紧密联系的，当给定了幅频特性，其相频特性也随
之而定，反之亦然。因此，可只根据幅频特性（或只根据相频特
性）对其进行分析或综合；而非最小相位系统则不然，在进行分
析或综合时，必须同时考虑其幅频特性与相频特性。
最小相位系统与非最小相位系统
Sunday, July 12, 2020
1
最小相位系统和非最小相位系统
最小相位系统和非最小相位系统 定义：在右半S平面上既无极点也无零点，同时无纯滞后环节 的系统是最小相位系统，相应的传递函数称为最小相位传递函 数；反之，在右半S平面上具有极点或零点，或有纯滞后环节 的系统是非最小相位系统，相应的传递函数称为非最小相位传 递函数。 在幅频特性相同的一类系统中，最小相位系统的相位移最小， 并且最小相位系统的幅频特性的斜率和相频特性的角度之间具 有内在的关系。
u
e e u
-u
2
2
ln ctgh = ln
2
e - e u
-u
2
2
为加权函数，曲线如图
Sunday, July 12, 2020
6
零度根轨迹非最小相位系统
问题。由于它是一种图解求根的方法，比较直观，避免了求解高阶系统
特征根的麻烦，所以，根轨迹法在工程实践中获得了广泛的应用。 采用根轨迹法分析和设计系统，必须绘制出根轨迹图。用数学解析
法去逐个求出闭环特征方程的根再绘制根轨迹图，十分困难且没有意义。
重要的是找到一些规律，以便根据开环传递函数与闭环传递函数的关系 以及开环传递函数零点和极点的分布，迅速绘出闭环系统的根轨迹。这 种作图方法的基础就是根轨迹方程。
第四章 根轨迹法
二、根轨迹方程
[例] 闭环传递函数为
( s) G(s) 1 G( s) H ( s)
R( s )
G( s) H ( s)
C ( s)
闭环特征方程是 1 G(s) H (s) 0
根轨迹增益
就其实质来说，根轨迹方程就是闭环的特征方程式 系统开环 传递函数 开环传递函数化成如下形式： 零点 m
K ( s z1 )(s z 2 ) ( s z m ) G( s) H ( s) ( s p1 )(s p 2 ) ( s p n )
K (s zi )
i 1
(s p
j 1
n
j
)
系统开环传 递函数极点
第四章 根轨迹法
i 1 j 1
m
n
0
s2 p2
(s 2 p1 ) (s2 p2 ) 180
s2 p1
s2
满足相角条件，所以s2在根轨迹上，即s2是该系统的闭环极 点。
第四章 根轨迹法
根轨迹方程 G(s)H(s) 1
G (s)H(s) K
' i 1 n i 1
(s z )
第12讲bode最小相位系统和非最小相位系统
(1)对数坐标图 (Bode diagram or logarithmic plot) (2)极坐标图 (Polar plot) (3)对数幅相图 (Log-magnitude versus phase plot)
对数幅频特性 对数频率 特性曲线
相频特性
20log G( j) dB G( j) ()
R(s) + -
E(s)
G(s)
C(s)
假设系统的开环传递函数为
G(s)
K (T1s 1)(T2s 1)(Tms 1) s (T1s 1)(T2s 1)(Tn s 1)
图5-21单位反馈控制系统
G(
j)
(
K (T1 j 1)(T2 j 1)(Tm j j) (T1 j 1)(T2 j 1)(Tn
n
n
时
40 log 40 log1 0 n
dB
所以高频渐近线与低频渐近线在
8
处相交。这个频率就是上述二阶因子的转角频率。
谐振频率谐振峰值
d g() 2(1 2 )(2 ) 2(2 )2 1 0
dt
n2
n2
n n
g ( )
2
2 n
(1
2 n
2
2)2
4
2 (1
2)
G( j)
n
n
L()
20 log
1 2 (
j
1
)
(
j
)2
20log
(1
2 n2
)2
(2
n
)2
n
n
低频渐近线为一条0分贝的水平线
在低频时，即当 n
-20log1=0dB
在高频时，即当 n
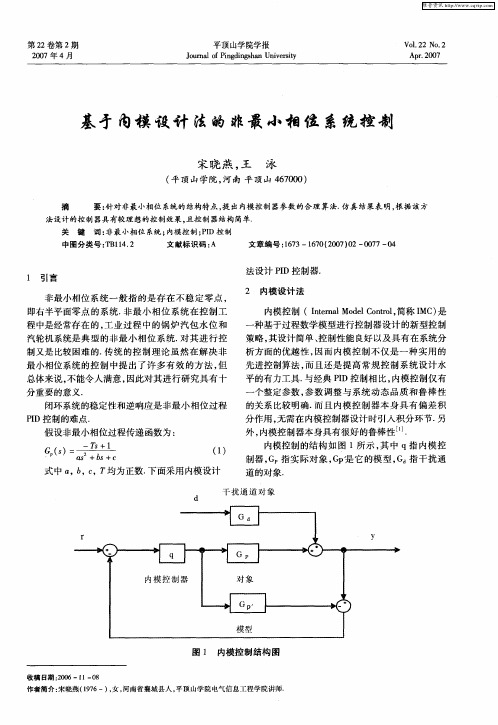
非最小相位系统中的内模控制
如 果 模 型精 确 ， 即Ｇ（ ） ｓ 一Ｇ（ ） 且 没 有 扰 动 ， ｓ， 即
作者简介 ： 尚继 良（ ９ ６ ）男 ， １ ５ ￣ ， 副教 授
维普资讯
文 章 编 号 ： ６ ２６ ８ （ ０ ７ ０ —２ ３ ０ １ ７ — ９ ７ ２ ０ ） ３０ ５ —３
非 最 小 相 位 系统 中的 内模 控 制
尚继 良，王 晓燕 ， 于 玮
（ 岛科 技 大 学 自动化 与 电子 工 程 学 院 ， 青 山东 青 岛 ， ６ ０ ２ ２ ６４ ）
输入 ， ｓ为 给定输 出 ， ｓ 为 干扰 输 入 ， ｓ 和 ｙ（） Ｄ（） Ｃ（）
（） Ｇ（） ｓ 一［ ｓ 一Ｇ（） Ｕ（） ｓ－ ｓ ＋Ｄ（） ｌ ｓ
（） ２
Ｇ （） 别 是 常 规 反馈 控 制 器 和 被 控 对象 的传 递 ｓ分
收 稿 日期 ： ０ ６ ０ — ９ ２ ０ — ９ ２
遍存 在 ， 其 进行 控 制 仍 然 较 难［ 。 当 系统 右 半 对 １ ］
平 面存在 奇数个 零点 时 ， 阶跃信 号 的作用下 ， 在 会
出现负调 ， 即其 被 控 量 开始 的变 化 方 向与后 来 的
变化 方 向相 反口 。这 就很 容 易 使 控 制 器 误 操 作 ， ］ 控制 作用 反 而 对 被 控 量 的 波 动 起 错 误 的 推 动 作
内模 控 制 （ＭＣ 的 概 念 是 由 Ｇａｃ Ｉ ） ｒｉ 人 于 ａ等 １ ８ 年 提 出的 ， ９２ 由于 它设 计 简单 、 踪 性 能好 、 跟 鲁
棒性 强 、 能消 除不可 测干 扰 ， ｓ为 对象 的预 测模 型 Ｇ（） 引。
所 重视 。而非 最小相 位 过程在 实 际控制 对象 中普
最小相位系统非最小相位系统一复杂系统开环传函可
L( ) 20 lg K
( ) 0
L(ω)/dB 20lgK
φ(ω)/(°)
01
ω
01
ω
2. 积分环节 G(s) 1
s
频率特性为
G( j )
1
1
j
e2
j
其幅频特性和相频特性为
A() 1/
奈氏曲线为：
Im
() 90
ω→∞ 0
当 0时，(0) 0;当 1 时，( 1 ) ;当 时，() 。
T
T4
2
不难看出相频特性曲线在半对数坐标系中对于( ω0, －45°)点是斜对称的，这是对数相频特性的一个特点。 当时间常数T变化时，对数幅频特性和对数相频特性的
形状都不变，仅仅是根据转折频率1/T的大小整条曲线
(描点法)
L() 20 lg 1 1 2T 2
20 lg 1 2T 2
() arctgT
L()/dB
0 0.1/T
-10 -20 -30
()/(°) 0°
0.1/T -45°
渐近线 渐近线
1/T
精确曲线
1/T
10/T
10/T
-90°
当ωT=1时, ω=1/T 称为交接频率, 或转 折频率、转角频率。
φ (ω )/(°)
0.1
ω
－90°
3. 微分环节 G(s) s
微分环节的频率特性为
j
G( j ) j e 2
其幅频特性和相频特性为 A( )
奈氏曲线为：
Im ( ) 90
ω→∞
ω＝0
0 Re
基于内模设计法的非最小相位系统控制
法设计 的控制 器具有较 理想的控制效果 ， 且控 制器结构 简单．
中 图分 类 号 ：Ｂ １ ． Ｔ １４ ２
１ 引言
法设计 ＰＤ控制 器・ Ｉ ２ 内模设 计法
非 最小相位 系统 一 般指 的是存 在 不 稳定 零 点 ， 即右半 平面零点 的系统 ． 最小 相 位 系统 在控 制 工 非 程 中是 经常存在 的 ， 工业 过程 中的锅 炉 汽 包水 位 和 汽轮机 系统是典 型 的非 最小 相 位 系统 ． 其进 行 控 对 制又是 比较 困难 的． 传统 的控 制 理论 虽 然 在解 决 非 最小相位 系统 的控 制 中提 出 了许 多 有 效 的方 法 ， 但 总体来说 ， 不能令人满 意 ， 因此对 其进 行研究 具有 十
１
Ｔ．
１ 。
）
（） ３
模控 制器代人 （ ）式 中就 可 以得 到 Ｇ （） ２ ｓ 的表 达
式． （ ）式进行 化简或近 似处理得 到如 （ ）式 所 对 ２ ３ 示 的形式 ， 就可 以求 出相应 的 ＰＤ参 数 ， Ｉ 而且 这 ３个 参 数都 只和内模控制器设 计时所 引入 的滤波 器 的参 数 Ａ有关 ， 以 Ａ的取值 直接 和控 制 系统 的性 能 以 所 及 鲁棒性有关 ， 户可 以按 照 实 际过 程 的要 求来 进 用
ＰＤ控制 的难 点． Ｉ 假设 非最小相位 过程传递 函数为 ：
㈤ ＝ （） １
分作 用 ， 无需在 内模控制 器设计 时 引入 积分 环节． 另 外， 内模控 制器本 身具有很好 的鲁棒性 …． 内模控制 的结 构 如 图 １所示 ， 中 ｑ指 内模控 其 制 器 ， 指实 际对 象 ， ｐ 它 的模 型 ， 指 干扰 通 Ｇ Ｇ是 Ｇ
基于自抗扰的非最小相位伺服系统控制
其负 调和 调 节 时 间是 相 互耦 合 的 ， 抑 制 了 系 统 的 负调通 常 会增加 调 节时 间 ， 造 成 系统调 节 的困难 。 本文 采用 自抗 扰 控 制 方 法 来 实 现 对 非 最小
＜ （ 是＋ １ ） 一ｚ ｌ （ 是 ） ＋ ｈ・ ２ （ 是 ）
ｚ
（ １ ）
渡过程 得 到 的信 号 和 扩张 状 态 观 测器 得 到 的信 号
２ 自抗 扰 控 制器 的控 制 算 法 与参 数
选 择
自抗扰 控制 技 术 是 中科 院 韩 京 清研 究 员 经 过
多年潜 心 研 究 、 发 展 完 善 的 一 种 非 线 性 自适 应 控
进行 非线 性组合 得 到 系统 的控 制 量 。一 般 采 用 式
确 的系 统零 极 点 位 置 ， 就 使 得 无 法 实 现 零 极 点 完
全对 消 ， 反而 会使 得 控 制 器 中包 含 不 稳 定 的极 点 ，
稳 定 零动 态 系统 ， 在 线 性 系 统 里 是 指 传 递 函数 中 含 有 正实部 零 点或 极 点 的 系 统 。与 最 小 相位 系统 相 比， 非最 小 相位 系统 调 节 的快 速性 较差 ， 对 系统
第１ １ 卷第 ３ 期
果 。其 中逆控 制 方 法 需 要 得 到 系 统 的 逆 模 型 ， 在 实际 系统 中要得 到 系统 的准 确 的 逆模 型是 很 困难
的； 而 另外 的一 些方 法 则需 要 建 立 经 验 规 则 ， 寻 找
变化 ， 而， ２ ２ （ ｔ ） 一ｊ 。 （ ） ， 这样 实现 了对输 入 信号 及
其 微分 的合 理跟 踪 。其离 散化 实现 形式 如式 （ １ ） ：
＜ （ 是＋ １ ） 一ｚ ｌ （ 是 ） ＋ ｈ・ ２ （ 是 ）
ｚ
（ １ ）
渡过程 得 到 的信 号 和 扩张 状 态 观 测器 得 到 的信 号
２ 自抗 扰 控 制器 的控 制 算 法 与参 数
选 择
自抗扰 控制 技 术 是 中科 院 韩 京 清研 究 员 经 过
多年潜 心 研 究 、 发 展 完 善 的 一 种 非 线 性 自适 应 控
进行 非线 性组合 得 到 系统 的控 制 量 。一 般 采 用 式
确 的系 统零 极 点 位 置 ， 就 使 得 无 法 实 现 零 极 点 完
全对 消 ， 反而 会使 得 控 制 器 中包 含 不 稳 定 的极 点 ，
稳 定 零动 态 系统 ， 在 线 性 系 统 里 是 指 传 递 函数 中 含 有 正实部 零 点或 极 点 的 系 统 。与 最 小 相位 系统 相 比， 非最 小 相位 系统 调 节 的快 速性 较差 ， 对 系统
第１ １ 卷第 ３ 期
果 。其 中逆控 制 方 法 需 要 得 到 系 统 的 逆 模 型 ， 在 实际 系统 中要得 到 系统 的准 确 的 逆模 型是 很 困难
的； 而 另外 的一 些方 法 则需 要 建 立 经 验 规 则 ， 寻 找
变化 ， 而， ２ ２ （ ｔ ） 一ｊ 。 （ ） ， 这样 实现 了对输 入 信号 及
其 微分 的合 理跟 踪 。其离 散化 实现 形式 如式 （ １ ） ：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3.2 极点配置
开环传递函数：
K Ts 1
设计反馈为比例环节： H K c 。 闭环传递函数变为：
(3)
K y G K Ts 1 x Hy G y KK x 1 GH 1 Ts 1 KK c c Ts 1 KK c 1 。只要调整 K c 使得 KK c 1 即可。 闭环系统的极点： s T
非最小相位系统的控制中， 需要抑制由不稳定零点引起的负调并同时缩短系统的调节时 间。 针对非最小相位系统负调与调节时间的相互影响及负调与不稳定零点的相互关系， 提出 将控制过程分为抑制负调阶段和跟踪输入阶段， 并适时改变系统不稳定零点数， 用遗传算法 统一优化各阶段的控制器参数。 仿真结果表明该控制方法大大减弱了负调， 并同时缩短了调 节时间，达到了良好的控制效果。
Nichols Chart 20 System: G Gain Margin (dB): -20 At frequency (rad/sec): 0 Closed Loop Stable? Yes
15
10 Open-Loop Gain (dB) System: G Phase Margin (deg): 84.3 Delay Margin (sec): 0.148 At frequency (rad/sec): 9.95 Closed Loop Stable? Yes
1
概念
对于闭环系统,如果它的开环传递函数极点或零点的实部小于或等于零,则称它是最小相 位系统。
2
开环传递函数中含有非最小相位系统
K Ts 1
(1)
开环传递函数：
可见开环传递函数含有一个非最小相位系统。 闭环传递函数：
K K Ts 1 K Ts K 1 1 Ts 1
闭环系统的极点： s
0
-10
-20 -90
-135
-180 10
-2
10
-1
10
0
10
1
10
2
Frequency (rad/sec)
Step Response 1.4
1.2
1
Amplitude
0.8
0.6
0.4
0.2
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Time (sec)
3
解决最小相位系统的方法3.1 50-5-10
-15 -180
-150 Open-Loop Phase (deg)
-120
-90
Bode Diagram Gm = -20 dB (at 0 rad/sec) , Pm = 84.3 deg (at 9.95 rad/sec) 20(2)
K 1 ，可见只要 K 1 ，就能保证闭环系统是稳定的。
T
2.1 K 1
假设系统开环传递函数为：
0.1 。 s 1
Nichols Chart
-20 System: G Gain Margin (dB): 20 At frequency (rad/sec): 0 Closed Loop Stable? No
-40
-50
-60 -90
-135
-180 10
-2
10
-1
10
0
10
1
10
2
Frequency (rad/sec)
14
x 10
5
Step Response
12
10
Amplitude
8
6
4
2
0 0
2
4
6
8
10
12
14
16
18
Time (sec)
2.2 K 1
假设系统开环传递函数为：
10 。 s 1
-25
-30 Open-Loop Gain (dB)
-35
-40
-45
-50
-55 -180
-150 Open-Loop Phase (deg)
-120
-90
Bode Diagram Gm = 20 dB (at 0 rad/sec) , Pm = Inf -20
-30 Magnitude (dB) Phase (deg)
稳态响应：
(4)
K 。 1 KK c
设计： KK c 1 ，并希望：
K K 1 1 Kc K 1 KK c
可以通过开环传递函数的稳态响应求出 K 值，再设计 K c 值。