应用数学基础习题课指导上下册全套课件
合集下载
《应用数学基础》 (谢政 著) 课后习题答案 国防工业出版社习题2解答

⎡λ + α ⎢ 0 ⎢ ⎢ 0 ⎢ ⎣ 0
0 λ +α 0 0
1 0 λ +α 0
0 ⎤ 1 ⎥ ⎥. 0 ⎥ ⎥ λ +α ⎦
+ 3i ( −1)] 0 −8 ⎤ [[ 2 −(λ + 1) λ + 11⎤ ⎡ 1 ⎡λ − 3 2 i ( −1)] 1,2 ⎢ ⎥ [ ] 0 →⎢ −8 ⎥ 解:(1) ⎢λ − 3 ⎥ ⎢ −3 λ + 1 −6 ⎥ ⎯⎯⎯⎯ ⎢ ⎥ ⎢ ⎥ λ λ − + − + 2 0 5 2 0 5 ⎣ ⎦ ⎣ ⎦
(2) 设目前农村人口与城镇人口相等,即 ⎢
解 (1) ⎢
q ⎤ ⎡ xn ⎤ ⎡ xn +1 ⎤ ⎡1 − p =⎢ ⎥ ⎥⎢ ⎥. ⎣ yn +1 ⎦ ⎣ p 1 − q ⎦ ⎣ yn ⎦ −q q ⎤ λ −1+ p ⎡1 − p = = (λ − 1)(λ − 1 + p + q) , ⎥ −p λ −1+ q ⎣ p 1− q⎦
Aα = λα , A α = A
m
m −1
( Aα ) = Am −1λα = λ Am −1α = λ mα
7. 将下列矩阵酉对角化.
A−1α = λ −1α
− 2 ,对应的特征向量分别为 (0,1, −i ) T , ( 2i,1, i ) T , (− 2i,1, i ) T ,由于此三个向量分
(2)
λI − ⎢
λ1 = 1, λ2 = 1 − p − q, ξ1 = ( q, p ) T , ξ 2 = (1, −1)T ,因此
q ⎤ ⎡ q 1 ⎤ ⎡1 0 ⎤ ⎡ q 1 ⎤ ⎡1 − p ⎢ p −1⎥ ⎢ p 1 − q ⎥ ⎢ p −1⎥ = ⎢ 0 1 − p − q ⎥ , ⎦ ⎣ ⎦ ⎣ ⎦⎣ ⎦ ⎣
应用数学基础下课件第二十六章常微分方程初步

1 2
y2
1 2
x2
c1.
所以其通解为y2 x2 c.
例2 确定镭的衰变速度与质量m成正比.
解 dm km, (k 0为比例系数),负号表示质量随时间增加而减少. dt
所以
dm dt
kdt,
(m
0), ln
m
kt
c1 ,
m ektc1 ekt ,即为衰变规律.由此可见镭的质量随时间增加而 按指数规律衰减.
若q(x) 0,即y ' py q称为一阶线性非齐次方程.
对于一阶线性齐次方程,其通解很容易解决.即 dy pdx, ln | y | y
pdx
c
',
y
ce
pdx
,
这里c为任意实数.
对于一阶线性非齐次方程,不能进行变量分离,求解稍困难些.
不难看出,一阶线性齐次方程y ' py 0是非齐次方程y ' py
x
(2)因为2x 2 yy ' 0, 所以y ' y ,即x2 y2 c为该微分方程的解;
(3)改写微分方程成ydy
x xdx, 两端积分可得
1
y2
1
x2
c '.
22
即x2 y2 c为该微分方程的解;
(4)因为x 1时, y 0,所以c 1,所求曲线方程为x2 y2 1(特解).
2
24
原方程的通解为 x y 1 sin(x y) x c 24
四、一阶线性微分方程
形如 dy py q称为一阶线性微分方程(!重点掌握!).这里p, dx
q均为x的连续函数.之所以称为线性,是指函数y及其导数y '都是 一次的. 若q(x) 0,即y ' py 0称为一阶线性齐次方程.
导数的应用习题课17页PPT文档
,又f(0)=f(π)=0,[
f
()]m
a
x
33 .
8
故当
x 3,y 2
3 4
时,
(xy)max
33 8
.
例6:证明不等式: ln x11(x 1 )212(1x )3(x0 ).
解:函数的定义域为(,0 ) (0,1) (1,) .
当x<0或x>1时, f(x) x x12x22x1.
x1 x x(x1)
f(x)x22(xx11)2. 故当x<0时, f(x)0;当x>1时, f(x)0.
当0<x<1时, f(x)2x x 2( x2 x 1)1,f(x)x2 2 (x x 1 1)2,
(2)若f(x)在区间[m,m+1]上单调递增,求m的取值
范围. 解:(1) f(x)3a2x2b,x
由题意得:
f(1)2 ab2 a1 f(1)3 3a2b3 b3.
(2) f(x ) 3 x 2 6 x 3 x (x 2 ) 0,解得x2]和[0,+∞).
故当0<x<1/2时,f(x)0;当1/2<x<1时, f(x)0.
因此,函数在(-∞,0)和(1/2,1)上是增函数,而在(0,1/2) 和(1,+∞)上是减函数.
例2:已知函数f(x)=ax3+bx2,曲线y=f(x)过点P(-1,2),
且在点P处的切线恰好与直线x-3y=0垂直.
(1)求a、b的值;
例3:试问:曲线y=x6/3上哪一点的法线在y轴上截距最小 ?(所谓法线是指:过曲线上一点与以此点为切点的 切线垂直的直线).
解:在已知曲线上任取一点(x, x6/3),则过该点的切线的 斜率为 ky2x5,从而法线的斜率为 12x5 .
高中数学第三章函数的应用习题课函数的应用课件新人教版必修1

=ln x,那么函数 y=f(x)的零点个数为( )
A.一定是 2
B.一定是 3
C.可能是 2 也可能是 3 D.可能是 0
解 (1)因为 f(x)是定义在 R 上的奇函数,当 x≥0 时,f(x)=x2 -3x,所以 f(x)=x-2-x23-x,3xx,≥x0<,0, 所以 g(x)=x-2-x24-x+4x3+,3x,≥x0<,0,由xx≥ 2-04,x+3=0, 解得 x=1 或 x=3;由x-<x02,-4x+3=0,解得 x=-2- 7. 所以函数 g(x)=f(x)-x+3 的零点的集合为{-2- 7,1,3}. 故选 D.
【训练 1】 设 f(x)=x3+bx+c 是[-1,1]上的增函数,且
f-12·f12<0,则方程 f(x)=0 在[-1,1]内(
)
A.可能有 3 个实根
B.可能有 2 个实根
C.有唯一实根
D.没有实根
解析 由于 f(x)=x3+bx+c 是[-1,1]上的增函数,且
f-12·f12<0,所以 f(x)在-12,12上有唯一零点,即方程 f(x) =0 在[-1,1]内有唯一实根.
2019/7/11
最新中小学教学课件
28
4.已测得(x,y)的两组值为(1,2),(2,5),现有两个拟合模型, 甲:y=x2+1,乙:y=3x-1.若又测得(x,y)的一组对应值为 (3,10.2),则选用________作为拟合模型较好. 解析 对于甲:x=3时,y=32+1=10,对于乙: x=3时,y=8,因此用甲作为拟合模型较好. 答案 甲
(1)写出图(1)表示的销售价格与时间的函数关系式 P=f(t),写 出图(2)表示的日销售量与时间的函数关系式 Q=g(t)及日销 售金额 M(元)与时间的函数关系 M=h(t); (2)乙商店销售同一种商品,在 4 月份采用另一种销售策略, 日销售金额 N(元)与时间 t(天)之间的函数关系为 N=-2t2- 10t+2 750,试比较 4 月份每天两商店销售金额的大小关系.
应用数学基础下课件第十七章定积分的应用

P(h, r)的直线方程为
y
r h
x
此圆锥体可看作由直线y
r h
x, x
0, x
h及x轴所围成的直角
三角形绕x轴旋转围成的.由旋转体体积的计算公式,得所求圆锥
体的体积
V
h
0
r h
2
x
dx
r2
h2
x3 3
h
0
1 r2h
3
三、求平面曲线弧长
现在来计算曲线y f (x)上相应于x从a到b的一段弧的长度.
0
0
R R2
x2
dx
4R arcsin
x R R 0
2 R
例9
求星形
x y
a cos2 a sin3
t t
,
(a
0)的全长(见图17
15).
解 由于星形线关于两个坐标轴对称,所以所求曲线的长度是
该曲线在第一象限内曲线长的4倍.取t为积分变量.
dx 3a cos2 t sin t dt
dy 3asin2 t cost dt
式中, y(t) 0;与分别为曲边左,右端所对应的参数值.
2.在极坐标系下的面积计算
设曲线的方程由极坐标给出:r r( ), , 求曲线
r r( ),半直线 , 所围成的曲边扇形的面积(见图
17-8 )
利用微元法,取极角为积分变量,变化区间为, ,在任
意子区, +d 上,曲边扇形面积的部分量可用处的极径r
区间为-2,2,其面积微元为dA
y 4 y 4 x2
(4 x2 )dx故所求图形面积为
A
2
(4 x2 )dx 2
2 (4 x2 )dx 32
经济应用数学基础(第二版)全书课件汇总整本书电子教案(最新)

xn 的极限, 记作
lim
n
xn
A
如: lim 1 0 ; lim n 1
n n
n n 1
1.2 极 限
【经济问题1-1】中老大每次分得的马匹数构成
的数列
17 2
17 18 2
17 182 2
17 18n1 2
17
易知
lim
n
18n1
2
0
1.2 极 限
2. 函数极限
定义1.5 如果当自变量 x取正值并无限增大时,函数
(2)由题意,收益函数为
R(Q) Q P Q(90 0.5Q) 90Q 0.5Q
L(Q) R(Q) C(Q) 1.5Q2 94Q 10
1.2 极限
1.2.1 极限概念
1. 数列极限
定义1.4 对于数列 ,xn如果当 无限n 增大时, xn
无限趋近于一个确定的常数 A,则称常数 为A 数列
2
3 x, 1 x 2
1
(1)求此函数的定义域并作出草图;-2 -1
12 -1
x
(2)求 f ( 1), f (1), f ( 4) 的值。
-2
2
3
解 (1)函数的定义域为 (1,2] ,
(2)f ( 1) 1 1 3 , f (1) 12 1, f (4) 3 4 5
22
2
lim f (x) lim (x 1) 1
x0
x0
lim f (x) lim (x 1) 1
x0
x0
因为 f (x) 的左极限和右极限都存在但不相等,所以
lim f (x)不存在。
x0
1.2 极 限
1.2.2 无穷小量与无穷大量
lim
n
xn
A
如: lim 1 0 ; lim n 1
n n
n n 1
1.2 极 限
【经济问题1-1】中老大每次分得的马匹数构成
的数列
17 2
17 18 2
17 182 2
17 18n1 2
17
易知
lim
n
18n1
2
0
1.2 极 限
2. 函数极限
定义1.5 如果当自变量 x取正值并无限增大时,函数
(2)由题意,收益函数为
R(Q) Q P Q(90 0.5Q) 90Q 0.5Q
L(Q) R(Q) C(Q) 1.5Q2 94Q 10
1.2 极限
1.2.1 极限概念
1. 数列极限
定义1.4 对于数列 ,xn如果当 无限n 增大时, xn
无限趋近于一个确定的常数 A,则称常数 为A 数列
2
3 x, 1 x 2
1
(1)求此函数的定义域并作出草图;-2 -1
12 -1
x
(2)求 f ( 1), f (1), f ( 4) 的值。
-2
2
3
解 (1)函数的定义域为 (1,2] ,
(2)f ( 1) 1 1 3 , f (1) 12 1, f (4) 3 4 5
22
2
lim f (x) lim (x 1) 1
x0
x0
lim f (x) lim (x 1) 1
x0
x0
因为 f (x) 的左极限和右极限都存在但不相等,所以
lim f (x)不存在。
x0
1.2 极 限
1.2.2 无穷小量与无穷大量
应用数学基础下课件第十五章导数的应用2
答案
2.确定函数y = x2 2x 3的单减区间.
答案
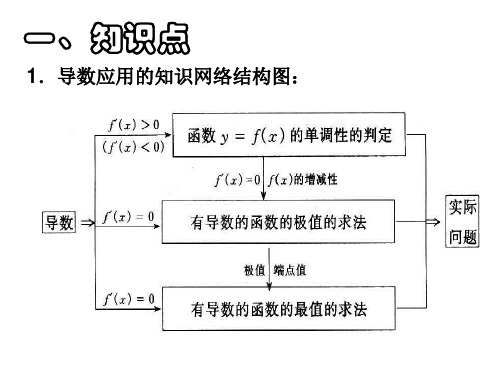
第二节 函数的极值及判定
定义
如果对x 附近的任意x(x x )都有f (x) f (x )成立,则f (x )
0
0
0
0
为极大值;若f (x) f (x )成立,则f (x )为极小值.
0
0
函数的极大,极小值统称极值,使函数取得极值的点极值点. 函数的极值是局部性的,它只限于x0的某一邻域内,通过函数 相比较才能显示出来.在一个区间上,函数可能有几个极大,
3
2
函数的图形如图15 4所示,在
1
点(1,2),(2,1)处有水平切线.
x
1
2
3
图154 例6示意图
例7 确定函数y 3 x2的单调区间.
解 因为
y'
23
1 x13
所以当x0时, y'为无穷大不存大;当x0时, y'0
区间(,0)上函数y 3 x2为单调减;当x 0时,
y' 0,区间(0,)上函数y 3 x2为单调增,函数的
图形如155所示
y
y 2 x2
O
x
图155 例7示意图
思考题
1.罗尔定理的三个条件是充要条件吗?能否去掉某个条
件?
答案
2.拉格朗日定理的结论有哪些形式?(举例至少写三种形式) 答案
3.请思考并写出罗尔定理与拉格朗日定理有何关系? 答案
课堂练习题
1.验证罗尔定理对y
=
lnsinx在
6
,
5
6
上的正确性.
例1 求函数y x2ex的极值. 解 因为, y' 2xex x2ex xex(2 x),令y' 0得驻点x 0,x 2. 当x0时, y'0;当0 x2时, y'0,当x2时y'0. 所以函数在x0处取得极小值y 0;在x2取得极大值y 4e2. 当函数在驻点处二阶导数存大时,有以下判定定理.
《应用数学基础》 (谢政 著) 课后习题答案 国防工业出版社习题1解答

−1
: Y → X 存在的充要条件是 Tx = 0 ⇒ x = 0 ;
−1 −1
(2) 若逆映射 T 存在,则 T 也是线性算子. 证明 (1) 由于 T 是满射,则 R (T ) = Y .
−1
必要性. 假设 T 的逆映射 T 以及 T 为单射可知 x = 0 .
: Y → X 存在, 则 T 为单射. 若 Tx = 0 , 则由 T 0 = 0
⎡0⎤ ⎢a ⎥ ⎢ ⎥, ⎢0⎥ ⎢ ⎥ ⎣c ⎦
⎡b ⎤ ⎢0⎥ ⎢ ⎥, ⎢d ⎥ ⎢ ⎥ ⎣0⎦
⎡0⎤ ⎢b ⎥ ⎢ ⎥, ⎢0⎥ ⎢ ⎥ ⎣d ⎦
案
⎡a ⎢0 ⎢ ⎢c ⎢ ⎣0
0 a 0 c
b 0 d 0
0⎤ b⎥ ⎥. 0⎥ ⎥ d⎦
9. 设 T 是三维线性空间 X 上的线性变换,它关于基 {e1 , e2 , e3 } 的矩阵是
2×2
⎧ ⎡1 ⎨⎢ ⎩ ⎣0
的矩阵. 解
⎡0 ⎢0 ⎣
2×2
1⎤ , 0⎥ ⎦
⎡0 ⎢1 ⎣
0⎤ , 0⎥ ⎦
⎡0 ⎢0 ⎣
0⎤ ⎫ ⎬ 1⎥ ⎦⎭
(1) 令 K = {TX |X ∈ ℝ
} ,则 K 为 ℝ 2×2 的线性子空间, T 为 ℝ 2×2 → K 上
的映射,且有 ∀X 1 , X 2 ∈ ℝ
0⎤ ⎡1 = b⎢ ⎥ 0⎦ ⎣0
b⎤ ⎡0 = b⎢ ⎥ d⎦ ⎣0
即 TE11 , TE12 , TE 21 , TE 22 关于基 {E11 , E12 , E 21 , E 22 } 的坐标依次为
网
课
因此 T 关于基 {E11 , E12 , E 21 , E 22 } 的矩阵为
: Y → X 存在的充要条件是 Tx = 0 ⇒ x = 0 ;
−1 −1
(2) 若逆映射 T 存在,则 T 也是线性算子. 证明 (1) 由于 T 是满射,则 R (T ) = Y .
−1
必要性. 假设 T 的逆映射 T 以及 T 为单射可知 x = 0 .
: Y → X 存在, 则 T 为单射. 若 Tx = 0 , 则由 T 0 = 0
⎡0⎤ ⎢a ⎥ ⎢ ⎥, ⎢0⎥ ⎢ ⎥ ⎣c ⎦
⎡b ⎤ ⎢0⎥ ⎢ ⎥, ⎢d ⎥ ⎢ ⎥ ⎣0⎦
⎡0⎤ ⎢b ⎥ ⎢ ⎥, ⎢0⎥ ⎢ ⎥ ⎣d ⎦
案
⎡a ⎢0 ⎢ ⎢c ⎢ ⎣0
0 a 0 c
b 0 d 0
0⎤ b⎥ ⎥. 0⎥ ⎥ d⎦
9. 设 T 是三维线性空间 X 上的线性变换,它关于基 {e1 , e2 , e3 } 的矩阵是
2×2
⎧ ⎡1 ⎨⎢ ⎩ ⎣0
的矩阵. 解
⎡0 ⎢0 ⎣
2×2
1⎤ , 0⎥ ⎦
⎡0 ⎢1 ⎣
0⎤ , 0⎥ ⎦
⎡0 ⎢0 ⎣
0⎤ ⎫ ⎬ 1⎥ ⎦⎭
(1) 令 K = {TX |X ∈ ℝ
} ,则 K 为 ℝ 2×2 的线性子空间, T 为 ℝ 2×2 → K 上
的映射,且有 ∀X 1 , X 2 ∈ ℝ
0⎤ ⎡1 = b⎢ ⎥ 0⎦ ⎣0
b⎤ ⎡0 = b⎢ ⎥ d⎦ ⎣0
即 TE11 , TE12 , TE 21 , TE 22 关于基 {E11 , E12 , E 21 , E 22 } 的坐标依次为
网
课
因此 T 关于基 {E11 , E12 , E 21 , E 22 } 的矩阵为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
件是必要条件但不是充分条件。
四、本章关键词
集合 不等式 命题
( 二)
常见问题分类与解法
本章主要介绍了集合、不等式及简易逻辑三部分内容,其 常见问题类型及解答方法如下。
一、集合与集合、元素与集合间的关系判断
这类问题解答的前提是:首先理解集合与集合、元素与
集合间的各种关系的含义,即明确元素与集合间的关系是“属
(3) 命题及命题的联结词,命题的四种形式;充要条件的概 念。
二、本章重点、难点
集合间的关系,不等式的性质,命题的相互关系是重点; 集合间的运算,求解不等式是难点。
三、对学习的建议
(1) 要注意元素与集合的关系是从属关系,集合与集合间的 关系是包含被包含的关系;相等关系;子集与真子集意义不 同;0、{0}、 三者的含意不同。
例2
设 1, 2,3, 4,5, 6, 7,8,9 , A 1,3,5, 7 , B 3, 4,5。试
写出集合:(1) A B;(2) A B;(3) 痧 B;(4) A
A
B 。
解 (1) A B 1,3,5, 1,3, 4,5, 7; 1,3,5, 7 3, 4,5 3,5; 3, 4,5 2, 4, 6,8,9 3, 4,5 4;
于”与“不属于”的从属关系,而集合与集合间的关系是“包 含”与“包含于”的包含关系;其次理解各种符号的含义,恰 当地运用符号。
例1 用适当的符号 ( ,, 刭, , ) 表示下列各组中的关系。
(1) 2 ______{x | 2x 4 0};
(2)
2 _____ Z;
(3) {1,3}_____{x | x 2 2 x 3 0};
目录
第一章 集合、不等式、简易逻辑.ppt 第二章 幂函数、指数函数、对数函数.ppt 第三章 任意角的三角函数.ppt 第四章 加法定理及其推论.ppt 第五章 反三角函数与简单的三角方程.ppt 第六章 平面向量和复数.ppt 第七章 空间图形.ppt 第八章 直 线.ppt 第九章 二次曲线.ppt 第十章 极坐标和参数方程.ppt 第十一章 数列与数学归纳法.ppt 第十二章 排列、组合与二项式定理.ppt
(4) 该组仍为两个集合间的关系. 在数轴上,通过二者 表示的数集范围可看出,{x |1 x 3} Ø {x | 1 x 4},即填 包含于符号“ Ø ” .
二、集合间的运算
集合间的运算主要有“交”、“并”、“差”、“补” 四种,要理解每种运算的规定,使用恰当的符号表示运算类 型,同时注意集合的元素,列举时不分次序、不要遗漏、不 要重复。
(4) {x |1 x 3}_____{x | 1 x 4}.
解
(1) 该组中“2”是元素,{x | 2 x 4 0}表示一集合,那么
二者间只可能是“属于”与“不属于”的关系. 显然,2 4 0,即 2 是属于集合 {x | 2 x 4 0} 的,故填属于符号“” .
用区间表示为:(, 2]; (3) 由于 | x 2 | 1,于是 1 x 2 1,故 1 x 3,即 原数集等同于数集 {x |1 x 3},用区间表示为 (1,3); (4) 由于 x 3 0,即 x 3,故原数集等同于 {x | x 3}, 用区间表示为 [3, ).
(2) 故
2 为一元素,Z 为整数集;又因为
2 不是整数,
2 Z,即填不属于符号“” .
(3) 该组左、右两边皆为集合. 左边集合中的元素有两 个: 1,3;右边集合 {x | x 2 2 x 3 0} 中的元素通过求解 方程 x 2 2 x 3 0 可看出,也是 1,3 两个元素,故二者 相等,填等号“ ” .
(2) 要正确理解集合的并与交定义中“或”与“且”两个字 的含义。
(3) x 2 a 2 (a 0) 的解不是 x a,而是 x a 或 x a; x 2 a 2 (a 0) 的解不是 x a,而是 a x a。
(4) 要注意命题都是陈述句,正确理解命题的四种形式间的 真值关系。 (5) 要注意有些条件是充分条件但不是必要条件,而有些条
第一章 (一) (二) (三) (四)
集合、不等式、简易逻辑 本章内容小结 常见问题分类及解法 思 课 考 堂 题 练 习
(一) 本章内容小结
一、本章主要内容
(1) 集合的概念,集合之间的关系及其运算;区间的几种形 式及其表示方法。 (2) 不等式的性质,一元二次不等式、分式不等式、绝对值
不等式的求解方法。
(3) ð A B ð 1,3,5,7
(4) ð A B ð 1,3, 4,5, 7 2, 6,8,9 .
三、区间的表示
理解区间作为一种数集的概念,要用正确的符号表示所 给区间。
例3
试将下列数集用区间表示。 (1) {x | 2 x 1 0}; (3) {x || x 2 | 1}; (2) {x | 2 x 0}; (4) {x | x 3 0}. 1 (1) 该数集中的数 x 满足:2 x 1 0,即 x ,于是 2 1 1 数集可表示为 x x ,用区间表示即为 , ; 2 2 (2) 由于 2 x 0,即 x 2,故原数集等同于 {x | x 2},
目录
第十三章 函数、极限与连续.ppt 第十四章 导数与微分.ppt 第十五章 导数的应用.ppt 第十六章 一元函数积分学.ppt 第十七章 定积分的应用.ppt 第十八章 多元函数微分学.ppt 第十九章 多元函数积分学.ppt 第二十章 概率论初步.ppt 第二十一章 数理统计基础.ppt 第二十二章 行 列 式.ppt 第二十三章 矩阵与线性方程组.ppt 第二十四章 线性规划初步.ppt 第二十五章 无穷级数.ppt 第二十六章 常微分方程.ppt 第二十七章 拉普拉斯变换.ppt
