susan算子检测角点 - 360文档中心

一种改进的SUSAN算子棋盘格角点亚像素检测算法

２１０２年第１期
文章编号：０６２７（０２０－０４０１０－５２１）１０６－４３
计算机与现代化ＪＵＮＩＹＩＮＡＨＡＩＡＪＵＸＡＤＩＵＳ
第１７期９
一
种改进的ＳＳＮ算子棋盘格角点亚像素检测算法ＵＡ
王瑞杨润泽尹晓春罗志海，，，
（．１军械工程学院机械制造教研室，河北石家庄０００；．５０３２中国人民解放军６０７部队，６７山西大同０７４）３０４摘要：ＵＡＳＳＮ算子在检测角点时，只以ＵＡＳＮ区域面积的大小作为判断准则，忽略ＵＡＳＮ区域形状的影响。因此，该算法对棋盘格标定板中的内角点与边缘点难以区分。针对此问题，文提出在ＳＳＮ圆模板内再次采用ＳＳＮ算子来实本ＵＡＵＡ现时棋盘格标定板角点的有效检测。此外，每个初定位角点的局部邻域内，用二次曲面拟合法得到角点的亚像素坐在采标。实验证明，所提出的算法准确、有效、适应性好，能为摄像机标定提供亚像素精度的角点信息。关键词：棋盘格；ＵＡＳＳＮ算子；角点检测；亚像素
ＡＮ’ ｈｐｎｄｔｃｉｇｆａｕｅｐｉｔ．Ｉ’ ｉｃｌｔｉｔｇｉｈｔｅｃｅｓｏｒｏｒｎｄｅｐｉｔｆｒｔｅＳＡＮａｇ・ＳｓａｅｉｅｅｔｅｔｒｏｎｓｔｓｄｆｕｔｏｄｓｎｕｓｈｈｓｂａｄｃｍｅｓａｄｅｇｏｎｓｏｈＵＳｏｎｉｉｌｉｈｒｔｍ．ＴｅｅｏｅａｏｈｒＵＡｃｒｕａｓＳａｄｄｗｔｉｅＳＳｉｕａｓｖｒｏｉｅｅｔｈｒｆｒｎｔｅＳＮｉｌｒｍａｋｉｄｅｉｎｔＵＡＮｃｒｌｒｍａｋｔｏｅｃｍｅｔｓｄｆＣ．Ｍｏｅｖｒｕ．Ｓｃｈｈｃｏｈｒｏｅ．ｓｂｐｘｌｃｏｄｎｔｓｃｒｅｓａｅｃｃｌｔｄｗｔｕｄｃＳｒｃｉｉｇｉｅｏｒｉａｅｏｎｒｒａｕａｅｉｑａｒＵｇｅｆｔ．ＥｐｒｍｅｔｌｒｓｈｈｗｔａｔｅｐｏｏｅｇｒｔｍａｌｈｉＨｔｎｘｅｉｎａｅｔｓｓｏｈｔｈｒｐｓｄａｏｈｈｒｌｉｓｈｇｒｃｓｎａｄｃｎｐｏｉｅｒｌｂｅｄｔｒｉｈｐｅｉｉｎｃｍｅａｃｌｒｔｎｉｈｐｅｉｉｎａｒｖｄｅｉｌａａｆｇ — ｒｃｓａｒａｉａｉ．ｏａｏｈｏｂｏＫｅｒｓｃｅｓｏｒｙｗｏｄ：ｈｓｂａｄ；ＳＳＵＡＮｐｒｔｒｏｒｄｔｃｉｎｕ－ｉｅｏｅａｏ；ｃｍｅｅｅｔ；ｓｂｐｘｌｏ

角点检测的几种基本方法

角点检测的几种基本方法角点检测(Corner Detection)是计算机视觉系统中用来获得图像特征的一种方法，广泛应用于运动检测、图像匹配、视频跟踪、三维建模和目标识别等领域中。

也称为特征点检测。

角点通常被定义为两条边的交点，更严格的说，角点的局部邻域应该具有两个不同区域的不同方向的边界。

而实际应用中，大多数所谓的角点检测方法检测的是拥有特定特征的图像点，而不仅仅是“角点”。

这些特征点在图像中有具体的坐标，并具有某些数学特征，如局部最大或最小灰度、某些梯度特征等。

现有的角点检测算法并不是都十分的鲁棒。

很多方法都要求有大量的训练集和冗余数据来防止或减少错误特征的出现。

角点检测方法的一个很重要的评价标准是其对多幅图像中相同或相似特征的检测能力，并且能够应对光照变化、图像旋转等图像变化。

Moravec角点检测算法Moravec角点检测算法是最早的角点检测算法之一。

该算法将角点定义为具有低“自相关性”的点。

算法会检测图像的每一个像素，将像素周边的一个邻域作为一个patch，并检测这个patch和周围其他patch的相关性。

这种相关性通过两个patch间的平方差之和(SSD)来衡量，SSD值越小则相似性越高。

如果像素位于平滑图像区域内，周围的patch都会非常相似。

如果像素在边缘上，则周围的patch在与边缘正交的方向上会有很大差异，在与边缘平行的方向上则较为相似。

而如果像素是各个方向上都有变化的特征点，则周围所有的patch都不会很相似。

Moravec会计算每个像素patch和周围patch的SSD最小值作为强度值，取局部强度最大的点作为特征点。

Harris角点检测算法Moravec角点检测算法有几个很明显的缺陷：1，强度值的计算并不是各向同性的，只有离散的8个45度角方向被考虑。

因为patch的评议比较最多只有8个方向；2，由于窗口是方形并且二元的，因此相应函数会有噪声；3，对边缘的相应太简单，因为强度值尽取SSD的最小值；FAST角点检测算法Smith 和 Brady在1997年提出了一种完全不同的角点提取方法，即“SUSAN (Smallest UnivalueSegment AssimilatingNucleus)”提取算子。

基于SUSAN检测算子的二维条码定位方法

基于SUSAN检测算子的二维条码定位方法周乐【摘要】以二维条码DataMatrix在实际应用中的图像为例，采用一种基于图像最优闽值的SUSAN检测算子，将复杂背景图像中的二维条码图像区域检测出来。

使用这种方法可以在最大程度上忽略复杂背景的干扰，实现二维条码的快速定位。

%Taking the image of the Data Matrix of two-dimensional bar code in practical applications as an example, the paper adopts the SUSAN detection operator based on the image optimal threshold, which can quickly find out 2D bar code image region from complex background image. This method could ignore the complex background interference in the greatest degree, and achieve location of 2D bar code quickly.【期刊名称】《微型机与应用》【年(卷),期】2012(031)009【总页数】4页(P35-37,40)【关键词】二维条码;Data;Matrix;最优阈值;SUSAN检测算子【作者】周乐【作者单位】西安建筑科技大学信息与控制工程学院,陕西西安710055【正文语种】中文【中图分类】TP391.44自动化数据采集技术是信息采集和处理的关键技术[1]，条码技术在自动化数据采集中占重要地位。

二维条码是在传统的一维条码基础上发展起来的。

传统的一维条码由于受信息容量的限制必须依赖数据库，而二维条码的信息密度高、信息容量大，可以不依赖于数据库。

二维条码不仅可以将数字、字符等信息存入编码，而且可以将人脸、指纹和虹膜等图像信息存入条码，因此二维条码在证件识读、人事管理、运输包装、POS系统和电子数据交换等方面得到广泛的应用[2]。

一种自适应阈值的角点检测算法

一种自适应阈值的角点检测算法摘要针对SUSAN算子只采用固定阈值和定位不够精确的问题，本文利用角点像素与其所在的角之间具有连通性的特点，给出了一种角点精确定位的改进方法，并采用了自适应阈值，在图像中每个像素的 SUSAN 模板内单独计算阈值 t，使其在各种不同的对比度下仍能正确提取出角点。

实验结果证明了该方法的有效性。

关键词 SUSAN 算法；角点提取；自适应阈值；图像连通性1 引言角点是图像上曲率足够高、并且位于图像中不同亮度区域交界处的点。

由于角点包含了很多的图像中的信息，因此，角点在图像匹配、运动物体的跟踪以及目标识别等方面有着广泛的应用。

如何快速准确的提取出图像中的角点成为了一个关键的问题。

SUSAN算法是由英国牛津大学的Brady首先提出的，它是一种直接利用图像灰度有效地进行边缘、角点检测的低层次图像处理算法。

它具有方法简单，抗噪能力强和处理速度快等特点。

本文首先介绍SUSAN角点提取的原理，然后分析了该算法的缺点，提出SUSAN模板中自适应阈值的选取的方法，并利用角点像素与其所在的角之间具有连通性的特点，给出了一种角点精确定位的改进方法。

2 SUSAN算法的基本原理[1]图1显示了一个在白色背景下的黑色的长方形，图中a，b，c，d，e五个位置分别是五个圆形的模板在图像中不同的位置，窗口的中心被称之为“核”。

窗口中所有具有与核相同或相似灰度的像素，把这些像素构成的区域称为USAN ( Univalue Segment Assimilating Nucleus)。

由图1可以看出，当核像素处在图像中的灰度一致区域时，USAN的面积会达到最大（超过一半），当核处在直边缘处约为最大值的一半，当核处在角点处更小，约为最大值的四分之一。

因此，利用USAN面积的上述变化性质可检测边缘或角点。

图1 SUSAN模板在图像中的几种位置本文所使用的是一个包含37个像素的圆形模板，半径为3.4个像素，如图2。

角点检测

角点检测角点检测算法可归纳为3类：基于灰度图像的角点检测、基于二值图像的角点检测、基于轮廓曲线的角点检测。

基于灰度图像的角点检测又可分为基于梯度、基于模板和基于模板梯度组合3类方法，其中基于模板的方法主要考虑像素领域点的灰度变化，即图像亮度的变化，将与邻点亮度对比足够大的点定义为角点。

常见的基于模板的角点检测算法有Kitchen-Rosenfeld角点检测算法，Harris角点检测算法、KLT角点检测算法及SUSAN角点检测算法。

和其他角点检测算法相比，SUSAN角点检测算法具有算法简单、位置准确、抗噪声能力强等特点。

2算法SUSAN是Smith和Brady提出的一种图像处理方法，该算法是基于像素领域包含若干元素的近似圆形模板，对每个像素基于该模板领域的图像灰度计算角点响应函数（CRF）的数值，如果大于某阈值且为局部极大值，则认为该点为角点。

角点的精度与圆形模板大小无关，圆形模板越大，检测的角点数越多，则计算量也越大，本文圆形模板包含37个元素，该近似圆形模板结构如图1所示。

SUSAN圆形模板与物体位置关系图[1]如图2所示为SUSAN圆形模板与物体的5种几何位置关系，对于图像中非纹理区域的任一点，在以它为中心的模板窗中存在一块亮度与其相同的区域，这块区域即为SUSAN的USAN （Univalve Segment Assimilating Nucleus）区域。

USAN区域包含了图像结构的重要信息，由图可知，当模板中心像素点位于区域内部时，USAN的面积最大，当该像素点位于区域边界时，则面积为最大的一半，当该像素点为角点时，USAN区域面积约为最大的1/4。

SUSAN根据不同位置时USAN区域的面积来考察当前像素点为区域内部点、边缘点或角点。

USAN区域面积通过圆模板内各像素与中心点像素比较得到的相似点的个数总和来表示，该相似比较函数为：函数其中（x0,y0），(x,y)分别为模板中心像素点和待比较像素点的坐标，t为相似度阈值，本文该值取整幅图像灰度最大值和最小值差值的1/10。

SUSAN检测算法概述

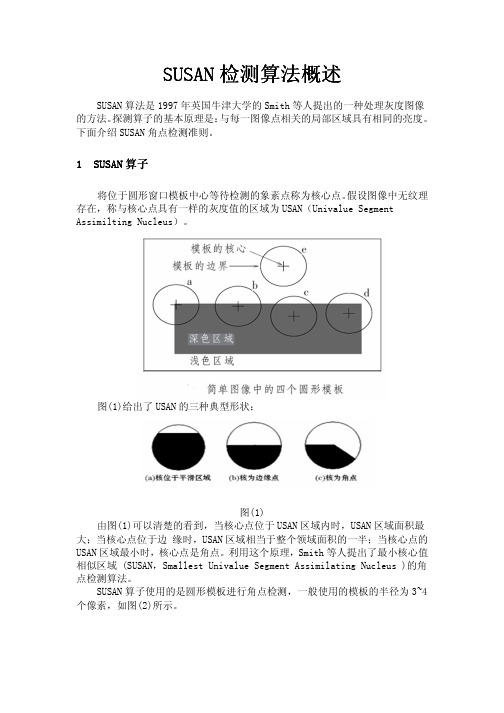
SUSAN检测算法检测算法概述概述概述SUSAN算法是1997年英国牛津大学的Smith等人提出的一种处理灰度图像的方法。

探测算子的基本原理是：与每一图像点相关的局部区域具有相同的亮度。

下面介绍SUSAN角点检测准则。

1SUSAN算子将位于圆形窗口模板中心等待检测的象素点称为核心点。

假设图像中无纹理存在，称与核心点具有一样的灰度值的区域为USAN（Univalue Segment Assimilting Nucleus）。

图(1)给出了USAN的三种典型形状：图(1)由图(1)可以清楚的看到，当核心点位于USAN区域内时，USAN区域面积最大；当核心点位于边缘时，USAN区域相当于整个领域面积的一半；当核心点的USAN区域最小时，核心点是角点。

利用这个原理，Smith等人提出了最小核心值相似区域 (SUSAN，Smallest Univalue Segment Assimilating Nucleus )的角点检测算法。

SUSAN算子使用的是圆形模板进行角点检测，一般使用的模板的半径为3~4个像素，如图(2)所示。

图(2) SUSAN圆形模板将模板中的各点亮度与核心点的亮度利用下面的函数进行比较，(1)在上式中为图像中像素的灰度值， t为灰度差别的阈值，为模板中心的像素，为其他的像素， C为比较函数。

模板中所有的像素都用这个函数进行比较，然后计算出函数C的和值n。

(2)和值n就是USAN(univalue segment assimilating nucleus)区域的像素个数，就是USAN区域的面积，然后把这个面积和几何阈值进行比较，得到最后的响应函数：(3)上式中，R为响应函数，g为阈值，通常在探测角点时取值为1/2模板的像素个数，当采用7×7的模板时，g=37×1/2。

2SUSAN算子的改进算法通常在实际的应用中，对于比较函数我们通常采用下面的比较函数：(4)采用这个函数可以使比较函数具有更好的稳定性，当图像中的像素亮度值有很小的变化后，对于c 的取值不会产生很大的影响。

图像角点

角点检测技术方法概述角点检测(Corner Detection)是计算机视觉系统中用来获得图像特征的一种方法，广泛应用于运动检测、图像匹配、视频跟踪、三维建模和目标识别等领域中。

也称为特征点检测。

角点通常被定义为两条边的交点，更严格的说，角点的局部邻域应该具有两个不同区域的不同方向的边界。

而实际应用中，大多数所谓的角点检测方法检测的是拥有特定特征的图像点，而不仅仅是“角点”。

这些特征点在图像中有具体的坐标，并具有某些数学特征，如局部最大或最小灰度、某些梯度特征等。

现有的角点检测算法并不是都十分的鲁棒。

很多方法都要求有大量的训练集和冗余数据来防止或减少错误特征的出现。

角点检测方法的一个很重要的评价标准是其对多幅图像中相同或相似特征的检测能力，并且能够应对光照变化、图像旋转等图像变化。

Moravec角点检测算法Moravec角点检测算法是最早的角点检测算法之一。

该算法将角点定义为具有低“自相关性”的点。

算法会检测图像的每一个像素，将像素周边的一个邻域作为一个patch，并检测这个patch和周围其他patch的相关性。

这种相关性通过两个patch间的平方差之和(SSD)来衡量，SSD值越小则相似性越高。

如果像素位于平滑图像区域内，周围的patch都会非常相似。

如果像素在边缘上，则周围的patch在与边缘正交的方向上会有很大差异，在与边缘平行的方向上则较为相似。

而如果像素是各个方向上都有变化的特征点，则周围所有的patch都不会很相似。

Moravec会计算每个像素patch和周围patch的SSD最小值作为强度值，取局部强度最大的点作为特征点。

Harris角点检测算法Moravec角点检测算法有几个很明显的缺陷：1，强度值的计算并不是各向同性的，只有离散的8个45度角方向被考虑。

因为patch的评议比较最多只有8个方向；2，由于窗口是方形并且二元的，因此相应函数会有噪声；3，对边缘的相应太简单，因为强度值尽取SSD的最小值；FAST角点检测算法Smith 和Brady在1997年提出了一种完全不同的角点提取方法，即“SUSAN (Smallest UnivalueSegment AssimilatingNucleus)”提取算子。

Harris与SUSAN原理及实验结果分析

Harris 与SUSAN 角点检测算法原理与实验结果分析一．Harris 算法原理Harris 角点检测算法的基本原理是取以目标像素点为中心的一个小窗口，计算窗口沿任何方向移动后的灰度变化，并用解析形式表达。

设以像素点(x,y)为中心的小窗口在X 方向上移动u ，y 方向上移动v ，Harris 给出了灰度变化度量的解析表达式：2,,|,|,,()(x y x y x u y v x y x y I I E w I I w u v o X Y ∂∂=-=++∂∂∑∑ (1.1)其中，,x y E 为窗口内的灰度变化度量；,x y w 为窗口函数，一般定义为222()/,x y x y w eσ+=；I 为图像灰度函数，略去无穷小项有： 222222,,[()()2]2x y x y x y x y E w u I v I uvI I Au Cuv Bv =++=++∑（1.2）将,x y E 化为二次型有： ,[]x y u E u v M v ⎡⎤=⎢⎥⎣⎦(1.3)M 为实对称矩阵： 2,2x y x x y x y y I I I M w I I I ∙⎤⎡=⎥⎢∙⎢⎥⎣⎦∑ (1.4)通过对角化处理得到： 11,200x y E R R λλ-⎛⎫= ⎪⎝⎭ (1.5)其中，R 为旋转因子，对角化处理后并不改变以u,v 为坐标参数的空间曲面的形状，其特征值反应了两个主轴方向的图像表面曲率。

当两个特征值均较小时，表明目标点附近区域为“平坦区域”；特征值一大一小时，表明特征点位于“边缘”上；只有当两个特征值均比较大时，沿任何方向的移动均将导致灰度的剧烈变化。

Harris 的角点响应函数(CRF)表达式由此而得到：2(,)det()(())CRF x y M k trace M =- (1.6) 其中：det(M)表示矩阵M 的行列式，trace(M)表示矩阵的迹。

当目标像素点的CRF 值大于给定的阈值时，该像素点即为角点。

susan算子角点提取在船舶舷号定位中的应用

susan算子角点提取在船舶舷号定位中的应
用
Susan算子是比较常用的角点检测算子，可以通过边缘的变换信息来检测图像的角点。

在船舶舷号定位方面，Susan算子用于检测船舷中的舷号角点信息，根据角点的分布状况来确定船舷的方向，进而定位船舷的位置。

Susan算子检测的角点信息，是船舷方向定位的关键基础，船舷舷号定位的精准度就取决于其处理效果：Susan算子能够较准确地在船舶舷号中检测出角点信息，有助于提高船舶检测定位精度。

同时，Susan算子不仅可以处理狭小的舷号角点信息，而且对图像中各种干扰也有较强的免疫性能，从而提高角点检测的精准度，有助于保障船舶舷号检测定位的精准度。

基于环形模板的SUSAN角点检测算法

２０１４年第１期
文章编号：ｌＯＯ９— ２５５２（２０１４）Ｏ１ — ００３１ — ０４中图分类号：ＴＰ３９１．４１文献标识码：Ａ
基于环形模板的ＳＵＳＡＮ角点检测算法
唐坚刚，任琳２，林新，李春
ｅｄｇｅｐｏｉｎｔ，ｉｎｃａｓｅｏｆｍｉｓｓｉｎｇｃｏｍｅｒ，ｔｈｅｎａｄｄｉｎｇａｄｉｓｃｒｅｔｅｒｉｎｇ－ｔｅｍｐｌａｔｅｒｔｏＳＵＳＡＮ ’Ｓｃｉｒｃｌｅｔｅｍｐｌａｔｅ，ａｎｄａｃｃｏｄｉｒｎｇｔｏｔｈｅｂｉｇｒｈｔｎｅｓｓｃｈａｎｇｅｔｉｍｅｓｏｆｒｔｏｄｉｓｔｉｎｇｕｉｓｈｔｈｅｐｏｉｎｔｉｓｃｏｍｅｒｏｒｎｏｔ．Ｔｈｅ
（１．上海医疗器械高等专科学校，上海２０００９３；２．上海理工大学，上海２０００９３）
摘
要：ＳＵＳＡＮ算子需要不断地调整 “ 相似性阈值 ” 才能获得更好的角点，它可以检测Ｘ型、Ｙ
型和Ｔ型，但是不能检测出特殊形状和复杂形状的角点。为了克服这些缺点，文中提出了一种自适应阈值的选择方法，使程序自动化，若角点的ＵＳＡＮ区域与边缘点的ＵＳＡＮ区域相同，则在ＳＵＳＡＮ的模板中叠加一个离散的环状模板ｒ，根据模板ｒ中的亮度变化次数来区分待测点是否是角点，以免遗漏角点。实验结果显示改进后的算法不仅省去手动调整阈值，大大提高程序运行