机械原理大作业(用复数矢量法求连杆速度、加速度+c语言程序实现)

合集下载

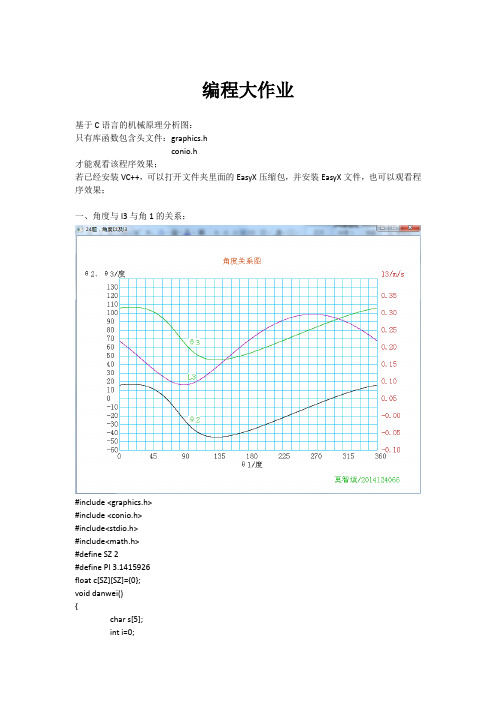
C语言机械原理编程,连杆运动分析图线

t=-k*40/20-120;
setcolor(GREEN);
line(m11,t11,m1,t);
m11=m1,t11=t;
k=l3;
m1=n*600/360;
t=-k*40/(0.05)-80;
setcolor(MAGENTA);
line(m12,t12,m1,t);
m12=m1,t12=t;
n+=0.1;
i+=10;
}
outtextxy(-85,-420, "θ2、θ3/度");
}
int main()
{
//创建大小为800 * 600的绘图窗口
initgraph(800, 600);
//设置原点(0, 0)为屏幕中央（Y轴默认向下为正）
setorigin(100, 500);
//使用白色填充背景
setbkcolor(WHITE);
//输出屏幕提示
settextcolor(BLACK);
setfont(18,0,"宋体");
danwei();
danwei1();
settextcolor(RED);
danwei2();
settextcolor(RGB(201, 62, 0));
outtextxy(240,-450, "角度关系图");
void matrixmultiplication(float a_2[2][2],float b_2[2][1],float y[2][1])
{
int i,j,k,a_column=2,a_row=2,b_row=1;
float temp;
for(i=0;i<a_column;i++)

机械原理大作业一连杆机构参考例子

机械原理大作业课程名称：机械原理设计题目：机械原理大作业院系：汽车工程学院车辆工程班级：1101201姓名：。

学号：。

指导教师：游斌弟大作业1 连杆机构运动分析1、运动分析题目如图所示机构，已知机构各构件的尺寸为280mm AB =,350mm BC =,320mm CD =,160mm AD =，175mm BE = 220mm EF =，25mm G x =，80mm G y =，构件1的角速度为110rad/s ω=，试求构件2上点F 的轨迹及构件5的角位移、角速度和角加速度，并对计算结果进行分析。

图 12、对机构进行结构分析该机构由I 级杆组RR （原动件1）、II 级杆组RRR （杆2、杆3）和II 级杆组RPR （滑块4及杆5）组成。

I 级杆组RR ，如图2所示；II 级杆组RRR ，如图3所示；II 级杆组RPR ，如图4所示。

图2 图 2图4 3、建立坐标系建立以点A为原点的固定平面直角坐标系4、各基本杆组运动分析的数学模型（1）同一构件上点的运动分析：如图5所示的构件AB,,已知杆AB 的角速度=10/rad s ω，AB 杆长i l =280mm,可求得B 点的位置B x 、B y ，速度xB v 、yB v ，加速度xB a 、yB a 。

=cos =280cos B i x l ϕϕ; =sin =280sin B i y l ϕϕ;图 3==-sin =-BxB i B dx v l y dt ωϕω； ==cos =;B yB i B dyv l x dt ωϕω222B 2==-cos =-BxB i d x a l x dt ωϕω；2222==-sin =-ByB i Bd y a l y dtωϕω。

图 4（2）RRRII 级杆组的运动分析如图6所示是由三个回转副和两个构件组成的II 级组。

已知两杆的杆长2l 、3l 和两个外运动副B 、D 的位置（B x 、B y 、D x 、D y ）、速度（ xB yB xD yD v v v v 、、、）图6和加速度（xB yB xD yD a a a a 、、、）。

哈工大机械原理大作业1 连杆机构运动分析牛头刨床学号5号

大作业1 连杆机构运动分析运动分析题目图1-13 牛头刨床机构简图一、按比例画出机构运动简图见A3图纸二、机构的结构分析及基本杆组的划分（1）机构的结构分析该机构为平面连杆机构，活动构件数n=5；有A、B、C、E、F五个转动副和B、F两个移动副，没有高副，故低副数PL=7，高副数PH=0。

机构的自由度F=3n-2PL-PH=3*5-2*7=1。

机构有确定运动轨迹。

（2）基本杆组的划分图1-13中，原动件构件1为Ⅰ级杆组，移除之后按照拆杆组法对机构进行拆分，可得由滑块2和杆3组成的RPRⅡ级杆组，以及由杆4和滑块5组成的RRPⅡ级杆组。

拆分图如下：图1-13-1 Ⅰ级杆组图1-13-2 RPRⅡ级杆组图1-13-3 RRPⅡ级杆组三、各杆组的运动分析数学模型图1-13-1 Ⅰ级杆组 x B =x A +l AB cos ϕy B =y A +l AB sin ϕ图1-13-2 RPR Ⅱ级杆组 x E =x B +(l CE -s)cos ϕj y E =y B +(l CE -s)sin ϕjϕj =arctan(B 0/A 0)A 0=xB -x CB 0=y B -y CS =2020B A + 图1-13-3 RRP Ⅱ级杆组F 的位置 x F =x E -l EF cos ϕiy F =y E +l EF sin ϕi ϕi =arcsin(A 1/l EF )A 1=H-H 1-y EF 的速度F 的加速度四、建立坐标系以A 为原点建立坐标系，则A （0,0）五、编程使用MATLAB 编写程序如下lAB=108;lCD=620;lEF=300;H1=350;H=635;xC=0;yC=-350;syms t;f=(255*pi/30)*t;xB=lAB*cos(f);yB=lAB*sin(f);A0=xB-xC;B0=yB-yC;S=sqrt(A0^2+B0^2);f1=atan(B0/A0);xE=xB+(lAB-S)*cos(f1);yE=yB+(lAB-S)*sin(f1);A1=H-H1-yE;f2=asin(A1/lEF);xF=xE-lEF*cos(f2);yF=yE+lEF*sin(f2);a=0:0.001:0.5;xF=subs(xF,t,a);plot(a,xF)title('位移x随时间t变化图像') xlabel('t(s)'),ylabel(X')lAB=108;lCD=620;lEF=300;H1=350;H=635;xC=0;yC=-350;syms t;f=(255*pi/30)*t;xB=lAB*cos(f);yB=lAB*sin(f);A0=xB-xC;B0=yB-yC;S=sqrt(A0^2+B0^2);f1=atan(B0/A0);xE=xB+(lAB-S)*cos(f1);yE=yB+(lAB-S)*sin(f1);A1=H-H1-yE;f2=asin(A1/lEF);xF=xE-lEF*cos(f2);yF=yE+lEF*sin(f2);vF=diff(xF,t);a=0:0.001:0.5;vF=subs(vF,t,a);plot(a,vF)title('速度v随时间t变化图像') xlabel('t(s)'),ylabel(V')lAB=108;lCD=620;lEF=300;H1=350;H=635;xC=0;yC=-350;syms t;f=(255*pi/30)*t;xB=lAB*cos(f);yB=lAB*sin(f);A0=xB-xC;B0=yB-yC;S=sqrt(A0^2+B0^2);f1=atan(B0/A0);xE=xB+(lAB-S)*cos(f1);yE=yB+(lAB-S)*sin(f1);A1=H-H1-yE;f2=asin(A1/lEF);xF=xE-lEF*cos(f2);yF=yE+lEF*sin(f2);aF=diff(xF,t,2);a=0:0.001:0.5;aF=subs(aF,t,a);plot(a,aF)title('加速度a随时间t变化图像') xlabel('t(s)'),ylabel(A')六、位移、速度、加速度图像位移xE随时间t变化图像速度vE随时间t变化图像加速度aE随时间t变化图像七、运动分析由MATLAB编程后绘制所得图线分析可知，牛头刨床的刨头F行程约为500mm，在0.06s~0.17s之间速度和加速度波动较大，在0.17s~0.29s 之间速度和加速度波动较小，这就保证了刨头在空行程时有急回运动，而在工作行程是由较均匀的切削速度，运动连续，且运动性能良好稳定。

机械原理大作业平面连杆机构报告

平面连杆机构的运动分析（题号：平面六杆机构）一、题目说明图示为一平面六杆机构。

设已知各构件的尺寸如表1所示，又知原动件1以等角速度ω1=1 rad/s沿逆时针方向回转，试求各从动件的角位移、角速度及角加速度以及E点的位移、速度及加速度的变化情况。

已知其尺寸参数如下表所示：二、题目分析1、建立封闭图形：L 1 + L 2= L 3+ L 4组号1ll2l 3 l 4 l 5 l 6 α A B C2-A2-B 2-C26.5 67.5 87.5 52.4 43.0 60l 2=116.6 l 2=111.6l 2=126.6L 1 + L 2= L 5+ L 6+AG2、机构运动分析：a 、角位移分析由图形封闭性得：⎪⎪⎩⎪⎪⎨⎧⋅-⋅+=+-⋅-⋅+⋅⋅-⋅+=+-⋅-⋅+⋅⋅=⋅+⋅+⋅=⋅+⋅55662'2221155662'222113322114332211sin sin )sin(sin sin cos cos )cos(cos cos sin sin sin cos cos cos θθθαπθθθθθαπθθθθθθθθL L y L L L L L x L L L L L L L L L L G G 将上式化简可得：⎪⎪⎩⎪⎪⎨⎧=⋅-⋅+-⋅+⋅-=⋅-⋅+-⋅+⋅⋅-=⋅-⋅⋅-=⋅-⋅G G y L L L L L x L L L L L L L L L L L 66552'233466552'2331133221143322sin sin )sin(sin cos cos )cos(cos sin sin sin cos cos cos θθαθθθθαθθθθθθθθb 、角速度分析上式对时间求一阶导数，可得速度方程：化为矩阵形式为：⎪⎪⎩⎪⎪⎨⎧=⋅⋅-⋅⋅+⋅-⋅+⋅⋅=⋅⋅+⋅⋅-⋅-⋅-⋅⋅-⋅⋅-=⋅⋅-⋅⋅⋅⋅=⋅⋅+⋅⋅-0cos cos )cos(cos 0sin sin )sin(sin cos cos cos sin sin sin 66655522'233366655522'2333111333222111333222ωθωθωαθωθωθωθωαθωθωθωθωθωθωθωθL L L L L L L L L L L L L L⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅-⋅⋅=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅-⋅⋅-⋅⋅⋅-⋅--⋅-⋅-⋅⋅⋅-00cos sin cos cos cos )cos(sin sin sin )sin(00cos cos 00sin sin 1111165326655332'26655332'233223322θθωωωωωθθθαθθθθαθθθθθL L L L L L L L L L L L L Lc 、角加速度分析：矩阵对时间求一阶导数，可得加速度矩阵2233222333'223355665'22335566622332233'22sin sin 0cos cos 00sin()sin sin sin cos()cos cos cos cos cos 00sin sin 00cos(L L L L L L L L L L L L L L L L L θθεθθεθαθθθεθαθθθεθθθθθα-⋅⋅⎡⎤⎡⎤⎢⎥⎢⎥⋅-⋅⎢⎥⎢⎥⋅=⎢⎥⎢⎥-⋅--⋅-⋅⋅⎢⎥⎢⎥⋅-⋅⋅-⋅⎣⎦⎣⎦-⋅⋅-⋅⋅⋅-211221123123355665'2223355666cos sin )cos cos cos 0sin()sin sin sin 0L L L L L L L L L θωθωωθθθωθαθθθω⎡⎤⋅⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⋅⎢⎥⎢⎥⎢⎥⋅+⋅⎢⎥⎢⎥⎢⎥⋅⋅-⋅⎢⎥⎢⎥⎢⎥⋅-⋅⋅-⋅⎢⎥⎣⎦⎣⎦⎣⎦d 、E 点的运动状态位移：⎩⎨⎧⋅-⋅+=⋅-⋅+=55665566sin sin cos cos θθθθL L y y L L x x G EG E速度：⎪⎩⎪⎨⎧⋅⋅-⋅⋅=⋅⋅+⋅⋅-=555666555666cos cos sin sin ωθωθωθωθL L v L L v yx E E 加速度：⎪⎩⎪⎨⎧⋅⋅-⋅⋅+⋅⋅+⋅⋅-=⋅⋅+⋅⋅+⋅⋅-⋅⋅-=5552555666266655525556662666cos sin cos sin sin cos sin cos εθωθεθωθεθωθεθωθL L L L a L L L L a yx E E三、流程图四、源程序#include<stdio.h>#include<stdlib.h>#include<math.h>#define PI 3.1415926#define N 4void Solutionangle(double [18],double ); /*矢量法求角位移*/void Solutionspeed(double [N][N],double [N],double [18],double ); /*角速度求解*/void Solutionacceleration(double [N][N],double [N][N],double [N],double [18]);/*角加速度求解*/void GaussianE(double [N][N],double [N],double [N]);/*高斯消去*/void FoundmatrixA(double [18],double [N][N]); //创建系数矩阵Avoid FoundmatrixB(double [18],double ,double [N]);//创建系数矩阵Bvoid FoundmatrixDA(double [18],double [N][N]);//创建矩阵DAvoid FoundmatrixDB(double [18],double ,double [N]);//创建矩阵DB//定义全局变量double l1=26.5,l2=111.6,l3=67.5,l4=87.5,l5=52.4,l6=43.0;double l2g=65.0,xg=153.5,yg=41.7,inang=60*PI/180,as1=1.0;//主函数void main(){int i,j;FILE *fp;double shuju[36][18];double psvalue[18],a[N][N],da[N][N],b[N],db[N],ang1;//建立文件，并制表头if((fp=fopen("filel","w"))==NULL){printf("Cann't open this file.\n");exit(0);}fprintf(fp,"\n The Kinematic Parameters of Point 5\n"); fprintf(fp," ang2 ang3 ang5 ang6"); fprintf(fp," as2 as3 as5 as6"); fprintf(fp," aas2 aas3 aas5 aas6");fprintf(fp," xe ye vex vey aex aey\n");//计算数据并写入文件for(i=0;i<36;i++){ang1=i*PI/18;Solutionangle(psvalue,ang1);FoundmatrixB(psvalue,ang1,b);FoundmatrixA(psvalue,a);Solutionspeed(a,b,psvalue,ang1);FoundmatrixDA(psvalue,da);FoundmatrixDB(psvalue,ang1,db);Solutionacceleration(a,da,db,psvalue);for(j=0;j<4;j++){shuju[i][j]=psvalue[j]*180/PI;}for(j=4;j<18;j++){shuju[i][j]=psvalue[j];}fprintf(fp,"\n");for(j=0;j<18;j++)fprintf(fp,"%12.3f",shuju[i][j]);}fclose(fp);//输出数据for(i=0;i<36;i++){ang1=i*PI/18;printf("\n输出ang1=%d时的求解\n",i*10);printf("angle angspeed angacceleration E:\n"); for(j=0;j<4;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=4;j<8;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=8;j<12;j++)printf("%lf\t",shuju[i][j]);printf("\n");for(j=12;j<18;j++)printf("%lf\t",shuju[i][j]);printf("\n");}}/*矢量法求角位移*/void Solutionangle(double value[18],double ang1){double xe,ye,A,B,C,phi,alpha,csn,ang5g,d2,d,ang2,ang3,ang5,ang6; A=2*l1*l3*sin(ang1);B=2*l3*(l1*cos(ang1)-l4);C=l2*l2-l1*l1-l3*l3-l4*l4+2*l1*l4*cos(ang1);ang3=2*atan((A+sqrt(A*A+B*B-C*C))/(B-C));if(ang3<0)//限定ang3大小{ang3=2*atan((A-sqrt(A*A+B*B-C*C))/(B-C));}ang2=asin((l3*sin(ang3)-l1*sin(ang1))/l2);xe=l4+l3*cos(ang3)+l2g*cos(ang2-inang);ye=l3*sin(ang3)+l2g*sin(ang2-inang);phi=atan2((yg-ye),(xg-xe));d2=(yg-ye)*(yg-ye)+(xg-xe)*(xg-xe);d=sqrt(d2);csn=(l5*l5+d2-l6*l6)/(2.0*l5*d);alpha=atan2(sqrt(1.0-csn*csn),csn);ang5g=phi-alpha;ang5=ang5g-PI;ang6=atan2(ye+l5*sin(ang5g)-yg,xe+l5*cos(ang5g)-xg);value[0]=ang2;value[1]=ang3;value[2]=ang5;value[3]=ang6;value[12]=xe;value[13]=ye;//限定角度大小for(int i=0;i<4;i++){while(value[i]>2*PI)value[i]-=2*PI;while(value[i]<0)value[i]+=2*PI;}}/*角速度求解*/void Solutionspeed(double a2[N][N],double b2[N],double value[18],double ang1) {double ang2,ang3;ang2=value[0];ang3=value[1];double p2[N];GaussianE(a2,b2,p2);value[4]=p2[0];value[5]=p2[1];value[6]=p2[2];value[7]=p2[3];value[14]=-l3*value[5]*sin(ang3)-l2g*value[4]*sin(ang2-inang);value[15]=l3*value[5]*cos(ang3)+l2g*value[4]*cos(ang2-inang);}/*角加速度求解*/void Solutionacceleration(double a3[N][N],double da3[N][N],double db3[N],double value[18]){int i,j;double ang2,ang3;ang2=value[0];ang3=value[1];double bk[N]={0};double p3[N];for(i=0;i<N;i++){for(j=0;j<N;j++){bk[i]+=-da3[i][j]*value[4+j];}bk[i]+=db3[i]*as1;}GaussianE(a3,bk,p3);value[8]=p3[0];value[9]=p3[1];value[10]=p3[2];value[11]=p3[3];value[16]=-l3*value[9]*sin(ang3)-l3*value[5]*value[5]*cos(ang3)-l2g*value[8]*si n(ang2-inang)-l2g*value[4]*value[4]*cos(ang2-inang);value[17]=l3*value[9]*cos(ang3)-l3*value[5]*value[5]*sin(ang3)+l2g*value[8]*cos (ang2-inang)-l2g*value[4]*value[4]*sin(ang2-inang);}/*高斯消去法解矩阵方程*/void GaussianE(double a4[N][N],double b4[N],double p4[N]){int i,j,k;double a4g[N][N],b4g[N],t;for(i=0;i<N;i++)for(j=0;j<N;j++)a4g[i][j]=a4[i][j];for(i=0;i<N;i++)b4g[i]=b4[i];//使主对角线上的值尽可能大if(a4g[0][0]<a4g[1][0] && a4g[0][1]>a4g[1][1]){for(j=0;j<N;j++){t=a4g[0][j];a4g[0][j]=a4g[1][j];a4g[1][j]=t;}t=b4g[0];b4g[0]=b4g[1];b4g[1]=t;}if(a4g[2][2]<a4g[3][2] && a4g[2][3]>a4g[3][3]){for(j=0;j<N;j++){t=a4g[2][j];a4g[2][j]=a4g[3][j];a4g[3][j]=t;}t=b4g[2];b4g[2]=b4g[1];b4g[3]=t;}//初等行变换for(j=0;j<N;j++)for(i=0;i<N;i++){if(i!=j){for(k=0;k<N;k++)if(k!=j){a4g[i][k]-=a4g[i][j]/a4g[j][j]*a4g[j][k];} b4g[i]-=b4g[j]*a4g[i][j]/a4g[j][j];a4g[i][j]=0;}}for(i=0;i<N;i++)b4g[i]/=a4g[i][i];p4[0]=b4g[0];p4[1]=b4g[1];p4[2]=b4g[2];p4[3]=b4g[3];}//创建系数矩阵Avoid FoundmatrixA(double value5[18],double a5[N][N]){double ang2,ang3,ang5,ang6;ang2=value5[0];ang3=value5[1];ang5=value5[2];ang6=value5[3]; a5[0][0]=-l2*sin(ang2);a5[0][1]=l3*sin(ang3);a5[1][0]=l2*cos(ang2);a5[1][1]=-l3*cos(ang3);a5[2][0]=-l2*sin(ang2)-l2g*sin(ang2-inang);a5[2][2]=l5*sin(ang5);a5[2][3]=l6*sin(ang6);a5[3][0]=l2*cos(ang2)+l2g*cos(ang2-inang);a5[3][2]=-l5*cos(ang5);a5[3][3]=-l6*cos(ang6);a5[0][2]=a5[0][3]=a5[1][2]=a5[1][3]=a5[2][1]=a5[3][1]=0;}//创建系数矩阵Bvoid FoundmatrixB(double value6[18],double ang1,double b6[N]){b6[0]=b6[2]=l1*sin(ang1)*as1;b6[1]=b6[3]=-l1*cos(ang1)*as1;}//创建矩阵DAvoid FoundmatrixDA(double value7[18],double da7[N][N]){double ang2,ang3,ang5,ang6,as2,as3,as5,as6;ang2=value7[0];ang3=value7[1];ang5=value7[2];ang6=value7[3]; as2=value7[4];as3=value7[5];as5=value7[6];as6=value7[7];da7[0][0]=-l2*as2*cos(ang2);da7[0][1]=l3*as3*cos(ang3);da7[1][0]=-l2*as2*sin(ang2);da7[1][1]=l3*as3*sin(ang3);da7[2][0]=as2*(-l2*cos(ang2)-l2g*cos(ang2-inang));da7[2][2]=as5*l5*cos(ang5);da7[2][3]=as6*l6*cos(ang6);da7[3][0]=as2*(-l2*sin(ang2)-l2g*sin(ang2-inang));da7[3][2]=as5*l5*sin(ang5);da7[3][3]=as6*l6*sin(ang6);da7[0][2]=da7[0][3]=da7[1][2]=da7[1][3]=da7[2][1]=da7[3][1]=0; }//创建矩阵DBvoid FoundmatrixDB(double value8[18],double ang1,double db8[N]){db8[0]=db8[2]=l1*as1*cos(ang1);db8[1]=db8[3]=l1*as1*sin(ang1);}五、计算结果及相关曲线图：A组：数据图像角位移角速度角加速度E点的位移、速度及加速度六、体会及建议：这次的作业给了我们一次锻炼机会，让我们基本掌握了平面六杆机构解析算法的基本原理，从理论到程序实践，每一步都环环相扣，每一个结果都息息相关，最终在我们共同的努力下完成了本次作业。

机械原理课程大作业

机械原理课程大作业基于MATLAB平面连杆机构运动学和动力学分析指导老师：王玉丹目录作业一：平面连杆机构运动学分析第2页作业二：平面连杆机构动力学分析第15页作业一L(AE)=70mm,L(AB)=40mm,L(EF)=60mm,L(DE)=35mm,L(CD)=75m m,L(BC)=50mm,原动件以等角速度W1=10rad/s回转。

试以图解法求在θ1=50°时C点的速度和加速度.对机构进行运动分析，写出C点的位置、速度及加速度方程。

解题过程：令AB=r1, BC=r2, CD=r3, DE=r4，AE=r6，EF=r8, AF=r7，角EAF=θ1。

分析：对机构进行位置分析由封闭形ABCDEA可得：r1+r2=r6+r3+r4 （1）由封闭图形AEFA可得：r7=r6+r8 （2）将（1）（2）两式整理可得：r2-r3-r4=-r1+r6-r8+r7=r6【一】（1）位置方程：【二】速度方程：【三】加速度方程：【四】根据位置方程式编制如下函数：【五】进行数据输入，运行程序进行运算。

根据上面分析的θ1 的极限位置取θ1 的范围为40°-55°并均分成15个元素：输出的P、矩阵的第二列到第四列分别是θ2 、θ3 、4θ4 的值，第一列是AF杆的长度r1’。

【六】第二步根据速度方程式编写如下函数：根据第一步得到的数据进行数据输入，运行程序计算各速度值。

程序如下：程序运行得到q矩阵，第一行到第三行分别是a2、a3、a4 的值，第四行是杆AF上滑块运动的速度，即F点的速度。

【七】第三步编写加速度计算函数：【八】根据第一步和第二步输入数据，运行程序得到各加速度的值：【1】计算C点在θ1 =55°，w1 =10rad/s时的速度，加速度：总结数据绘出各构件的位置、速度和加速度的表格如下：【2】输出图像1）角位置程序及输出的图像：2）F点速度程序及输出的图像：3）角加速度程序及输出的图像：4）F点的加速度程序及输出图像：作业二在图示的正弦机构中，已知：L(AB)=100mm,h1=120mm,h2=80mm, W1=10rad/s(常数)，滑块2和构件3的重量分别为，G2 =40 N 和G3 =100 N,质心S2 和S3 的位置如图所示，加于构件3上的生产阻力Fr=400 N，构件1的重力和惯性力略去不计。

平面连杆机构运动分析c语言版 - 机械原理课程设计

机械原理课程设计平面连杆机构运动分析（VC++语言版）第一章机构运动分析的目的和方法一、运动分析的目的当设计新的机械时，或是分析现有机械的工作性能时，都必须先计算其机构的运动参数，也就是进行机构的运动分析。

通过位移或轨迹分析，可以确定机构的外廓、某些构件运动所需的空间或判断它们运动时是否相互干涉；可以考察某构件能否实现预定位置变化的要求，或某构件上某点能否实现预定轨迹变化的要求。

通过速度分析，可以确定机构中从动件的速度变化规律能否满足工作要求。

进行生产能力和功率的计算；还能对进一步做机构的加速度分析和受力分析提供必要的数据，也是机构运动方程求解的基础。

通过加速度分析，可以确定机构各构件及构件上某些点的加速度，了解机构加速度的变化规律；是计算惯性力进行动力分析、考察机构动力平衡、防止振动和噪音的基础。

二、基于直角坐标法的运动分析直角坐标法的要点是以点的运动为基础贯穿整个分析过程。

作运动分析时先求机构中某些特殊点的运动，再根据点的运动计算机构的角运动。

第二章连杆机构运动分析的直角坐标法原理一、平面机构的组成原理我们知道，机构具有确定运动的条件是其原动件的数目应等于其所具有的自由度的数目。

因此，如将机构及和机架相联的原动件与其余构件拆分开，则有其余构件构成的构件组必然是一个自由度为零的构件组。

而这个自由度为零的构件组，有时还可以再拆成更简单的自由度为零的构件组。

我们把最后不能再拆的最简单的自由度为零的构件组称为组成机构的基本杆组。

含有高副的平面机构，可以按一定条件用低副替代高副而化成平面低副机构。

这样，任何机构都可以看成是有若干个基本杆组依次联结于原动件和机架上而构成的。

最简单的基本杆组是有两个构件和三个低副构成，称为Ⅱ级组，是应用最多的基本杆组，我们把同一构件上两点的运动分析及常见的Ⅱ级组的运动分析分别编写成独立的子程序，对机构进行运动分析时，仅需调用相应的子程序即可。

二、连杆机构运动分析的直角坐标法原理将机构放在直角坐标系中，选择其上的某些特殊点如铰链点、几何关节、机构质心等作为考察对象。

哈工大机械原理大作业连杆机构运动分析29

机械原理大作业一课程名称：机械原理设计题目：连杆机构运动分析-29院系：机电工程学院班级：设计者：学号：指导教师：设计时间：哈尔滨工业大学一、设计题目(29)二、VB编程得到动画、轨迹、位移、速度、加速度线图1.用VB编写程序得到的机构动画2.构件2上的E点轨迹4.构件7的速度线图三、计算说明书(一)建立机构运动分析数学模型对机构进行结构分析，找出基本杆组1.基本杆组划分a)杆件1为原动件b)构件2、3为RRR型II级杆组c)构件4、5为RRR型II级杆组d)构件6、7为RRP型II级杆组2.结构分析与自由度计算机构为平面连杆机构，活动构件数n=7,L P =10,转动副为9个，移动副为1个，高副为0个，则机构自由度为F=3n-2P L -P H =3x7-2x10=1。

各基本杆组的运动分析数学模型1.原动件（I 级构件）图1（1）位置分析B 点位置方程cos sin B A i iBA i i x x l y y l ϕϕ=+⎧⎨=+⎩ （1-1）（2）速度分析把（1-1）对时间t 求导得B 速度方程sin cos B B A i i i BB A i i i dx x x l dt dy y y l dt ϕϕϕϕ⎫==-⎪⎪⎬⎪==+⎪⎭g g g g g g （1-2）（3）加速度分析把（2-2）对时间他求导得B 加速度方程222222cos sin sin cos B B A i i i i i i BB A i i i i i i d x x x l l dt d y y y l l dt ϕϕϕϕϕϕϕϕ⎫==--⎪⎪⎬⎪==-+⎪⎭g g g g g g g g g g g g g g （1-3）上式中 i i d dt ϕϕω==g22i i d dtϕϕα==g g 2. RRR 杆组的运动分析3.RRP杆组的运动分析图2（1）位置分析内运动副C 的位置方程cos cos sin sin sin cos C B i i K j j jCB i i K j j j x x l x s l y y l y s l ϕϕϕϕϕϕ=+=+-⎧⎪⎨=+=++⎪⎩ （2-1）i l 的转角 0arcsin()ji j iA l l ϕϕ+=+ （2-2）式中0()sin ()cos B k j B K j A x x y y ϕϕ=---满足装配条件0j i A l l +≤ 滑块D 相对参考点K 的位移为sin cos cos sin C k j jC K j jjjx x l y y l s ϕϕϕϕ-+--==（2-3）滑块D 的位置方程 cos sin D K iD K ix x s y y s ϕϕ=+⎧⎨=+⎩ （2-4）（2）速度分析杆i l 的角速度123sin cos j ji i Q Q Q ϕϕωϕ-+==g（2-5）滑块D 沿导路的移动速度 123cos sin i i i iQ l Q l s Q ϕϕ-+=g（2-6）式中1(sin cos )K B j j j j Q x x s l ϕϕϕ=--+ggg2(cos sin )K B j j j j Q y y s l ϕϕϕ=-+-g g g3sin sin cos cos i i j i i j Q l l ϕϕϕϕ=+内运动副C 的速度为sin cos C B i i iC B i i ix x l y y l ϕϕϕϕ⎧=-⎪⎨⎪=+⎩gg gg g g （2-7）外移动副D 的速度为cos sin sin cos D K i j jD K i j j x x s s y y s s ϕϕϕϕϕϕ⎧=+-⎪⎨⎪=++⎩gg g g g g g g（2-8）（3）加速度分析杆i l 的角加速度453sin s j ji i Q Q co Q ϕϕεϕ-+==g g（2-9）滑块D 沿导路移动的加速度为453cos sin i i i i Q l Q l s Q ϕϕ--=g g （2-10）式中224cos (sin cos )(cos sin )2sin K B i i i j j j j j j j j j j Q x x l s l s l s ϕϕϕϕϕϕϕϕϕϕ=-+-+---g g g g g g g g g g225sin (cos sin )(sin cos )2cos K B i i i j j j j j j j j j j Q y y l s l s l s ϕϕϕϕϕϕϕϕϕϕ=-++--++g g g g g g g g g g内运动副C 的加速度22cos sin sin cos C B i i i j i j C B i i i j i jx x l l y y l l ϕϕϕϕϕϕϕϕ⎧=--⎪⎨⎪=-+⎩g gg g g g g g gg g g g g（2-11）滑块D 的加速度22cos sin cos 2sin sin cos sin 2cos D K j j j j j j jD K j j j j j j jx x s s s s y y s s s s ϕϕϕϕϕϕϕϕϕϕϕϕϕϕ⎧=+---⎪⎨⎪=++-+⎩g g g g g g g g g g gg g g g g g g gg g g（2-12）以上为基本杆组的通用分析，根据已知条件进行赋值均在程序中体现(二) 计算流程框图（见下页）(三)VB编写程序清单'定义变量Dim xA As Double 'A点的坐标、速度、加速度Dim yA As DoubleDim vxA As DoubleDim vyA As DoubleDim axA As DoubleDim ayA As DoubleDim xB As Double 'B点Dim yB As DoubleDim vxB As DoubleDim vyB As DoubleDim axB As DoubleDim ayB As DoubleDim xD As Double 'D点Dim yD As DoubleDim vxD As DoubleDim vyD As DoubleDim axD As DoubleDim ayD As DoubleDim xE As Double 'E点Dim yE As DoubleDim vxE As DoubleDim vyE As DoubleDim axE As DoubleDim ayE As DoubleDim xG As Double 'G点Dim yG As DoubleDim vxG As DoubleDim vyG As DoubleDim axG As DoubleDim ayG As DoubleDim xH As Double 'H点Dim yH As DoubleDim vxH As DoubleDim vyH As DoubleDim axH As DoubleDim ayH As DoubleDim xM As Double 'M点Dim yM As DoubleDim vxM As DoubleDim vyM As DoubleDim axM As DoubleDim xN As Double '参考点NDim yN As DoubleDim vxN As DoubleDim vyN As DoubleDim axN As DoubleDim ayN As DoubleDim xK As Double 'K点Dim yK As DoubleDim vxK As DoubleDim vyK As DoubleDim axK As DoubleDim ayK As DoubleDim delt1 As Double 'AB杆初始转角Dim L1 As Double 'AB杆长Dim f1 As Double 'AB杆转角Dim w1 As Double 'AB杆角速度Dim e1 As Double 'AB杆角加速度Dim L2 As Double 'BC杆Dim f2 As DoubleDim w2 As DoubleDim e2 As DoubleDim L3 As Double 'CD杆Dim f3 As DoubleDim w3 As DoubleDim e3 As DoubleDim LBE As Double 'BE杆Dim delt2 As DoubleDim L4 As Double 'EF杆Dim f4 As DoubleDim w4 As DoubleDim e4 As DoubleDim LFG As Double 'FG杆Dim f5 As DoubleDim w5 As DoubleDim e5 As DoubleDim deltGH As Double 'GH杆Dim LGH As DoubleDim L6 As Double 'HM（HK）杆Dim f6 As DoubleDim w6 As DoubleDim e6 As DoubleDim Lj As Double 'MK杆Dim wj As DoubleDim ej As DoubleDim ss As Double '移动副K的位移Dim vss As Double '移动副K的速度Dim ass As Double '移动副K的加速度Dim pi As DoubleDim pa As DoubleDim i As DoubleDim fj1 As DoublePrivate Sub Command1_Click() '点E的轨迹Picture1.Scale (-50, 250)-(600, -100)Picture1.Line (-50, 0)-(600, 0) 'XPicture1.Line (0, 250)-(0, -100) 'YFor i = -50 To 600 Step 50 'X轴坐标Picture1.DrawStyle = 2Picture1.Line (i, 250)-(i, -100)Picture1.CurrentX = i - 0: Picture1.CurrentY = 0 Picture1.Print iNext iFor i = -100 To 250 Step 50 'Y轴坐标Picture1.DrawStyle = 2Picture1.Line (-50, i)-(600, i)Picture1.CurrentX = -20: Picture1.CurrentY = i + 7 Picture1.Print iNext iFor fj1 = 0 To 360 Step 0.01f1 = fj1 * paCall RR1Call RRR1Call RR2Picture1.PSet (xE, yE)Next fj1End SubPrivate Sub Command2_Click() '求点G的位移Picture2.Scale (-20, 300)-(380, 200)Picture2.Line (-20, 0)-(380, 0) 'XPicture2.Line (0, 300)-(0, 200) 'YFor i = 0 To 360 Step 30 'X轴坐标Picture2.DrawStyle = 2Picture2.Line (i, 300)-(i, 0)Picture2.CurrentX = i - 10: Picture2.CurrentY = 0Picture2.Print iNext iFor i = 200 To 300 Step 10 'Y轴坐标Picture2.Line (0, i)-(380, i)Picture2.CurrentX = -25: Picture2.CurrentY = i Picture2.Print iNext iFor fj1 = 0 To 360 Step 0.01f1 = fj1 * paCall RR1Call RRR1Call RR2Call RRR2Call RR3Call RRP1Picture2.PSet (fj1, ss)Next fj1End SubPrivate Sub Command3_Click() '求点G的速度Picture3.Scale (-30, 600)-(380, -600)Picture3.Line (-30, 0)-(380, 0) 'XPicture3.Line (0, 600)-(0, -600) 'YFor i = 0 To 360 Step 30 'X轴坐标Picture3.DrawStyle = 2Picture3.Line (i, 600)-(i, -600)Picture3.CurrentX = i - 10: Picture3.CurrentY = 0 Picture3.Print iNext iFor i = -600 To 600 Step 50 'Y轴坐标Picture3.Line (0, i)-(380, i)Picture3.CurrentX = -28: Picture3.CurrentY = i Picture3.Print iNext iFor fj1 = 0 To 360 Step 0.01f1 = fj1 * paCall RR1Call RRR1Call RR2Call RRR2Call RR3Call RRP1Picture3.PSet (fj1, vss)Next fj1End SubPrivate Sub Command4_Click() '求点G的加速度Picture4.Scale (-20, 20000)-(380, -10000)Picture4.Line (-20, 0)-(380, 0) 'XPicture4.Line (0, 20000)-(0, -10000) 'YFor i = 0 To 360 Step 30 'X轴坐标Picture4.DrawStyle = 2Picture4.Line (i, 20000)-(i, -10000)Picture4.CurrentX = i - 10: Picture4.CurrentY = 0 Picture4.Print iNext iFor i = -10000 To 20000 Step 1000 'Y轴坐标Picture4.Line (0, i)-(380, i)Picture4.CurrentX = -25: Picture4.CurrentY = i + 5 Picture4.Print iNext iFor fj1 = 0 To 360 Step 0.01f1 = fj1 * paCall RR1Call RRR1Call RR2Call RRR2Call RR3Call RRP1Picture4.PSet (fj1, ass)Next fj1End SubPrivate Sub Form_Load() '赋初值xA = 0yA = 0vxA = 0vyA = 0axA = 0ayA = 0xD = 730yD = -138vxD = 0vyD = 0axD = 0ayD = 0xG = 465yG = -248vxG = 0vyG = 0axG = 0ayG = 0xN = 545yN = 0vxN = 0vyN = 0axN = 0ayN = 0delt1 = 0L1 = 200w1 = 10e1 = 0L2 = 670L3 = 350delt2 = 0LBE = 335L4 = 380LFG = 130deltGH = 56 * paLGH = 100L6 = 486Lj = 0fj = pi / 2wj = 0ej = 0pi = 3.14pa = pi / 180End SubPublic Sub RR1() '杆ABxB = xA + L1 * Cos(f1 + delt1)yB = yA + L1 * Sin(f1 + delt1)vxB = vxA - w1 * L1 * Sin(f1 + delt1)vyB = vyA + w1 * L1 * Cos(f1 + delt1)axB = axA - w1 ^ 2 * L1 * Cos(f1 + delt1) - e1 * L1 * Sin(f1 + delt1) ayB = ayA - w1 ^ 2 * L1 * Sin(f1 + delt1) + e1 * L1 * Cos(f1 + delt1) End SubPublic Sub RRR1() '杆BCDDim xC As DoubleDim yC As DoubleDim vxC As DoubleDim vyC As DoubleDim axC As DoubleDim ayC As DoubleDim LBD As DoubleDim JCBD As DoubleDim val1 As DoubleDim fDB As DoubleDim C2 As DoubleDim C3 As DoubleDim S2 As DoubleDim S3 As DoubleDim G11 As DoubleDim G12 As DoubleDim G13 As DoubleLBD = Sqr((xD - xB) ^ 2 + (yD - yB) ^ 2)If LBD > L2 + L3 And LBD < Abs(L2 - L3) ThenIf MsgBox("RRR杆组杆长不符合要求", vbOKOnly, "提示") = 1 Then EndElseEnd IfElseEnd IfIf LBD < L2 + L3 And LBD > Abs(L2 - L3) Thenval1 = (L2 ^ 2 + LBD ^ 2 - L3 ^ 2) / (2 * L2 * LBD)JCBD = Atn(-val1 / Sqr(-val1 * val1 + 1)) + 2 * Atn(1)ElseEnd IfIf LBD = L2 + L3 ThenJCBD = 0ElseEnd IfIf LBD = Abs(L2 - L3) ThenIf L2 > L3 ThenJCBD = 0ElseEnd IfIf L2 < L3 ThenJCBD = piElseEnd IfElseEnd IfIf xD > xB And yD >= yB Then '第一象限fDB = Atn((yD - yB) / (xD - xB))ElseEnd IfIf xD = xB And yD > yB ThenfDB = pi * 2ElseEnd IfIf xD < xB And yD >= yB Then '第二象限fDB = pi + Atn((yD - yB) / (xD - xB)) ElseEnd IfIf xD < xB And yD < yB Then '第三象限fDB = pi + Atn((yD - yB) / (xD - xB)) ElseEnd IfIf xB = xD And yD < yB ThenfDB = 3 * pi / 2ElseEnd IfIf xD > xB And yD <= yB Then '第四象限fDB = 2 * pi + Atn((yD - yB) / (xD - xB)) ElseEnd Iff2 = fDB + JCBDxC = xB + L2 * Cos(f2)yC = yB + L2 * Sin(f2)If xC > xD And yC >= yD Then '第一象限f3 = Atn((yC - yD) / (xC - xD))ElseEnd IfIf xC = xD And yC > yD Thenf3 = pi / 2ElseEnd IfIf xC < xD And xC >= xD Then '第二象限f3 = pi + Atn((yC - yD) / (xC - xD))ElseEnd IfIf xC < xD And xC < xD Then '第三象限f3 = pi + Atn((yC - yD) / (xC - xD))ElseEnd IfIf xC = xD And xC < xD Thenf2 = 3 * pi / 2ElseEnd IfIf xC > xD And xC <= xD Then '第四象限f2 = 2 * pi + Atn((yC - yD) / (xC - xD))ElseEnd IfC2 = L2 * Cos(f2)S2 = L2 * Sin(f2)C3 = L3 * Cos(f3)S3 = L3 * Sin(f3)G11 = C2 * S3 - C3 * S2w2 = (C3 * (vxD - vxB) + S3 * (vyD - vyB)) / G11w3 = (C2 * (vxD - vxB) + S2 * (vyD - vyB)) / G11vxC = vxB - w2 * L2 * Sin(f2)vyC = vyB + w2 * L2 * Cos(f2)G12 = axD - axB + w2 ^ 2 * C2 - w3 ^ 2 * C3G13 = ayD - ayB + w2 ^ 2 * S2 - w3 ^ 2 * S3e2 = (G12 * C3 + G13 * S3) / G11e3 = (G12 * C2 + G13 * S2) / G11axC = axB - e2 * L2 * Sin(f2) - w2 ^ 2 * L2 * Cos(f2)ayC = ayB - e2 * L2 * Cos(f2) - w2 ^ 2 * L2 * Sin(f2)End SubPublic Sub RR2() '杆BExE = xB + LBE * Cos(f2 + delt2)yE = yB + LBE * Sin(f2 + delt2)vxE = vxB - w2 * LBE * Sin(f2 + delt2)vyE = vyB + w2 * LBE * Cos(f2 + delt2)axE = axB - w2 ^ 2 * LBE * Cos(f2 + delt2) - e2 * LBE * Sin(f2 + delt2) ayE = ayB - w2 ^ 2 * LBE * Sin(f2 + delt2) + e2 * LBE * Cos(f2 + delt2) End SubPublic Sub RRR2() '杆EFGDim xF As DoubleDim yF As DoubleDim vxF As DoubleDim vyF As DoubleDim axF As DoubleDim ayF As DoubleDim LEG As DoubleDim JFEG As DoubleDim val2 As DoubleDim fGE As DoubleDim C4 As DoubleDim C5 As DoubleDim S4 As DoubleDim S5 As DoubleDim G21 As DoubleDim G22 As DoubleDim G23 As DoubleLEG = Sqr((xG - xE) ^ 2 + (yG - yE) ^ 2)If LEG > L4 + LFG And LEG < Abs(L4 - LFG) ThenIf MsgBox("RRR杆组杆长不符合要求", vbOKOnly, "提示") = 1 Then EndElseEnd IfElseEnd IfIf LEG < L4 + LFG And LEG > Abs(L4 - LFG) Thenval2 = (L4 ^ 2 + LEG ^ 2 - LFG ^ 2) / (2 * L4 * LEG)JFEG = Atn(-val2 / Sqr(-val2 * val2 + 1)) + 2 * Atn(1)ElseEnd IfIf LEG = L4 + LFG ThenJFEG = 0ElseEnd IfIf LEG = Abs(L4 - LFG) ThenIf L4 > LFG ThenJFEG = 0ElseEnd IfIf L4 < LFG ThenJFEG = piElseEnd IfElseEnd IfIf xG > xE And yG >= yE Then '第一象限fGE = Atn((yG - yE) / (xG - xE))ElseEnd IfIf xG = xE And yG > yE ThenfGE = pi * 2ElseEnd IfIf xG < xE And yG >= yE Then '第二象限fGE = pi + Atn((yG - yE) / (xG - xE)) ElseEnd IfIf xG < xE And yG < yE Then '第三象限fGE = pi + Atn((yG - yE) / (xG - xE)) ElseEnd IfIf xE = xG And yG < yE ThenfGE = 3 * pi / 2ElseEnd IfIf xG > xE And yG <= yE Then '第四象限fGE = 2 * pi + Atn((yG - yE) / (xG - xE)) ElseEnd Iff4 = fGE - JFEGxF = xE + L4 * Cos(f4)yF = yE + L4 * Sin(f4)If xF > xG And yF >= yG Then '第一象限f5 = Atn((yF - yG) / (xF - xG))ElseEnd IfIf xF = xG And yF > yG Thenf5 = pi / 2ElseEnd IfIf xF < xG And xF >= xG Then '第二象限f5 = pi + Atn((yF - yG) / (xF - xG))ElseEnd IfIf xF < xG And xF < xG Then '第三象限f5 = pi + Atn((yF - yG) / (xF - xG))ElseEnd IfIf xF = xG And xF < xG Thenf4 = 3 * pi / 2ElseEnd IfIf xF > xG And xF <= xG Then '第四象限f4 = 2 * pi + Atn((yF - yG) / (xF - xG)) ElseEnd IfC4 = L4 * Cos(f4)S4 = L4 * Sin(f4)C5 = LFG * Cos(f5)S5 = LFG * Sin(f5)G21 = C4 * S5 - C5 * S4w4 = (C5 * (vxG - vxE) + S5 * (vyG - vyE)) / G21w5 = (C4 * (vxG - vxE) + S4 * (vyG - vyE)) / G21vxF = vxE - w4 * L4 * Sin(f4)vyF = vyE + w4 * L4 * Cos(f4)G22 = axG - axE + w4 ^ 2 * C4 - w5 ^ 2 * C5G23 = ayG - ayE + w4 ^ 2 * S4 - w5 ^ 2 * S5e4 = (G22 * C5 + G23 * S5) / G21e5 = (G22 * C4 + G23 * S4) / G21axF = axE - e4 * L4 * Sin(f4) - w4 ^ 2 * L4 * Cos(f4)ayF = ayE - e4 * L4 * Cos(f4) - w4 ^ 2 * L4 * Sin(f4)End SubPublic Sub RR3() '杆GHxH = xG + LGH * Cos(f5 + deltGH)yH = yG + LGH * Sin(f5 + deltGH)vxH = vxG - w5 * LGH * Sin(f5 + deltGH)vyH = vyG + w5 * LGH * Cos(f5 + deltGH)axH = axG - w5 ^ 2 * LGH * Cos(f5 + deltGH) - e5 * LGH * Sin(f5 + deltGH) ayH = ayG - w5 ^ 2 * LGH * Sin(f5 + deltGH) + e5 * LGH * Cos(f5 + deltGH) End SubPublic Sub RRP1() '杆组H(M)KDim A0 As DoubleDim Q1 As DoubleDim Q2 As DoubleDim Q3 As DoubleDim Q4 As DoubleDim Q5 As DoubleDim val3 As DoubleA0 = Lj + (yN - yH) * Cos(fj) - (xN - xH) * Sin(fj)val3 = A0 / L6fi = Atn(val3 / Sqr(-val3 * val3 + 1)) + fjxM = xH + L6 * Cos(fi)yM = yH + L6 * Sin(fi)ss = (xM - xN) * Cos(fj) + (yM - yN) * Sin(fj)xK = xN + ss * Cos(fj)yK = yN + ss * Sin(fj)Q1 = vxN - vxH - wj * (ss * Sin(fj) + Lj * Cos(fj))Q2 = vyN - vyH + wj * (ss * Cos(fj) - Lj * Sin(fj))Q3 = L6 * Sin(fi) * Sin(fj) + L6 * Cos(fi) * Cos(fj)w6 = (-Q1 * Sin(fj) + Q2 * Cos(fj)) / Q3vss = -(Q1 * L6 * Cos(fi) + Q2 * L6 * Sin(fi)) / Q3vxM = vxH - w6 * L6 * Sin(fi)vyM = vyH + w6 * L6 * Cos(fi)vxK = vxN + vss * Cos(fj) - ss * wj * Sin(fj)vyK = vyN + vss * Sin(fj) + ss * wj * Cos(fj)Q4 = axN - axH + w6 ^ 2 * L6 * Cos(fi) - ej * (ss * Sin(fj) + Lj * Cos(fj)) - wj ^ 2 * (ss * Cos(fj) - Lj * Sin(fj)) - 2 * vss * wj * Sin(fj)Q5 = ayN - ayH + w6 ^ 2 * L6 * Sin(fi) + ej * (ss * Cos(fj) - Lj * Sin(fj)) - wj ^ 2 * (ss * Sin(fj) + Lj * Cos(fj)) + 2 * vss * wj * Cos(fj)e6 = (-Q4 * Sin(fj) + Q5 * Cos(fj)) / Q3ass = (-Q4 * L6 * Cos(fi) - Q5 * L6 * Sin(fi)) / Q3axM = axH - e6 * L6 * Sin(fi) - w6 ^ 2 * L6 * Cos(fi)ayM = ayH + e6 * L6 * Cos(fi) - w6 ^ 2 * L6 * Sin(fi)axK = axN + ass * Cos(fj) - ss * ej * Sin(fj) - ss * wj ^ 2 * Cos(fj) - 2 * vss * wj * Sin(fj)ayK = ayN + ass * Sin(fj) + ss * ej * Cos(fj) - ss * wj ^ 2 * Sin(fj) + 2 * vss * wj * Cos(fj)End Sub(四)计算结果分析用VB编程可得构件6的位移、速度、加速度图像，由图像可得机构运动一个周期内每个时刻的运动参数值，较为直观。

哈工大机械原理大作业连杆机构9

机械原理大作业大作业一：连杆机构运动分析学生姓名：学号：指导教师：丁刚完成时间：机电工程学院机械设计系制二〇一八年四月连杆机构运动分析1题目（9）图1 设计题目在图1所示的机构中，已知l AB=60mm，l BC=180mm，l DE=200mm，l CD=120mm，l EF=300mm，h=80mm，h1=85mm，h2=225mm，构件1以等角速度ω1=100rad/s 转动。

求在一个运动循环中，滑块5的位移、速度和加速度曲线。

2分析结构1、杆1为RR主动件，绕A以ω1 转动，自由度1.2、4杆和滑块5为RRP II级杆组.，自由度0.3、2，3杆组成II级杆组RRR，自由度0.总共自由度为F=5*3-2*7=1 .由上述的杆组类型，确认出所需运动分析数学模型：同一构件上的点、RRP、RRR。

3.杆组法对平面连杆机构进行运动分析3.1对主动件杆1 RR I级构件的分析主动杆1转角：φ= [0°,360°) δ=0°,则φ’=ω1=100 rad/s角加速度φ’’=0.已知h2=225mm, h=80mm, l AB=60mm 所以A（225mm,80mm）A点速度(0,0),加速度(0,0)B点位置(x A+l AB*cos(φ), Y A+l AB*sin(φ))B点速度(-l AB*sin(φ), l AB*cos(φ)),加速度(-l AB*cos(φ), -l AB*sin(φ))3.2RRRII 级杆组分析（模型参考教材P37-38）图3 如图所示两个构件组成II 级杆组。

已知了B 的位置（x B ，y B ）= (x A +l AB *cos(φ), Y A +l AB *sin(φ)),速度（x ’B ，y ’B ）和加速度（x ’’B ,y ’’B ）, 已知运动副D （0,0），还可知，x ’D =y ’D =0, x ’’D =y ’’D =0. l BC =180 mm, l CD = 120mm所以，x c =x D +l CD *cos(φi)= x B +l BC *cos(φj) y c =x D +l CD *sin(φi)= x B +l BC *sin(φi) 对于φ的求解： A 0=2*l CD （x B -x D ） B 0=2*l BC （y B -y D ） C 0=l CD 2+ l BD 2- l BC 2为了保证机构的装配正常：l BD ≤l CD + l BC AND l BD ≥Abs （l CD - l BC ）可求3杆的转角φi=2*arctan(（B 0±sqrt （A 02 + B 02- C 02））/（A 02+ C 02)），角速度w3=φi ’和角加速度α3= φi ’’3.3 同一构件上的点(模型参考书P35-36)Φiφjφi已知D(0,0),速度(0,0),加速度(0,0),3杆转角φi 角速度φi’角加速度φi’’，Φi和它的导数在3.2都有体现LDE= 200mm可求出E的坐标,速度,加速度.x E =x c+lCE*cos(φi)y E =x C+lCE*sin(φi)同样地，速度、加速度通过求导即可得出算式，可以编出程序。

哈工大机械原理大作业连杆

哈工大机械原理大作业连杆Modified by JACK on the afternoon of December 26, 2020Harbin Institute of Technology机械原理大作业一课程名称：机械原理设计题目：连杆机构运动分析院系：机电工程学院班级：设计者：学号：指导教师：设计时间：1.运动分析题目(11)在图所示的六杆机构中，已知：AB l =150mm, AC l =550mm, BD l =80mm, DE l =500mm,曲柄以等角速度1w =10rad/s 沿逆时针方向回转，求构件3的角速度、角加速度和构件5的位移、速度、加速度。

2.机构的结构分析建立以点A 为原点的固定平面直角坐标系A-x, y,如下图：机构结构分析该机构由Ⅰ级杆组RR （原动件1）、Ⅱ级杆组RPR （杆2及滑块3）和Ⅱ级杆组RRP （杆4及滑块5）组成。

3.建立组成机构的各基本杆组的运动分析数学模型原动件1（Ⅰ级杆组RR ）由图所示，原动件杆1的转角a=0-360°，角速度1w =10rad/s ，角加速度1a =0,运动副A 的位置坐标A x =A y =0,速度(A ，A)，加速度（A ，A ），原动件1的长度AB l =150mm 。

求出运动副B 的位置坐标（B x , B y ）、速度（B ，B ）和加速度（B ，B ）。

杆2、滑块3杆组（RPR Ⅱ级杆组）已出运动副B 的位置（B x , B y ）、速度（B ，B ）和加速度（B ，B ），已知运动副C 的位置坐标C x =0, C y =550mm,速度，加速度，杆长AC l =550mm 。

求出构件2的转角b,角速度2w 和角加速度2a . 构件二上点D 的运动已知运动副B 的位置（B x , B y ）、速度（B ，B ）、加速度（B ，B ），已经求出构件2的转角b ，角速度2w 和角加速度2a ，杆BD 的长度BD l =80mm 。

哈工大机械原理大作业连杆机构

H a r b i n I n s t i t u t e o f T e c h n o l o g y连杆机构运动分析课程名称：机械原理设计题目：院系：班级：设计者：学号：指导教师：设计时间：哈尔滨工业大学一、连杆机构运动分析已知机构各构件的尺寸为AB=100mm，BC=2.73AB，CD=1.36AB，CG=2.36AB，BG=4.9AB，AF=2.36AB，AD=2.87AB，DF=2AB，GE=1.45AB，EF=2.82AB，GM=1.36AB，MK=1.91AB，KD=0.54AB，KF=2.81AB，HF=3.1AB，DH=3.63AB， =135 ，构件1的角速度为w1=10rad/s。

试求构件2上点G的轨迹以及构件4、构件6和构件8的角位移、角速度与角加速度。

并对计算结果进行分析。

二、机构的结构分析，组成机构的基本杆组划分该机构由一个I级杆组以及若干个II级杆组组成。

I 级杆组为：原动件1。

II级杆组为：杆2与杆CD（RRR杆组）、滑块G、杆4（RPR杆组）、杆5、杆6（RRR 杆组）、杆7与杆8（RRR杆组）。

I级杆组 1（原动件与机架）II 级杆组 1（RRR 杆2与杆CD ）II 级杆组 2（RPR 杆4与滑块3）II 级杆组 3(RRR 杆5与杆6)II 级杆组 4（RRR 杆7与杆8）三、各基本杆组的运动分析数学模型1) 根据机构运动简图，运动副A 为固定点，其位置、速度、加速度,,,,a a ax ay ax ayx y v v a a ,和杆AB 的角位移、角速度、角加速度,,ab ab ab ϕωα均已知，并且杆AB 长度为AB l 已知，使用同一构件上点的运动分析模型，可以计算出B 点的位置、速度以及加速度,,,,b b bx by bx byx y v v a a ,。

2) 已知运动副D 的位置、速度、加速度,,,,d d dx dy dx dyx y v v a a ,，以及杆CD 的长度CD l 、杆BC 的长度BC l ，B 点的参数上面已求出，使用RRRII 级杆组运动分析模型，可以求解出运动副C 的位置、速度、加速度,,,,c c cx cy cx cyx y v v a a ,，以及杆BC 的角位移、角速度、角加速度,,bc bc bc ϕωα。

机械原理第三章3-9复数矢量法

l1 l2 l3 l4
i1
以复数形式表示为： l 1e
l 2 ei 2 l4 l 3ei3
(a)
注意：角以x轴的正向逆时针度量。
一、铰链四杆机构
l 1e
i1
l 2 e
i 2
l4 l 3e
i 3
(a)
按欧拉公式展开得：
l 1 (cos 1 i sin 1 ) l2 (cos 2 i sin 2 ) l4 l3 (cos 3 i sin 3 )
将(a)式对时间求导数得：
(a)
l 11ie
l 11ie
i1
l 2 2ie
e
i 2
l 3 3ie
i 3 (c)
为消去2，(c)式两边乘以
i (1 2 )
i 2
l 2 2ie
i ( 2 2 )
l 3 3ie
i ( 3 2 )
按欧拉公式展开：取实部得：
2 2 2 1 2 3
一、铰链四杆机构
同理得： 2
2 2 l33 l112 cos(1 3 ) l22 cos(2 3 ) 2 l2 sin(2 3 )
注意: 角加速度的正负号表示角速度的变化趋势，角加速度与角速度同号时，表示加速；异号时表示减速。
的一元二次方程，由此解出
tan(3 / 2)
B A2 B 2 C 2 3 2arctan AC
的装配模式; “-” 表示虚线所示的装配模式。
3解中的正负号，表明有两个解。“+”表示实线所示
一、铰链四杆机构
y B 1
2 1 1
2
C 3
3
4
D x

哈工大机械原理大作业——凸轮——1号

哈工大机械原理大作业——凸轮——1号Harbin Institute of Technology机械原理大作业2课程名称：机械原理设计题目：凸轮机构设计院系：机电工程学院哈尔滨工业大学一、设计题目：设计直动从动件盘形凸轮机构，其原始参数见表1序号升程（mm)升程运动角（º）升程运动规律升程许用压力角（º）回程运动角（º）回程运动规律回程许用压力角（º）远休止角（º）近休止角（º）7 70 90 正弦加速度30 80 3-4-5多项式70 95 95二、凸轮推杆升程、回程运动方程及推杆位移、速度、加速度线图：（1）凸轮推杆升程运动方程：正弦加速度：0≪φ≪Φ0s=h[φΦ0−12πsin(2πΦ0φ)]v=ℎω1Φ0[1−cos(2πΦ0φ)]a =2πℎω122sin (2π0φ) (2) 凸轮推杆回程运动方程： 3-4-5多项式：πϕπ36533637≤≤ s =h [1−(10T 23−15T 24+6T 25)]v =−30ℎω1Φ0′T 22(1−2T 2) a =−60ℎω12′2T 2(1−3T 2+2T 22) 式中：T 2=φ−(Φ0+Φs )Φ0′[]⎭⎬⎫⎩⎨⎧Φ-Φ-Φ+=)(cos 12/0'0s h s ϕπ[])(sin 20''1s hw v Φ+Φ-ΦΦ-=ϕππ[])(cos20'2'0212s hw a Φ+Φ-ΦΦ-=ϕππ（3）运用Matlab 软件进行编程，令1w =w =10rad/s ，程序如下：syms h w f0 fs f0s fss a1 a2 l1 l2 t2 s v a F f dsf h=70; w=10;f0=90*pi/180; fs=95*pi/180; f0s=80*pi/180; fss=95*pi/180; a1=30*pi/180; a2=70*pi/180; l1=0; l2=0;F=0.1:360; f=F*pi/180;t2=(f-(f0+fs))/f0s;s=70.*(f/f0-1/(2*pi).*sin(2*pi*f/f0)).*(F<=90)+70.*(F>90&F<=185)+70*(1-(10*(t2).^3-15*(t2).^4+6*(t2).^5)).*(F>185&F<=265)+0.*(F>265&F<=360);+0.*(F>265&F<=360); +0.*(F>265&F<=360); plot(F,s)画图得到推杆位移线图：推杆速度线图：推杆加速度线图：三、凸轮机构的s d ds-ϕ线图，并依次确定凸轮的基圆半径和偏距：plot(dsf,s)凸轮机构的s d ds-ϕ线图：确定凸轮的基圆半径和偏距:由上图和许用压力角可知凸轮基圆半径：r0 = 75mm ，偏距e = 33mm 。

哈工大机械原理大作业2-29

设计说明书1 设计题目如图所示直动从动件盘形凸轮机构，其原始参数见表2-1。

从表2-1中选择一组凸轮机构的原始参数，据此设计该凸轮机构。

2、推杆升程、回程运动方程及位移、速度、加速度线图2.1凸轮运动分析推程运动方程; 01cos 2h s πϕ⎡⎤⎛⎫=-⎢⎥ ⎪Φ⎝⎭⎣⎦100sin 2h v πωπϕ⎛⎫=⎪ΦΦ⎝⎭221200cos 2h a πωπϕ⎛⎫= ⎪ΦΦ⎝⎭回程运动方程：()'1s s hϕ-Φ+Φ⎡⎤=-⎢⎥Φ⎣⎦1'hvω=-Φa=2.2求位移、速度、加速度线图MATLAB源程序pi=3.1415926;c=pi/180;h=140;f0=120;fs=45;f01=90;fs1=105;%升程阶段f=0:1:360;for n=0:f0s(n+1)=h/2*(1-cos(pi/f0*f(n+1)));v(n+1)=pi*h/(2*f0*c)*sin(pi/f0*f(n+1));a(n+1)=pi^2*h/(2*f0^2*c^2)*cos(pi/f0*f(n+1));end%远休止阶段for n=f0:f0+fss(n+1)=140;v(n+1)=0;a(n+1)=0;end%回程阶段for n=f0+fs:f0+fs+f01s(n+1)=h*(1-(f(n+1)-(f0+fs))/f01);v(n+1)=-h/(f01*c);a(n+1)=0;end;%近休止阶段for n=f0+fs+f01:360;s(n+1)=0;v(n+1)=0;a(n+1)=0;endfigure(1);plot(f,s,'r');xlabel('\phi/\circ');ylabel('s/mm');grid on;title('推杆位移线图')figure(2);plot(f,v,'r');xlabel('\phi/\circ');ylabel('v/\ommiga');grid on;title('推杆速度线图') figure(3);plot(f,a,'r');xlabel('\phi/\circ');ylabel('a/\ommiga');grid on;title('推杆加速度线图')2.3位移、速度、加速度线图3 凸轮机构的dssdϕ-线图，确定基圆半径和偏心距3.1理论分析机构压力角α应按下式计算：以d s/dφ为横坐标，以s(φ)为纵坐标，可作出d s/dφ-s(φ)曲线如图4-16所示，再作斜直线D t d t 与升程的[d s/dφ-s(φ)]曲线相切并使与纵坐标夹角为升程[α]，则D t d t线的右下方为选择凸轮轴心的许用区。

机械原理(2015春)用解析法作机构的运动分析

w32 l3
2、矩阵法（1）位置分析：
位置方程：
整理：解此方程可得
（2）速度分析：
将位置方程对时间求一次导数写成矩阵形式
解此矩阵方程可得
（3）加速度分析
速度方程：将此速度方程对时间求一次导数，得加速度方程：
解此方程可得
3、杆组法
（1）基本原理
B
拆杆组
B+
（2）杆组法运动分析子程序
(1)单杆构件的运动分析子程序
用杆组法进行机构运动分析时，要正确拆分杆组，在调用各杆组运动分析的子程序时，首先要根据机构的初始位置判断该杆组的装配形式，确定位置模式系数M(+1或-1），再去调用子程序。主程序调用子程序时注意形参与实参之间的对应关系。
学会如何把一个复杂问题转化为用计算机解决的问题，是培养解决问题能力的锻炼机会。
已知：xA , yA, l, vA, aA 求：xB, yB , vB , aB
位置分析：速度分析：
rB = rA + l
xB = xA + l cosj yB = yA + l sinj
将位置方程对时间求一次导数，得速度方程，带入已知量，求出未知量
加速度分析：
将速度方程对时间求一次导数，得加速度方程，带入已知量，求出未知量
- l3w3程可得：
a3
=
l1w12
cos(q1
- q2 ) + w22l2 - l3w32 l3 sin(q3 - q2 )
cos(q 3
- q2 )
a2
=
-
l1w12
cos(q1
- q3 ) - w22l2 cos(q2 l3 sin(q2 - q3 )

哈工大机械原理大作业(连杆机构)

三、建立数学模型
建立坐标系：以C为原点，水平方向为X轴，CA所在直线为Y轴建立直角坐标系（如图4）。
取曲柄1水平且位于A点右侧为初始时刻，设曲柄1角速度为w，由题意知w= =8.5π rad/s………………（1）
设曲柄1转角为θ，则B点坐标：
xB=ιABcosθ=ιABcoswt
yB=H1+ιABsinθ=H1+ιABsinwt………………（2）
form=1:length(t)-1
ddxF(m)=(dxF(m+1)-dxF(m))/0.0001;
end
ddxF(length(t))=ddxF(length(t)-1);
figure
plot(t,ddxF)
title('¼ÓËÙ¶ÈÍ¼Ïñ');
xlabel('t /s'),ylabel('v /(m/s^2)');
输出图像：
xE(m)=yE(m)/k(m);
xF(m)=xE(m)-(-H^2+lEF^2-yE(m)^2+2*yE(m)*H)^(1/2)+0.1142;
end
form=1:length(t)-1
dxF(m)=(xF(m+1)-xF(m))/0.0001;
end
dxF(length(t))=dxF(length(t)-1);
∵ιEF+ιCE>H且ιCE<H
∴E点始终在F点的右下方
∴xF<xE,所以x2舍去，只取xF=x1……………（8）
∴点F坐标为（xF，H）
当t=0时，可得F点初始位置坐标，不妨设为（xo,H）。
则F点位移（通过计算，t=0时，得xo=-0.1142）

用矢量方程图解法作机构的速度及加速度分析

1 3
C
? 21LAB ? CB AB BC
由图解法得到
B3点的绝对速度 vB3v pb3，方向p→b3 B3 点相对于 B2 点的速度 vB3B2v pb3，方向b2→ b3
b3 p
b2
3v pb3LBC，顺时针方向
n t r k aB3 aB3 aB3 aB2 aB3B2 aB3B2
B
pቤተ መጻሕፍቲ ባይዱ
速度影像的用途对于同一构件，由两点的速度可求任意点的速度。举例求BC中间点E的速度
A
C E B
bc上中间点e为E点的影像联接pe，就代表E点的绝对速度vE。
a
e
c
p
b
② 加速度关系设已知角速度，A点加速度aA和B 点加速度aB的方向。 A、B两点间加速度关系式 n t a B a A a BA a BA 大小 ? √ 2LAB ? 方向 √ √ B→A BA
a
c
⑶ 两构件上重合点之间的运动关系
转动副移动副
v B1 v B 2
重合点
B
a B1 a B 2
C
vB2 vB3
A 2 1
aB 2 aB 3
2
B
3

1 A

重合点
D C
① 速度关系
大小方向
牵连运动
相对运动 1 2
A B 3
vB3 vB2 vB3B2
选加速度比例尺a (ms2mm) ，在任意点 p 作图，使aAa pa，anBA=aab 由图解法得到 aBa pb，方向p→b atBAa bb，方向b→b aBAa ab，方向a→b

5.1 连杆的速度和加速度

x
y x
0
相应的角速度矢量：
k x x k y y k k z z
角速度算子 s( ) 和角速度矢量是角速度的两种描述，在任意矢径p处引起的线速度 vp 可表示为：
A A A A vp B RBvp s( AB )B RB p
vBo A vBo 0
A A A A vp B RBvp 2s( AB )B RBvp s( AB )B RB p s( AB )s( AB )B RB p
因为角速度矢量是自由矢量，若已知｛C｝相对｛B｝的转动角速度，则｛C｝相对｛A｝的转动角速度和角加速度矢量为：
i
vci i vi i i i pci
i
vci i vi i i i pci i i (i i i pci )
i 1
移动关节的连杆运动的传递
当关节i+1是移动关节时，连杆i+1相对坐标系｛i+1｝的z轴移动，没有转动，旋转矩阵是常数矩阵，相应的传递关系为：
i 1
i1 ii1 Rii
i1 ii1 Rii
i 1
i 1
vi1 ii1 R(i vi i i i pi 1 ) di1i 1zi1
动力学逆问题－－已知操作臂的运动（关节位移、速度和加速度），求出所需的关节力或力矩
动力学的目的：动力学正问题与操作臂的仿真研究有关，逆问题是为零实时控制的需要，利用动力学模型，实现最优控制，以期达到良好的动态性能和最优指标动力学的用途：机器人动力学模型主要用于机器人的设计和离线编程。本章体系结构：为了建立机器人动力学方程，本章首先讨论机器人运动的瞬时状况，对其进行速度分析和加速度分析，研究连杆的静力学平衡问题。然后利用达朗贝尔原理，将静力学平衡条件用于动力学问题。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

机原大作业
题3-23
班级：
学号：
姓名：
指导老师：
题目
3-23 在图示机构中，已知原动件1以等角速度w1=10rad/s 逆时针转动，l AB =100mm ， l BC =300mm ，e=30mm 。

试用复数矢量法求构件2的转角θ2、角速度w2和角加速度α2，构件3的速度v 3和加速度a 3。

（1）建立封闭矢量多边形
L1+L2=L4+e (a) L1e iθ1+L2e iθ2=L4 (b)
=>{L1cosθ1+L2cosθ2=L4
L1sinθ1+L2sinθ2=e
(c)
联立可得
L4=[l 22
−(e −l 1sinθ1)2]1/2+l 1cosθ1 （d ）
θ2=arctan [e−l 1cosθ1
l
4−l 1cosθ1
] (e)
(2)速度分析
将试(b)对时间t 求导，可得
il 1w 1e iθ1+il 2w 2e iθ2=l 4
(f) 将上式虚部和实部分开，并联解可得 l 4
=v 3=−[w 1l 1sin (θ1−θ2)]/cosθ2 w 2=−
l 1cosθ1
l 2sinθ2w 1
(3)加速度分析
将式（f）对时间进行求导，可得
-l1w12e iθ1+il2w2e iθ1−l2w22e iθ2=l4
将上式虚部和实部分开，并联解可得
w2=α2=−(w12l1sinθ1+w22l2sinθ2)/(l2cosθ2)
l4=a3=[−w12l1cos(θ1−θ2)+w22l2]/ cosθ2
(4)程序代码（c语言）
#include<stdio.h>
#include<math.h>
#define pi 0.1745329
#define pai 3.1415926
int main()
{
double w1=10,l1=0.1,l2=0.3,e=0.03,j1=0,j2,w2,a2,v3,a3,l4;
double j2hudu;
FILE *fp;
fp=fopen("d:\\jiyuandazuoye.txt","w");
int i;
for(i=0;i<=180;i++)
{
l4=sqrt(fabs(l2*l2-((e-l1*sin(j1*pi))*(e-l1*sin(j1*pi)))))+l1*cos(j1*pi);
j2hudu=atan((e-l1*cos(j1*pi))/(l4-l1*cos(j1*pi)));
j2=pai*j2hudu;
v3=-(w1*l1*sin((j1*pi-j2hudu))/cos(j2hudu));
w2=-(l1*w1*cos(j1*pi))/(l2*sin(j2hudu));
a2=-(w1*w1*l1*sin(j1*pi)+w2*w2*l2*sin(j2hudu))/(l2*cos(j2hudu));
a3=(-w1*w1*l1*cos(pi*j1-j2hudu)+w2*w2*l2)/cos(j2hudu);
fprintf(fp,"j1=%.3f l4=%.3f j2=%.3f w2=%.3f a2=%.3f v3=%.3f a3=%.3f\n",j1,l4,j2,w2,a2,v3,a3);
j1+=2;
}
fclose(fp);
return 0;
}
（5）图像。