完全平方公式的几何背景专题训练试题精选附复习资料
1-6 完全平方公式(分层练习)(解析版)

第一章整式的乘除1.6完全平方公式精选练习一、单选题1.(2022秋·福建泉州·八年级校考期末)已知a、b不同的两个实数,且满足0ab>、2242a b ab+=-,当a b-为整数时,ab的值为()A.34或12B.1C.34D.14或34A .12xyB .24xyC .24xy -D .12xy-【答案】C【分析】先利用完全平方公式去括号,再求值即可.【详解】解:22(23)(23)x y x y A -=++,222241294129x xy y x xy y A -+=+++,24A xy =-,故选:C .【点睛】本题考查整式的混合运算,解题关键是掌握完全平方公式.3.(2022秋·全国·八年级专题练习)已知2283a b a b =+-=,,则ab 的值为()A .32B .3C .﹣12D .5222021202120222022b =-⨯+,在下列判断结果正确是().A .a b >B .a b<C .a b=D .无法判断【答案】C【分析】根据完全平方公式的变形,将b 化简,进而与a 比较即可求解【详解】解:202120221a =⨯+,222021202120222022b =-⨯+()22021202220212022=-+⨯202120221=⨯+,故a b =.故选C .【点睛】本题考查了完全平方公式的变形,掌握完全平方公式的变形是解题的关键.5.(2022秋·全国·八年级专题练习)如图所示分割正方形,各图形面积之间的关系,验证了一个等式,这个等式是()A .()222y x y xy x +=++B .()2222y x y xy x +=++C .()()22y x y x y x-=-+D .()()22y x y x xy+--=4【答案】D【分析】此图形中,一个大正方形的面积-小正方形的面积=四个矩形的面积.【详解】解:如图,大正方形的面积()2y x =+,小正方形的面积()2y x =-,四个长方形的面积4xy =,则由图形知,大正方形的面积-小正方形的面积=四个矩形的面积,即()()22y x y x xy +--=4.故选:D .【点睛】本题考查了完全平方公式的几何背景.应从整体和部分两方面来理解完全平方公式的几何意义;主要围绕图形面积展开分析.6.(2022秋·全国·八年级期末)图(1)是一个长为2a ,宽为2b a b (>)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空余的部分的面积是()A .abB .()2+a b C .()2a b -D .22a b -【答案】C【分析】根据中间部分的四边形是正方形,表示出边长,则面积可以求得.【详解】解:中间部分的四边形是正方形,边长是+2a b b a b -=-,则面积是()2a b -.故选:C .【点睛】本题考查了完全平方公式的几何背景,求出正方形的边长是解答本题的关键.二、填空题7.(2022秋·福建泉州·八年级校考期末)若22m m -=,那么()()()21223m m m -++-+的值为________.【答案】4【分析】先去括号,再合并同类项,然后把22m m -=代入化简后的式子进行计算即可解答.【详解】()()()21223m m m -++-+222143m m m =-++-+222m m =-,当22m m -=,原式()22224m m =-=⨯=,故答案为:4.【点睛】本题考查了整式的混合运算-化简求值,准确熟练地进行计算是解题的关键.8.(2022秋·湖北武汉·八年级校考期末)计算()()55a b c a b c -++-=____________.【答案】2221025a b bc c -+-【分析】利用平方差公式和完全平方公式进行计算即可得.【详解】解:原式()()55a b c a b c ⎡⎤⎡⎤=--+-⎣⎦⎣⎦()225a b c =--()2221025a b bc c =--+2221025a b bc c =-+-,故答案为:2221025a b bc c -+-.【点睛】本题考查了平方差公式和完全平方公式,熟记乘法公式是解题关键.9.(2022秋·湖北武汉·八年级校考期末)24x kx -+是完全平方式,则k =____________.【答案】4±【分析】根据完全平方公式()2222a b a ab b ±=±+即可得.【详解】解:22242x kx x kx -+=-+ 是完全平方式,()22222x kx x ∴-+=±,22444x kx x x ∴-+=±+,4k ∴=±,故答案为:4±.【点睛】本题考查了完全平方式,熟记公式是解题关键.10.(2021春·贵州贵阳·八年级贵阳市第十七中学校考期中)如果()22164x mx x -+=+,那么m =______.【答案】8-【分析】把右边的完全平方公式展开,根据多项式相等,比较两边对应项的系数,即可求得m 的值.【详解】解:()228164x x x +=++ ,2281616mx x x x ∴+++-=,8m ∴-=,8m ∴=-,故答案为:8-.【点睛】本题考查了完全平方公式,两个多项式的相等,应用完全平方公式展开是关键.三、解答题11.(2022秋·河北保定·八年级统考期末)计算:(1)()()24322a a a a ++⋅;(2)()()()2322x x x +++-.【答案】(1)418a ;(2)2265x x ++.【分析】(1)根据同底数幂的乘法、幂的乘方和积的乘方的运算法则展开,再合并同类项即可.(2)根据乘法公式展开,再合并同类项即可.【详解】(1)解:()()24322a a a a ++⋅44416a a a =++418a =;(2)解:()()()2322x x x +++-22694x x x =+++-2265x x =++.【点睛】本题考查了整式的运算,熟练掌握整式的运算法则是解题的关键.12.(2022秋·吉林长春·八年级统考期中)先化简,再求值:()()()2311x x x -++-,其中=1x -.【答案】610x -+,16【分析】利用完全平方公式,平方差公式进行计算,然后把x 的值代入化简后的式子进行计算即可解答.【详解】解:原式22691x x x =-++-610x =-+当=1x -时,原式()()611016=-⨯-+=.【点睛】本题考查了整式的混合运算-化简求值,准确熟练地进行计算是解题的关键.一、填空题1.(2022秋·山东滨州·八年级校考期末)已知5x y a a a ⋅=,()4xy a a =,则x y +=________,xy =______,22x y +=__________.【答案】5417【分析】根据同底数幂的乘法和幂的乘方运算法则,即可求出x y +和xy 的值,再根据完全平方公式即可求出22x y +的值.【详解】解:∵5x y a a a ⋅=,()4xy a a =,∴5x y +=,4xy =,∴()2222252417x y x x y y =+-=-=+⨯,故答案为:5,4,17.【点睛】本题主要考查了同底数幂的乘法运算法则,幂的乘方运算法则,完全平方公式,解题的关键是掌握同底数幂的乘法,底数不变,指数相加;幂的乘方,底数不变,指数相乘;完全平方公式()2222a b a ab b ±=±+.2.(2022秋·湖北·八年级统考期末)已知:0x >,1x x-=1x x +=_____.【详解】解:∵1x x-=,0x >∴1x x +==是完全平方式,则的值为______.【答案】9或1-##1-或9【分析】根据完全平方公式的特点:首平方,尾平方,首尾两数积的两倍在中央求解即可.【详解】解:∵()22425x m x +-+是完全平方式,∴()2425m x x -=±⨯,整理得:2810m -=或2810m -=-,解得9m =或1m =-,故答案为:9或1-.【点睛】本题考查完全平方式,记住完全平方式的特征是解题的关键,形如222a ab b ±+这样的式子是完全平方式,属于中考常考题型.4.(2022秋·北京海淀·七年级清华附中校考期末)已知2810m m -+=,则22128m m m -+=______.5.(2022秋·天津和平·八年级天津一中校考期末)(1)已知,,则的值为______.(2)已知()249x y +=,2227x y +=,则()2x y -的值为______.(3)已知x 满足()()222022202412x x -+-=,则()22023x -的值为______.【答案】3955【分析】(1)将22xy +变形为()+-22xy xy ,再代入已知条件计算即可;(2)将22x y +变形为()+-22x y xy ,再代入已知条件,即可求出xy 值,将()2x y -变形为()24x y xy +-,代入即可求解.(3)将()()222022202412x x -+-=变形为()()22202312023112x x -+++-=,则()()22202311202312x x -++--=⎡⎤⎣⎦,将2023x -看做成一个整体,化简即可求得()22023x -的值.【详解】解:(1)∵7x y +=,5xy =,∴22x y +()22x y xy=+-2725=-⨯39=,故答案为:39;(2)∵()249x y +=∴22249x xy y ++=∵2227x y +=,∴11xy =,∴()2x y -222x xy y =-+()24x y xy=+-49411=-⨯故答案为:5;(3)∵()()222022202412x x -+-=,∴()()22202312023112x x -+++-=,()()22202311202312x x -++--=⎡⎤⎣⎦,()()()()222023220231122023202312x x x x -+-++--+-=,()222023212x -+=,()220235x -=,故答案为:5.【点睛】本题考查完全平方公式的应用,熟练掌握利用完全平方公式变形求代数式值是解题的关键.二、解答题6.(2022秋·全国·八年级专题练习)已知3a b +=,4ab =-,求下列各式的值.(1)2()a b -;(2)225a ab b -+.【答案】(1)25(2)37【分析】(1)利用完全平方差公式变形即可求解;(2)利用完全平方公式变形,将式子用含a b +、ab 的式子表示,再代入求解.【详解】(1)解:224a b a b ab-=+-()()()2344=-⨯-25=(2)解:2222527a ab b a ab b ab-+=++-27a b ab=+-()9(28)=--37=【点睛】本题考查了完全平方公式及其变形式,根据公式的特征进行变形是求解的关键.7.(2022秋·陕西渭南·八年级校考阶段练习)(1)证明:相邻两个奇数的平方的差是8的倍数.(注释:两个奇数的平方的差:两个奇数各自平方,然后相减)(2)证明:任意两个奇数的平方的差是4的倍数.(3)已知1139273m m ⨯⨯=,求m 的值.【答案】(1)见解析;(2)见解析;(3)2【分析】(1)表示出相邻两个奇数为:21n +,23n +,列出他们平方的差进行计算即可;(2)表示相互两个奇数为:21n +,21m +,列出他们平方的差进行计算即可;(3)将9m ,27m 转化为底数为3的形式,再利用幂的乘方和同底数幂的乘方运算即可.【详解】(1)证明:相邻两个奇数的平方的差是8的倍数.(注释:两个奇数的平方的差:两个奇数各自平方,然后相减)设:这两个奇数为:21n +,23n +(注:设为2n -1,2n +1也可以)()()222321n n ++-()224129441n n n n =++-++88n =+则:()8881n n +=+是8的倍数,∴相邻两个奇数的平方的差是8的倍数.(2)证明:任意两个奇数的平方的差是4的倍数.设:这两个奇数为:21n +,21m +()()222121n m +-+()22441441n n m m =++-++224444n n m m=+--则:()222244444n n m m n n m m +--=+--是4的倍数,∴任意两个奇数的平方的差是4的倍数.(3)已知1139273m m ⨯⨯=,求m 的值.()()23113333mm⨯⨯=1231133m m ++=12311m m ++=2m =.【点睛】本题考查完全平方公式的运算及同底数幂的乘法和幂的乘方的运算,熟练运用公式及法则是解决问题的关键.8.(2022秋·河南周口·八年级校联考阶段练习)如图1是一个长为2a ,宽为2b 的长方形,沿图中虚线剪开分成四块完全一样的小长方形,然后按如图2的形状拼成一个正方形.(1)图2中的阴影部分的正方形的边长是______;(2)用两种不同的方法求图中阴影部分的面积,并写出三个代数式()2a b +,()2a b -,ab 之间的等量关系;(3)根据(2)中的等量关系,解决问题:若10x y +=,16xy =,求x y -的值;(4)根据(2)中的等量关系,直接写出1m m+和1m m -之间的关系;若2410m m -+=,分别求出1m m +和21m m ⎛⎫- ⎪⎝⎭的值.【答案】(1)a b-(2)方法一:()2a b -,方法二:()24a b ab +-,()()224a b a b ab -=+-或()()224a b a b ab +=-+(3)6±(4)1m m +的值为4,21m m ⎛⎫- ⎪⎝⎭的值为12【分析】(1)图2中,大正方形的边长为:a b +,横着看,a b +是由两个b 和阴影正方形的边长构成,相减便得阴影正方形边长;(2)方法一:图1中已求出阴影正方形的边长,边长乘边长即为面积;方法二:图2长方形面积减图2非阴影部分面积,即为阴影部分面积;(3)运用(2)中关系可得()()224x y x y xy -=+-,代入求解即可;(4)将m 视为a ,1m 视为b ,按照上述结论即可解决.【详解】(1)解:阴影部分的正方形的边长为:a b b b a b +--=-,故答案为:a b -;(2)阴影部分的面积:方法一:利用整体思想,边长为()a b -的正方形其面积为()2a b -,方法二:利用分割思想,阴影部分面积=边长为()a b +的大正方形面积-4个长为a 宽为b 的。
(完整版)完全平方公式专项练习50题(有答案)

完全平方公式专项练习知识点:完全平方公式:(a+b)2=a 2+2ab+b 2 (a-b)2=a 2-2ab+b 2两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
1、完全平方公式也可以逆用,即a 2+2ab+b 2=(a+b)2 a 2-2ab+b 2=(a-b)22、能否运用完全平方式的判定①有两数和(或差)的平方即:(a+b)2或 (a-b)2或 (-a-b)2或 (-a+b)2②有两数平方,加上(或减去)它们的积的2倍,且两数平方的符号相同。
即:a 2+2ab+b 2或a 2-2ab+b 2-a 2-2ab-b 2或 -a 2+2ab-b 2专项练习:1.(a +2b )22.(3a -5)23..(-2m -3n )24. (a 2-1)2-(a 2+1)25.(-2a +5b )26.(-21ab 2-32c )2 7.(x -2y )(x 2-4y 2)(x +2y )8.(2a +3)2+(3a -2)29.(a -2b +3c -1)(a +2b -3c -1);10.(s -2t )(-s -2t )-(s -2t )2;11.(t -3)2(t +3)2(t 2+9)2.12. 972;13. 20022;14. 992-98×100;15. 49×51-2499.16.(x -2y )(x +2y )-(x +2y )217.(a +b +c )(a +b -c )18.(2a +1)2-(1-2a )219.(3x -y )2-(2x +y )2+5x (y -x )20.先化简。
再求值:(x +2y )(x -2y )(x 2-4y 2),其中x =2,y =-1.21.解关于x 的方程:(x +41)2-(x -41)(x +41)=41. 22.已知x -y =9,x ·y =5,求x 2+y 2的值.23.已知a (a -1)+(b -a 2)=-7,求222b a +-ab 的值.24.已知a +b =7,ab =10,求a 2+b 2,(a -b )2的值.25.已知2a -b =5,ab =23,求4a 2+b 2-1的值.26.已知(a +b )2=9,(a -b )2=5,求a 2+b 2,ab 的值.27.已知 2()16,4,a b ab +==求223a b +与2()a b -的值。
七下第九章完全平方公式几何背景题训练(有答案)
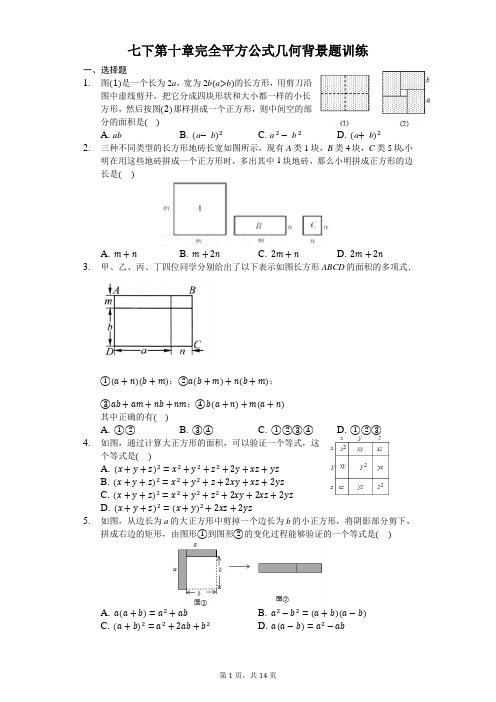
七下第十章完全平方公式几何背景题训练一、选择题1.图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是()A. abB. (a−b)2 C. a 2−b 2 D. (a+b)22.三种不同类型的长方形地砖长宽如图所示,现有A类1块,B类4块,C类5块.小明在用这些地砖拼成一个正方形时,多出其中1块地砖,那么小明拼成正方形的边长是()A. m+nB. m+2nC. 2m+nD. 2m+2n3.甲、乙、丙、丁四位同学分别给出了以下表示如图长方形ABCD的面积的多项式.①(a+n)(b+m);②a(b+m)+n(b+m);③ab+am+nb+nm;④b(a+n)+m(a+n)其中正确的有()A. ①②B. ③④C. ①②③④D. ①②③4.如图,通过计算大正方形的面积,可以验证一个等式,这个等式是()A. (x+y+z)2=x2+y2+z2+2y+xz+yzB. (x+y+z)2=x2+y2+z+2xy+xz+2yzC. (x+y+z)2=x2+y2+z2+2xy+2xz+2yzD. (x+y+z)2=(x+y)2+2xz+2yz5.如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分剪下,拼成右边的矩形,由图形①到图形②的变化过程能够验证的一个等式是()A. a(a+b)=a2+abB. a2−b2=(a+b)(a−b)C. (a+b)2=a2+2ab+b2D. a(a−b)=a2−ab6.如图,将边长为a的正方形剪去一个边长为b的正方形,再将剩余图形沿虚线剪开,拼成一个长方形,通过计算,剪接接前后两个图形中阴影部分的面积可以验证等式()A. (a±b)2=a2±2ab+b2B. a2±2ab+b2=(a±b)2C. (a+b)(a−b)=a2−b2D. a2−b2=(a+b)(a−b)7.如图,将图1中阴影部分拼成图2,根据两个图形中阴影部分的关系,可以验证下列哪个计算公式()A. (a+b)(a−b)=a2−b2B. (a−b)2=a2−2ab+b2C. (a+b)2=a2+2ab+b2D. (a+b)2=(a−b)2+4ab8.有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的面积之和为()A. 7B. 12C. 13D. 259.如图,有三种卡片,分别是边长为a的正方形卡片1张,边长为b的正方形卡片4张和长宽为a、b的长方形卡片4张,现使用这9张卡片拼成一个大的正方形,则这个大的正方形边长为()A. a+3bB. 2a+bC. a+2bD. 4ab二、填空题10.如图,边长为2m+3的正方形纸片剪出一个边长为m+3的正方形之后,剩余部分可剪拼成一个长方形,若拼成的长方形一边长为m,则这个长方形的周长为___________.11.如图,如图1是边长为a的正方形剪去边长为1的小正方形,图2是边长为(a−1)的正方形,图3是宽为(a−1)的长方形.记图1、图2、图3中阴影部分的面积分别为S1、S2、S3,若S1+S2=S3,则图3中长方形的长为________.(用a的式子表示)12.动手操作:如图1是一个长为2a,宽为2b的大长方形,沿图中的虚线剪开分成四个大小相同的小长方形,然后按照图2所示再拼成一个大正方形.提出问题:(1)观察图1,大长方形的面积为_______________;(2)观察图2,大正方形的面积为_______________;(3)利用图2中阴影部分面积的不同求法,请写出三个代数式(a+b)2,(a−b)2,ab之间的一个等量关系:_______________;问题解决:(4)根据上述(3)中得到的等量关系,解决下列问题:若x−y=6,xy=7,则x+y=_______________.13.探究:利用图中的三种材料各若干可以拼出一些长方形来解释某些等式.(1)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图所示的A__块,B___块,C__块.(2)要拼出一个长边3a+b的正方形,需要如图所示的A__块,B_____块,C_____块.(3)现有4块A,12块B,则再需要____块C,就可以拼成一个正方形。
完全平方公式、平方差公式的几何背景

专题完全平方公式、平方差公式的几何背景【例7】(2012•遵义)如图,从边长为(a+1)cm的正方形纸片中剪去一个边长为(a-1)cm的正方形(a>1),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则该矩形的面积是( C )A.2cm2 B2acm2 C.4acm2 D.(a2-1)cm2分析:先求出正方形的边长,继而得出面积,然后根据空白部分的面积=正方形的面积-矩形的面积即可得出答案.解答:解:由题意可得,正方形的边长为(m+n),故正方形的面积为(m+n)2,又∵原矩形的面积为4mn,∴中间空的部分的面积=(m+n)2-4mn=(m-n)2.故选C.【例8】(2012•白银)如图,边长为(m+3)的正方形纸片,剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是()A.m+3 B.m+6 C.2m+3 D.2m+6分析:由于边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个矩形(不重叠无缝隙),那么根据正方形的面积公式,可以求出剩余部分的面积,而矩形一边长为3,利用矩形的面积公式即可求出另一边长.解答:解:依题意得剩余部分为(m+3)2-m2=m2+6m+9-m2=6m+9,而拼成的矩形一边长为3,∴另一边长是396m=2m+3.故选C.【变式训练】15.(2012四川绵阳)图(1)是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( C )A.2mn B.(m+n)2 C.(m-n)2 D.m2-n216.如图所示,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( C )A.(a-b)2=a2-2ab+b2 B.(a+b)2=a2+2ab+b2C.a2-b2=(a+b)(a-b) D.a2+ab=a(a+b)17.图①是一个边长为(m+n)的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( B )A.(m+n)2-(m-n)2=4mnB.(m+n)2-(m2+n2)=2mnC.(m-n)2+2mn=m2+n2D.(m+n)(m-n)=m2-n218.(2012广东佛山)如图,边长为m+4的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形,若拼成的矩形一边长为4,则另一边长为2m+4 .19.如图,边长为a的正方形中有一个边长为b的小正方形,若将图1的阴影部分拼成一个长方形,如图2,比较图1和图2的阴影部分的面积,你能得到的公式是a2-b2=(a+b)(a-b).20.利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是(a-b)2=a2-2ab+b2 .21.阅读材料并回答问题:我们知道,完全平方式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,如:(2a+b)(a+b)=2a2+3ab+b2,就可以用图(1)或图(2)等图形的面积表示.(1)请写出图(3)所表示的代数恒等式: .(2)试画一个几何图形,使它的面积表示:(a+b)(a+3b)=a2+4ab+3b2;(3)请仿照上述方法另写一个含有a,b的代数恒等式,并画出与它对应的几何图形.解:(1)(2a+b)(a+2b)=2a2+5ab+2b2;(2)(答案不唯一);(3)恒等式是(a+2b)(a+b)=a2+3ab+2b2,如图所示.(答案不唯一)。
第03讲 平方差和完全平方公式(知识解读+真题演练+课后巩固)(解析版)

第03讲平方差和完全平方公式1.掌握平方差和完全平方公式结构特征,并能从广义上理解公式中字母的含义;2.学会运用平方差和完全平方公式进行计算.了解公式的几何意义,能利用公式进行乘法运算;3.能灵活地运用运算律与乘法公式简化运算.4.能用平方差和完全平方公式的逆运算解决问题知识点1:平方差公式平方差公式:22()()a b a b a b+-=-语言描述:两个数的和与这两个数的差的积,等于这两个数的平方差.注意:在这里,b a ,既可以是具体数字,也可以是单项式或多项式.知识点2:平方差公式的特征抓住公式的几个变形形式利于理解公式.但是关键仍然是把握平方差公式的典型特征:既有相同项,又有“相反项”,而结果是“相同项”的平方减去“相反项”的平方.常见的变式有以下类型:①位置变化,(x +y )(-y +x )=x 2-y 2②符号变化,(-x +y )(-x -y )=(-x )2-y 2=x 2-y 2③指数变化,(x 2+y 2)(x 2-y 2)=x 4-y 4④系数变化,(2a +b )(2a -b )=4a 2-b 2⑤换式变化,[xy +(z +m )][xy -(z +m )]=(xy )2-(z +m )2=x 2y 2-(z +m )(z +m )=x 2y 2-(z 2+zm +zm +m 2)=x 2y 2-z 2-2zm -m 2⑥增项变化,(x -y +z )(x -y -z )=(x -y )2-z 2=(x -y )(x -y )-z 2=x 2-xy -xy +y 2-z 2=x 2-2xy +y 2-z 2知识点3:完全平方公式完全平方公式:()2222a b a ab b+=++2222)(b ab a b a +-=-两数和(差)的平方等于这两数的平方和加上(减去)这两数乘积的两倍注意:公式特点:左边是两数的和(或差)的平方,右边是二次三项式,是这两数的平方和加(或减)这两数之积的2倍.以下是常见的变形:()2222a b a b ab +=+-()22a b ab=-+()()224a b a b ab+=-+知识点4:拓展、补充公式2222222a b c ab ac bc=+++++(a+b+c)222112a a a±=+±(a )2()()()x p x q x p q x pq ++=+++;2233()()a b a ab b a b ±+=± ;33223()33a b a a b ab b ±=±+±;2222()222a b c a b c ab ac bc ++=+++++.【题型1平方差公式运算】【典例1】(2023春•渭南期中)计算(3a +2)(3a ﹣2)=9a 2﹣4.【答案】9a 2﹣4.【解答】解:(3a +2)(3a ﹣2)=9a 2﹣4.故答案为:9a 2﹣4.【变式1-1】(2023春•蕉城区校级月考)若a +b =1,a ﹣b =2022,则a 2﹣b 2=2022.【答案】2022.【解答】解:∵a +b =1,a ﹣b =2022,∴(a+b)(a﹣b)=a2﹣b2=1×2022=2022.故答案为:2022.【变式1-2】(2023春•双峰县期末)(4a+b)(﹣b+4a)=16a2﹣b2.【答案】16a2﹣b2.【解答】解:原式=(4a)2﹣b2=16a2﹣b2.故答案为:16a2﹣b2.【变式1-3】(2023春•埇桥区期末)计算:(2x﹣3y)(3y+2x)=4x2﹣9y2.【答案】4x2﹣9y2.【解答】解:(2x﹣3y)(3y+2x)=(2x)2﹣(3y)2=4x2﹣9y2.故答案为:4x2﹣9y2.【典例2】(2023春•佛冈县期中)19992﹣1998×2002.【答案】﹣3995.【解答】解:原式=(2000﹣1)2﹣(2000﹣2)×(2000+2)=20002﹣4000+1﹣20002+4=﹣3995.【变式2-1】(2023•皇姑区校级开学)简便运算:20222﹣2020×2024.【答案】4.【解答】解:20222﹣2020×2024=20222﹣(2022﹣2)×(2022+2)=20222﹣(20222﹣4)=20222﹣20222+4=4.【变式2-2】(2023春•安乡县期中)计算:20222﹣2021×2023.【答案】1.【解答】解:20222﹣2021×2023.=20222﹣(2022﹣1)×(2022+1)=20222﹣20222+1=1.【变式2-3】(2023春•渭滨区期末)用整式乘法公式计算:899×901+1.【答案】810000.【解答】解:899×901+1=(900﹣1)×(900+1)+1=9002﹣1+1=810000.【题型2平方差公式的逆运算】【典例3】(2023春•海阳市期末)已知x+2y=13,x2﹣4y2=39,则多项式x﹣2y的值是3.【答案】3.【解答】解:∵x+2y=13,x2﹣4y2=39,∴x2﹣4y2=(x+2y)(x﹣2y)=39,∴x﹣2y=3.故答案为:3.【变式3-1】(2023春•辽阳期末)若m2﹣n2=6,且m+n=3,则n﹣m等于﹣2.【答案】﹣2.【解答】解:∵(m+n)(m﹣n)=m2﹣n2,∴m﹣n=(m2﹣n2)÷(m+n)=6÷3=2,∴n﹣m=﹣2,故答案为:﹣2.【变式3-2】(2023春•广饶县期中)已知实数a,b满足a2﹣b2=40,a﹣b=4,则a+b的值为10.【答案】10.【解答】解:∵a2﹣b2=40,∴(a+b)(a﹣b)=40,∵a﹣b=4,∴a+b=10.故答案为:10.【变式3-3】(2023春•甘州区校级期末)若m2﹣n2=6,m+n=3,则=1.【答案】1.【解答】解:∵m2﹣n2=6,m+n=3,∴(m﹣n)(m+n)=6,则m﹣n的值是2,∴=1.故答案为:1.【题型3平方差公式的几何背景】【典例4】(2023春•东昌府区校级期末)如图,在边长为a的正方形中挖去一个边长为b的小正方形(a>b),把余下的部分剪拼成垄一个矩形.(1)通过计算两个图形的面积(阴影部分的面积),可以验证的等式是:B.A.a2﹣2ab+b2=(a﹣b)2B.a2﹣b2=(a+b)(a﹣b)C.a2+ab=a(a+b)D.a2﹣b2=(a﹣b)2(2)应用你从(1)选出的等式,完成下列各题:①已知:a+b=7,a2﹣b2=28,求a﹣b的值;②计算:;【答案】(1)B;(2)a﹣b=4;(3).【解答】解:(1)第一个图形面积为a2﹣b2,第二个图形的面积为(a+b)(a ﹣b),∴可以验证的等式是:a2﹣b2=(a+b)(a﹣b),故答案为:B;(2)∵a+b=7,a2﹣b2=28,∴(a+b)(a﹣b)=28,即7(a﹣b)=28,∴a﹣b=4;(3)原式=(1﹣)×(1+)×(1﹣)×(1+)×(1﹣)×(1+)×...×(1﹣)×(1+)=××××××...××=×=.【变式4-1】(2023春•高明区月考)乘法公式的探究及应用.(1)如图1到图2的操作能验证的等式是D.(请选择正确的一个)A.a2﹣2ab+b2=(a﹣b)2B.a2+ab=a(a+b)C.(a﹣b)2=(a+b)2﹣4abD.a2﹣b2=(a+b)(a﹣b)(2)当4m2=12+n2,2m+n=6时,则2m﹣n=2;(3)运用你所得到的公式,计算下列各题:①20232﹣2022×2024;②2×(3+1)×(32+1)×(34+1)×(38+1)×(316+1)+1.【答案】(1)D;(2)2;(3)①1;②332.【解答】解:(1)如图,图1中阴影面积为a2﹣b2,图2的阴影面积为(a+b)(a﹣b),∴图1到图2的操作能验证的等式是a2﹣b2=(a+b)(a﹣b),故答案为:D;(2)∵4m2=12+n2,∴4m2﹣n2=12即(2m+n)(2m﹣n)=12,∵2m+n=6,∴2m﹣n=2,故答案为:2;(3)①20232﹣2022×2024=20232﹣(2023﹣1)×(2023+1)=20232﹣20232+1=1;②2×(3+1)×(32+1)×(34+1)×(38+1)×(316+1)+1=(3﹣1)×(3+1)×(32+1)×(34+1)×(38+1)×(316+1)+1=(32﹣1)×(32+1)×(34+1)×(38+1)×(316+1)+1=(34﹣1)×(34+1)×(38+1)×(316+1)+1=(38﹣1)×(38+1)×(316+1)+1=(316﹣1)×(316+1)+1=332﹣1+1=332.【变式4-2】(2023春•清远期末)如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).(1)根据上述操作利用阴影部分的面积关系得到的等式:C(选择正确的一个)A.a2﹣2ab+b2=(a﹣b)2;B.a2+ab=a(a+b);C.a2﹣b2=(a+b)(a﹣b),D.(a﹣b)2=(a+b)2﹣4ab(2)请应用(1)中的等式,解答下列问题:(1)计算:2022×2024﹣20232;(2)计算:3(22+1)(24+1)(28+1)…(264+1)+1.【答案】(1)C;(2)①﹣1,2128.=a2﹣b2.根据图2知:S阴影=(a+b)(a 【解答】解:(1)根据图1知:S阴影﹣b),∴a2﹣b2=(a+b)(a﹣b),故选:C.(2)①原式=(2023﹣1)(2023+1)﹣20232=20232﹣12﹣20232=﹣1.②原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(264+1)+1=(22﹣1)(22+1)(24+1)(28+1)…(264+1)+1=(24﹣1)(24+1)(28+1)…(264+1)+1=(2128﹣1)+1=2128.【变式4-3】(2023春•屏南县期中)乘法公式的探究及应用:如图,在边长为a 的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪成两个直角梯形后,再拼成一个等腰梯形.(1)通过计算左、右两图的阴影部分面积,可以得到乘法公式:(a+b)(a﹣b)=a2﹣b2;(2)利用上述乘法公式计算:①1002﹣98×102;②(2m+n﹣p)(2m+n+p).【答案】(1)(a+b)(a﹣b)=a2﹣b2;(2)①4;②4m2+4mn+n2﹣p2.【解答】解:(1)两个图形中阴影部分面积一致,大小正方形面积之差等于等腰梯形的面积,且等腰梯形的高为大小正方形边长差,故;故答案为:(a+b)(a﹣b)=a2﹣b2;(2)①1002﹣98×102=1002﹣(100﹣2)(100+2)=1002﹣(1002﹣22)=1002﹣1002+22=4②(2m+n﹣p)(2m+n+p)=(2m+n)2﹣p2=4m2+4mn+n2﹣p2.【题型4完全平方公式】【典例5】(2023春•砀山县校级期末)计算:(x+4)2﹣x2=8x+16.【答案】8x+16.【解答】解:(x+4)2﹣x2=x2+8x+16﹣x2=8x+16,故答案为:8x+16.【变式5-1】(2023春•威宁县期末)已知x2+y2=10,xy=2,则(x﹣y)2=6.【答案】见试题解答内容【解答】解:∵x2+y2=10,xy=2,∴(x﹣y)2=x2+y2﹣2xy=10﹣4=6.故答案为:6.【变式5-2】(2023春•东港市期中)若(2x﹣m)2=4x2+nx+9,则n的值为±12.【答案】±12.【解答】解:∵(2x﹣m)2=4x2﹣4mx+m2,∴m2=9,∴m=±3,∴n=﹣4m=±12.故答案为:±12.【变式5-3】(2023春•未央区校级月考)计算:(x+2)2+(1﹣x)(2+x).【答案】3x+6.【解答】解:原式=x2+4x+4+2+x﹣2x﹣x2=3x+6.【题型5完全平方公式下得几何背景】【典例6】(2023秋•绿园区校级月考)为创建文明校园环境,高校长制作了“节约用水”“讲文明,讲卫生”等宣传标语,标语由如图①所示的板材裁剪而成,其为一个长为2m,宽为2n的长方形板材,将长方形板材沿图中虚线剪成四个形状和大小完全相同的小长方形标语,在粘贴过程中,同学们发现标语可以拼成图②所示的一个大正方形.(1)用两种不同方法表示图②中小正方形(阴影部分)面积:=(m﹣n)2;方法一:S小正方形=(m+n)2﹣4mn;方法二:S小正方形(2)(m+n)2,(m﹣n)2,4mn这三个代数式之间的等量关系为(m+n)2=(m﹣n)2+4mn;(3)根据(2)题中的等量关系,解决如下问题:①已知:a﹣b=5,ab=﹣6,求:(a+b)2的值;②已知:a﹣=1,求:的值.【答案】(1)(m﹣n)2,(m+n)2﹣4mn;(2)(m+n)2=(m﹣n)2+4mn;(3)①1;②5.【解答】解:(1)方法1:;方法2:,故答案为:(m﹣n)2,(m+n)2﹣4mn;(2)∵(m+n)2=m2+2mn+n2,(m﹣n)2+4mn=m2﹣2mn+n2+4mn=m2+2mn+n2,∴(m+n)2=(m﹣n)2+4mn,故答案为:(m+n)2=(m﹣n)2+4mn;(3)①a﹣b=5,ab=﹣6,∴(a+b)2=(a﹣b)2+4ab,=52+4×(﹣6)=25+(﹣24)=1;②=12+4=1+4=5.【变式6-1】(2023春•甘州区校级期中)图1是一个长为2x、宽为2y的长方形,沿图中虚线用剪刀剪成四个完全相同的小长方形,然后按图2所示拼成一个正方形.(1)你认为图2中的阴影部分的正方形的边长等于x﹣y.(2)试用两种不同的方法求图2中阴影部分的面积.方法1:(x﹣y)2;方法2:(x+y)2﹣4xy.(3)根据图2你能写出下列三个代数式之间的等量关系吗?代数式:(x+y)2,(x﹣y)2,4xy.(x+y)2=(x﹣y)2+4xy(4)根据(3)题中的等量关系,解决如下问题:若x+y=4,xy=3,则(x﹣y)2=4.【答案】见试题解答内容【解答】解:(1)图②中的阴影部分的小正方形的边长=x﹣y;故答案为:(x﹣y);(2)方法①(x﹣y)2;方法②(x+y)2﹣4xy;故答案为:(x﹣y)2,(x+y)2﹣4xy;(3)(x+y)2=(x﹣y)2+4xy;故答案为:(x+y)2=(x﹣y)2+4xy;(4)(x﹣y)2=(x+y)2﹣4xy=42﹣12=4故答案为:4.【变式6-2】(2023•永修县校级开学)如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四个小长方形,然后按图②的方式拼成一个正方形.(1)请用两种不同的方法求图②中阴影部分的面积(直接用含m,n的代数式表示).方法一:(m+n)2﹣4mn;方法二:(m﹣n)2.(2)根据(1)的结论,请你写出代数式(m+n)2,(m﹣n)2,mn之间的等量关系.(3)根据(2)题中的等量关系,解决如下问题:已知实数a,b满足:a+b =6,ab=5,求a﹣b的值.【答案】(1)(m+n)2﹣4mn,(m﹣n)2;(2)代数式(m+n)2,(m﹣n)2,mn之间的等量关系可表示为:(m+n)2﹣4mn=(m﹣n)2;(3)±4.【解答】解:(1)由题意得,图②中阴影部分的面积为(m+n)2﹣4mn或(m﹣n)2,故答案为:(m+n)2﹣4mn,(m﹣n)2;(2)由(1)题可得,(m+n)2﹣4mn=(m﹣n)2,∴代数式(m+n)2,(m﹣n)2,mn之间的等量关系可表示为:(m+n)2﹣4mn=(m﹣n)2;(3)由(2)题结果可得,(a+b)2﹣4ab=(a﹣b)2,∴a﹣b=±,∴当a+b=6,ab=5时,a﹣b=±=±==±4.【变式6-3】(2023春•湖州期中)阅读理解:若x满足(30﹣x)(x﹣10)=160,求(30﹣x)2+(x﹣10)2的值.解:设30﹣x=a,x﹣10=b.则(30﹣x)(x﹣10)=ab=160,a+b=(30﹣x)+(x﹣10)=20,(30﹣x)2+(x﹣10)2=a2+b2=(a+b)2﹣2ab=202﹣2×160=80.解决问题:(1)若x满足(2021﹣x)2+(x﹣2018)2=2020.求(2021﹣x)(x﹣2018)的值;(2)如图,在矩形ABCD中,AB=20,BC=12,点E、F是BC、CD上的点,且BE=DF=x.分别以FC、CE为边在矩形ABCD外侧作正方形CFGH 和CEMN,若矩形CEPF的面积为160平方单位,求图中阴影部分的面积和.【答案】(1)﹣;(2)384.【解答】解:(1)设2021﹣x=a,x﹣2008=b.则a+b=3,而(2021﹣x)2+(x﹣2018)2=2020=a2+b2,∴(2020﹣x)(x﹣2018)=ab===﹣;(2)由AB=20,BC=12,BE=DF=x,则CE=12﹣x,CF=20﹣x,∵矩形CEPF的面积为160平方单位,∴(12﹣x)(20﹣x)=160,∴S=CE2+FC2=(12﹣x)2+(20﹣x)2,阴影部分设12﹣x=m,20﹣x=n,则mn=160,m﹣n=﹣8,∴S=CE2+FC2=(12﹣x)2+(20﹣x)2,阴影部分=m2+n2=(m﹣n)2+2mn=64+320=384,即阴影部分的面积为384.【题型6完全平方公式的逆运算】【典例7】(2023春•永丰县期中)已知:a2+b2=3,a+b=2.求:(1)ab的值;(2)(a﹣b)2的值;(3)a4+b4的值.【答案】(1);(2)2;(3).【解答】解:(1)∵a+b=2,∴(a+b)2=4,即a2+2ab+b2=4,∵a2+b2=3,∴3+2ab=4,∴ab=;(2)(a﹣b)2=(a+b)2﹣4ab=4﹣4×=2;(3)a4+b4=(a2+b2)2﹣2a2b2=(a2+b2)2﹣2(ab)2=32﹣2×()2=9﹣=.【变式7-1】(2023春•都昌县期末)已知实数m,n满足m+n=6,mn=﹣3.(1)求(m+2)(n+2)的值;(2)求m2+n2的值.【答案】(1)13;(2)42.【解答】解:(1)因为m+n=6,mn=﹣3,所以(m+2)(n+2)=mn+2m+2n+4=mn+2(m+n)+4=﹣3+2×6+4=13.(2)m2+n2=(m+n)2﹣2mn=62﹣2×(﹣3)=36+6=42.【变式7-2】(2023春•周村区期末)若x+y=2,且(x+3)(y+3)=12.(1)求xy的值;(2)求x2+3xy+y2的值.【答案】见试题解答内容【解答】解:(1)∵(x+3)(y+3)=12,∴xy+3x+3y+9=12,则xy+3(x+y)=3,将x+y=2代入得xy+6=3,则xy=﹣3;(2)当xy=﹣3、x+y=2时,原式=(x+y)2+xy=22+(﹣3)=4﹣3=1.【变式7-3】(2022秋•大安市期末)已知m﹣n=6,mn=4.(1)求m2+n2的值.(2)求(m+2)(n﹣2)的值.【答案】(1)44;(2)﹣12.【解答】解:(1)因为m﹣n=6,mn=4,所以m2+n2=(m﹣n)2+2mn=62+2×4=36+8=44;(2)因为m﹣n=6,mn=4,所以(m+2)(n﹣2)=mn﹣2m+2n﹣4=mn﹣2(m﹣n)﹣4=4﹣2×6﹣4=﹣12.1.(2023•深圳)下列运算正确的是()A.a3•a2=a6B.4ab﹣ab=4C.(a+1)2=a2+1D.(﹣a3)2=a6【答案】D【解答】解:A,a3•a2=a3+2=a5,故A选项错误,不合题意;B,4ab﹣ab=3ab,合并同类项结果错误,故B选项错误,不合题意;C,(a+1)2=a2+2a+1,故C选项错误,不合题意;D,(﹣a3)2=a3×2=a6,故D选项正确,符合题意;故选:D.2.(2022•赤峰)已知(x+2)(x﹣2)﹣2x=1,则2x2﹣4x+3的值为()A.13B.8C.﹣3D.5【答案】A【解答】解:(x+2)(x﹣2)﹣2x=1,x2﹣4﹣2x=1,x2﹣2x=5,所以2x2﹣4x+3=2(x2﹣2x)+3=2×5+3=10+3=13,故选:A.3.(2022•百色)如图,是利用割补法求图形面积的示意图,下列公式中与之相对应的是()A.(a+b)2=a2+2ab+b2B.(a﹣b)2=a2﹣2ab+b2C.(a+b)(a﹣b)=a2﹣b2D.(ab)2=a2b2【答案】A【解答】解:根据题意,大正方形的边长为a+b,面积为(a+b)2,由边长为a的正方形,2个长为a宽为b的长方形,边长为b的正方形组成,所以(a+b)2=a2+2ab+b2.故选:A.4.(2022•兰州)计算:(x+2y)2=()A.x2+4xy+4y2B.x2+2xy+4y2C.x2+4xy+2y2D.x2+4y2【答案】A【解答】解:(x+2y)2=x2+4xy+4y2.故选:A.5.(2023•凉山州)已知y2﹣my+1是完全平方式,则m的值是±2.【答案】±2.【解答】解:∵y2﹣my+1是完全平方式,y2﹣2y+1=(y﹣1)2,y2﹣(﹣2)y+1=(y+1)2,∴﹣m=﹣2或﹣m=2,∴m=±2.故答案为:±2.6.(2023•雅安)若a+b=2,a﹣b=1,则a2﹣b2的值为2.【答案】2.【解答】解:∵a+b=2,a﹣b=1,∴a2﹣b2=(a+b)(a﹣b)=2×1=2.故答案为:2.7.(2023•江西)化简:(a+1)2﹣a2=2a+1.【答案】2a+1.【解答】解:原式=a2+2a+1﹣a2=2a+1,故答案为:2a+1.8.(2022•遵义)已知a+b=4,a﹣b=2,则a2﹣b2的值为8.【答案】8.【解答】解:∵a+b=4,a﹣b=2,∴a2﹣b2=(a+b)(a﹣b)=4×2=8,故答案为:8.9.(2022•乐山)已知m2+n2+10=6m﹣2n,则m﹣n=4.【答案】4.【解答】解:∵m2+n2+10=6m﹣2n,∴m2﹣6m+9+n2+2n+1=0,即(m﹣3)2+(n+1)2=0,∴m=3,n=﹣1,∴m﹣n=4,故答案为:4.10.(2022•大庆)已知代数式a2+(2t﹣1)ab+4b2是一个完全平方式,则实数t的值为或﹣..【答案】见试题解答内容【解答】解:根据题意可得,(2t﹣1)ab=±(2×2)ab,即2t﹣1=±4,解得:t=或t=.故答案为:或﹣.11.(2022•滨州)若m+n=10,mn=5,则m2+n2的值为90.【答案】90.【解答】解:∵m+n=10,mn=5,∴m2+n2=(m+n)2﹣2mn=102﹣2×5=100﹣10=90.故答案为:90.12.(2022•德阳)已知(x+y)2=25,(x﹣y)2=9,则xy=4.【答案】4.【解答】解:∵(x+y)2=x2+y2+2xy=25,(x﹣y)2=x2+y2﹣2xy=9,∴两式相减得:4xy=16,则xy=4.故答案为:413.(2023•兰州)计算:(x+2y)(x﹣2y)﹣y(3﹣4y).【答案】x2﹣3y.【解答】解:原式=x2﹣4y2﹣(3y﹣4y2)=x2﹣4y2﹣3y+4y2=x2﹣3y.14.(2022•六盘水)如图,学校劳动实践基地有两块边长分别为a,b的正方形秧田A,B,其中不能使用的面积为M.(1)用含a,M的代数式表示A中能使用的面积a2﹣M;(2)若a+b=10,a﹣b=5,求A比B多出的使用面积.【答案】(1)a2﹣M;(2)50.【解答】解:(1)A中能使用的面积=大正方形的面积﹣不能使用的面积,即a2﹣M,故答案为:a2﹣M;(2)A比B多出的使用面积为:(a2﹣M)﹣(b2﹣M)=a2﹣b2=(a+b)(a﹣b)=10×5=50,答:A比B多出的使用面积为50.1.(2023春•市南区校级期中)下列算式能用平方差公式计算的是()A.(2a+b)(2b﹣a)B.(x+1)(﹣x﹣1)C.(3x﹣y)(﹣3x+y)D.(﹣m﹣n)(﹣m+n)【答案】D【解答】解:∵(2a+b)(2b﹣a)不符合平方差公式的特点,∴选项A不符合题意;∵(x+1)(﹣x﹣1)=﹣(x+1)2,∴选项B不符合题意;∵(3x﹣y)(﹣3x+y)=﹣(3x﹣y)2,∴选项C不符合题意;∵(﹣m+n)(﹣m﹣n)=(﹣m)2﹣n2,∴选项D符合题意;故选:D.2.(2022秋•睢阳区期末)如图1,在边长为a的正方形中剪去一个边长为b(b<a)的小正方形,把剩下部分拼成一个梯形(如图2),利用这两个图形的面积,可以验证的等式是()A.a2+b2=(a+b)(a﹣b)B.(a﹣b)2=a2﹣2ab+b2 C.(a+b)2=a2+2ab+b2D.a2﹣b2=(a+b)(a﹣b)【答案】D【解答】解:∵图1中的阴影部分面积为:a2﹣b2,图2中阴影部分面积为:(2b+2a)(a﹣b),∴a2﹣b2=(2b+2a)(a﹣b),即a2﹣b2=(a+b)(a﹣b),故选:D.3.(2022秋•嵩县期末)已知x+y=8,xy=12,则x2﹣xy+y2的值为()A.42B.28C.54D.66【答案】B【解答】解:∵x+y=8,xy=12,∴原式=(x+y)2﹣3xy=82﹣3×12=64﹣36=28.故选:B.4.(2022秋•海口期末)等式(﹣a﹣1)()=a2﹣1中,括号内应填入.A.a+1B.﹣1﹣a C.1﹣a D.a﹣1【答案】C【解答】解:结合题意,可知相同项是﹣a,相反项是1和﹣1,∴空格中应填:1﹣a.故选:C.5.(2022秋•离石区期末)若二次三项式x2+kx+4是一个完全平方式,则k的值是()A.4B.﹣4C.±2D.±4【答案】D【解答】解:中间项为加上或减去x和2乘积的2倍,故k=±4.故选:D.6.(2023春•攸县期末)若x2﹣y2=3,则(x+y)2(x﹣y)2的值是()A.3B.6C.9D.18【答案】C【解答】解:∵x2﹣y2=(x+y)(x﹣y)=3,∴原式=32=9,故选:C.7.(2022秋•邹城市校级期末)已知x2+2(m﹣1)x+9是一个完全平方式,则m的值为()A.4B.4或﹣2C.±4D.﹣2【答案】B【解答】解:∵x2+2(m﹣1)x+9是一个完全平方式,∴2(m﹣1)=±6,解得:m=4或m=﹣2,故选:B.8.(2022秋•渝北区校级期末)化简:(x+2y)2﹣(x+y)(3x﹣y).【答案】﹣2x2+2xy+5y2.【解答】解:原式=x2+4xy+4y2﹣(3x2﹣xy+3xy﹣y2)=x2+4xy+4y2﹣3x2+xy﹣3xy+y2=﹣2x2+2xy+5y2.9.(2023春•渭滨区期中)请你参考黑板中老师的讲解,用乘法公式进行简便计算:利用乘法公式有时可以进行简便计算.例1:1012=(100+1)2=1002+2×100×1+1=10201;例2:17×23=(20﹣3)(20+3)=202﹣32=391.(1)9992;(2)20222﹣2021×2023.【答案】(1)998001;(2)1.【解答】解:(1)原式=(1000﹣1)2=10002﹣2×1000×1+1=1000000﹣2000+1=998001;(2)20222﹣(2022﹣1)×(2022+1)=20222﹣20222﹣+1=1.10.(2022秋•龙湖区期末)请认真观察图形,解答下列问题:(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简)(2)由(1),你能得到怎样的等量关系?请用等式表示;(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14.求:①a+b的值;②a2﹣b2的值.【答案】见试题解答内容【解答】解:(1)两个阴影图形的面积和可表示为:a2+b2,(a+b)2﹣2ab,(2)a2+b2=(a+b)2﹣2ab,(3)①∵a2+b2=53,ab=14,∴(a+b)2=a2+b2+2ab=53+2×14=81,∴a+b=±9,又∵a>0,b>0,∴a+b=9.②∵(a﹣b)2=a2+b2﹣2ab=53﹣2×14=25∴a﹣b=±5又∵a>b>0,∴a﹣b=5∴a2﹣b2=(a+b)(a﹣b)=9×5=45.11.(2022秋•高安市期末)已知a+b=7,ab=﹣2.求:(1)a2+b2的值;(2)(a﹣b)2的值.【答案】(1)53.(2)57.【解答】解:(1)∵a+b=7,ab=﹣2,∴(a+b)2=a2+b2+2ab=a2+b2+(﹣4)=49.∴a2+b2=53.(2)∵a+b=7,ab=﹣2,∴(a﹣b)2=a2+b2﹣2ab=a2+b2﹣(﹣4)=53+4=57.12.(2022•荆门)已知x+=3,求下列各式的值:(1)(x﹣)2;(2)x4+.【答案】(1)5;(2)47.【解答】解:(1)∵=,∴===﹣4x•=32﹣4=5;(2)∵=,∴=+2=5+2=7,∵=,∴=﹣2=49﹣2=47.13.(2022秋•阳城县期末)从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).(1)上述操作能验证的等式是C;(请选择正确的一个)A.a2﹣2ab+b2=(a﹣b)2B.b2+ab=b(a+b)C.a2﹣b2=(a+b)(a﹣b)D.a2+ab=a(a+b)(2)应用你从(1)选出的等式,完成下列各题:①已知x2﹣4y2=12,x+2y=4,求x的值.②计算:.【答案】(1)C;(2);(3).【解答】解:(1)第一个图形中阴影部分的面积是a2﹣b2,第二个图形的面积是(a+b)(a﹣b),则a2﹣b2=(a+b)(a﹣b).故选:C;(2)①∵x2﹣4y2=(x+2y)(x﹣2y),∴12=4(x﹣2y),得:x﹣2y=3,联立,①+②,得2x=7,解得:x=;②=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)(1﹣)(1+)==×=.14.(2023春•威海期中)利用简便方法计算:(1)501×499+1;(2)0.125×104×8×104.【答案】见试题解答内容【解答】解:(1)原式=(500+1)×(500﹣1)+1=5002﹣1+1=5002=250000;(2)原式=(0.125×8)×(104×104)=108.15.(2022秋•南昌期末)图1是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.(1)求图2中的阴影部分的正方形的周长;(2)观察图2,请写出下列三个代数式(a+b)2,(a﹣b)2,ab之间的等量关系;(3)运用你所得到的公式,计算:若m、n为实数,且mn=﹣3,m﹣n=4,试求m+n的值.(4)如图3,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=8,两正方形的面积和S1+S2=26,求图中阴影部分面积.【答案】答:(1)4a﹣4b;(2)(a﹣b)2=(a﹣b)2+4ab;(3)m+n=±2;=.(4)S阴影【解答】解:(1)阴影部分的正方形边长为a﹣b,故周长为4(a﹣b)=4a﹣4b,故答案为:4a﹣4b;(2)大正方形面积可以看作四个矩形面积加阴影面积,故可表示为:4ab+(a ﹣b)2,大正方形边长为a+b,故面积也可以表达为:(a+b)2,因此(a+b)2=(a﹣b)2+4ab,故答案为:(a+b)2=(a﹣b)2+4ab;(3)由(2)可知:(m+n)2=(m﹣n)2+4mn,已知m﹣n=4,mn=﹣3,所以(m+n)2=16+4×(﹣3)=4,所以m+n=±2;故m+n的值为±2;(4)设AC=a,BC=b,因为AB=8,S1+S2=26,所以a+b=8,a2+b2=26,因为(a+b)2=a2+b2+2ab,所以64=26+2ab,解得ab=19,由题意:∠ACF=90°,=ab=.所以S阴影16.(2022秋•丹棱县期末)阅读下列文字,我们知道对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:(1)写出图2中所表示的数学等式(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac =38,求a2+b2+c2的值;(3)图3中给出了若干个边长为a和边长为b的小正方形纸片.若干个长为a和宽为b的长方形纸片,利用所给的纸片拼出一个几何图形,使得计算它的面积能得到数学公式:2a2+5ab+2b2=(2a+b)(a+2b).【答案】见试题解答内容【解答】解:(1)根据题意,大矩形的面积为:(a+b+c)(a+b+c)=(a+b+c)2,各小矩形部分的面积之和=a2+2ab+b2+2bc+2ac+c2,∴等式为(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.(2)a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc=112﹣2×38=45.(3)如图所示。
完全平方公式专项练习50题(有答案)

完全平方公式专项练习知识点:完全平方公式:(a+b)2=a 2+2ab+b 2 (a-b)2=a 2-2ab+b 2两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
1、完全平方公式也可以逆用,即a 2+2ab+b 2=(a+b)2 a 2-2ab+b 2=(a-b)22、能否运用完全平方式的判定①有两数和(或差)的平方即:(a+b)2或 (a-b)2或 (-a-b)2或 (-a+b)2②有两数平方,加上(或减去)它们的积的2倍,且两数平方的符号相同。
即:a 2+2ab+b 2或a 2-2ab+b 2-a 2-2ab-b 2或 -a 2+2ab-b 2专项练习:1.(a +2b )22.(3a -5)23..(-2m -3n )24. (a 2-1)2-(a 2+1)25.(-2a +5b )26.(-21ab 2-32c )2 7.(x -2y )(x 2-4y 2)(x +2y )8.(2a +3)2+(3a -2)29.(a -2b +3c -1)(a +2b -3c -1);10.(s -2t )(-s -2t )-(s -2t )2;11.(t -3)2(t +3)2(t 2+9)2.12. 972;13. 20022;14. 992-98×100;15. 49×51-2499.16.(x -2y )(x +2y )-(x +2y )217.(a +b +c )(a +b -c )18.(2a +1)2-(1-2a )219.(3x -y )2-(2x +y )2+5x (y -x )20.先化简。
再求值:(x +2y )(x -2y )(x 2-4y 2),其中x =2,y =-1.21.解关于x 的方程:(x +41)2-(x -41)(x +41)=41. 22.已知x -y =9,x ·y =5,求x 2+y 2的值.23.已知a (a -1)+(b -a 2)=-7,求222b a +-ab 的值. 24.已知a +b =7,ab =10,求a 2+b 2,(a -b )2的值. 25.已知2a -b =5,ab =23,求4a 2+b 2-1的值. 26.已知(a +b )2=9,(a -b )2=5,求a 2+b 2,ab 的值.27.已知 2()16,4,a b ab +==求223a b +与2()a b -的值。
完全平方公式专项练习50题(有答案)

完全平方公式专项练习知识点:完全平方公式:(a+b)2=a 2+2ab+b 2 (a-b)2=a 2-2ab+b 2两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
1、完全平方公式也可以逆用,即a 2+2ab+b 2=(a+b)2 a 2-2ab+b 2=(a-b)22、能否运用完全平方式的判定①有两数和(或差)的平方即:(a+b)2或 (a-b)2或 (-a-b)2或 (-a+b)2②有两数平方,加上(或减去)它们的积的2倍,且两数平方的符号相同。
即:a 2+2ab+b 2或a 2-2ab+b 2-a 2-2ab-b 2或 -a 2+2ab-b 2专项练习:1.(a +2b )22.(3a -5)23..(-2m -3n )24. (a 2-1)2-(a 2+1)25.(-2a +5b )26.(-21ab 2-32c )2 7.(x -2y )(x 2-4y 2)(x +2y )8.(2a +3)2+(3a -2)29.(a -2b +3c -1)(a +2b -3c -1);10.(s -2t )(-s -2t )-(s -2t )2;11.(t -3)2(t +3)2(t 2+9)2.12. 972;13. 20022;14. 992-98×100;15. 49×51-2499.16.(x -2y )(x +2y )-(x +2y )217.(a +b +c )(a +b -c )18.(2a +1)2-(1-2a )219.(3x -y )2-(2x +y )2+5x (y -x )20.先化简。
再求值:(x +2y )(x -2y )(x 2-4y 2),其中x =2,y =-1.21.解关于x 的方程:(x +41)2-(x -41)(x +41)=41. 22.已知x -y =9,x ·y =5,求x 2+y 2的值.23.已知a (a -1)+(b -a 2)=-7,求222b a +-ab 的值. 24.已知a +b =7,ab =10,求a 2+b 2,(a -b )2的值. 25.已知2a -b =5,ab =23,求4a 2+b 2-1的值. 26.已知(a +b )2=9,(a -b )2=5,求a 2+b 2,ab 的值.27.已知 2()16,4,a b ab +==求223a b +与2()a b -的值。
专题1.6 完全平方公式(分层练习,五大类型)(原卷版)

专题1.6 完全平方公式(分层练习,五大类型)考查题型一、利用整式的乘法公式进行计算1.化简:(x﹣2)2+(x+3)(x+1).2.计算:(1)a3•a2•a4+(﹣a)2;(2)(x+y)2﹣x(2y﹣x).考查题型二、利用完全平方公式之间的关系进行计算3.已知x+y=6,x2+y2=22.求:(1)xy的值;(2)(x﹣y)2﹣4的值.4.已知a﹣b=4,ab=3,求:(1)a2+b2;(2)(a﹣2)(b+2)的值.5.计算:(1)已知a m=3,a n=2,求a2m+3n的值.(2)若(x+y)2=16,(x﹣y)2=12,求xy的值.6.已知2x2﹣2x=1,求代数式(x﹣1)2+(x+3)(x﹣3)的值.7.解答题:(1)若x+y=8,x2+y2=40,求xy的值;(2)若(4﹣x)x=3,求(4﹣x)2+x2的值.8.若x+y=6,且(x+2)(y+2)=23.(1)求xy的值;(2)求x2+6xy+y2的值.考查题型三、利用非负整数解相关问题9.从这两个公式中,我们可以看到,完全平方公式的展开式由三项构成,分别是a2、b2和±2ab.现有一个多项式为x4+4x2,请你再添加一个单项式使其成为一个多项式的完全平方你可以添加哪几个单项式?请直接写出答案.10.已知一个三角形的三边长分别是5、x、(x+1),且有x2+25=(x+1)2,求其他两边的长.考查题型四、利用几何背景说明完全平方公式及应用公式求值11.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,若a+b=4,a2+b2=10,求剩下的钢板的面积.12.若x满足(9﹣x)(x﹣4)=4,求(4﹣x)2+(x﹣9)2的值.解:设9﹣x=a,x﹣4=b,则(9﹣x)(x﹣4)=ab=4,a+b=(9﹣x)+(x﹣4)=5,∴(9﹣x)2+(x﹣4)2=(a+b)2﹣2ab=52﹣2×4=17.请仿照上面的方法求解下面问题:(1)若x满足(5﹣x)(x﹣2)=2,求(5﹣x)2+(x﹣2)2的值.(2)若x满足(6﹣x)(3﹣x)=1,求代数式(9﹣2x)2的值.(3)已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=3,CF=5,长方形EMFD的面积是48,分别以MF、DF作正方形,求阴影部分的面积.13.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.(1)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系;(2)若要拼出一个面积为(a+2b)(a+b)的矩形,则需要A号卡片1张,B号卡片2张,C号卡片张.(3)根据(1)题中的等量关系,解决如下问题:①已知:a+b=5,a2+b2=11,求ab的值;②已知(x﹣2019)2+(x﹣2021)2=20,求x﹣2020的值.14.探究规律并解决问题.(1)比较a2+b2与2ab的大小(用“>”“<”或“=”填空):①当a=3,b=3时,a2+b22ab;②当a=2,b=时,a2+b22ab;③当a=﹣2,b=3时,a2+b22ab.(2)通过上面的填空,猜想a2+b2与2ab的大小关系,并说明理由.考查题型五、利用杨辉三角探究规律15.观察下列算式,尝试问题解决:杨辉三角形是一个由数字排列成的三角形数表,一般形式如图所示,其中每一横行都表示(a+b)n(此处n=0,1,2,3,4,5..)的计算结果中的各项系数:(1)请根据上题中的杨辉三角系数集”,仔细观察下列各式中系数的规律,并填空:(a+b)1=a+b各项系数之和1+1=2=21(a+b)2=a2+2ab+b2各项系数之和1+2+1=4=22(a+b)3=a3+3a2b+3ab2+b3各项系数之和1+3+3+1=8=23①请补全下面展开式的系数:(a﹣b)6=a6+a5b+15a4b2+a3b3+15a2b4﹣6ab5+b6②请写出(a+b)10各项系数之和:(2)设(x+1)17=a17x17+a16x16+…+a1x+a0,求a1+a2+a3+…+a16+a17的值.(3)你能在(2)的基础上求出a2+a4+a6+…+a14+a16的值吗?若能,请写出过程.一、单选题1.下列计算中,结果正确的是()A.(﹣pq)3=p3q3B.x4+x4=x8C.(a﹣b)2=a2﹣b2D.(a2)3=a62.若x+y=4,xy=3,则x2+y2=()A.7B.10C.16D.223.如果x2+2ax+9是一个完全平方式,则a的值是()A.3B.6C.±6D.±34.已知x+y=3,xy=﹣2,则x2﹣xy+y2的值是()A.11B.15C.3D.75.如图,根据计算长方形ABCD的面积,可以说明下列哪个等式成立()A.(a+b)2=a2+2ab+b2B.(a﹣b)2=a2﹣2ab+b2C.(a+b)(a﹣b)=a2﹣b2D.a(a+b)=a2+ab6.小华在利用完全平方公式计算一个二项整式的平方时,不小心用墨水把中间一项的系数染黑了,得到正确的结果为a2■ab+9b2,则中间一项的系数是()A.6B.﹣6C.6或﹣6D.187.将一块边长为a米的正方形广场进行扩建,扩建后的正方形边长比原来长2米,则扩建后广场面积增大了()A.4平方米B.(a2+4)平方米C.(2a+4)平方米D.(4a+4)平方米8.如图,M是AG的中点,B是AG上一点,分别以AB、BG为边,作正方形ABCD和正方形BGFE,连接MD和MF.设AB=a,BG=b,且a+b=10,ab=6,则图中阴影部分的面积为()A.46B.53C.59D.63二、填空题9.多项式9x2+1加上一个单项式后,使它能成为一个多项式的完全平方,那么加上的单项式可以是(填上一个你认为正确的即可).10.若a+b=4,ab=2,则代数式a2+b2+4ab的值是.11.关于x的二次三项式4x2+mx+1是完全平方式,则m=.12.若边长为a,b的长方形周长为10,面积为5,则a2+b2的值是.三、解答题13.先化简,再求值:,其中x=﹣3,.14.若x+y=6,且(x+2)(y+2)=24.(1)求xy的值;(2)求x2+3xy+y2的值.15.已知a+b=6,ab=﹣27,求下列各式的值.(1)a2+b2;(2)a2+b2﹣ab.16.已知2a2﹣3a﹣4=0,求的值.17.已知多项式A=(m﹣3)2﹣(2﹣m)(2+m)+2.(1)化简多项式A;(2)若x2﹣2mx+4是一个完全平方式,求A的值.18.下面是小颖化简整式的过程,仔细阅读后解答所提出的问题.解:x(x+2y)﹣(x+1)2+2x=(x2+2xy)﹣(x2+2x+1)+2x第一步=x2+2xy﹣x2+2x+1+2x第二步=2xy+4x+1第三步(1)小颖的化简过程从第步开始出现错误,错误的原因是.(2)写出此题正确的化简过程.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
完全平方公式的几何背景专题训练试题精选一.选择题(共6小题)1.(2010•丹东)图①是一个边长为()的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是()()(m﹣n)2﹣n2 A.()2﹣(m﹣n)2=4 B.()2﹣(m22)=2 C.(m﹣n)2+222D.2.利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:()22+22.你根据图乙能得到的数学公式是()B.(a﹣b)22﹣22C.a()2D.a(a﹣b)2﹣A.()(a﹣b)2﹣b23.如图,你能根据面积关系得到的数学公式是()A.a2﹣b2=()(a﹣b)B.()22+22C.(a﹣b)22﹣22D.a()24.如图(1),是一个长为2a宽为2b(a>b)的矩形,用剪刀沿矩形的两条对角轴剪开,把它分成四个全等的小矩形,然后按图(2)拼成一个新的正方形,则中间空白部分的面积是()A.B.()2C.(a﹣b)2D.a2﹣b25.如图的图形面积由以下哪个公式表示()B.(a﹣b)22﹣22C.()22+22D.a2﹣b2=()(a﹣b)A.a2﹣b2(a﹣b)(a﹣b)6.如果关于x的二次三项式x2﹣16是一个完全平方式,那么m的值是()A.8或﹣8 B.8C.﹣8 D.无法确定二.填空题(共7小题)7.(2014•玄武区二模)如图,在一个矩形中,有两个面积分别为a2、b2(a>0,b>0)的正方形.这个矩形的面积为(用含a、b的代数式表示)8.如图,边长为(2)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为2,则另一边长是.(用含m的代数式表示)9.有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的面积之和为.10.如图1和图2,有多个长方形和正方形的卡片,图1是选取了2块不同的卡片,拼成的一个图形,借助图中阴影部分面积的不同表示可以用来验证等式a()2成立.根据图2,利用面积的不同表示方法,写出一个代数恒等式.11.如图,正方形广场的边长为a米,中央有一个正方形的水池,水池四周有一条宽度为的环形小路,那么水池的面积用含a、b的代数式可表示为平方米.12.如图,请写出三个代数式()2、(a﹣b)2、之间的等量关系是.13.如图,长为a,宽为b的四个小长方形拼成一个大正方形,且大正方形的面积为64,中间小正方形的面积为16,则,.三.解答题(共10小题)14.阅读学习:数学中有很多等式可以用图形的面积来表示.如图1,它表示(2n)()2+32n2,(1)观察图2,请你写出()2,(a﹣b)2,之间的关系.(2)小明用8个一样大的长方形,(长为a,宽为b),拼成了如图甲乙两种图案,图案甲是一个正方形,图案甲中间留下了一个边长为2的正方形;图形乙是一个长方形.①a2﹣44b2= ②.15.【学习回顾】我们已经知道,根据几何图形的面积关系可以说明完全平方公式,说明如下:如图1,正方形的面积=正方形的面积+(长方形的面积+长方形的面积)+正方形的面积.即:()22+22.【思考问题】还有一些等式也可以用上述方式加以说明,请你尝试完成.如图2,长方形的面积=长方形的面积+长方形的面积﹣长方形的面积﹣的面积,即:(2a﹣b)()= .【尝试实践】计算(2)()= .仿照上述方法,画图并说明.16.阅读下列文字,我们知道对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式,例如由图1可以得到(2b)()2+32b2.请解答下列问题:(1)写出图2中所表示的数学等式;(2)利用(1)中所得到的结论,解决下面的问题:已知11,38,求a222的值;(3)图3中给出了若干个边长为a和边长为b的小正方形纸片.若干个长为a和宽为b的长方形纸片,利用所给的纸片拼出一个几何图形,使得计算它的面积能得到数学公式:2a2+52b2=(2)(2b).17.如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形.(1)图2的空白部分的边长是多少?(用含的式子表示)(2)若27,且3,求图2中的空白正方形的面积.(3)观察图2,用等式表示出(2a﹣b)2,和(2)2的数量关系.18.动手操作:如图①是一个长为2a,宽为2b的长方形,沿图中的虚线剪开分成四个大小相等的长方形,然后按照图②所示拼成一个正方形.提出问题:(1)观察图②,请用两种不同的方法表示阴影部分的面积;问题解决:根据上述(2)中得到的等量关系,解决下列问题:已知:6,3.求:(x﹣y)2的值.19.图①是一个长为2a,宽为2b的长方形,沿图中虚线剪开,可分成四块小长方形.(1)将图①中所得的四块长为a,宽为b的小长方形拼成一个正方形(如图②).请利用图②中阴影部分面积的不同表示方法,直接写出代数式()2、(a﹣b)2、之间的等量关系是;(2)根据(2)题中的等量关系,解决如下问题:已知8,7,则m﹣;(3)将如图①所得的四块长为a,宽为b的小长方形不重叠地放在长方形的内部(如图③),未被覆盖的部分(两个长方形)用阴影表示.若左下角与右上角的阴影部分的周长之差为4,且小长方形的周长为8,则每一个小长方形的面积为.20.把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接和,若两正方形的边长满足10,20,你能求出阴影部分的面积吗?21.阅读材料并填空:我们知道,完全平方式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式样也可以用这种形式表示,如:(2)()=2a2+32,就可以用图(1),或图(2)等图形的面积表示.请你写出图(3)所表示的代数恒等式.请你写出图(4)所表示的代数恒等式.22.图1是一个长为2x、宽为2y的长方形,沿图中虚线用剪刀剪成四个完全相同的小长方形,然后按图2所示拼成一个正方形.(1)你认为图2中的阴影部分的正方形的边长等于.(2)试用两种不同的方法求图2中阴影部分的面积.方法1:;方法2:.(3)根据图2你能写出下列三个代数式之间的等量关系吗?代数式:()2,(x﹣y)2,4.(4)根据(3)题中的等量关系,解决如下问题:若4,3,则(x﹣y)2= .23.已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.(1)你认为图乙中阴影部分的正方形的边长等于多少?.(2)请用两种不同的方法求图乙中阴影部分的面积.方法一:;方法二:.(3)观察图乙,你能写出下列三个代数式之间的等量关系吗?()2;(m﹣n)2;(4)根据(3)题中的等量关系,解决如下问题:若8,5,求(a﹣b)2的值.完全平方公式的几何背景专题训练试题精选参考答案与试题解析一.选择题(共6小题)1.(2010•丹东)图①是一个边长为()的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是()A.()2﹣(m﹣n)2=4 B.()2﹣(m22)=2 C.(m﹣n)2+222D.()(m﹣n)2﹣n2考点:完全平方公式的几何背景.专题:计算题;压轴题.分析:根据图示可知,阴影部分的面积是边长为的正方形减去中间白色的正方形的面积m22,即为对角线分别是2m,2n的菱形的面积.据此即可解答.解答:解:()2﹣(m22)=2.故选B.点评:本题是利用几何图形的面积来验证()2﹣(m22)=2,解题关键是利用图形的面积之间的相等关系列等式.2.利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲,我们A.()(a﹣b)2﹣b2B.(a﹣b)22﹣22C.a()2D.a(a﹣b)2﹣考点:完全平方公式的几何背景.分析:根据图形,左上角正方形的面积等于大正方形的面积减去两个矩形的面积,然后加上多减去的右下角的小正方形的面积.解答:解:大正方形的面积=(a﹣b)2,还可以表示为a2﹣22,∴(a﹣b)22﹣22.故选B.点评:正确列出正方形面积的两种表示是得出公式的关键,也考查了对完全平方公式的理解能力.3.如图,你能根据面积关系得到的数学公式是()A.a2﹣b2=()(a﹣b)B.()22+22C.(a﹣b)22﹣22D.a()2考点:完全平方公式的几何背景.分析:根据图形得出阴影部分的面积是(a﹣b)2和b2,剩余的矩形面积是(a﹣b)b和(a﹣b)b,即大阴影部分的面积是(a﹣b)2,即可得出选项.解答:解:从图中可知:阴影部分的面积是(a﹣b)2和b2,剩余的矩形面积是(a ﹣b)b和(a﹣b)b,即大阴影部分的面积是(a﹣b)2,∴(a﹣b)22﹣22,故选C.点评:本题考查了完全平方公式的应用,主要考查学生的阅读能力和转化能力,题目比较好,有一定的难度.4.如图(1),是一个长为2a宽为2b(a>b)的矩形,用剪刀沿矩形的两条对角轴剪开,把它分成四个全等的小矩形,然后按图(2)拼成一个新的正方形,则中间空白部分的面积是()A.B.()2C.(a﹣b)2D.a2﹣b2考点:完全平方公式的几何背景.分先求出正方形的边长,继而得出面积,然后根据空白部分的面积=正方形的解答:解:由题意可得,正方形的边长为(),故正方形的面积为()2,又∵原矩形的面积为4,∴中间空的部分的面积=()2﹣4(a﹣b)2.故选C.点评:此题考查了完全平方公式的几何背景,求出正方形的边长是解答本题的关键,难度一般.5.如图的图形面积由以下哪个公式表示()A.a2﹣b2(a﹣b)(a﹣b)B.(a﹣b)22﹣22C.()22+22D.a2﹣b2=()(a﹣b)考点:完全平方公式的几何背景.分析:通过图中几个图形的面积的关系来进行推导.解答:解:根据图形可得出:大正方形面积为:()2,大正方形面积=4个小图形的面积和22,∴可以得到公式:()22+22.故选:C.点本题考查了完全平方公式的推导过程,运用图形的面积表示是解题的关键.6.如果关于x的二次三项式x2﹣16是一个完全平方式,那么m的值是()A.8或﹣8 B.8C.﹣8 D.无法确定考点:完全平方公式的几何背景.分析:根据两平方项确定出这两个数,再根据乘积二倍项列式求解即可.解答:解:∵x2﹣16是一个完全平方式,∴﹣±2×4•x,解得±8.故选A.点评:本题是完全平方公式的考查,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.注意积的2倍的符号,避免漏解.二.填空题(共7小题)7.(2014•玄武区二模)如图,在一个矩形中,有两个面积分别为a2、b2(a>0,b>0)的正方形.这个矩形的面积为()2(用含a、b的代数式表示)考点:完全平方公式的几何背景.析:解答:解;∵两个小矩形的长为a,宽为b,∴正方形的边长为:∴它的面积为:()2故答案为:()2点评:本题主要考查完全平方公式的几何表示,运用不同方法表示阴影部分面积是解题的关键.8.如图,边长为(2)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为2,则另一边长是22 .(用含m的代数式表示)考点:完全平方公式的几何背景.专题:几何图形问题.分析:由于边长为(2)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个矩形(不重叠无缝隙),那么根据正方形的面积公式,可以求出剩余部分的面积,而矩形一边长为2,利用矩形的面积公式即可求出另一边长.解解:依题意得剩余部分为而拼成的矩形一边长为2,∴另一边长是(44)÷2=22.故答案为:22.点评:本题主要考查了多项式除以单项式,解题关键是熟悉除法法则.9.有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B 的面积之和为13 .考点:完全平方公式的几何背景.分析:设正方形A的边长为a,正方形B的边长为b,由图形得出关系式求解即可.解答:解:设正方形A的边长为a,正方形B的边长为b,由图甲得a2﹣b2﹣2(a﹣b)=1即a22﹣21,由图乙得()2﹣a2﹣b2=12,212,所以a22=13,故答案为:13.点本题主要考查了完全平方公式的几何背景,解题的关键是根据图形得出数10.如图1和图2,有多个长方形和正方形的卡片,图1是选取了2块不同的卡片,拼成的一个图形,借助图中阴影部分面积的不同表示可以用来验证等式a()2成立.根据图2,利用面积的不同表示方法,写出一个代数恒等式()(2b)2+2b2+3 .考点:完全平方公式的几何背景.专题:计算题.分析:表示阴影部分的面积有两种方法:①大长方形的面积=()(2b),②3个正方形的面积加上3个矩形的面积a222,推出即可.解答:解:由图2可知:阴影部分的面积是:①()(2b),②a2222+2b2+3,∴()(2b)2+2b2+3,故答案为:()(2b)2+2b2+3.点评:本题考查了完全平方公式的几何背景的应用,关键是检查学生能否正确表示图形中阴影部分的面积,题目具有一定的代表性,考查了学生的理解能力、观察图形的能力等11.如图,正方形广场的边长为a米,中央有一个正方形的水池,水池四周有一条宽度为的环形小路,那么水池的面积用含a、b的代数式可表示为a2﹣44b2或(a﹣2b)2平方米.考点:完全平方公式的几何背景.专题:几何图形问题.分析:根据图示计算出中央正方形的水池的边长,然后根据正方形的面积公式来计算水池的面积.解答:解:水池的边长是:a﹣2b,所以,正方形水池的面积是(a﹣2b)(a﹣2b)2﹣44b2或(a﹣2b)(a﹣2b)=(a﹣2b)2.故答案是:a2﹣44b2或(a﹣2b)2.点评:本题考查对完全平方公式几何意义的理解.解题时,主要围绕图形面积展开分析.12.如图,请写出三个代数式()2、(a﹣b)2、之间的等量关系是)2=(a﹣b)2+4 .考点:完全平方公式的几何背景.分析:通过观察图形知:()2,(a﹣b)2,分别表示的是大正方形、空白部分的正方形及小长方形的面积.解答:解:由图可以看出,大正方形面积=阴影部分的正方形的面积+四个小长方形的面积,即:()2=(a﹣b)2+4,故答案为:()2=(a﹣b)2+4.点评:此题考查了学生观察、分析图形解答问题的综合能力,关键是通过观察图形找出各图形之间的关系.13.如图,长为a,宽为b的四个小长方形拼成一个大正方形,且大正方形的面积为64,中间小正方形的面积为16,则 6 , 2 .考点:完全平方公式的几何背景.分先求出大正方形的边长为:,小正方形的边长为:a﹣b,再列出方程组求解.解答:解:大正方形的边长为:,小正方形的边长为:a﹣b 即:解得故答案为:6,2.点评:本题的关键是求出大正方形的边长和小正方形的边长.列出方程组.三.解答题(共10小题)14.阅读学习:数学中有很多等式可以用图形的面积来表示.如图1,它表示(2n)()2+32n2,(1)观察图2,请你写出()2,(a﹣b)2,之间的关系()2﹣(a﹣b)2=4 .(2)小明用8个一样大的长方形,(长为a,宽为b),拼成了如图甲乙两种图案,图案甲是一个正方形,图案甲中间留下了一个边长为2的正方形;图形乙是一个长方形.①a2﹣44b2= 4 ②60 .考点:完全平方公式的几何背景.专数形结合.分析:根据图形的面积公式来进行分析即可得到.解答:解:(1)()2﹣(a﹣b)2=4;(2)①4 ②60点评:该题目考查了利用图形的面积来得到数学公式,关键是灵活进行数学结合来分析.15.【学习回顾】我们已经知道,根据几何图形的面积关系可以说明完全平方公式,说明如下:如图1,正方形的面积=正方形的面积+(长方形的面积+长方形的面积)+正方形的面积.即:()22+22.【思考问题】还有一些等式也可以用上述方式加以说明,请你尝试完成.如图2,长方形的面积=长方形的面积+长方形的面积﹣长方形的面积﹣正方形的面积,即:(2a﹣b)()= 2a2﹣﹣b2.【尝试实践】计算(2)()= 2a2+32.仿照上述方法,画图并说明.考点:完全平方公式的几何背景.分析:(1)利用长方形的面积=长方形的面积+长方形的面积﹣长方形的面积﹣正方形的面积计算.(2)利用长方形的面积=正方形的面积+正方形的面积+长方形的面积+长方形的面积+长方形的面积+正方形的面积计算.解答:解:(1)长方形的面积=长方形的面积+长方形的面积﹣长方形的面积﹣正方形的面积,即:(2a﹣b)()=2a2﹣﹣b2.故答案为:正方形,2a2﹣﹣b2.(2)(2)()=2a2+32.如图,故答案为:2a2﹣﹣b2.点评:本题主要考查了完全平方公式的几何背景,解题的关键是通过几何图形之间的数量关系对公式做出几何解释.16.阅读下列文字,我们知道对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式,例如由图1可以得到(2b)()2+32b2.请解答下列问题:(1)写出图2中所表示的数学等式()2222+222 ;(2)利用(1)中所得到的结论,解决下面的问题:已知11,38,求a222的值;(3)图3中给出了若干个边长为a和边长为b的小正方形纸片.若干个长为a和宽为b的长方形纸片,利用所给的纸片拼出一个几何图形,使得计算它的面积能得到数学公式:2a2+52b2=(2)(2b).考点:完全平方公式的几何背景.分析:(1)根据数据表示出矩形的长与宽,再根据矩形的面积公式写出等式的左边,再表示出每一小部分的矩形的面积,然后根据面积相等即可写出等式.(2)根据利用(1)中所得到的结论,将11,38作为整式代入即可求出.(3)找规律,根据公式画出图形,拼成一个长方形,使它满足所给的条件.解答:解:(1)根据题意,大矩形的面积为:()()=()2,各小矩形部分的面积之和2+22+222,∴等式为()2222+222.(2)a222 =()2﹣2﹣2﹣2=112﹣2×38=45.(3)如图所示点评:本题考查了完全平方公式的几何背景,根据矩形的面积公式分整体与部分两种思路表示出面积,然后再根据同一个图形的面积相等即可解答.17.如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形.(1)图2的空白部分的边长是多少?(用含的式子表示)(2)若27,且3,求图2中的空白正方形的面积.(3)观察图2,用等式表示出(2a﹣b)2,和(2)2的数量关系.考点:完全平方公式的几何背景.分析:(1)观察由已知图形,得到四个小长方形的长为2a,宽为b,那么图2中的空白部分的正方形的边长是小长方形的长减去小长方形的宽.(2)通过观察图形,大正方形的边长为小长方形的长和宽的和.图2中空白部分的正方形的面积为大正方形的面积减去四个小长方形的面积.(3)通过观察图形知:(2)2 (2a﹣b)2 8.分别表示的是大正方形、空白部分的正方形及小长方形的面积.解答:解:(1)图2的空白部分的边长是2a﹣b(2)由图21﹣2可知,小正方形的面积=大正方形的面积﹣4个小长方形的面积,∵大正方形的边长=27,∴大正方形的面积=(2)2=49,又∵4个小长方形的面积之和=大长方形的面积=4a×288×3=24,∴小正方形的面积=(2a﹣b)2=49﹣24=25(3)由图2可以看出,大正方形面积=空白部分的正方形的面积+四个小长方形的面积即:(2)2﹣(2a﹣b)2=8.点评:此题考查了学生观察、分析图形解答问题的综合能力,以及对列代数式、代数式求值的理解与掌握.关键是通过观察图形找出各图形之间的关系.18.动手操作:如图①是一个长为2a,宽为2b的长方形,沿图中的虚线剪开分成四个大小相等的长方形,然后按照图②所示拼成一个正方形.提出问题:(1)观察图②,请用两种不同的方法表示阴影部分的面积;(2)请写出三个代数式()2,(a﹣b)2,之间的一个等量关系.问题解决:根据上述(2)中得到的等量关系,解决下列问题:已知:6,3.求:(x﹣y)2的值.考完全平方公式的几何背景.点:专题:几何图形问题.分析:(1)第一种方法为:大正方形面积﹣4个小长方形面积,第二种表示方法为:阴影部分正方形的面积;(2)利用()2﹣4(a﹣b)2可求解.解答:提出问题:解:(1)()2﹣4或(a﹣b)2(2)()2﹣4(m﹣n)2问题解决:(3)(x﹣y)2=()2﹣4∵6,3.∴(x﹣y)2=36﹣9=25.点评:本题考查了完全平方公式的几何背景.解决问题的关键是读懂题意,找到所求的量的等量关系.本题更需注意要根据所找到的规律做题.19.图①是一个长为2a,宽为2b的长方形,沿图中虚线剪开,可分成四块小长方形.(1)将图①中所得的四块长为a,宽为b的小长方形拼成一个正方形(如图②).请利用图②中阴影部分面积的不同表示方法,直接写出代数式()2、(a﹣b)2、之间的等量关系是(a﹣b)2=()2﹣4 ;(2)根据(2)题中的等量关系,解决如下问题:已知8,7,则m﹣±6;(3)将如图①所得的四块长为a,宽为b的小长方形不重叠地放在长方形的内部(如图③),未被覆盖的部分(两个长方形)用阴影表示.若左下角与右上角的阴影部分的周长之差为4,且小长方形的周长为8,则每一个小长方形的面积为3 .考点:完全平方公式的几何背景.分析:(1)利用大正方形的面积减4个小长方形的面积等于小正方形的面积求解;(2)利用公式(m﹣n)2=()2﹣4求解即可;(3)由左下角与右上角的阴影部分的周长之差为4,得出﹣844,由小长方形的周长为8,得出2()=8,联立得出a,b的值即可求出小长方形的面积.解答:解:(1)(a﹣b)2=()2﹣4.故答案为:(a﹣b)2=()2﹣4.(2)∵8,7,∴(m﹣n)2=()2﹣464﹣28=36,∴m﹣±6故答案为:±6.(3)设长方形为m,为n,右上角部分的阴影周长为:2(n﹣﹣a)左下角部分的阴影周长为:2(m﹣2﹣2b)∵左下角与右上角的阴影部分的周长之差为4,∴﹣844,又∵2()=8,∴解得3,1,∴每一个小长方形的面积为3×1=3.故答案为:3.点评:本题考查了完全平方公式的几何背景,解题的关键是通过几何图形之间的数量关系解决问题.20.把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接和,若两正方形的边长满足10,20,你能求出阴影部分的面积吗?考点:完全平方公式的几何背景.分(1)此题根据面积的不同求解方法,可得到不同的表示方法.一种可以是析: 3个正方形的面积和6个矩形的面积,种是大正方形的面积,可得等式()2222+222,(2)利用S阴影=正方形的面积+正方形的面积﹣三角形的面积﹣三角形的面积求解.解答:(1)()2222+222(2)∵10,20,∴S阴影22﹣()•b﹣a 222﹣()2﹣×102﹣×20=50﹣30=20.点评:本题考查了完全平方公式几何意义,解题的关键是注意图形的分割与拼合,会用不同的方法表示同一图形的面积.21.阅读材料并填空:我们知道,完全平方式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式样也可以用这种形式表示,如:(2)()=2a2+32,就可以用图(1),或图(2)等图形的面积表示.请你写出图(3)所表示的代数恒等式()22+22.请你写出图(4)所表示的代数恒等式(2)(2b)=2a2+52b2.分析:求出长方形的长和宽,根据长方形的面积公式求出即可.解答:解:图(3)所表示的代数恒等式是()()=()22+22,图(4)所表示的代数恒等式是(2)(2b)=2a2+52b2,故答案为:()22+22,(2)(2b)=2a2+52b2.点评:本题考查了完全平方公式的应用,主要考查学生的阅读能力和转化能力,题目比较好,有一定的难度.22.图1是一个长为2x、宽为2y的长方形,沿图中虚线用剪刀剪成四个完全相同的小长方形,然后按图2所示拼成一个正方形.(1)你认为图2中的阴影部分的正方形的边长等于x﹣y .(2)试用两种不同的方法求图2中阴影部分的面积.方法1:(x﹣y)2 ;方法2:()2﹣4 .(3)根据图2你能写出下列三个代数式之间的等量关系吗?代数式:()2,(x﹣y)2,4.()2=(x﹣y)2+4(4)根据(3)题中的等量关系,解决如下问题:若4,3,则(x﹣y)2= 4 .分析:(1)图①分成了4个长为x,宽为y的长方形,图②中的阴影部分的小正方形的边长等于x﹣y,大正方形的边长等于;(2)直接利用正方形的面积公式得到②中阴影部分的面积为(x﹣y)2;也可以用大正方形的面积减去4个长方形的面积即②()2﹣4;(3)利用面积之间的关系易得()2=(x﹣y)2+4.解答:解:(1)图②中的阴影部分的小正方形的边长﹣y;故答案为:(x﹣y);(2)方法①(x﹣y)2;方法②()2﹣4;故答案为:(x﹣y)2 ,()2﹣4;(3)()2=(x﹣y)2+4;故答案为:()2=(x﹣y)2+4;(4)(x﹣y)2=()2﹣442﹣12=4故答案为:4.点评:本题考查了列代数式:根据题中的已知数量利用代数式表示其他相关的量.23.已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.(1)你认为图乙中阴影部分的正方形的边长等于多少?m﹣n .(2)请用两种不同的方法求图乙中阴影部分的面积.方法一:()2﹣4 ;方法二:(m﹣n)2.(3)观察图乙,你能写出下列三个代数式之间的等量关系吗?()2;(m﹣n)2;(4)根据(3)题中的等量关系,解决如下问题:若8,5,求(a﹣b)2的值.考点:完全平方公式的几何背景.分析:平均分成后,每个小长方形的长为m,宽为n.(1)正方形的边长=小长方形的长﹣宽;(2)第一种方法为:大正方形面积﹣4个小长方形面积,第二种表示方法为:阴影部分为小正方形的面积;(3)利用()2﹣4(m﹣n)2可求解;(4)利用(a﹣b)2=()2﹣4可求解.解答:解:(1)m﹣n;(2)()2﹣4或(m﹣n)2;(3)()2﹣4(m﹣n)2;(4)(a﹣b)2=()2﹣4,。
