环路计算,补偿和仿真
几种环路稳定性仿真方法介绍

几种环路稳定性仿真方法介绍奚义义【期刊名称】《电子世界》【年(卷),期】2016(000)018【总页数】2页(P133-134)【作者】奚义义【作者单位】法雷奥汽车内部控制(深圳)有限公司【正文语种】中文自从闭环系统概念提出以来,闭环系统已经广泛应用于汽车工业中,例如:引擎控制系统,空调控制系统。
然而闭环系统的引入可能会引起震荡。
为了避免出现震荡,目前VLS (Valeo Lighting System)通过仿真,计算以及测试来保证闭环系统的稳定性。
这篇文章主要介绍目前VLS线性闭环系统几种利用Pspice的仿真分析方法,然而在进行环路仿真时,断开点的选择尤为重要,对两种不同环路仿真分析方法获取的开环传递函数与环路断开点输入输出阻抗的关系进行介绍,分析其优缺点,并在此基础上引入S.ROSENSTARK 不依赖于环路阻抗的环路分析方法。
2.1 VLS 线性系统介绍目前VLS大部分的线性闭环系统满足图1所示的构造,Vref(s):输入基准信号,G(s):误差放大增益;H(s):功率放大级的增益;Vout(s):电压输出信号;Zin(s):误差放大级输入阻抗。
对于上图的闭环系统,对其开环传递函数推导如下:设定,并在误差放大和功率放大级之间断开环路①,其开环传递函数T(s)为:上式是闭环系统的开环传递函数,下面我们将会对常用的环路仿真分析方法进行介绍。
2.2 VLS 两种环路仿真分析方法介绍目前VLS环路分析方法主要两种,为了能够传递函数与输入输出阻抗之间的关系,两种方法选择断开点阻抗不是理想的②:第一种方法[1][2]:在环路中插入一个交流源U1,交流源两端电压的比值即为环路开环传递函数;第二种方法:在环路中插入一个无穷大的电感并在环路的断开点的输入端注入交流信号Us,分析电感两端电压比值即为环路开环传递函数。
VLS常用的两种环路分析方法,下面对其获得的开环传递函数进行分析。
对于上面的两种环路的分析方法都有局限,测试结果依赖于Zin(s)与Zout (s),下面分析将会展示具体的影响。
loop gain的仿真原理

loop gain的仿真原理
Loopgain是指控制回路中环路增益的值,它是控制回路稳定性
的关键参数之一。
为了准确地评估控制回路的稳定性,需要进行loop gain的仿真。
loop gain的仿真主要分为两个步骤:建立数学模型和进行仿真计算。
在建立数学模型时,需要考虑控制回路中各个元件的特性参数,并将它们转化为数学方程。
然后,通过相应的仿真软件进行仿真计算,得到loop gain的值。
在进行仿真计算时,需要应用一定的输入信号,比如正弦波或方波,以模拟实际的控制回路情况。
同时,要注意控制回路中各个元件的频率响应特性,以保证仿真结果的准确性。
除了建立数学模型和进行仿真计算外,还可以通过实际测试来验证控制回路的稳定性。
实际测试可以利用现代数字示波器等高精度测试设备,对控制回路进行全面的测试和分析。
总之,loop gain的仿真是控制回路设计和优化的重要手段之一,可以帮助工程师更加准确地评估控制回路的稳定性,并优化回路设计。
- 1 -。
开关电源环路补偿设计

开关电源环路补偿设计开关电源环路补偿设计在开关电源设计中,环路补偿是至关重要的一步。
环路补偿的正确设计可以提高电源的稳定性和效率,从而提供更为可靠的电源输出。
本文将针对开关电源的环路补偿设计,从三个方面进行阐述。
一、开关电源环路补偿的基本原理开关电源的环路补偿,是指将部分输出信号回馈到反馈端口,通过正反馈作用来改善系统的动态性能。
补偿的目的,是使电源输出稳定,对负载的响应性更好。
为了实现这一目的,设计师需要对开关电源的基本原理有深入的理解。
在开关电源中,电容、电感和频率之间的相互影响是至关重要的。
通过合理的组合设计,可以提高电源的效率,降低功耗。
二、开关电源环路补偿的设计方法开关电源的环路补偿设计方法,需要综合考虑多个参数,如响应时间、阻尼稳定性、相位裕度等。
其中,响应时间涉及到电路响应时间、电源传输函数以及负载条件,需要根据具体情况予以调整。
阻尼稳定性关系到系统的稳态稳定性,需要根据不同负载条件下的阻尼因素予以设计。
相位裕度涉及到极点间距,可以通过更改反馈回路的增益稳定性来达到较好的效果。
三、开关电源环路补偿的优化在实际电路中,由于电容、电感和负载等多种因素的影响,开关电源环路补偿存在一定的误差。
优化环路补偿,可以通过在电路中加入滤波电容、降低负载电感等措施,提高电源输出的稳定性。
此外,在滤波器的选型方面,选择与系统肖特基二极管参数相匹配的器件,可以较为有效地降低噪声和振荡。
总之,开关电源环路补偿对整个系统的性能至关重要。
一个合理的补偿设计将使电源输出变得更加稳定、高效,具有更好的响应性。
因此,在开发开关电源的过程中,我们应该时刻保持对环路补偿原理的理解,并综合考虑各种参数和因素,以达到最优的设计效果。
反馈环路补偿设计-简述实例(TL431 PC817)

15 .1
参数设计步骤(5)
5、确定EA补偿网络的零点和极点位置。 Fez=1/3Fc=500Hz Fep>3Fc=4.5kHz 取5k 6、计算反馈环路参数。 设R2=Vref/250uA=10K,则R1=R2*Vo/Vref=47k 取51k。 R4=Vf/1mA=1.2/1=1.2K.取1k。 R3≥(V0-Vf-Vref)/10=830.取 1k
参数设计步骤(6)
7、计算R5,C1,C2. R5=Axo*R1=15.1*51=770K 取680k C1=1/Fez*2*3.14*680k=468.3nF 取470nF C2=C1/2*3.14*680k*Fep=0.234nF 取270pF
补充说明
电路中的光耦传输比取100%。 调整动态补偿网络参数,一般是应用实验的方 法。这里是简单说了计算过程。
设计要点一
系统的反馈类型有电流型和电压型,应依照 相对应的工作模式确定传导函数。这里就已 电流反馈形式的PWM芯片为例介绍 在FALYBACK中又有CCM、DCM、RCM三 种电路工作模式。对于哪种模式的电路都不 重要,因为它取决于芯片自身。 在设计完成变压器、EMI滤波、安规元件、芯 片周围电路、输出电路后才能进行设计反馈 反馈电路结构中通常采用放大器+光耦形式
VC C +1 2
R R3
R1
A PC8 1 7
R4 C2 C1 R5 TL4 3 1 R2
参数设计步骤(1)
1.
确定输入到输出的DC增益 140 12V (1 0.48) N(1 D) R O 1A A DC 23 (1 D) R S (1 0.48) 1.5
Saber仿真在开关电源产品设计中的应用

Saber仿真在开关电源产品设计中的应用
充电状态时,最低电压为42V
Saber仿真在开关电源产品设计中的应用
驱动波形和谐振电流波形如下
Saber仿真在开关电源产品设计中的应用
谐振电容电压波形
Saber仿真在开关电源产品设计中的应用
从以上仿真可以看出,在所有工作区间,开 关频率最低为180kHz(58V满载输出时)。 谐振电容的电压最大有效值为366V(58V满 载输出时)。 谐振电感电流和励磁电感电流均在58V满载输 出时达到最大值。 以上结论和相关数据,对于磁性器件损耗计 算和仿真,谐振电容选型,开关频率参数设 定等具有指导性意义。
Saber仿真在开关电源产品设计中的应用 在所有的解决方案中,平均电流控制模式的CCM BOOST PFC电路应用最为成熟,广泛应用于中大功 率电源场合。 但是,一般单路CCM BOOST PFC电路在1~3kW的 功率范围内可以达到最佳的设计效果。在3kW以上 的应用中,单路PFC电路的优化设计将变得困难。 在此背景下,交错并联PFC电路引起大家的关注和 重视。其每个并联支路的设计思路与单路PFC电路 完全相同,因此可以获得体积,布局和热设计的优 化设计结果。而两路之间错相180°控制,开关纹 波可以相互抵消,因此可以简化输入EMI滤波器的 设计。
Saber仿真在开关电源产品设计中的应用
负载动态电压波形(更改431补偿电容为47nF,3842 COMP 端电阻为2k)
负载动态调整时间缩小到2ms左右,电压过冲降到15.4V
Saber仿真在开关电源产品设计中的应用
本文由于写作时间的关系,不再对环路进行 详细的计算和仿真。 关于环路补偿部分的计算和仿真,请参考本 人在21世纪电源网论坛发的文章《环路补 偿—计算和仿真》。 反激电路在DCM模式下的传递函数在张兴柱 博士的公司网站上()可以找 到相关资料。
CCM模式APFC电路设计

CCM模式APFC电路设计传统的工频交流整流电路,因为整流桥后面有一个大的电解电容来稳定输出电压,所以使电网的电流波形变成了尖脉冲,滤波电容越大,输入电流的脉宽就越窄,峰值越高,有效值就越大。
这种畸变的电流波形会导致一些问题,比如无功功率增加、电网谐波超标造成干扰等。
功率因数校正电路的目的,就是使电源的输入电流波形按照输入电压的变化成比例的变化。
使电源的工作特性就像一个电阻一样,而不在是容性的。
目前在功率因数校正电路中,最常用的就是由BOOST变换器构成的主电路。
而按照输入电流的连续与否,又分为DCM、CRM、CCM模式。
DCM模式,因为控制简单,但输入电流不连续,峰值较高,所以常用在小功率场合。
CCM模式则相反,输入电流连续,电流纹波小,适合于大功率场合应用。
介于DCM和CCM之间的CRM称为电流临界连续模式,这种模式通常采用变频率的控制方式,采集升压电感的电流过零信号,当电流过零了,才开通MOS管。
这种类型的控制方式,在小功率PFC电路中非常常见。
今天我们主要谈适合大功率场合的CCM模式的功率因数校正电路的设计。
要设计一个功率因数校正电路,首先我们要给出我们的一些设计指标,我们按照一个输出500W左右的APFC电路来举例:已知参数:交流电源的频率fac——50Hz最低交流电压有效值Umin——85Vac最高交流电压有效值Umax——265Vac输出直流电压Udc——400VDC输出功率Pout——600W最差状况下满载效率η——92%开关频率fs——65KHz输出电压纹波峰峰值Voutp-p——10V那么我们可以进行如下计算:1,输出电流Iout=Pout/Udc=600/400=1.5A2,最大输入功率Pin=Pout/η=600/0.92=652W3,输入电流最大有效值Iinrmsmax=Pin/Umin=652/85=7.67A4,那么输入电流有效值峰值为Iinrmsmax*1.414=10.85A5,高频纹波电流取输入电流峰值的20%,那么Ihf=0.2*Iinrmsmax=0.2*10.85=2.17A6,那么输入电感电流最大峰值为:ILpk=Iinrmsmax+0.5*Ihf=10.85+0.5*2.17=11.94A7,那么升压电感最小值为Lmin=(0.25*Uout)/(Ihf*fs)=(0.25*400)/(2.17*65KHz)=709uH8,输出电容最小值为:Cmin=Iout/(3.14*2*fac*Voutp-p)=1.5/(3.14*2*50*10)=477.7uF,实际电路中还要考虑hold up时间,所以电容容量可能需要重新按照hold up的时间要求来重新计算。
SABER实践教程(关于saber在电源仿真中的几个技巧)
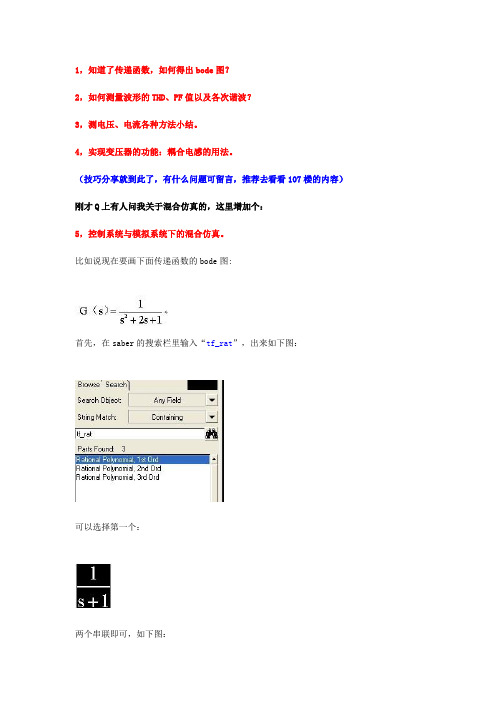
1,知道了传递函数,如何得出bode图?2,如何测量波形的THD、PF值以及各次谐波?3,测电压、电流各种方法小结。
4,实现变压器的功能:耦合电感的用法。
(技巧分享就到此了,有什么问题可留言,推荐去看看107楼的内容)刚才Q上有人问我关于混合仿真的,这里增加个:5,控制系统与模拟系统下的混合仿真。
比如说现在要画下面传递函数的bode图:首先,在saber的搜索栏里输入“tf_rat”,出来如下图:可以选择第一个:两个串联即可,如下图:这样就实现了上面的传递函数。
这里的source需要用到控制系统下的,可搜“c_sin”,选择第一个,如下:当然了,不一定非要这个,因为可以通过接口转换来实现,这是后话。
关于tf_rat的设置如下:这样就实现了函数:1/(s+1)最后的连接图:先netlist再DC分析然后小信号分析,看下面设置:最后的bode图:至此,bode图已经画出来了,很简单哈,剩下的就是自己去分析了~这里附上上面仿的附件,方便下载。
双击轴线,AXIS ATTRIBUTE对话框里的GRID increment可以调制轴线等分间距!!路径中不能有中文,要在全英文下看波形可以放大的,选中托一下即可。
要恢复回来,按下面按钮:不错,既然你仿出来了,你再试试这个传递函数哈:怎么跟上图差不多呢关于区别,你看看:这样看就出来区别了,哈哈怎么把两个波形放在同一个图中的?讲讲波形计算器吧,比如如何把某一个电流扩大十倍,电压扩大十倍便找个简单的电流扩大十20倍的小例子这是一个电流波形,点出计算器来点击图形右侧的电流标号i(l.lr),标号呈现白色表示选中,然后在计算器光标处左键按一下,右键再按一下,至此i(l.lr)添加到计算器中了。
其次在光标处输出20*,再次输入内容的话,以前的内容自动清除,从而计算器自动生成了i(l.lr)*20,这样计算器完成了计算。
计算其中delete为删除键。
最后点击Δ左边的绿色波形图,电流扩大十倍后如下图所示在saber,常用的电容就一种,可以不分极性的,如下:,如何测量波形的THD、PF值以及各次谐波在PFC的仿真以及并网逆变中,经常需要测量波形的THD,PF值,看各次谐波的大小。
SABER 环路计算,补偿和仿真

BUCK 电路的环路计算,补偿和仿真Xia Jun 2010-8-14 本示例从简单的BUCK 电路入手,详细说明了如何进行电源环路的计算和补偿,并通过saber 仿真验证环路补偿的合理性。
一直以来,环路的计算和补偿都是开关电源领域的“难点”,很多做开关电源研发的工程师要么对环路一无所知,要么是朦朦胧胧,在产品的开发过程中,通过简单的调试来确定环路补偿参数。
而这种在实验室里调试出来的参数真的能满足各种实际的使用情况吗?能保证电源产品在高低温的情况下,在各种负载条件下,环路都能够稳定吗?能保证在负载跳变的情况下收敛吗?太多的未知数,这是产品开发的大忌。
我们必须明明白白的知道,环路的稳定性如何?相位裕量是多少?增益裕量是多少?高低温情况下这些值又会如何变化?在一些对动态要求非常严格的场合,我们如何折中考虑环路稳定性和动态响应之间的关系?有的放矢,通过明确的计算和仿真,我们的产品设计才是科学的,合理的,可靠的。
我们的目标是让产品经得起市场的检验,让客户满意,让自己放心。
一切从闭环系统的稳定性说起,在自动控制理论中,根据乃奎斯特环路稳定性判据,如果负反馈系统在穿越频率点的相移为180°,那么整个闭环系统是不稳定的。
很多人可能对这句话很难理解,虽然自动控制理论几乎是所有大学工科学生的必修课,可大部分是是抱着应付的态度的,学完就忘了。
那就再给大家讲解一下吧。
等式:V out=[Vin-V out*H(S)]*G(S)公式:Vout Vin G S ()1G S ()H S ()⋅+G(S)/(1+G(S)*H(S))就称之为系统的闭环传递函数,如果1+G(S)*H(S)=0,那么闭环系统的输出值将会无限大,此时闭环系统是不收敛的,也即是不稳定的。
G(S)*H(S)是系统的开环传递函数,当G(S)*H(S)=-1时,以S=j ω带入,即获得开环系统的频域响应为G(j ω)*H(j ω)=-1,此时频率响应的增益和相角分别为:gain =‖-1‖=1angle=tan -1(0/-1)=180°从上面的分析可以看出,如果扰动信号经过G(S)和H(S)后,模不变,相位改变180°,那么这个闭环系统就是不稳定的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
BUCK 电路的环路计算,补偿和仿真Xia Jun 2010-8-14 本示例从简单的BUCK 电路入手,详细说明了如何进行电源环路的计算和补偿,并通过saber 仿真验证环路补偿的合理性。
一直以来,环路的计算和补偿都是开关电源领域的“难点”,很多做开关电源研发的工程师要么对环路一无所知,要么是朦朦胧胧,在产品的开发过程中,通过简单的调试来确定环路补偿参数。
而这种在实验室里调试出来的参数真的能满足各种实际的使用情况吗?能保证电源产品在高低温的情况下,在各种负载条件下,环路都能够稳定吗?能保证在负载跳变的情况下收敛吗?太多的未知数,这是产品开发的大忌。
我们必须明明白白的知道,环路的稳定性如何?相位裕量是多少?增益裕量是多少?高低温情况下这些值又会如何变化?在一些对动态要求非常严格的场合,我们如何折中考虑环路稳定性和动态响应之间的关系?有的放矢,通过明确的计算和仿真,我们的产品设计才是科学的,合理的,可靠的。
我们的目标是让产品经得起市场的检验,让客户满意,让自己放心。
一切从闭环系统的稳定性说起,在自动控制理论中,根据乃奎斯特环路稳定性判据,如果负反馈系统在穿越频率点的相移为180°,那么整个闭环系统是不稳定的。
很多人可能对这句话很难理解,虽然自动控制理论几乎是所有大学工科学生的必修课,可大部分是是抱着应付的态度的,学完就忘了。
那就再给大家讲解一下吧。
等式:V out=[Vin-V out*H(S)]*G(S)公式:VoutVin G S ()1G S ()H S ()⋅+G(S)/(1+G(S)*H(S))就称之为系统的闭环传递函数,如果1+G(S)*H(S)=0,那么闭环系统的输出值将会无限大,此时闭环系统是不收敛的,也即是不稳定的。
G(S)*H(S)是系统的开环传递函数,当G(S)*H(S)=-1时,以S=j ω带入,即获得开环系统的频域响应为G(j ω)*H(j ω)=-1,此时频率响应的增益和相角分别为:gain =‖-1‖=1angle=tan -1(0/-1)=180°从上面的分析可以看出,如果扰动信号经过G(S)和H(S)后,模不变,相位改变180°,那么这个闭环系统就是不稳定的。
但是,别忘了,这是负反馈系统,信号经过H(S)之后,本身就有180°的相移,所以,针对负反馈的闭环系统而言,其描述为:如果扰动信号经过系统主电路和反馈系统之后,其模不变,相位也不变,那么这个系统是不稳定的。
为什么相位也不变?因为G(S)*H(S)造成的180°相移和负反馈本身造成的180°相移,两者叠加之后是360°,所以等于相位不变。
什么是穿越频率?G(S)*H(S)对应的增益为1(即幅值不变)的频率即为穿越频率。
换算为dB 单位:20log1=0dB 。
理论上来说,在穿越频率点上,只要相移不是180°,那么系统就是稳定的。
但是由于模拟系统的离散性(即所有器件的特性都不是固定不变的,随时间和温度在不断的变化),如果相移很接近180°,这时闭环系统是条件稳定的,即有可能进入不稳定状态。
所以为了避免这种情况,要求在穿越频率点上,开环传递函数G(S)*H(S)的相移应该与180°保持足够的裕量。
这个裕量选取多少比较合适呢?目前在工程应用上通常选取45°,即要求传递函数G(S)*H(S)的相移应该小于135°,这是兼顾考虑环路稳定性和动态响应速度的折中值,理论上来说裕量越大越好,但过大的相位裕量会导致动态响应变慢(过阻尼特性)。
为了保证足够的相位裕量,我们希望开环传递函数的增益曲线以-1的斜率穿越0dB线。
如果开环传递函数的增益曲线在穿越频率点的斜率为-2,那么意味着有接近180°的相移,这将导致相位裕量明显不足,而如果斜率为-1,那么通常意味着相位有45°以上的裕量。
增益曲线的斜率是如何来的?主电路或反馈补偿电路中,每产生一个极点,开环传递函数的增益曲线斜率在该极点的转折频率点上就会增加-1,相反的,每产生一个零点,开环传递函数的增益曲线斜率在该零点的转折频率点上就会增加+1。
不同斜率下的相位裕量如下图所示:从上图可以看出,如果开环传递函数以-2的斜率穿越0dB线,那么相移接近180°,如果以-1的斜率穿越0dB线,那么相移接近90°。
从上图也可以看出,如果两者的穿越频率(fc)相同,那么在0Hz频率点上,-2斜率下降的开环传递函数的增益远远大于-1斜率下降的开环传递函数,这有什么意义呢?这就是静态增益,决定了输出值与给定值之间的静态误差。
假如给定值是10V,希望输出也是10V,以-1斜率下降的开环传递函数的静态增益是20dB,以-2斜率下降的开环传递函数的静态增益是40dB,两者的输出静态误差分别为:10V*(1/10)=1V,10V*(1/100)=0.1V,可见静态误差相差是多么巨大!所以,我们期望静态增益越大越好。
除此之外,开环传递函数的斜率还对动态响应有巨大影响。
假如穿越频率fc依然相同,一个开环传递函数的斜率为-1,另外一个为-2,负载从90%突然跳变到10%,那么此时的输出电压必然会从一个稳态值变化到另外一个稳态值,这中间的暂态过程称之为动态响应。
对动态响应影响最大的是穿越频率fc,我们希望fc越大越好,当然为了避免开关频率对控制环路的影响,fc必须远小于开关频率,一般取fc小于1/6的开关频率,一般的开关电源对于动态响应要求并不十分苛刻,通常fc都小于开关频率的1/10。
那么开环传递函数的斜率对于动态响应有什么影响呢?如下图所示:从上图我们看到,开环传递函数斜率为-2的情况下,输出电压呈现明显的欠阻尼振荡,输出电压快速达到下一个稳态值并过冲,随后围绕稳态值阻尼振荡。
开环传递函数斜率为-1的情况下,输出电压呈现明显的过阻尼特性,从一个稳态值缓慢的变化到下一个稳态值。
过阻尼的缓慢变化和欠阻尼的多次振荡都不是我们想要的情况,我们希望动态发生时,输出能够快速变化到稳定值,同时又不会产生反复的震荡。
那么我们可以结合上面的两种情况,对开环传递函数的斜率做出适当的变化,以达到较快的动态响应速度。
如下图所示:从上图可以看出,在(1/2)fc频率处,开环传递函数的斜率由-2变成-1,可以达到较快的动态响应,由于传递函数以-1的效率穿越0dB线,也可以获得足够的相位裕量。
同时由于从0Hz~(1/2)fc之间,开环传递函数以-2斜率衰减,可以获得很高的静态增益,从而使得静态误差非常的小。
在这里需要说明的是,考核相位裕量,只需在穿越频率点的相位裕量足够就可以了,在fc之前的相位裕量不必严格满足裕量要求。
通过上面的分析,我们已经对环路稳定性,相位裕量,动态响应有了初步的了解,下面我们就要进入实例,来初步理解如何进行环路补偿的计算和仿真。
还是从最简单的拓扑——buck电路入手吧。
CCM情况下控制(占空比d)到输出(电压V o)的小信号传递函数:这个公式是怎么来的?大多数的教材上都有推导过程,我们不需要知道如何去推导主电路的传递函数,这些已经被研究的很透彻了,我们只需要拿过来用就可以了。
在此推荐一下张兴柱博士的公司网站:,张老师已经把常用拓扑的传递函数都推导出来并放在网站上面了。
下面开始计算,mathcad,不会用的请举手,同志们,时代在进步,要跟上潮流啊!做简单的设定,输入Vg=20V,占空比0.5,输出10V,负载电阻1Ω,其他设定如下:这是一个典型的低通滤波器,低频时增益保持不变,在LC产生的双极点处(频率为1.16kHz),增益曲线以-2的斜率衰减,在电解电容的ESR产生的零点处(频率为4.5kHz),增益曲线的斜率由-2变成-1。
那么相位的变化情况如何呢?看起来还不错,电容ESR引起的零点部分抵消了LC双极点导致的相移,使得在穿越频率点上还保持足够的相位裕量:从上面的计算中,可以获得主电路传递函数G(S)的穿越频率为7.2kHz,相位裕量为62.4°。
看来我们不需要做补偿啊,穿越频率够大,在穿越频率点上传递函数增益曲线的斜率为-1,相位裕量也大于45°,只要让H(S)=1就可以保证开环传递函数G(S)*H(S)获得足够的相位裕量。
可是,静态增益实在太低了,只有26dB,我们要消除静态误差,就必须使得增益曲线从0Hz开始就以-1或-2的斜率下降,补偿是不可避免的。
下面就几种典型的补偿方式做一下介绍:1. 单极点补偿3. 单零单极补偿5. 单零双极补偿6. 双零双极补偿根据以上的各种补偿电路,我们应该选择哪一个呢?为了提高静态增益,我们需要在原点处产生一个极点,所以如果要做最简单的补偿,我们应该采用单零单极补偿电路。
假如我们希望开环传递函数G(S)*H(S)的穿越频率为10kHz,而前面计算的G(S)的穿越频率为7.2kHz,那么H(S)将把整体的穿越频率往后推延2.8kHz。
H(S)由两部分组成,一部分是我们需要设计的补偿环节K(S),另一部分是PWM的调制比,即占空比与调制锯齿波电压幅值之间的比例,称之为Fm,如下图所示:当V E=V P时,占空比为1,所以Fm=1/V P。
H(S)=K(S)*Fm,所以开环传递函数为:G(S)*K(S)*Fm。
K(S)*Fm在10kHz频率点的增益为20log(R2*Fm/R1),而G(S)在10kHz频率点的增益为:,即-3.573dB。
所以有:20log(R2*Fm/R1)=3.573假定V P=5V。
设定反馈分压电阻为Rf1=3kΩ,Rf2=1kΩ,如下图所示:在小信号分析时,运放的正极接地,由于运放正负极之间的虚短特性,运放的负极等效于接地,此时R f2被短接,R f1即为补偿网络的电阻R1,即R1=3kΩ。
据此可以求出:R2=22.6 kΩ希望补偿电路的零点频率为1/2fc,即可求出C1=4.425nF,取标准值4.7nF。
计算完成之后,让我们来看看补偿的效果吧:根据计算结果,穿越频率为10.08kHz,相位裕量为60.6°。
OK,计算完成了,结果是相当完美的,完全达到了我们的设计要求,那么仿真的情况会如何呢?会与计算吻合吗?下面就让我们通过saber的环路仿真来体验一下环路测试的效果吧。
不幸的是,我还无法实现闭环仿真来验证开环传递函数G(S)*H(S)的增益和相位曲线,幸运的是,开环仿真还是可以进行的,我们可以分别对Fm*G(S)和K(S)进行开环仿真,与计算结果进行对比和相互验证。
要实现频域的环路仿真,就必须用到saber中的环路扫描仪tdsa,它能够向环路注入频率可变的正弦波信号,通过测试反馈信号,获得两者之间的增益和相位关系。
